Abstract
Optical modulators for optical interconnects require a small size, small voltage, high speed and wide working spectrum. For this purpose, we developed Si slow-light Mach-Zehnder modulators via a 180 nm complementary metal-oxide-semiconductor process. We employed 200 μm lattice-shifted photonic crystal waveguides with interleaved p-n junctions as phase shifters. The group index spectrum of slow light was almost flat at ng ≈ 20 but exhibited ±10% fluctuation over a wavelength bandwidth of 20 nm. The cutoff frequency measured in this bandwidth ranged from 15 to 20 GHz; thus, clear open eyes were observed in the 25 Gbps modulation. However, the fluctuation in ng was reflected in the extinction ratio and bit-error rate. For a stable error-free operation, a 1 dB margin is necessary in the extinction ratio. In addition, we constructed a device with varied values of ng and confirmed that the extinction ratio at this speed was enhanced by larger ng up to 60. However, this larger ng reduced the cutoff frequency because of increased phase mismatch between slow light and radio frequency signals. Therefore, ng available for 25 Gbps modulation is limited to up to 40 for the current device design.
1. Introduction
The Si photonics platform enables the fabrication of dense photonic integrated circuits and reduces their production cost, thanks to the strong optical confinement of high-index-contrast Si devices and the utilization of the matured complementary metal-oxide-semiconductor (CMOS) process, respectively. It is well suited for the development of components and subsystems for optical interconnects in data centers and high-performance computers. For these cases, optical modulators are key [1,2,3,4,5,6] and a wide working spectrum and wide working temperature range are particularly required in optical interconnects, in addition to small size, low loss, low drive voltage and high speed.
Previous studies on Si modulators have mainly used a phase shift generated by carrier plasma dispersion in p-n-doped rib waveguides. Resonator-type modulators such as microring devices often show good performance with a small size, but the working spectrum is very limited and cannot operate stably without complicated thermal stabilizations [7,8,9]. Therefore, most studies have employed Mach-Zehnder (MZ) devices, enabling a wide working spectrum and, hence, operating over a wide temperature range without thermal stabilizations when they use a symmetric circuit. However, MZ circuits typically need a long phase shifter length of several millimeters to obtain a sufficient extinction ratio (ER) [1,2,3,4,5,6], resulting in high power consumption. To overcome this constraint, we have developed photonic crystal waveguide (PCW) MZ modulators. They are constructed via a CMOS process, with a phase shifter length L significantly reduced by the slow-light effect [10,11,12,13,14,15]. For slow light with a low group velocity υg, the slowdown factor is usually expressed by the group index ng ≡ c/υg, where c is the light velocity in a vacuum. Values of ng are observed to be between 3 and 4 for Si rib waveguides, while Si PCWs easily produce ng > 20 [10]. In a simplified model, the phase shift Δφ in a waveguide with an equivalent modal index change induced by carrier plasma dispersion, Δneq, is expressed as [15,16]
where k0 = 2π/λ is the wave number in a vacuum and ωb is the photonic band frequency. As Δφ is proportional to ng, the same value for Δφ can be expected even for smaller L and Δneq by employing a large ng. Furthermore, we developed lattice-shifted PCWs (LSPCWs) that generate low-dispersion (LD) slow light, showing an almost constant ng over the wide wavelength range of 10–20 nm for transverse-electric (TE) polarization [10]. In our recent study, we observed eye opening at some selected wavelengths and the unchanged 10 Gbps operation was confirmed for a wavelength bandwidth of 16.9 nm at wavelength λ ~ 1550 nm and a temperature range of 19–124 °C in a device with L = 90 μm [11]. Moreover, an interleaved p-n junction was employed, which increases the overlap of a depletion region with the slow-light mode and thus increases Δneq. This succeeded in the 25 Gbps modulation in a device with L = 200 μm with a drive voltage of Vpp = 1.75 V (on the panel of pulse pattern generator, PPG) [15]. In this study, we observed an ER of 3 dB, although the excess modulation loss (ML), which usually helps to increase the ER, was moderately suppressed to 0.8 dB.
A concern in using such LD slow light in practical modulators is the small fluctuations of ng in a working spectrum. These fluctuations are considered to be primarily caused by the reflection at the ends of the LSPCW and may be suppressed by technical improvements. However, for the fundamental improvement of the fabrication accuracy, a more advanced CMOS process is required, which increases the production cost. It is important to estimate how severely modulation characteristics reflect fluctuations in ng and thus modify requirements accordingly. In this study, we investigated modulation characteristics over the wide working spectrum. We measured the frequency response, ER, and bit-error rate (BER) in detail and evaluated the relation with ng, and revealed the condition that satisfies requirements for optical interconnects.
2. Device
Figure 1a shows the schematic of the Si LSPCW MZ modulator with the interleaved p-n junction. The details of the structure, theoretical modal behaviors, and fundamental modulation characteristics can be seen in Reference [15]. Third-row-shifted LSPCWs with a central p-n junction and SiO2 cladding as phase shifters were employed; these exhibit typical LD slow light. The phase shifter length was fixed at L = 200 μm and parameters of the LSPCW were a (lattice constant) = 400 nm, 2r (hole diameter) = 220 nm, and s (lattice shift) = 95 nm. An interleaved p-n junction with a comb period of wx = 300 nm and a comb depth of wy = 600 nm was used. The p- and n-type doping concentrations were given as NA = 9.5 × 1017 cm−3 and ND = 5.7 × 1017 cm−3, respectively, and the p+ and n+ doping concentrations for electrical contacts were NA+ = 1.0 × 1019 cm−3 and ND+ = 1.0 × 1019 cm−3, respectively. To avoid the strong free carrier absorption in heavily doped regions, a distance of ~4 μm across the p-n junction was set. As radio frequency (RF) electrodes of the phase shifters, coplanar waveguides consisting of an Al electrode for signal (S) and two Al electrodes for ground (G) were employed. No termination resistors were used, to simplify the device layout. In addition, 36.5 μm TiN heaters were integrated inside the SiO2 cladding above the same LSPCWs, and were used for setting the initial phase of each MZ arm. The total footprint of the device excluding the input and output waveguides was ~400 × 500 μm2, but they could be reduced to ~50 × 250 μm2 if we shrink the electrodes and neglect the RF pads.
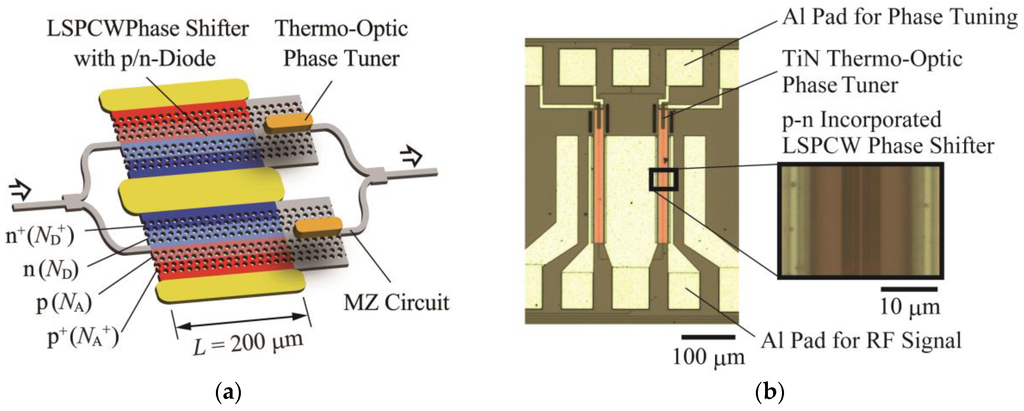
Figure 1.
Si LSPCW MZ modulator. (a) Schematic. Interleaved p-n junction was employed but not shown in this figure; (b) Microscope image of fabricated device.
The devices were constructed on a 200 mm silicon-on-insulator (SOI) wafer, using a 180 nm CMOS process at the Institute of Micro-Electronics foundry service with a KrF excimer laser exposure at λ = 248 nm. The original thickness of the Si slab in the SOI wafer was 220 nm, but was subsequently thinned to 210 nm by thermal oxidation. The thickness of the SiO2 BOX layer was 2 μm. Fourteen mask layers were used: two layers for the waveguides, four layers for the p-n junctions, two layers for the heaters and thermal isolation trench, four layers for RF and DC electrodes, contact holes, and contact pads, and two layers for the formation of waveguide end facets with spot size converters (SSC). For the waveguide layers, phase-shift masks were applied to improve the resolution to approximately 100 nm. Figure 1b shows the microscope image of the fabricated device.
First, we measured the fundamental slow-light characteristics of the device. Using objective lenses or compact lens modules, we input light from and output light to single mode fibers with the SSC consisting of SiO2 waveguides and Si inverse tapers located at the chip facets. Figure 2a shows the transmission spectrum normalized by the transmission in a Si wire waveguide of the same length. The device exhibits a flat transmission band at λ = 1550–1570 nm with a maximum transmission of −5 dB. This excess loss came from the two 1 × 2 couplers in the MZ circuit (<0.5 dB in total), the propagation loss in the LSPCW (~3 dB), and the coupling loss between the LSPCW and Si wire (~1.5 dB in total). More than 60% of the LSPCW loss is due to the free-carrier absorption, which is expected to be reduced by optimizing the doping. Therefore, the excess loss is expected to fall by ~3 dB in future studies. Since the Si wire for the optical wiring had a 4 dB/cm propagation loss and a <0.1 dB loss at 90° bends, which corresponds to a 2 dB loss for ~4.5-mm-long wiring with six bends, the total on-chip loss of the device was 7 dB. Figure 2b shows the ng spectrum measured by the modulation phase shift method. The device exhibited the LD band with ng ≈ 20 and bandwidth Δλ ≈ 20 nm. We have reported higher ng of 50–60 by modifying the lattice shift. However, in that case, the working spectrum was narrowed to less than 10 nm due to the constraint of the ng-bandwidth product [10], and the strong back-scattering in the PCW, with some disordering, produced irregular oscillations. In this study, since we set ng to be moderately low, the ng spectrum was sufficiently wide and looks to be almost flat with no irregular oscillations. The ±10% variation of ng observed in the ng spectrum is considered to be due to the Fabry-Perot resonance in the LSPCW [17].
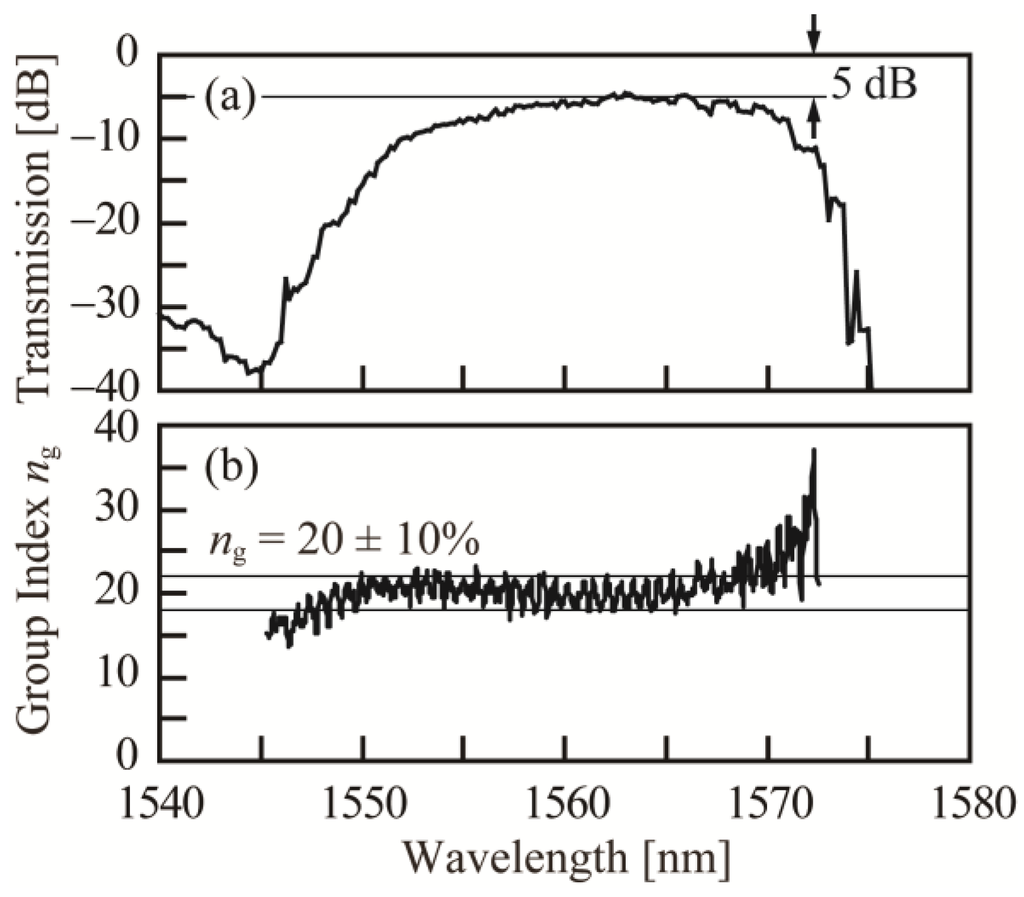
Figure 2.
Slow-light characteristics of fabricated device. (a) Transmission spectrum; (b) ng spectrum.
3. Frequency Response
The frequency response was measured using a vector network analyzer (VNA, Anritsu 37269E-R, Atsugi, Japan). Small sinusoidal signals from the VNA were applied to the RF electrode of a single MZ arm through an RF probe (typical insertion loss is 0.8 dB), and the modulated signals were then returned to the VNA through an erbium-doped fiber amplifier (EDFA, Alnair Labs CPA-100-CL, Shinagawa, Japan), a band-pass filter (BPF, Alnair Labs CVF-220-CL, Shinagawa, Japan) and an opto-electronic (OE) converter (Anritsu MN4765, Atsugi, Japan). Figure 3 shows S11 for the RF signals reflected to the output port of the VNA and S21 for the modulated optical signals that were input into the VNA. As previously mentioned, the device did not have termination resistors, and thus S11 becomes 0 dB at low frequencies. At high frequencies, on the other hand, the RF signals tend to attenuate during the transmission due to the parasitic resistance at the p-n junction, which decreases S11 gradually. The dip appearing at 19 GHz is considered to be caused by the excitation of the coupled slotline mode. This will be suppressed by symmetrizing the GSG RF electrode, which was designed asymmetrically in this fabrication, and the connection between the two G electrodes [4,18]. In any case, the reflection of the RF signals generates a voltage on the electrode two times greater than the set value at the PPG at low frequencies, 1.7 times greater at 12 GHz exhibiting S11 = −3 dB, and 1.4–1.5 times greater at 15 GHz exhibiting S11 = −6 dB. This enhances the total modulation efficiency while relatively degrading the high-frequency response.
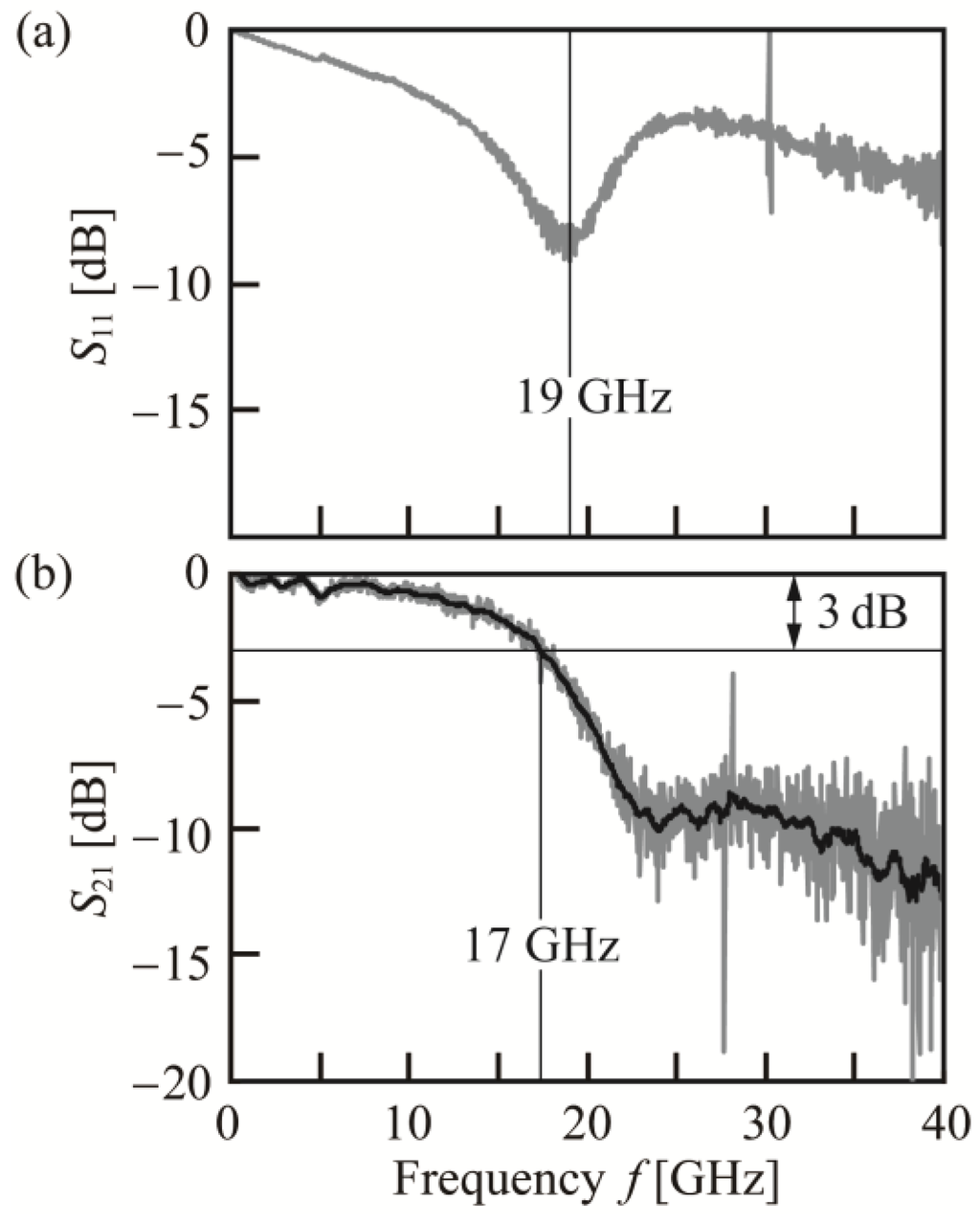
Figure 3.
Measured S parameters: (a) S11; (b) EO S21 at λ = 1554 nm. Gray line shows raw data. Black line shows averaged values within each ~0.5 GHz range.
For the electro-optic (EO) S21 measurement, a TE-polarized laser light at λ = 1554 nm was coupled to the SSC through a polarization-maintaining single mode fiber with a lens module. The coupling loss was 3.5 dB, including a 1 dB loss inside the lens module (7 dB in total for the input and output). The total insertion loss from fiber to fiber was approximately 14 dB including a 7 dB on-chip loss. Furthermore, the total loss from the laser source to the output fiber was 21 dB, including losses at the polarization controller and some junctions between fibers. Therefore, the laser power was raised to 16.5 dBm and S21 was measured. The cutoff frequency f3dB was 17 GHz, which is sufficient for the 25 Gbps operation. In general, f3dB is constrained by the RC time constant. We have reported the calculation of the resistance R and capacitance C at the p-n junction using the commercial simulator Lumerical DEVICE in Reference [15]. Modeling the Si layer sandwiched by the SiO2 BOX layer and top SiO2 cladding (both insulators), they were calculated to be 96 Ω (146 Ω including 50 Ω internal resistance in the PPG connected in series with the R) and ~60 fF at Vb = −2.2 × 2 V, respectively, for the current design. Their product gives f3dB = 18 GHz, which almost agrees with the measured value.
The f3dB could be constrained by the phase mismatch between the slow light and RF signals. The decreased ratio of the modulation depth, η(f), is expressed as
where nRF is the refractive index for RF signals, c is the light velocity in a vacuum, and θ0 is the initial phase mismatch. EO S21 is expressed using electro-electronic (EE) S21 for RF signals as
For typical traveling-wave modulators, a small phase mismatch is compensated by optimizing the design. In slow-light modulators, on the other hand, this issue is more complicated due to the large differences between group velocities. Let us assume that f = 12.5 GHz is a critical frequency for 25 Gbps modulation. Then, for ng = 20, nRF = 2 and L = 200 μm, η(f) is calculated to be higher than 0.95 when θ0 is optimized. Thus, the phase mismatch issue is not so severe. However, if either ng, L or f is larger than their present values, it will become a limiting factor to the frequency response; η(f) will be less than 0.9 when ng ≥ 32, L ≥ 340 μm or f ≥ 22 GHz.
We measured the frequency response spectrum R(f, λ) by changing λ in steps of 0.02 nm in the LD band within the range λ = 1550–1558 nm. Figure 4 shows the measured results as a color plot, as well as the measured ng spectrum and calculated f3dB spectrum from Equations (2) and (3). R(f, λ) exhibits fluctuations, which are considered to reflect the ng spectrum, although they do not agree completely. The ng spectrum shows a relatively large and slow oscillation with an averaged period of 0.7 nm, and a small and fast oscillation with an averaged period smaller than 0.2 nm. This large and slow oscillation roughly corresponds to the fluctuations in R(f, λ) at f > 20 GHz, and therefore may correspond to the effect of the phase mismatch at higher f. On the other hand, f3dB depicted by the boundary between red and yellow regions only exhibits the small and fast fluctuation, lying between 15 and 20 GHz, with the exception of three wavelengths that show f3dB = 12–13 GHz. Thus, the frequency response of this device satisfies the requirement for the 25 Gbps operation over the wide wavelength range.
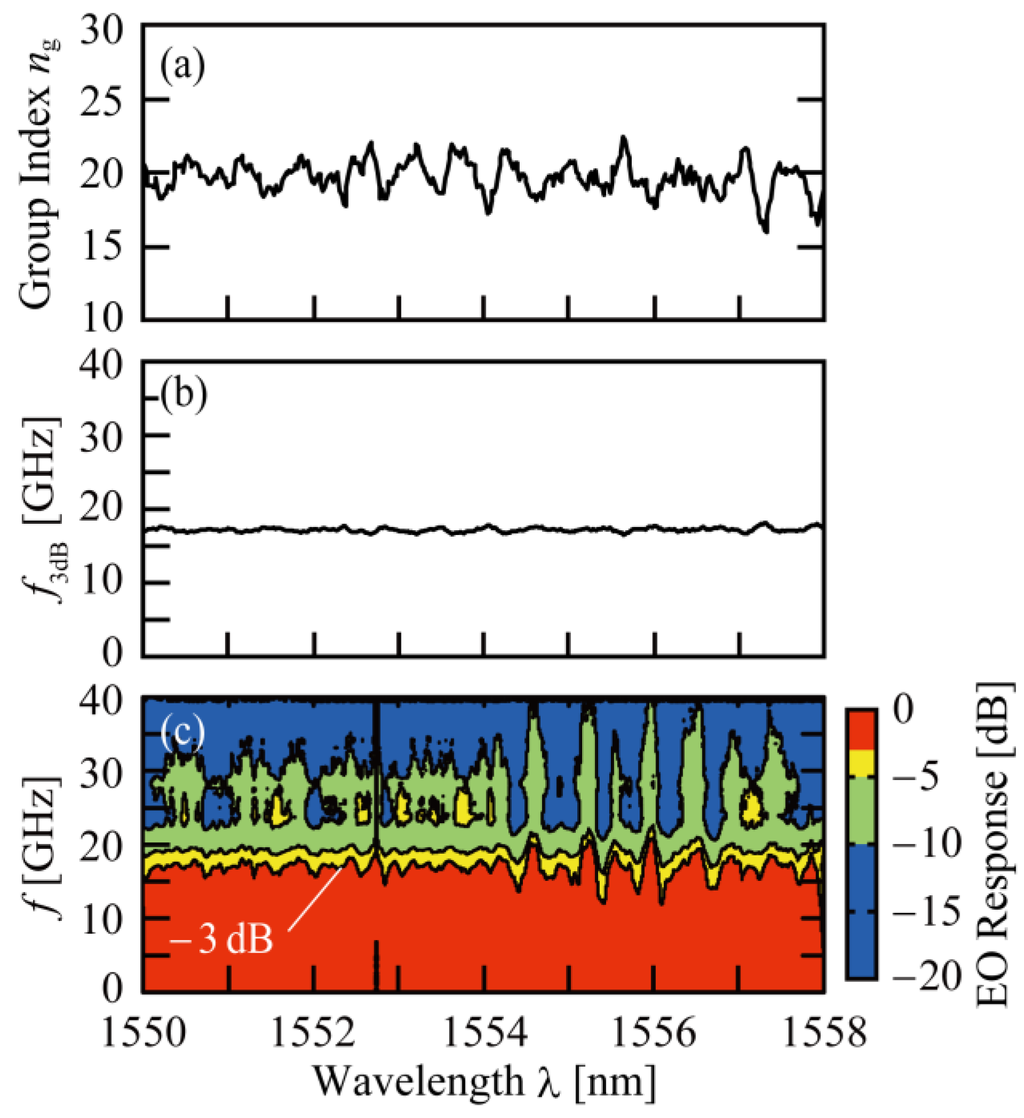
Figure 4.
Fluctuations in frequency response over the wide wavelength range: (a) ng spectrum; (b) f3dB spectrum calculated from Equations (2) and (3) with the measured ng and EE S21 estimated with R = 96 Ω and C = 50 fF; (c) Frequency response spectrum R(f, λ) obtained from the averaged response at each λ, such as those represented by the black line in Figure 3b. The f3dB is shown by the boundary between red and yellow regions. The fluctuation in the measurement setup was smaller than 1 GHz.
4. Signal Modulation
The 25 Gbps signal modulation was investigated over the wide wavelength range, using the non-return-to-zero (NRZ) pseudo-random-bit sequence (PRBS). Although the voltages from PPG (Anritsu MP1800A, Atsugi, Japan) were set as Vb ≈ −1 V and Vpp = 2.0 V, actual applied voltages should be modified by the open-ended electrodes, as mentioned above. The operation was first measured at λ = 1561 nm. Since the device and measurement setup had losses as outlined above, the output light from the device was amplified using EDFA and BPF, and then received and analyzed by an optical sampling oscilloscope (Keysight 86100C, 86109A, Santa Rosa, CA, USA). Figure 5a shows the eye pattern when the initial phase of the MZ arms was adjusted so that ER ≈ 3 dB was obtained. The open eye was observed with ML = 0.5 dB, which is comparable to that in a previous study [15]. Figure 5b shows a clearer open eye with ER = 3.9 dB when the ML was slightly increased to 1 dB.
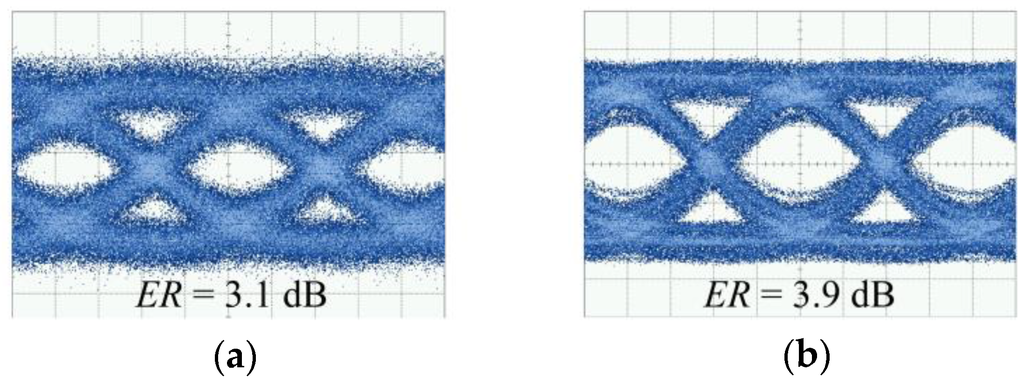
Figure 5.
The 25 Gbps eye patterns of modulated light: (a) ML = 0.5 dB and (b) 1.0 dB with PRBS lengths of 231 − 1 and 27 − 1, respectively.
Next, ER was repeatedly measured, changing the wavelength in steps of 0.5 nm between the range λ = 1549.5–1565.5 nm. The initial phase was adjusted such that the output intensity with no Vpp was decreased to 2 dB lower than the maximum, thus giving ML = 2 − ER/2. This is almost the same condition as that in Figure 5. Figure 6 shows the spectra of ER and ng. Although they do not agree completely, they exhibit similar patterns. ER ranges between 2 and 3 dB and fluctuates by ~1 dB. Furthermore, ER and BER were measured, within the range λ = 1558–1560 nm in steps of 0.2 nm. For the BER measurement, amplified light was detected by an OE converter (Agilent 11982A) after passing through a variable optical attenuator, where the electrical signal was incident on an error detector module (Anritsu MU183040B) after removing the DC components. Voltages from the PPG and initial phase were set similarly to those presented in Figure 6. Figure 7a shows BER measured as a function of the received powers Pr at the OE converter. The error-free operation of BER < 10−11 was confirmed. Figure 7 compares the BER and ER spectra measured in steps of 0.2 nm in the range of λ = 1558–1560 nm. ER fluctuated by 1 dB, similarly to that in Figure 6. In other words, the BER finally reflects the fluctuations in ng through those in the ER. This indicates that a margin larger than 1 dB is necessary in ER for a stable, error-free operation. For optical interconnects, ER is required to be larger than 3 dB, although it depends on the specifications of the transmitter and receiver. However, for the modulator described in this study, ER should be greater than 4 dB, including the margin. This is achieved by increasing the ML by 0.5 dB and the loss is compensated by increasing the output power from the light source or reducing the passive losses.
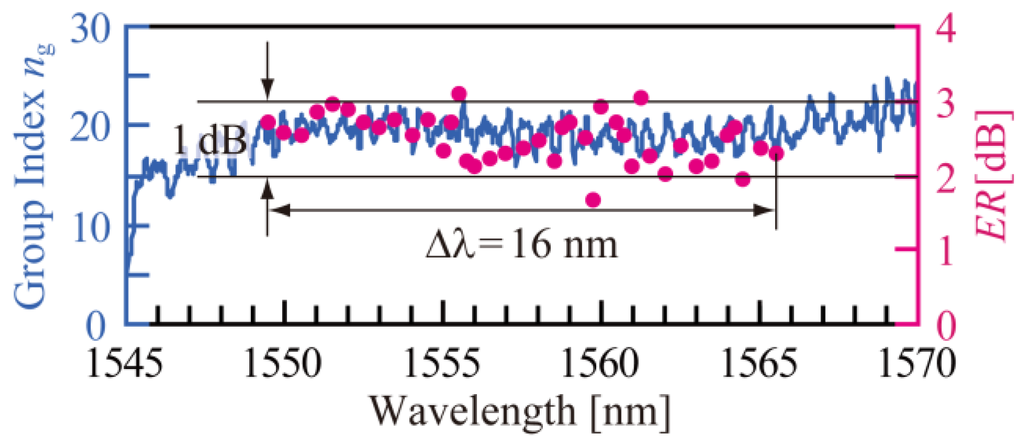
Figure 6.
Spectra of ng and ER measured at 25 Gbps. Operating condition was similar to that for Figure 5.
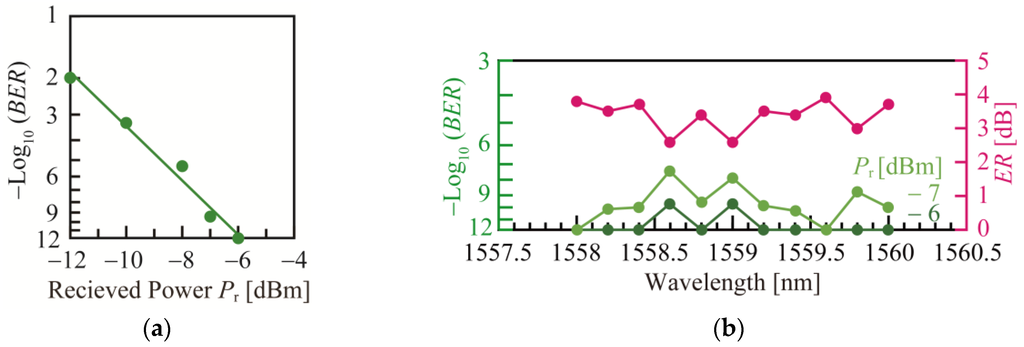
Figure 7.
BER characteristics at 25 Gbps for 27 − 1 bit NRZ-PRBS signals: (a) BER at λ = 1559.6 nm; (b) BER and ER at λ = 1558–1560 nm.
5. Slow-Light Enhancement
Thus far, the modulation characteristics have been presented with a fixed ng ≈ 20. In this section, the characteristics for a varied ng are presented. For a SiO2-cladded PCW, without a lattice shift, ng increases as λ increases towards the photonic band edge. Since this increase is smaller than that in air-bridge structures which have been extensively studied in the past, this allows for a wide scan of ng and the comprehensive investigation of the slow-light enhancement, by only changing λ. Here, the PCW was designed with specifications of a = 400 nm, 2r = 200 nm, and s = 0 nm. Due to different fabrication lots, doping concentrations were lower than those given above, i.e., NA = 4.8 × 1017 cm−3 and ND = 4.8 × 1017 cm−3, and the p-n junction profile was linear. Therefore, the modulation efficiency should be lower than that in the device described in the previous sections. The absolute value of the efficiency was neglected, while focusing on the relative change of the modulation characteristics with ng.
Figure 8 presents the measured ng spectrum, with the f3dB spectrum calculated in the same way as that for Figure 4b, and measured R(f, λ) at λ = 1534–1540 nm. It is shown that ng changes widely from 20 to 60 within this range. The calculated f3dB decreases with the increasing ng, showing the influence of the phase mismatch. The f3dB estimated from the measured R(f, λ) was 10–20 GHz at ng ≈ 20, but then fell to less than 10 GHz for higher ng, which almost agrees with the calculated one. Thus, some solution to suppress the phase mismatch is necessary when ng is increased to enhance Δφ. Solutions need to slow down the RF signals and/or to shift back the phase of the RF signals inside the electrode. For the former, a slow-wave electrode consisting of a loaded transmission line has previously been studied [6,19,20,21,22]. However, their slow-down factors are too small to compensate the phase mismatch. For the latter, it is possible to add a delay line, such as a meander line; however, this will increase the device footprint as its length will be in the order of millimeters. Furthermore, the fluctuations in f3dB in Figure 8 become particularly large at ng > 40, possibly caused by the oscillation of ng. As previously mentioned, a large ng generates strong back-scattering and, in particular, enlarges the spectral oscillation. A more advanced CMOS process is necessary to completely improve this situation, which may be costly. Alternatively, ng can be set to no higher than 40 if the current CMOS process is used, with the application of the slow light to the modulator.
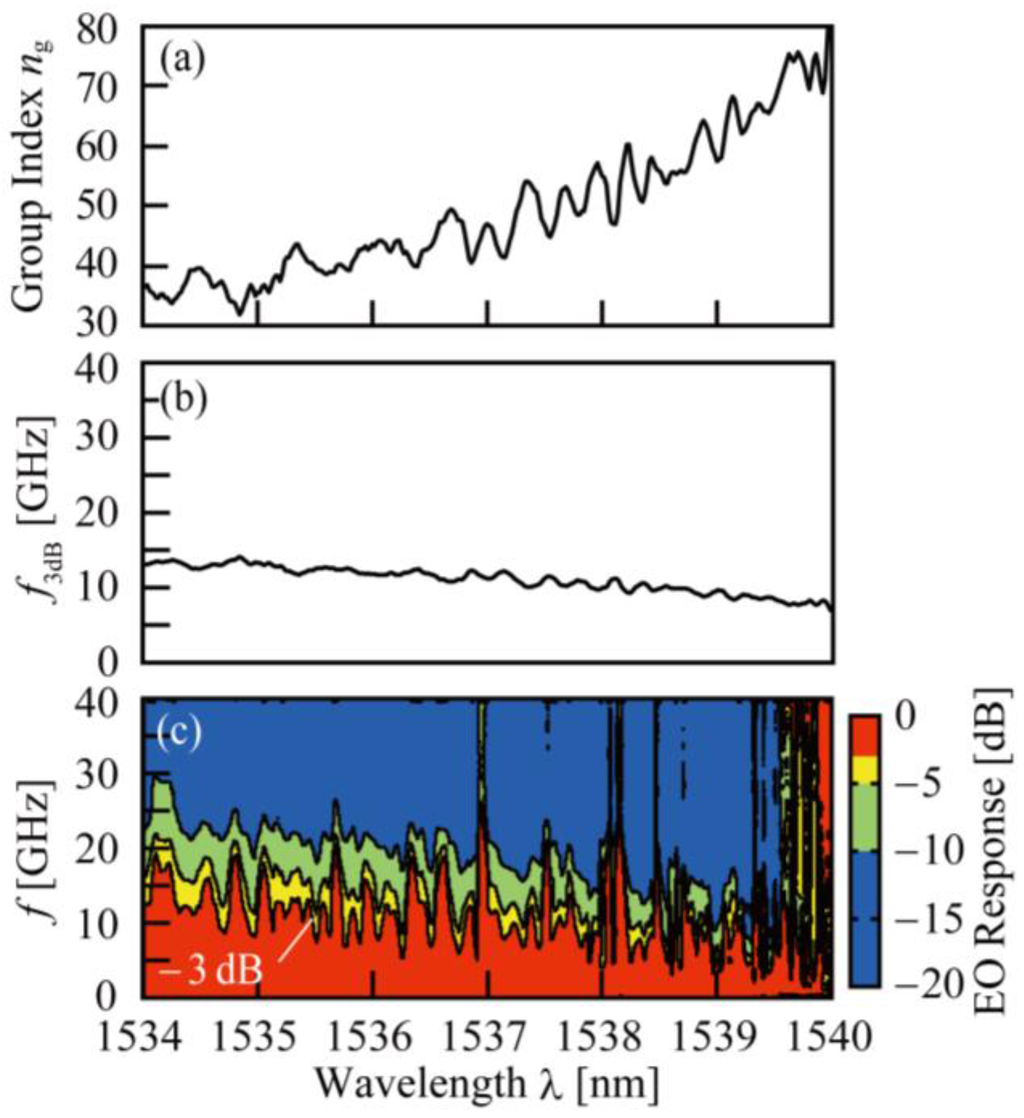
Figure 8.
Characteristics of PCW device without lattice shifts in the wide wavelength range: (a) ng spectrum; (b) f3dB spectrum calculated from Equations (2) and (3) with the measured ng and EE S21 estimated with R = 96 Ω and C = 50 fF; (c) Frequency response spectrum R(f, λ).
Figure 9 shows the result of the signal modulations. Although the voltages are the same as for Figure 5, the initial phase was set such that the transmission with no Vpp was reduced to 9 dB lower than the maximum, resulting in a large ML, and, hence, compensating for the low modulation efficiency. The ER was 2.5 dB at ng = 25, but increased to 8.1 dB at ng = 64. Figure 10 shows Δφ estimated from the ER as a function of ng. As expected from Equation (1), Δφ is almost proportional to ng, and therefore confirms the slow-light enhancement in the modulation efficiency. Equation (1) also indicates that Δφ depends on Δneq, which is determined by the overlap between the guided mode and the depletion region of the p-n junction. If the distribution of the slow-light mode changes with ng, Δneq would also change. Inversely speaking, the proportional behaviors between Δφ and ng suggest that the distribution is almost unchanged or is less severe for the modulator performance in this range. Equations (2) and (3) and the results in Figure 8 also suggest that such large ng makes the phase mismatch more severe and decreases Δφ. However, it is not apparent in Figure 10 because the slow-light enhancement in Equation (1) might be more dominant for the 25 Gbps PRBS signals whose major frequency components are lying at <12.5 GHz.
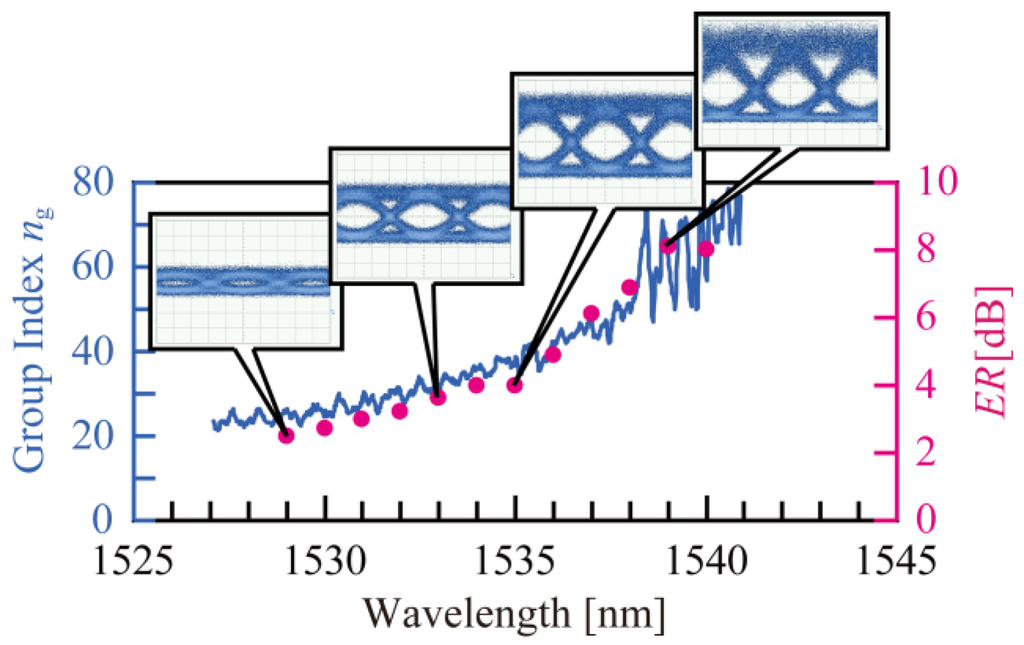
Figure 9.
The ng spectrum of PCW device without lattice shifts and ER at 25 Gbps modulation. Set voltages were the same as those for Figure 5.
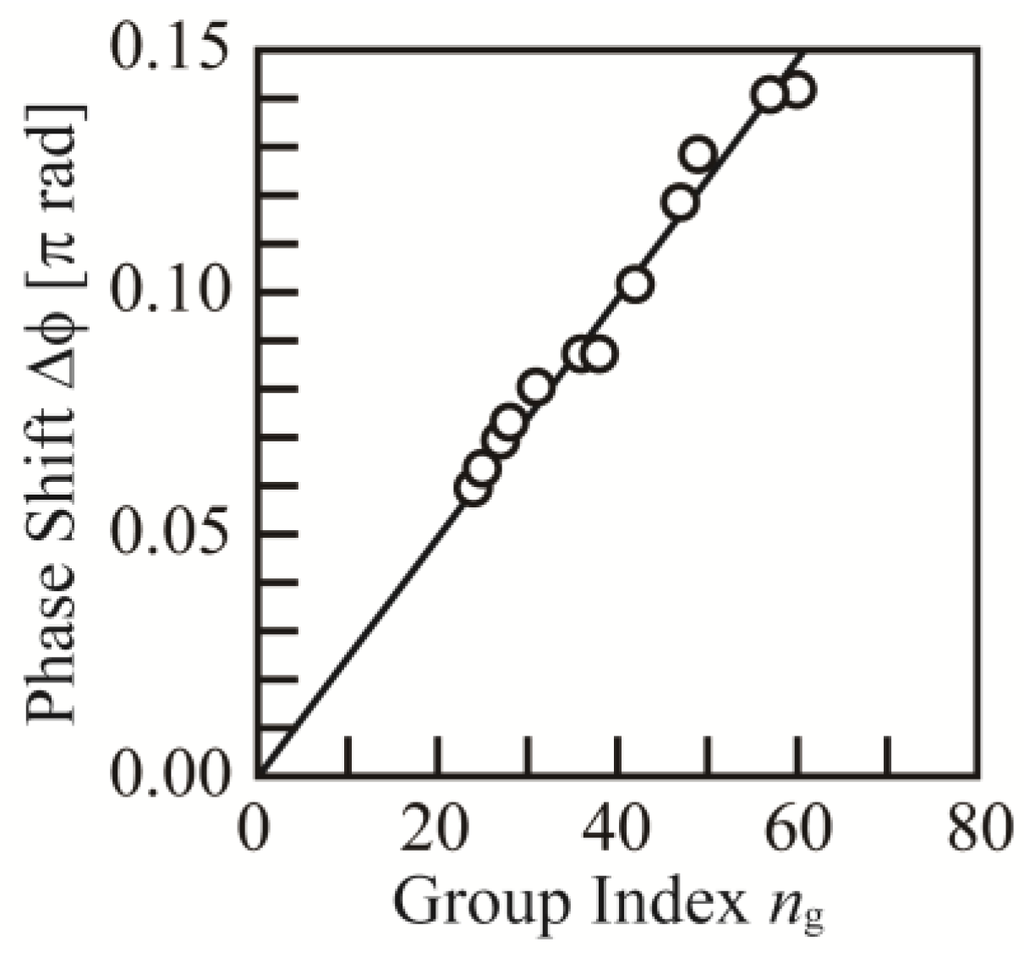
Figure 10.
The Δφ estimated from ER as a function of ng.
6. Conclusions
Si lattice-shifted photonic crystal slow-light modulators were constructed using a 180 nm CMOS process, with a phase shifter length as short as 200 μm. The frequency response, ER, and BER were measured in wide wavelength ranges, with fluctuations observed, perhaps due to the oscillation in the group index ng spectrum. The device with ng ≈ 20 showed a wide working spectrum of 20 nm and a sufficient frequency response for the 25 Gbps modulation. A higher ng up to 60 is available by modifying the lattice shift but the working spectrum is comparably narrowed, which is the major constraint of the slow-light effect. Even for the moderately low ng ≈ 20, the ±10% fluctuation was observed in the ng spectrum, which was reflected in ER and BER. Therefore, a margin larger than 1 dB is necessary in ER for stable, error-free operation, which can be achieved by adding a 0.5 dB modulation loss, comparably increasing the light source power and/or reducing passive losses. The ER was simply increased by increasing ng; however, the frequency response was degraded simultaneously. This degradation was considered to be due to the phase mismatch between slow light and RF signals, which will be more problematic beyond 25 Gbps. Results suggest that ng should be set to less than 40 to avoid this degradation and avoid irregularly large oscillations in ER, which is particularly enhanced by slow light.
Acknowledgments
This work was partly supported by the New Energy and Industrial Technology Development Organization (NEDO), Japan.
Author Contributions
Yosuke Hinakura, Yosuke Terada and Toshihiko Baba conceived and designed the experiments; Yosuke Terada, Takuya Tamura and Toshihiko Baba designed the devices; Yosuke Hinakura and Yosuke Terada performed the experiments; Yosuke Hinakura analyzed the data; Toshihiko Baba contributed experiment systems, analysis tools; Yosuke Hinakura and Toshihiko Baba wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef]
- Thomson, D.J.; Gardes, F.Y.; Fedeli, J.M.; Zlatanovic, S.; Hu, Y.; Kuo, B.P.P.; Myslivets, E.; Alic, N.; Radic, S.; Mashanovich, G.Z.; et al. 50-Gb/s silicon optical modulator. IEEE Photonics Technol. Lett. 2012, 24, 234–236. [Google Scholar] [CrossRef]
- Yang, L.; Ding, J. High-speed silicon Mach-Zehnder optical modulator with large optical bandwidth. J. Lightwave Technol. 2014, 32, 966–970. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Xiao, X.; Li, Z.; Yu, Y.; Yu, J. Demonstration and characterization of high-speed silicon depletion-mode Mach-Zehnder modulators. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 23–32. [Google Scholar] [CrossRef]
- Akiyama, S.; Imai, M.; Baba, T.; Akagawa, T.; Hirayama, N.; Noguchi, Y.; Seki, M.; Koshino, K.; Toyama, M.; Horikawa, T.; et al. Compact PIN-diode-based silicon modulator using side-wall-grating waveguide. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 74–84. [Google Scholar] [CrossRef]
- Ding, R.; Liu, Y.; Ma, Y.; Yang, Y.; Li, Q.; Lim, A.E.J.; Lo, G.Q.; Bergman, K.; Baehr-Jones, T.; Hochberg, M. High-speed silicon modulator with slow-wave electrodes and fully independent differential drive. J. Lightwave Technol. 2014, 32, 2240–2247. [Google Scholar] [CrossRef]
- Timurdogan, E.; Sorace-Agaskar, C.M.; Sun, J.; Hosseini, E.S.; Biberman, A.; Watts, M.R. An ultralow power athermal silicon modulator. Nat. Commun. 2014, 5, 4008. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Chang, E.; Amberg, P.; Shubin, I.; Lexau, J.; Liu, F.; Thacker, H.; Djordjevic, S.S.; Lin, S.; Luo, Y.; et al. A high-speed, tunable silicon Photonic ring modulator integrated with ultra-efficient active wavelength control. Opt. Express 2014, 22, 12628–12633. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Wade, M.T.; Lee, Y.; Orcutt, J.S.; Alloatti, L.; Georgas, M.S.; Waterman, A.S.; Shainline, J.M.; Avizienis, R.R.; Lin, S.; et al. Single-chip microprocessor that communicates directly using light. Nature 2015, 528, 534–538. [Google Scholar] [CrossRef] [PubMed]
- Tamura, T.; Kondo, K.; Terada, Y.; Hinakura, Y.; Ishikura, N.; Baba, T. Silica-Clad Silicon Photonic Crystal Waveguides for Wideband Dispersion-Free Slow Light. J. Lightwave Technol. 2015, 33, 3034–3040. [Google Scholar] [CrossRef]
- Nguyen, H.C.; Sakai, Y.; Shinkawa, M.; Ishikura, N.; Baba, T. 10 Gb/s operation of photonic crystal silicon optical modulators. Opt. Express 2011, 19, 13000–13007. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.C.; Sakai, Y.; Shinkawa, M.; Ishikura, N.; Baba, T. Photonic crystal silicon optical modulators: Carrier-injection and depletion at 10 Gb/s. IEEE J. Quantum Electron. 2012, 48, 210–220. [Google Scholar] [CrossRef]
- Nguyen, H.C.; Hashimoto, S.; Shinkawa, M.; Baba, T. Compact and fast photonic crystal silicon optical modulators. Opt. Express 2012, 20, 22465–22474. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.C.; Yazawa, N.; Hashimoto, S.; Otsuka, S.; Baba, T. Sub-100 μm photonic crystal Si optical modulators: Spectral, athermal, and high-speed performance. IEEE J. Sel. Top Quantum Electron. 2013, 19, 127–137. [Google Scholar] [CrossRef]
- Terada, Y.; Ito, H.; Nguyen, H.C.; Baba, T. Theoretical and experimental investigation of low-voltage and low-loss 25-Gbps Si photonic crystal slow light Mach-Zehnder modulators with interleaved p/n junction. Front. Phys. 2014, 2, 1–9. [Google Scholar] [CrossRef]
- Brosi, J.M.; Koos, C.; Andreani, L.C.; Waldow, M.; Leuthold, J.; Freude, W. High-speed low-voltage electro-optic modulator with a polymer-infiltrated silicon photonic crystal waveguide. Opt. Express 2008, 16, 4177–4191. [Google Scholar] [CrossRef] [PubMed]
- O’Faolain, L.; Schulz, S.A.; Beggs, D.M.; White, T.P.; Spasenović, M.; Kuipers, L.; Morichetti, F.; Melloni, A.; Mazoyer, S.; Hugonin, J.P.; et al. Loss engineered slow light waveguides. Opt. Express 2010, 18, 27627–27638. [Google Scholar] [CrossRef] [PubMed]
- Ponchak, G.E.; Papapolymerou, J.; Tentzeris, M.M. Excitation of coupled slotline mode in finite-ground CPW with unequal ground-plane widths. IEEE Trans. Microwave Theory Technol. 2005, 53, 713–717. [Google Scholar] [CrossRef]
- Shin, J.H.; Sakamoto, S.R.; Dagli, N. Conductor loss of capacitively loaded slow wave electrodes for high-speed photonic devices. J. Lightwave Technol. 2011, 29, 48–52. [Google Scholar] [CrossRef]
- Chen, H.W.; Kuo, Y.H.; Bowers, J.E. 25 Gb/s hybrid silicon switch using a capacitively loaded traveling wave electrode. Opt. Express 2010, 18, 1070–1075. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, G.L.; Mason, T.G.B.; Yu, P.K.L. Analysis of segmented traveling-wave optical modulators. J. Lightwave Technol. 2004, 22, 1789–1796. [Google Scholar] [CrossRef]
- Jaeger, N.A.; Lee, Z.K. Slow-wave electrode for use in compound semiconductor electrooptic modulators. IEEE J. Quantum Electron. 1992, 28, 1778–1784. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).