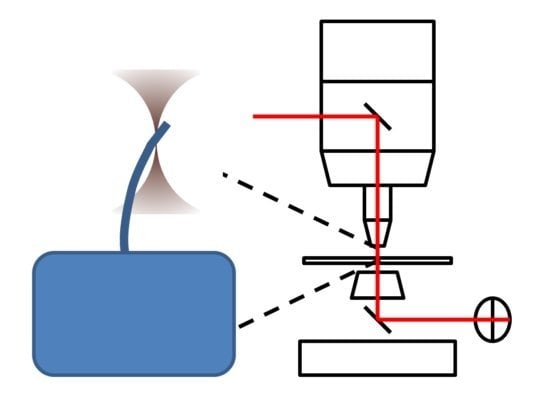
A Model for the Force Exerted on a Primary Cilium by an Optical Trap and the Resulting Deformation
Abstract
:1. Introduction
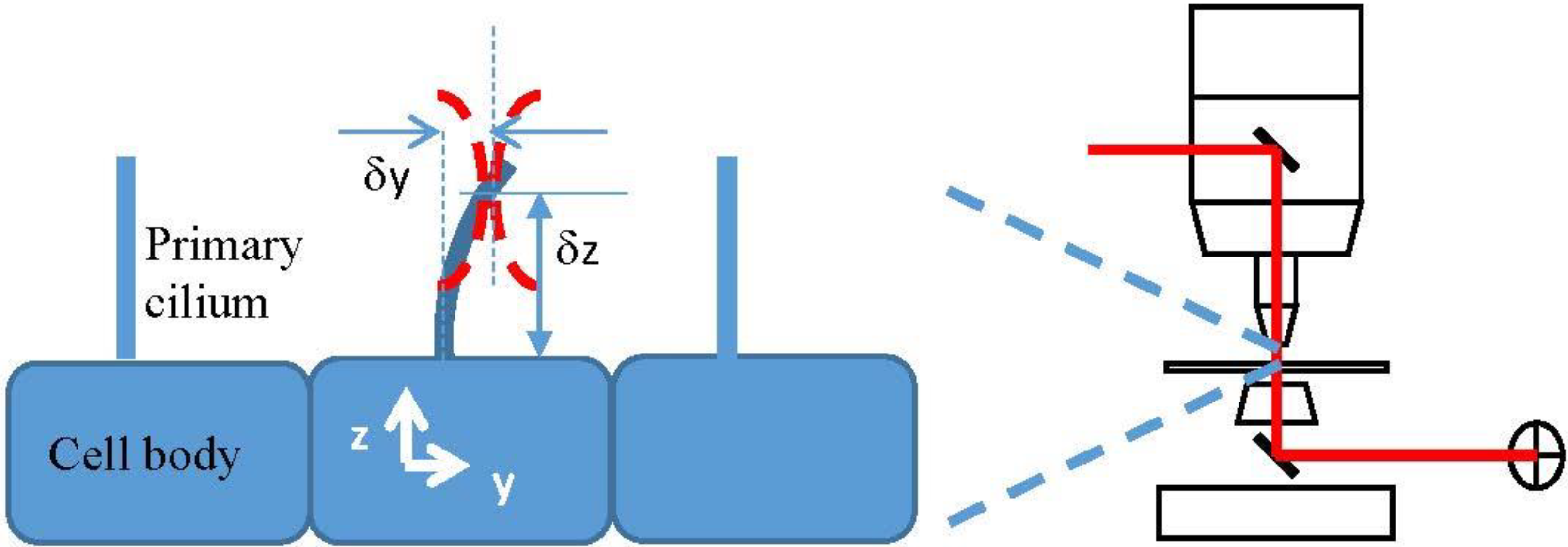
The Electric Field and the discrete dipole approximation (DDA)
- Electric field field amplitude
- Trap beam waist
- Trap beam diameter at dipole ‘i’
- Wavenumber
- Rayleigh length
- Radius of curvature
- Radial coordinate
- P the optical power
- NA the numerical aperture of the focusing lens, and
- δx, δy, δz are the displacement of the center of the beam waist from the coordinate origin, which we place at the center of the base of the cilium.
2. Results
2.1. The Force on a Dipole and the Force Density
2.2. The z Dependence of the Force Density and the Bending of a Cilium
2.3. The General Case
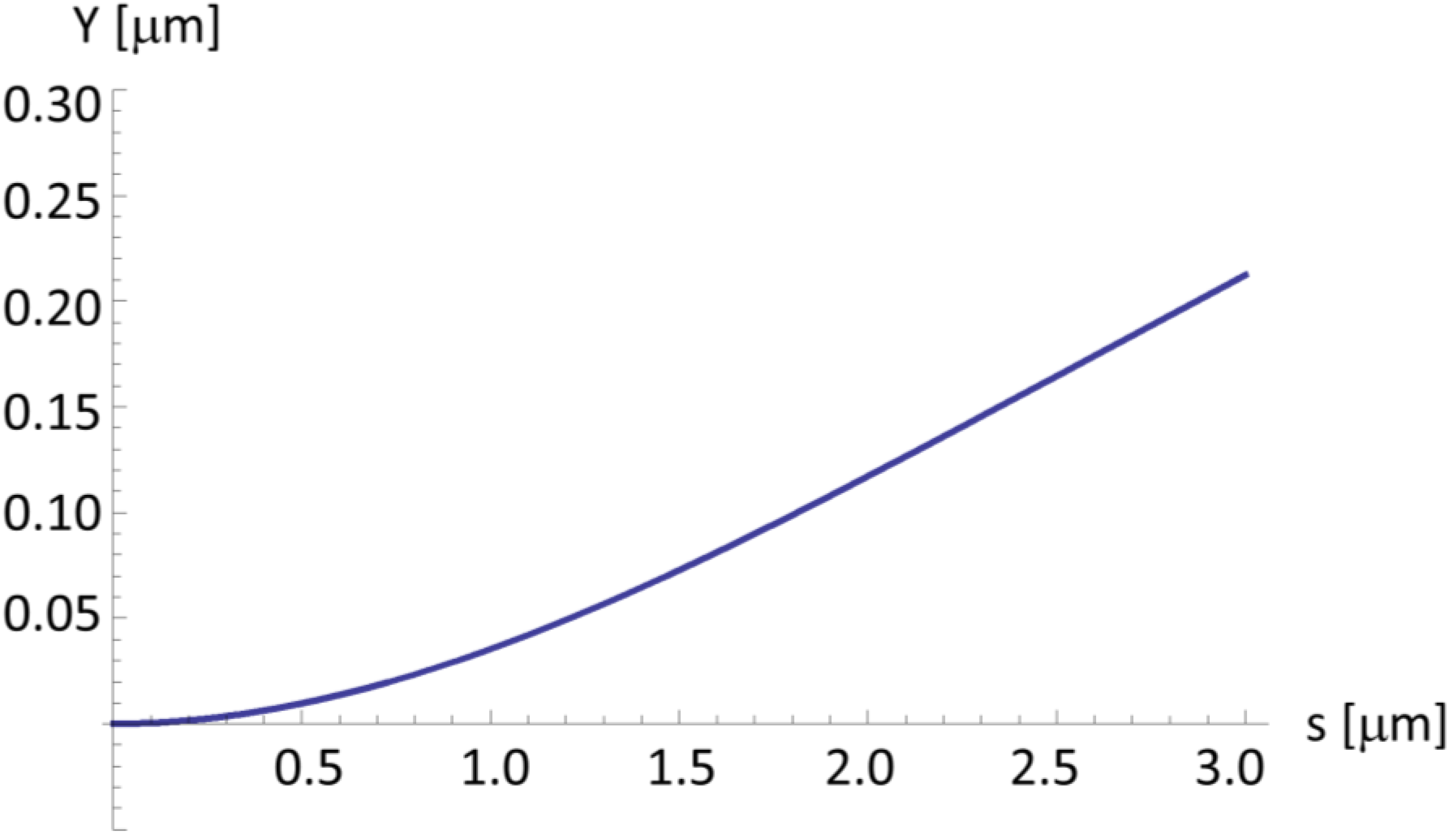
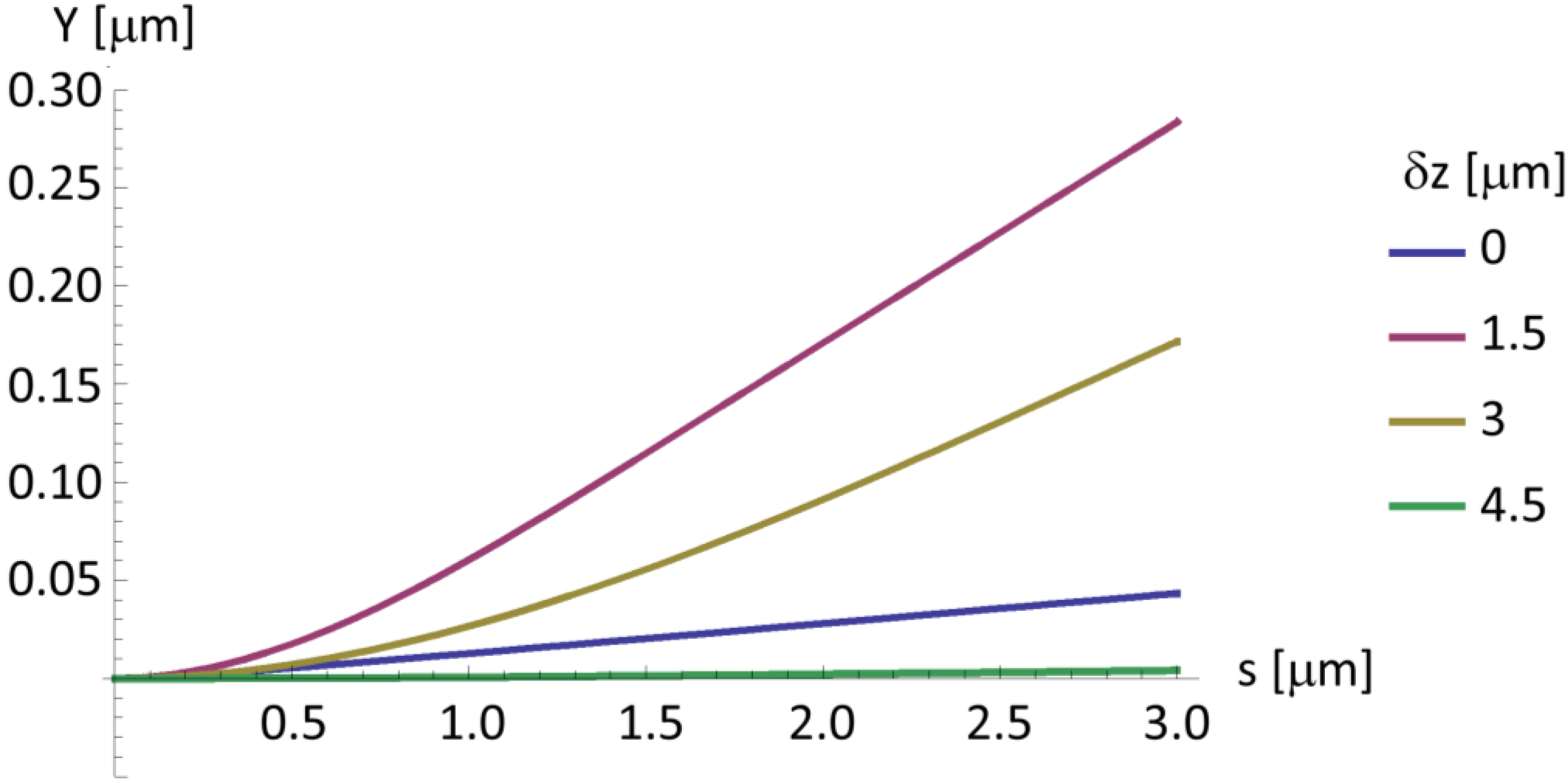
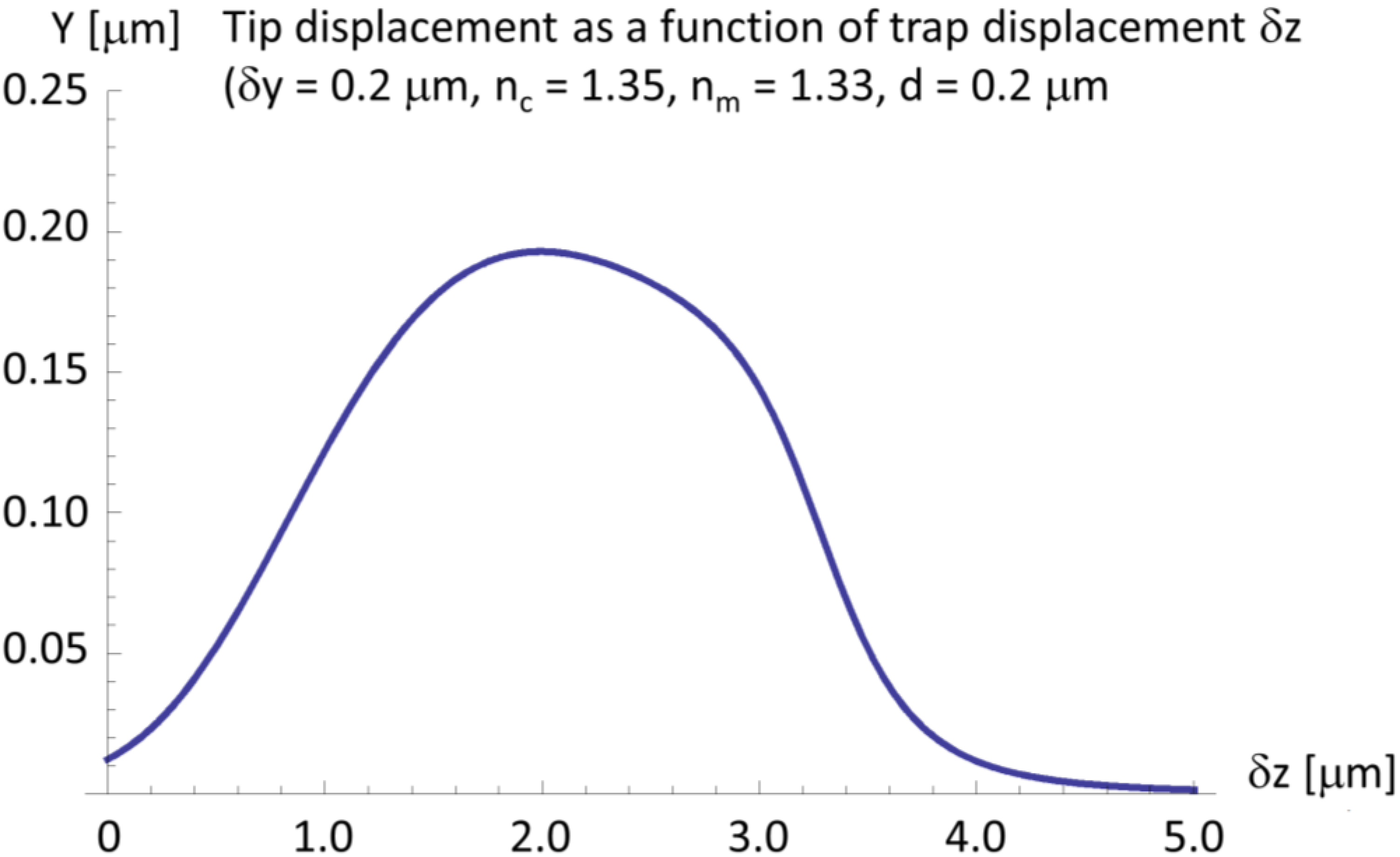
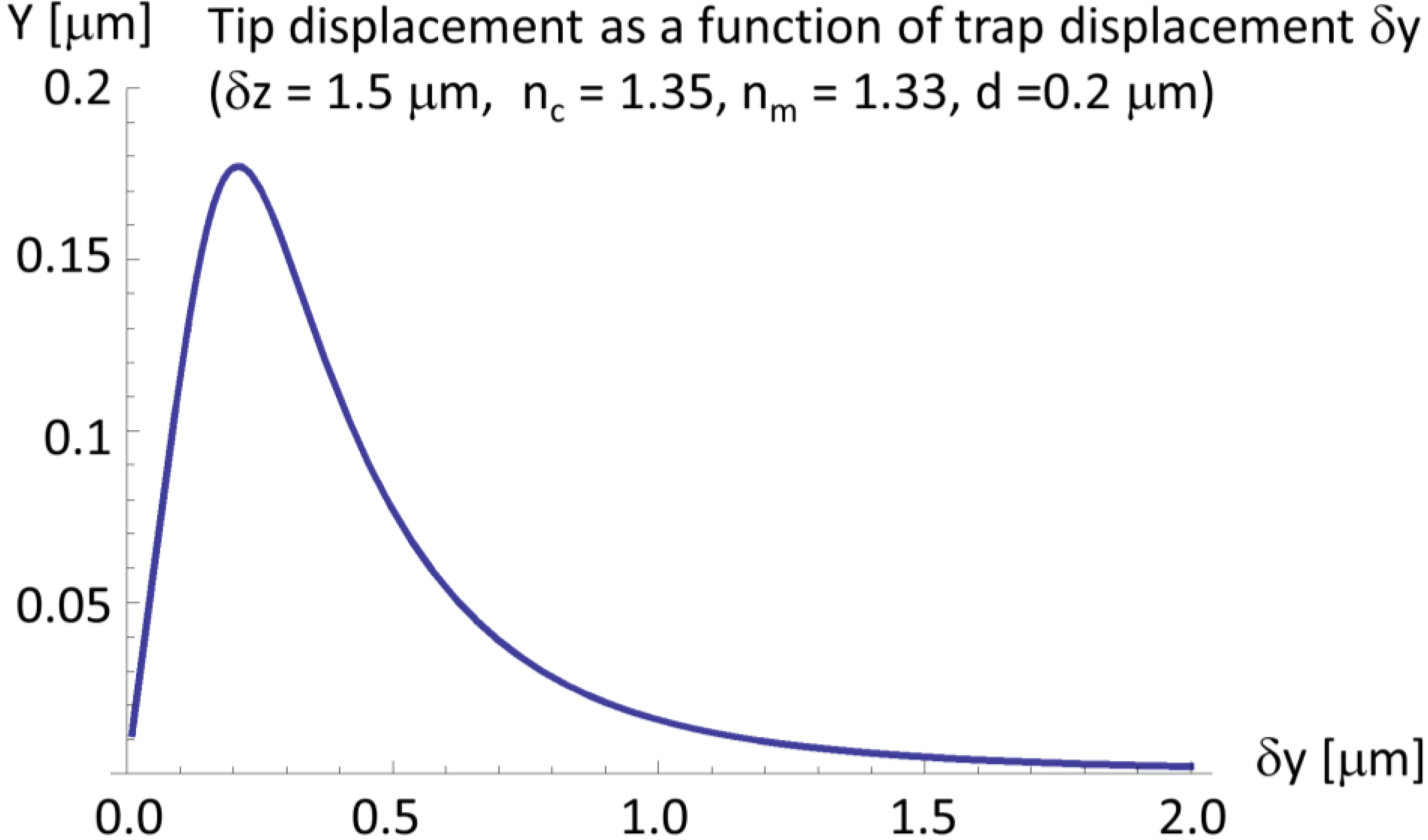
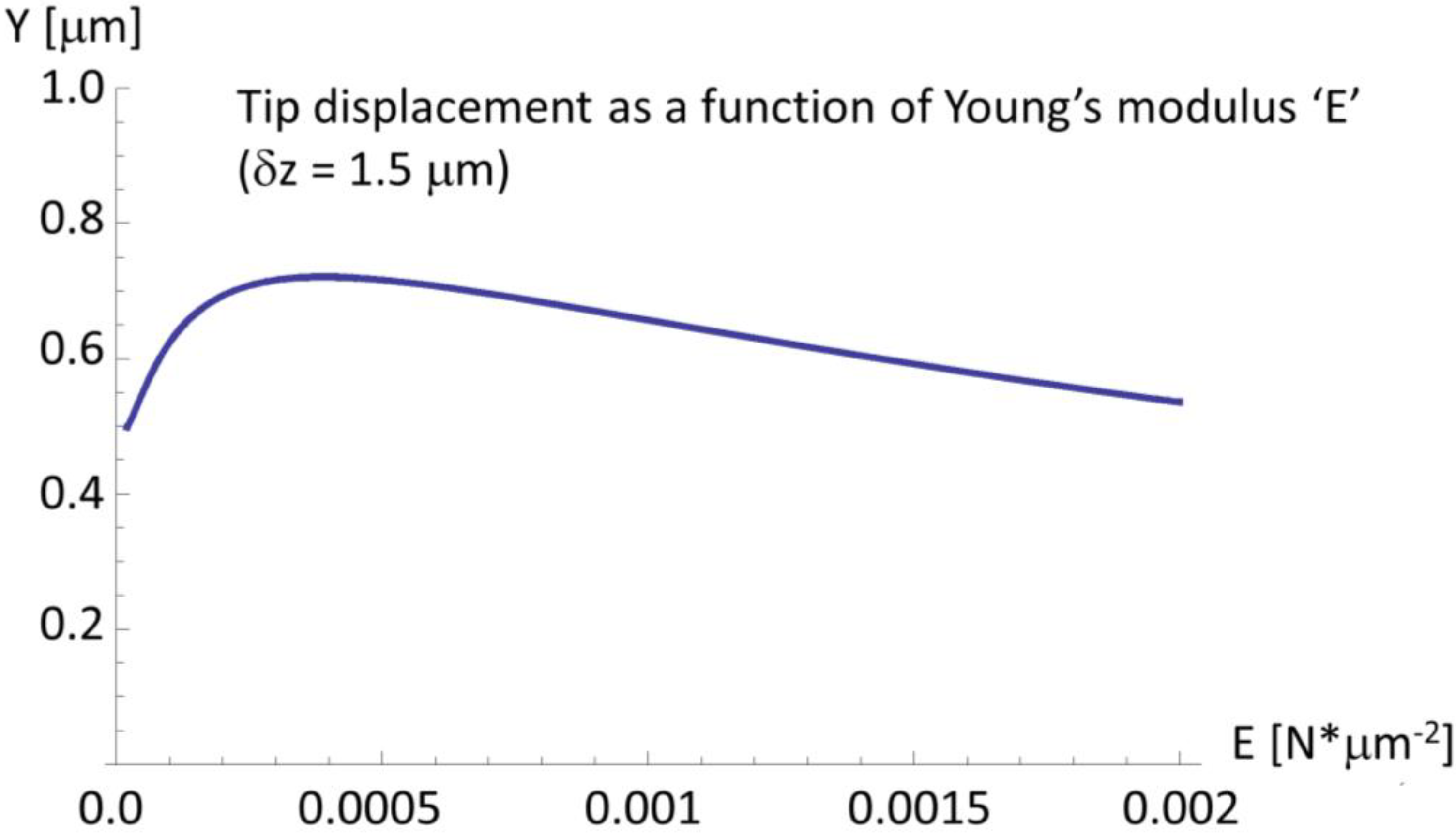
2.4. A Very Narrow Cylinder
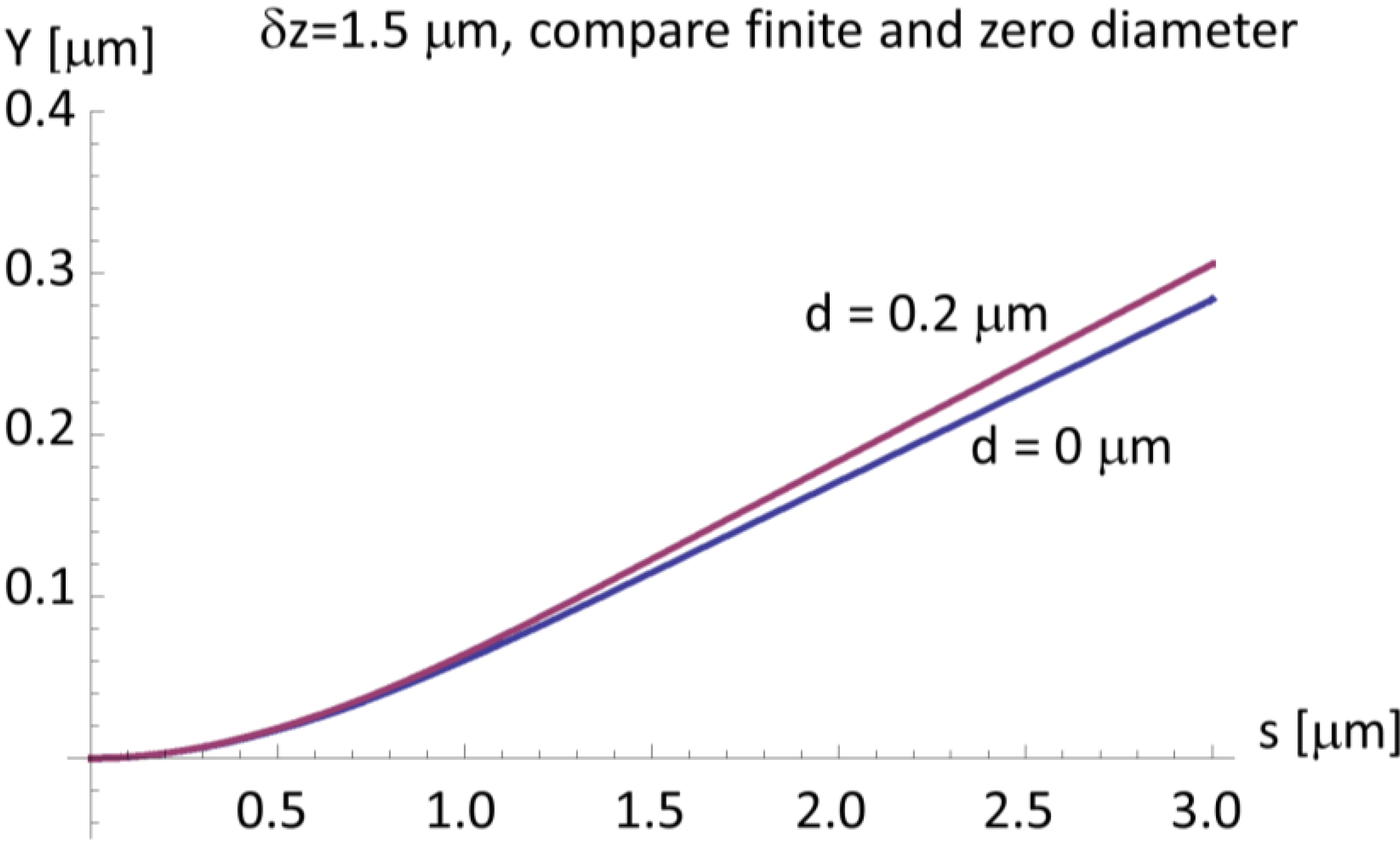
3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
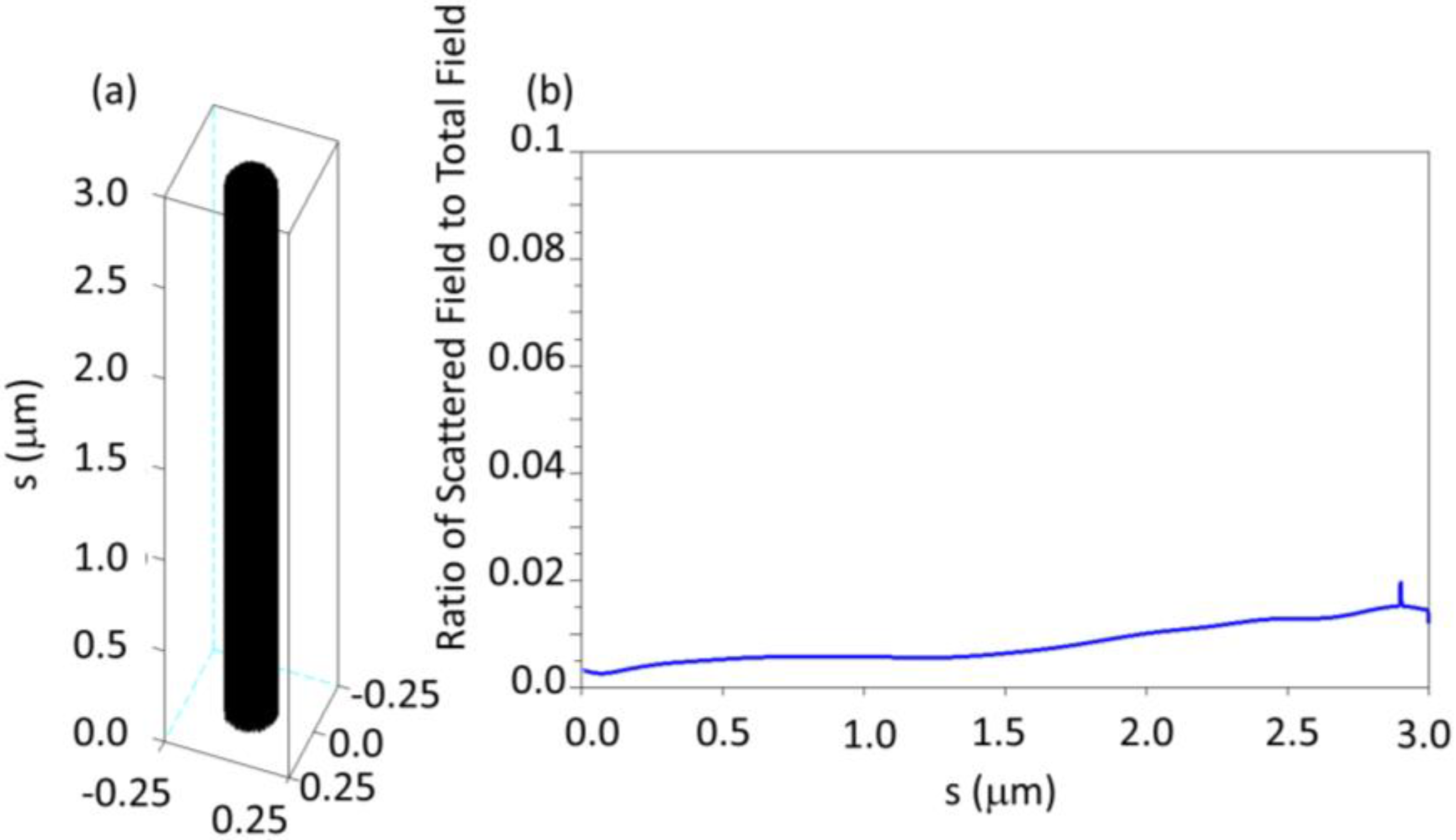
Appendix A: Using the DDA to Calculate the Scattered Electric Field
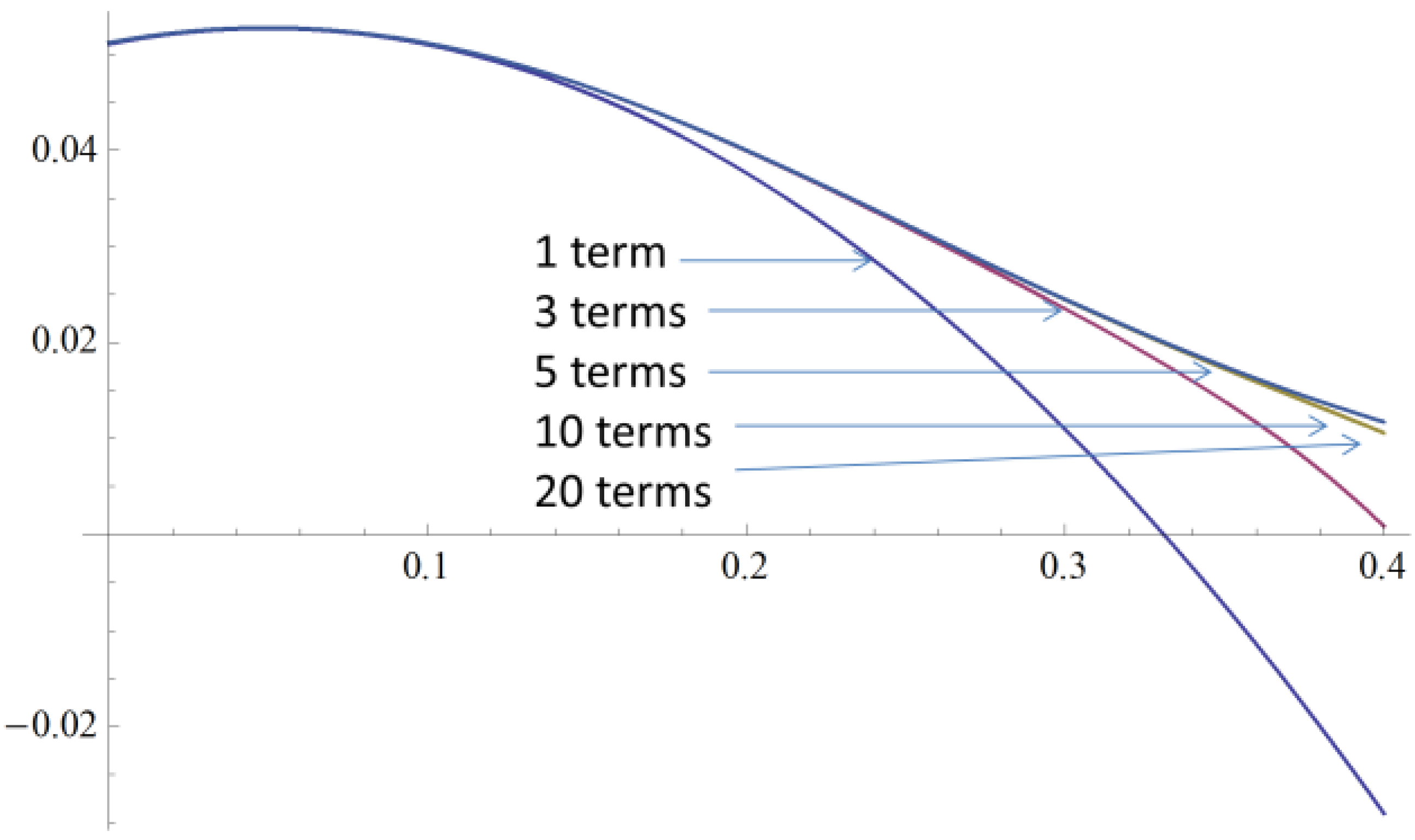
Appendix B: Series Solution for the Force on a Cylinder
Conflict of Interest
References
- Praetorius, H.A.; Spring, K.R. The renal cell primary cilium functions as a flow sensor. Curr. Opin. Nephrol. Hypertens 2003, 12, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Miyoshi, K.; Kasahara, K.; Miyazaki, I.; Asanuma, M. Factors that influence primary cilium length. Acta Med. Okayama 2011, 65, 279–285. [Google Scholar] [PubMed]
- Rikmenspoel, R. Elastic properties of the sea urchin sperm flagellum. Biophysical journal 1966, 6, 471–479. [Google Scholar] [CrossRef]
- Baba, S.A. Flexural rigidity and elastic constant of cilia. J. Exp. Biol. 1972, 56, 459–467. [Google Scholar] [PubMed]
- Schwartz, E.A.; Leonard, M.L.; Bizios, R.; Bowser, S.S. Analysis and modeling of the primary cilium bending response to fluid shear. Am. J. Physiol. 1997, 272, F132–F138. [Google Scholar] [PubMed]
- Resnick, A.; Hopfer, U. Force-response considerations in ciliary mechanosensation. Biophys. J. 2007, 93, 1380–1390. [Google Scholar] [CrossRef] [PubMed]
- Resnick, A.; Hopfer, U. Mechanical stimulation of primary cilia. Front. Biosci. 2008, 13, 1665–1680. [Google Scholar] [CrossRef] [PubMed]
- Mans, D.A.; Voest, E.E.; Giles, R.H. All along the watchtower: Is the cilium a tumor suppressor organelle? Biochim. Biophys. Acta 2008, 1786, 114–125. [Google Scholar] [PubMed]
- Jenkins, P.M.; McEwen, D.P.; Martens, J.R. Olfactory cilia: Linking sensory cilia function and human disease. Chem. Senses 2009, 34, 451–464. [Google Scholar] [CrossRef] [PubMed]
- Veland, I.R.; Awan, A.; Pedersen, L.B.; Yoder, B.K.; Christensen, S.T. Primary cilia and signaling pathways in mammalian development, health and disease. Nephron Physiol. 2009, 111, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Peterson, M.A. Geometry of ciliary dynamics. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 011923. [Google Scholar] [CrossRef]
- Kim, S.; Dynlacht, B.D. Assembling a primary cilium. Curr. Opin. Cell Biol. 2013, 25, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Fisch, C.; Dupuis-Williams, P. Ultrastructure of cilia and flagella—Back to the future! Biol. Cell 2011, 103, 249–270. [Google Scholar] [CrossRef] [PubMed]
- Pozrikidis, C. Shear flow past slender elastic rods attached to a plane. Int. J. Solids Struct. 2011, 48, 137–143. [Google Scholar] [CrossRef]
- Eloy, C.; Lauga, E. Kinematics of the most efficient cilium. Phys. Rev. Lett. 2012, 109, 038101. [Google Scholar] [CrossRef] [PubMed]
- Hilfinger, A.; Chattopadhyay, A.K.; Julicher, F. Nonlinear dynamics of cilia and flagella. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 051918. [Google Scholar] [CrossRef]
- Young, Y.N.; Downs, M.; Jacobs, C.R. Dynamics of the primary cilium in shear flow. Biophys. J. 2012, 103, 629–639. [Google Scholar] [CrossRef] [PubMed]
- Battle, C. Mechanics & Dynamics of the Primary Cilium; Georg-August-Universität Göttingen: Göttingen, Germany, 2013. [Google Scholar]
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Felgner, H.; Frank, R.; Schliwa, M. Flexural rigidity of microtubules measured with the use of optical tweezers. J. Cell Sci. 1996, 109, 509–516. [Google Scholar] [PubMed]
- Wiggins, C.H.; Riveline, D.; Ott, A.; Goldstein, R.E. Trapping and wiggling: Elastohydrodynamics of driven microfilaments. Biophys. J. 1998, 74, 1043–1060. [Google Scholar] [CrossRef]
- Glaser, J.; Hoeprich, D.; Resnick, A. Near real-time measurement of forces applied by an optical trap to a rigid cylindrical object. Opt. Eng. 2014, 53. [Google Scholar] [CrossRef]
- Ren, K.F.; Grehan, G.; Gouesbet, G. Scattering of a gaussian beam by an infinite cylinder in the framework of generalized lorenz-mie theory: Formulation and numerical results. J. Opt. Soc. Am. A 1997, 14, 3014–3025. [Google Scholar] [CrossRef]
- Kozaki, S. Scattering of a gaussian-beam by an inhomogeneous dielectric cylinder. J. Opt. Soc. Am. 1982, 72, 1470–1474. [Google Scholar] [CrossRef]
- Lock, J.A. Scattering of a diagonally incident focused gaussian beam by an infinitely long homogeneous circular cylinder. J. Opt. Soc. Am. A 1997, 14, 640–652. [Google Scholar]
- Ling, L.; Zhou, F.; Huang, L.; Li, Z.Y. Optical forces on arbitrary shaped particles in optical tweezers. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Simpson, S.H.; Hanna, S. Application of the discrete dipole approximation to optical trapping calculations of inhomogeneous and anisotropic particles. Opt. Express 2011, 19, 16526–16541. [Google Scholar] [CrossRef] [PubMed]
- Yurkin, M.A.; Hoekstra, A.G.; Brock, R.S.; Lu, J.Q. Systematic comparison of the discrete dipole approximation and the finite difference time domain method for large dielectric scatterers. Opt. Express 2007, 15, 17902–17911. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Thomas, E.L. Optical forces and optical torques on various materials arising from optical lattices in the lorentz-mie regime. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
- Wriedt, T. A review of elastic light scattering theories. Part. Part. Syst. Char. 1998, 15, 67–74. [Google Scholar] [CrossRef]
- Verghese, E.; Zhuang, J.; Saiti, D.; Ricardo, S.D.; Deane, J.A. In vitro investigation of renal epithelial injury suggests that primary cilium length is regulated by hypoxia-inducible mechanisms. Cell Biol. Int. 2011, 35, 909–913. [Google Scholar] [CrossRef] [PubMed]
- Barton, J.P.; Alexander, D.R. 5th-order corrected electromagnetic-field components for a fundamental gaussian-beam. J. Appl. Phys. 1989, 66, 2800–2802. [Google Scholar] [CrossRef]
- Gu, M. Advanced Optical Imaging Theory; Springer: Berlin, Germany; New York, NY, USA, 2000; p. 214. [Google Scholar]
- Segel, L.A.; Handelman, G.H. Mathematics Applied to Continuum Mechanics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; p. 590. [Google Scholar]
- Downs, M.E.; Nguyen, A.M.; Herzog, F.A.; Hoey, D.A.; Jacobs, C.R. An experimental and computational analysis of primary cilia deflection under fluid flow. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 2–10. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.F.; Ganatos, P.; Weinbaum, S. Transmission of steady and oscillatory fluid shear stress across epithelial and endothelial surface structures. Phys. Fluids 2005. [Google Scholar] [CrossRef]
- Liu, W.; Xu, S.; Woda, C.; Kim, P.; Weinbaum, S.; Satlin, L.M. Effect of flow and stretch on the [ca2+]i response of principal and intercalated cells in cortical collecting duct. Am. J. Physiol. 2003, 285, F998–F1012. [Google Scholar]
- Ibrahim, S.M.; Patel, B.P.; Nath, Y. Modified shooting approach to the non-linear periodic forced response of isotropic/composite curved beams. Int. J. Nonlinear Mech. 2009, 44, 1073–1084. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lofgren, I.; Resnick, A. A Model for the Force Exerted on a Primary Cilium by an Optical Trap and the Resulting Deformation. Photonics 2015, 2, 604-618. https://doi.org/10.3390/photonics2020604
Lofgren I, Resnick A. A Model for the Force Exerted on a Primary Cilium by an Optical Trap and the Resulting Deformation. Photonics. 2015; 2(2):604-618. https://doi.org/10.3390/photonics2020604
Chicago/Turabian StyleLofgren, Ian, and Andrew Resnick. 2015. "A Model for the Force Exerted on a Primary Cilium by an Optical Trap and the Resulting Deformation" Photonics 2, no. 2: 604-618. https://doi.org/10.3390/photonics2020604