Chirality in Optical Trapping and Optical Binding
Abstract
:1. Introduction
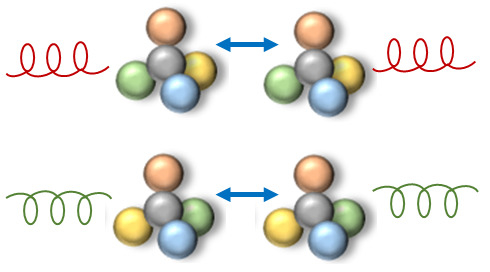
2. Chirality in Optical Trapping
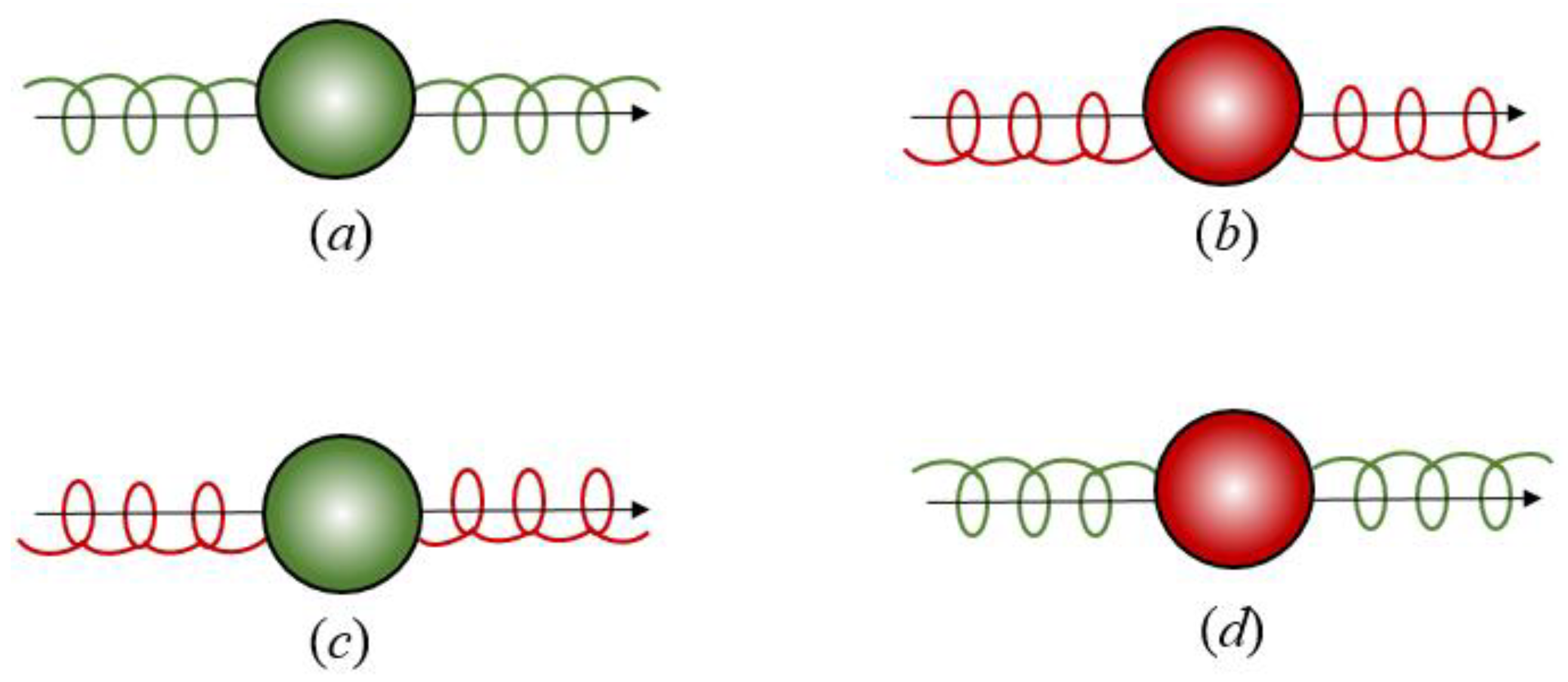
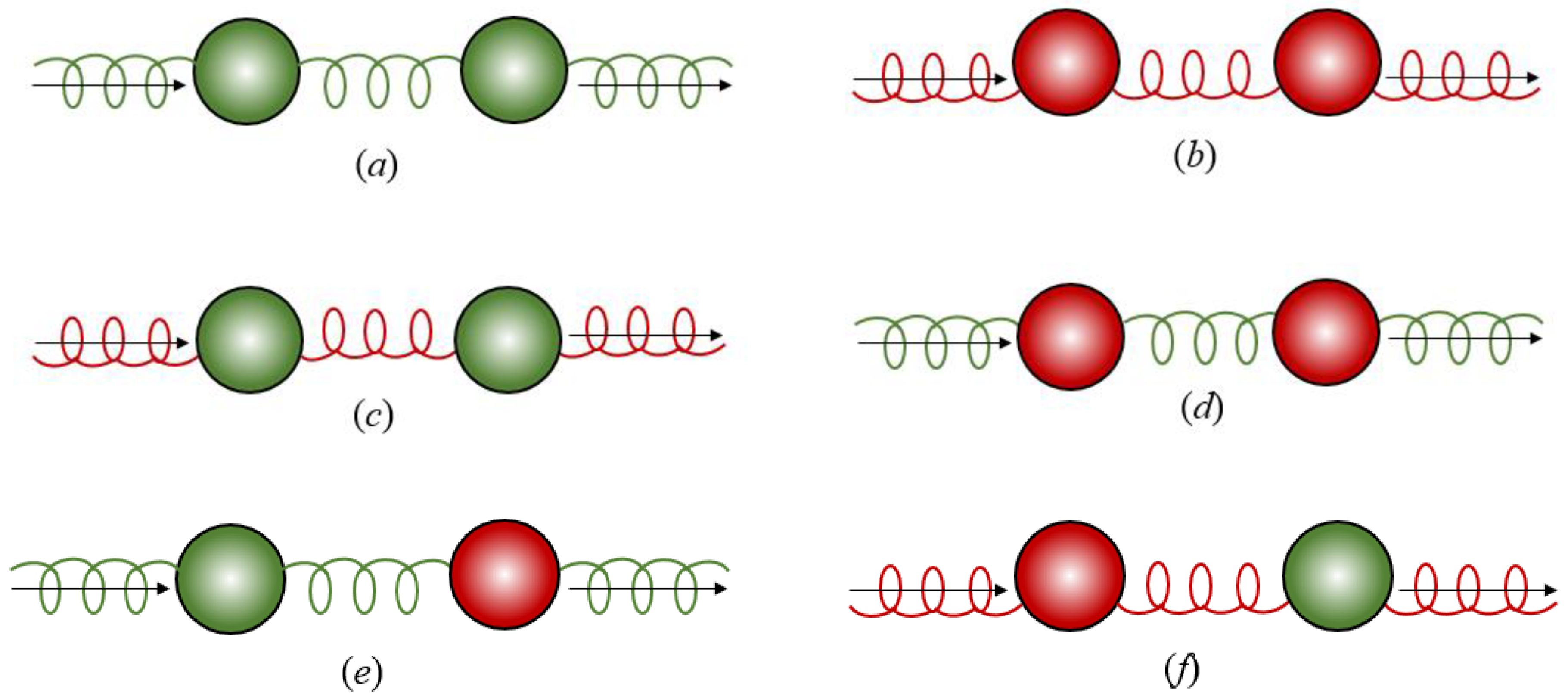
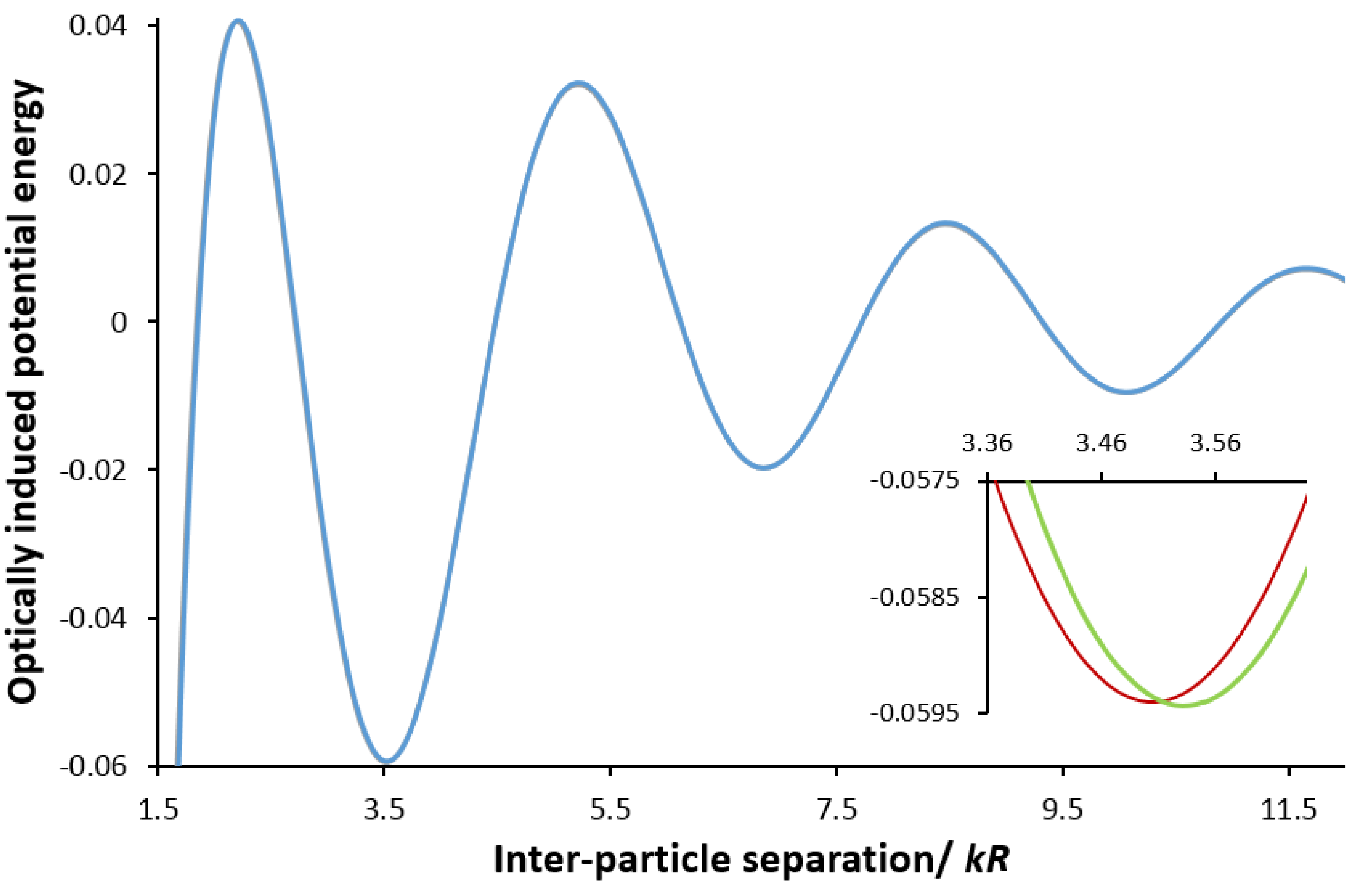
3. Chirality in Optical Binding
Acknowledgments
Conflict of Interest
References
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.; Bjorkholm, J.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, M. Multiple traps created with an inclined dual-fiber system. Opt. Express 2009, 17, 21680–21690. [Google Scholar] [CrossRef]
- Kotsifaki, D.G.; Makropoulou, M.; Serafetinides, A.A. Efficient and low cost multiple optical trap, based on interference. Optik 2013, 124, 617–621. [Google Scholar] [CrossRef]
- Ren, Y.-X.; Wu, J.-G.; Chen, M.; Li, H.; Li, Y.-M. Stability of novel time-sharing dual optical tweezers using a rotating tilt glass plate. Chinese. Phys. Lett. 2010, 27, 028703. [Google Scholar] [CrossRef]
- Dasgupta, R.; Verma, R.S.; Gupta, P.K. Microfluidic sorting with blinking optical traps. Opt. Lett. 2012, 37, 1739–1741. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.M.; Bowman, R.W.; Linnenberger, A.; Dienerowitz, M.; Phillips, D.B.; Carberry, D.M.; Miles, M.J.; Padgett, M.J. A compact holographic optical tweezers instrument. Rev. Sci. Instrum. 2012, 83, 113107. [Google Scholar] [CrossRef]
- Yevnin, M.; Kasimov, D.; Gluckman, Y.; Ebenstein, Y.; Roichman, Y. Independent and simultaneous three-dimensional optical trapping and imaging. Biomed. Opt. Express 2013, 4, 2087–2094. [Google Scholar] [CrossRef]
- Shaw, L.; Preece, D.; Rubinsztein-Dunlop, H. Kinect the dots: 3D control of optical tweezers. J. Opt. 2013, 15, 075303. [Google Scholar] [CrossRef]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Yan, Z.; Jureller, J.E.; Sweet, J.; Guffey, M.J.; Pelton, M.; Scherer, N.F. Three-dimensional optical trapping and manipulation of single silver nanowires. Nano Lett. 2012, 12, 5155–5161. [Google Scholar] [CrossRef]
- Decombe, J.-B.; Mondal, S.K.; Kumbhakar, D.; Pal, S.S.; Fick, J. Single and multiple microparticle trapping using non-Gaussian beams from optical fiber nanoantennas. IEEE J. Sel. Top. Quant. 2015, 21, 1–6. [Google Scholar] [CrossRef]
- Dawood, F.; Qin, S.; Li, L.; Lin, E.Y.; Fourkas, J.T. Simultaneous microscale optical manipulation, fabrication and immobilisation in aqueous media. Chem. Sci. 2012, 3, 2449–2456. [Google Scholar] [CrossRef]
- Ghadiri, R.; Weigel, T.; Esen, C.; Ostendorf, A. Microassembly of complex and three-dimensional microstructures using holographic optical tweezers. J. Micromech. Microeng. 2012, 22, 065016. [Google Scholar] [CrossRef]
- Palima, D.; Glückstad, J. Gearing up for optical microrobotics: micromanipulation and actuation of synthetic microstructures by optical forces. Laser Photon. Rev. 2013, 7, 478–494. [Google Scholar] [CrossRef]
- Phillips, D.B.; Grieve, J.A.; Olof, S.N.; Kocher, S.J.; Bowman, R.; Padgett, M.J.; Miles, M.J.; Carberry, D.M. Surface imaging using holographic optical tweezers. Nanotechnology 2011, 22, 285503. [Google Scholar] [CrossRef] [PubMed]
- Phillips, D.B.; Gibson, G.M.; Bowman, R.; Padgett, M.J.; Hanna, S.; Carberry, D.M.; Miles, M.J.; Simpson, S.H. An optically actuated surface scanning probe. Opt. Express 2012, 20, 29679–29693. [Google Scholar] [CrossRef]
- Ma, B.; Yao, B.; Peng, F.; Yan, S.; Lei, M.; Rupp, R. Optical sorting of particles by dual-channel line optical tweezers. J. Opt. 2012, 14, 105702. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Z.; Qu, S. Living cell manipulation in a microfluidic device by femtosecond optical tweezers. Opt. Laser Eng. 2014, 55, 150–154. [Google Scholar] [CrossRef]
- Capitanio, M.; Pavone, F.S. Interrogating biology with force: Single molecule high-resolution measurements with optical tweezers. Biophys. J. 2013, 105, 1293–1303. [Google Scholar] [CrossRef]
- Li, M.; Wang, M.D. Unzipping single DNA molecules to study nucleosome structure and dynamics. Methods Enzymol. 2012, 513, 29–58. [Google Scholar] [CrossRef]
- Monico, C.; Capitanio, M.; Belcastro, G.; Vanzi, F.; Pavone, F. Optical methods to study protein-DNA interactions in vitro and in living cells at the single-molecule level. Int. J. Mol. Sci. 2013, 14, 3961–3992. [Google Scholar] [CrossRef] [PubMed]
- Heller, I.; Hoekstra, T.P.; King, G.A.; Peterman, E.J.G.; Wuite, G.J.L. Optical tweezers analysis of DNA–protein complexes. Chem. Rev. 2014, 114, 3087–3119. [Google Scholar] [CrossRef]
- Chowdhury, S.; Thakur, A.; Svec, P.; Wang, C.; Losert, W.; Gupta, S. Automated manipulation of biological cells using gripper formations controlled by optical tweezers. IEEE T. Autom. Sci. Eng. 2014, 11, 338–347. [Google Scholar] [CrossRef]
- Jeorrett, A.H.; Neale, S.L.; Massoubre, D.; Gu, E.; Henderson, R.K.; Millington, O.; Mathieson, K.; Dawson, M.D. Optoelectronic tweezers system for single cell manipulation and fluorescence imaging of live immune cells. Opt. Express 2014, 22, 1372–1380. [Google Scholar] [CrossRef]
- Smith, D.E. Single-molecule studies of viral DNA packaging. Curr. Opin. Virol. 2011, 1, 134–141. [Google Scholar] [CrossRef]
- Pang, Y.; Song, H.; Kim, J.H.; Hou, X.; Cheng, W. Optical trapping of individual human immunodeficiency viruses in culture fluid reveals heterogeneity with single-molecule resolution. Nat. Nanotechnol. 2014, 9, 624–630. [Google Scholar] [CrossRef]
- Veigel, C.; Schmidt, C.F. Moving into the cell: single-molecule studies of molecular motors in complex environments. Nat. Rev. Mol. Cell Biol. 2011, 12, 163–176. [Google Scholar] [CrossRef]
- Bentley, R. Chirality in Biology. In Encyclopedia of Molecular Cell Biology and Molecular Medicine; Meyers, R.A., Ed.; Wiley-VCH: Weinheim, Germany, 2006; pp. 579–618. [Google Scholar]
- Barron, L.D. Chirality and life. Space Sci. Rev. 2008, 135, 187–201. [Google Scholar] [CrossRef]
- Mori, K. Bioactive natural products and chirality. Chirality 2011, 23, 449–462. [Google Scholar] [CrossRef]
- Cintas, P.; Amabilino, D.B. Biochirality: Origins, Evolution and Molecular Recognition; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Timsit, Y. DNA self-assembly: From chirality to evolution. Int. J. Mol. Sci. 2013, 14, 8252–8270. [Google Scholar] [CrossRef] [PubMed]
- Senge, M.; Ryan, A.; Letchford, K.; MacGowan, S.; Mielke, T. Chlorophylls, symmetry, chirality, and photosynthesis. Symmetry 2014, 6, 781–843. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, J.; Koschny, T.; Kafesaki, M.; Soukoulis, C.M. Chiral metamaterials: simulations and experiments. J. Opt. A: Pure Appl. Opt. 2009, 11, 114003. [Google Scholar] [CrossRef]
- Valev, V.K.; Baumberg, J.J.; Sibilia, C.; Verbiest, T. Chirality and chiroptical effects in plasmonic nanostructures: fundamentals, recent progress, and outlook. Adv. Mater. 2013, 25, 2517–2534. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Mutlu, M.; Ozbay, E. Chiral metamaterials: from optical activity and negative refractive index to asymmetric transmission. J. Opt. 2013, 15, 023001. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Wang, Y.; Chen, H. Emerging chirality in nanoscience. Chem. Soc. Rev. 2013, 42, 2930–2962. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Leeder, J.M.; Coles, M.M.; Andrews, D.L. Signatures of material and optical chirality: Origins and measures. Chem. Phys. Lett. 2015, 626, 106–110. [Google Scholar] [CrossRef]
- Bendix, P.M.; Jauffred, L.; Norregaard, K.; Oddershede, L.B. Optical trapping of nanoparticles and quantum dots. IEEE J. Sel. Top. Quant. 2014, 20, 15–26. [Google Scholar] [CrossRef]
- Tinguely, J.-C.; Ding, M.; Brambilla, G.; Hohenau, A.; Krenn, J.R.; Hellesø, O.G. Nanostructured fibre tip for trapping of nanoparticles. Proc. SPIE 2014, 8999, 89991D. [Google Scholar] [CrossRef]
- Gelfand, R.M.; Wheaton, S.; Gordon, R. Cleaved fiber optic double nanohole optical tweezers for trapping nanoparticles. Opt. Lett. 2014, 39, 6415–6417. [Google Scholar] [CrossRef]
- Thirunamachandran, T. Intermolecular interactions in the presence of an intense radiation field. Mol. Phys. 1980, 40, 393–399. [Google Scholar] [CrossRef]
- Burns, M.M.; Fournier, J.-M.; Golovchenko, J.A. Optical binding. Phys. Rev. Lett. 1989, 63, 1233–1236. [Google Scholar] [CrossRef] [PubMed]
- Tatarkova, S.A.; Carruthers, A.E.; Dholakia, K. One-dimensional optically bound arrays of microscopic particles. Phys. Rev. Lett. 2002, 89, 283901. [Google Scholar] [CrossRef] [PubMed]
- Singer, W.; Frick, M.; Bernet, S.; Ritsch-Marte, M. Self-organized array of regularly spaced microbeads in a fiber-optical trap. J. Opt. Soc. Am. B 2003, 20, 1568–1574. [Google Scholar] [CrossRef]
- Karásek, V.; Čižmár, T.; Brzobohatý, O.; Zemánek, P.; Garcés-Chávez, V.; Dholakia, K. Long-range one-dimensional longitudinal optical binding. Phys. Rev. Lett. 2008, 101, 143601. [Google Scholar] [CrossRef] [PubMed]
- Gherardi, D.M.; Carruthers, A.E.; Čižmár, T.; Wright, E.M.; Dholakia, K. A dual beam photonic crystal fiber trap for microscopic particles. Appl. Phys. Lett. 2008, 93, 041110. [Google Scholar] [CrossRef]
- Brzobohatý, O.; Čižmár, T.; Karásek, V.; Šiler, M.; Dholakia, K.; Zemánek, P. Experimental and theoretical determination of optical binding forces. Opt. Express 2010, 18, 25389–25402. [Google Scholar] [CrossRef] [PubMed]
- Demergis, V.; Florin, E.-L. Ultrastrong optical binding of metallic nanoparticles. Nano Lett. 2012, 12, 5756–5760. [Google Scholar] [CrossRef]
- Yan, Z.; Gray, S.K.; Scherer, N.F. Potential energy surfaces and reaction pathways for light-mediated self-organization of metal nanoparticle clusters. Nat. Commun. 2014, 5, 3751. [Google Scholar] [CrossRef] [PubMed]
- Čižmár, T.; Dávila Romero, L.C.; Dholakia, K.; Andrews, D.L. Multiple optical trapping and binding: New routes to self-assembly. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 102001. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Optically induced forces and torques: Interactions between nanoparticles in a laser beam. Phys. Rev. A 2005, 72, 033816. [Google Scholar] [CrossRef]
- Rodríguez, J.; Dávila Romero, L.C.; Andrews, D.L. Optical binding in nanoparticle assembly: Potential energy landscapes. Phys. Rev. A 2008, 78, 043805. [Google Scholar] [CrossRef]
- Dávila Romero, L.C.; Andrews, D.L. A retarded coupling approach to intermolecular interactions. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 085403. [Google Scholar] [CrossRef]
- Hernandez, R.J.; Mazzulla, A.; Pane, A.; Volke-Sepulveda, K.; Cipparrone, G. Attractive-repulsive dynamics on light-responsive chiral microparticles induced by polarized tweezers. Lab Chip 2013, 13, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Donato, M.G.; Hernandez, J.; Mazzulla, A.; Provenzano, C.; Saija, R.; Sayed, R.; Vasi, S.; Magazzù, A.; Pagliusi, P.; Bartolino, R.; et al. Polarization-dependent optomechanics mediated by chiral microresonators. Nat. Commun. 2014, 5, 3656. [Google Scholar] [CrossRef] [PubMed]
- Tkachenko, G.; Brasselet, E. Helicity-dependent three-dimensional optical trapping of chiral microparticles. Nat. Commun. 2014, 5, 4491. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, D.E.; Silveirinha, M.G. Optical tractor beam with chiral light. 2015. [Google Scholar]
- Dienerowitz, M.; Mazilu, M.; Dholakia, K. Optical manipulation of nanoparticles: A review. J. Nanophoton. 2008, 2, 021875. [Google Scholar] [CrossRef]
- Marago, O.M.; Jones, P.H.; Gucciardi, P.G.; Volpe, G.; Ferrari, A.C. Optical trapping and manipulation of nanostructures. Nat. Nanotechnol. 2013, 8, 807–819. [Google Scholar] [CrossRef] [Green Version]
- Bowman, R.W.; Padgett, M.J. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef]
- Barron, L.D. Molecular Light Scattering and Optical Activity, 1st ed.; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Bradshaw, D.S.; Andrews, D.L. Interparticle interactions: Energy potentials, energy transfer, and nanoscale mechanical motion in response to optical radiation. J. Phys. Chem. A 2013, 117, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V.V.; Letokhov, V.S. Gradient optical force on atoms: beyond dipole approximation. Opt. Commun. 1996, 126, 45–48. [Google Scholar] [CrossRef]
- Gübitz, G.; Schmid, M.G. Chiral separation principles in chromatographic and electromigration techniques. Mol. Biotechnol. 2006, 32, 159–179. [Google Scholar] [CrossRef]
- Subramanian, G. Chiral Separation Techniques: A Practical Approach; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Ward, T.J.; Baker, B.A. Chiral separations. Anal. Chem. 2008, 80, 4363–4372. [Google Scholar] [CrossRef] [PubMed]
- Ahuja, S. Chiral Separation Methods for Pharmaceutical and Biotechnological Products; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Marcos, F.H.C.; Powers, T.R.; Stocker, R. Separation of microscale chiral objects by shear flow. Phys. Rev. Lett. 2009, 102, 158103. [Google Scholar] [CrossRef] [PubMed]
- Eichhorn, R. Microfluidic sorting of stereoisomers. Phys. Rev. Lett. 2010, 105, 034502. [Google Scholar] [CrossRef] [PubMed]
- Bogunovic, L.; Fliedner, M.; Eichhorn, R.; Wegener, S.; Regtmeier, J.; Anselmetti, D.; Reimann, P. Chiral particle separation by a nonchiral microlattice. Phys. Rev. Lett. 2012, 109, 100603. [Google Scholar] [CrossRef] [PubMed]
- Meinhardt, S.; Smiatek, J.; Eichhorn, R.; Schmid, F. Separation of chiral particles in micro- or nanofluidic channels. Phys. Rev. Lett. 2012, 108, 214504. [Google Scholar] [CrossRef] [PubMed]
- Aristov, M.; Eichhorn, R.; Bechinger, C. Separation of chiral colloidal particles in a helical flow field. Soft Matter 2013, 9, 2525–2530. [Google Scholar] [CrossRef] [PubMed]
- Baranova, N.; Zel'Dovich, B.Y. Separation of mirror isomeric molecules by radio-frequency electric field of rotating polarization. Chem. Phys. Lett. 1978, 57, 435–437. [Google Scholar] [CrossRef]
- Schamel, D.; Pfeifer, M.; Gibbs, J.G.; Miksch, B.; Mark, A.G.; Fischer, P. Chiral colloidal molecules and observation of the propeller effect. J. Am. Chem. Soc. 2013, 135, 12353–12359. [Google Scholar] [CrossRef] [PubMed]
- Tkachenko, G.; Brasselet, E. Spin controlled optical radiation pressure. Phys. Rev. Lett. 2013, 111, 033605. [Google Scholar] [CrossRef] [PubMed]
- Tkachenko, G.; Brasselet, E. Optofluidic sorting of material chirality by chiral light. Nat. Commun. 2014, 5, 3577. [Google Scholar] [CrossRef] [PubMed]
- Faryad, M.; Lakhtakia, A. The circular Bragg phenomenon. Adv. Opt. Photon. 2014, 6, 225–292. [Google Scholar] [CrossRef]
- Patterson, D.; Doyle, J.M. Sensitive chiral analysis via microwave three-wave mixing. Phys. Rev. Lett. 2013, 111, 023008. [Google Scholar] [CrossRef] [PubMed]
- Patterson, D.; Schnell, M.; Doyle, J.M. Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature 2013, 497, 475–477. [Google Scholar] [CrossRef]
- Patterson, D.; Schnell, M. New studies on molecular chirality in the gas phase: enantiomer differentiation and determination of enantiomeric excess. Phys. Chem. Chem. Phys. 2014, 16, 11114–11123. [Google Scholar] [CrossRef]
- Shubert, V.A.; Schmitz, D.; Patterson, D.; Doyle, J.M.; Schnell, M. Identifying enantiomers in mixtures of chiral molecules with broadband microwave spectroscopy. Angew. Chem. Int. Ed. 2014, 53, 1152–1155. [Google Scholar] [CrossRef]
- Butcher, D.T.; Buhmann, S.Y.; Scheel, S. Casimir–Polder forces between chiral objects. New J. Phys. 2012, 14, 113013. [Google Scholar] [CrossRef]
- Shang, Q.-C.; Wu, Z.-S.; Qu, T.; Li, Z.-J.; Bai, L.; Gong, L. Analysis of the radiation force and torque exerted on a chiral sphere by a Gaussian beam. Opt. Express 2013, 21, 8677–8688. [Google Scholar] [CrossRef] [PubMed]
- Ding, K.; Ng, J.; Zhou, L.; Chan, C.T. Realization of optical pulling forces using chirality. Phys. Rev. A 2014, 89, 063825. [Google Scholar] [CrossRef]
- Wang, S.B.; Chan, C.T. Lateral optical force on chiral particles near a surface. Nat. Commun. 2014, 5, 3307. [Google Scholar] [CrossRef] [PubMed]
- Salam, A.; Meath, W.J. On the control of excited state relative populations of enantiomers using circularly polarized pulses of varying durations. J. Chem. Phys. 1997, 106, 7865–7868. [Google Scholar] [CrossRef]
- Salam, A.; Meath, W.J. On enantiomeric excesses obtained from racemic mixtures by using circularly polarized pulsed lasers of varying durations. Chem. Phys. 1998, 228, 115–129. [Google Scholar] [CrossRef]
- González, L.; Hoki, K.; Kröner, D.; Leal, A.S.; Manz, J.; Ohtsuki, Y. Selective preparation of enantiomers by laser pulses: From optimal control to specific pump and dump transitions. J. Chem. Phys. 2000, 113, 11134–11142. [Google Scholar] [CrossRef]
- González, L.; Kröner, D.; Solá, I.R. Separation of enantiomers by ultraviolet laser pulses in H2POSH: π pulses versus adiabatic transitions. J. Chem. Phys. 2001, 115, 2519–2529. [Google Scholar] [CrossRef]
- Hoki, K.; González, L.; Fujimura, Y. Control of molecular handedness using pump-dump laser pulses. J. Chem. Phys. 2002, 116, 2433–2438. [Google Scholar] [CrossRef]
- Král, P.; Thanopulos, I.; Shapiro, M.; Cohen, D. Two-step enantio-selective optical switch. Phys. Rev. Lett. 2003, 90, 033001. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Salam, A. On chiral selectivity of enantiomers using a circularly polarized pulsed laser under resonant and off-resonant conditions. Chem. Phys. 2006, 324, 367–375. [Google Scholar] [CrossRef]
- Li, Y.; Bruder, C.; Sun, C.P. Generalized Stern-Gerlach effect for chiral molecules. Phys. Rev. Lett. 2007, 99, 130403. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.Z.; Wei, L.F. Distinguishing left- and right-handed molecules using two-step coherent pulses. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 185402. [Google Scholar] [CrossRef]
- Li, X.; Shapiro, M. Spatial separation of enantiomers by coherent optical means. J. Chem. Phys. 2010, 132, 041101. [Google Scholar] [CrossRef]
- Li, X.; Shapiro, M. Theory of the optical spatial separation of racemic mixtures of chiral molecules. J. Chem. Phys. 2010, 132, 194315. [Google Scholar] [CrossRef]
- Eilam, A.; Shapiro, M. Spatial separation of dimers of chiral molecules. Phys. Rev. Lett. 2013, 110, 213004. [Google Scholar] [CrossRef] [PubMed]
- Canaguier-Durand, A.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Mechanical separation of chiral dipoles by chiral light. New J. Phys. 2013, 15, 123037. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Chiral discrimination in optical trapping and manipulation. New J. Phys. 2014, 16, 103021. [Google Scholar] [CrossRef]
- Cameron, R.P.; Barnett, S.M.; Yao, A.M. Discriminatory optical force for chiral molecules. New J. Phys. 2014, 16, 013020. [Google Scholar] [CrossRef]
- Cameron, R.P.; Yao, A.M.; Barnett, S.M. Diffraction gratings for chiral molecules and their applications. J. Phys. Chem. A 2014, 118, 3472–3478. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Laser optical separation of chiral molecules. Opt. Lett. 2015, 40, 677–680. [Google Scholar] [CrossRef]
- Bradshaw, D.S.; Andrews, D.L. Electromagnetic trapping of chiral molecules: Orientational effects of the irradiating beam. J. Opt. Soc. Am. B 2015, 32, B25–B31. [Google Scholar] [CrossRef]
- Salam, A. On the effect of a radiation field in modifying the intermolecular interaction between two chiral molecules. J. Chem. Phys. 2006, 124, 014302. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Chiral discrimination in optical binding. Phys. Rev. A 2015, in press. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light, 3rd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Kostur, M.; Schindler, M.; Talkner, P.; Hänggi, P. Chiral separation in microflows. Phys. Rev. Lett. 2006, 96, 014502. [Google Scholar] [CrossRef]
- Eichhorn, R. Enantioseparation in microfluidic channels. Chem. Phys. 2010, 375, 568–577. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradshaw, D.S.; Forbes, K.A.; Leeder, J.M.; Andrews, D.L. Chirality in Optical Trapping and Optical Binding. Photonics 2015, 2, 483-497. https://doi.org/10.3390/photonics2020483
Bradshaw DS, Forbes KA, Leeder JM, Andrews DL. Chirality in Optical Trapping and Optical Binding. Photonics. 2015; 2(2):483-497. https://doi.org/10.3390/photonics2020483
Chicago/Turabian StyleBradshaw, David S., Kayn A. Forbes, Jamie M. Leeder, and David L. Andrews. 2015. "Chirality in Optical Trapping and Optical Binding" Photonics 2, no. 2: 483-497. https://doi.org/10.3390/photonics2020483
APA StyleBradshaw, D. S., Forbes, K. A., Leeder, J. M., & Andrews, D. L. (2015). Chirality in Optical Trapping and Optical Binding. Photonics, 2(2), 483-497. https://doi.org/10.3390/photonics2020483