Objectivisation In Simplified Quantum Brownian Motion Models

Abstract

The birth of objective properties from the subjective quantum world has been one of the key questions in the quantum-to-classical transition. Based on recent results in the field, we study it in a quantum mechanical model of a boson-boson interaction—quantum Brownian motion. Using various simplifications, we prove a formation for thermal environments of, so called, spectrum broadcast structures, responsible for perceived objectivity. In the quantum measurement limit we prove that this structure is always formed, providing the characteristic timescales. Including self-Hamiltonians of the environment, we show the exponential scaling of the effect with the size of the environment. Finally, in the full model we numerically study the influence of squeezing in the initial state of the environment, showing broader regions of formation than for non-squeezed thermal states.

1. Introduction

Quantum measurement inevitably disturbs a state of a measured system, unless very special conditions are met [1]. This is in stark contrast with the classical physics we are used to, where a state of the system is believed to exist objectively, independently of the observation. A pioneering attempt to resolve this situation has been initiated by Zurek and collaborators through the quantum Darwinism program (see, e.g., [2] and the references therein), which is an advance form of the theory decoherence (see, e.g., [3]). In essence, it relies on two fundamental observations. First, in usual situations a quantum system S interacts with multiple environments $E_1,\cdots ,E_N$ and the information about the system is learned not directly but through an observation of some portion, which we call $fE$, of those environments. Hence, studying information content, deposited through decoherence in the portions of environment is of key importance. Second, what lies at the heart of objectivity is information redundancy: If the same information about the system (or more precisely about its state) is present in many fractions of the environment and can be accessed by independent observers without disturbing the system, it appears to be objective [2]. This information redundancy has been studied in several emblematic models of decoherence, e.g., in quantum Brownian motion [4], in spin-$1/2$ systems [5], and for a small dielectric sphere illuminated by photons [6], suggesting that the objectivisation of certain properties indeed takes place in those models.

However, this approach is based on a certain scalar criterion for objectivity, probing the scaling of the quantum mutual information between the system and the observed environment fraction with the size of this fraction [2]. Although very suggestive, the sufficiency of this criterion remains open, as pointed out in [7], where a deeper structural analysis has been developed, based on the most fundamental description of a quantum system—its state (see also [8], strengthening some aspects of [7]). In brief, using an operational definition of objectivity from [2] and, surprisingly, the Bohr non-disturbance condition [9] it has been shown in an abstract, model- and dynamics-independent setting that the necessary and sufficient condition for appearance of an objective state of the system is formation of a, so called, spectrum broadcast structure [7]:

$${\varrho }_{S:fE}=\sum _i{p}_i|{\xi }_i\rangle \langle {\xi }_i|\otimes {\varrho }_i^{E_1}\otimes \cdots \otimes {\varrho }_i^{E_{fN}},{\varrho }_i^{E_k}{\varrho }_{i^{\prime }\ne i}^{E_k}=0$$

(1)

where $fE$ denotes the observed fraction of the environment E, $\{|{\xi }_i\rangle \}$ is a pointer basis, $p_i=\langle {\xi }_i|{\varrho }_{0S}|{\xi }_i\rangle$ initial pointer probabilities, and ${\varrho }_i^{E_1},\cdots ,{\varrho }_i^{E_{fN}}$ some states of the observed environments $E_1,\cdots ,E_{fN}$ with mutually orthogonal supports. The process of formation of this structure is called state information broadcasting and is similar to quantum state broadcasting [10]. However, only a part of the initial state ${\varrho }_{0S}$ is broadcasted—the probabilities $p_i=\langle {\xi }_i|{\varrho }_{0S}|{\xi }_i\rangle$. The name comes from the fact that all the reduced states of the environments have the same spectrum $\left\{p_i\right\}$ as the decohered state of the system and such structures first appeared in a different context in [11]. As seen from Equation (1), if a spectrum brodcast structure has been formed, the observers trying to determine the state of the system from the environment will all get the same results i with the same probabilities $p_i$, due to the non-overlapping supports of the environmental states, and the state of the system will stay unchanged. This leads to the objectivisation of the states $|{\xi }_i\rangle$. Formally, state information broadcasting can be described as a quantum channel:

$${\Lambda }^{S\to fE}\left({\varrho }_{0S}\right)=\sum _i\langle {\xi }_i|{\varrho }_{S0}|{\xi }_i\rangle {\varrho }_i^{E_1}\otimes \cdots \otimes {\varrho }_i^{E_{fN}}$$

(2)

Formation of such structures has been recently theoretically confirmed for the mentioned models of decoherence: the illuminated sphere model [12], spin-$1/2$ systems [13], and in quantum Brownian motion [14] (see e.g., [3,15] for an introduction to the model). The last study, although introduced a novel concept of a dynamical objectivisation with time evolving structure Equation (1), relied in its final stage on the numerics, due to a complicated nature of appearing expressions. In the present work, we further analyze quantum Brownian motion model and, at an expense of various simplifications, we obtain analytical estimates on the speed of formation of the spectrum broadcast structure as a function of time and the size of the environment. Moreover, in the full model we numerically study the effect of squeezing in the initial state of the environment.

2. Results

2.1. The General Mechanism

We illustrate our method, first developed in [7,12], on a general interaction Hamiltonian of the von Neumann measurement type [1]:

$$\widehat{H}=\widehat{A}\otimes \sum _{k=1}^N{\widehat{B}}_k,$$

(3)

where $\widehat{A}$, ${\widehat{B}}_k$ are some observables of the system and the k-th environment respectively, assumed for simplicity to have discrete spectra (for a treatment of observables with continuous spectra see [14]) and we have neglected the self-Hamiltonians of the system and the environments. We assume that the strengths of each interaction in Equation (3) are vanishingly small (one can imagine adding small coupling constants $g_k$ there; we however do not do it for simplicity’s sake). Diagonalizing $\widehat{A}$, leads to the time evolution of a controlled unitary type, with the system controlling the environment:

$$\widehat{U}\left(t\right)=\sum _a|a\rangle \langle a|\otimes \underset{k=1}{\overset{N}{⨂}}{e}^{-iat{\widehat{B}}_k}$$

(4)

The basic object of our study [7,12,14] is the post-interaction state ${\varrho }_{S:fE}\left(t\right)$ of the system S and the observed fraction of the environment $fE$ (of the size $fN$, $0<f<1$), obtained with the above $\widehat{U}\left(t\right)$. The observed fraction is not the whole environment as some losses are necessary for the decoherence (as it happens in realistic situations). We obtain:

$${\varrho }_{S:fE}\left(t\right)=t{r}_{(1-f)E}\left[\widehat{U}\left(t\right){\varrho }_{0S}\otimes \underset{k=1}{\overset{N}{⨂}}{\varrho }_{0k}\widehat{U}{\left(t\right)}^{†}\right]$$

$$=\sum _a\langle a|{\varrho }_{0S}|a\rangle |a\rangle \langle a|\otimes \underset{k=1}{\overset{fN}{⨂}}{e}^{-iat{\widehat{B}}_k}{\varrho }_{0k}{e}^{iat{\widehat{B}}_k}$$

(5)

$$+\sum _{a\ne a^{\prime }}{\Gamma }_{a,a^{\prime }}\left(t\right)\langle a|{\varrho }_{0S}|a^{\prime }\rangle |a\rangle \langle a^{\prime }|\otimes \underset{k=1}{\overset{fN}{⨂}}{e}^{-iat{\widehat{B}}_k}{\varrho }_{0k}{e}^{i{a}^{\prime }t{\widehat{B}}_k}$$

(6)

where:

$${\Gamma }_{a,a^{\prime }}\left(t\right)=\prod _{k\in (1-f)E}tr\left[e^{-iat{\widehat{B}}_k}{\varrho }_{0k}{e}^{i{a}^{\prime }t{\widehat{B}}_k}\right]$$

(7)

is the usual decoherence factor between the states $|a\rangle$, $|a^{\prime }\rangle$ and $(1-f)E$ denotes the lost (unobserved) fraction of the environment. We then check for the spectrum broadcast structure Equation (1) formation in two steps.

First, we take care of the vanishing of the off-diagonal part Equation (6), which is the well known decoherence process. Vanishing of Equation (6) in the trace norm is fully controlled (assuming of course coherences between different as in the system’s initial state${\varrho }_{0S}$) by the modulus $|{\Gamma }_{a,a^{\prime }}\left(t\right)|$, so it is enough to check if $|{\Gamma }_{a,a^{\prime }}\left(t\right)|\approx 0$ with time. Note that decoherence is a result of the losses and therefore decoherence factor depends only on the unobserved fraction of the environment. The basis $\{|a\rangle \}$ becomes then the pointer basis, which as we pointed out earlier [12] is arguably put by hand to some extent. Developing a framework where this basis appears truly dynamically would be a very interesting task (if at all possible).

Second, we check if the post-interaction states of the environments ${\varrho }_{ka}\left(t\right)=e^{-iat{\widehat{B}}_k}{\varrho }_{0k}{e}^{iat{\widehat{B}}_k}$ have non-overlapping suports ${\varrho }_a\left(t\right){\varrho }_{a^{\prime }}\left(t\right)\approx 0$. This is equivalent to their perfect one-shot distinguishability through projective measurements on their supports. However, due to the assumed weak interaction Equation (3) one cannot expect that for states of the individual environments. In fact, for a vanishingly weak interaction, the states ${\varrho }_{ka}\left(t\right)$ are almost identical for different a and hence carry a vanishingly small amount of information about the system (the index a of an eigenstate of the observable $\widehat{A}$ in this case). Thus, we perform an environment coarse-graining and divide the observed fraction of the environment $fE$ in Equation (5) into $\mathcal{M}$ fractions (assumed equal for simplicity) of a size $fN/\mathcal{M}=mN$. This grouping into macrofractions can be also seen as representing detection thresholds of real-life detectors. Since at some point we are interested in a thermodynamic-type of a limit $N\to \infty$ it is important that those fractions scale with N (hence the name "macrofractions"). Due to no direct interactions between different parts of the environment (cf. Equation (3)), post-interaction states of each macrofraction are simply products ${\varrho }_a^{mac}\left(t\right)={⨂}_{k\in mac}{\varrho }_a\left(t\right)$. We assume that a single macrofraction is a minimal portion of the environment providing the observers with information about the central system and therefore it is enough to consider the distinguishability at the level of a single macrofraction. We use the generalized overlap [16], $B({\varrho }_1,{\varrho }_2)=tr\sqrt{\sqrt{{\varrho }_1}{\varrho }_2\sqrt{{\varrho }_1}}$, as the most convenient measure due to its scaling with the tensor product:

$$B_{a,a^{\prime }}^{mac}\left(t\right)=B\left({\varrho }_a^{mac}\left(t\right),{\varrho }_{a^{\prime }}^{mac}\left(t\right)\right)=\prod _{k\in mac}B\left({\varrho }_{ka}\left(t\right),{\varrho }_{k{a}^{\prime }}\left(t\right)\right)$$

(8)

Vanishing of $B_{a,a^{\prime }}^{mac}\left(t\right)$ is equivalent to ${\varrho }_a^{mac}\left(t\right)$, ${\varrho }_{a^{\prime }}^{mac}\left(t\right)$ being perfectly distinguishable [16].

Thus, if one is able to prove that for some initial states ${\varrho }_{0k}$ (and other possible parameters of the model) both:

$$|{\Gamma }_{a,a^{\prime }}\left(t\right)|\approx 0,B_{a,a^{\prime }}^{mac}\left(t\right)\approx 0$$

(9)

then this is equivalent to a formation of the spectrum broadcast structure Equation (1):

$${\varrho }_{S:fE}\approx \sum _a{p}_a|a\rangle \langle a|\otimes {\varrho }_a^{ma{c}_1}\otimes \cdots \otimes {\varrho }_a^{ma{c}_{\mathcal{M}}},{\varrho }_a^{ma{c}_j}{\varrho }_{a^{\prime }\ne a}^{ma{c}_j}\approx 0$$

(10)

and the convergence is in the trace norm. By [7] this, in turn, means that the states $|a\rangle$ of the decohered system become objective as the information about the index a has been redundantly copied and stored in the environment and is accessible without disturbing the system through projective measurements on the supports of ${\varrho }_a^{mac}$.

2.2. Model of Quantum Brownian Motion

We begin with briefly describing the model [3,15] and the results of [14]. The central system S is modeled as a harmonic oscillator of a mass M and a frequency Ω, linearly coupled to a bath of oscillators:

$$\widehat{H}=\frac{{\widehat{P}}^2}{2M}+\frac{M{\Omega }^2{\widehat{X}}^2}{2}+\sum _{k=1}^N\left(\frac{{\widehat{p}}_k^2}{2m_k}+\frac{m_k{\omega }_k^2{\widehat{x}}_k^2}{2}\right)+\widehat{X}\otimes \sum _{k=1}^N{C}_k{\widehat{x}}_k$$

(11)

where we assume the units in which $\hslash =1$, ${\widehat{x}}_k,{\widehat{p}}_k$ describe the k-th environmental oscillator and $C_k$ are the coupling constants. The central assumption is that the system is very massive compared to the environments: $M\gg m_k$ for every k. The formation of the broadcast state is measured by two scalar functions: the well known decoherence factor, associated with a loss of some of the environments and a generalized overlap [16], measuring distinguishability of macroscopic states of the observed environments. The whole system is initialized in a product state ${\varrho }_{0S}\otimes {⨂}_k{\varrho }_{0k}$, where about the central systems’ initial state ${\varrho }_{0S}$ we only assume that it has coherences in the position X. Apart from the last subsection, the environments are assumed to be in a thermal state with the same temperature T. The noise in the environment is a highly non-trivial factor, compared to pure initial states (as in e.g., [4]), both conceptually, as the noise can prevent accumulation of information in the environment although decoherence has taken place, and technically [12,14]. We are interested in collective effects, where a single environment couples very weakly to the system. Otherwise, it could "learn" enough about the system to decohere it—a situation trivial from a point of view of studying information flow into different parts of the environment. In QBM this means that the environmental oscillators are off-resonance:

$${\omega }_k\ll \Omega \text{or}{\omega }_k\gg \Omega \text{for}\text{all}k$$

(12)

Because a single environment acquires vanishingly small amount of information in the course of the interaction, we have proposed [12] to group the observed environments into fractions, scaling with the total number of the environments N, so called macrofractions. This is at the level of such coarse-grained environment where one can expect an appearance of a spectrum broadcast structure. This method is analogous to e.g., description of liquids: each point of a liquid (a macro-fraction here) is in reality composed of a suitable large number of microparticles (individual environments). Same technique is also used in a mathematical approach to von Neumann measurements using, so called, macroscopic observables (see, e.g., [17] and the references therein).

Another characteristic feature of our method [14] is that instead of introducing the usual continuum approximation of the environments, characterized by a continuous spectral density function [3,15], we work with a discrete bath of oscillators with random frequencies ${\omega }_k$ (this method is adapted from the spin systems [18]). Under such conditions, we have obtained analytical expressions for the decoherence and distinguishability factors, denoted ${\Gamma }_{X,X^{\prime }}\left(t\right)$ and $B_{X,X^{\prime }}^{mac}\left(t\right)$ respectively, between two different initial positions $X,X^{\prime }$ (or in fact states of motion in a certain sense) of the central system [14]:

$$\left|{\Gamma }_{X,X^{\prime }}\left(t\right)\right|=exp\left[-\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in (1-f)E}{|{\alpha }_k\left(t\right)|}^2\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)\right]$$

(13)

$$B_{X,X^{\prime }}^{mac}\left(t\right)=exp\left[-\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in mac}{|{\alpha }_k\left(t\right)|}^2\text{th}\left(\frac{\beta {\omega }_k}{2}\right)\right]$$

(14)

$${|{\alpha }_k\left(t\right)|}^2=\frac{C_k^2{\omega }_k}{2m_k{({\omega }_k^2-{\Omega }^2)}^2}\left[{\left(cos{\omega }_{k}t-cos\Omega t\right)}^2+{\left(sin{\omega }_{k}t-\frac{\Omega }{{\omega }_k}sin\Omega t\right)}^2\right]$$

(15)

where $(1-f)E$ is the unobserved (traced out) fraction of the environment, $mac$ denotes one of the observed macrofractions, and $\beta =1/k_{B}T$ is the inverse temperature. Due to the random character of ${\omega }_k$, these are complicated almost periodic functions of time. Numerical analysis in [14], assuming independently, identically distributed (i.i.d.) ${\omega }_k$s with a uniform distribution over a spectrum interval far from the resonance, shows that if the macrofraction sizes are large enough for a given temperature, the broadcast structure is formed, certified by vanishing of both of the above functions. These results are in accord with the earlier results of [4], which suggested there is indeed some objectivisation in the model, in the sense that we confirm the objectivisation but using a very different, more fundamental approach [7], based directly on quantum states and for a much wider and more realistic class of the environment initial states—thermal states. Below, using various simplifications, we further study formation of the structure Equation (1) analytically as well as the effect of squeezing in the initial thermal state.

2.3. Full Quantum Measurement Limit And Exact Timescales

We first consider a highly simplified model, with dominating interaction term and completely neglecting self-Hamiltonians of both the system and the environment:

$$\widehat{H}\approx \widehat{X}\otimes \sum _{k=1}^N{C}_k{\widehat{x}}_k$$

(16)

This is called Quantum Measurement Limit due to the fact that the Hamiltonian represents an ideal von Neumann measurement of the system observable $\widehat{X}$ by the environments [1]. Such a simplified model will allow us to obtain the character and the timescales of the broadcast structure formation. The corresponding evolution is of the controlled unitary type with X as the control parameter:

$$\widehat{U}\left(t\right)=\int dX|X\rangle \langle X|\otimes \underset{k=1}{\overset{N}{⨂}}\widehat{D}\left(-\frac{i{C}_{k}t}{\sqrt{2}}X\right)$$

(17)

where $\widehat{D}\left(\alpha \right)=e^{\alpha a^{†}-{\alpha }^{*}a}$ is the displacement operator and we have set the oscillators masses and the frequencies to unity. This leads to the following decoherence and distinguishability factors [14]:

$$\left|{\Gamma }_{X,X^{\prime }}\left(t\right)\right|=exp\left[-\frac{{(X-X^{\prime })}^2}{2}{t}^2\text{cth}\frac{\beta }{2}\sum _{k\in (1-f)E}{C}_k^2\right]$$

(18)

$$B_{X,X^{\prime }}^{mac}\left(t\right)=exp\left[-\frac{{(X-X^{\prime })}^2}{2}{t}^2\text{th}\frac{\beta }{2}\sum _{k\in mac}{C}_k^2\right]$$

(19)

One immediately sees that unlike in the full model, in the quantum measurement limit there is always a formation of the spectrum broadcast structure, and hence objectivisation of the system’s position X, described by the Gaussian decay in time of $\left|{\Gamma }_{X,X^{\prime }}\left(t\right)\right|$, $B_{X,X^{\prime }}^{mac}\left(t\right)$. Quite surprisingly, one does not even have to assume random coupling constants $C_k$ as e.g., in the spin systems [18]. If however, one assumes random i.i.d. $C_k$ with a finite average $\overline{C^2}<\infty$, more can be said as the sum ${\sum }_k{C}_k^2$ above can be approximated using the law of large numbers for large macrofraction sizes:

$$\left|{\Gamma }_{X,X^{\prime }}\left(t\right)\right|\underset{N\to \infty }{\approx }exp\left[-(1-f)N\frac{{(X-X^{\prime })}^2}{2}\overline{C^2}{t}^2\text{cth}\frac{\beta }{2}\right]=e^{-(1-f)N{\left(\frac{t}{{\tau }_D}\right)}^2}$$

(20)

$$B_{X,X^{\prime }}^{mac}\left(t\right)\underset{N\to \infty }{\approx }exp\left[-mN\frac{{(X-X^{\prime })}^2}{2}\overline{C^2}{t}^2\text{th}\frac{\beta }{2}\right]=e^{-mN{\left(\frac{t}{{\tau }_B}\right)}^2}$$

(21)

where $(1-f)N$ and $mN$, $f,m\in (0,1)$, are the sizes of the unobserved macrofraction $(1-f)E$ and (one of the) observed one $mac$ respectively. The characteristic timescales of decoherence and distinguishability are given by, respectively:

$$\frac{1}{{\tau }_D}=\left|X-X^{\prime }\right|\sqrt{\frac{\text{cth}(\beta /2)}{2}\overline{C^2}}$$

(22)

$$\frac{1}{{\tau }_B}=\left|X-X^{\prime }\right|\sqrt{\frac{\text{th}(\beta /2)}{2}\overline{C^2}}$$

(23)

with the second being in general larger than the first for a given temperature T. This is the effect of noise—it obviously slows down the accumulation of information in environmental macrofractions (cf. [12]).

2.4. Partial Quantum Measurement Limit And Time Averages

Inclusion of the self-Hamiltonians of the environment:

$$\widehat{H}=\sum _{k=1}^N\left(\frac{{\widehat{p}}_k^2}{2m_k}+\frac{m_k{\omega }_k^2{\widehat{x}}_k^2}{2}\right)+\widehat{X}\otimes \sum _{k=1}^N{C}_k{\widehat{x}}_k$$

(24)

still allows for an exact solution, following e.g., the method of [14]:

$$\widehat{U}\left(t\right)=\int dX|X\rangle \langle X|\otimes \underset{k=1}{\overset{N}{⨂}}\widehat{D}\left({\alpha }_k\left(t\right)X\right)e^{i{\zeta }_k\left(t\right)X^2}$$

(25)

$${\alpha }_k\left(t\right)=-\frac{C_k}{\sqrt{2m_k{\omega }_k^3}}\left[e^{i{\omega }_{k}t}-1\right],{\zeta }_k\left(t\right)=\frac{C_k^2}{2m_k{\omega }_k^3}\left[{\omega }_{k}t-sin\left({\omega }_{k}t\right)\right]$$

(26)

For random ${\omega }_k$, the decoherence and distiguishability factors become almost periodic functions of time:

$$\left|{\Gamma }_{X,X^{\prime }}\right|=exp\left[\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in (1-f)E}\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)\frac{C_k^2\left(cos{\omega }_{k}t-1\right)}{m_k{\omega }_k^3}\right]$$

(27)

$$B_{X,X^{\prime }}^{mac}\left(t\right)=exp\left[\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in mac}\text{th}\left(\frac{\beta {\omega }_k}{2}\right)\frac{C_k^2\left(cos{\omega }_{k}t-1\right)}{m_k{\omega }_k^3}\right]$$

(28)

They are simpler than in the full model [14], as e.g., there is no frequency mixing between the environmental bands and the central system, but still too complicated for an immediate analytical studies (which will be the subject of an independent work). We believe the law of large numbers will prove useful again here. What, however, can be evaluated are the time averages $〈|{\Gamma }_{X,X^{\prime }}|〉={lim}_{\tau \to \infty }\frac{1}{\tau }{\int }_0^{\tau }dt|{\Gamma }_{X,X^{\prime }}\left(t\right)|$, $〈B_{X,X^{\prime }}^{mac}〉={lim}_{\tau \to \infty }\frac{1}{\tau }{\int }_0^{\tau }dt{B}_{X,X^{\prime }}^{mac}\left(t\right)$, noting that the amplitudes of the cosines in Equations (27) and (28) are all non-negative. Using a theorem from [19] one obtains (see Methods):

$$〈\left|{\Gamma }_{X,X^{\prime }}\right|〉=exp\left[-\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in (1-f)E}\frac{C_k^2\text{cth}(\beta {\omega }_k/2)}{m_k{\omega }_k^3}\right]\prod _{k\in (1-f)E}{\text{I}}_0\left[\frac{{(X-X^{\prime })}^2{C}_k^2\text{cth}(\beta {\omega }_k/2)}{2m_k{\omega }_k^3}\right]$$

(29)

$$〈B_{X,X^{\prime }}^{mac}〉=exp\left[-\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in mac}\frac{C_k^2\text{th}(\beta {\omega }_k/2)}{m_k{\omega }_k^3}\right]\prod _{k\in mac}{\text{I}}_0\left[\frac{{(X-X^{\prime })}^2{C}_k^2\text{th}(\beta {\omega }_k/2)}{2m_k{\omega }_k^3}\right]$$

(30)

where ${\text{I}}_0\left(z\right)=(1/\pi ){\int }_0^{\pi }d\theta e^{zcos\theta }$ is the modified Bessel function of the first kind. The rationale behind studying time averages is that since the functions themselves are non-negative, vanishing of the time averages is a good measure of the functions being practically zero. We are again interested in the scaling of the averages with the macrofraction sizes, for simplicity assuming them here to be equal: $\#(1-f)E=\#mac=mN$, $m\in (0,1)$. We also assume $C_k$ to be only mass-dependent (and not random) [14], $C_k=\sqrt{\frac{M{m}_k{\tilde{\gamma }}_0}{\pi }}$, with M the mass of the central system and ${\tilde{\gamma }}_0$ some constant. The scaling can be evaluated in the large separation limit:

$$\frac{\sqrt{M{\tilde{\gamma }}_0}|X-X^{\prime }|}{{\omega }_k^{3/2}}\gg 1\text{for}\text{every}k$$

(31)

which allows one to use the asymptotic expansion ${\text{I}}_0\left(x\right)\approx e^x/\sqrt{2\pi x}$. Assuming further low temperature limit, $\beta \to \infty$ (from Equation (28) $B_{X,X^{\prime }}^{mac}$ rises with T), one obtains:

$$〈\left|{\Gamma }_{X,X^{\prime }}\right|〉\approx \prod _{k=1}^{mN}\frac{{\omega }_k^{3/2}}{\sqrt{M{\tilde{\gamma }}_0}|X-X^{\prime }|}$$

(32)

and the same for $〈B_{X,X^{\prime }}^{mac}〉$, as $\text{th}(\beta {\omega }_k/2)\approx 1\approx \text{cth}(\beta {\omega }_k/2)$ in Equations (29) and (30). We perform further averaging over the random frequencies ${\omega }_k$, assuming [14] they are i.i.d. with a uniform distribution over a spectrum interval Δ, centered at some $\overline{\omega }\gg \Delta$. This gives:

$$\overline{〈\left|{\Gamma }_{X,X^{\prime }}\right|〉}={\int }_{\overline{\omega }-\frac{\Delta }{2}}^{\overline{\omega }+\frac{\Delta }{2}}\prod _j\frac{d{\omega }_j}{\Delta }〈\left|{\Gamma }_{X,X^{\prime }}\right|〉\approx e^{-mN\left(log\frac{\sqrt{M{\tilde{\gamma }}_0}|X-X^{\prime }|}{{\overline{\omega }}^{3/2}}\right)}$$

(33)

and the same for the distinguishability factor, due to the assumed low temperature limit:

$$\overline{〈B_{X,X^{\prime }}^{mac}〉}={\int }_{\overline{\omega }-\frac{\Delta }{2}}^{\overline{\omega }+\frac{\Delta }{2}}\prod _j\frac{d{\omega }_j}{\Delta }〈\left|B_{X,X^{\prime }}^{mac}\right|〉\approx e^{-mN\left(log\frac{\sqrt{M{\tilde{\gamma }}_0}|X-X^{\prime }|}{{\overline{\omega }}^{3/2}}\right)}$$

(34)

This is the desired scaling. One sees that whenever Equation (31) holds, for low temperatures, both averages exponentially decay in the thermodynamic limit $N\to \infty$, indicating formation of the spectrum broadcast state.

2.5. Squeezed Thermal States in The Full Model

We now switch to the full model Equation (11) and analyze the effect of squeezing in the initial thermal state of the environment, assuming:

$${\varrho }_{0k}=\widehat{S}\left(r\right){\varrho }_{kT}\widehat{S}{\left(r\right)}^{†}$$

(35)

where $\widehat{S}\left(r\right)=e^{\frac{r}{2}({\widehat{a}}^2-{\widehat{a}}^{†2})}$ is the squeezing operator and ${\varrho }_{kT}$ are the thermal oscillator states. Simple calculation shows that it is enough to substitute in Equations (13) and (14) $|{\alpha }_k{\left(t\right)|}^2$ for:

$${|{\tilde{\alpha }}_k\left(t\right)|}^2=\text{ch}\left(2r\right)\left[{\left|{\alpha }_k\left(t\right)\right|}^2-\text{th}\left(2r\right)\text{Re}{\alpha }_k^2\left(t\right)\right]$$

(36)

$$\text{Re}{a}_k{\left(t\right)}^2=\frac{C_k^2}{4m_k{\omega }_k}\{\frac{1}{{({\omega }_k+\Omega )}^2}\left\{cos\left[2({\omega }_k+\Omega )t\right]-2cos\left[({\omega }_k+\Omega )t\right]\right\}+\frac{1}{{({\omega }_k-\Omega )}^2}\left\{cos\left[2({\omega }_k-\Omega )t\right]-2cos\left[({\omega }_k-\Omega )t\right]\right\}+\frac{1}{{\omega }_k^2-{\Omega }^2}\left\{cos2\left({\omega }_{k}t\right)-cos\left[\left({\omega }_k-\Omega \right)t\right]-cos\left[\left({\omega }_k+\Omega \right)t\right]\right\}+\frac{3{\omega }_k^2+{\Omega }^2}{{({\omega }_k^2-{\Omega }^2)}^2}\}$$

(37)

From Equation (36) one sees that for large squeezing, $|{\tilde{\alpha }}_k{\left(t\right)|}^2$ grows exponentially as $e^{2r}$, enabling a formation of the broadcast structure as the most problematic term in Equation (14) decay as $\text{th}(\beta {\omega }_k/2)\approx \beta {\omega }_k/2$ for high temperatures. This reflects the fact that large squeezing decreases the noise, increasing the information capacity of the environment. The plots in Figure 1 confirm this. From Figure 1a it can be seen that for a moderate macrofractions of 10 oscillators only with a help of a large squeezing $logr>0$ the negative effect of the temperature can be overcome, and both functions are damped indicating formation of the spectrum broadcast structure.

For 30 oscillators, Figure 1b, the effect of random phases in Equations (13) and (14) is much stronger, the functions are much more damped for the chosen parameters range, and hence the plateau of a broadcast structure formation is much larger. Quite surprisingly, there is a bump around $logr=0$ where the formation is suppressed, most probably due to a constructive interference in Equations (36) and (37).

The parameters for the numerics are as follows [14]: For the central system we assume $M={10}^{-5}$ kg, $\Omega =3\times {10}^8$ s⁻¹; the frequencies ${\omega }_k$ are i.i.d. and uniformly distributed in the interval $3\cdots 6\times {10}^9$ s⁻¹ to satisfy the off-resonance condition Equation (12); we set $|X-X^{\prime }|={10}^{-9}$ m. We assume here that the coupling constants $C_k$ depend only on the masses, $C_k\equiv 2\sqrt{\frac{M{m}_k{\tilde{\gamma }}_0}{\pi }}$, where ${\tilde{\gamma }}_0=0.33\times {10}^{18}$ s⁻² is a constant. Thus, we do not assume the dependence on the ${\omega }_k$, as it is the case, e.g., for the Ohmic spectral density [4].

The averaging time was set at fairy large $1s$. Finally, as in the previous section, we assume a symmetric situation where the size of the traced macro-fraction $(1-f)E$ in Equation (13) is the same as the size of the observed one $mac$ in Equation (14).

Figure 1. Time averaged decoherence $\langle |{\Gamma }_{X,X^{\prime }}|\rangle$ (green; lower surfaces) and distinguishability $\langle B_{X,X^{\prime }}^{mac}\rangle$ (magenta; upper surfaces) factors as functions of the temperature T and squeezing r (both on the logarithmic scale) of the environment. The set of random frequencies ${\omega }_k$ was generated once per plot. The traced over and observed macrofractions, $(1-f)E$ and $mac$, are assumed to be of the same size. Both plots simultaneously approaching zero indicates formation of the spectrum broadcast structure for a given $(r,T)$. (a) 10 oscillators; (b) 30 oscillators.

Figure 1. Time averaged decoherence $\langle |{\Gamma }_{X,X^{\prime }}|\rangle$ (green; lower surfaces) and distinguishability $\langle B_{X,X^{\prime }}^{mac}\rangle$ (magenta; upper surfaces) factors as functions of the temperature T and squeezing r (both on the logarithmic scale) of the environment. The set of random frequencies ${\omega }_k$ was generated once per plot. The traced over and observed macrofractions, $(1-f)E$ and $mac$, are assumed to be of the same size. Both plots simultaneously approaching zero indicates formation of the spectrum broadcast structure for a given $(r,T)$. (a) 10 oscillators; (b) 30 oscillators.

3. Discussion

Our results can be grouped into three groups. First, neglecting the self-Hamiltonians of the system and the environments completely we have shown that there is always a formation of the spectrum broadcast structure for thermal environments, irrespective of how high the temperature is, if one waits long enough and/or takes large enough macrofractions. The derived Gaussian character of this formation together with characteristic timescales has not been obtained before. An application of the law of large numbers allowed us to obtain the exponential scaling of the decay with the environment size. Although very basic here, we believe this method will make analytical studies of the full model possible.

Second, in a more complicated model including self-Hamiltonians of the environments we have shown using a form of ergodicity for almost periodic functions [19], an exponential decay of infinite-time averages of both decoherence and distinguishability factors in the low temperature limit and for large separations of the systems’ initial positions $X,X^{\prime }$. Again, this is a novel result, compared to the earlier studies [4,14]. The large separation assumption opens here an interesting possibility of a space coarse-grained spectrum broadcast structure, where such a structure appears for large distances but not for small distances. This would lead to a sort of a macroscopic objectivity, emerging only at large scales. This concept will be a subject of further research.

Finally, we have numerically studied the effect of squeezing in the thermal environment in the full model. To our knowledge, such studies have not been performed before in the context of objectivisation (in [4] the system was initialized in a squeezed state, but the environment was initially in the ground state). Squeezing obviously increases the informational capacity of the environment, while the temperature destroys it. This leads to an interplay between squeezing and heating of the environment and our results show that in general large enough squeezing will dominate the noise due to the temperature. We had to rely on the numerics as the appearing almost periodic functions are quite complicated. 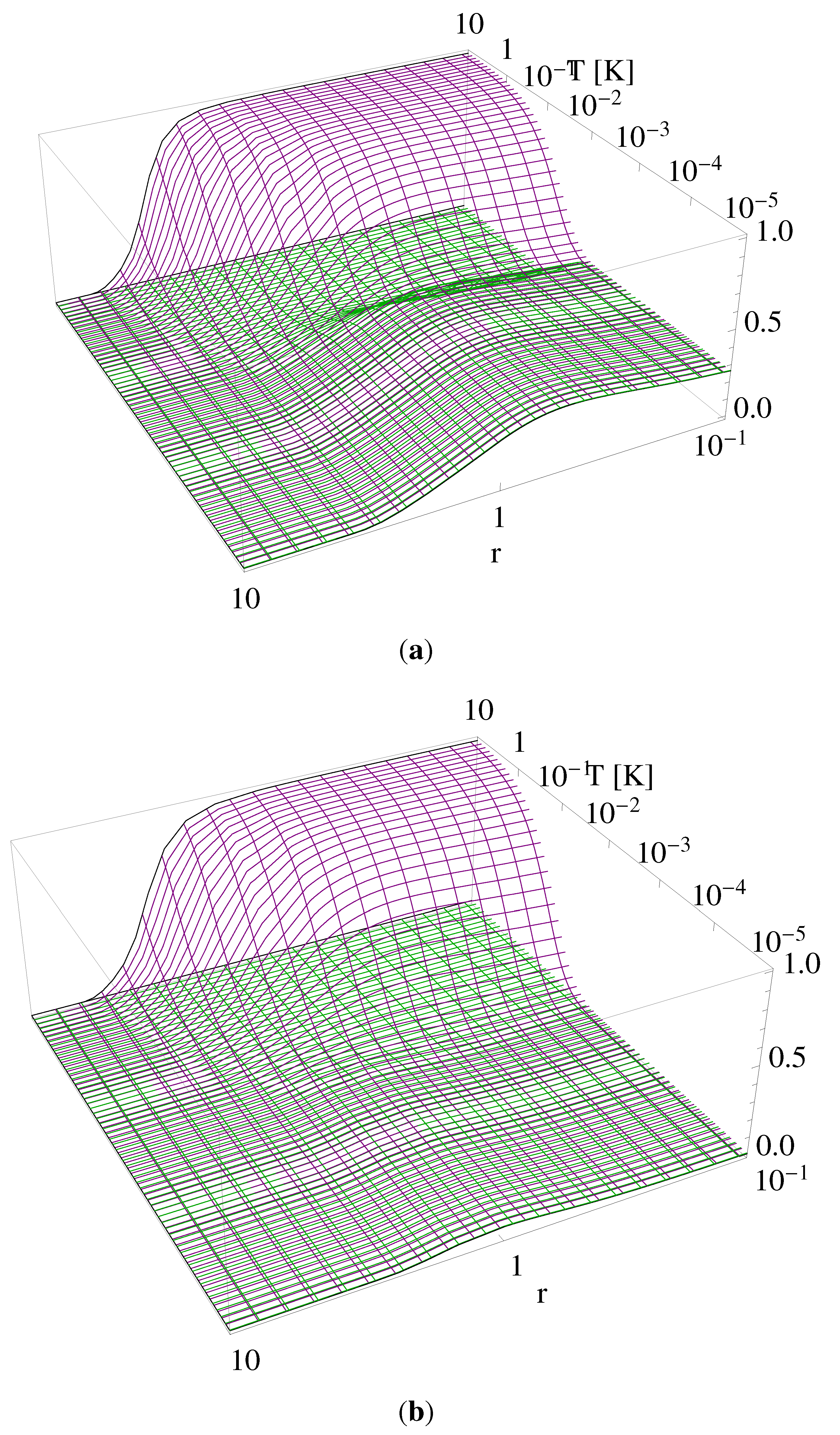However, as mentioned above, we hope the law of large numbers together with possible additional simplifications, e.g., the low temperature limit, will open a way for obtaining analytical estimates on the timescale of the objectivisation.

4. Methods

4.1. Time Averages of Almost Periodic Functions with Positive Coefficients

We will show the passage from Equations (27) and (28) to Equations (29) and (30). We evaluate the time average:

$$\underset{\tau \to \infty }{lim}\frac{1}{\tau }{\int }_0^{\tau }dtexp\left[\frac{{(X-X^{\prime })}^2}{2}\sum _{k\in (1-f)E}\frac{C_k^{2}cos{\omega }_{k}t}{m_k{\omega }_k^3}\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)\right]$$

(38)

The crucial step is to use one of the results from [19], which states a form of ergodicity for such functions. Namely, due to the positive amplitudes of the trigonometric functions, the time average can be substituted with the ensemble average (average over the angles in this case). This gives:

$$\underset{\tau \to \infty }{lim}\frac{1}{\tau }{\int }_0^{\tau }dt\prod _{k\in (1-f)E}exp\left[\frac{{(X-X^{\prime })}^2}{2}\frac{C_k^{2}cos{\omega }_{k}t}{m_k{\omega }_k^3}\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)\right]$$

(39)

$$=\prod _{k\in (1-f)E}\frac{1}{2\pi }{\int }_0^{2\pi }d{\theta }_{k}exp\left[\frac{{(X-X^{\prime })}^2}{2}\frac{C_k^2}{m_k{\omega }_k^3}\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)cos{\theta }_k\right]$$

(40)

$$=\prod _{k\in (1-f)E}{\text{I}}_0\left[\frac{{(X-X^{\prime })}^2}{2}\frac{C_k^2}{m_k{\omega }_k^3}\text{cth}\left(\frac{\beta {\omega }_k}{2}\right)\right]$$

(41)

where the last step is the standard Bessel integral, giving the modified Bessel function of the first kind: ${\text{I}}_0\left(z\right)=(1/\pi ){\int }_0^{\pi }d\theta e^{zcos\theta }$.