Squeezed Phonon Wave Packet Generation by Optical Manipulation of a Quantum Dot

Abstract

In solid-state physics, the quantized lattice vibrations, i.e., the phonons, play a vital role. Phonons, much like photons, satisfy bosonic commutation relations, and therefore, various concepts well-known in quantum optics can be transferred to the emerging field of phononics. Examples are non-classical states and, in particular, squeezed states. We discuss the generation of phonon squeezing by optically exciting a quantum dot and show that by excitation with detuned continuous wave laser fields, sequences of squeezed phonon wave packets are created, which are emitted from the quantum dot region into the surrounding material.

1. Introduction

Phonons are the quantized vibrations of the crystal lattice. They are, in many ways, similar to photons, i.e., the quanta of the electromagnetic field, because both phonons and photons satisfy bosonic commutation relations. Various types of quantum states of photons have been extensively studied in the past [1,2]. A particular class for bosons are squeezed states [3,4], which, for photons, can be routinely generated, e.g., by parametric down-conversion, and which can be used to provide higher measurement precision, e.g., in gravitational wave detectors [5]. This is possible, because squeezing allows one to reduce the quantum mechanical fluctuations of one observable below its vacuum value at the cost of enlarged fluctuations of the conjugate observable.

The concept of squeezing can directly be transferred to other bosonic excitations, like the motion of an atom in a trap [6,7] or the vibrations of a nanoresonator [8,9,10,11]. Furthermore, the search for and analysis of squeezed phonon states in various solid state systems has been the subject of many experimental [12,13,14,15,16], as well as theoretical [17,18,19,20,21,22,23,24] investigations in the past years. For phonons, the lattice displacement and the momentum of the motion of the lattice ions are a conjugate pair of variables, which enter in the Heisenberg uncertainty principle. Squeezing therefore corresponds to reducing the fluctuations of one of these variables at the expense of the other one.

The phenomenon of squeezing is often introduced for the case of a single mode. For photons, this can be achieved, e.g., by considering light in a microcavity [25,26]. For some phonon systems, an effective reduction to a single mode with well-defined frequency is possible as well, such as for longitudinal optical phonons with negligible dispersion or for phonons at van Hove singularities in the phonon density of states. Many investigations in the past have concentrated on phonon squeezing in such systems [12,13,14,19,20,24,27]. When the phonon system cannot be reduced to a single mode and modes with a continuum of frequencies contribute to the displacement and momentum of the lattice ions, a localized excitation leads to the creation of traveling phonon wave packets [28]. These wave packets can also exhibit squeezing [22].

While in some ionic crystals, a direct optical excitation of some optical phonon modes by infrared light is possible, the typical excitation of phonons occurs indirectly via an optical excitation of the electronic system. By means of the electron-phonon interaction, the excitation is then partially transferred to the phonon system, which opens up the possibility for an indirect, optical control of the phonon states [16,19,22,24]. A simple, localized electronic system, which can be well controlled optically, is given by a semiconductor quantum dot (QD). The optical excitation of the QD by laser pulses can create wave packets or sequences of wave packets of acoustic phonons [28], which are emitted from the QD into the surrounding material. In this paper, we will analyze the fluctuation properties of such wave packets emitted from a QD that is driven by a continuous wave (CW) field and discuss under which conditions squeezing can emerge. In particular, we will show that while for excitations by laser fields resonant to the exciton-transition energy, no squeezing occurs, for detuned excitations, sequences of squeezed wave packets can be emitted from the QD.

2. Theoretical Model

We will study the properties of phonons generated by the optical excitation of a self-assembled semiconductor QD. Typically, in these systems, the coupling via the deformation potential to longitudinal acoustic (LA) phonons has been found to be the most efficient one [29]. Therefore, we will restrict ourselves to this type of phonon. The relevant quantity for the study of squeezing is the lattice displacement $\widehat{\mathbf{u}}(\mathbf{r},t)$, which for LA phonons is given by:

$$\widehat{\mathbf{u}}(\mathbf{r},t)=-i\sqrt{\frac{\hslash }{2\rho V}}\sum _{\mathbf{q}}\frac{1}{\sqrt{{\omega }_{\mathbf{q}}}}\left({\widehat{b}}_{\mathbf{q}}^{\phantom{†}}{e}^{i\mathbf{q}·\mathbf{r}}-{\widehat{b}}_{\mathbf{q}}^{†}{e}^{-i\mathbf{q}·\mathbf{r}}\right)\frac{\mathbf{q}}{q}$$

(1)

where ${\widehat{b}}_{\mathbf{q}}^{†}$ (${\widehat{b}}_{\mathbf{q}}^{\phantom{†}}$) are the creation (annihilation) operators for a phonon with wave vector $\mathbf{q}$ and energy $\hslash {\omega }_{\mathbf{q}}$, satisfying the commutation relation $\left[{\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}},{\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}\right]={\delta }_{\mathbf{q},{\mathbf{q}}^{\prime }}$, V is the normalization volume of the phonon modes and ρ the crystal density. Assuming isotropic bulk phonons, the dispersion relation reduces to ${\omega }_{\mathbf{q}}=c_{\mathrm{l}}q$, with $c_{\mathrm{l}}$ being the longitudinal sound velocity. The conjugate variable to the lattice displacement is the momentum given by $\widehat{\pi }=V_{\mathrm{e}}\rho \partial \widehat{\mathbf{u}}/\partial t$ with $V_{\mathrm{e}}$ being the volume of the elementary cell. We will restrict ourselves to a system with spherical symmetry; therefore, all quantities only depend on the radial coordinate r [22].

To study phonon squeezing, we have to look at the fluctuations of displacement and momentum given by $\Delta u=\sqrt{\langle {\widehat{\mathbf{u}}}^2\rangle -{\langle \widehat{\mathbf{u}}\rangle }^2}$ and analogous for $\widehat{\pi }$. The uncertainties for displacement and momentum have to fulfill the Heisenberg uncertainty principle given by:

$${(\Delta u)}^2{(\Delta \pi )}^2\ge \frac{1}{4}{\hslash }^2$$

(2)

Because the Heisenberg limit is given for the product of the quantities, there is the freedom to lower the fluctuations of one variable at the cost of the other, which is often understood as squeezing. We will take as a reference the vacuum fluctuations and define squeezing as the case when the fluctuations of one of the variables drops below its respective vacuum value $\Delta u_{\mathrm{vac}}$ and $\Delta {\pi }_{\mathrm{vac}}$ defined by:

$$\begin{array}{ccc}\hfill {(\Delta u_{\mathrm{vac}})}^2& =& \frac{\hslash }{2\rho V}\sum _{\mathbf{q},{\mathbf{q}}^{\prime }}\frac{1}{\sqrt{{\omega }_{\mathbf{q}}{\omega }_{{\mathbf{q}}^{\prime }}}}\frac{\mathbf{q}·{\mathbf{q}}^{\prime }}{q{q}^{\prime }}〈\left[{\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}},{\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}\right]〉=\frac{\hslash }{2\rho V}\sum _{\mathbf{q}}\frac{1}{{\omega }_{\mathbf{q}}}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {(\Delta {\pi }_{\mathrm{vac}})}^2& =& \frac{\hslash \rho V_{\mathrm{e}}^2}{2V}\sum _{\mathbf{q},{\mathbf{q}}^{\prime }}\sqrt{{\omega }_{\mathbf{q}}{\omega }_{{\mathbf{q}}^{\prime }}}\frac{\mathbf{q}·{\mathbf{q}}^{\prime }}{q{q}^{\prime }}〈\left[{\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}},{\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}\right]〉=\frac{\hslash \rho V_{\mathrm{e}}^2}{2V}\sum _{\mathbf{q}}{\omega }_{\mathbf{q}}\hfill \end{array}$$

(4)

For a single mode (setting $V_{\mathrm{e}}=V$) or optical modes with a fixed frequency ${\omega }_0$, the vacuum fluctuations satisfy the minimum uncertainty product. However, for LA phonons, it turns out that already in the case of the vacuum state, the Heisenberg limit is exceeded [22].

For our further investigations, we restrict ourselves to the lattice displacement and define the quantity $D_u$ as the normalized deviation of the squared fluctuations of the displacement from their vacuum value, i.e.,

$$D_u(r,t)=\frac{{[\Delta u(r,t)]}^2-{(\Delta u_{\mathrm{vac}})}^2}{{(\Delta u_{\mathrm{vac}})}^2}$$

(5)

With this definition, squeezing is directly reflected by $D_u<0$. For brevity, we will refer to $D_u$ as fluctuations in the following. Written explicitly in terms of expectation values of the phonon creation and annihilation operators, $D_u$ reads:

$$\begin{array}{ccc}\hfill D_u(r,t)& =& +\frac{\hslash }{\rho V}\frac{1}{{(\Delta u_{\mathrm{vac}})}^2}\sum _{\mathbf{q},{\mathbf{q}}^{\prime }}\frac{1}{\sqrt{{\omega }_{\mathbf{q}}{\omega }_{{\mathbf{q}}^{\prime }}}}\frac{\mathbf{q}·{\mathbf{q}}^{\prime }}{q{q}^{\prime }}\left(\langle {\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}{\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}}\rangle -\langle {\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}\rangle \langle {\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}}\rangle \right)e^{i(\mathbf{q}-{\mathbf{q}}^{\prime })·\mathbf{r}}\hfill \end{array}$$

$$\begin{array}{ccc}& & -\frac{\hslash }{\rho V}\frac{1}{{(\Delta u_{\mathrm{vac}})}^2}\sum _{\mathbf{q},{\mathbf{q}}^{\prime }}\frac{1}{\sqrt{{\omega }_{\mathbf{q}}{\omega }_{{\mathbf{q}}^{\prime }}}}\frac{\mathbf{q}·{\mathbf{q}}^{\prime }}{q{q}^{\prime }}Re\left[\left(\langle {\widehat{b}}_{\mathbf{q}}{\widehat{b}}_{{\mathbf{q}}^{\prime }}\rangle -\langle {\widehat{b}}_{\mathbf{q}}\rangle \langle {\widehat{b}}_{{\mathbf{q}}^{\prime }}\rangle \right)e^{i(\mathbf{q}+{\mathbf{q}}^{\prime })·\mathbf{r}}\right]\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& \equiv & D_{\langle b^{†}b\rangle }(r,t)+D_{\langle bb\rangle }(r,t)\hfill \end{array}$$

(7)

In this way, the fluctuations can be separated into two parts. The first part $D_{\langle b^{†}b\rangle }(r,t)$ is the fluctuations related to operators, which are off-diagonal generalizations of the phonon occupation ${\widehat{n}}_{\mathbf{q}}={\widehat{b}}_{\mathbf{q}}^{†}{\widehat{b}}_{\mathbf{q}}^{\phantom{†}}$. It can be shown that $D_{\langle b^{†}b\rangle }(r,t)$ is always positive. The second part $D_{\langle bb\rangle }(r,t)$ is the fluctuations of a two-phonon coherence. In the case of purely incoherent phonons, i.e., $\langle {\widehat{b}}_{\mathbf{q}}^{†}\rangle =\langle {\widehat{b}}_{\mathbf{q}}^{\phantom{†}}\rangle =\langle {\widehat{b}}_{\mathbf{q}}{\widehat{b}}_{{\mathbf{q}}^{\prime }}\rangle =0$ and $\langle {\widehat{b}}_{{\mathbf{q}}^{\prime }}^{†}{\widehat{b}}_{{\mathbf{q}}^{\phantom{\prime }}}^{\phantom{†}}\rangle ={\widehat{n}}_{\mathbf{q}}{\delta }_{{\mathbf{qq}}^{\prime }}$, only the first part remains, leading to $D_u>0$. Squeezing therefore requires the presence of two-phonon coherences. Indeed, it is well known from quantum optics that operators of the form ${\widehat{b}}^2$ and ${\widehat{b}}^{†2}$ appear in the squeezing operator for a single mode and, in this way, are crucial for the reduction of fluctuations below the vacuum limit [1].

We will study the fluctuation properties of phonons generated by optical excitation of a QD. Because a detailed description of the theory can be found in previous papers (see, e.g., [28]), we will only briefly summarize the main aspects here. We consider a QD in the strong confinement limit driven by a circularly polarized light field, such that a description of the QD by a two-level system consisting of the ground state $|g\rangle$ and the single exciton state $|x\rangle$ with the exciton energy $\hslash {\omega }_{\mathrm{x}}$ is appropriate. The coupling to bulk LA phonons takes place via the pure dephasing mechanism, i.e., phonon-induced transitions to other electronic states are neglected. The system can be optically controlled via a laser field $E\left(t\right)$, which is described in the usual dipole and rotating wave approximation. Then, the Hamiltonian of the system reads:

$$\widehat{H}=\hslash {\omega }_{\mathrm{x}}|x\rangle \langle x|-M{E}^{(+)}|x\rangle \langle g|-M^{*}{E}^{(-)}|g\rangle \langle x|+\sum _{\mathbf{q}}\hslash {\omega }_{\mathbf{q}}{\widehat{b}}_{\mathbf{q}}^{†}{\widehat{b}}_{\mathbf{q}}^{}+\sum _{\mathbf{q}}\hslash \left(g_{\mathbf{q}}{\widehat{b}}_{\mathbf{q}}+g_{\mathbf{q}}^{*}{\widehat{b}}_{\mathbf{q}}^{†}\right)|x\rangle \langle x|$$

(8)

Here, $g_{\mathbf{q}}$ is the exciton-phonon coupling matrix element and M is the dipole matrix element. The excitation, which we consider here is a smoothly switched on CW excitation with the laser frequency ${\omega }_{\mathrm{L}}$. In terms of the Rabi frequency $\Omega \left(t\right)=\frac{2}{\hslash }M{E}^{(+)}\left(t\right)e^{i{\omega }_{\mathrm{L}}t}$, the excitation is modeled by:

$$\Omega \left(t\right)=\frac{{\Omega }_{\mathrm{R}}}{2}\left[erf\left(\frac{t}{\tau }\right)+1\right]$$

(10)

where τ defines the duration of the switch-on process, while ${\Omega }_{\mathrm{R}}$ determines the strength of the CW excitation after it has been switched on.

In the system, different types of resonance conditions can be fulfilled. First, the laser excitation is resonant, when the laser frequency ${\omega }_{\mathrm{L}}$ matches the frequency of the exciton transition. Here, the renormalization of the exciton energy due to the electron-phonon interaction (the polaron shift) has to be taken into account, leading to ${\tilde{\omega }}_{\mathrm{x}}={\omega }_{\mathrm{x}}-{\sum }_{\mathbf{q}}{\left|g_{\mathbf{q}}\right|}^2/{\omega }_{\mathbf{q}}$. Thus, the laser excitation is called resonant if ${\omega }_{\mathrm{L}}={\tilde{\omega }}_{\mathrm{x}}$. If this condition is not met, we call the excitation detuned and introduce the detuning $\hslash \delta \omega =\hslash {\omega }_{\mathrm{L}}-\hslash {\tilde{\omega }}_{\mathrm{x}}$. This is schematically shown in Figure 1a.

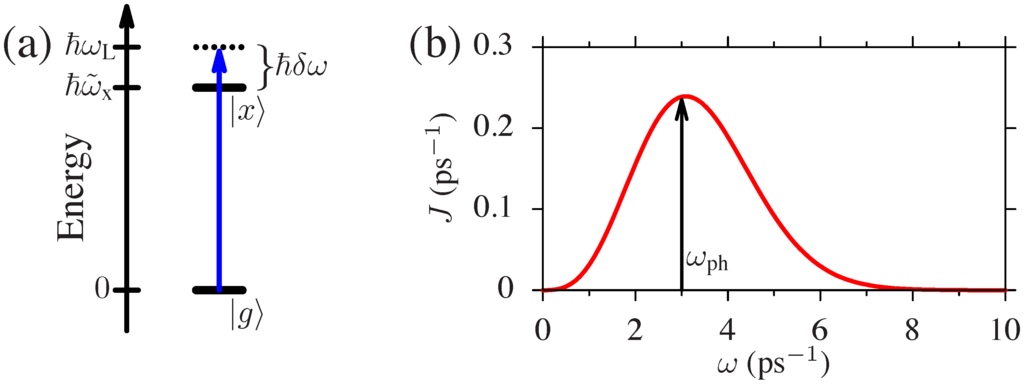
Figure 1. (a) Schematic plot of the two-level model with the optical excitation; (b) phonon spectral density for a QD with a 5-nm diameter.

Figure 1. (a) Schematic plot of the two-level model with the optical excitation; (b) phonon spectral density for a QD with a 5-nm diameter.

A second type of resonance is introduced by the exciton-phonon coupling. The efficiency of this coupling is quantified by the phonon spectral density:

$$J\left(\omega \right)=\sum _{\mathbf{q}}{|g_{\mathbf{q}}|}^2\delta (\omega -{\omega }_{\mathbf{q}})$$

(10)

Assuming for simplicity a spherical QD geometry with harmonic confinement potentials for electrons and holes, the spectral density reads:

$$J\left(\omega \right)=\frac{{\omega }^3}{4{\pi }^2\rho \hslash c_{\mathrm{l}}^5}{\left(D_{\mathrm{e}}{e}^{-{\left(\frac{\omega a_{\mathrm{e}}}{2c_{\mathrm{l}}}\right)}^2}-D_{\mathrm{h}}{e}^{-{\left(\frac{\omega a_{\mathrm{h}}}{2c_{\mathrm{l}}}\right)}^2}\right)}^2$$

(11)

where $D_{\mathrm{e}}$ ($D_{\mathrm{h}}$) are the deformation potentials of electrons (holes) and $a_{\mathrm{e}}$ ($a_{\mathrm{h}}$) are the spatial widths of the electron (hole) wave functions. We take GaAs material parameters [29] and a QD with $L=a_{\mathrm{e}}2\sqrt{ln2}=5\mathrm{nm}$ diameter (full width at half maximum of the electron density), as well as $a_{\mathrm{h}}=0.87a_{\mathrm{e}}$. Figure 1b shows $J\left(\omega \right)$ for this QD. It is seen that $J\left(\omega \right)$ is maximal at a finite phonon frequency ${\omega }_{\mathrm{ph}}$. The coupling between the exciton and phonon system is most efficient when the time $T_{\mathrm{ph}}=2\pi /{\omega }_{\mathrm{ph}}$ (roughly the time the phonons need to travel across the QD) matches the period of the Rabi oscillation of the exciton system. A more transparent interpretation of this resonance between light-induced and phonon-related dynamics can be obtained within the dressed state picture. The dressed states are the eigenstates of the coupled QD-light system. They are split by the energy $\hslash {\tilde{\Omega }}_{\mathrm{R}}=\hslash \sqrt{{\Omega }_{\mathrm{R}}^2+\delta {\omega }^2}$ [30], where ${\tilde{\Omega }}_{\mathrm{R}}$ is the effective Rabi frequency. In this picture, phonons can induce transitions between the dressed states, and the transitions are most efficient when the splitting coincides with the maximum of the spectral density [31,32,33]. For the QD parameters taken in this paper, the resonant phonon time is $T_{\mathrm{ph}}=2\pi /{\omega }_{\mathrm{ph}}\approx 2\mathrm{ps}$. We note that the coupling is only efficient for phonons with frequencies between 1 and $7{\mathrm{ps}}^{-1}$.

In general, the optical excitation of the QD leads to the generation of a mean lattice displacement $\langle \widehat{u}(r,t)\rangle$, which, for symmetry reasons, has only a radial component and which essentially corresponds to the dynamics of a classical strain field. In the case of a spherical QD and LA phonons, this leads to traveling spherical waves, which decay $\sim r^{-1}$. Accordingly the fluctuations decay $\sim r^{-2}$. To compensate for this geometrical decay, we plot the scaled quantities:

$$\tilde{u}(r,t)=\left(\frac{r}{1\mathrm{nm}}\right)\langle \widehat{u}(r,t)\rangle \text{and}{\tilde{D}}_u(r,t)=\left(\frac{r^2}{1{\mathrm{nm}}^2}\right)D_u(r,t)$$

(12)

While in the case of excitation by ultrafast laser pulses, the coupled QD-phonon dynamics can be calculated analytically [22,34], for arbitrary excitations, no exact analytical results are known. Therefore, we use a numerical calculation on the level of a fourth-order correlation expansion [35,36], which has been shown to provide very reliable results in the parameter range studied here [37]. The complete set of equations for our model can be found in [36] (Equations (3)–(6) and (A1)–(A9)).

3. Results and Discussion

We will first study the fluctuation properties for two different excitation strengths. One is chosen such that the Rabi frequency is in resonance with the phonon coupling, while the other is much stronger and far above the resonance condition. After that, we will give an overview of the occurrence of squeezing for various coupling strengths. To focus on the excitation-induced properties of the phonons, we restrict ourselves to the temperature $T=0\mathrm{K}$, such that before switching on the light field $D_u=0$. Initially, both the exciton and the phonon system are taken to be in their respective ground state. The exciton is driven by an optical CW field that is switched on according to Equation (9) with $\tau =0.5\mathrm{ps}$.

3.1. Rabi Frequency Resonant with Phonon Coupling

We start our discussion with a Rabi frequency ${\Omega }_{\mathrm{R}}=3{\mathrm{ps}}^{-1}={\omega }_{\mathrm{ph}}$, which is in resonance with the phonon coupling. Figure 2 shows the results for this excitation; it is structured as follows: The three different detunings $\hslash \delta \omega =+0.5,0$ and $-0.5\mathrm{meV}$ are shown from left to right. In the upper row ((a), (c) and (e)), we show the exciton occupation $f\left(t\right)=\langle |x\rangle \langle x|\rangle$ (solid red lines), as well as the Rabi frequency $\Omega \left(t\right)$ (dashed blue lines) in the lower panels and the mean lattice displacement $\tilde{u}$ in the top panels. In the lower row ((b), (d) and (f)), we show the fluctuations ${\tilde{D}}_u(r,t)$ in the lower panels and their temporal profiles at $r=20\mathrm{nm}$ in the upper panels.

Let us first briefly discuss the upper row of Figure 2, i.e., (a), (c) and (e). The case of resonant excitation with $\hslash \delta \omega =0\mathrm{meV}$ has been extensively studied in [28], and we refer to that paper for further details on the dynamics of the lattice displacement. The exciton occupation f (shown in the lower panel) performs the well-known Rabi oscillations with the Rabi frequency ${\Omega }_{\mathrm{R}}$ that are damped in time due to the coupling to the LA phonons [30,38]. The upper panel of Figure 2c shows the lattice displacement $\tilde{u}$ (note that the values are scaled according to Equation (12)) plotted against time and distance from the QD. Every excitation of the exciton leads to the emission of a wave packet with a negative amplitude. Accordingly, each destruction of the exciton creates a wave packet with positive displacement. As the amplitude of the Rabi oscillation decays quite fast, also the amplitudes of the emitted phonons get smaller from one wave packet to the next one. Note that the oscillation period of the phonon wave packets is determined by the Rabi frequency ${\Omega }_{\mathrm{R}}$. Moving to detuned excitations in Figure 2a,e, the overall behavior is rather similar. The oscillations now occur with the effective Rabi frequency ${\tilde{\Omega }}_{\mathrm{R}}\approx 3.1{\mathrm{ps}}^{-1}$, which is, however, only slightly different from ${\Omega }_{\mathrm{R}}$. For positive detuning, the exciton occupation relaxes towards a slightly higher value, and for negative detuning, a slightly lower value compared to the resonant excitation is reached. These different long-time values can be best understood in the dressed state picture. At low temperatures, when no phonon absorption processes are possible, only transitions from the upper to the lower dressed state by phonon emission occur, such that, finally, only the lower dressed state is populated [37]. Thus, the final exciton populations seen in Figure 2 reflect the different contributions of the exciton state to the lower dressed state: at resonance, this state is an equal superposition of the ground and exciton state; for positive detuning, it is more exciton-like; and for negative detuning, it is more ground state-like. Since the initial state before switching on the light field is the ground state, phonon emission is more pronounced for positive detuning than for negative detuning.

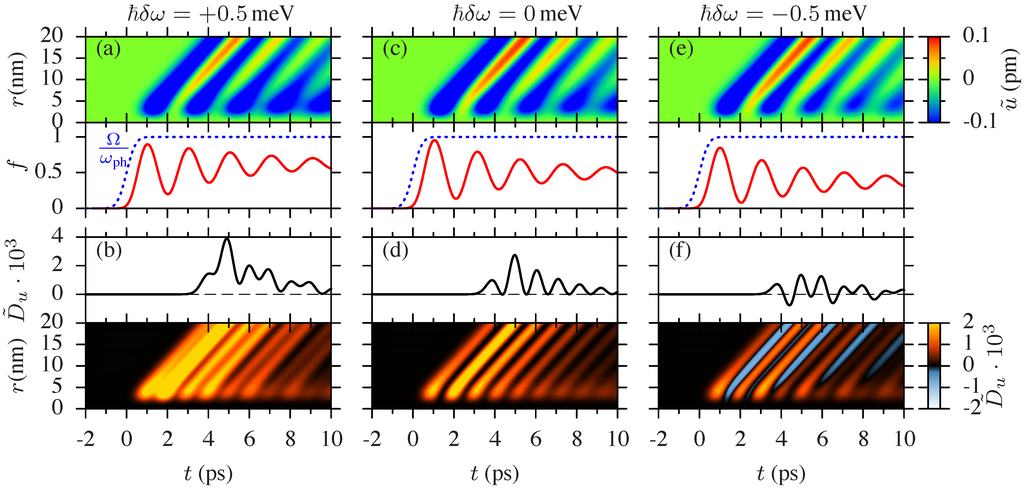
Figure 2. (a,c,e) Mean lattice displacement $\tilde{u}(r,t)$ (upper panel); Rabi frequency Ω (dashed blue) and occupation f of the exciton state (solid red) (lower panel); (b,d,f) fluctuations of the lattice displacement ${\tilde{D}}_u(r,t)$ (lower panel), as well as their temporal profiles at $r=20\mathrm{nm}$ (upper panel): (a,b) positive detuning $\hslash \delta \omega =+0.5\mathrm{meV}$; (c,d) resonant excitation $\hslash \delta \omega =0\mathrm{meV}$; (e,f) negative detuning $\hslash \delta \omega =-0.5\mathrm{meV}$.

Figure 2. (a,c,e) Mean lattice displacement $\tilde{u}(r,t)$ (upper panel); Rabi frequency Ω (dashed blue) and occupation f of the exciton state (solid red) (lower panel); (b,d,f) fluctuations of the lattice displacement ${\tilde{D}}_u(r,t)$ (lower panel), as well as their temporal profiles at $r=20\mathrm{nm}$ (upper panel): (a,b) positive detuning $\hslash \delta \omega =+0.5\mathrm{meV}$; (c,d) resonant excitation $\hslash \delta \omega =0\mathrm{meV}$; (e,f) negative detuning $\hslash \delta \omega =-0.5\mathrm{meV}$.

The focus of this paper is the fluctuations of the lattice displacement ${\tilde{D}}_u$, which are plotted in the bottom row of Figure 2, i.e., (b), (d) and (f). The overall spatio-temporal structure (shown in the lower panels) follows the behavior of the displacement. The top panels show a temporal profile of the fluctuations at $r=20\mathrm{nm}$. For the resonant excitation (Figure 2d), in addition to the emission of coherent phonon wave packets, also an increase of the fluctuations above the vacuum level is found. It can be clearly seen that the fluctuations never go below zero, thus, the state is never squeezed. Having a more detailed look, we see that the maxima of the fluctuations appear exactly between the wave packets in the lattice displacement, where the slope of $\tilde{u}$ is the largest, and that the fluctuations become minimal when there is a maximum or minimum in the displacement. This shows that the fluctuations oscillate with twice the Rabi frequency, i.e., $2{\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$. Typically, an oscillation with twice the characteristic frequency of the phonon system is an indicator of squeezing, in particular in single mode systems. However, it has been found in other systems, as well, that oscillations with the double frequency may also appear without squeezing [19].

For a positive detuning of $\hslash \delta \omega =+0.5\mathrm{meV}$ in Figure 2b, we again see an oscillatory behavior of the fluctuations. Also in this case, the fluctuations are strictly positive; thus, no squeezing occurs. Furthermore, we see in the profile that the oscillation contains more than just twice the effective Rabi frequency, such that the oscillation looks rather irregular. In contrast, for the case of a negative detuning of $\hslash \delta \omega =-0.5\mathrm{meV}$, the fluctuations clearly fall below zero on the slope of each wave packet. This means that the emitted wave packets are squeezed, and even a sequence of squeezed wave packets is generated by excitation with a CW light field. These findings are in line with other studies, where squeezed phonons arising from negatively detuned excitation of an electronic system were found [12,24]. In those studies, phonons with a fixed frequency, like optical phonons or phonons at van Hove singularities, were investigated. This means that the phonons have a vanishing group velocity, such that they do not move in space. The new feature in our system studied here is that the LA phonons form squeezed traveling wave packets that leave the QD.

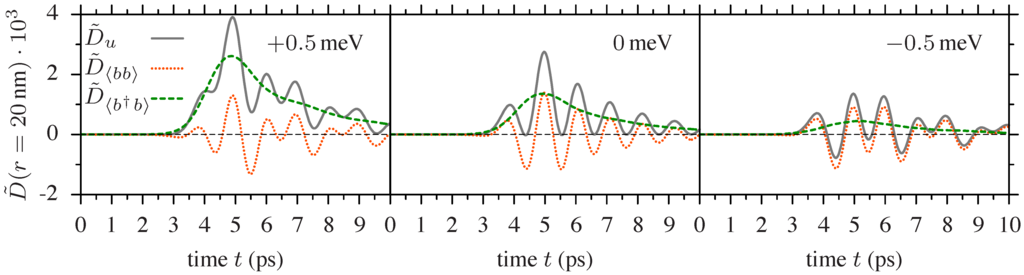
Figure 3. Fluctuations of the lattice displacement ${\tilde{D}}_u$ (solid grey), the two-phonon coherence ${\tilde{D}}_{\langle bb\rangle }$ (dotted orange) and the phonon occupation ${\tilde{D}}_{\langle b^{†}b\rangle }$ (dashed green) for $\hslash \delta \omega =0\mathrm{meV}$ (center), $+0.5\mathrm{meV}$ (left) and $-0.5\mathrm{meV}$ (right). All curves are calculated for $r=20\mathrm{nm}$.

Figure 3. Fluctuations of the lattice displacement ${\tilde{D}}_u$ (solid grey), the two-phonon coherence ${\tilde{D}}_{\langle bb\rangle }$ (dotted orange) and the phonon occupation ${\tilde{D}}_{\langle b^{†}b\rangle }$ (dashed green) for $\hslash \delta \omega =0\mathrm{meV}$ (center), $+0.5\mathrm{meV}$ (left) and $-0.5\mathrm{meV}$ (right). All curves are calculated for $r=20\mathrm{nm}$.

To analyze the fluctuations ${\tilde{D}}_u$ in more detail, we show the temporal profile at $r=20\mathrm{nm}$ again in Figure 3 (solid grey line), where we now distinguish between the two contributions ${\tilde{D}}_{\langle b^{†}b\rangle }$ (dashed green line) and ${\tilde{D}}_{\langle bb\rangle }$ (dotted orange line) defined in Section 2. We remind that ${\tilde{D}}_{\langle b^{†}b\rangle }$ describes the fluctuations of the phonon occupations, and in this way, it includes the heating processes of the phonon system, while ${\tilde{D}}_{\langle bb\rangle }$ refers to the fluctuations of the two-phonon coherence. Let us first concentrate on ${\tilde{D}}_{\langle b^{†}b\rangle }$. The behavior of these fluctuations is smooth and does not show any oscillatory behavior for any detuning, but they form roughly the mean value of the oscillatory full fluctuations ${\tilde{D}}_u$. In contrast, for ${\tilde{D}}_{\langle bb\rangle }$, an oscillatory behavior is seen. For resonant excitation, we see that it goes approximately with twice the Rabi frequency, i.e., $2{\Omega }_{\mathrm{R}}$. For detuned excitation, a spectral analysis shows that the oscillation is composed of two frequencies, approximately $2{\tilde{\Omega }}_{\mathrm{R}}$ and ${\tilde{\Omega }}_{\mathrm{R}}$. It is interesting to note that an oscillation of the fluctuations with double and single phonon frequency was also found for squeezed longitudinal optical phonons after pulsed optical excitation [19].

To understand whether squeezing occurs, we have to compare the strength of the two contributions ${\tilde{D}}_{\langle b^{†}b\rangle }$ and ${\tilde{D}}_{\langle bb\rangle }$. For resonant excitation, the two parts have the same strength, such that they can compensate for each other. The minima in ${\tilde{D}}_u$ reach exactly zero, and no squeezing occurs. For positive detuning, as discussed above, the relaxation from the upper to the lower dressed state is associated with an increased phonon emission. When we think of ${\tilde{D}}_{\langle b^{†}b\rangle }$ to represent heating processes of the phonon bath, it is easy to understand that for a positive detuning, the fluctuations ${\tilde{D}}_{\langle b^{†}b\rangle }$ are larger than in the resonant case. It turns out that here, the heating processes always exceed the squeezing processes represented by ${\tilde{D}}_{\langle bb\rangle }$. Therefore, the total fluctuations ${\tilde{D}}_u$ are always positive, and no squeezing occurs. For negative detuning, the lower dressed state has a larger ground state contribution, such that phonon emission processes are reduced compared to the resonant case, i.e., the heating is suppressed. Accordingly, ${\tilde{D}}_{\langle b^{†}b\rangle }$ is much smaller than ${\tilde{D}}_{\langle bb\rangle }$, and the total fluctuations are dominated by the two-phonon coherence, thus leading to squeezing.

3.2. Rabi Frequency out of Resonance with Phonon Coupling

A drawback of the excitation with a Rabi frequency of ${\Omega }_{\mathrm{R}}\approx {\omega }_{\mathrm{ph}}$ is the fact that the dephasing of the exciton is quite strong, such that the dynamics is limited to a short period of time. To avoid this pronounced damping in time, we now double the amplitude of the CW field to ${\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$. In [28], we have shown that for Rabi frequencies in this region, a long sequence of wave packets can be emitted, because the exciton and the phonon system become increasingly decoupled and the dephasing mechanisms are suppressed. For a discussion of the mean lattice displacement $\tilde{u}$ we again refer to [28]. Figure 4a shows the fluctuations of the lattice displacement as a function of time and distance from the QD for the three detunings $\hslash \delta \omega =+0.5,0$ and $-0.5\mathrm{meV}$. For the resonant excitation (central panel), only positive fluctuations are visible. After two large wave packets at the beginning that result from the switch-on process, all remaining amplitudes are almost of the same size. This reflects the very inefficient dephasing of the exciton state. Turning to detuned excitations, a surprising result is found for the fluctuations: not only for a negative detuning (Figure 4a bottom), but also for a positive detuning (Figure 4a top), pronounced negative fluctuations appear. We want to point out that in Section 3.1 and in previous studies on similar systems, squeezed phonon states were only found for optical excitation energies smaller than the exciton transition [6,24]. For positive detunings, only enhanced fluctuations were observed [6,24].

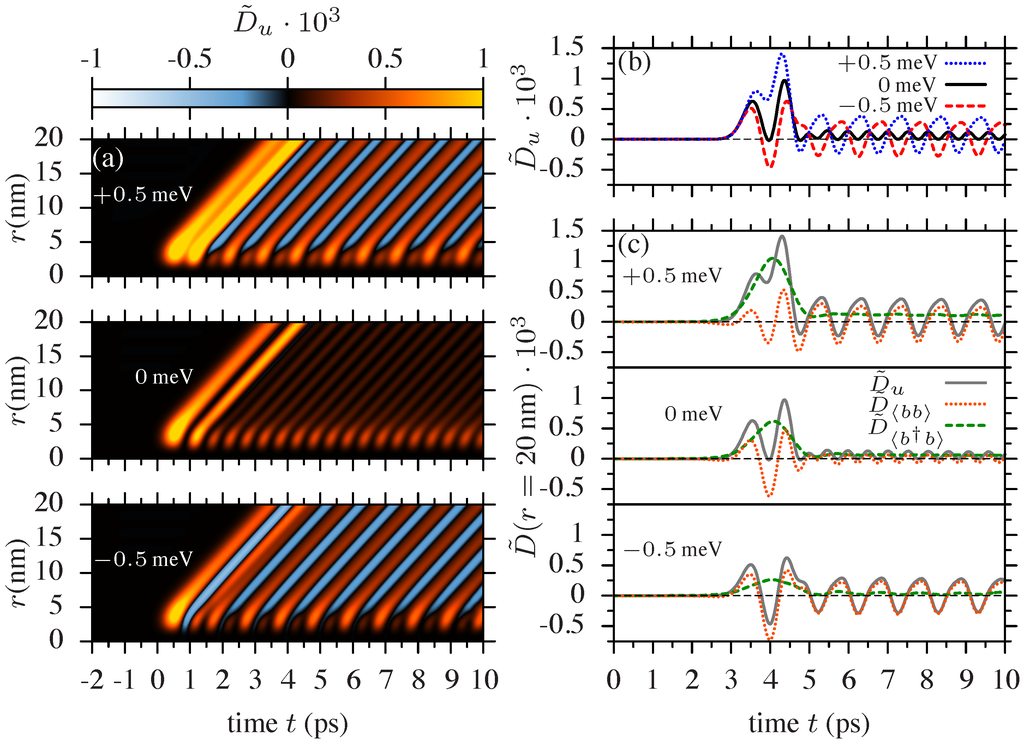
Figure 4. (a) Fluctuations of the lattice displacement ${\tilde{D}}_u(r,t)$ as a function of t and r for a Rabi frequency ${\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$; (b) temporal shape of the fluctuations of the lattice displacement ${\tilde{D}}_u$ from (a) at $r=20\mathrm{nm}$; (c) same as Figure 3 but for ${\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$.

Figure 4. (a) Fluctuations of the lattice displacement ${\tilde{D}}_u(r,t)$ as a function of t and r for a Rabi frequency ${\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$; (b) temporal shape of the fluctuations of the lattice displacement ${\tilde{D}}_u$ from (a) at $r=20\mathrm{nm}$; (c) same as Figure 3 but for ${\Omega }_{\mathrm{R}}=6{\mathrm{ps}}^{-1}$.

To take a closer look at the temporal structure of the fluctuations, in Figure 4b, we have plotted the profile of ${\tilde{D}}_u$ for $r=20\mathrm{nm}$ for the three cases of the detuning $\hslash \delta \omega =+0.5$ (dotted blue line), 0 (solid black line) and $-0.5\mathrm{meV}$ (dashed red line). In the case of a resonant excitation (solid black), the minima of the fluctuations again reach zero, but never become negative. The frequency of this oscillation is approximately twice the Rabi frequency of the system, i.e., $\approx 12{\mathrm{ps}}^{-1}$. Note that, here, ${\tilde{\Omega }}_{\mathrm{R}}\approx 6.04{\mathrm{ps}}^{-1}$, which essentially agrees with ${\Omega }_{\mathrm{R}}$. For the detuned cases (dashed red and dotted blue lines), the overall amplitude of the oscillation is enlarged, such that both reach negative values. Both curves look quite similar, but have a phase shift of π. It is also clearly visible that the dominant frequency of the oscillation for the detuned cases is approximately the single Rabi frequency ${\tilde{\Omega }}_{\mathrm{R}}$, while the fast component with about $2{\tilde{\Omega }}_{\mathrm{R}}$ is weaker.

We again want to analyze the separate contributions to the fluctuations ${\tilde{D}}_u$. The results are shown in Figure 4c in the same way as in Figure 3. We recover some features from the previous case of strong phonon coupling at ${\Omega }_{\mathrm{R}}=3{\mathrm{ps}}^{-1}$. The fluctuations of the phonon occupation ${\tilde{D}}_{\langle b^{†}b\rangle }$ (dashed green lines) again get larger for positive detuning and smaller for negative detuning; however, they are much smaller than in the case of strong phonon coupling. This is due to the fact that the phonon spectral density at $\omega ={\Omega }_{\mathrm{R}}$ is much smaller now. The curves still do not exhibit a distinct oscillating structure, but are more or less constant after the strong wave packet from the switch-on process of the optical field that appears around $t=4\mathrm{ps}$. It also still holds that the contributions ${\tilde{D}}_{\langle b^{†}b\rangle }$ form the mean value for the full fluctuations ${\tilde{D}}_u$ (solid grey lines). However, the important difference from Figure 2 is the fact that the fluctuations of the two-phonon coherence ${\tilde{D}}_{\langle bb\rangle }$ (dotted orange lines) clearly get larger than ${\tilde{D}}_{\langle b^{†}b\rangle }$ for detuned excitations nearly independent of the sign of the detuning, which is quite remarkable. Additionally, as the previous discussion still holds, the phonon wave packets are squeezed when the two-phonon contributions dominate.

3.3. Dependence on Rabi Frequency

Let us now draw a complete picture and study the fluctuations as a function of the Rabi frequency. In Figure 5 (left panel), we plot the profiles of the fluctuations ${\tilde{D}}_u$ at $r=20\mathrm{nm}$ in a contour plot as a function of time t and Rabi frequency ${\Omega }_{\mathrm{R}}$ for the three different detunings. As expected, for zero detuning, we do not see any squeezing. For negative detuning, we find that for almost all Rabi frequencies ${\Omega }_{\mathrm{R}}$, squeezing occurs. For positive detuning, the situation turns out to be more complicated. While for small Rabi frequencies up to about ${\Omega }_{\mathrm{R}}=3{\mathrm{ps}}^{-1}$, no squeezing occurs, for higher Rabi frequencies around $6{\mathrm{ps}}^{-1}$, the fluctuations exhibit clear squeezing. We mention that also the lattice momentum exhibits no squeezing for resonant excitation and may exhibit squeezing for detuned excitations. We additionally plot the fluctuations of the phonon occupations ${\tilde{D}}_{\langle b^{†}b\rangle }$ (middle panel) and the fluctuations of the two-phonon coherence ${\tilde{D}}_{\langle bb\rangle }$ (right panel). Here, we can clearly see the difference between the three detunings. While for negative detuning, the fluctuations of the phonon occupations ${\tilde{D}}_{\langle b^{†}b\rangle }$ are very small, for positive detuning, they become very strong. However, the important feature is that the main contributions of ${\tilde{D}}_{\langle b^{†}b\rangle }$ are restricted to frequencies around ${\Omega }_{\mathrm{R}}=3{\mathrm{ps}}^{-1}$. This reflects the fact that only in this range of Rabi frequencies does pronounced phonon emission from the upper to the lower dressed state occur. The shape of this area in the plot does not change, but the detuning only contributes to a scaling of it, which can be understood from the fact that with increasing detuning, the contribution of the exciton state to the lower dressed state increases, and thus, more phonons are generated in the relaxation process. On the other hand, the strength of the fluctuations of the two-phonon coherence ${\tilde{D}}_{\langle bb\rangle }$ are very similar for all three detunings. The main difference is that for zero detuning, they are strongest around ${\Omega }_{\mathrm{R}}=3{\mathrm{ps}}^{-1}$ and become small for ${\Omega }_{\mathrm{R}}\gtrsim 6{\mathrm{ps}}^{-1}$, while in the detuned cases, also significant contributions arise from larger Rabi frequencies.

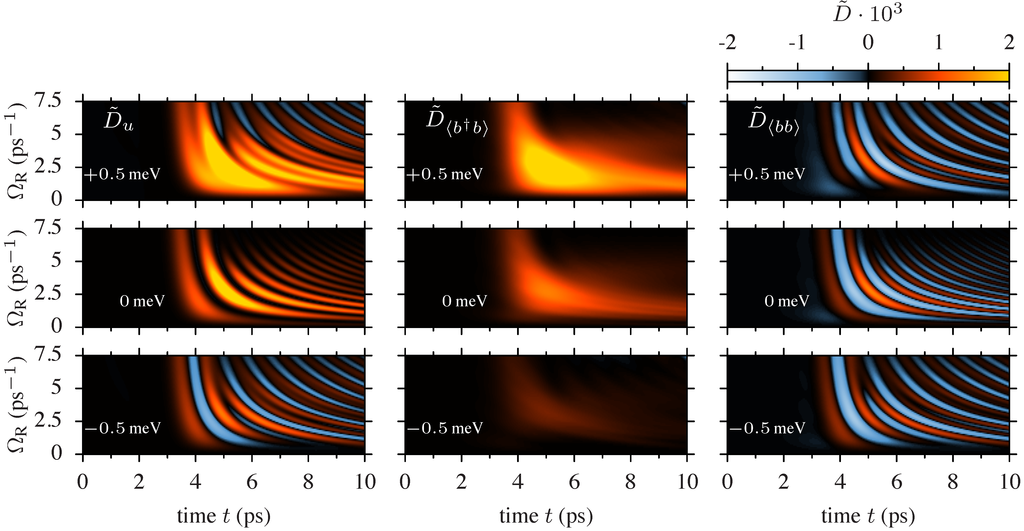
Figure 5. Fluctuations of the lattice displacement ${\tilde{D}}_u$ (left), ${\tilde{D}}_{\langle b^{†}b\rangle }$ (center) and ${\tilde{D}}_{\langle bb\rangle }$ (right) at $r=20\mathrm{nm}$ plotted against time t and Rabi frequency ${\Omega }_{\mathrm{R}}$ for the detunings $\delta \omega =+0.5\mathrm{meV}$ (top); $0\mathrm{meV}$ (middle) and $-0.5\mathrm{meV}$ (bottom).

Figure 5. Fluctuations of the lattice displacement ${\tilde{D}}_u$ (left), ${\tilde{D}}_{\langle b^{†}b\rangle }$ (center) and ${\tilde{D}}_{\langle bb\rangle }$ (right) at $r=20\mathrm{nm}$ plotted against time t and Rabi frequency ${\Omega }_{\mathrm{R}}$ for the detunings $\delta \omega =+0.5\mathrm{meV}$ (top); $0\mathrm{meV}$ (middle) and $-0.5\mathrm{meV}$ (bottom).

4. Conclusions

Phonon squeezing is in many ways similar to photon squeezing, but also, some pronounced differences appear. Relevant quantities for the phonons are the lattice displacement and momentum, which are, for LA phonons, defined by many modes. In this paper, we have analyzed the fluctuation properties of the lattice displacement of LA phonons that are emitted from an optically-driven QD. We have studied different excitation strengths of a CW field and different detunings. Our studies were focused on the lattice displacement; however, the lattice momentum behaves mostly in an analogous way. For optical excitation in resonance with the transition energy of the exciton system, no squeezing was found; however, an oscillation of the fluctuations with twice the Rabi frequency occurred. This is similar to the appearance of contributions with twice the phonon frequency in the case of optical phonon fluctuations after impulsive excitation [19]. For negatively detuned excitations, we have shown that for all excitation strengths, squeezing appears, in agreement with studies on similar systems [1,12,24]. For positive detuning, we found that the appearance of squeezing is determined by the heating of the phonon system. While for strong phonon coupling, the heating dominates, and no squeezing occurs, for weak phonon coupling at high Rabi frequencies, the squeezing prevails.