Moiré Effect with Refraction

Abstract

The moiré effect has been considered in various objects, such as coplanar layers, hollow shells, and volumetric three-dimensional objects (e.g., parallelepipeds, prisms, cylinders, and LED cubes). However, the moiré effect in refracting objects filled with a transparent substance (such as liquid or glass) has not yet been investigated. We performed a theoretical and experimental study of the moiré effect in rectangular and cylindrical containers with a refractive substance. The formulas for the magnification coefficient and the moiré period in rectangular and cylindrical refracting objects were obtained. The experiments confirm the theory. This study is essential for understanding the physical properties of the moiré effect with refraction. The results can be used to measure the level and refractive index.

1. Introduction

The moiré effect is a physical phenomenon that occurs in superimposed periodic or nearly periodic structures or their projections [1,2]. Moiré patterns appear as relatively broad stripes, with periods that differ from the original structures.

The principle of moiré pattern formation is shown in Figure 1.

Figure 1a shows two grids with parallel lines and similar but not equal periods that overlap, i.e., are visible through each other, which illustrates the key point: the low-frequency moiré pattern has a new period that is absent in the original grids. Moiré patterns appear in the overlap region (the dashed rectangle in the middle of Figure 1a); however, closer inspection reveals that it contains a mixture of the original grids and new patterns. The mixture can be seen above and below the overlap region. To see the moiré patterns themselves, a low-pass filter should be applied. The pure moiré patterns are shown inside the dashed rectangle, and their period is significantly greater than the period of either grid. Furthermore, Figure 1b shows the intensity profile along a horizontal line in the middle of the overlap region.

Figure 2 shows all signals along with their spectra. The spectral peaks of the moiré patterns are located significantly closer to the beginning of the spectral region, and therefore, there is no fundamental difficulty in filtering them out of the mixture.

Most often, the moiré effect is considered in coplanar layers [1,4,5,6,7], particularly in twistronics and two-dimensional materials [8,9,10,11], twisted bilayers [12,13,14], and interesting cases of tri- and multi-layered structures [15,16].

Sometimes (although relatively rarely), the effect is studied in non-coplanar layers [17,18,19] or hollow three-dimensional objects bounded by flat or curved surfaces of macro- [20,21,22,23,24,25] and nano-objects [26,27,28], including

(a)

Parallel planes (sides of a rectangular parallelepiped) [2,29,30];

(b)

Non-parallel planes of a wedge (triangular prism) [20];

(c)

Cylinder [21,22,23,24], in particular, single-walled (SWNT) [31,32,33] and double-walled nanotubes (DWNT) [34,35];

(d)

Their combinations [36];

(e)

Multilayered volumetric structures (e.g., LED cubes) [37].

However, to the author’s knowledge, the moiré effect in objects filled with a refractive substance (e.g., thick glass or transparent containers filled with liquid), except for a few papers [38,39,40], has not yet been investigated.

The paper examines rectangular and cylindrical containers. The former can be called a box. We used the first-order approximation (small angles).

2. Materials and Methods

Consider a symmetric 3D object filled with a refractive substance (such as water or glass), as shown in Figure 3. The surface of the liquid is horizontal (parallel to the xy-plane). We used line grids with vertical lines (perpendicular to the xy-plane) attached to the object’s surfaces without folds or gaps. Thus, we consider flat facets (parallelepiped) and curved (cylinder).

The refraction is significant only on the frontal surface of an object (near the camera), but on the rear surface (far from the camera), refraction is not taken into account.

The origin is at the center of the object, see Figure 4. The observer (camera) is located at point C. The distance from the origin to the camera is L. The camera viewing angle is α:

$$\tan \alpha ={\displaystyle \frac{y_0}{l}}$$

(1)

where y₀ is the ordinate of the intersection point (x₀, y₀) of the camera ray with the near surface, and l is the distance from the camera to the intersection.

In a filled object, the apparent (visible) size of the object is changed because of the refractive substance inside the object. The intersection points of the refracted and the extended rays with the far surface are (x₂, y₂) and (x₁, y₁). The relative refractive magnification M shows how much the visible size is larger than the physical size (the physical intersection of the ray with the far surface); formally, it is defined as the ratio of the visible and physical sizes.

The refractive magnification coefficient M indicates how much the visible (apparent) size exceeds the physical size (the intersection of the original ray with the far surface); formally, it is defined as the ratio of the apparent size to the physical size:

$$M={\displaystyle \frac{y_{vis}}{y_{ph}}}$$

(2)

where the physical and visual (perceived) sizes are as follows:

$$y_{ph}=y_2$$

(3)

$$y_{vis}=y_1$$

(4)

It should be noted that M is a dimensionless quantity that has no specific units of measurement.

Snell’s law, in general, is represented as follows:

$$\mathit{sin}r={\displaystyle \frac{\mathit{sin}i}{n}}$$

(5)

where n is the refractive index of the medium (a dimensionless quantity, such as 1 for air and 1.33 for water); for small angles,

$$r={\displaystyle \frac{i}{n}}$$

(6)

where n is the refractive index, i and r are the angles of incidence and refraction,

$$i=\phi +\alpha$$

(7)

$$r=\phi +\psi$$

(8)

In the formulas above, the angle φ is the angle between the abscissa and the intersection point,

$$\tan \phi ={\displaystyle \frac{y_0}{x_0}}$$

(9)

and the angle ψ is a portion of the refraction angle above the line parallel to the abscissa.

Based on geometry,

$$y_1=y_0+\left(x_0-x_1\right)\mathit{tan}\alpha$$

(10)

$$y_2=y_0+\left(x_0-x_2\right)\mathit{tan}\psi$$

(11)

Thus, for small angles, the refractive magnification coefficient is

$$M={\displaystyle \frac{y_0+\left(x_0-x_1\right)\alpha }{y_0+\left(x_0-x_2\right)\psi }}$$

(12)

(The refractive magnification M for the far grid will be calculated in Section 3.1.)

The ratio of grid wavenumbers/periods ρ is defined as

$$\rho ={\displaystyle \frac{k_{near}}{k_{far}}}={\displaystyle \frac{{\lambda }_{far}}{{\lambda }_{near}}}$$

(13)

where k is the wavenumber and λ is the period.

The geometrical ratio of grids ρ is the ratio of the physical periods (as the grids are technically constructed). However, the effective size of the far grid changes due to the refraction in the filled object,

$${\lambda }_{far}^{eff}=M{\lambda }_{far}$$

(14)

and thus

$${\rho }^{eff}=M\rho$$

(15)

The fundamental property of the moiré effect [1,2] is that the moiré wavenumber is equal to the difference in the wavenumbers of the grids projected onto the same plane,

$$k_M={k^{\prime }}_{FAR}-{k^{\prime }}_{NEAR}$$

(16)

The projected wavenumbers and moiré wavenumbers will be calculated in Section 3.2.

For the parallelepiped, we used the relative quantity

$$\widehat{L}={\displaystyle \frac{L}{W}}$$

(17)

where W is the half-width of the parallelepiped.

Similarly, in formulas related to the cylinder, we use relative quantities

$$\tilde{x}={\displaystyle \frac{x}{R}}$$

(18)

$$\tilde{y}={\displaystyle \frac{y}{R}}$$

(19)

$$\tilde{L}={\displaystyle \frac{L}{R}}$$

(20)

where R is the radius of the cylinder.

The relative quantities defined by Equations (17)–(20) are the dimensionless ratios that have no unit of measurement.

3. Results

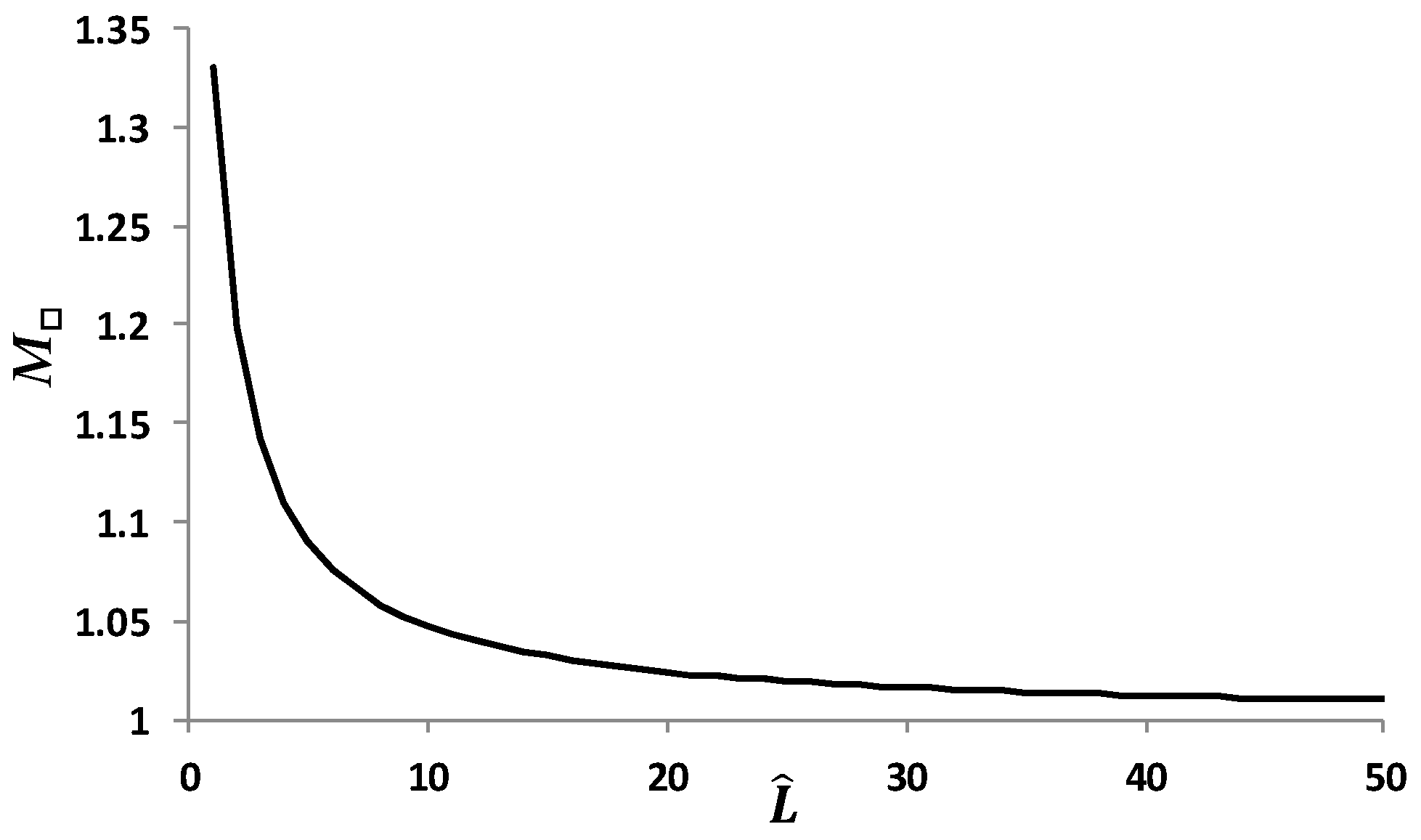
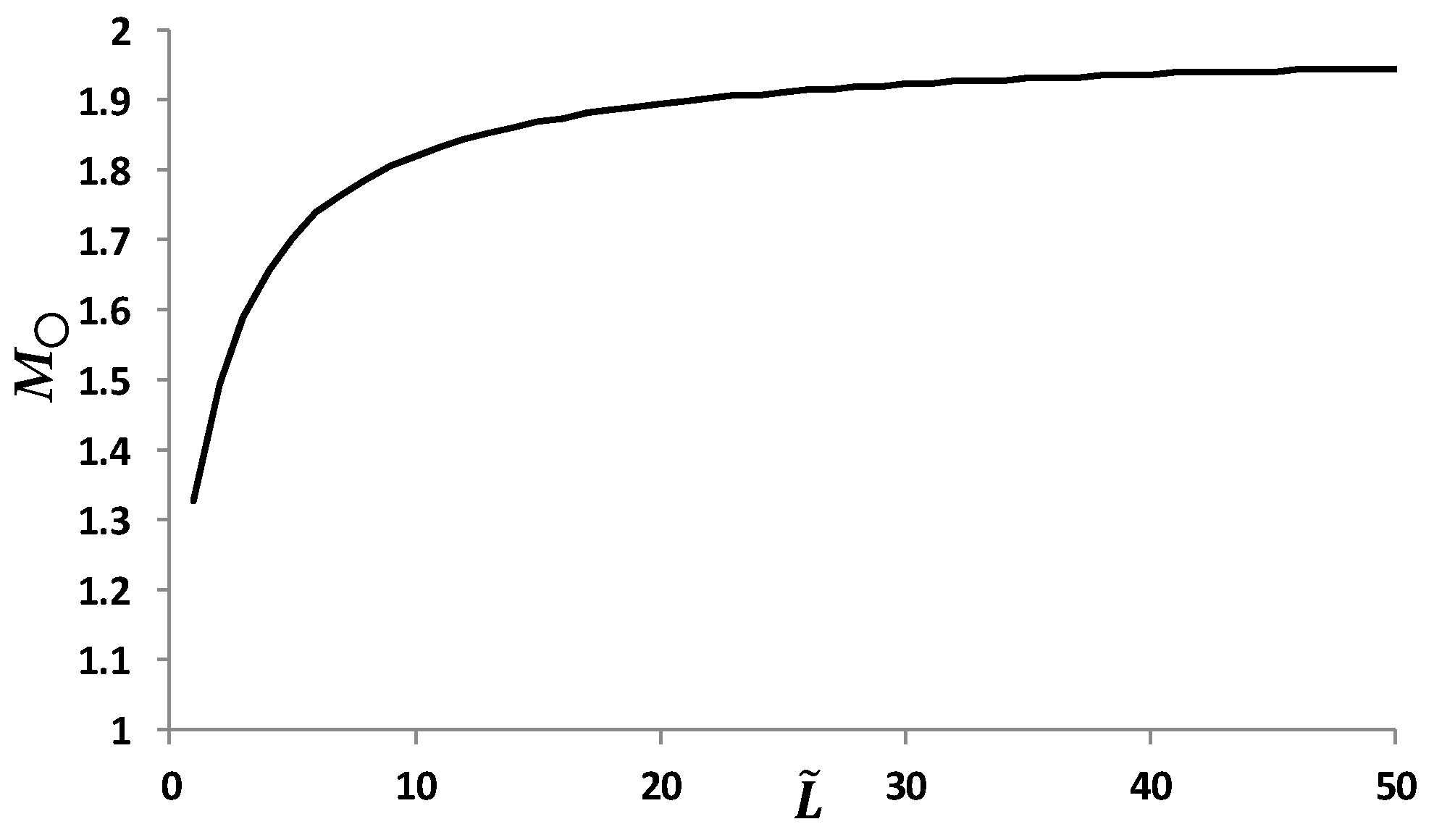
3.1. Refractive Magnification

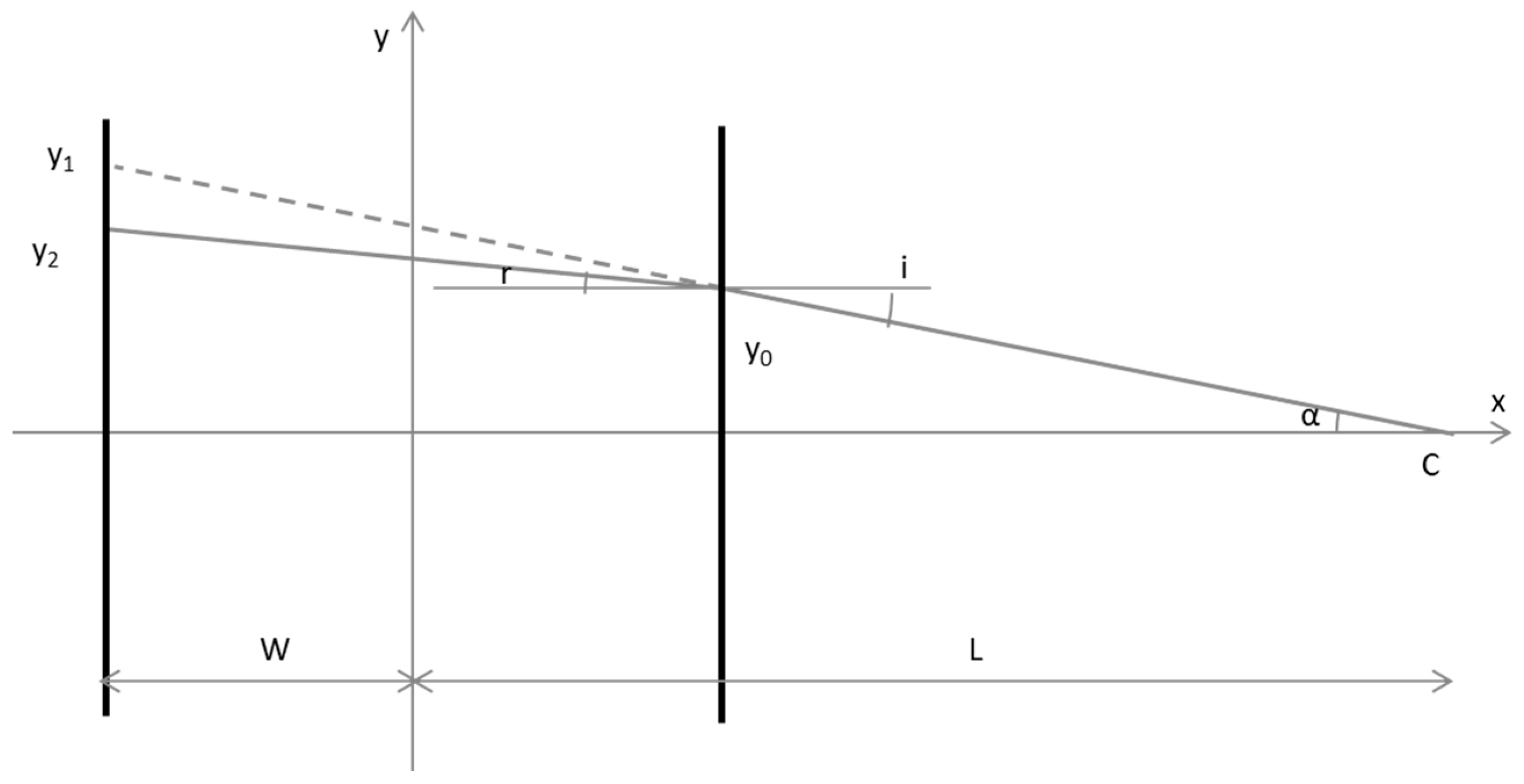
3.1.1. Refractive Magnification in a Parallelepiped

The symmetric parallelepiped is shown in Figure 5. Both surfaces are parallel to the ordinate, and x₀ − x₁ = x₀ − x₂ = 2W. The angles are as follows:

$$i=\alpha$$

(21)

$$r=\psi$$

(22)

For small angles, Equations (10) and (11) are as follows:

$$y_1=\left(L+W\right)\alpha$$

(23)

$$y_2=\left(L-W\right)\alpha +2W{\displaystyle \frac{\alpha }{n}}$$

(24)

From Equation (12), we obtain the refractive magnification in the filled parallelepiped,

$$M_{◻}={\displaystyle \frac{L+W}{L+\nu W}}$$

(25)

where, for convenience of deriving the formulas, we defined the coefficient ν as follows:

$$\nu ={\displaystyle \frac{2- n}{n}}$$

(26)

N.B. In the water, the coefficient ν equals 0.5.

Using the relative quantity Equation (17) and the above coefficient, Equation (25) becomes

$$M_{◻}={\displaystyle \frac{\widehat{L}+1}{\widehat{L}+\nu }}$$

(27)

We consider M as a distance function. Other quantities are parameters and are formally denoted by subscripts and superscripts in the formulas.

For n > 1, the denominator is smaller than the numerator. Thus, M > 1, and a water layer (with parallel sides) magnifies images of objects behind it.

For $\widehat{L}=1$, the refractive magnification $M_{◻}\left(1\right)=n$. At large distances, the refractive magnification is $M_{◻}^{\left(n\right)}(\infty )=1$ in both water and air.

For n > 1, the derivative of Equation (27) is negative. Therefore, the refractive magnification as a function of the distance decreases from n to 1, as shown in Figure 6, where the calculated refractive magnification in water slightly exceeds 1.

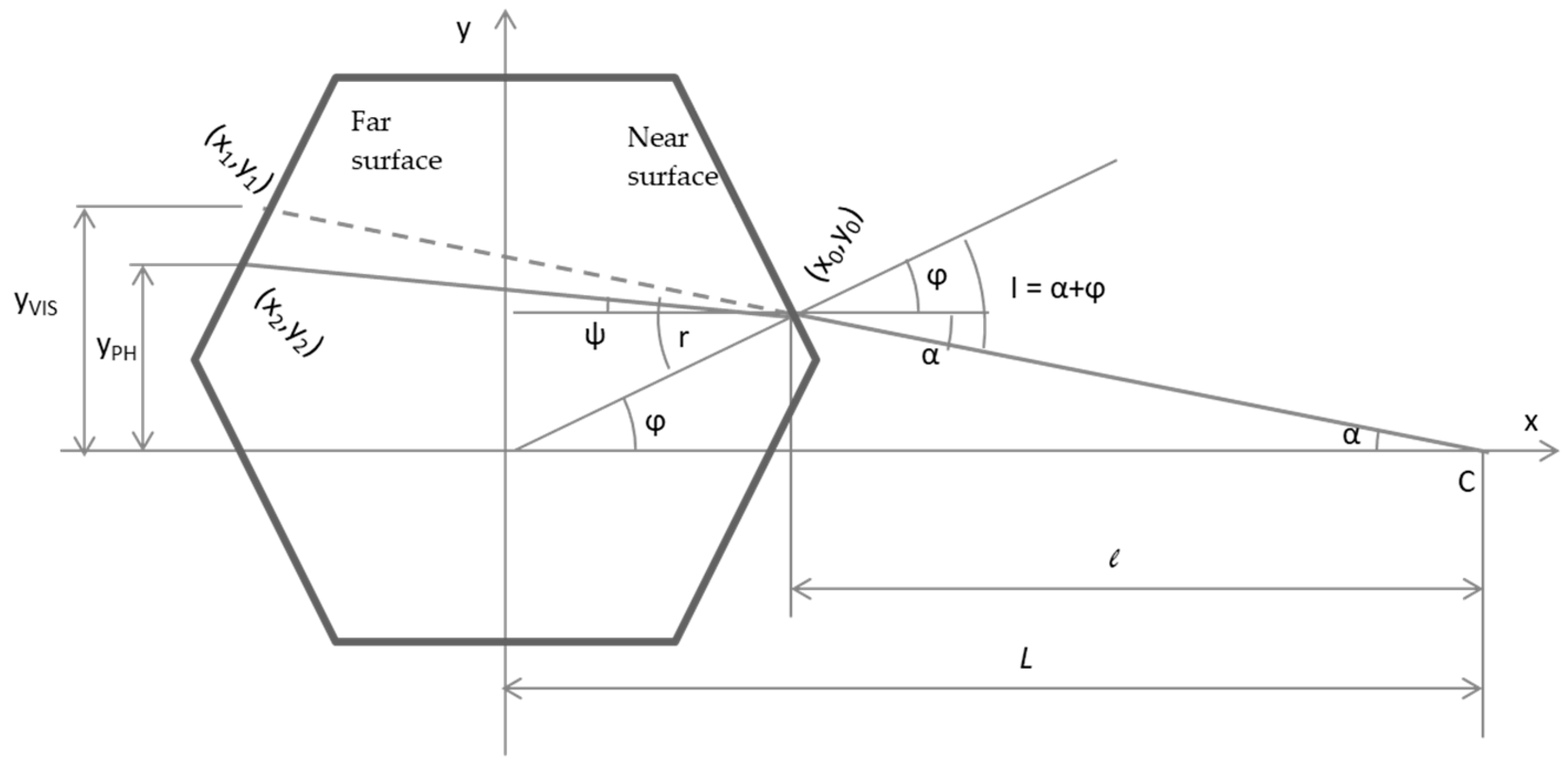
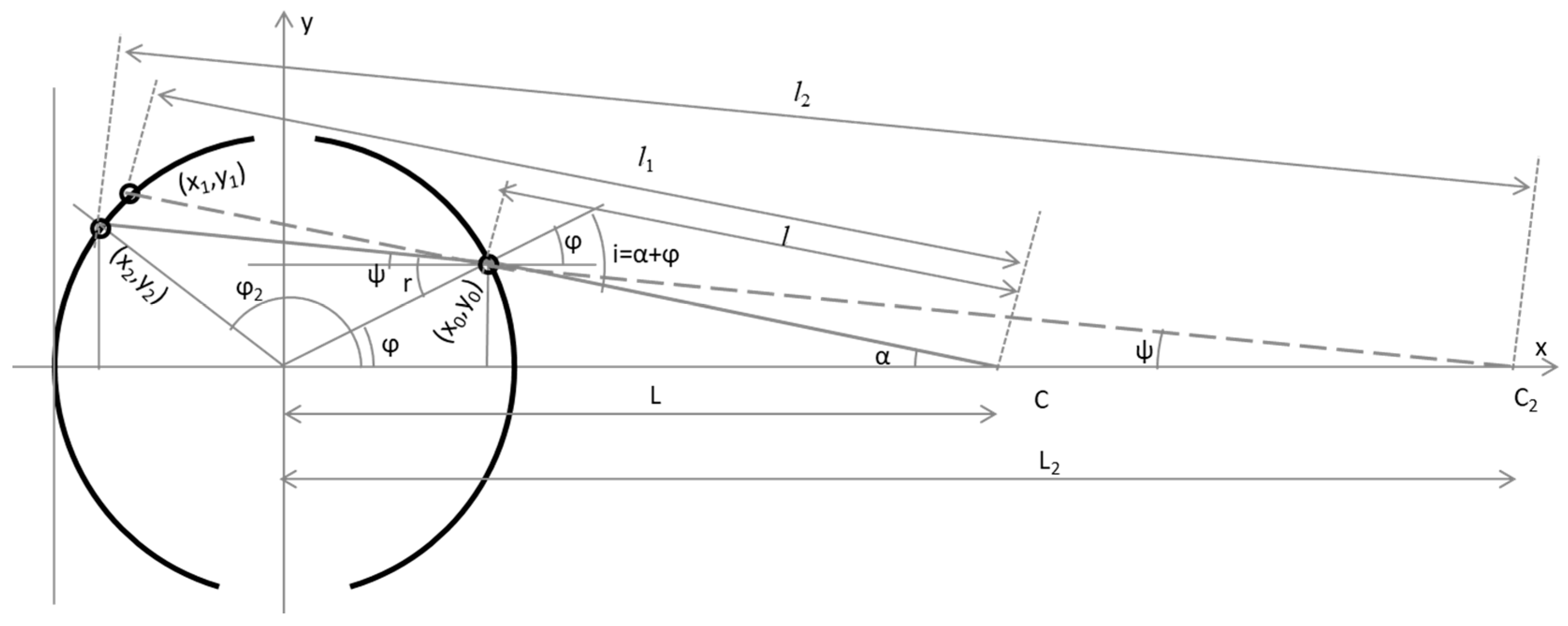
3.1.2. Refractive Magnification in a Cylinder

The geometry of our problem (see Figure 7) is similar to the central projection discussed in [2]. Note the second, imaginary point C₂ at the intersection of the extended refracted ray with the abscissa; L₂ and l₂ are distances to it. The angles α and ψ are small, but the angles φ₁ and φ₂ are not.

According to [2], the coordinates of the intersection point of the camera ray with the cylindrical surface are as follows:

$$\tilde{x}=\tilde{L}-\tilde{l}\mathit{cos}\alpha$$

(28)

$$\tilde{y}=\tilde{l}\mathit{sin}\alpha$$

(29)

where L is the distance from the center of the cylinder to the camera, and l is the distance from the camera to the intersection point:

$$\tilde{l}=\tilde{L}\mathit{cos}\alpha \pm \sqrt{1-{\tilde{L}}^2{\mathit{sin}}^2\alpha }$$

(30)

where the upper sign refers to the concave half of the cylinder (far from the camera), and the lower sign refers to the convex half (near the camera).

Near Surface

On the near (refracting) surface, for small angles, we have from Equation (30),

$$\tilde{l}=\tilde{L}-1$$

(31)

From geometry, using Equation (31), the formulas Equations (28) and (29) can be rewritten for small angles,

$${\tilde{x}}_0=1$$

(32)

$${\tilde{y}}_0=\left(\tilde{L}-1\right)\alpha$$

(33)

$$\phi =\tilde{l}\alpha =\left(\tilde{L}-1\right)\alpha$$

(34)

On the near surface, the incident angle given by Equation (7) can be expressed using Equation (34),

$$i=\alpha +\left(\tilde{L}-1\right)\alpha =\tilde{L}\alpha$$

(35)

Then, from Equation (6),

$$r={\displaystyle \frac{\tilde{L}\alpha }{n}}$$

(36)

From Equations (8), (36) and (34), we obtain the first formula for ψ,

$$\psi =r-\phi =\left({\displaystyle \frac{1-n}{n}}\tilde{L}+1\right)\alpha$$

(37)

Far Surface

There are two intersections of the physical and extended rays with the far surface; for them, we have the following:

$${\tilde{l}}_1=\tilde{L}+1$$

(38)

$${\tilde{l}}_2={\tilde{L}}_2+1$$

(39)

$${\tilde{x}}_1=-1$$

(40)

$${\tilde{y}}_1=\left(\tilde{L}+1\right)\alpha$$

(41)

$${\tilde{x}}_2=-1$$

(42)

$${\tilde{y}}_2=\left({\tilde{L}}_2+1\right)\psi$$

(43)

Therefore, in the first order approximation, the intersections 1 and 2 have the same abscissas but different ordinates.

Using geometry and Equations (32) and (33), we obtain the second formula for ψ

$$\tan \psi ={\displaystyle \frac{{\tilde{y}}_0}{{\tilde{L}}_2-{\tilde{x}}_0}}={\displaystyle \frac{\left(\tilde{L}-1\right)\alpha }{{\tilde{L}}_2-1}}$$

(44)

Combining two Equations (37) and (44) for ψ (small angle), we obtain

$${\displaystyle \frac{\tilde{L}-1}{{\tilde{L}}_2-1}}={\displaystyle \frac{1-n}{n}}\tilde{L}+1$$

(45)

We solve Equation (45) for ${\tilde{L}}_2$:

$${\tilde{L}}_2={\displaystyle \frac{\tilde{L}}{n}}{\displaystyle \frac{1}{\frac{1-n}{n}\tilde{L}+1}}$$

(46)

Formula for Refractive Magnification in a Cylinder

Substitute Equations (46) and (37) into Equation (43),

$${\tilde{y}}_2=\left(\nu \tilde{L}+1\right)\alpha$$

(47)

Using the visible size Equations (3) and (41), and the physical size Equations (4) and (47), the refractive magnification in the cylinder according to Equation (2) is equal to

$$M_{◯}={\displaystyle \frac{\tilde{L}+1}{\nu \tilde{L}+1}}$$

(48)

When $\tilde{L}$ = 1, $M_{◯}\left(1\right)=n$. At large distances, the refractive magnification in the cylinder is constant and depends on the refractive index,

$$M_{◯}(\infty )\approx {\displaystyle \frac{1}{\nu }}$$

(49)

For n > 1, the derivative of Equation (48) with respect to distance is positive, so the function increases from n to the above value (in water, to approximately 2).

The calculated refractive magnification in the cylinder filled with water is shown in Figure 8, where it is slightly less than 2 (at large distances, it is approximately twice the refractive magnification in the box).

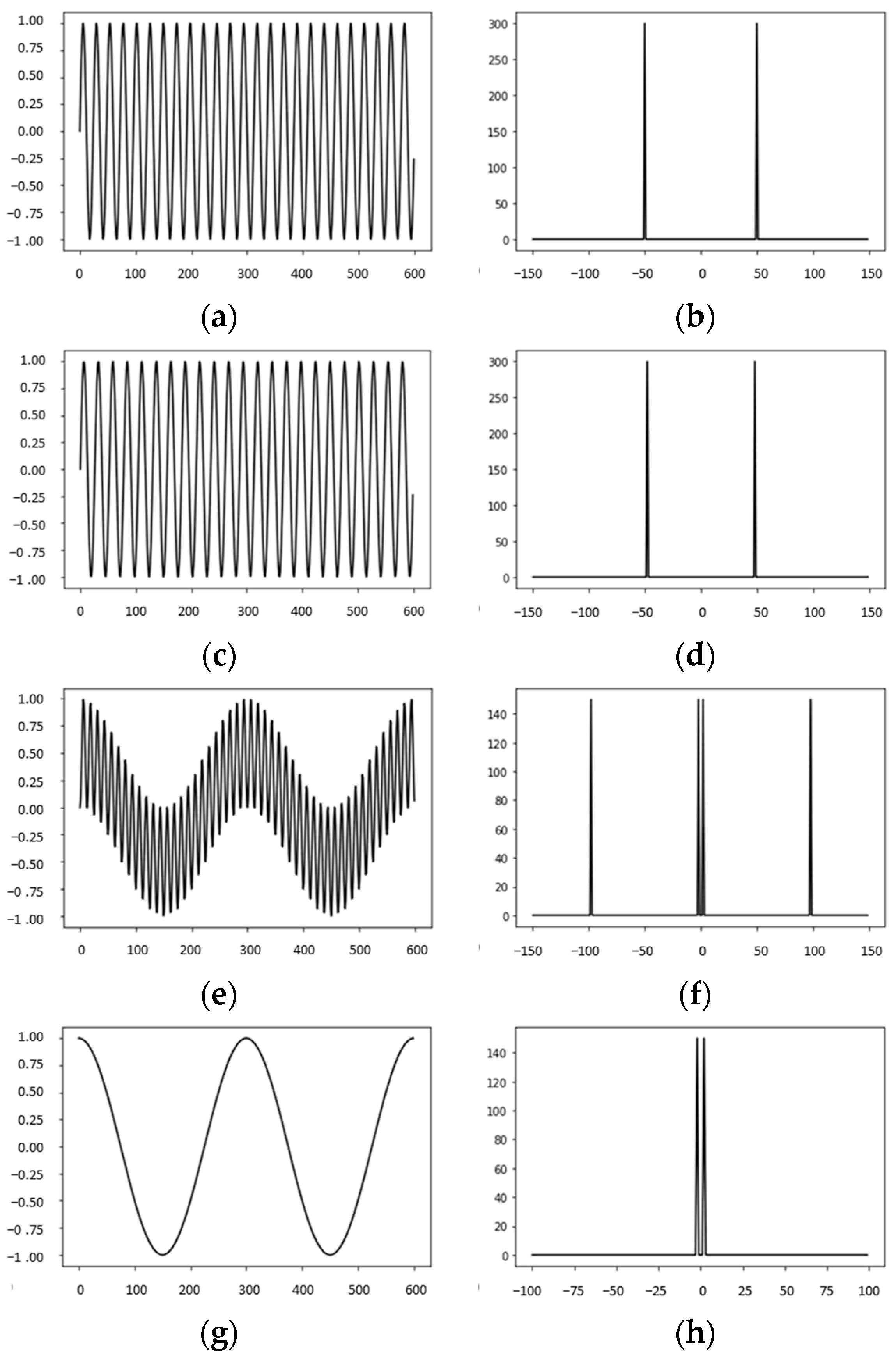
3.2. Moiré Effect

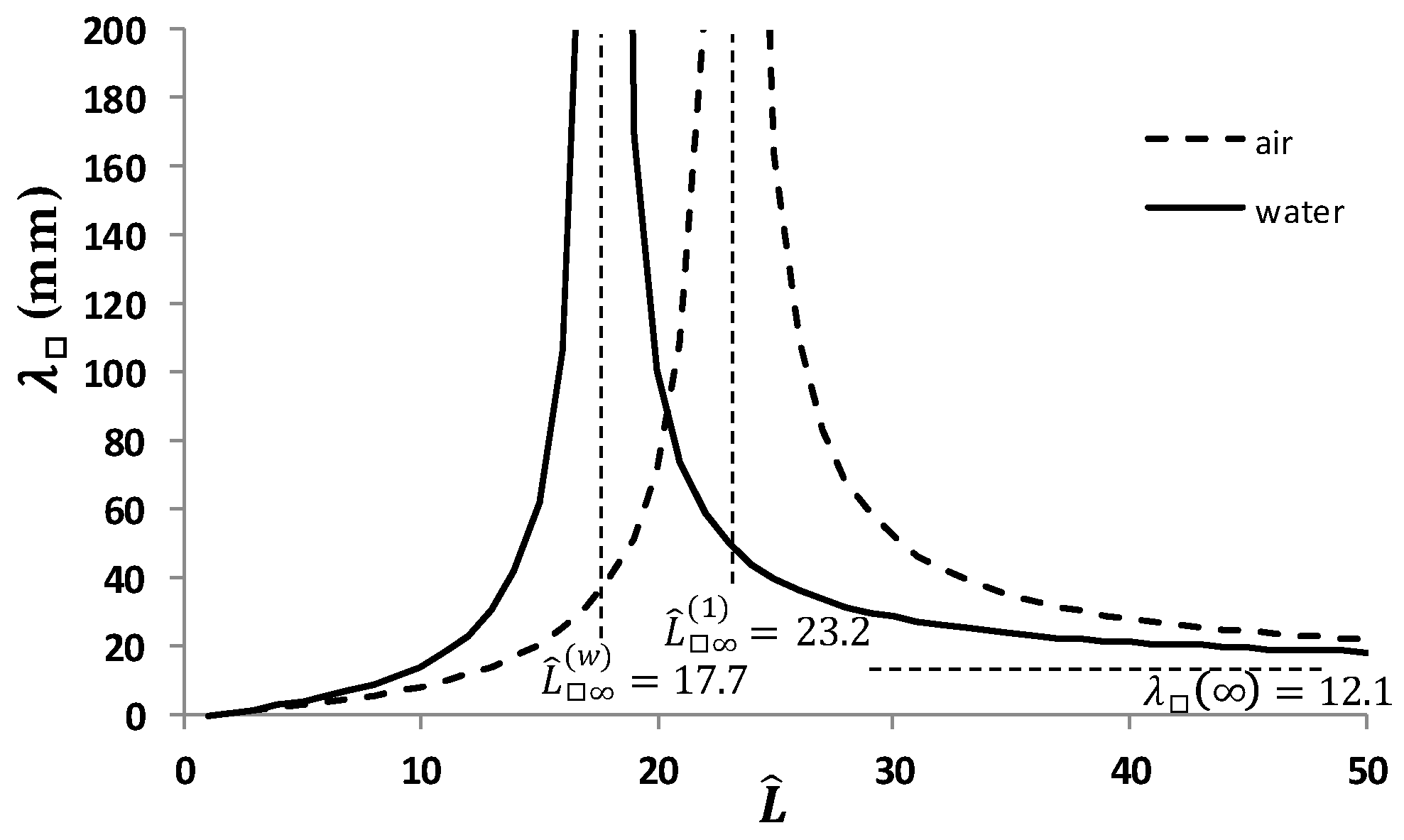
3.2.1. Moiré Effect in Parallelepiped

Let us find the second period projected on the first plane of the empty rectangular container based on the geometry. From the similar triangles in Figure 5, given y₂ = λ₂, y₁ = λ_2′), we obtain

$${\lambda }_2\prime ={\displaystyle \frac{L-W}{L+W}}{\lambda }_2$$

(50)

where ${\displaystyle \frac{L-W}{L+W}}$ can be called a projection coefficient. Correspondingly,

$$k_2\prime ={\displaystyle \frac{L+W}{L-W}}{k}_2$$

(51)

The first projected period coincides with itself. Then, according to the fundamental formula Equation (16), the moiré wavenumber is,

$$k_m={\displaystyle \frac{L+W}{L-W}}{k}_2-k_1$$

(52)

In the filled container, the far grid increases in the refracting substance (see Equation (15)), so using Equation (13) and the relative quantity Equation (17), we have

$$k_M=k_{near}\left({\displaystyle \frac{1}{\rho M_{◻}}}{\displaystyle \frac{\widehat{L}+1}{\widehat{L}-1}}-1\right)$$

(53)

Substituting M_◻ from Equation (27) into Equation (53), we obtain the moiré wavenumber in the parallelepiped,

$$k_{M◻}={\displaystyle \frac{k_{near}}{\rho }}{\displaystyle \frac{\left(1-\rho \right)\widehat{L}+\left(\nu +\rho \right)}{\widehat{L}-1}}$$

(54)

The corresponding moiré period is

$${\lambda }_{◻}={\lambda }_{near}\left|{\displaystyle \frac{\rho \left(\widehat{L}-1\right)}{\left(1-\rho \right)\widehat{L}+\left(\nu +\rho \right)}}\right|$$

(55)

Similar to the magnification M, we consider the moiré period as a function of distance.

When $\widehat{L}=1$, the function according to Equation (55) is zero. When $\widehat{L}=\infty$,

$${\lambda }_{◻}(\infty )={\lambda }_{near}\left|{\displaystyle \frac{\rho }{1-\rho }}\right|$$

(56)

The period reaches infinity at the distance where the denominator is zero:

$${\widehat{L}}_{◻\infty }={\displaystyle \frac{\nu +\rho }{\rho -1}}$$

(57)

The derivative of the function under the modulus operator in Equation (55) is positive, so the function 1/k rises, reaching infinity at the intermediate point given by Equation (57). However, the period (the modulus of the inverse k) increases and decreases.

The calculated moiré period is shown in Figure 9 for air and water; characteristic lines are also indicated.

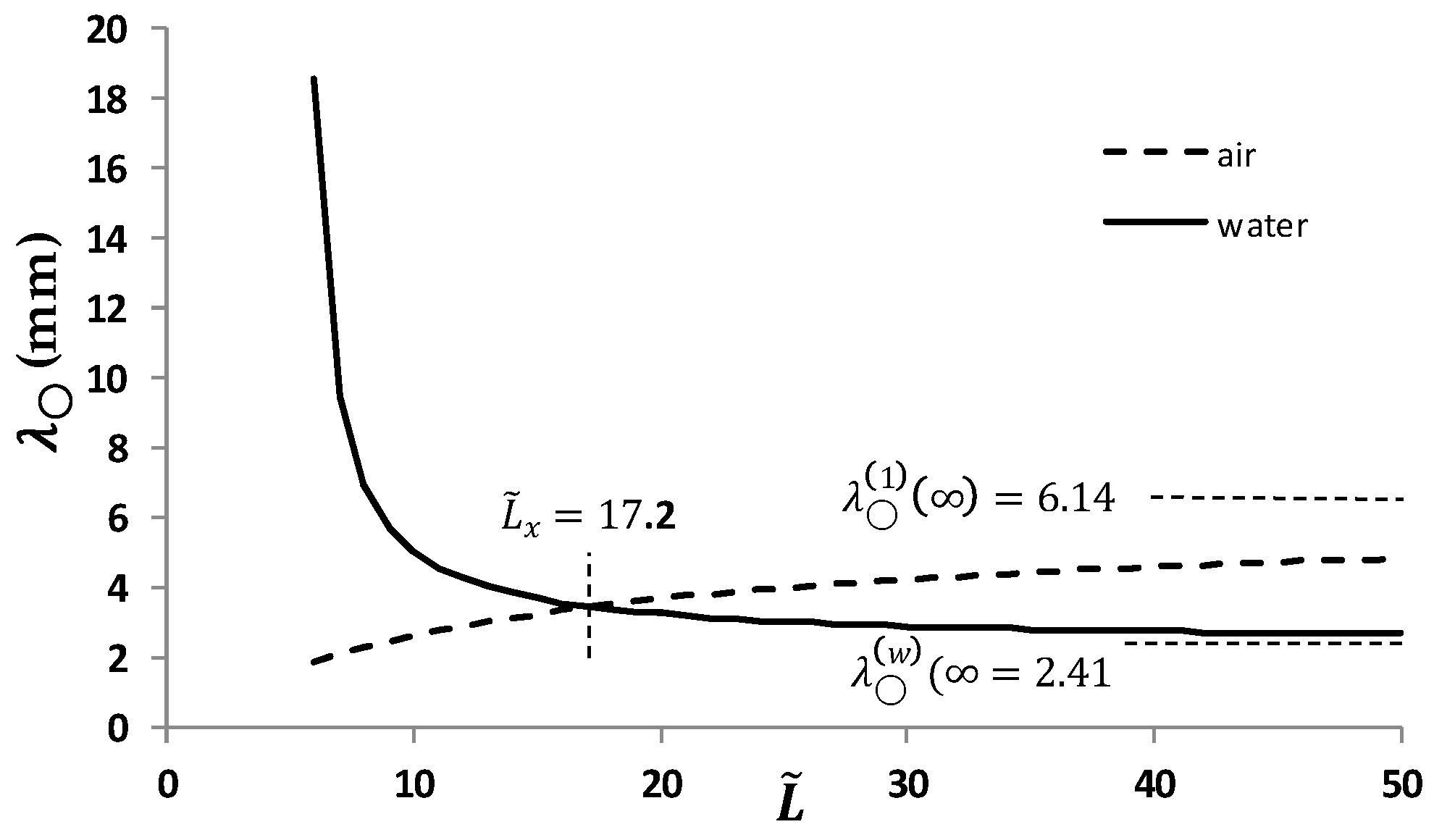
3.2.2. Moiré Effect in a Cylinder

The projected wavenumber of a cylindrical surface is known (see Equation (3.64) in [2]), see also [21] with a different position of the origin,

$$k^{\prime }=k{\cos }^2\alpha {\displaystyle \frac{\Lambda \pm 1}{\tilde{L}}}$$

(58)

where the auxiliary quantity Λ is defined as

$$\Lambda ={\displaystyle \frac{\tilde{L}\cos \alpha }{\sqrt{1-{\tilde{L}}^2{\sin }^2\alpha }}}$$

(59)

(For small angles, $\Lambda \approx \tilde{L}$.)

The moiré wavenumber can be obtained from Equation (58) based on the fundamental formula Equation (16); for small angles, we have

$$k_{M◯}\approx k_{NEAR}{\displaystyle \frac{1}{\tilde{L}}}\left({\displaystyle \frac{\tilde{L}+1}{M_{◯}{\rho }_0}}-\left(\tilde{L}-1\right)\right)$$

(60)

Using the refractive magnification Equation (48), we obtain

$$k_{M◯}=k_{NEAR}{\displaystyle \frac{1}{{\rho }_0\tilde{L}}}\left(\left(\nu -{\rho }_0\right)\tilde{L}+\left({\rho }_0+1\right)\right)$$

(61)

The corresponding moiré period is

$${\lambda }_{◯}={\lambda }_{NEAR}\left|{\displaystyle \frac{{\rho }_0\tilde{L}}{\left(\nu -{\rho }_0\right)\tilde{L}+\left(1+{\rho }_0\right)}}\right|$$

(62)

At $\tilde{L}=1$, the period is

$${\lambda }_{◯}(1)={\lambda }_{NEAR}{\displaystyle \frac{n{\rho }_0}{2}}$$

(63)

At $\tilde{L}=\infty$,

$${\lambda }_{◯}(\infty )={\lambda }_{near}\left|{\displaystyle \frac{{\rho }_0}{\nu -{\rho }_0}}\right|$$

(64)

The asymptotes in air and water are, respectively,

$${\lambda }_{◯}^{\left(1\right)}(\infty )={\lambda }_{near}\left|{\displaystyle \frac{{\rho }_0}{1-{\rho }_0}}\right|$$

(65)

$${\lambda }_{◯}^{\left(w\right)}(\infty )={\lambda }_{near}\left|{\displaystyle \frac{{\rho }_0}{\frac{1}{2}-{\rho }_0}}\right|$$

(66)

The moiré period reaches infinity when the denominator of Equation (62) is zero:

$${\widehat{L}}_{◯\infty }={\displaystyle \frac{1+{\rho }_0}{{\rho }_0-\nu }}$$

(67)

The derivative of the function under the modulus in Equation (62) (the inverse k in Equation (61)) is positive, i.e., the function under the modulus increases. However, in water, the right branch of the period (the absolute value) decreases, so the functions in water and in air intersect. The intersection point L_x can be found from the condition

$${\displaystyle \frac{1}{k_{◯}^{\left(1\right)}}}=-{\displaystyle \frac{1}{k_{◯}^{\left(w\right)}}}$$

(68)

and

$${\tilde{L}}_x={\displaystyle \frac{{\rho }_0+1}{{\rho }_0-\frac{1}{n}}}$$

(69)

The calculated periods are shown in Figure 10 for air and water (ρ = 0.86); characteristic points and lines are also indicated.

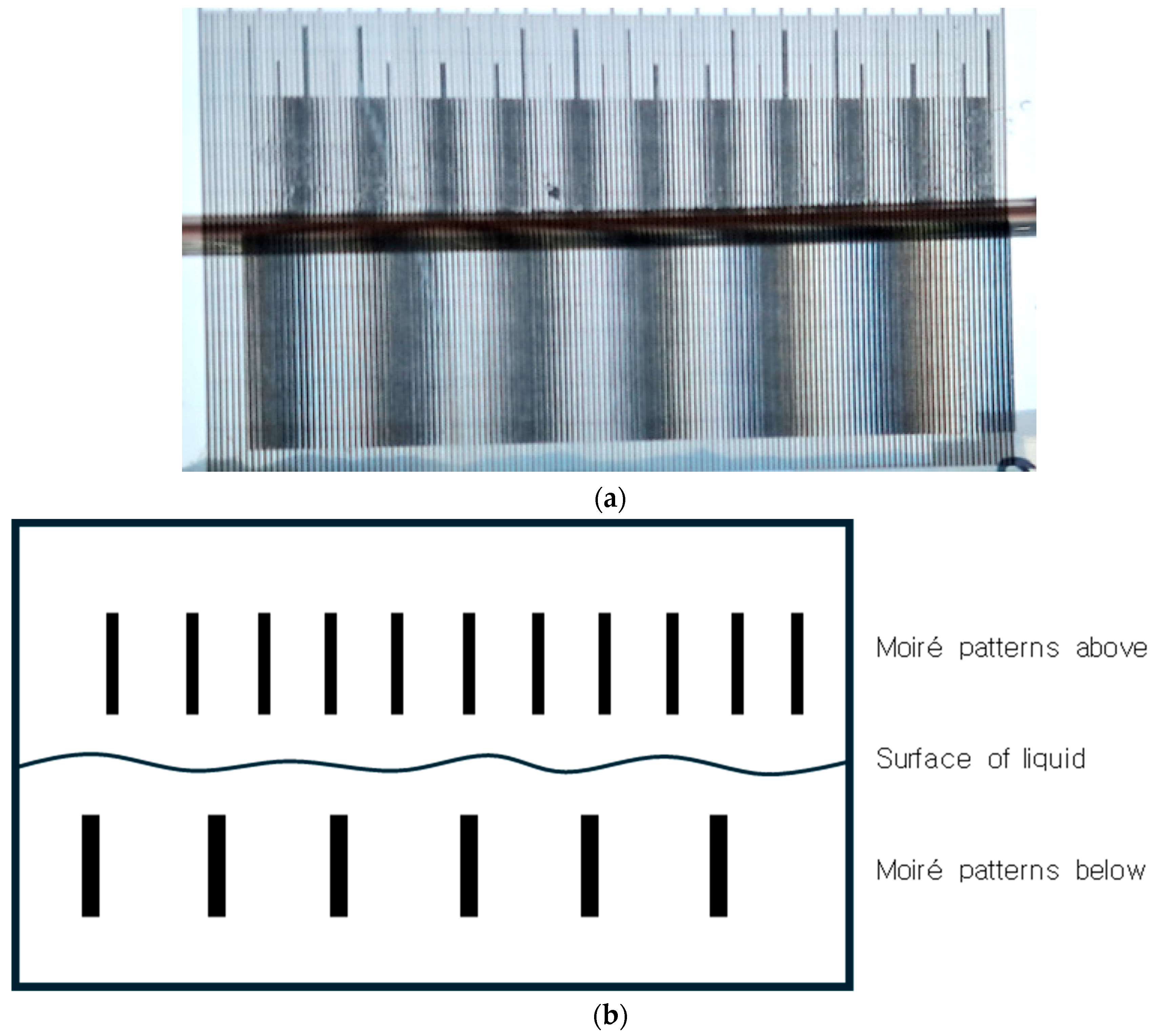
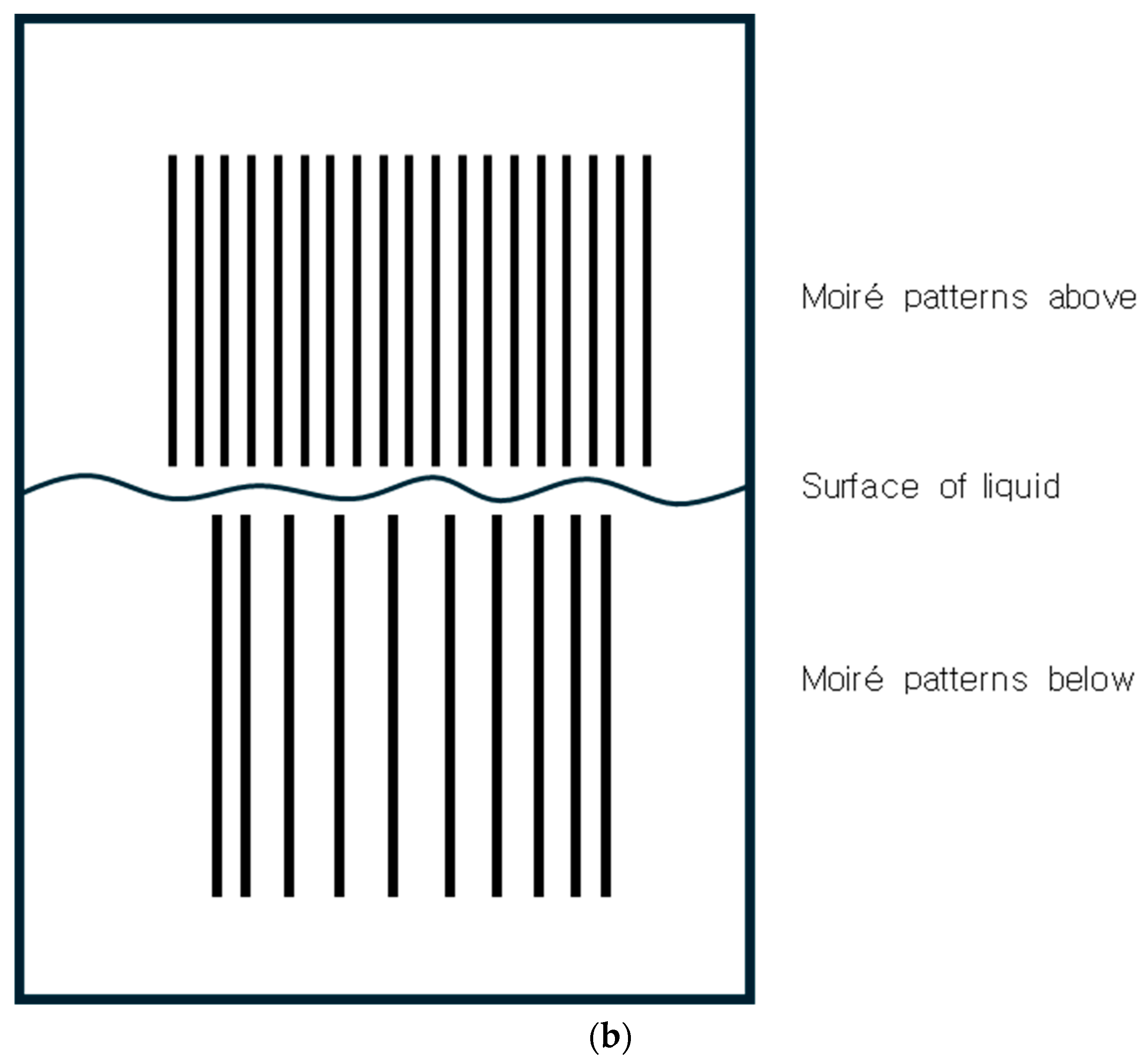
3.3. Experiments

The dimensions of the transparent plastic objects we used in experiments were as follows. The width of the rectangular container was 4.8 cm (W = 2.4 cm), other dimensions were 30 cm × 18 cm. The diameter of the cylindrical container was 7.4 cm (R = 3.7 cm); the height was 10 cm. In the first experiment, the grid period was 1 mm; the same for the front surfaces of both objects in the second experiment. The rear surfaces in the second experiment had grid periods of 1.09 mm (the box) and 0.89 mm (the cylinder).

The FHD2K cameras used in the experiments were the DRGO web camera, resolution 1080p (Dareum International, Goyang, Republic of Korea), and the mobile phone Galaxy S5, with a resolution of 1920 × 1080 (Samsung Electronics, Suwon, Republic of Korea).

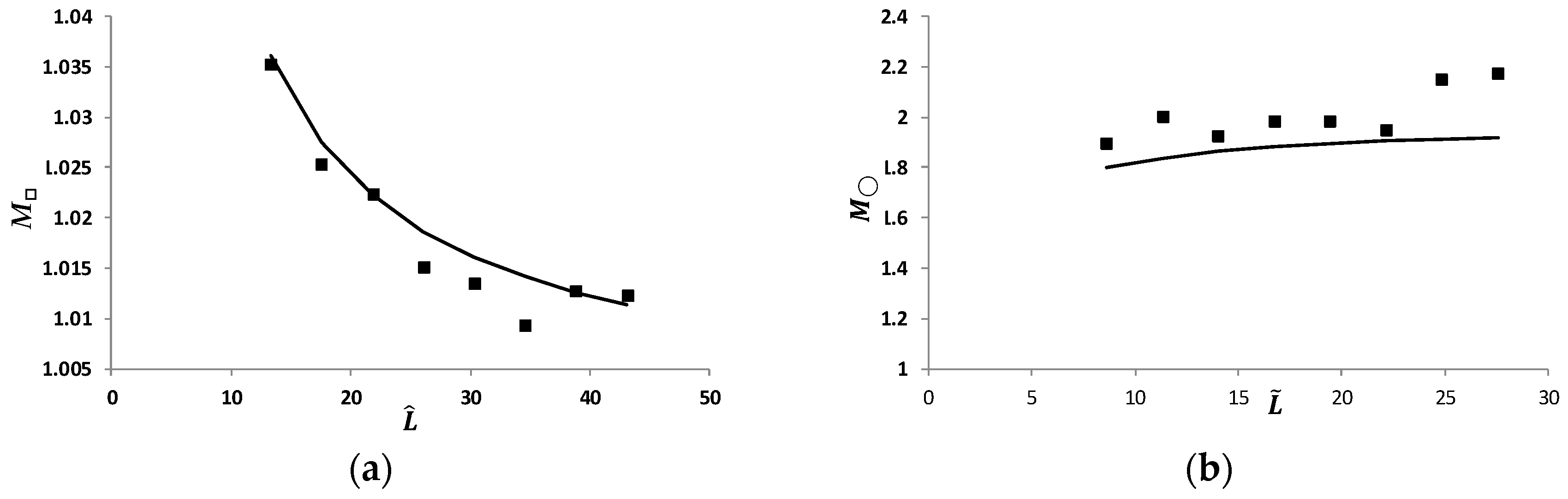
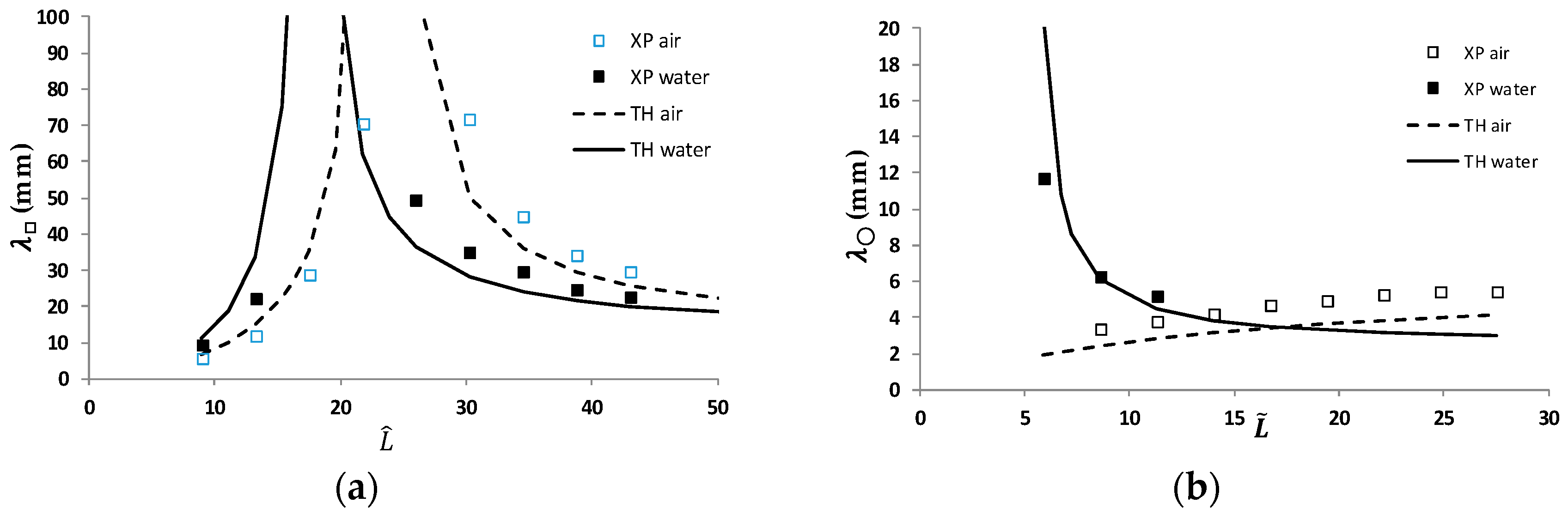
3.3.1. Experimental Refractive Magnification

The moiré magnification was measured by the apparent size of the entire grid attached to the far surface (the white lines with arrows in Figure 11 and Figure 12) photographed through the container above and below the surface of the liquid (the camera axis was horizontal, directed along the x-axis to the origin).

The graph is shown in Figure 13a for the rectangular water tank with 2W = 4.8 cm; the deviation of experiments from the theory (Equation (48)) is 0.2%. In the cylinder with R = 3.7 cm (see Figure 13b), the deviation from Equation (62) is 7.8%.

Note that all visible grid lines are uniformly distributed across the rectangular container. In contrast, within a narrow angular range of the cylindrical surface (near the projection of the cylinder’s axis [4]), there are only a few nearly equidistant lines.

3.3.2. Experimental Moiré Period

Examples of moiré patterns in the box and the cylinder with two grids at near and far surfaces are shown in Figure 14 and Figure 15, together with the scheme. As in the previous experiment with a single grid (Figure 12 and Figure 13), the camera axis was horizontal and directed to the origin; the photographs show the yz-plane above and below the water surface.

The moiré period was measured as follows. The size of several periods of the moiré patterns was measured in pixels. The known width of the grid was also measured in pixels, allowing the pixel-per-millimeter ratio to be calculated for a given photograph. Then the moiré period in mm can be determined. The results are presented in Figure 16 for the objects shown in Figure 14 and Figure 15: the box with 2W = 4.8 cm (ρ = 1.09) and the cylinder with R = 3.7 cm (ρ = 0.86).

4. Discussion

The analytic expressions for a parallelepiped and a cylinder are somewhat similar. The formal difference between the refractive magnification Equation (48) for a cylinder and the corresponding formula for a parallelepiped Equation (27) lies in the position of the coefficient ν in the denominator. Similarly, Equations (55) and (62) differ in the signs and positions of the coefficients (1 ± ρ) and ($\nu$ ± ρ).

The physical meaning of the refractive medium is to increase the effective distance to the camera, which can be seen at the extended backward refracted ray (beyond point C) in Figure 5 and Figure 7 (point C₂ in the latter case). This means that in a camera with a horizontal axis (parallel to the water surface), we can observe the moiré effect as if from two different distances simultaneously. These differences manifest themselves, in particular, as differences in the sizes and periods of the moiré patterns between the two regions.

In a cylindrical water tank, the accuracy of the refractive magnification measurements based on RMSE is lower than in a box, since the number of grid lines is smaller (e.g., 20 vs. 140). The deviation of the measured moiré period from the theory (RMSE) is about 25% for the box and cylinder, probably for the same reason, since the typical number of the measured moiré fringes was less than ten.

The main sources of experimental errors are irregular grid, tilted grid, non-parallel grid lines on the front and back surfaces, unevenly distributed moiré patterns (out of the angular range on a cylinder or on an inclined parallelepiped), camera axis not perpendicular to the front surface, a small number of grid lines, etc. We have always tried to take into account the possibility of such errors and avoid them as much as possible.

Note that the peak heights at a certain distance are theoretically infinite (as, for example, in Figure 9), and therefore, the data cannot be correctly presented in graphs. It should also be noted that the RMSE criterion may fail near sharp edges of functions that could theoretically be infinite, as in Figure 16.

As the sample size increases, the standard deviation of the sample approaches the actual standard deviation, the variability of the sampling distribution decreases, and accuracy increases.

According to Equation (27), the refractive magnification in the box at a short distance is $M_{◻}^{\left(n\right)}\left(\widehat{L}\to 1\right)=n$, which is 33% greater than 1 for water; this is the case of a scuba diver underwater, for whom L << W. To independently confirm this value, one can recall that when wearing a flat scuba mask, objects underwater appear 33% larger than they are, as noted in [41,42,43].

Equation (55) with n = 1 is the functional analog of the formula for the moiré period in air [18], where the first grid is at the origin. The expression in parentheses in Equation (60) with M = 1 and ρ = 1 is equal to 2, i.e., the same coefficient as in Equation (3.115) in [2] (the moiré wavenumber in a single-layered cylinder without refraction).

We considered the approximation of small angles. Practically, it means that results are valid for the angles less than 8° from the camera axis with 1% accuracy and for the angles less than 18° with 5% accuracy.

Compared with the moiré effect without refraction, the moiré period in the rectangular box is similar, but the distance of the infinite period is shifted, as shown in Equation (57) and Figure 9. However, in a cylinder, the ascending function is replaced by a descending one, as shown in Figure 10.

In this study, we examined the static moiré effect. In future research, we plan to examine moiré with refraction in motion, when objects are moving, in the hopes of discovering interesting visual effects.

Potential applications include measuring the refractive index and liquid level. The measured period of grid lines or moiré patterns, as well as the use of Equations (27) or (55), can indicate the refractive index; however, the latter will have higher accuracy due to the magnification. Liquid level can be measured by comparing the spatial frequencies of moiré patterns above and below the surface.

5. Conclusions

The moiré effect in flat and cylindrical objects with refraction was investigated. Formulas for the magnification coefficient and the moiré period were derived. The theory was confirmed experimentally. Previously published studies confirmed the cases without refraction.

We considered the approximation of small angles (within the angular range of approximately ±18°).

This study is important for understanding the physical properties of the moiré effect with significant refraction. The results can be used in practice for measuring the refractive index or the liquid level.