On the “Bi-Phase” of Fluorescence to Scattering with Single-Fiber Illumination and Detection: A Quasi-Analytical Photon-Transport Approach Operated with Center-Illuminated Area Detection
Abstract
1. Introduction
2. Preliminary Remarks
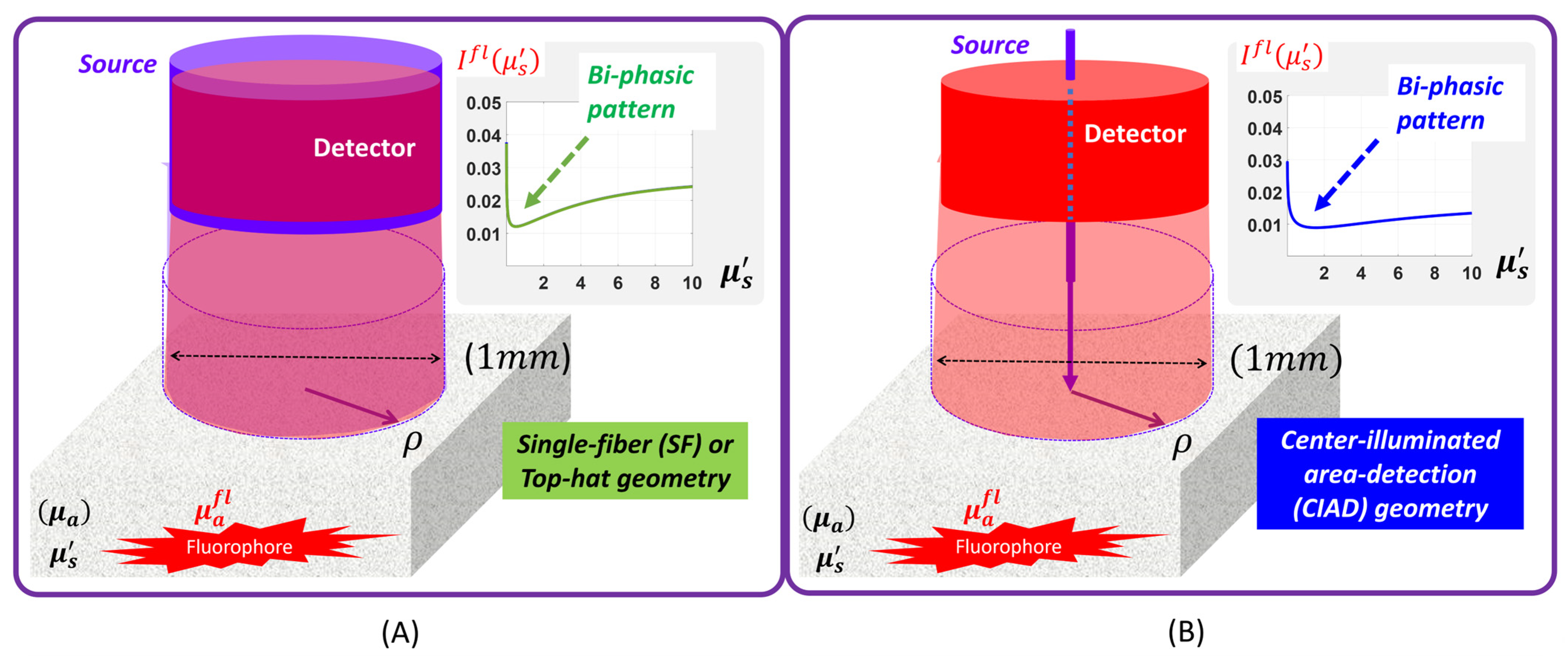
2.1. Correspondence of the Patterns of Fluorescence Projected Between SF and CIAD
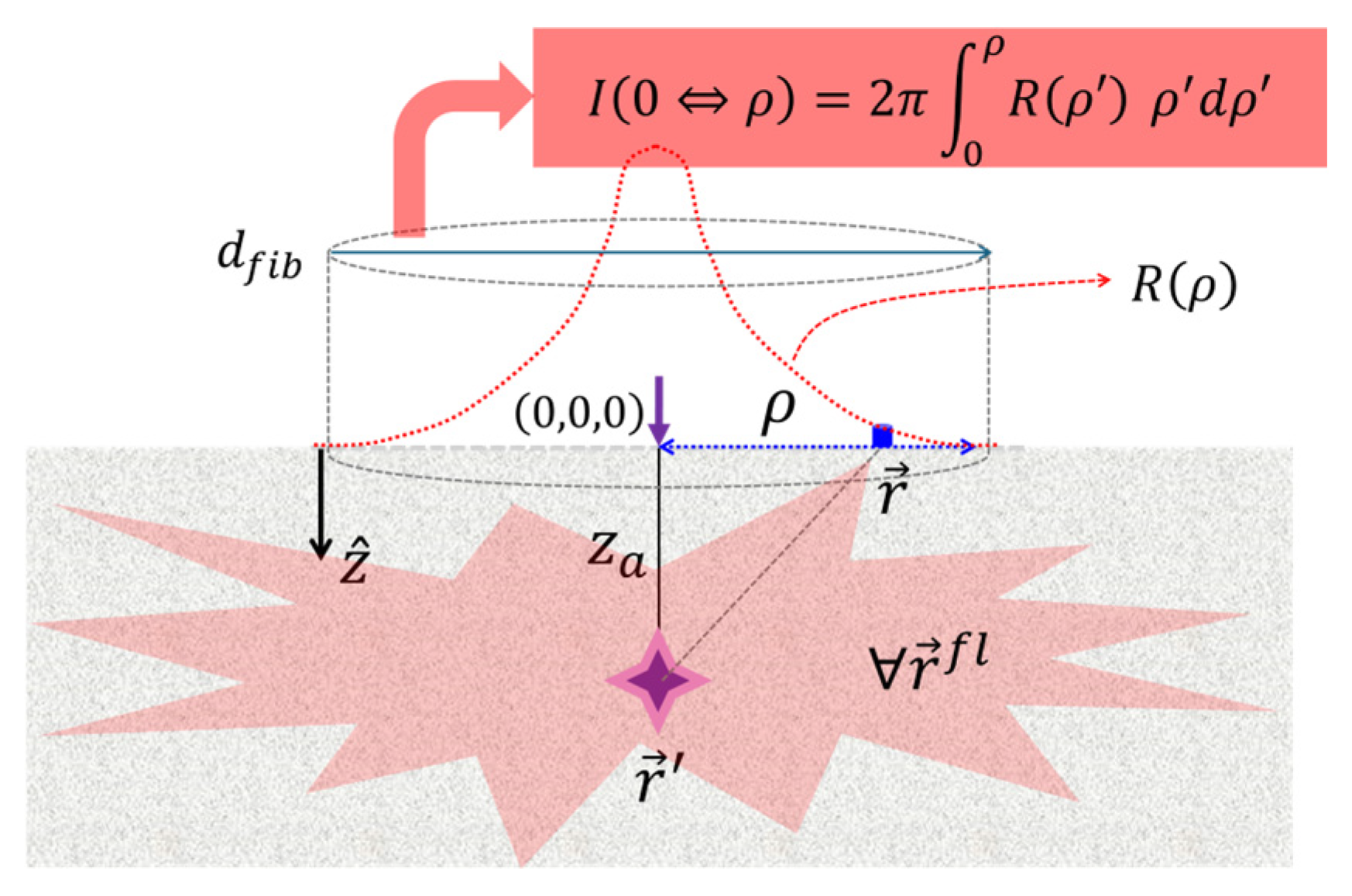
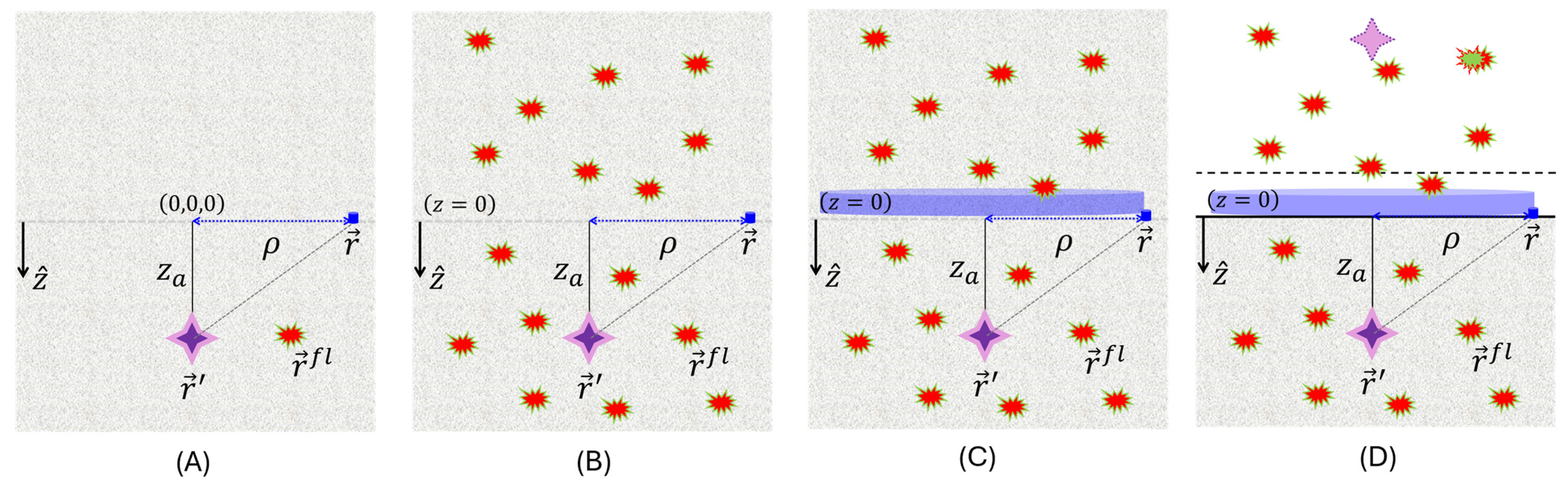
2.2. General Notations and Geometrical Considerations
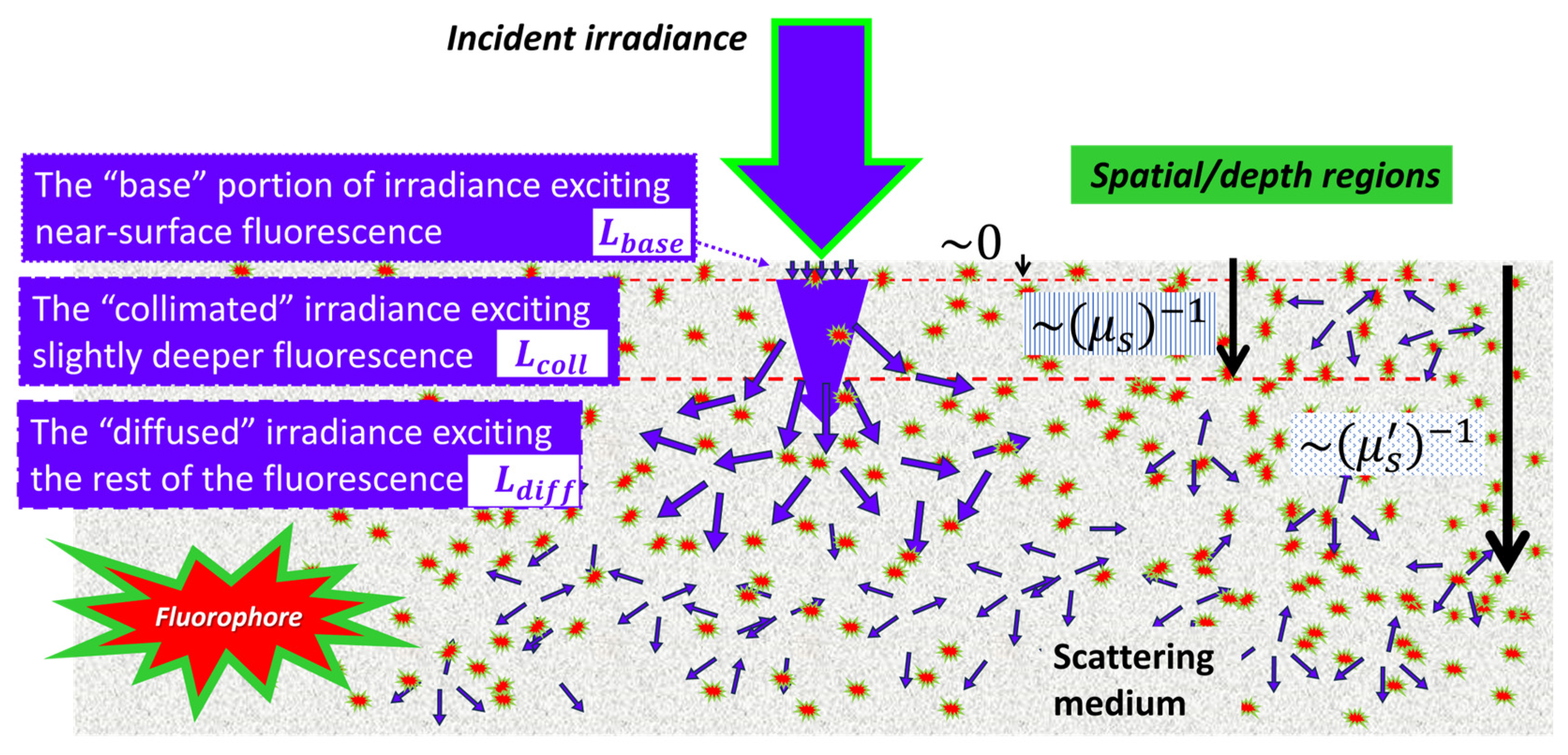
2.3. Decomposition of Radiance Exciting the Fluorescence in CIAD Geometry
2.4. Analytical Routes to a Terminal Form of the Diffuse Proportion of Fluorescence in CIAD Geometry
3. Analytical Approach
3.1. The “Base” Proportion of Fluorescence Associated with Radiative Transfer Treatment of the Irradiation of Excitation on the Extreme Outer Part of the Medium
3.2. The “Collimated” Proportion of Fluorescence Associated with Radiative Transfer Treatment of the Irradiation of Excitation over Approximately One Scattering Path Length
3.3. The “Diffuse” Proportion of Fluorescence Associate with the Diffuse Transport of the Irradiance of Excitation
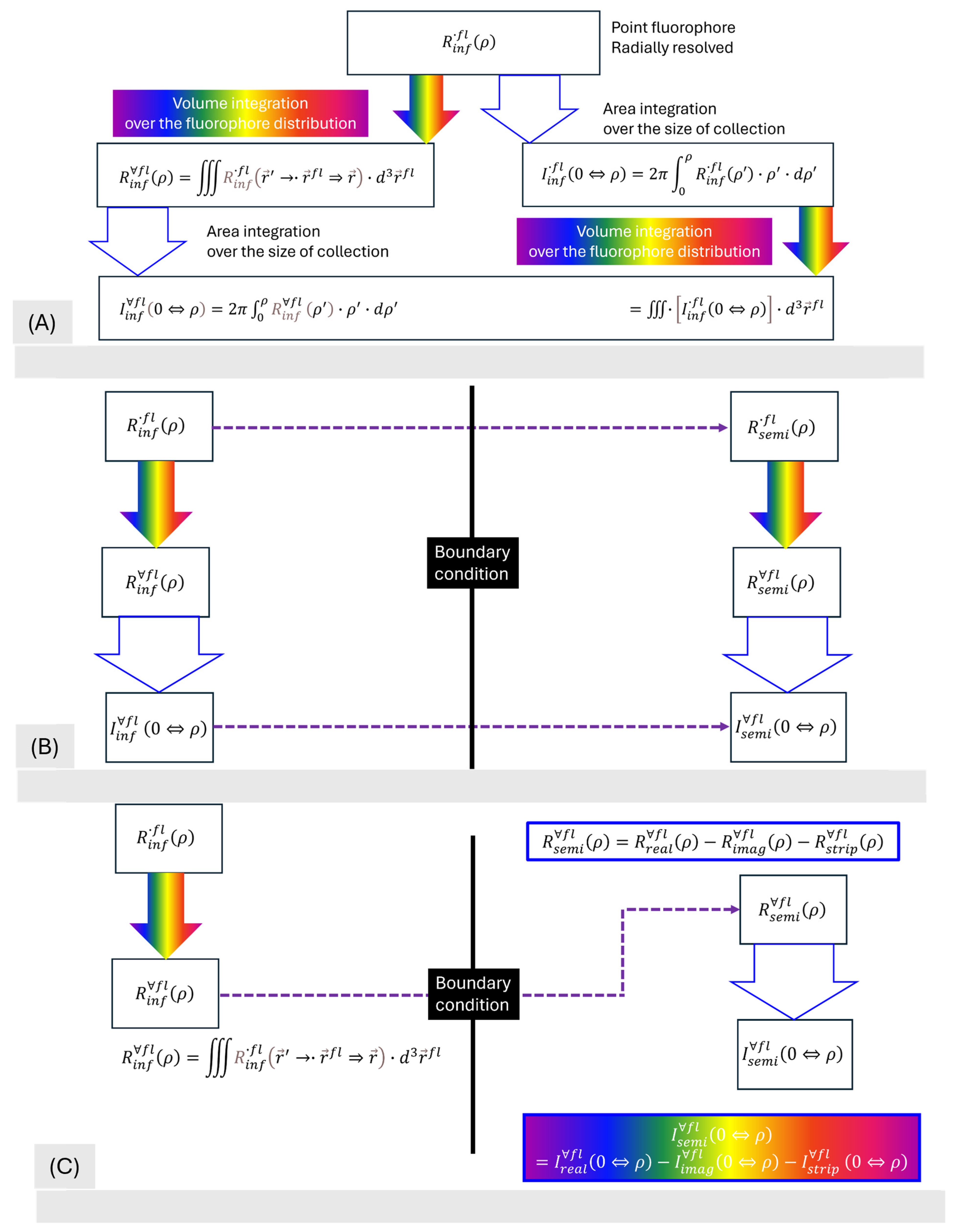
3.3.1. From Point Fluorophore to All Fluorophores
3.3.2. From Point Detection to Area Detection
3.3.3. The Implementation of a Type-III Boundary Condition
3.4. The Terminal Combined Form of the Fluorescence of CIAD
4. Numerical Implementations to Compare Patterns Projected for CIAD and for SF
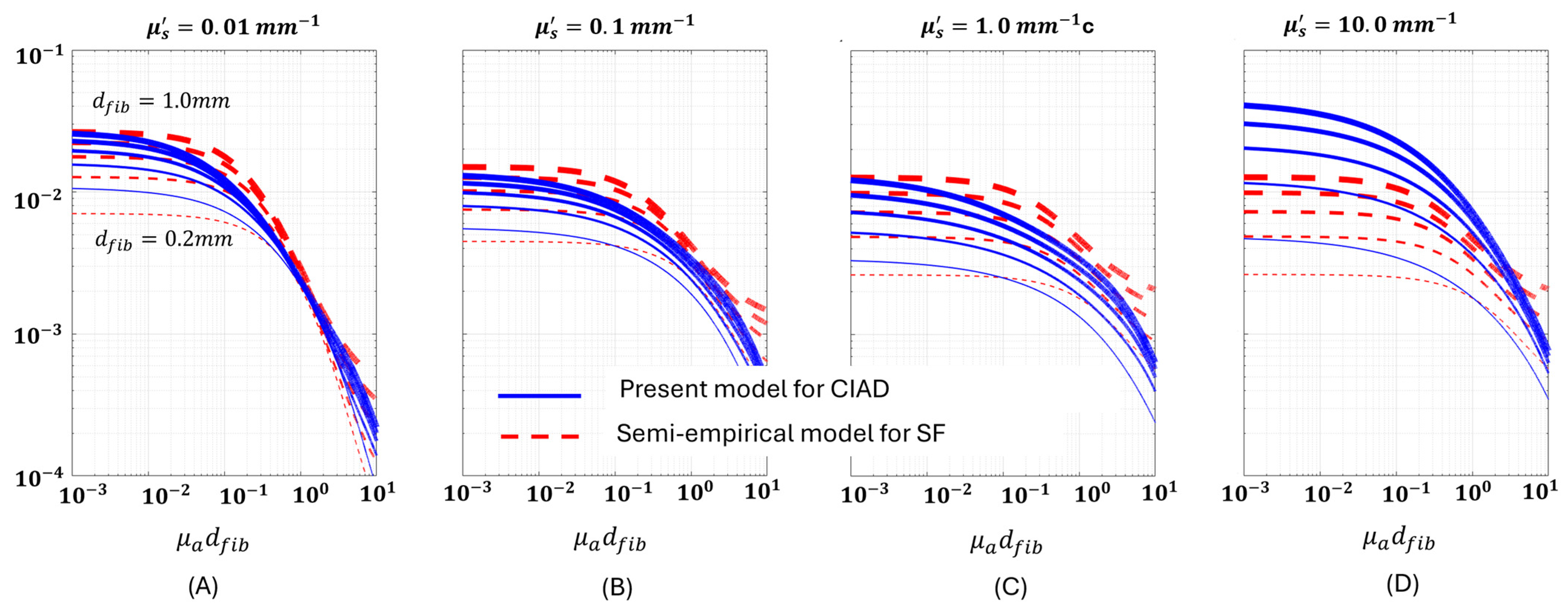
4.1. Fluorescence Versus Dimensionless Scattering Projected for CIAD in Comparison to That for SF
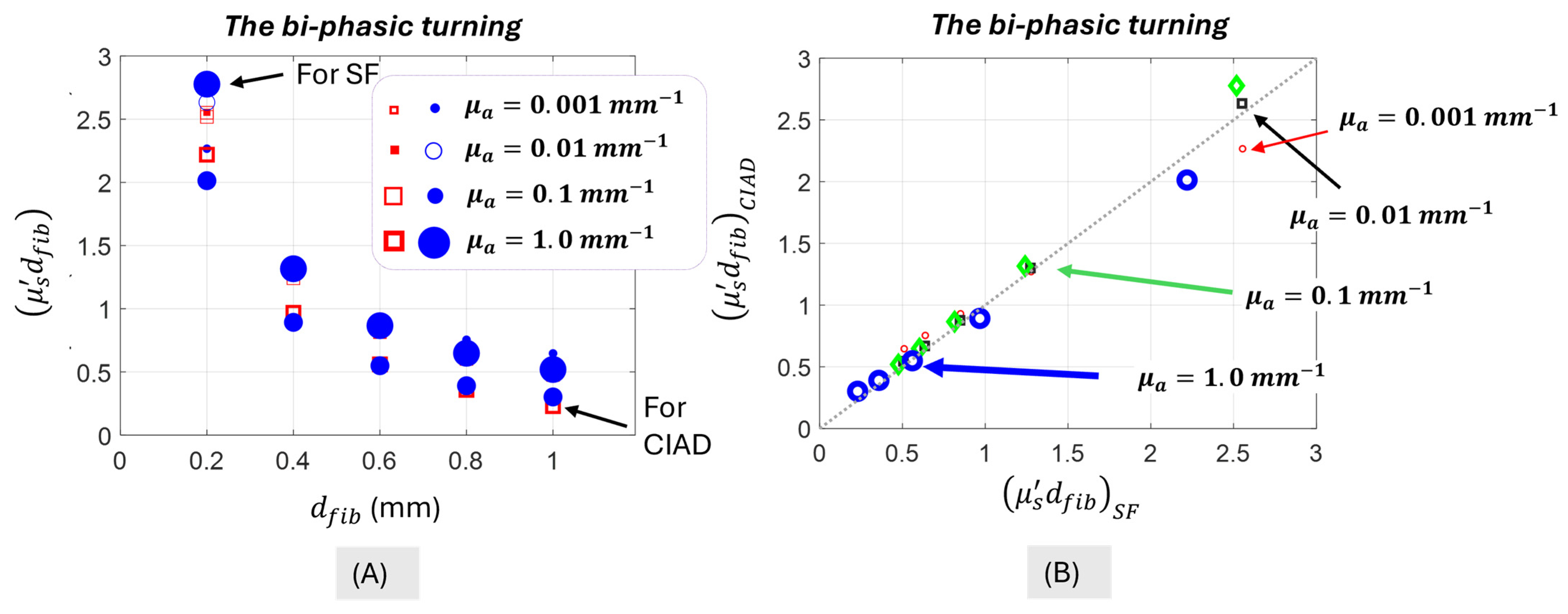
4.2. The Bi-Phasic Turning Point
4.3. Fluroescence Versus Absorption Projected for CIAD in Comparison to That for SF
5. Discussions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Scalability Between Equation (30) and Equation (29)
References
- Voulgarelis, S.; Fathi, F.; Stucke, A.G.; Daley, K.D.; Kim, J.; Zimmerman, M.A.; Hong, J.C.; Starkey, N.; Allen, K.P.; Yu, B. Evaluation of visible diffuse reflectance spectroscopy in liver tissue: Validation of tissue saturations using extracorporeal circulation. J. Biomed. Opt. 2021, 26, 055002. [Google Scholar] [CrossRef] [PubMed]
- Makuła, P.; Pacia, M.; Macyk, W. How To Correctly Determine the Band Gap Energy of Modified Semiconductor Photocatalysts Based on UV–Vis Spectra. J. Phys. Chem. Lett. 2018, 9, 6814–6817. [Google Scholar] [CrossRef] [PubMed]
- Dupuis, G.; Elias, M.; Simonot, L. Pigment Identification by Fiber-Optics Diffuse Reflectance Spectroscopy. Appl. Spectrosc. 2002, 56, 1329–1336. [Google Scholar] [CrossRef]
- Reeves, J.B.; Zapf, C.M. Mid-infrared Diffuse Reflectance Spectroscopy for Discriminant Analysis of Food Ingredients. J. Agric. Food Chem. 1998, 46, 3614–3622. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Saha, P.S.; Korfhage, M.O.; Zhu, C. Non-contact optical spectroscopy for tumor-sensitive diffuse reflectance and fluorescence measurements on murine subcutaneous tissue models: Monte Carlo modeling and experimental validations. Biomed. Opt. Express 2023, 14, 5418–5439. [Google Scholar] [CrossRef]
- Piao, D.; Borron, H.; Hawxby, A.; Wright, H.; Rubin, E.M. Effects of capsule on surface diffuse reflectance spectroscopy of the subcapsular parenchyma of a solid organ. J. Biomed. Opt. 2018, 23, 121602. [Google Scholar] [CrossRef]
- De Boer, L.L.; Bydlon, T.M.; Van Duijnhoven, F.; Vranken Peeters, M.-J.T.F.D.; Loo, C.E.; Winter-Warnars, G.A.O.; Sanders, J.; Sterenborg, H.J.C.M.; Hendriks, B.H.W.; Ruers, T.J.M. Towards the use of diffuse reflectance spectroscopy for real-time in vivo detection of breast cancer during surgery. J. Transl. Med. 2018, 16, 367. [Google Scholar] [CrossRef]
- Yu, B.; Fu, H.L.; Ramanujam, N. Instrument independent diffuse reflectance spectroscopy. J. Biomed. Opt. 2011, 16, 011010. [Google Scholar] [CrossRef]
- Piao, D.; O’Hara, J.; Bukkapatnam, S.; Ekin, S. Towards Non-Contact Glucose Sensing in Aqueous Turbid Medium at ∼1.1 Meters Distance. IEEE Photonics J. 2020, 12, 1–23. [Google Scholar] [CrossRef]
- Utzinger, U.; Richards-Kortum, R.R. Fiber optic probes for biomedical optical spectroscopy. J. Biomed. Opt. 2003, 8, 121–147. [Google Scholar] [CrossRef]
- Prahl, S.A. A Semi-Analytic Model for Fiber-Based Fluorescence Measurements. In Proceedings of the Biomedical Topical Meeting, Miami, FL, USA, 7–10 April 2002; OSA: Miami Beach, FL, USA; p. WD8. [Google Scholar]
- Pfefer, T.J.; Schomacker, K.T.; Ediger, M.N.; Nishioka, N.S. Light propagation in tissue during fluorescence spectroscopy with single-fiber probes. IEEE J. Sel. Top. Quantum Electron. 2001, 7, 1004–1012. [Google Scholar] [CrossRef]
- Kanick, S.C.; Van Der Leest, C.; Aerts, J.G.J.V.; Hoogsteden, H.C.; Kaščáková, S.; Sterenborg, H.J.C.M.; Amelink, A. Integration of single-fiber reflectance spectroscopy into ultrasound-guided endoscopic lung cancer staging of mediastinal lymph nodes. J. Biomed. Opt. 2010, 15, 017004. [Google Scholar] [CrossRef] [PubMed]
- De Roode, L.M.; De Boer, L.L.; Sterenborg, H.J.C.M.; Ruers, T.J.M. Tissue-probe contact assessment during robotic surgery using single-fiber reflectance spectroscopy. Biomed. Opt. Express 2024, 15, 6756. [Google Scholar] [CrossRef] [PubMed]
- Piao, D.; McKeirnan, K.L.; Sultana, N.; Breshears, M.A.; Zhang, A.; Bartels, K.E. Percutaneous single-fiber reflectance spectroscopy of canine intervertebral disc: Is there a potential for in situ probing of mineral degeneration? Lasers Surg. Med. 2014, 46, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Kanick, S.C.; Robinson, D.J.; Sterenborg, H.J.C.M.; Amelink, A. Monte Carlo analysis of single fiber reflectance spectroscopy: Photon path length and sampling depth. Phys. Med. Biol. 2009, 54, 6991–7008. [Google Scholar] [CrossRef]
- Denzer, M.L.; Piao, D.; Pfeiffer, M.; Mafi, G.; Ramanathan, R. Novel needle-probe single-fiber reflectance spectroscopy to quantify sub-surface myoglobin forms in beef psoas major steaks during retail display. Meat Sci. 2024, 210, 109439. [Google Scholar] [CrossRef]
- Pogue, B.; Testorf, M.; McBride, T.; Osterberg, U.; Paulsen, K. Instrumentation and design of a frequency-domain diffuse optical tomography imager for breast cancer detection. Opt. Express 1997, 1, 391. [Google Scholar] [CrossRef]
- Hariri Tabrizi, S.; Mahmoud Reza Aghamiri, S.; Farzaneh, F.; Amelink, A.; Sterenborg, H.J.C.M. Single fiber reflectance spectroscopy on cervical premalignancies: The potential for reduction of the number of unnecessary biopsies. J. Biomed. Opt. 2013, 18, 017002. [Google Scholar] [CrossRef]
- Alerstam, E.; Svensson, T.; Andersson-Engels, S.; Spinelli, L.; Contini, D.; Mora, A.D.; Tosi, A.; Zappa, F.; Pifferi, A. Single-fiber diffuse optical time-of-flight spectroscopy. Opt. Lett. 2012, 37, 2877–2879. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Ken, C.-F.; Hsu, C.-W.; Liu, Y.-G. Real time in vivo investigation of superoxide dynamics in zebrafish liver using a single-fiber fluorescent probe. Biomed. Opt. Express 2013, 4, 1702–1709. [Google Scholar] [CrossRef]
- Zlobina, N.V.; Budylin, G.S.; Tseregorodtseva, P.S.; Andreeva, V.A.; Sorokin, N.I.; Kamalov, D.M.; Strigunov, A.A.; Armaganov, A.G.; Kamalov, A.A.; Shirshin, E.A. In vivo assessment of bladder cancer with diffuse reflectance and fluorescence spectroscopy: A comparative study. Lasers Surg. Med. 2024, 56, 496–507. [Google Scholar] [CrossRef] [PubMed]
- Gabriëls, R.Y.; Van Heijst, L.E.; Hooghiemstra, W.T.R.; Van Der Waaij, A.M.; Kats-Ugurlu, G.; Karrenbeld, A.; Robinson, D.J.; Tenditnaya, A.; Ntziachristos, V.; Gorpas, D.; et al. Detection of Early Esophageal Neoplastic Barrett Lesions with Quantified Fluorescence Molecular Endoscopy Using Cetuximab-800CW. J. Nucl. Med. 2023, 64, 803–808. [Google Scholar] [CrossRef] [PubMed]
- Kanick, S.C.; Sterenborg, H.J.C.M.; Amelink, A. Empirical model of the photon path length for a single fiber reflectance spectroscopy device. Opt. Express 2009, 17, 860–871. [Google Scholar] [CrossRef] [PubMed]
- Diamond, K.R.; Patterson, M.S.; Farrell, T.J. Quantification of fluorophore concentration in tissue-simulating media by fluorescence measurements with a single optical fiber. Appl. Opt. 2003, 42, 2436–2442. [Google Scholar] [CrossRef]
- Stepp, H.; Beck, T.; Beyer, W.; Pfaller, C.; Schuppler, M.; Sroka, R.; Baumgartner, R. Measurement of fluorophore concentration in turbid media by a single optical fiber. Med. Laser Appl. 2007, 22, 23–34. [Google Scholar] [CrossRef]
- Hoy, C.L.; Gamm, U.A.; Sterenborg, H.J.C.M.; Robinson, D.J.; Amelink, A. Method for rapid multidiameter single-fiber reflectance and fluorescence spectroscopy through a fiber bundle. J. Biomed. Opt. 2013, 18, 107005. [Google Scholar] [CrossRef]
- Van Leeuwen-van Zaane, F.; Gamm, U.A.; Van Driel, P.B.A.A.; Snoeks, T.J.; De Bruijn, H.S.; Van Der Ploeg-van Den Heuvel, A.; Sterenborg, H.J.C.M.; Löwik, C.W.; Amelink, A.; Robinson, D.J. Intrinsic photosensitizer fluorescence measured using multi-diameter single-fiber spectroscopy in vivo. J. Biomed. Opt. 2014, 19, 015010. [Google Scholar] [CrossRef]
- Dablouk, M.O.; Buckley, K.; Eustace, D.; Jansen, M.; Bermingham, N.; Lim, C.; Kamel, M.; Mohammed, W.; O’Sullivan, M.G.J. Use of a Single-Fiber Optical Probe for the Detection of Tumor Fluorescence in High-Grade Glioma. Oper. Neurosurg. 2025, 29, 34–40. [Google Scholar] [CrossRef]
- Kanick, S.C.; Robinson, D.J.; Sterenborg, H.J.C.M.; Amelink, A. Semi-empirical model of the effect of scattering on single fiber fluorescence intensity measured on a turbid medium. Biomed. Opt. Express 2012, 3, 137–152. [Google Scholar] [CrossRef]
- Kanick, S.C.; Robinson, D.J.; Sterenborg, H.J.C.M.; Amelink, A. Extraction of intrinsic fluorescence from single fiber fluorescence measurements on a turbid medium. Opt. Lett. 2012, 37, 948–950. [Google Scholar] [CrossRef]
- Gamm, U.A.; Hoy, C.L.; Van Leeuwen–Van Zaane, F.; Sterenborg, H.J.C.M.; Kanick, S.C.; Robinson, D.J.; Amelink, A. Extraction of intrinsic fluorescence from single fiber fluorescence measurements on a turbid medium: Experimental validation. Biomed. Opt. Express 2014, 5, 1913–1925. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Calculation of the coupling coefficient in strained step index plastic optical fibers. Appl. Opt. 2008, 47, 4935–4939. [Google Scholar] [CrossRef] [PubMed]
- Mateo, J.; Losada, M.A.; Garcés, I.; Zubia, J. Global characterization of optical power propagation in step-index plastic optical fibers. Opt. Express 2006, 14, 9028–9035. [Google Scholar] [CrossRef] [PubMed]
- Simović, A.; Savović, S.; Drljača, B.; Djordjevich, A. Influence of intermediate layer on transmission characteristics of W-type optical fibers. Opt. Laser Technol. 2014, 57, 209–215. [Google Scholar] [CrossRef]
- Hurand, S.; Chauny, L.-A.; El-Rabii, H.; Joshi, S.; Yalin, A.P. Mode coupling and output beam quality of 100–400 μm core silica fibers. Appl. Opt. 2011, 50, 492–499. [Google Scholar] [CrossRef]
- Faber, D.J.; Post, A.L.; Sterenborg, H.J.C.M.; Van Leeuwen, T.G. Analytical model for diffuse reflectance in single fiber reflectance spectroscopy. Opt. Lett. 2020, 45, 2078–2081. [Google Scholar] [CrossRef]
- Piao, D. A new model-perspective on the threshold radius of lasing of a spherical random medium. Waves Random Complex Media 2024, 1–33. [Google Scholar] [CrossRef]
- Sun, T.; Piao, D.; Yu, L.; Murari, K. Diffuse photon-remission associated with single-fiber geometry may be a simple scaling of that collected over the same area when under centered-illumination. Opt. Lett. 2021, 46, 4817–4820. [Google Scholar] [CrossRef]
- Post, A.L.; Faber, D.J.; Sterenborg, H.J.C.M.; Van Leeuwen, T.G. Subdiffuse scattering and absorption model for single fiber reflectance spectroscopy. Biomed. Opt. Express 2020, 11, 6620–6633. [Google Scholar] [CrossRef]
- Post, A.L.; Faber, D.J.; Sterenborg, H.J.C.M.; Van Leeuwen, T.G. Experimental validation of a recently developed model for single-fiber reflectance spectroscopy. J. Biomed. Opt. 2021, 26, 025004. [Google Scholar] [CrossRef]
- Sun, T.; Piao, D. Diffuse photon remission associated with the center-illuminated-area-detection geometry: Part I, an approach to the steady-state model. Appl. Opt. 2022, 61, 9143–9153. [Google Scholar] [CrossRef]
- Sun, T.; Piao, D. Diffuse photon remission associated with the center-illuminated–area-detection geometry. II. Approach to the time-domain model. Appl. Opt. 2023, 62, 3880–3891. [Google Scholar] [CrossRef] [PubMed]
- Vitkin, E.; Turzhitsky, V.; Qiu, L.; Guo, L.; Itzkan, I.; Hanlon, E.B.; Perelman, L.T. Photon diffusion near the point-of-entry in anisotropically scattering turbid media. Nat. Commun. 2011, 2, 587. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, D. Selective imaging of surface fluorescence with very high aperture microscope objectives. J. Biomed. Opt. 2001, 6, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Hyde, D.E.; Farrell, T.J.; Patterson, M.S.; Wilson, B.C. A diffusion theory model of spatially resolved fluorescence from depth-dependent fluorophore concentrations. Phys. Med. Biol. 2001, 46, 369–383. [Google Scholar] [CrossRef]
- Haskell, R.C.; Svaasand, L.O.; Tsay, T.-T.; Feng, T.-C.; Tromberg, B.J.; McAdams, M.S. Boundary conditions for the diffusion equation in radiative transfer. J. Opt. Soc. Am. A 1994, 11, 2727–2741. [Google Scholar] [CrossRef]
- Sun, T.; Piao, D. Simple analytical total diffuse reflectance over a reduced-scattering-pathlength scaled dimension of [10−5, 10−1 ] from a medium with HG scattering anisotropy. Appl. Opt. 2019, 58, 9279–9289. [Google Scholar] [CrossRef]
- Piao, D.; Zhang, A.; Xu, G. Photon diffusion in a homogeneous medium bounded externally or internally by an infinitely long circular cylindrical applicator V Steady-state fluorescence. J. Opt. Soc. Am. A 2013, 30, 791–805. [Google Scholar] [CrossRef]
- Li, X.D.; O’Leary, M.A.; Boas, D.A.; Chance, B.; Yodh, A.G. Fluorescent diffuse photon density waves in homogeneous and heterogeneous turbid media: Analytic solutions and applications. Appl. Opt. 1996, 35, 3746–3758. [Google Scholar] [CrossRef]
- Soubret, A.; Ntziachristos, V. Fluorescence molecular tomography in the presence of background fluorescence. Phys. Med. Biol. 2006, 51, 3983–4001. [Google Scholar] [CrossRef]
- Aronson, R. Boundary conditions for diffusion of light. J. Opt. Soc. Am. A 1995, 12, 2532–2539. [Google Scholar] [CrossRef]
- Piao, D.; Patel, S. Simple empirical master–slave dual-source configuration within the diffusion approximation enhances modeling of spatially resolved diffuse reflectance at short-path and with low scattering from a semi-infinite homogeneous medium. Appl. Opt. 2017, 56, 1447–1452. [Google Scholar] [CrossRef]
- Abookasis, D.; Shemesh, D.; Litwin, A.; Siegelmann, H.T.; Didkovsky, E.; Ad-El, D.D. Single probe light reflectance spectroscopy and parameter spectrum feature extraction in experimental skin cancer detection and classification. J. Biophotonics 2023, 16, e202300001. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, Seventh; Academic Press: Burlington, MA, USA; ISBN 0-12-373637-4.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piao, D. On the “Bi-Phase” of Fluorescence to Scattering with Single-Fiber Illumination and Detection: A Quasi-Analytical Photon-Transport Approach Operated with Center-Illuminated Area Detection. Photonics 2025, 12, 904. https://doi.org/10.3390/photonics12090904
Piao D. On the “Bi-Phase” of Fluorescence to Scattering with Single-Fiber Illumination and Detection: A Quasi-Analytical Photon-Transport Approach Operated with Center-Illuminated Area Detection. Photonics. 2025; 12(9):904. https://doi.org/10.3390/photonics12090904
Chicago/Turabian StylePiao, Daqing. 2025. "On the “Bi-Phase” of Fluorescence to Scattering with Single-Fiber Illumination and Detection: A Quasi-Analytical Photon-Transport Approach Operated with Center-Illuminated Area Detection" Photonics 12, no. 9: 904. https://doi.org/10.3390/photonics12090904
APA StylePiao, D. (2025). On the “Bi-Phase” of Fluorescence to Scattering with Single-Fiber Illumination and Detection: A Quasi-Analytical Photon-Transport Approach Operated with Center-Illuminated Area Detection. Photonics, 12(9), 904. https://doi.org/10.3390/photonics12090904


_Piao.png)

