Design of Grating-Embedded Tantalum Pentoxide Microring Resonators with Piezoelectric Tunability
Abstract
1. Introduction
2. Design Principle
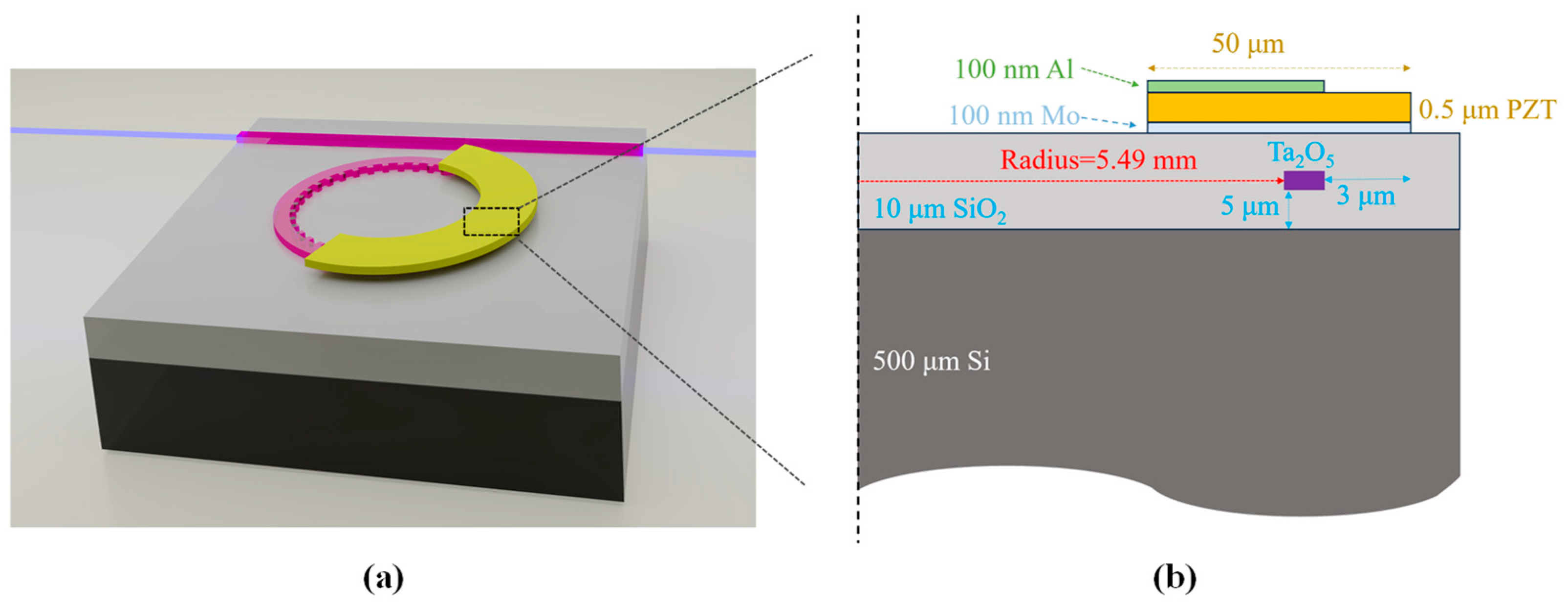
2.1. Design of the Microresonator
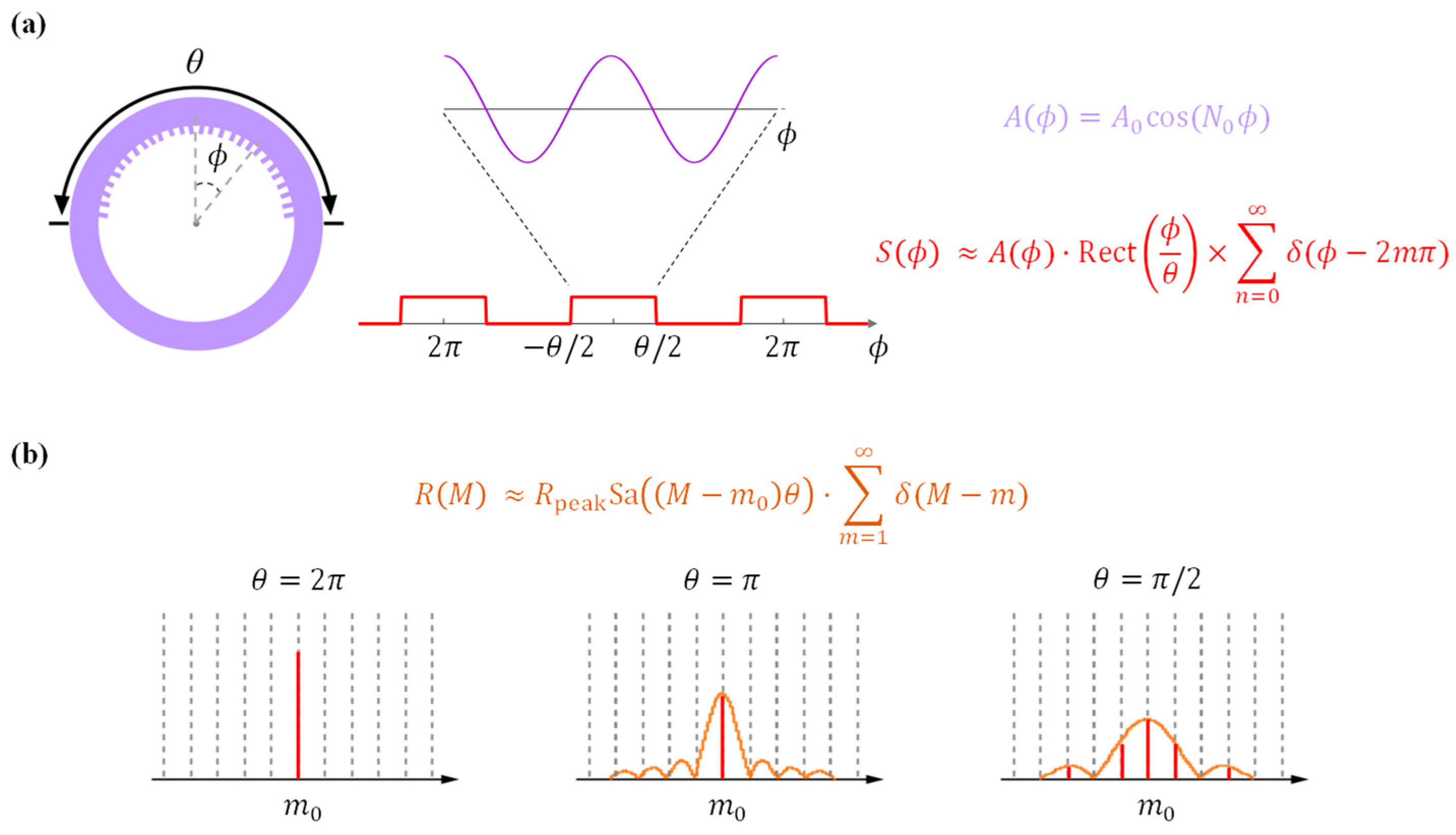
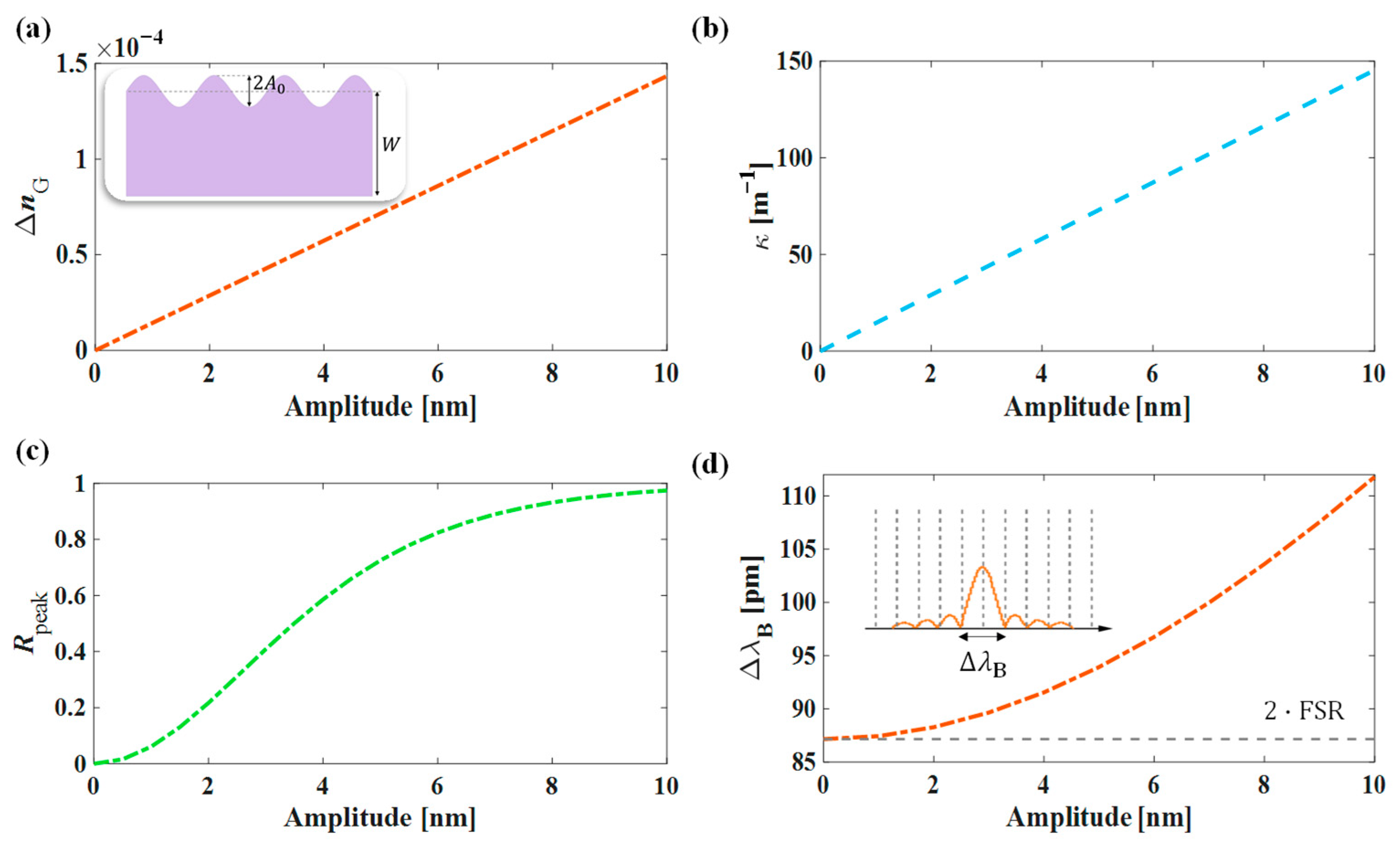
2.2. Design of Bragg Grating
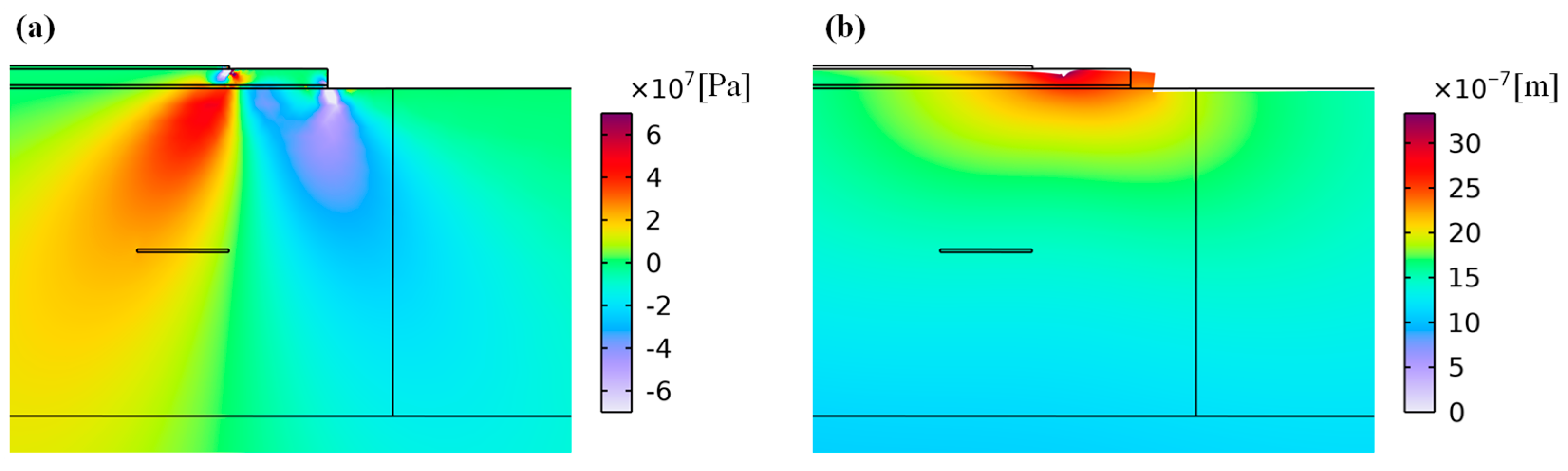
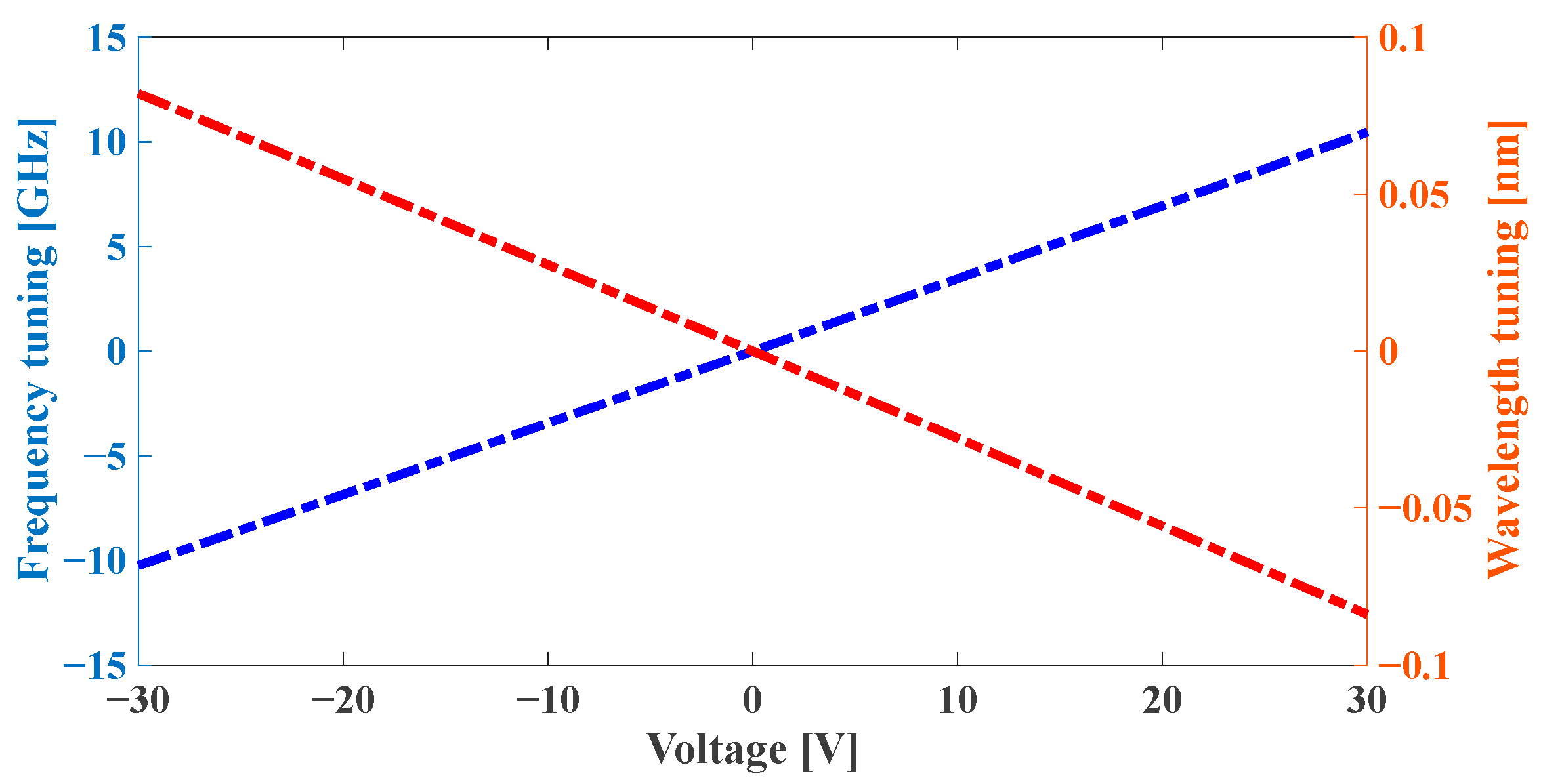
2.3. Design of Piezoelectric Actuator
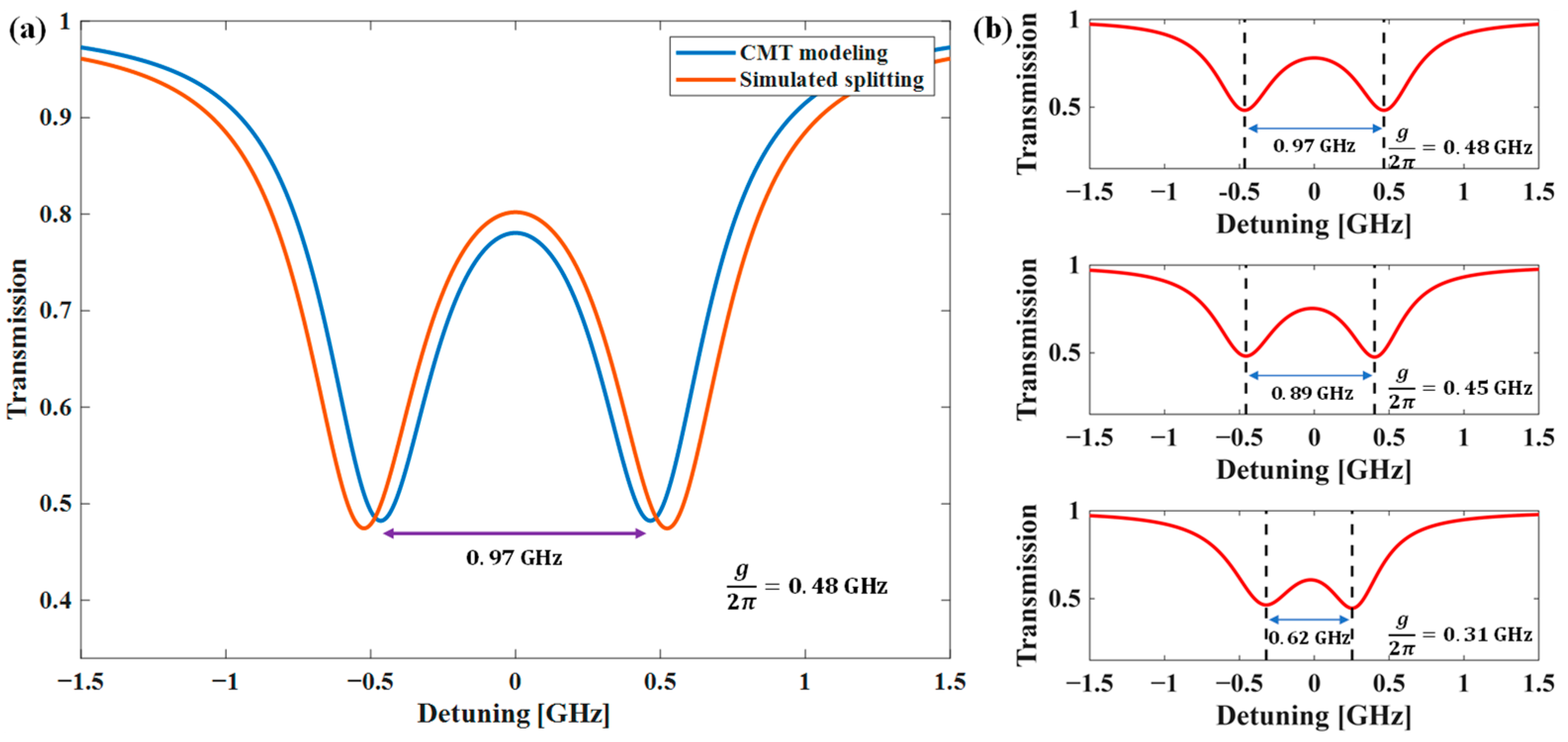
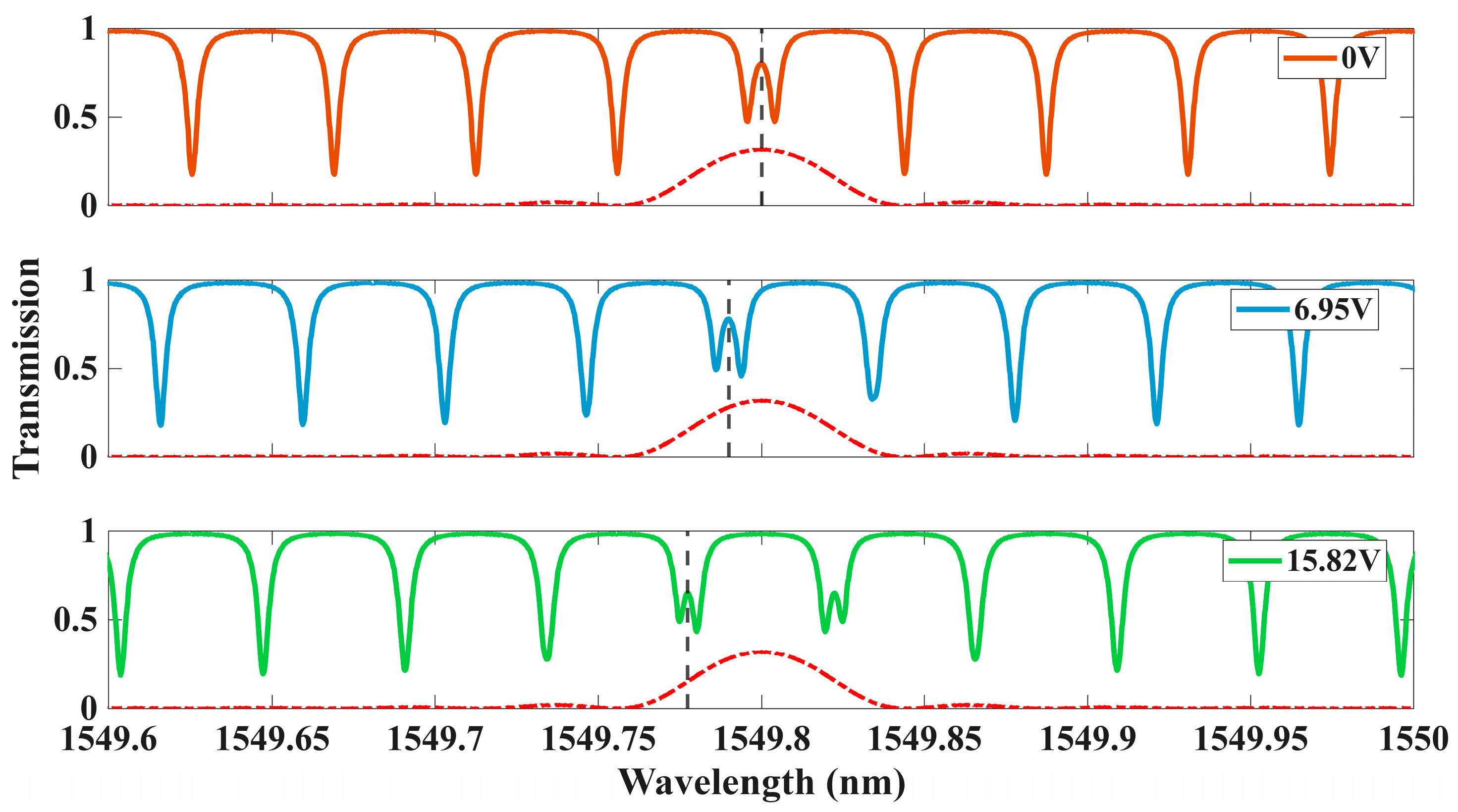
3. Resonance Splitting Modeling Using Coupled-Mode Theory
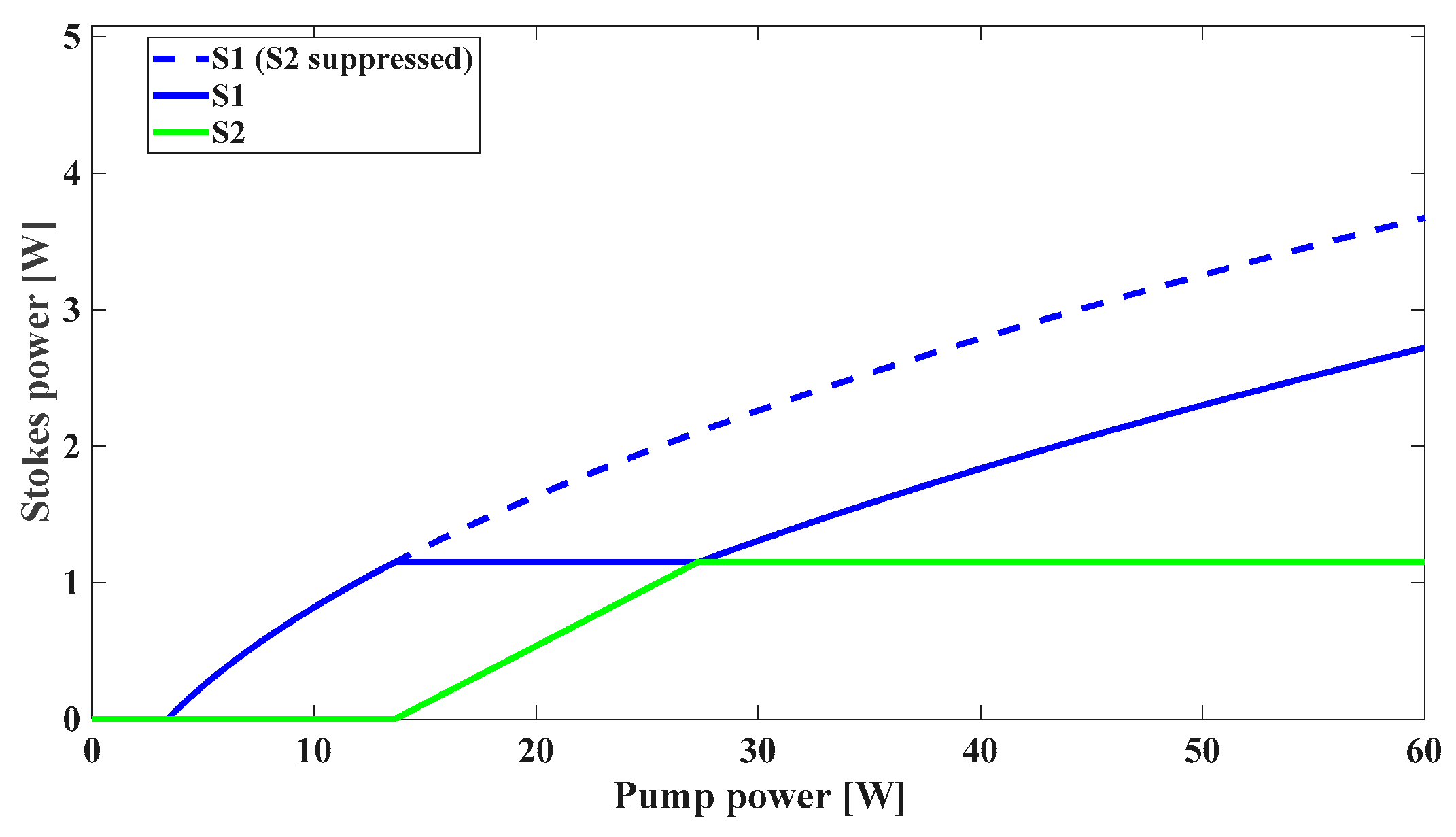
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kikuchi, K. Fundamentals of Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Blumenthal, D.J.; Ballani, H.; Behunin, R.O.; Bowers, J.E.; Costa, P.; Lenoski, D.; Morton, P.A.; Papp, S.B.; Rakich, P.T. Frequency-Stabilized Links for Coherent WDM Fiber Interconnects in the Datacenter. J. Light. Technol. 2020, 38, 3376–3386. [Google Scholar] [CrossRef]
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed Optical Fiber Sensing: Review and Perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Mazur, M.; Fontaine, N.; Chen, H.; Dallachiesa, L.; Ryf, R. Use of Optical Coherent Detection for Environmental Sensing. J. Light. Technol. 2023, 41, 3350–3357. [Google Scholar] [CrossRef]
- Ip, E.; Fang, J.; Li, Y.; Wang, Q.; Huang, M.-F.; Salemi, M.; Huang, Y.-K. Distributed Fiber Sensor Network Using Telecom Cables as Sensing Media: Technology Advancements and Applications [Invited]. J. Opt. Commun. Netw. 2022, 14, A61–A68. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, L.; Huang, S.; Ma, T.; Liu, F.; Yonezawa, H.; Zhang, Y.; Xiao, M. Sensing and Tracking Enhanced by Quantum Squeezing. Photon. Res. 2019, 7, A14–A26. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical Atomic Clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Wang, B.; Yang, Z.; Zhang, X.; Yi, X. Vernier Frequency Division with Dual-Microresonator Solitons. Nat. Commun. 2020, 11, 3975. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Lee, H.; Vahala, K.J. Microwave Synthesizer Using an On-Chip Brillouin Oscillator. Nat. Commun. 2013, 4, 2097. [Google Scholar] [CrossRef] [PubMed]
- Morton, P.A.; Morton, M.J. High-Power, Ultra-Low Noise Hybrid Lasers for Microwave Photonics and Optical Sensing. J. Light. Technol. 2018, 36, 5048–5057. [Google Scholar] [CrossRef]
- Otterstrom, N.T.; Behunin, R.O.; Kittlaus, E.A.; Wang, Z.; Rakich, P.T. A Silicon Brillouin Laser. Science 2018, 360, 1113–1116. [Google Scholar] [CrossRef]
- Ye, K.; Klaver, Y.; Jimenez Gordillo, O.A.; Botter, R.; Daulay, O.; Morichetti, F.; Melloni, A.; Marpaung, D. Brillouin and Kerr Nonlinearities of a Low-Index Silicon Oxynitride Platform. APL Photonics 2023, 8, 051302. [Google Scholar] [CrossRef]
- Rodrigues, C.C.; Schilder, N.J.; Zurita, R.O.; Magalhães, L.S.; Shams-Ansari, A.; Alegre, T.P.M.; Lončar, M.; Wiederhecker, G.S. On-Chip Backward Stimulated Brillouin Scattering in Lithium Niobate Waveguides. In Proceedings of the 2024 Conference on Lasers and Electro-Optics (CLEO), Charlotte, NC, USA, 5–10 May 2024; pp. 1–2. [Google Scholar]
- Liu, K.; Wang, J.; Chauhan, N.; Harrington, M.W.; Nelson, K.D.; Blumenthal, D.J. Integrated Photonic Molecule Brillouin Laser with a High-Power Sub-100-mHz Fundamental Linewidth. Opt. Lett. 2024, 49, 45–48. [Google Scholar] [CrossRef]
- Nelson, K.D.; Puckett, M.W.; Wu, J. A Ring-Laser Gyro Based on Stimulated Brillouin Scattering in Silicon Nitride Waveguides. In Proceedings of the 2020 IEEE Research and Applications of Photonics in Defense Conference (RAPID), Miramar Beach, FL, USA, 10–12 August 2020; pp. 1–3. [Google Scholar]
- Behunin, R.O.; Otterstrom, N.T.; Rakich, P.T.; Gundavarapu, S.; Blumenthal, D.J. Fundamental Noise Dynamics in Cascaded-Order Brillouin Lasers. Phys. Rev. A 2018, 98, 023832. [Google Scholar] [CrossRef]
- Wang, M.; Liu, C.; Zhou, X.; Li, J.; Wang, Z.; Yang, D.-Q.; Yang, Q.-F.; Li, B.-B. Cascading-Induced Fundamental Linewidth Enhancement of a Microcavity Brillouin Laser. ACS Photonics 2025, 12, 2318–2324. [Google Scholar] [CrossRef]
- Puckett, M.; Bose, D.; Nelson, K.; Blumenthal, D.J. Higher Order Cascaded SBS Suppression Using Gratings in a Photonic Integrated Ring Resonator Laser. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; pp. 1–2. [Google Scholar]
- Kheyri, M.; Zhang, S.; Bi, T.; Pal, A.; Zhang, H.; Zhang, Y.; Alabbadi, A.; Yan, H.; Ghosh, A.; Hill, L.; et al. On-Chip Microresonator Dispersion Engineering via Segmented Sidewall Modulation. Photon. Res. 2025, 13, 367–372. [Google Scholar] [CrossRef]
- Moille, G.; Lu, X.; Stone, J.; Westly, D.; Srinivasan, K. Fourier Synthesis Dispersion Engineering of Photonic Crystal Microrings for Broadband Frequency Combs. Commun. Phys. 2023, 6, 144. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Zeng, J.; Yu, S. Broadband and Accurate Electric Tuning of On-Chip Efficient Nonlinear Parametric Conversion. Optica 2025, 12, 424–432. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, W.; You, M.; Yu, X.; Ding, N.; Cheng, W.; Li, Z.; Tang, X.; Guo, F.; Lu, D.; et al. Tantalum Pentoxide Integrated Photonics: A Promising Platform for Low-Loss Planar Lightwave Circuits with Low Thermo-Optic Coefficients. ACS Photonics 2025, 12, 684–695. [Google Scholar] [CrossRef]
- Goede, M.; Dijkstra, M.; Chang, L.; Acharyya, N.; Kozyreff, G.; Obregon, R.; Martinez, E.; García-Blanco, S. Mode-Splitting in a Microring Resonator for Self-Referenced Biosensing. Opt. Express 2020, 29, 346–358. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, J.; Li, J.; Chen, Y.; Li, J.; Duan, J.; Xu, X.; Wang, J. High-Order Autler–Townes Splitting in Electrically Tunable Photonic Molecules. Photonics Res. 2024, 12, 1794. [Google Scholar] [CrossRef]
- Geng, Z.; Cheng, W.; Yan, Z.; Yi, Q.; Liu, Z.; You, M.; Yu, X.; Wu, P.; Ding, N.; Tang, X.; et al. Low-Loss Tantalum Pentoxide Photonics with a CMOS-Compatible Process. Opt. Express 2024, 32, 12291–12302. [Google Scholar] [CrossRef]
- Liu, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.W.; Nelson, K.D.; Behunin, R.O.; Rakich, P.T.; Blumenthal, D.J. Ultralow 0.034 dB/m Loss Wafer-Scale Integrated Photonics Realizing 720 Million Q and 380 μW Threshold Brillouin Lasing. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef]
- Zhao, Q.; Harrington, M.; Isichenko, A.; Liu, K.; Behunin, R.; Papp, S.; Rakich, P.; Hoyt, C.; Fertig, C.; Blumenthal, D. Integrated Reference Cavity with Dual-Mode Optical Thermometry for Frequency Correction. Optica 2021, 8, 1481–1487. [Google Scholar] [CrossRef]
- Blumenthal, D.; LIU, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.; Nelson, K.; Behunin, R.; Rakich, P. Supplementary Document for Ultra-Low 0.034 dB/m Loss Wafer-Scale Integrated Photonics Realizing 720 Million Q and 380 μW Threshold Brillouin Lasing—5717781.Pdf. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef]
- Yu, S.-P.; Cole, D.C.; Jung, H.; Moille, G.T.; Srinivasan, K.; Papp, S.B. Spontaneous Pulse Formation in Edgeless Photonic Crystal Resonators. Nat. Photonics 2021, 15, 461–467. [Google Scholar] [CrossRef]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design: From Devices to Systems; Cambridge University Press: Cambridge, UK, 2015; ISBN 978-1-316-23711-3. [Google Scholar]
- You, M.; Liu, Z.; Cheng, W.; Tang, X.; Ding, N.; Li, Z.; Wang, M.; Shen, L.; Zhao, Q. Athermal Tantalum Pentoxide Mach-Zehnder Interferometers Based on Structural Compensation Method. IEEE Photonics J. 2025, 17, 1–8. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Dong, B.; Skehan, J.C.; Zervas, M.; Kippenberg, T.J.; Bhave, S.A. Hybrid Integrated Photonics Using Bulk Acoustic Resonators. Nat. Commun. 2020, 11, 3073. [Google Scholar] [CrossRef]
- Stanfield, P.R.; Leenheer, A.J.; Michael, C.P.; Sims, R.; Eichenfield, M. CMOS-Compatible, Piezo-Optomechanically Tunable Photonics for Visible Wavelengths and Cryogenic Temperatures. Opt. Express 2019, 27, 28588–28605. [Google Scholar] [CrossRef]
- He, J.; You, M.; Liu, Z.; Li, Z.; Cheng, W.; Ding, N.; Tang, X.; Hou, J.; Zhao, Q. Simulation of Stress-Optic Microresonator Modulator. Available online: https://cn.comsol.com/paper/simulation-of-stress-optic-microresonator-modulator-137612 (accessed on 1 January 2025).
- Bu, G.; Ciplys, D.; Shur, M.; Schowalter, L.J.; Schujman, S.; Gaska, R. Electromechanical Coupling Coefficient for Surface Acoustic Waves in Single-Crystal Bulk Aluminum Nitride. Appl. Phys. Lett. 2004, 84, 4611–4613. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 6.0. www.comsol.com. COMSOL AB. Stockholm, Sweden.
- Fang, D.; Li, F.; Liu, B.; Zhang, Y.; Hong, J.; Guo, X. Advances in Developing Electromechanically Coupled Computational Methods for Piezoelectrics/Ferroelectrics at Multiscale. Appl. Mech. Rev. 2013, 65, 0802. [Google Scholar] [CrossRef]
- Huang, M. Stress Effects on the Performance of Optical Waveguides. Int. J. Solids Struct. 2003, 40, 1615–1632. [Google Scholar] [CrossRef]
- Zhao, Q.; Behunin, R.O.; Rakich, P.T.; Chauhan, N.; Isichenko, A.; Wang, J.; Hoyt, C.; Fertig, C.; Lin, M.H.; Blumenthal, D.J. Low-Loss Low Thermo-Optic Coefficient Ta2O5 on Crystal Quartz Planar Optical Waveguides. APL Photonics 2020, 5, 116103. [Google Scholar] [CrossRef]
- Nakagawa, Y.; Yawata, M.; Kakio, S. Enhancement of Photoelastic Constant of Optical Thin Film Waveguide Assisted by Surface Acoustic Wave. Ultrasonics 2000, 38, 590–593. [Google Scholar] [CrossRef]
- Souza, M.C.M.M.; Rezende, G.F.M.; Barea, L.A.M.; Wiederhecker, G.S.; Frateschi, N.C. Modeling Quasi-Dark States with Temporal Coupled-Mode Theory. Opt. Express 2016, 24, 18960–18972. [Google Scholar] [CrossRef]
- Suh, W.; Wang, Z.; Fan, S. Temporal Coupled-Mode Theory and the Presence of Non-Orthogonal Modes in Lossless Multimode Cavities. IEEE J. Quantum Electron. 2004, 40, 1511–1518. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Haus, H.A.; Foresi, J.; Laine, J.-P. Microring Resonator Channel Dropping Filters. J. Light. Technol. 1997, 15, 998–1005. [Google Scholar] [CrossRef]
- LIU, K.; Wang, J.; Chauhan, N.; Harrington, M.; Nelson, K.; Blumenthal, D. Supplementary Document for Integrated Photonic Molecule Brillouin Laser with High Power Sub-100-mHz Fundamental Linewidth—6720603.Pdf. Opt. Lett. 2024, 49, 45–48. [Google Scholar] [CrossRef]

| Parameter | Value | Reference |
|---|---|---|
[C/m2] | [37] | |
[GPa] | [36] | |
| [36] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; You, M.; Liu, Z.; Zhou, J.; Ding, N.; Zhang, Z.; Li, Z.; Tang, X.; Cheng, W.; Hou, J.; et al. Design of Grating-Embedded Tantalum Pentoxide Microring Resonators with Piezoelectric Tunability. Photonics 2025, 12, 903. https://doi.org/10.3390/photonics12090903
He J, You M, Liu Z, Zhou J, Ding N, Zhang Z, Li Z, Tang X, Cheng W, Hou J, et al. Design of Grating-Embedded Tantalum Pentoxide Microring Resonators with Piezoelectric Tunability. Photonics. 2025; 12(9):903. https://doi.org/10.3390/photonics12090903
Chicago/Turabian StyleHe, Jiazhao, Mingjian You, Zhenyu Liu, Junke Zhou, Ning Ding, Ziming Zhang, Zhengqi Li, Xingyu Tang, Weiren Cheng, Jiaxin Hou, and et al. 2025. "Design of Grating-Embedded Tantalum Pentoxide Microring Resonators with Piezoelectric Tunability" Photonics 12, no. 9: 903. https://doi.org/10.3390/photonics12090903
APA StyleHe, J., You, M., Liu, Z., Zhou, J., Ding, N., Zhang, Z., Li, Z., Tang, X., Cheng, W., Hou, J., Wang, S., & Zhao, Q. (2025). Design of Grating-Embedded Tantalum Pentoxide Microring Resonators with Piezoelectric Tunability. Photonics, 12(9), 903. https://doi.org/10.3390/photonics12090903






