Design of a Modified Moiré Varifocal Metalens Based on Fresnel Principles
Abstract
1. Introduction
2. Materials and Methods
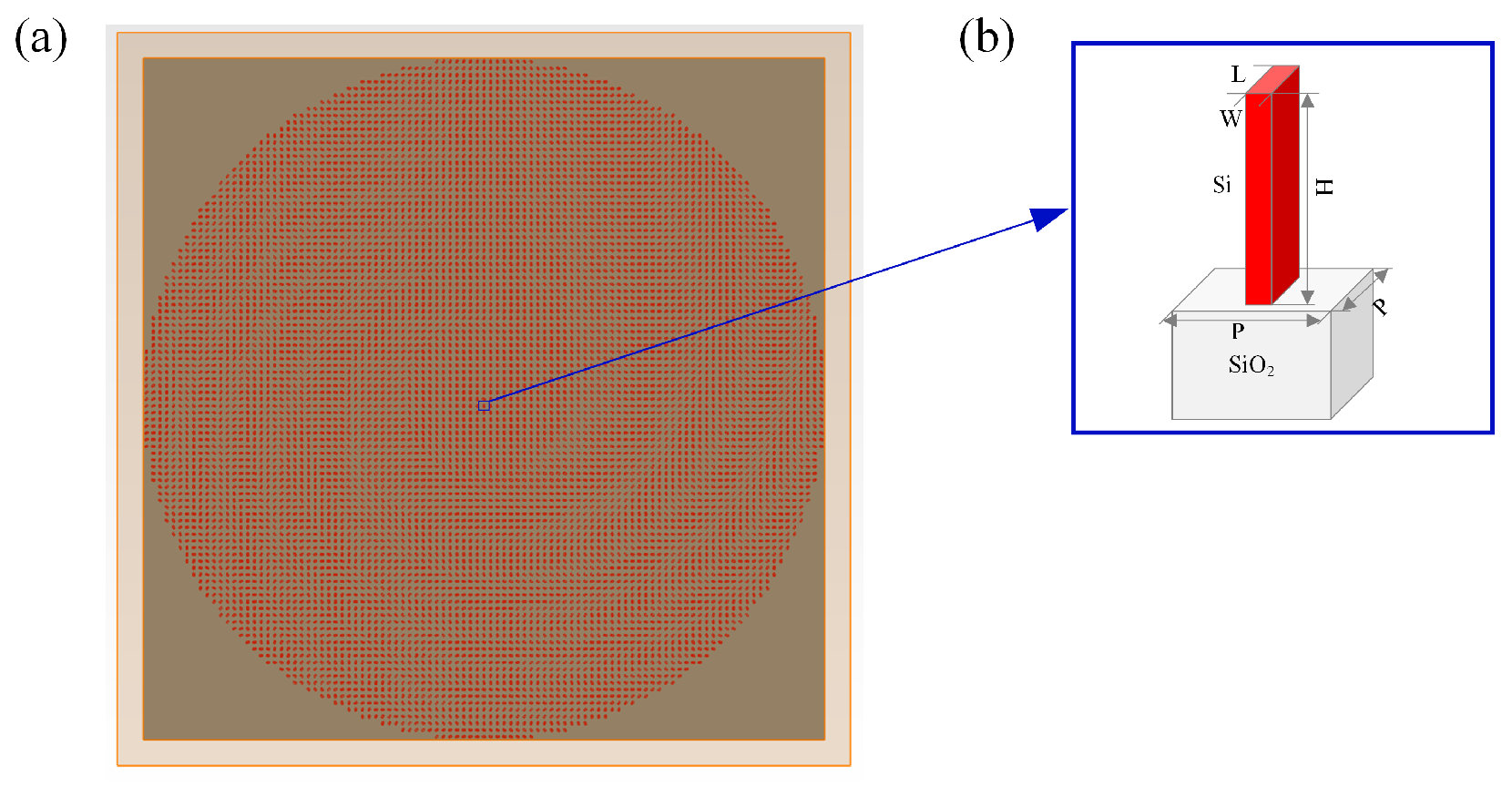
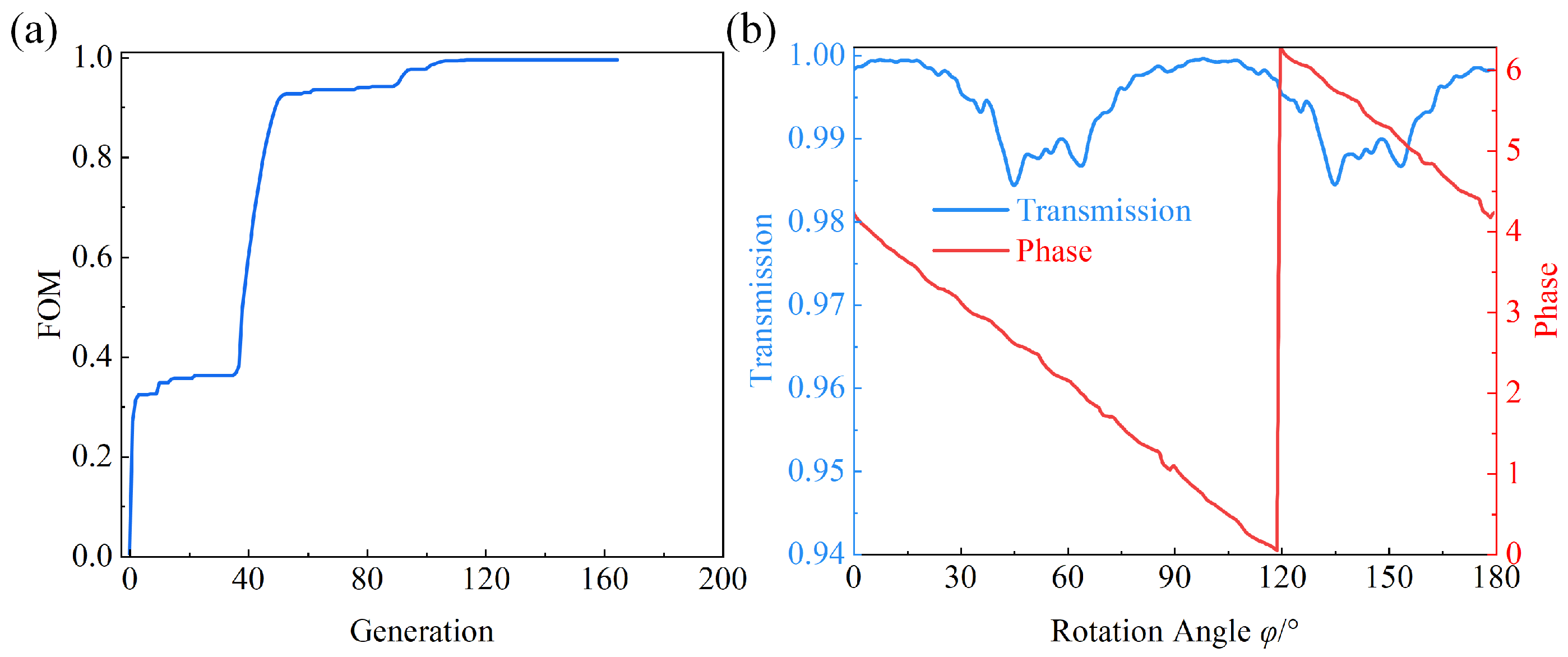
2.1. Design of Nano-Units for Varifocal Metalens
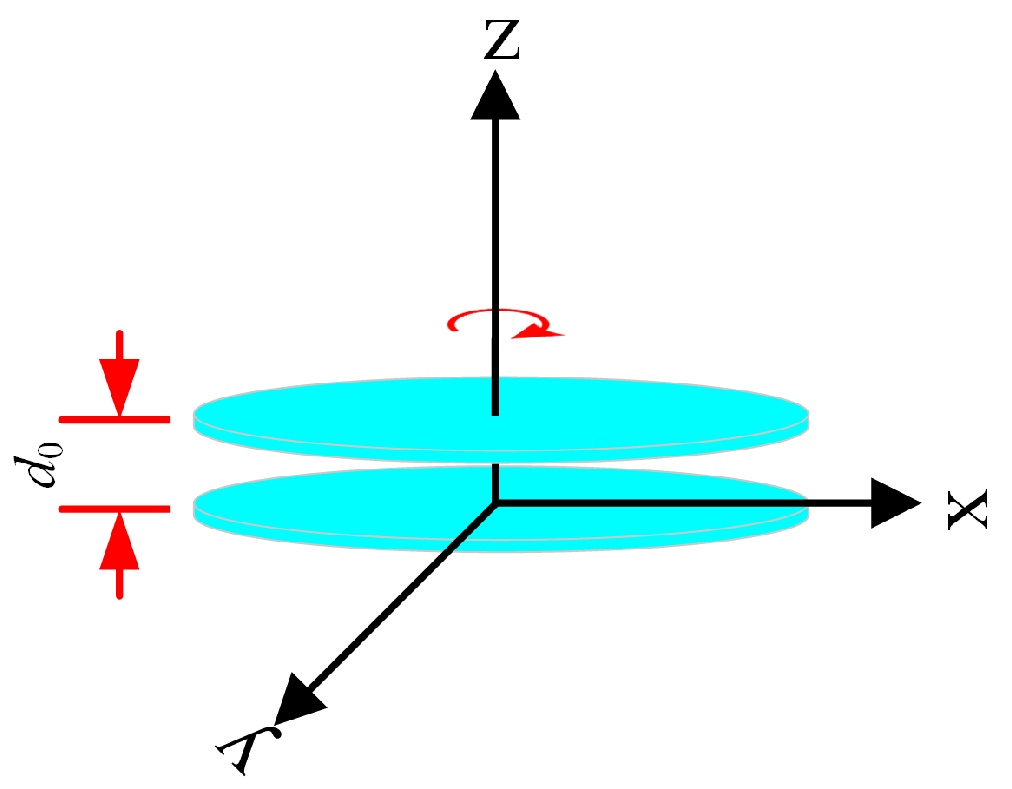
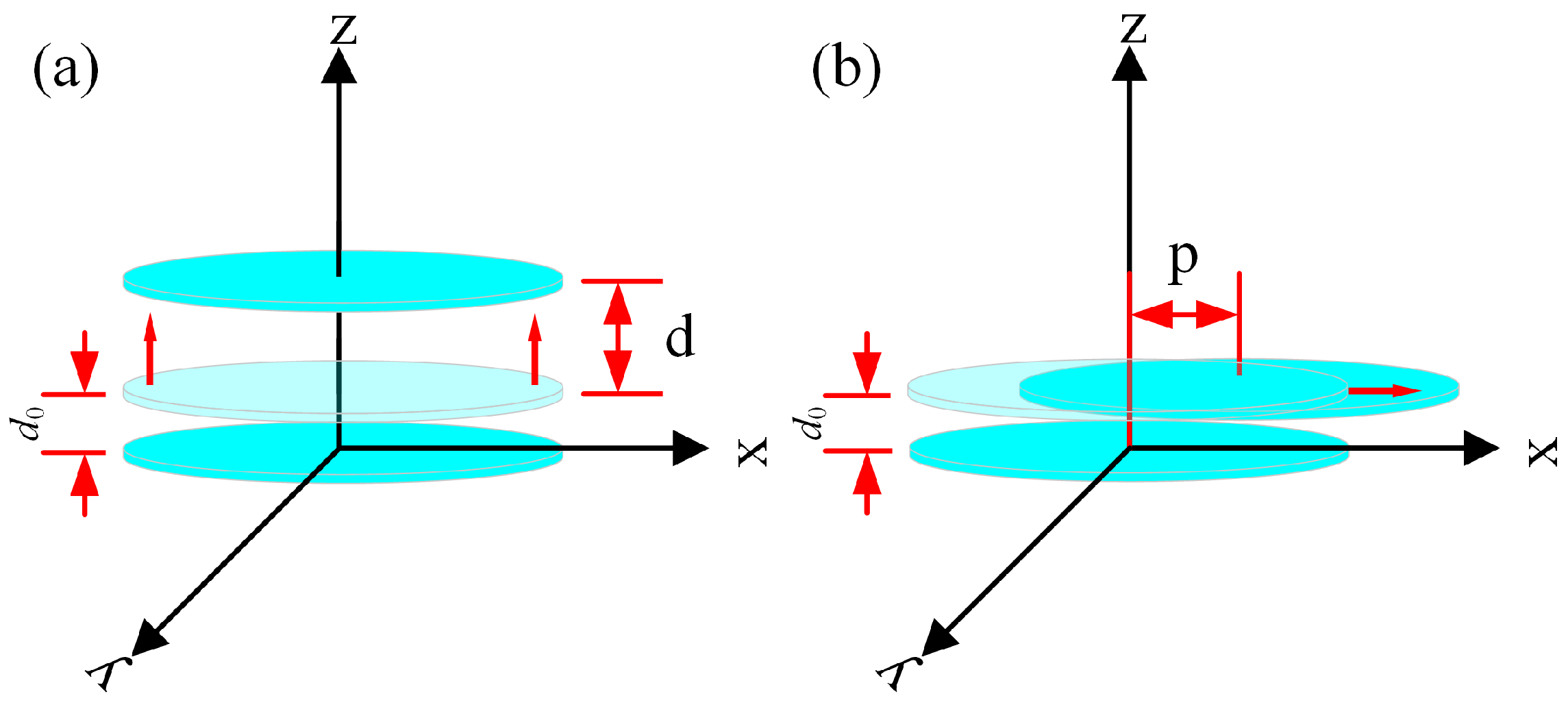
2.2. Design of the Modified Varifocal Metalens
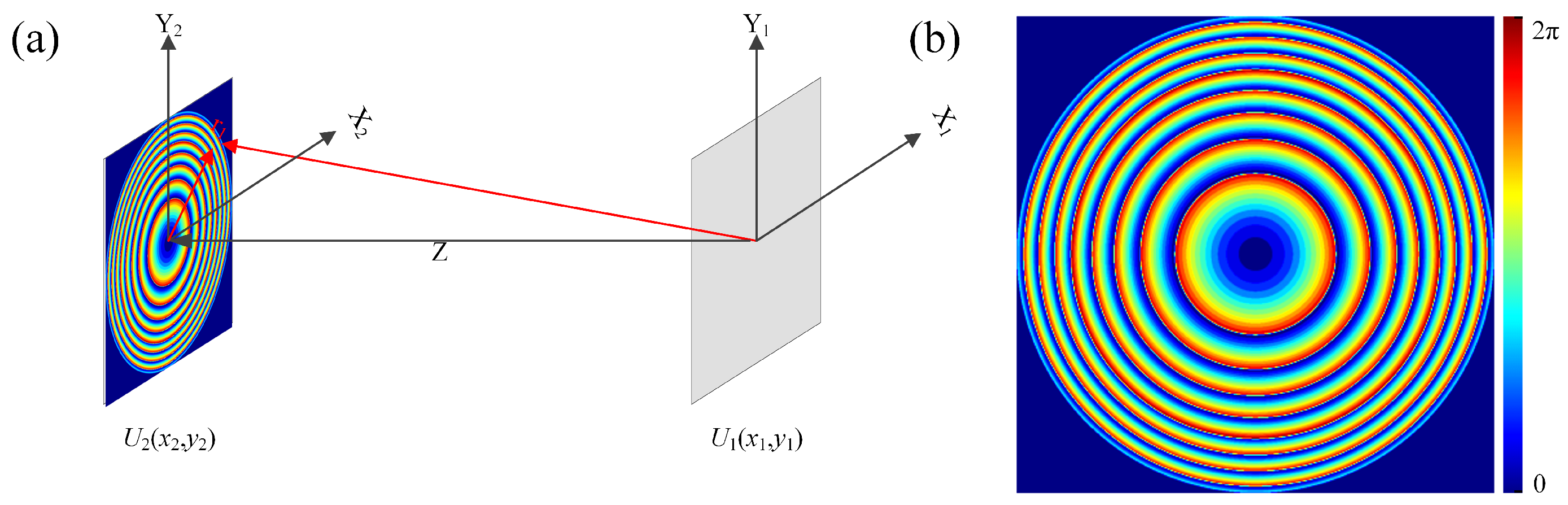
2.3. Phase Design Based on Fresnel
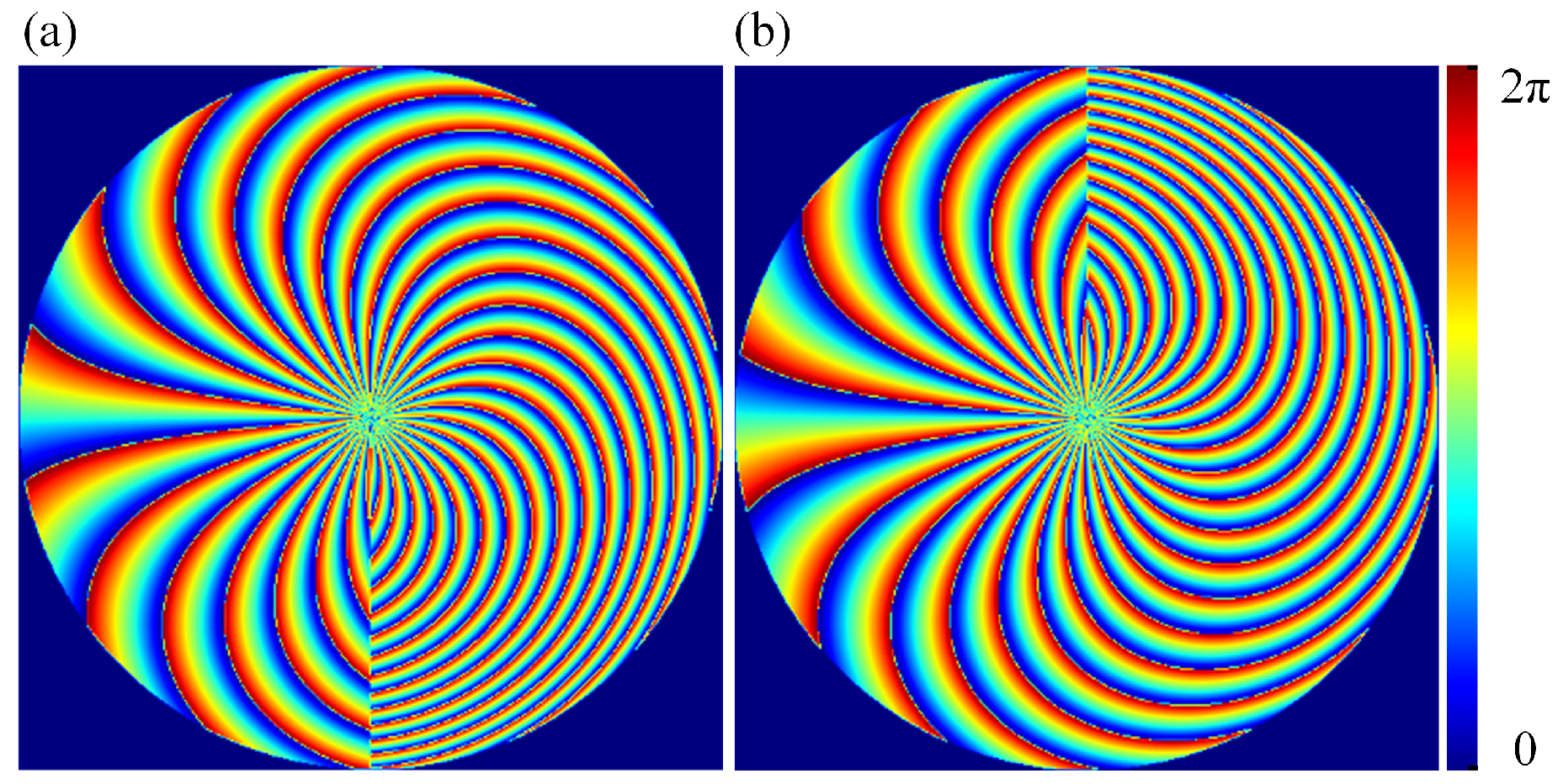
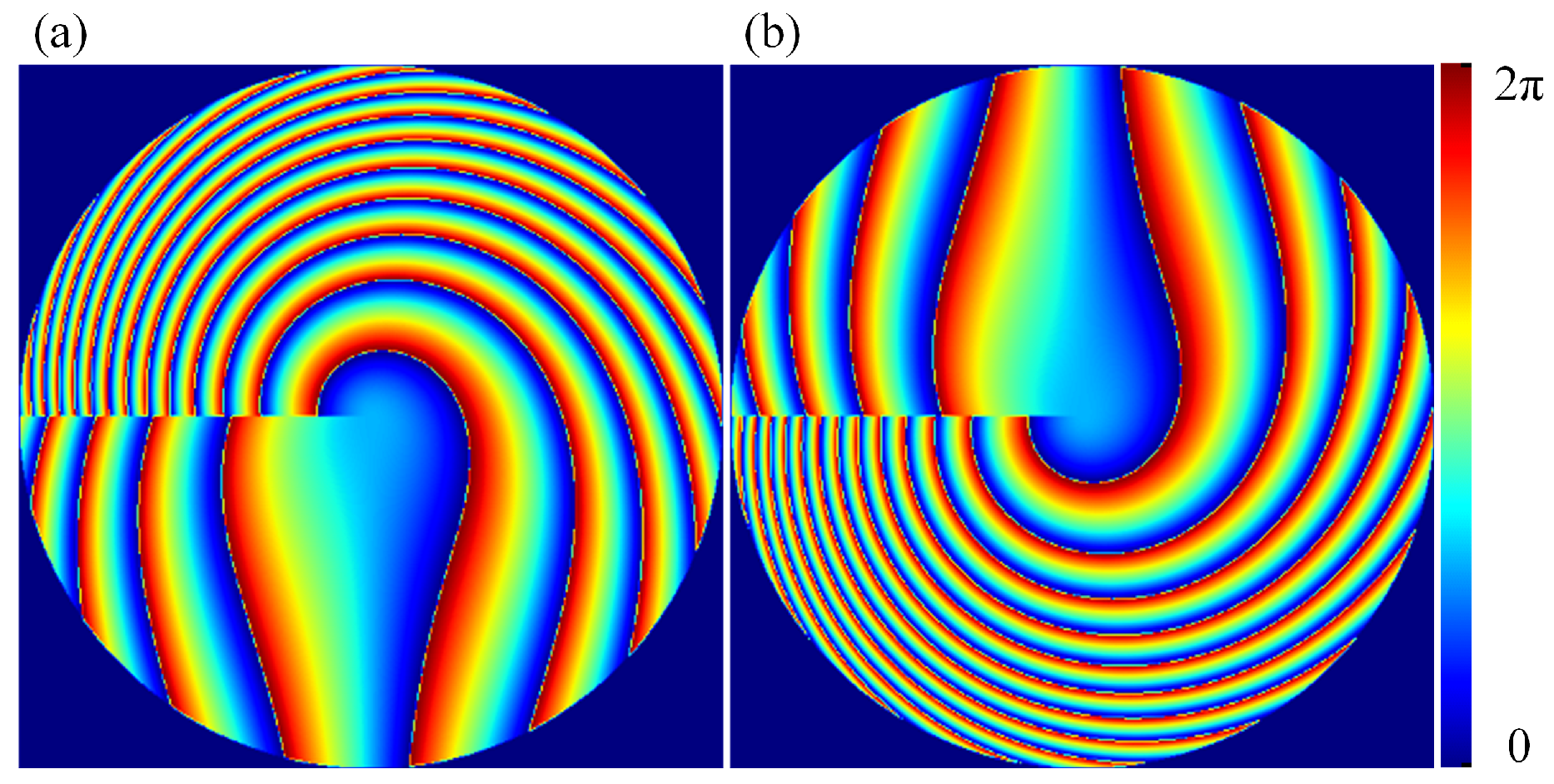
2.4. Design of Fresnel-Based Moiré Varifocal Metalens
3. Results and Discussion
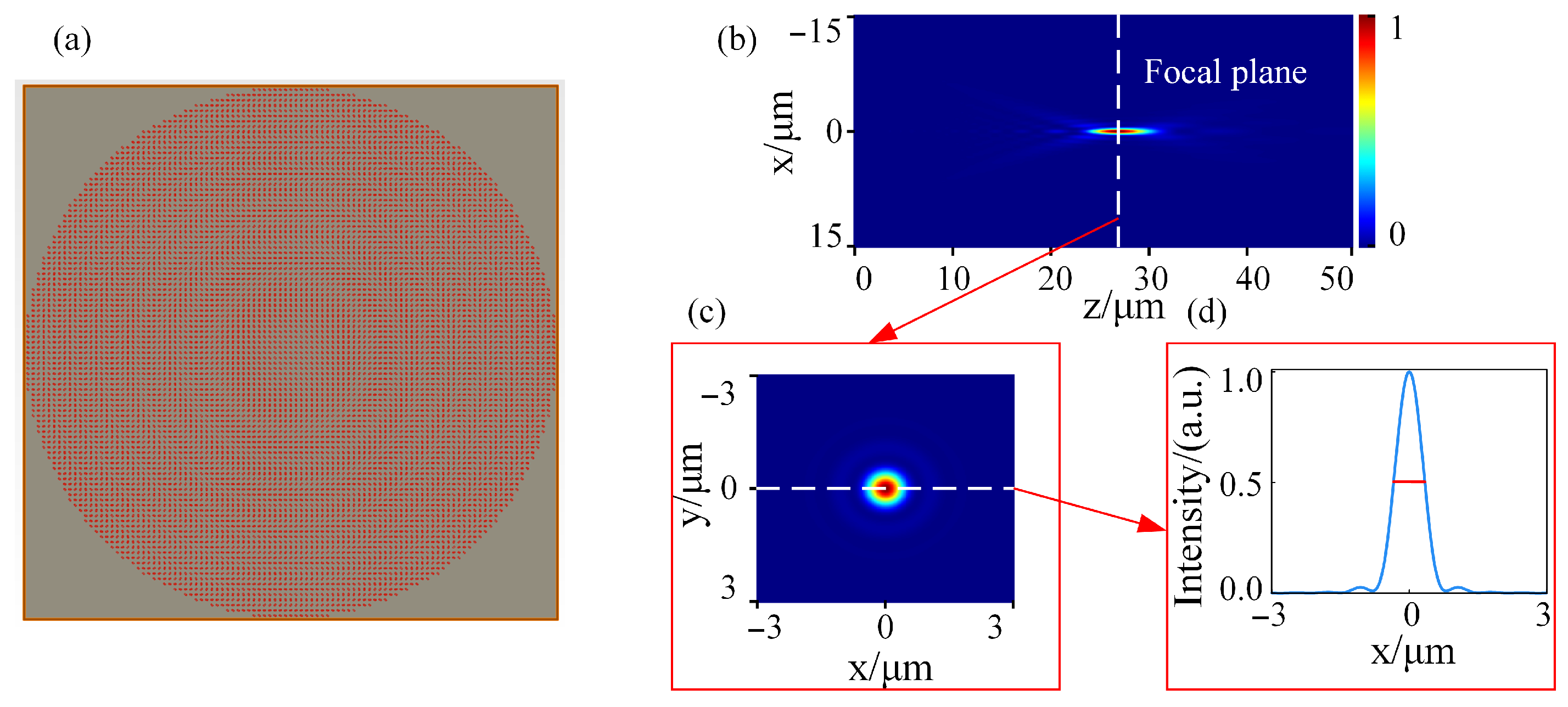
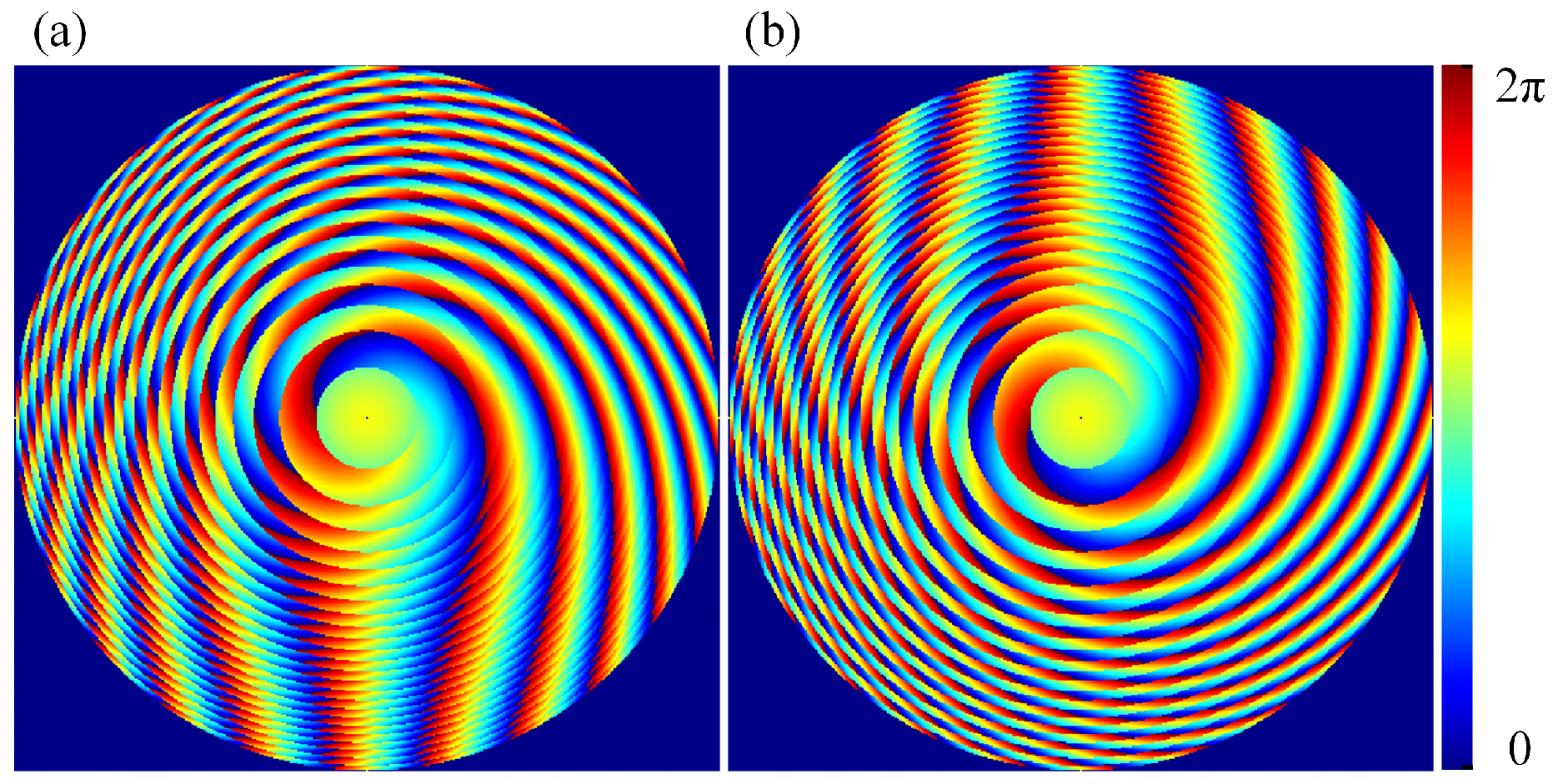
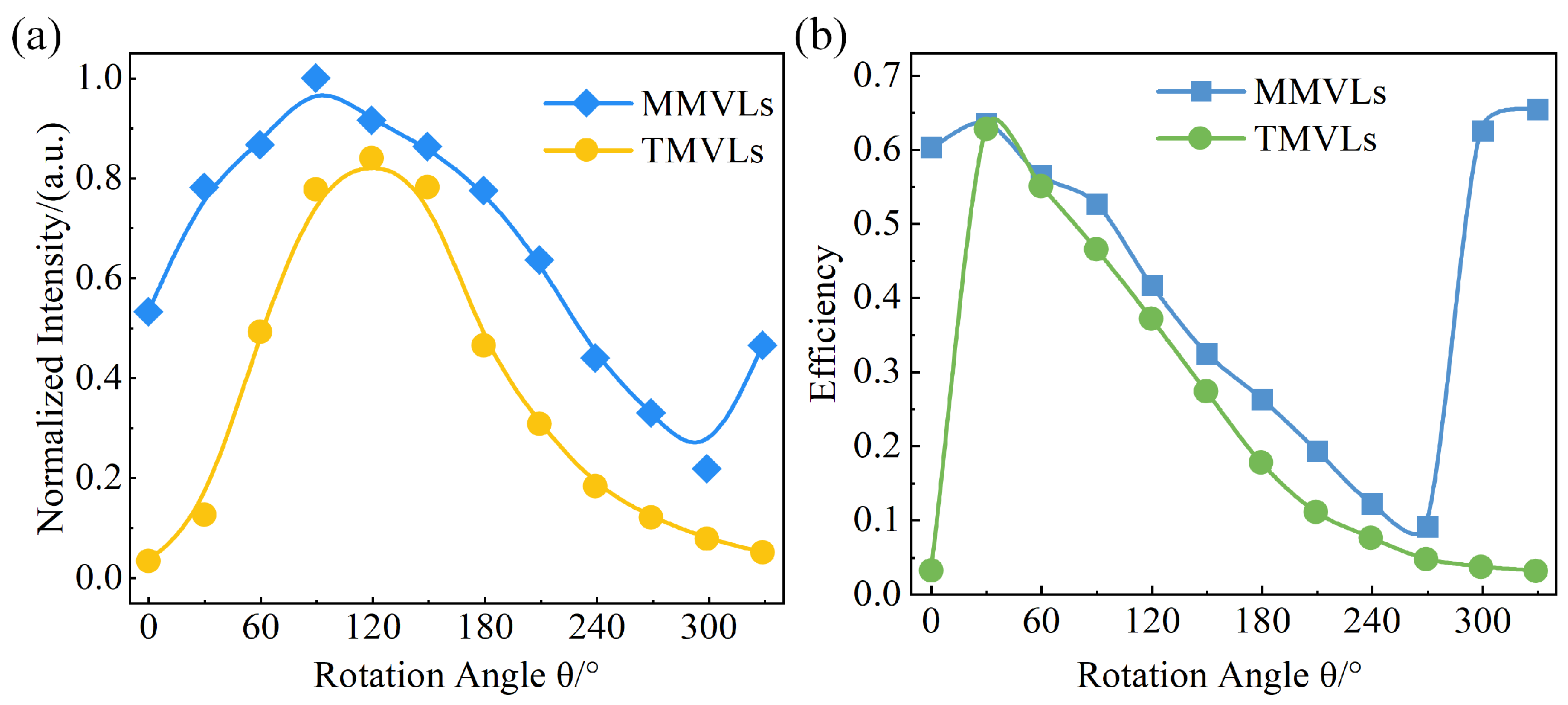
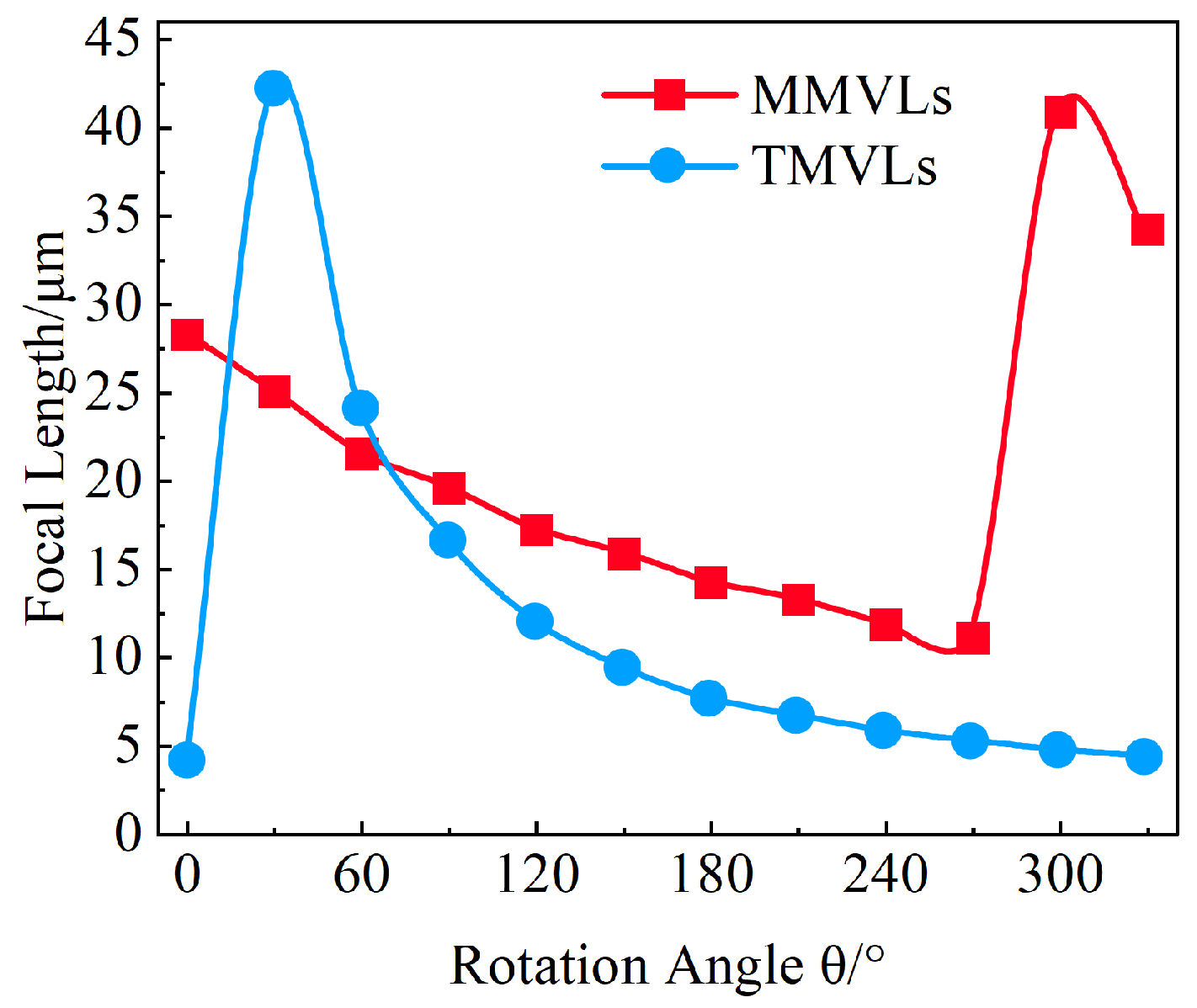
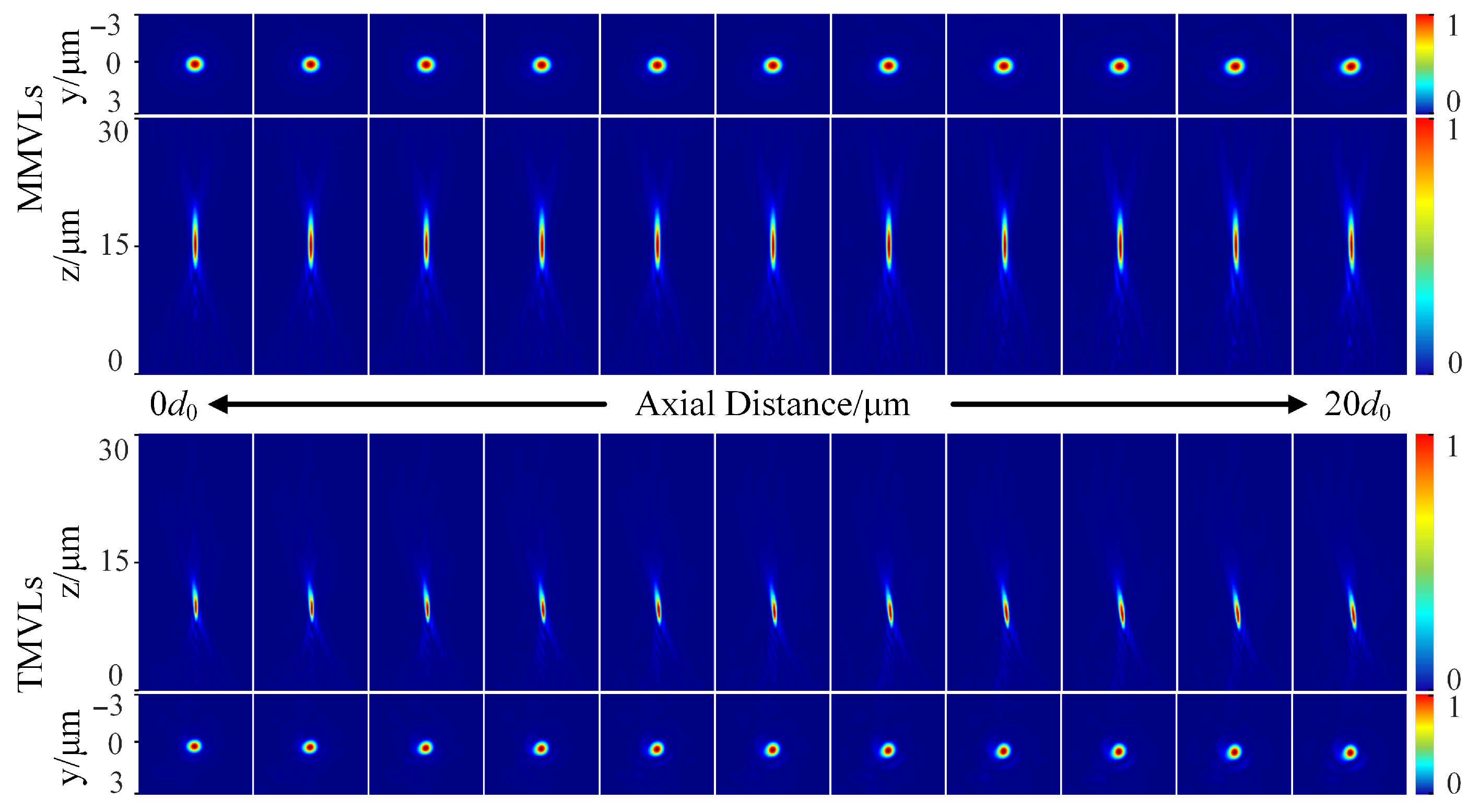
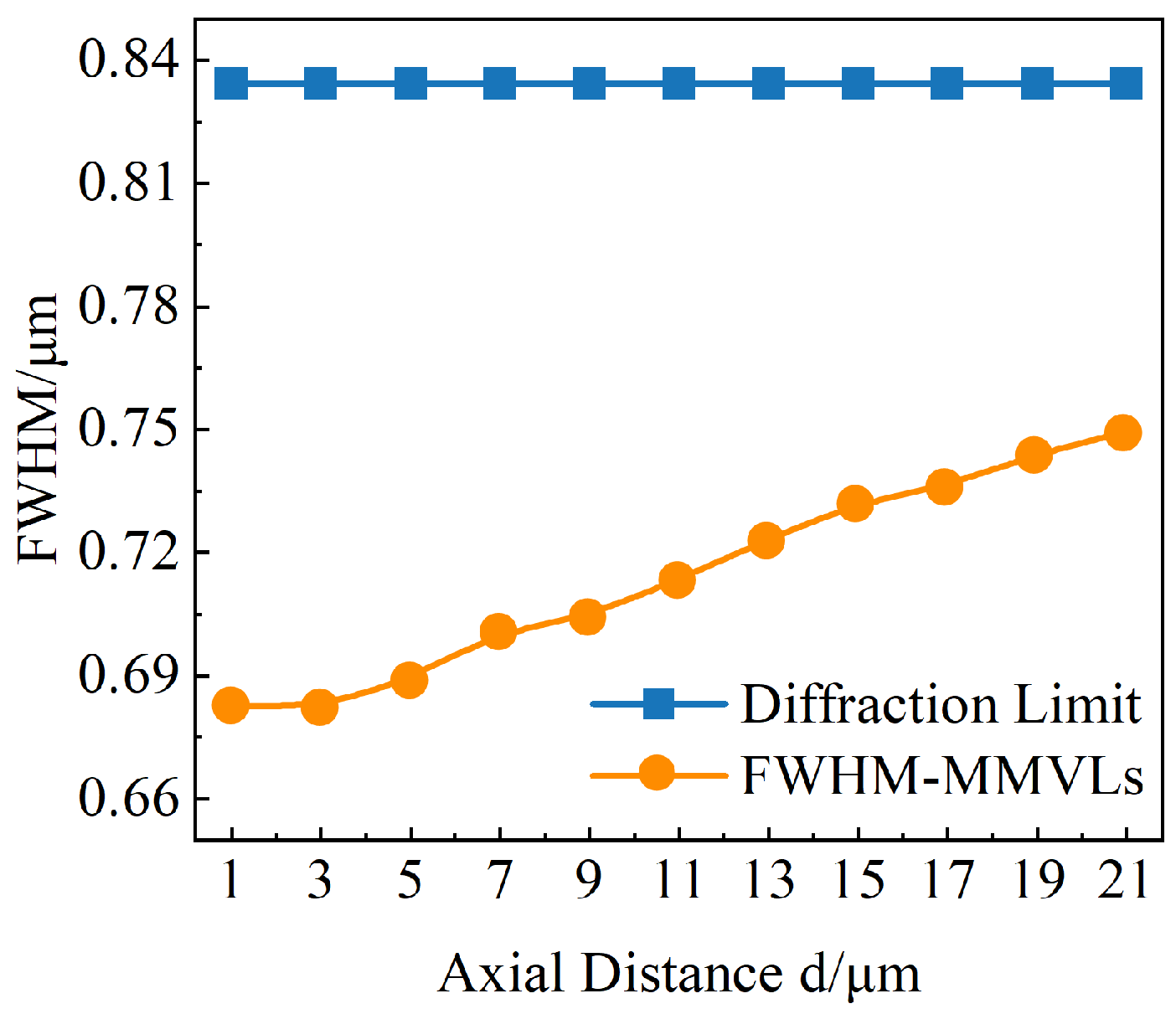
3.1. Varifocal Experiment
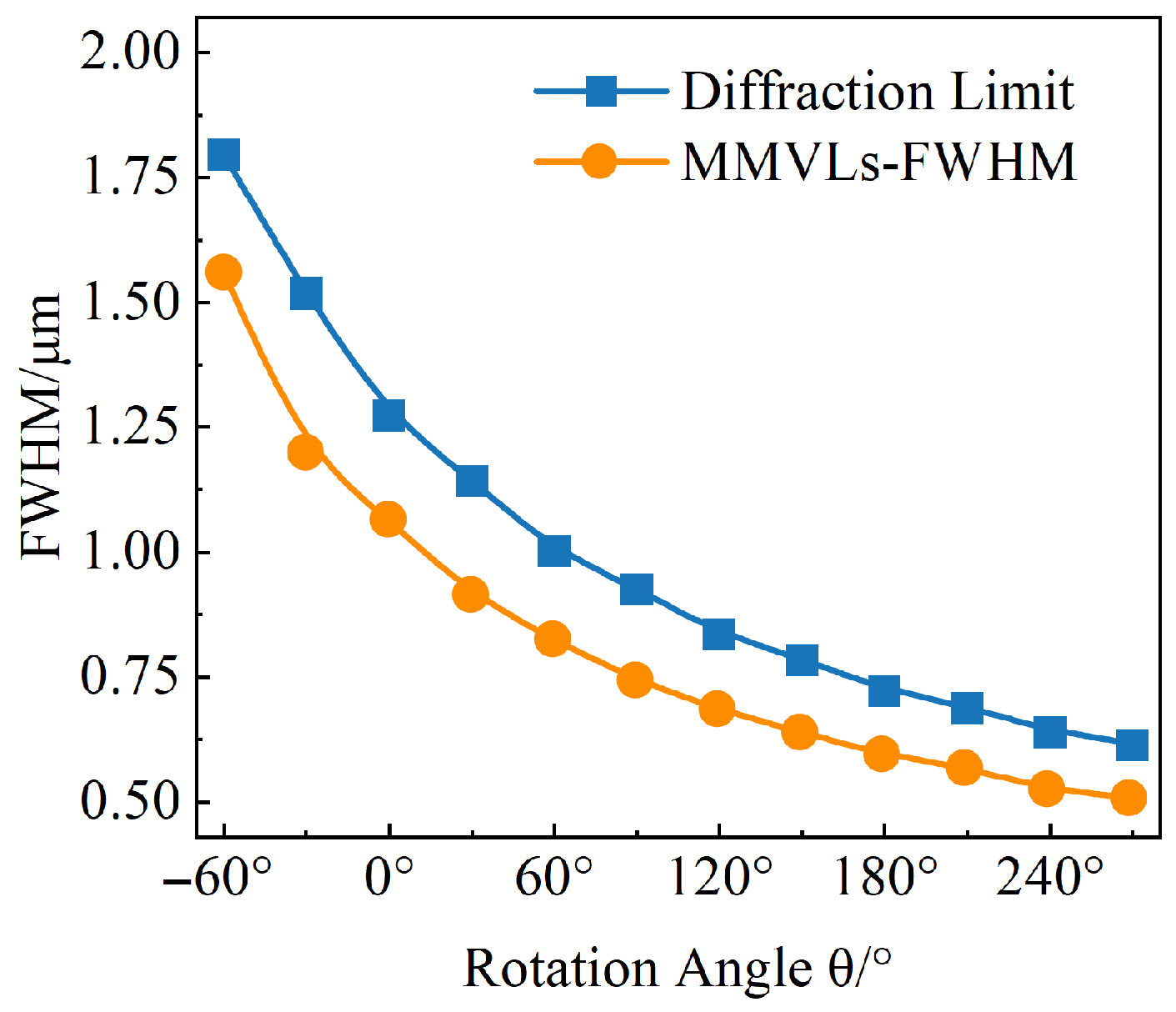
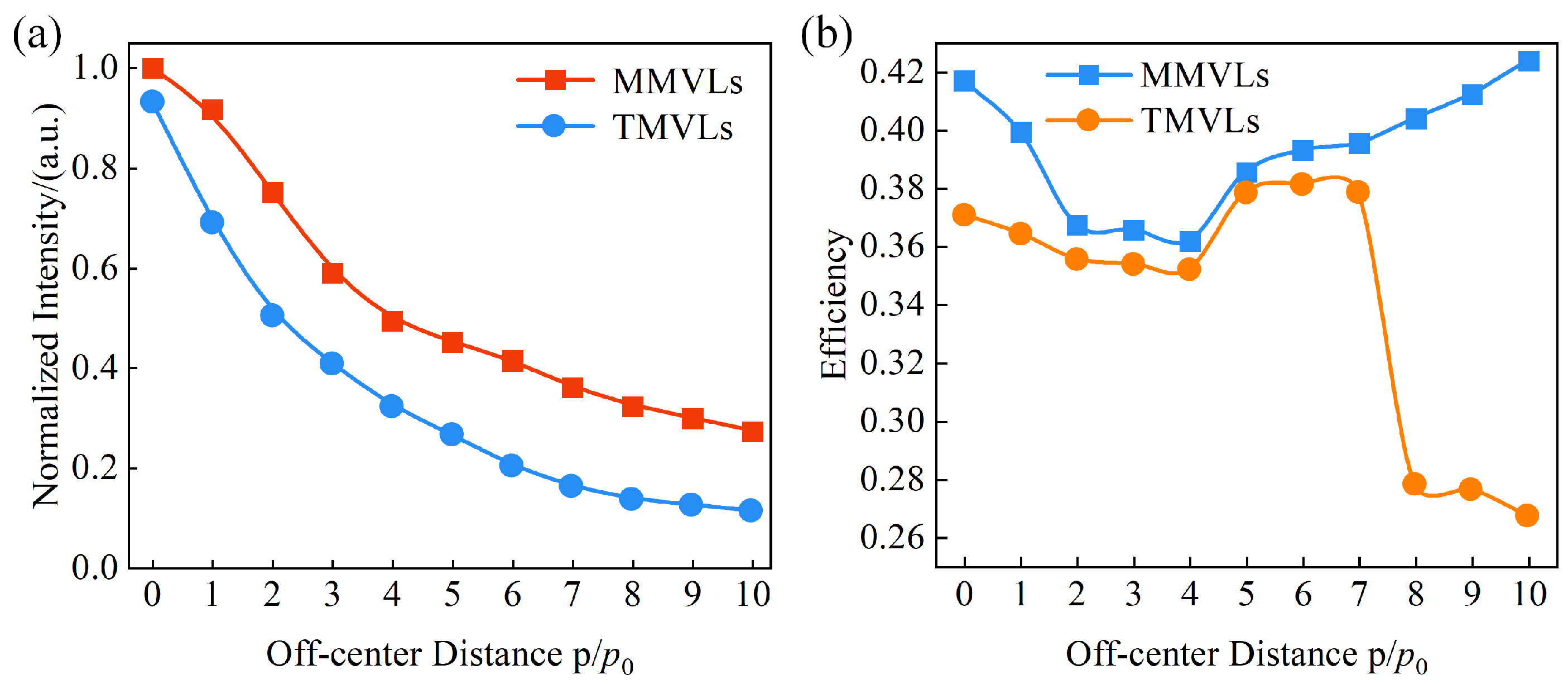
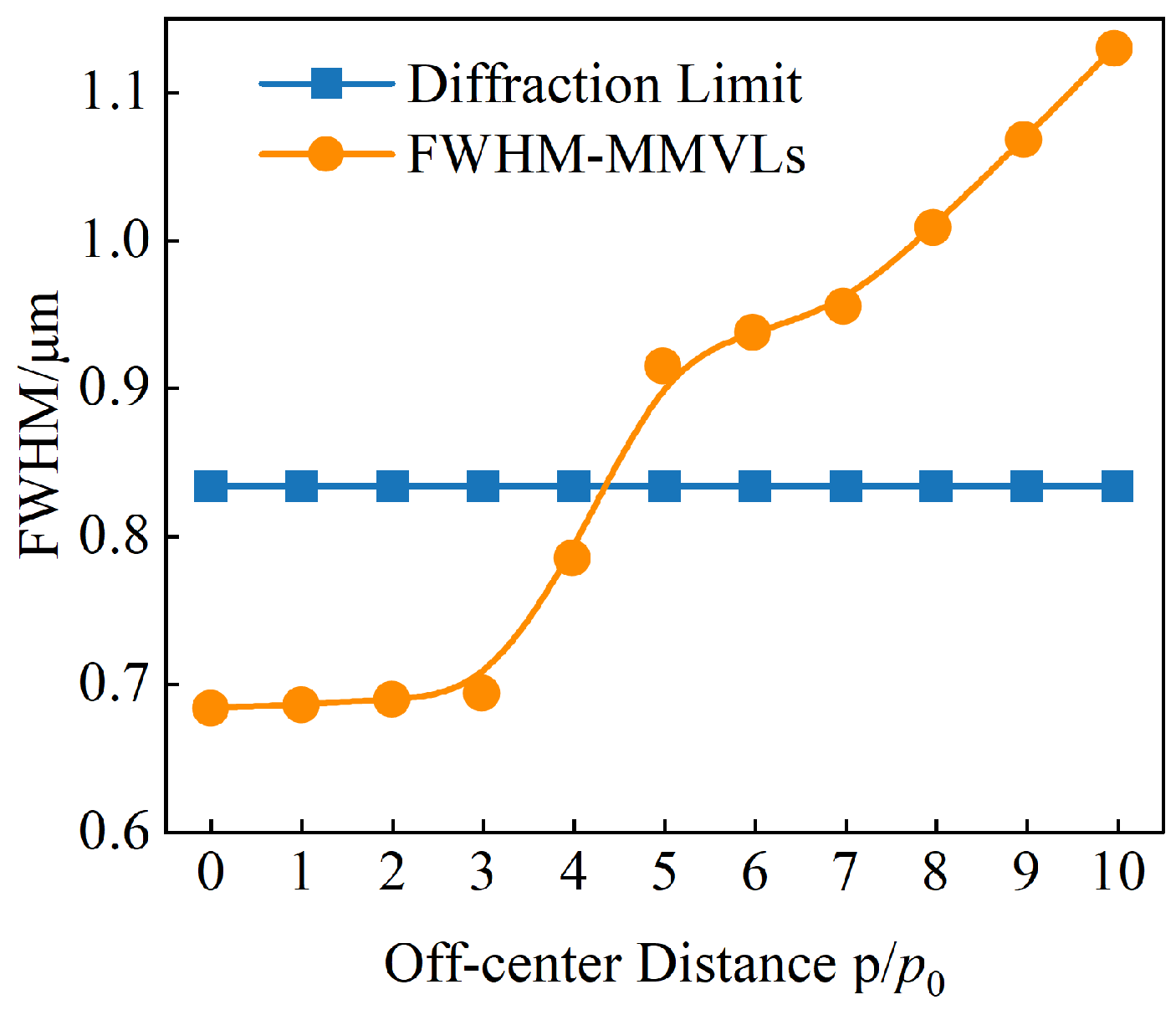
3.2. Robustness Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drexler, W.; Morgner, U.; Ghanta, R.K.; Kärtner, F.X.; Schuman, J.S.; Fujimoto, J.G. Ultrahigh-resolution ophthalmic optical coherence tomography. Nat. Med. 2001, 7, 502–507. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.D.; Mandella, M.J.; Contag, C.H.; Kino, G.S. Dual-axis confocal microscope for high-resolution in vivo imaging. Opt. Lett. 2003, 28, 414–416. [Google Scholar] [CrossRef]
- Fujimoto, J.G. Optical coherence tomography for ultrahigh resolution in vivo imaging. Nat. Biotechnol. 2003, 21, 1361–1367. [Google Scholar] [CrossRef]
- Ge, X.; Chen, S.; Chen, S.; Liu, L. High resolution optical coherence tomography. J. Light. Technol. 2021, 39, 3824–3835. [Google Scholar] [CrossRef]
- Mazlin, V.; Xiao, P.; Dalimier, E.; Grieve, K.; Irsch, K.; Sahel, J.A.; Fink, M.; Boccara, A.C. In vivo high resolution human corneal imaging using full-field optical coherence tomography. Biomed. Opt. Express 2018, 9, 557–568. [Google Scholar] [CrossRef]
- Marini, M.; Nardini, A.; Martínez Vázquez, R.; Conci, C.; Bouzin, M.; Collini, M.; Osellame, R.; Cerullo, G.; Kariman, B.; Farsari, M.; et al. Microlenses fabricated by two-photon laser polymerization for cell imaging with non-linear excitation microscopy. Adv. Funct. Mater. 2023, 33, 2213926. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Xu, J.; Sun, X.; Zhao, X.; Li, H.; Liu, Y.; Tian, J.; Hao, X.; Kong, X.; et al. The development of microscopic imaging technology and its application in micro-and nanotechnology. Front. Chem. 2022, 10, 931169. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Yang, D. Application of time lenses for high speed fiber-optic communication systems. In Proceedings of the 2009 4th International Conference on Computers and Devices for Communication (CODEC), Kolkata, India, 14–16 December 2009; IEEE: Washington, DC, USA, 2009; pp. 1–6. [Google Scholar]
- Tian, J.; Guo, T.; He, N.; Du, J.; Huang, Q.; Hong, X.; Fei, C.; Wang, Y.; Zhang, T.; Zhang, J.; et al. Wide-field-of-view modulating retro-reflector system based on a telecentric lens for high-speed free-space optical communication. IEEE Photonics J. 2023, 15, 1–8. [Google Scholar] [CrossRef]
- Enger, J.; Goksör, M.; Ramser, K.; Hagberg, P.; Hanstorp, D. Optical tweezers applied to a microfluidic system. Lab A Chip 2004, 4, 196–200. [Google Scholar] [CrossRef]
- Fällman, E.; Schedin, S.; Jass, J.; Andersson, M.; Uhlin, B.E.; Axner, O. Optical tweezers based force measurement system for quantitating binding interactions: System design and application for the study of bacterial adhesion. Biosens. Bioelectron. 2004, 19, 1429–1437. [Google Scholar] [CrossRef]
- Homburg, O.; Hauschild, D.; Kubacki, F.; Lissotschenko, V. Efficient beam shaping for high-power laser applications. In Proceedings of the Laser Source and System Technology for Defense and Security II, Kissimmee, FL, USA, 17–18 April 2006; SPIE: Philadelphia, PA, USA, 2006; Volume 6216, pp. 48–55. [Google Scholar]
- Laskin, A.; Kaiser, P.; Laskin, V.; Ostrun, A. Laser beam shaping for biomedical microscopy techniques. In Proceedings of the Biophotonics: Photonic Solutions for Better Health Care V, Brussels, Belgium, 4–7 April 2016; SPIE: Philadelphia, PA, USA, 2016; Volume 9887, pp. 251–260. [Google Scholar]
- Kubby, J.A. Adaptive Optics for Biological Imaging; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hampson, K.M.; Turcotte, R.; Miller, D.T.; Kurokawa, K.; Males, J.R.; Ji, N.; Booth, M.J. Adaptive optics for high-resolution imaging. Nat. Rev. Methods Prim. 2021, 1, 68. [Google Scholar] [CrossRef] [PubMed]
- Gaunekar, A.S.; Widdowson, G.P.; Srikanth, N.; Guangneng, W. Design and development of a high precision lens focusing mechanism using flexure bearings. Precis. Eng. 2005, 29, 81–85. [Google Scholar] [CrossRef]
- Dadkhah, A.; Jiao, S. Optical coherence tomography-guided dynamic focusing for combined optical and mechanical scanning multimodal photoacoustic microscopy. J. Biomed. Opt. 2019, 24, 121906. [Google Scholar] [CrossRef]
- Li, H.; Chen, H.; Li, X.; Song, H.; Wang, D. Structural optical design of multi-group, high zoom ratio optical systems. Opt. Commun. 2024, 551, 130022. [Google Scholar] [CrossRef]
- Ren, H.; Wu, S.T. Variable-focus liquid lens. Opt. Express 2007, 15, 5931–5936. [Google Scholar] [CrossRef] [PubMed]
- Pan, M.; Fu, Y.; Zheng, M.; Chen, H.; Zang, Y.; Duan, H.; Li, Q.; Qiu, M.; Hu, Y. Dielectric metalens for miniaturized imaging systems: Progress and challenges. Light. Sci. Appl. 2022, 11, 195. [Google Scholar] [CrossRef]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.; Chen, H.T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Ren, M.X.; Wu, W.; Cai, W.; Pi, B.; Zhang, X.Z.; Xu, J.J. Reconfigurable metasurfaces that enable light polarization control by light. Light. Sci. Appl. 2017, 6, e16254. [Google Scholar] [CrossRef]
- Xiao, X.; Zhao, Y.; Ye, X.; Chen, C.; Lu, X.; Rong, Y.; Deng, J.; Li, G.; Zhu, S.; Li, T. Large-scale achromatic flat lens by light frequency-domain coherence optimization. Light. Sci. Appl. 2022, 11, 323. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Lu, X.; Lv, H.; Mou, Z.; Zhou, C.; Teng, S. Bifocal metalens with diverse polarization combination. Plasmonics 2021, 16, 575–579. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- Shalaginov, M.Y.; An, S.; Zhang, Y.; Yang, F.; Su, P.; Liberman, V.; Chou, J.B.; Roberts, C.M.; Kang, M.; Rios, C.; et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat. Commun. 2021, 12, 1225. [Google Scholar] [CrossRef] [PubMed]
- Afridi, A.; Canet-Ferrer, J.; Philippet, L.; Osmond, J.; Berto, P.; Quidant, R. Electrically driven varifocal silicon metalens. Acs Photonics 2018, 5, 4497–4503. [Google Scholar] [CrossRef]
- Yang, F.; Dao, K.P.; An, S.; Qiu, X.; Zhang, Y.; Hu, J.; Gu, T. Design of continuously tunable varifocal metalenses. J. Opt. 2023, 25, 115102. [Google Scholar] [CrossRef]
- Chen, K.; Feng, Y.; Monticone, F.; Zhao, J.; Zhu, B.; Jiang, T.; Zhang, L.; Kim, Y.; Ding, X.; Zhang, S.; et al. A reconfigurable active Huygens’ metalens. Adv. Mater. 2017, 29, 1606422. [Google Scholar] [CrossRef]
- Huang, Z.; Hu, B.; Liu, W.; Liu, J.; Wang, Y. Dynamical tuning of terahertz meta-lens assisted by graphene. J. Opt. Soc. Am. B 2017, 34, 1848–1854. [Google Scholar] [CrossRef]
- Huang, P.S.; Chu, C.H.; Huang, S.H.; Su, H.P.; Tanaka, T.; Wu, P.C. Varifocal metalenses: Harnessing polarization-dependent superposition for continuous focal length control. Nano Lett. 2023, 23, 10432–10440. [Google Scholar] [CrossRef]
- Wang, M.; Lee, J.S.; Aggarwal, S.; Farmakidis, N.; He, Y.; Cheng, T.; Bhaskaran, H. Varifocal metalens using tunable and ultralow-loss dielectrics. Adv. Sci. 2023, 10, 2204899. [Google Scholar] [CrossRef]
- Zhang, J.C.; Yao, J.; Tsai, D.P. Meta-lens based on multi-level phase-change. J. Appl. Phys. 2024, 136, 053101. [Google Scholar] [CrossRef]
- Shen, Y.; Shen, Z.; Wang, Y.; Xu, D.; Hu, W. Electrically tunable terahertz focusing modulator enabled by liquid crystal integrated dielectric metasurface. Crystals 2021, 11, 514. [Google Scholar] [CrossRef]
- Bosch, M.; Shcherbakov, M.R.; Won, K.; Lee, H.S.; Kim, Y.; Shvets, G. Electrically actuated varifocal lens based on liquid-crystal-embedded dielectric metasurfaces. Nano Lett. 2021, 21, 3849–3856. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.; Faraon, A. MEMS-tunable dielectric metasurface lens. Nat. Commun. 2018, 9, 812. [Google Scholar] [CrossRef]
- Han, Z.; Colburn, S.; Majumdar, A.; Böhringer, K.F. MEMS-actuated metasurface Alvarez lens. Microsyst. Nanoeng. 2020, 6, 79. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Liu, X.N.; Zhou, Y.; Zhang, J.; Liu, S.B.; Li, L. Varifocal diffractive lens based on microfluidics. Opt. Lasers Eng. 2024, 174, 107955. [Google Scholar] [CrossRef]
- Wei, S.; Cao, G.; Lin, H.; Yuan, X.; Somekh, M.; Jia, B. A varifocal graphene metalens for broadband zoom imaging covering the entire visible region. ACS Nano 2021, 15, 4769–4776. [Google Scholar] [CrossRef] [PubMed]
- Bernet, S.; Ritsch-Marte, M. Adjustable refractive power from diffractive moiré elements. Appl. Opt. 2008, 47, 3722–3730. [Google Scholar] [CrossRef] [PubMed]
- Bernet, S.; Harm, W.; Ritsch-Marte, M. Demonstration of focus-tunable diffractive Moiré-lenses. Opt. Express 2013, 21, 6955–6966. [Google Scholar] [CrossRef]
- Cui, Y.; Zheng, G.; Chen, M.; Zhang, Y.; Yang, Y.; Tao, J.; He, T.; Li, Z. Reconfigurable continuous-zoom metalens in visible band. Chin. Opt. Lett. 2019, 17, 111603. [Google Scholar] [CrossRef]
- Sun, C.; Zeng, Z.; Wang, W.; Du, L.; Chen, X.; Leng, J.; Li, J.; Liu, Q.; Wen, Z.; Qi, P.; et al. An Ultra-Broadband Modified Moiré Varifocal Metalens with High Alignment Tolerance for Terahertz Wave. Laser Photonics Rev. 2025, 19, 2401935. [Google Scholar] [CrossRef]
- Lei, Y.; Liang, B.; Xiao, J.; Duan, J.; Lu, Z.; Wang, S.; Hu, Q.; Wang, Z.; Gong, Y. A 3-D-printed lens antenna with tunable Varifocal based on the Moiré effect. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 2301–2305. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, J.; Dong, Y.; Wang, J. Full-dimensional geometric-phase spatial light metamodulation. Nano Lett. 2024, 24, 9229–9236. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.L.; Liu, J.L.; Yue, J.X.; Qin, L.; Zhang, J.Y.; Li, X.; Song, C.X.; Zhang, Z.S.; Chen, H.; Chang, Y.C.; et al. Design of a polarization-insensitive broadband achromatic metalens for mid-wave infrared detector. Opt. Lett. 2024, 49, 5563–5566. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Sakuma, S.; Kera, K.; Uozumib, N.; Arai, F. Measurement of the mechanical properties of single Synechocystis sp. strain PCC6803 cells in different osmotic concentrations using a robot-integrated microfluidic chip. Lab A Chip 2018, 18, 1241–1249. [Google Scholar] [CrossRef]
- Luo, Y.; Chu, C.H.; Vyas, S.; Kuo, H.Y.; Chia, Y.H.; Chen, M.K.; Shi, X.; Tanaka, T.; Misawa, H.; Huang, Y.-Y.; et al. Varifocal metalens for optical sectioning fluorescence microscopy. Nano Lett. 2021, 21, 5133–5142. [Google Scholar] [CrossRef]
- Wang, C.; Yu, Z.; Zhang, Q.; Sun, Y.; Tao, C.; Wu, F.; Zheng, Z. Metalens eyepiece for 3D holographic near-eye display. Nanomaterials 2021, 11, 1920. [Google Scholar] [CrossRef]
- Mou, Z.; Lu, X.; Lv, H.; Han, Y.; Yue, Q.; Wang, S.; Teng, S. Metasurface array illuminator based on Fresnel holography. Optics Lasers Eng. 2020, 131, 106146. [Google Scholar] [CrossRef]
- Ouyang, X.; Zeng, Y.; Wang, Z.; Bo, B.; Lai, F.; Zhang, C.; Qiu, C.w.; Song, Q.; Yu, S.; Kivshar, Y.; et al. Ultra narrowband geometric-phase resonant metasurfaces. Proc. Natl. Acad. Sci. USA 2025, 122, e2420830122. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, D.; Sun, S.; Zhang, L.; Li, X. Design of a Modified Moiré Varifocal Metalens Based on Fresnel Principles. Photonics 2025, 12, 888. https://doi.org/10.3390/photonics12090888
Chang D, Sun S, Zhang L, Li X. Design of a Modified Moiré Varifocal Metalens Based on Fresnel Principles. Photonics. 2025; 12(9):888. https://doi.org/10.3390/photonics12090888
Chicago/Turabian StyleChang, Di, Shuiping Sun, Lieshan Zhang, and Xueyan Li. 2025. "Design of a Modified Moiré Varifocal Metalens Based on Fresnel Principles" Photonics 12, no. 9: 888. https://doi.org/10.3390/photonics12090888
APA StyleChang, D., Sun, S., Zhang, L., & Li, X. (2025). Design of a Modified Moiré Varifocal Metalens Based on Fresnel Principles. Photonics, 12(9), 888. https://doi.org/10.3390/photonics12090888




