Optical Communication Performance of Cylindrical Vector Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence
Abstract
1. Introduction
2. Theory
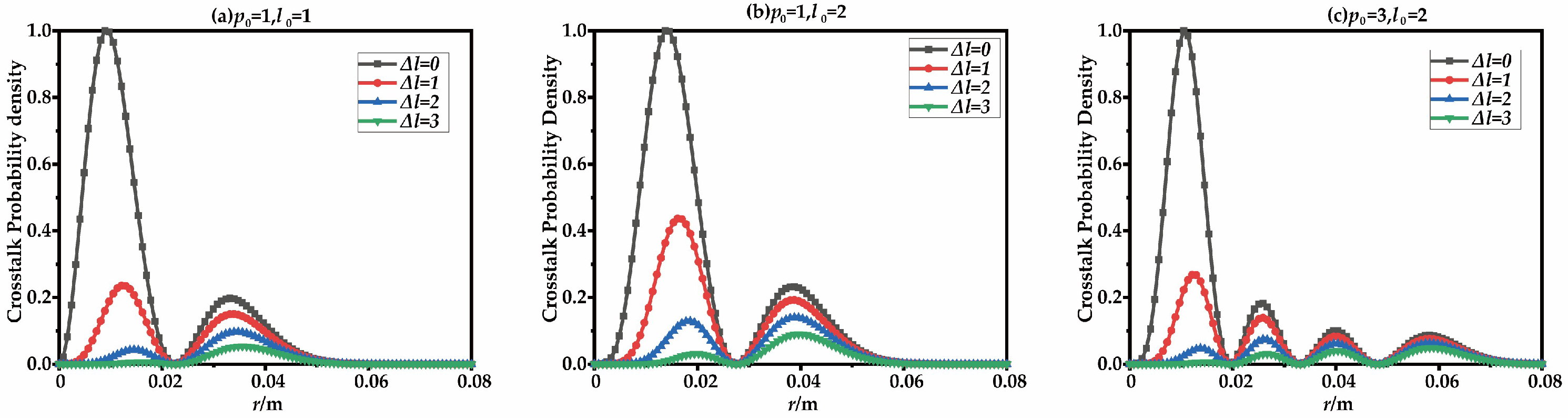
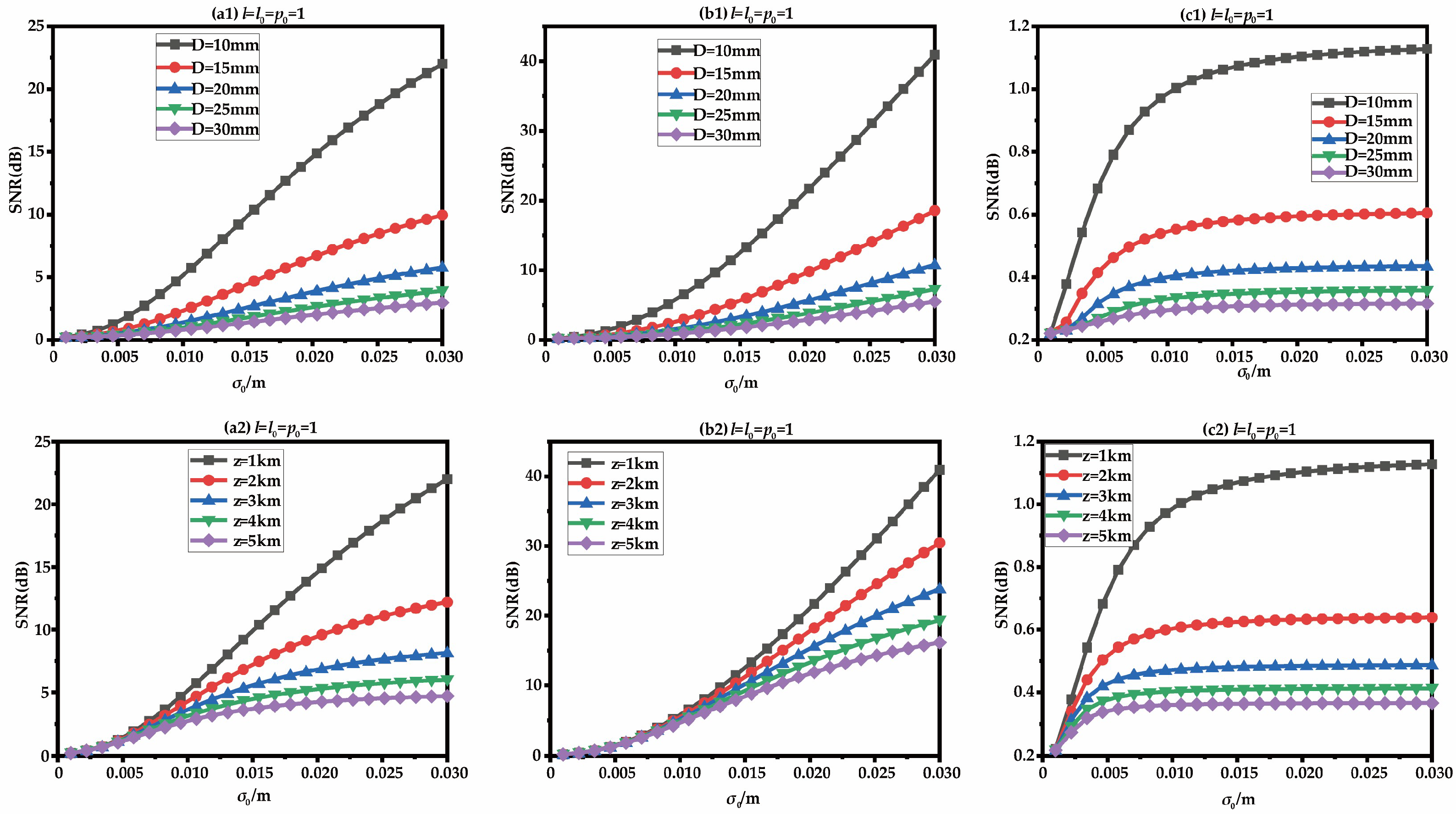
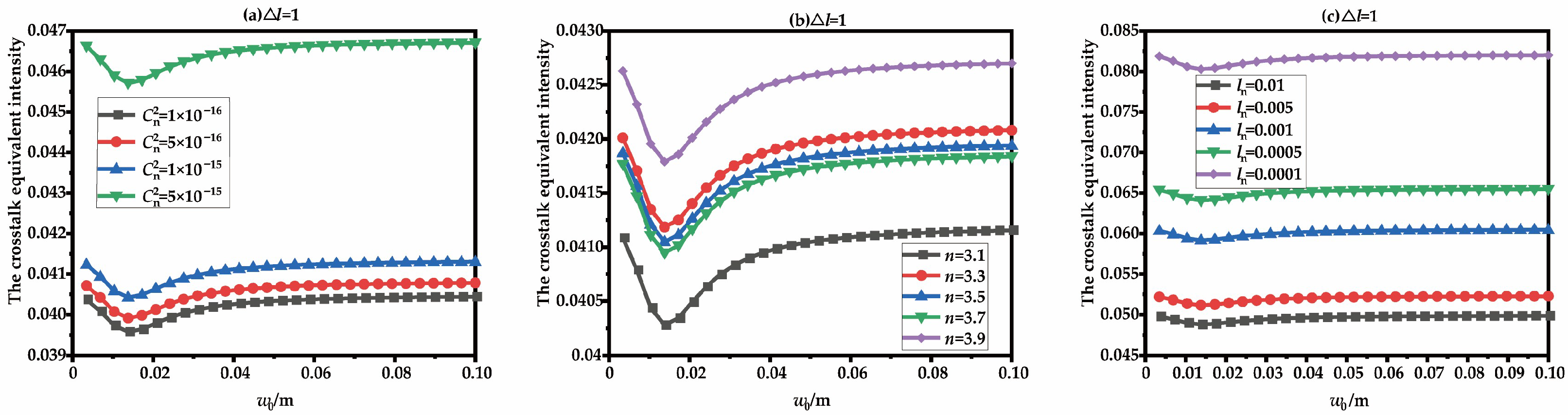
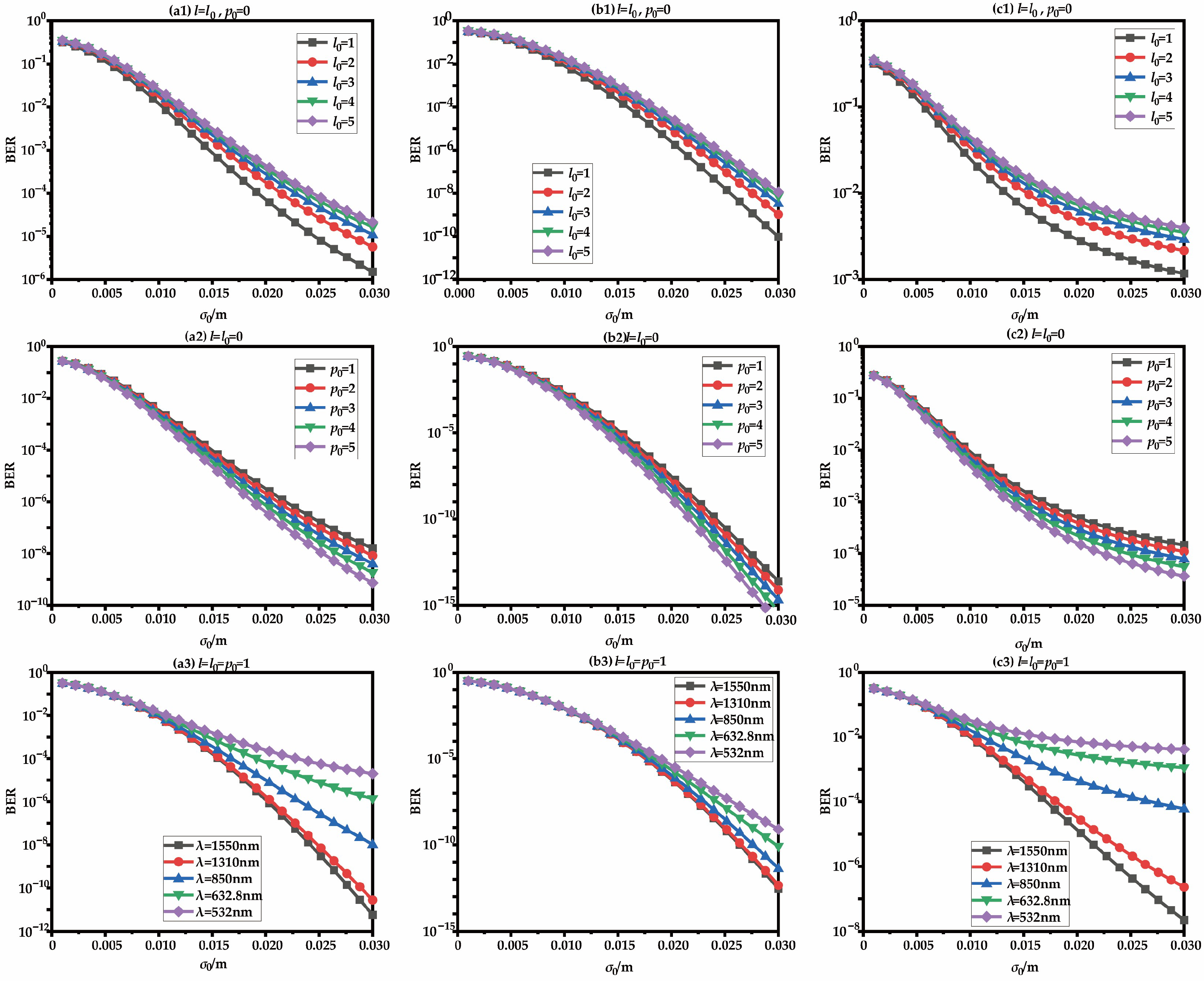
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2022, 11, 645–680. [Google Scholar] [CrossRef]
- Willner, A.E.; Zhao, Z.; Liu, C.; Zhang, R.; Song, H.; Pang, K.; Manukyan, K.; Song, H.; Su, X.; Xie, G.; et al. Perspectives on advances in high-capacity, free-space communications using multiplexing of orbital-angular-momentum beams. APL Photonics 2021, 6, 030901. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, D.; Li, C.; Duan, S.; Zhang, H.; Lin, W.; Liu, H.; Liu, B. Bidirectional high-purity structured light beams transformation based on multi-plane light conversion. Opt. Express 2025, 33, 7155–7170. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, Y.; Liu, X.; Ma, Y.; Cai, Y.; Ponomarenko, S.A.; Liu, X. Deep learning and random light structuring ensure robust free-space communications. Appl. Phys. Lett. 2024, 124, 214103. [Google Scholar] [CrossRef]
- Panchal, P.; Naik, D.N.; Narayanamurthy, C.S. Insensitivity of higher order topologically charged Laguerre–Gaussian beams to dynamic turbulence impact. Opt. Commun. 2021, 495, 127023. [Google Scholar] [CrossRef]
- Wang, S.; Qin, W.; Guan, T.; Liu, J.; Cai, Q.; Zhang, S.; Zhou, L.; Zhang, Y.; Wu, Y.; Tao, Z. Flexible generation of structured terahertz fields via programmable exchange-biased spintronic emitters. eLight 2024, 4, 11. [Google Scholar] [CrossRef]
- Ni, J.; Ji, S.; Wang, Z.; Liu, S.; Hu, Y.; Chen, Y.; Li, J.; Li, X.; Chu, J.; Wu, D.; et al. Unidirectional unpolarized luminescence emission via vortex excitation. Nat. Photonics 2023, 17, 601–606. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wang, C. Generation and expansion of Laguerre-Gaussian beams. J. Opt. 2022, 51, 910–926. [Google Scholar] [CrossRef]
- Ohtake, Y.; Ando, T.; Fukuchi, N.; Matsumoto, N.; Ito, H.; Hara, T. Universal generation of higher-order multiringed Laguerre-Gaussian beams by using a spatial light modulator. Opt. Lett. 2007, 32, 1411–1413. [Google Scholar] [CrossRef]
- Minoofar, A.; Su, X.; Zhou, H.; Zhang, R.; Alishahi, F.; Zou, K.; Song, H.; Pang, K.; Zach, S.; Tur, M.; et al. Experimental demonstration of sub-THz wireless communications using multiplexing of Laguerre-Gaussian beams when varying two different modal indices. J. Light. Technol. 2022, 40, 3285–3292. [Google Scholar] [CrossRef]
- Arya, S.; Chung, Y.H. High-performance and high-capacity ultraviolet communication with orbital angular momentum. IEEE Access 2019, 7, 116734–116740. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, Z.; Dedo, M.I.; Guo, K. The orbital angular momentum encoding system with radial indices of Laguerre–Gaussian beam. IEEE Photonics J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Xie, G.; Ren, Y.; Yan, Y.; Huang, H.; Ahmed, N.; Li, L.; Zhao, Z.; Bao, C.; Tur, M.; Ashrafi, S.; et al. Experimental demonstration of a 200-Gbit/s free-space optical link by multiplexing Laguerre–Gaussian beams with different radial indices. Opt. Lett. 2016, 41, 3447–3450. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Zhu, Y.; Wang, D.; Zhang, Y.; Hu, Z.; Cheng, M. Bessel–Gauss photon beams with fractional order vortex propagation in weak non-Kolmogorov turbulence. Photonics Res. 2016, 4, 30–34. [Google Scholar] [CrossRef]
- Ge, X.; Shang, Y.; Mi, Z.; Zhao, Z.; Zhang, L.; Wang, B.; Lei, C.; Man, Z. Crosstalk mitigation of a controllable annular auto-focusing vortex beam array in a turbulent atmosphere. Opt. Express 2024, 32, 12449–12461. [Google Scholar] [CrossRef]
- Chen, M.; Roux, F.S. Influence of the least-squares phase on optical vortices in strongly scintillated beams. Phys. Rev. A 2009, 80, 013824. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Y.; Guo, L.; Li, P.; Zhang, Y.; Wu, H.; Huang, L. Distortion sensing of off-axis vortex beams enabled by a differentiable neural model. Opt. Express 2025, 33, 24272–24291. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Huang, Y.; Wang, F.; Liu, X.; Gbur, G.; Cai, Y. Scintillation properties of a partially coherent vector beam with vortex phase in turbulent atmosphere. Opt. Express 2019, 27, 26676–26688. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Zhu, J.; Xu, M.; Pu, M.; Wang, S. Continuous-wave degenerate cavity laser for optical imaging in scattering media. Opt. Lett. 2024, 49, 4350–4353. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, K.; Zhang, C.; Liang, J.; Deng, S.; Hong, P.; Zou, B.; Liang, Y. Caustic analysis of partially coherent self-accelerating beams: Investigating self-healing properties. Phys. Rev. A 2024, 109, 043529. [Google Scholar] [CrossRef]
- Xu, W.; Ning, S.; Zhang, F. Review of partially coherent diffraction imaging. Acta Phys. Sin. 2021, 70, 214201. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, X.; Wang, F.; Chen, Y.; Cai, Y. Research progress on manipulating spatial coherence structure of light beam and its applications. Prog. Quant. Electron. 2023, 91, 100486. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Peng, X.; Liu, L.; Cai, Y.; Wang, F. Real-time synthesis of twisted Gaussian Schell-model beams and their applications in suppressing the turbulence-induced scintillation and beam wander. Opt. Lett. 2025, 50, 4342–4345. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhou, Z.; Yuan, X. Research on performance of convex partially coherent flat-topped beams in vertical atmospheric turbulent paths. Opt. Commun. 2021, 482, 126577. [Google Scholar] [CrossRef]
- Ming, G.; Yan, L.; Hong, L.; Lei, G. Polarization properties of polarized and partially coherent Electromagnetic Gaussian-Schell model pulse beams on slant path in turbulent atmosphere. Infrared Phys. Technol. 2014, 67, 98–106. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Liu, L.; Yuan, Y.; Cai, Y. Experimental study of the scintillation index of a radially polarized beam with controllable spatial coherence. Appl. Phys. Lett. 2013, 103, 091102. [Google Scholar] [CrossRef]
- Gu, Y.; Korotkova, O.; Gbur, G. Scintillation of nonuniformly polarized beams in atmospheric turbulence. Opt. Lett. 2009, 34, 2261–2263. [Google Scholar] [CrossRef]
- Dong, Y.; Cai, Y.; Zhao, C.; Yao, M. Statistics properties of a cylindrical vector partially coherent beam. Opt. Express 2011, 19, 5979–5992. [Google Scholar] [CrossRef]
- Nie, Z.; Shi, G.; Li, D.; Zhang, X.; Wang, Y.; Song, Y. Tight focusing of a radially polarized Laguerre–Bessel–Gaussian beam and its application to manipulation of two types of particles. Phys. Lett. A 2015, 379, 857–863. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Z.; Qu, J.; Huang, W. The tight focusing properties of Laguerre-Gaussian-correlated Schell-model beams. J. Mod. Opt. 2016, 63, 1429–1437. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, Y.; Wu, H.; Chen, H.; Sheng, Z.; Qu, J. Focus shaping of the radially polarized Laguerre-Gaussian-correlated Schell-model vortex beams. Opt. Express 2018, 26, 20076–20088. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, Y.; Dan, Y. Evolution properties of partially coherent radially polarized Laguerre-Gaussian vortex beams in an anisotropic turbulent atmosphere. Opt. Express 2021, 29, 34986–35002. [Google Scholar] [CrossRef]
- Huang, K.; Xu, Y.; Li, Y. Average intensity of a Laguerre—Gaussian vector vortex beam through inhomogeneous atmospheric turbulence. Photonics 2023, 10, 1189. [Google Scholar] [CrossRef]
- Chen, R.; Dong, Y.; Wang, F.; Cai, Y. Statistical properties of a cylindrical vector partially coherent beam in turbulent atmosphere. Appl. Phys. B 2013, 112, 247–259. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, H.; Yuan, Y.; Gao, Y.; Liang, C.; Ponomarenko, S.; Cai, Y. High-fidelity information transmission through the turbulent atmosphere utilizing partially coherent cylindrical vector beams. Adv. Photon. Res. 2024, 6, 2400137. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Eyyuboglu, H.; Baykal, Y. Average intensity and spreading of partially coherent standard and elegant Laguerre-Gaussian beams in turbulent atmosphere. Prog. Electromagn. Res. 2010, 103, 33–56. [Google Scholar] [CrossRef][Green Version]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Paterson, C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef]
- Ma, Z.; Zhao, W.; Zhao, J.; Liu, J.; Jing, Q.; Dou, J.; Li, B.; Hu, Y. Generation of arbitrary higher-order Poincaré sphere beam from a ring fiber laser with cascaded Q-plates. Opt. Laser Technol. 2022, 156, 108552. [Google Scholar] [CrossRef]
- Zhuang, Y.; Yang, Q.; Wu, P.; Zhang, W.; Ren, Y.; Liu, H. Vortex beam array generated by a volume compound fork grating in lithium niobite. Results Phys. 2021, 24, 104083. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Ruiz, I.; Cottrell, D.M. Decomposition of radially and azimuthally polarized beams using a circular-polarization and vortex-sensing diffraction grating. Opt. Express 2010, 18, 7173–7183. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, J.; Gbur, G.; Korotkova, O. Evolution of the orbital angular momentum flux density of partially coherent vortex beams in atmospheric turbulence. Front. Phys. 2020, 10, 1073662. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Xu, J.; Wang, J.; Jia, J. Orbital angular momentum crosstalk of single photons propagation in a slant non-Kolmogorov turbulence channel. Opt. Commun. 2011, 284, 1132–1138. [Google Scholar] [CrossRef]
- Wang, S.C.H.; Plonus, M.A.; Ouyang, C.F. Irradiance scintillations of a partially coherent source in extremely strong turbulence. Appl. Opt. 1979, 18, 1133–1135. [Google Scholar] [CrossRef] [PubMed]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Chen, M.; Lin, Y.; Zhang, Y. Signal/noise ratio of orbital angular momentum modes for a partially coherent modified Bessel-correlated beam in a biological tissue. J. Opt. Soc. Am. A 2017, 34, 2046–2051. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Dong, K.; Shi, C.; Al-Ahsab, H.T.M.; Guo, L.; Yi, X.; Wang, P.; Li, J. Enhancing Performance of Air–Ground OAM Communication System Utilizing Vector Vortex Beams in the Atmosphere. Photonics 2022, 10, 41. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Yao, L.; Gao, Y.; Zhang, H.; Yuan, Y.; Guo, B.; Shi, H. Optical Communication Performance of Cylindrical Vector Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence. Photonics 2025, 12, 883. https://doi.org/10.3390/photonics12090883
Liu M, Yao L, Gao Y, Zhang H, Yuan Y, Guo B, Shi H. Optical Communication Performance of Cylindrical Vector Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence. Photonics. 2025; 12(9):883. https://doi.org/10.3390/photonics12090883
Chicago/Turabian StyleLiu, Meng, Linxuan Yao, Yaru Gao, Hui Zhang, Yangsheng Yuan, Bohan Guo, and Huimin Shi. 2025. "Optical Communication Performance of Cylindrical Vector Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence" Photonics 12, no. 9: 883. https://doi.org/10.3390/photonics12090883
APA StyleLiu, M., Yao, L., Gao, Y., Zhang, H., Yuan, Y., Guo, B., & Shi, H. (2025). Optical Communication Performance of Cylindrical Vector Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence. Photonics, 12(9), 883. https://doi.org/10.3390/photonics12090883




