Diopter Measurement of Human Eye Based on Dual-Focus Swept Source Optical Coherence Tomography
Abstract
1. Introduction
2. Methods
2.1. System
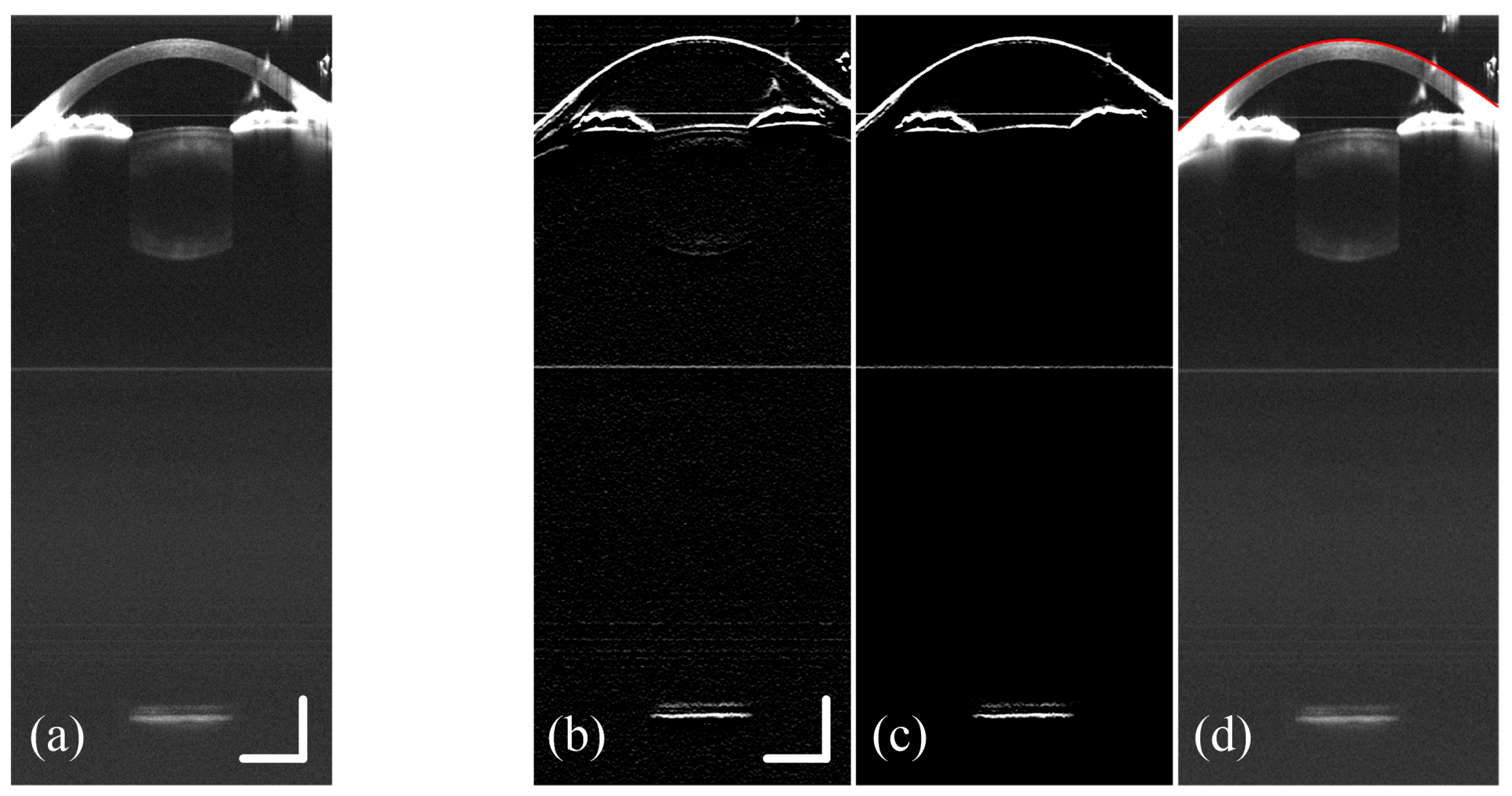
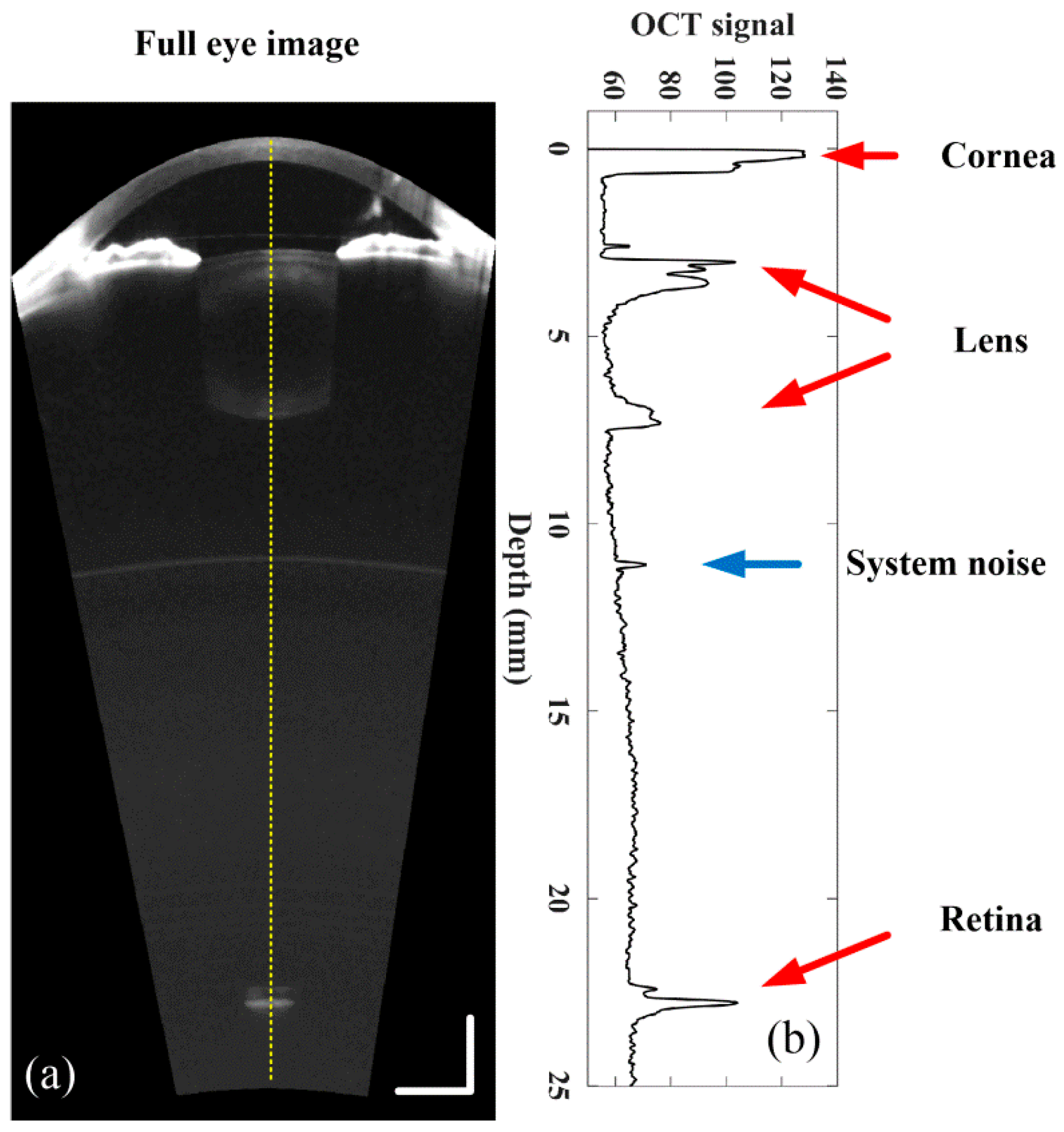
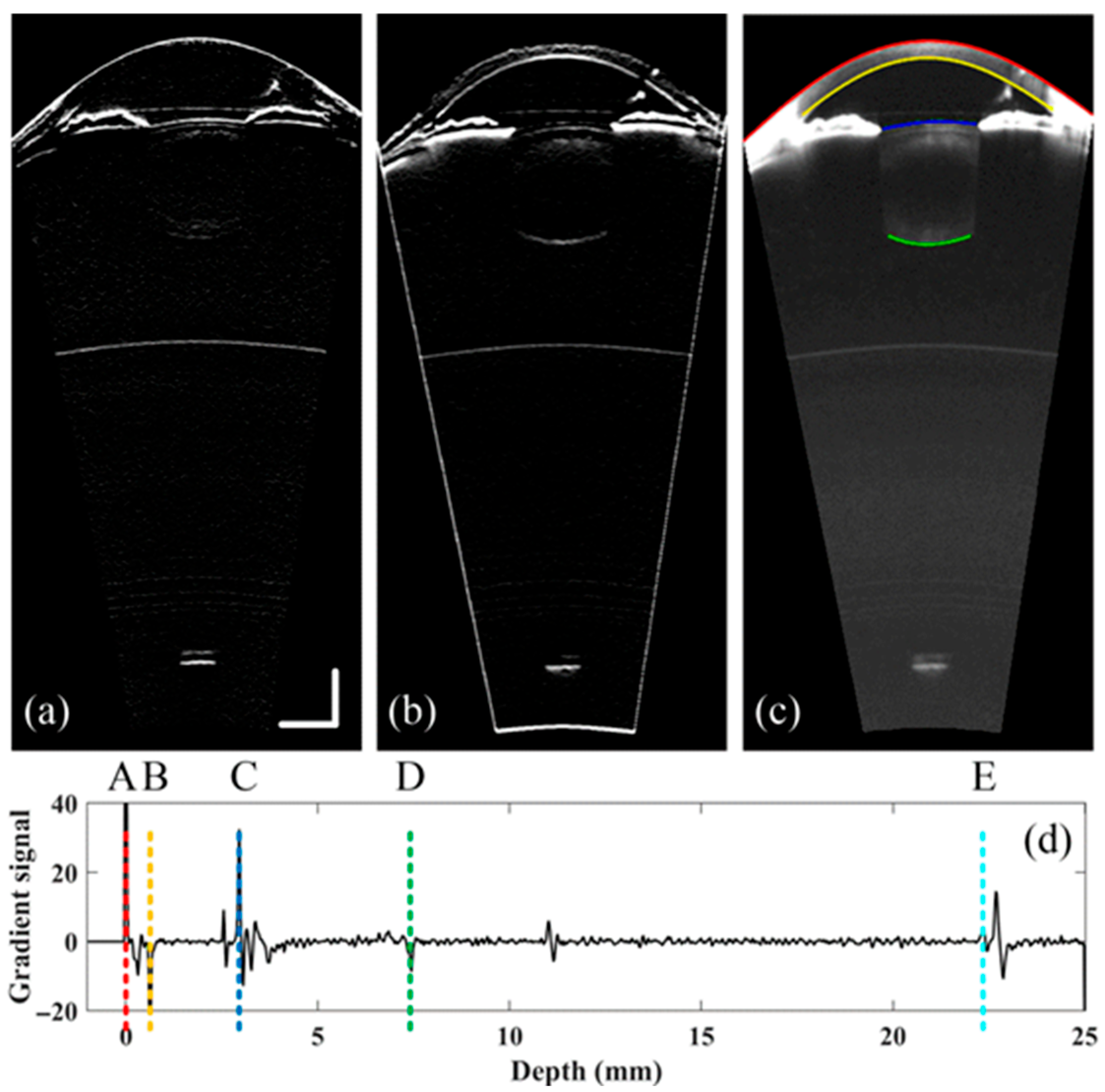
2.2. Refraction Correction, Boundary Detection and Curvature Calculation
2.3. Calculation of Diopter
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACD | Anterior chamber depth |
| AL | Axial length |
| CASC | Corneal anterior surface curvature |
| CC | Corneal curvature |
| CCT | Corneal center thickness |
| CNV | Choroidal neovascularization |
| CPSC | Corneal posterior surface curvature |
| FD-OCT | Fourier domain OCT |
| LASC | Lens anterior surface curvature |
| LCT | Lens center thickness |
| LPSC | Lens posterior surface curvature |
| OCT | Optical coherence tomography |
| RAC | Anterior cornea curvature radius |
| RAL | Anterior lens curvature radius |
| RPC | Posterior cornea curvature radius |
| RPE | Retinal pigment epithelium |
| RPL | Posterior lens curvature radius |
| SD-OCT | Spectral domain OCT |
| SER | Spherical equivalent refraction |
| SS-OCT | Swept source OCT |
| TD-OCT | Time domain OCT |
| VCD | Vitreous chamber depth |
| VCSEL | Vertical-cavity surface-emitting lasers |
References
- Wajuihian, S.O.; Mashige, K.P. Gender and age distribution of refractive errors in an optometric clinical population. J. Optom. 2021, 14, 315–327. [Google Scholar] [CrossRef]
- Haarman, A.E.G.; Enthoven, C.A.; Tideman, J.W.L.; Tedja, M.S.; Verhoeven, V.J.M.; Klaver, C.C.W. The Complications of Myopia: A Review and Meta-Analysis. Investig. Ophthalmol. Vis. Sci. 2020, 61, 49. [Google Scholar] [CrossRef] [PubMed]
- Terao, N.; Koizumi, H.; Kojima, K.; Kusada, N.; Nagata, K.; Yamagishi, T.; Yoneda, K.; Yoshii, K.; Kinoshita, S.; Sotozono, C. Short axial length and hyperopic refractive error are risk factors of central serous chorioretinopathy. Br. J. Ophthalmol. 2020, 104, 1260–1265. [Google Scholar] [CrossRef] [PubMed]
- Ha, A.; Kim, C.Y.; Shim, S.R.; Chang, I.B.; Kim, Y.K. Degree of Myopia and Glaucoma Risk: A Dose-Response Meta-analysis. Am. J. Ophthalmol. 2022, 236, 107–119. [Google Scholar] [CrossRef]
- Gaurisankar, Z.S.; van Rijn, G.A.; Lima, J.E.E.; Ilgenfritz, A.P.; Cheng, Y.; Haasnoot, G.W.; Luyten, G.P.M.; Beenakker, J.W.M. Correlations between ocular biometrics and refractive error: A systematic review and meta-analysis. Acta Ophthalmol. 2019, 97, 735–743. [Google Scholar] [CrossRef]
- Zhang, Z.; Mu, J.; Wei, J.; Geng, H.; Liu, C.; Yi, W.; Sun, Y.; Duan, J. Correlation between refractive errors and ocular biometric parameters in children and adolescents: A systematic review and meta-analysis. BMC Ophthalmol. 2023, 23, 472. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef]
- Fercher, A.F.; Hitzenberger, C.K.; Drexler, W.; Kamp, G.; Sattmann, H. In Vivo Optical Coherence Tomography. Am. J. Ophthalmol. 1993, 116, 113–114. [Google Scholar] [CrossRef]
- Murthy, R.K.; Haji, S.; Sambhav, K.; Grover, S.; Chalam, K.V. Clinical applications of spectral domain optical coherence tomography in retinal diseases. Biomed. J. 2016, 39, 107–120. [Google Scholar] [CrossRef]
- Izatt, J.A.; Hee, M.R.; Swanson, E.A.; Lin, C.P.; Huang, D.; Schuman, J.S.; Puliafito, C.A.; Fujimoto, J.G. Micrometer-scale resolution imaging of the anterior eye in vivo with optical coherence tomography. Arch. Ophthalmol. 1994, 112, 1584–1589. [Google Scholar] [CrossRef] [PubMed]
- Garcia Marin, Y.F.; Alonso-Caneiro, D.; Vincent, S.J.; Collins, M.J. Anterior segment optical coherence tomography (AS-OCT) image analysis methods and applications: A systematic review. Comput. Biol. Med. 2022, 146, 105471. [Google Scholar] [CrossRef]
- Geevarghese, A.; Wollstein, G.; Ishikawa, H.; Schuman, J.S. Optical Coherence Tomography and Glaucoma. Annu. Rev. Vis. Sci. 2021, 7, 693–726. [Google Scholar] [CrossRef]
- Rosales, P.; Wendt, M.; Marcos, S.; Glasser, A. Changes in crystalline lens radii of curvature and lens tilt and decentration during dynamic accommodation in rhesus monkeys. J. Vis. 2008, 8, 18. [Google Scholar] [CrossRef]
- Xie, X.; Sultan, W.; Corradetti, G.; Lee, J.Y.; Song, A.; Pardeshi, A.; Yu, F.; Chopra, V.; Sadda, S.R.; Xu, B.Y.; et al. Assessing accommodative presbyopic biometric changes of the entire anterior segment using single swept-source OCT image acquisitions. Eye 2021, 36, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Milani, P.; Montesano, G.; Rossetti, L.; Bergamini, F.; Pece, A. Vessel density, retinal thickness, and choriocapillaris vascular flow in myopic eyes on OCT angiography. Graefe’s Arch. Clin. Exp. Ophthalmol. 2018, 256, 1419–1427. [Google Scholar] [CrossRef]
- Jiao, H.; Hill, L.J.; Downie, L.E.; Chinnery, H.R. Anterior segment optical coherence tomography: Its application in clinical practice and experimental models of disease. Clin. Exp. Optom. 2021, 102, 208–217. [Google Scholar] [CrossRef] [PubMed]
- Mirzayev, I.; Gündüz, A.K.; Aydın Ellialtıoğlu, P.; Gündüz, Ö.Ö. Clinical applications of anterior segment swept-source optical coherence tomography: A systematic review. Photodiagnosis Photodyn. Ther. 2023, 42, 103334. [Google Scholar] [CrossRef] [PubMed]
- Wojtkowski, M.; Leitgeb, R.; Kowalczyk, A.; Bajraszewski, T.; Fercher, A.F. In vivo human retinal imaging by Fourier domain optical coherence tomography. J. Biomed. Opt. 2002, 7, 457–463. [Google Scholar] [CrossRef]
- Tañá-Rivero, P.; Orts-Vila, P.; Tañá-Sanz, P.; Ramos-Alzamora, M.; Montés-Micó, R. Assessment of corneal epithelial thickness mapping by spectral-domain optical coherence tomography. Front. Med. 2024, 11, 1459636. [Google Scholar] [CrossRef]
- Garza León, M.; Li, Y.; Gokul, A.; McGhee, C.; Ziaei, M. Repeatability and agreement of biometric measurements using spectral domain anterior segment optical coherence tomography and Scheimpflug tomography in keratoconus. PLoS ONE 2021, 16, e0248659. [Google Scholar] [CrossRef]
- Baumann, B.; Pircher, M.; Götzinger, E.; Hitzenberger, C.K.J.O.e. Full range complex spectral domain optical coherence tomography without additional phase shifters. Opt. Express 2007, 15, 13375–13387. [Google Scholar] [CrossRef]
- Grulkowski, I.; Gora, M.; Szkulmowski, M.; Gorczynska, I.; Szlag, D.; Marcos, S.; Kowalczyk, A.; Wojtkowski, M. Anterior segment imaging with Spectral OCT system using a high-speed CMOS camera. Opt. Express 2009, 17, 4842–4858. [Google Scholar] [CrossRef]
- Targowski, P.; Wojtkowski, M.; Kowalczyk, A.; Bajraszewski, T.; Szkulmowski, M.; Gorczyńska, I. Complex spectral OCT in human eye imaging in vivo. Opt. Commun. 2004, 229, 79–84. [Google Scholar] [CrossRef]
- Feng, Y.; Reinstein, D.Z.; Nitter, T.; Archer, T.J.; McAlinden, C.; Chen, X.; Bertelsen, G.; Utheim, T.P.; Stojanovic, A. Heidelberg Anterion Swept-Source OCT Corneal Epithelial Thickness Mapping: Repeatability and Agreement With Optovue Avanti. J. Refract. Surg. 2022, 38, 356–363. [Google Scholar] [CrossRef]
- Mohan, R.R.; Asawaworarit, R.; Satitpitakul, V.; Taweekitikul, P.; Pongpirul, K. Agreement of total corneal power between 2 swept-source optical coherence tomography and Scheimpflug tomography in normal and keratoconic patients. PLoS ONE 2022, 17, e0268856. [Google Scholar] [CrossRef]
- Rao, A.; Langenbucher, A.; Szentmáry, N.; Cayless, A.; Hoffmann, P.; Wendelstein, J.; Cooke, D. Repeatability of biometric measures from the IOLMaster 700 in a cataractous population. PLoS ONE 2024, 19, e0297869. [Google Scholar] [CrossRef]
- Liu, J.J.; Grulkowski, I.; Kraus, M.F.; Potsaid, B.; Lu, C.D.; Baumann, B.; Duker, J.S.; Hornegger, J.; Fujimoto, J.G. In vivo imaging of the rodent eye with swept source/Fourier domain OCT. Biomed. Opt. Express 2013, 4, 351–363. [Google Scholar] [CrossRef][Green Version]
- Grulkowski, I.; Liu, J.J.; Potsaid, B.; Jayaraman, V.; Lu, C.D.; Jiang, J.; Cable, A.E.; Duker, J.S.; Fujimoto, J.G. Retinal, anterior segment and full eye imaging using ultrahigh speed swept source OCT with vertical-cavity surface emitting lasers. Biomed. Opt. Express 2012, 3, 2733–2751. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Shao, Y.; Tao, A.; Jiang, H.; Liu, C.; Zhang, H.; Wang, J. Axial Biometry of the Entire Eye Using Ultra-Long Scan Depth Optical Coherence Tomography. Am. J. Ophthalmol. 2014, 157, 412–420.e412. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gotzinger, E.; Pircher, M.; Leitgeb, R.; Baumann, B.; Hitzenberger, C.K. Quadruple depth range spectral domain optical coherence tomography for imaging of the anterior eye segment. In Proceedings of the SPIE Photonics West—BIOS, San Jose, CA, USA, 24–29 January 2009. [Google Scholar]
- Grajciar, B.; Pircher, M.; Hitzenberger, C.K.; Findl, O.; Fercher, A.F. High sensitive measurement of the human axial eye length in vivo with Fourier domain low coherence interferometry. Opt. Express 2008, 16, 2405–2414. [Google Scholar] [CrossRef] [PubMed]
- Izatt, J.A.; Holmes, J.; Fujimoto, J.G.; Hattersley, S.; Stone, N.; Tuchin, V.V.; Bazant-Hegemark, F.; Barr, H. Multi-channel Fourier domain OCT system with superior lateral resolution for biomedical applications. In Proceedings of the Coherence Domain Optical Methods and Optical Coherence Tomography in Biomedicine XII, San Jose, CA, USA, 21–23 January 2008. [Google Scholar]
- Dai, C.; Zhou, C.; Fan, S.; Chen, Z.; Chai, X.; Ren, Q.; Jiao, S. Optical coherence tomography for whole eye segment imaging. Opt. Express 2012, 20, 6109–6115. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, J.; Jiao, S. Dual channel dual focus optical coherence tomography for imaging accommodation of the eye. Opt. Express 2009, 17, 8947–8955. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; Li, L.; Li, Q.; Dai, C.; Ren, Q.; Jiao, S.; Zhou, C. Dual band dual focus optical coherence tomography for imaging the whole eye segment. Biomed. Opt. Express 2015, 6, 2481–2493. [Google Scholar] [CrossRef] [PubMed]
- ANSI Z136.1; Safe Use of Lasers. American National Standards Institute: Orlando, FL, USA, 2022.
- IEC 60825-1; Safety of Laser Products—Part 1: Equipment Classi-fication and Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Podoleanu, A.; Charalambous, I.; Plesea, L.; Dogariu, A.; Rosen, R. Correction of distortions in optical coherence tomography imaging of the eye. Phys. Med. Biol. 2004, 49, 1277–1294. [Google Scholar] [CrossRef]
- Von Helmholtz, H. Helmholtz’s Treatise on Physiological Optics; Optical Society of America: Washington, DC, USA, 1925; Volume 3. [Google Scholar]
- Lotmar, W.J. Theoretical eye model with aspherics. J. Opt. Soc. Am. 1971, 61, 1522–1529. [Google Scholar] [CrossRef]
- Grand, Y.L.; Hage, S.G.E. Physiological Optics; Wiley-Blackwell: Hoboken, NJ, USA, 1980. [Google Scholar]
- Atchison, D.A.; Thibos, L.N. Optical models of the human eye. Clin. Exp. Optom. 2021, 99, 99–106. [Google Scholar] [CrossRef]
- Savini, G.; Hoffer, K.J.; Schiano-Lomoriello, D. Agreement between lens thickness measurements by ultrasound immersion biometry and optical biometry. J. Cataract Refract. Surg. 2018, 44, 1463–1468. [Google Scholar] [CrossRef]
- Meng, W.; Butterworth, J.; Malecaze, F.; Calvas, P. Axial Length of Myopia: A Review of Current Research. Ophthalmologica 2011, 225, 127–134. [Google Scholar] [CrossRef]
- Martin, R. Cornea and anterior eye assessment with slit lamp biomicroscopy, specular microscopy, confocal microscopy, and ultrasound biomicroscopy. Indian J. Ophthalmol. 2018, 66, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.; Chan, T.C.Y.; Prakash, G.; Jhanji, V. Applications of corneal topography and tomography: A review. Clin. Exp. Ophthalmol. 2018, 46, 133–146. [Google Scholar] [CrossRef]
- Chan, T.C.Y.; Biswas, S.; Yu, M.; Jhanji, V. Comparison of corneal measurements in keratoconus using swept-source optical coherence tomography and combined Placido–Scheimpflug imaging. Acta Ophthalmol. 2016, 95, e486–e494. [Google Scholar] [CrossRef] [PubMed]



| Medium | Refractive Index |
|---|---|
| Cornea | 1.387 |
| Aqueous humor | 1.342 |
| Lens | 1.415 |
| Vitreous | 1.341 |
| Average | 1.3549 |
| CCT | ACD | LCT | VCD | AL | |
|---|---|---|---|---|---|
| Dual-focus SS-OCT | 0.51 | 3.14 | 3.82 | 19.62 | 27.09 |
| Lenstar 900 | 0.54 | 3.12 | 3.99 | 19.58 | 27.23 |
| Accommodative Stimulus | CCT | LCT | ACD | VCD | CASC | CPSC | LASC | LPSC |
|---|---|---|---|---|---|---|---|---|
| Subject 1 | ||||||||
| 0D | 0.65 | 4.00 | 3.56 | 17.07 | 7.82 | 6.64 | 10.94 | 6.21 |
| 1D | 0.66 | 4.02 | 3.52 | 17.08 | 7.82 | 6.65 | 10.13 | 6.01 |
| 2D | 0.65 | 4.05 | 3.49 | 17.09 | 7.83 | 6.65 | 9.50 | 5.72 |
| 3D | 0.67 | 4.11 | 3.47 | 17.03 | 7.83 | 6.64 | 9.38 | 5.64 |
| 4D | 0.64 | 4.16 | 3.42 | 17.06 | 7.84 | 6.65 | 9.10 | 5.53 |
| 5D | 0.65 | 4.18 | 3.36 | 17.09 | 7.84 | 6.67 | 8.69 | 5.28 |
| 6D | 0.66 | 4.22 | 3.35 | 17.05 | 7.84 | 6.66 | 8.54 | 5.18 |
| Subject 2 | ||||||||
| 0D | 0.62 | 4.07 | 3.23 | 16.96 | 7.75 | 6.62 | 11.35 | 6.54 |
| 1D | 0.63 | 4.10 | 3.21 | 16.94 | 7.77 | 6.62 | 10.73 | 6.26 |
| 2D | 0.63 | 4.13 | 3.18 | 16.95 | 7.78 | 6.62 | 9.82 | 6.03 |
| 3D | 0.61 | 4.15 | 3.14 | 16.98 | 7.78 | 6.63 | 9.10 | 5.88 |
| 4D | 0.61 | 4.19 | 3.11 | 16.98 | 7.78 | 6.62 | 8.53 | 5.54 |
| 5D | 0.61 | 4.23 | 3.08 | 16.95 | 7.80 | 6.64 | 8.26 | 5.32 |
| 6D | 0.61 | 4.26 | 3.07 | 16.95 | 7.79 | 6.64 | 8.01 | 5.23 |
| Subject 3 | ||||||||
| 0D | 0.56 | 4.39 | 3.46 | 17.26 | 7.86 | 6.51 | 12.32 | 6.12 |
| 1D | 0.55 | 4.43 | 3.36 | 17.33 | 7.86 | 6.52 | 11.73 | 6.05 |
| 2D | 0.56 | 4.45 | 3.27 | 17.39 | 7.86 | 6.52 | 11.24 | 6.01 |
| 3D | 0.58 | 4.47 | 3.26 | 17.37 | 7.87 | 6.52 | 10.28 | 5.96 |
| 4D | 0.58 | 4.49 | 3.19 | 17.42 | 7.87 | 6.52 | 9.75 | 5.65 |
| 5D | 0.57 | 4.54 | 3.16 | 17.40 | 7.87 | 6.52 | 9.04 | 5.57 |
| 6D | 0.57 | 4.57 | 3.13 | 17.40 | 7.88 | 6.64 | 8.46 | 5.22 |
| Subject 4 | ||||||||
| 0D | 0.53 | 3.80 | 3.33 | 16.71 | 7.63 | 6.29 | 11.24 | 6.67 |
| 1D | 0.53 | 3.84 | 3.24 | 16.76 | 7.63 | 6.30 | 10.55 | 6.65 |
| 2D | 0.53 | 3.88 | 3.22 | 16.73 | 7.64 | 6.30 | 10.02 | 6.63 |
| 3D | 0.52 | 3.95 | 3.10 | 16.79 | 7.64 | 6.30 | 9.10 | 6.60 |
| 4D | 0.52 | 4.02 | 3.09 | 16.74 | 7.64 | 6.31 | 8.18 | 6.55 |
| 5D | 0.51 | 4.06 | 3.07 | 16.72 | 7.66 | 6.32 | 7.57 | 6.47 |
| 6D | 0.51 | 4.07 | 3.06 | 16.73 | 7.65 | 6.32 | 7.14 | 6.41 |
| Subject 5 | ||||||||
| 0D | 0.60 | 3.93 | 3.31 | 14.90 | 7.70 | 6.69 | 10.59 | 6.11 |
| 1D | 0.59 | 3.96 | 3.28 | 14.90 | 7.71 | 6.27 | 10.28 | 6.01 |
| 2D | 0.60 | 3.98 | 3.27 | 14.89 | 7.71 | 6.10 | 9.94 | 5.93 |
| 3D | 0.59 | 4.04 | 3.19 | 14.91 | 7.72 | 6.14 | 9.32 | 5.77 |
| 4D | 0.59 | 4.09 | 3.16 | 14.89 | 7.72 | 6.05 | 8.72 | 5.61 |
| 5D | 0.58 | 4.17 | 3.11 | 14.87 | 7.72 | 5.99 | 7.99 | 5.50 |
| 6D | 0.58 | 4.23 | 3.08 | 14.84 | 7.72 | 6.35 | 7.36 | 5.38 |
| Accommodative Stimulus | Corneal Refractive Power | Lens Refractive Power | SER |
|---|---|---|---|
| Subject 1 | |||
| 0D | 42.195 | 21.406 | −1.586 |
| 1D | 42.206 | 22.456 | −2.341 |
| 2D | 42.142 | 23.701 | −3.123 |
| 3D | 42.137 | 24.013 | −3.267 |
| 4D | 42.078 | 24.572 | −3.648 |
| 5D | 42.098 | 25.711 | −4.466 |
| 6D | 42.091 | 26.053 | −4.656 |
| Subject 2 | |||
| 0D | 42.606 | 20.442 | −0.779 |
| 1D | 42.483 | 21.436 | −1.300 |
| 2D | 42.420 | 22.657 | −2.110 |
| 3D | 42.425 | 23.673 | −2.914 |
| 4D | 42.426 | 25.144 | −3.899 |
| 5D | 42.310 | 26.076 | −4.413 |
| 6D | 42.372 | 26.651 | −4.867 |
| Subject 3 | |||
| 0D | 41.812 | 20.730 | −1.471 |
| 1D | 41.819 | 21.222 | −1.930 |
| 2D | 41.822 | 21.618 | −2.312 |
| 3D | 41.765 | 22.416 | −2.848 |
| 4D | 41.765 | 23.618 | −3.708 |
| 5D | 41.763 | 24.484 | −4.374 |
| 6D | 41.811 | 26.049 | −5.478 |
| Subject 4 | |||
| 0D | 43.033 | 20.602 | −1.517 |
| 1D | 43.050 | 21.163 | −2.096 |
| 2D | 43.004 | 21.664 | −2.511 |
| 3D | 43.016 | 22.660 | −3.502 |
| 4D | 42.970 | 23.892 | −4.579 |
| 5D | 42.893 | 24.960 | −5.481 |
| 6D | 42.931 | 25.813 | −6.298 |
| Subject 5 | |||
| 0D | 42.955 | 22.317 | −0.862 |
| 1D | 42.555 | 22.831 | −0.967 |
| 2D | 42.336 | 23.331 | −1.219 |
| 3D | 42.302 | 24.368 | −2.177 |
| 4D | 42.238 | 25.503 | −3.163 |
| 5D | 42.172 | 26.804 | −4.311 |
| 6D | 42.517 | 28.150 | −5.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhang, B.; Xiang, B.; Liu, J.; Ma, Z.; Lv, H.; Yu, Y.; Zhao, Y.; Yang, Y.; Luan, J.; et al. Diopter Measurement of Human Eye Based on Dual-Focus Swept Source Optical Coherence Tomography. Photonics 2025, 12, 856. https://doi.org/10.3390/photonics12090856
Jiang H, Zhang B, Xiang B, Liu J, Ma Z, Lv H, Yu Y, Zhao Y, Yang Y, Luan J, et al. Diopter Measurement of Human Eye Based on Dual-Focus Swept Source Optical Coherence Tomography. Photonics. 2025; 12(9):856. https://doi.org/10.3390/photonics12090856
Chicago/Turabian StyleJiang, Huiwen, Binyin Zhang, Ben Xiang, Jian Liu, Zhenhe Ma, Hongyu Lv, Yao Yu, Yuqian Zhao, Yanqiu Yang, Jingmin Luan, and et al. 2025. "Diopter Measurement of Human Eye Based on Dual-Focus Swept Source Optical Coherence Tomography" Photonics 12, no. 9: 856. https://doi.org/10.3390/photonics12090856
APA StyleJiang, H., Zhang, B., Xiang, B., Liu, J., Ma, Z., Lv, H., Yu, Y., Zhao, Y., Yang, Y., Luan, J., & Wang, Y. (2025). Diopter Measurement of Human Eye Based on Dual-Focus Swept Source Optical Coherence Tomography. Photonics, 12(9), 856. https://doi.org/10.3390/photonics12090856






