MGFormer: Super-Resolution Reconstruction of Retinal OCT Images Based on a Multi-Granularity Transformer
Abstract
1. Introduction
- We propose MGFormer, a novel Transformer-based SR framework that features a multi-granularity attention mechanism specifically designed for OCT image reconstruction.
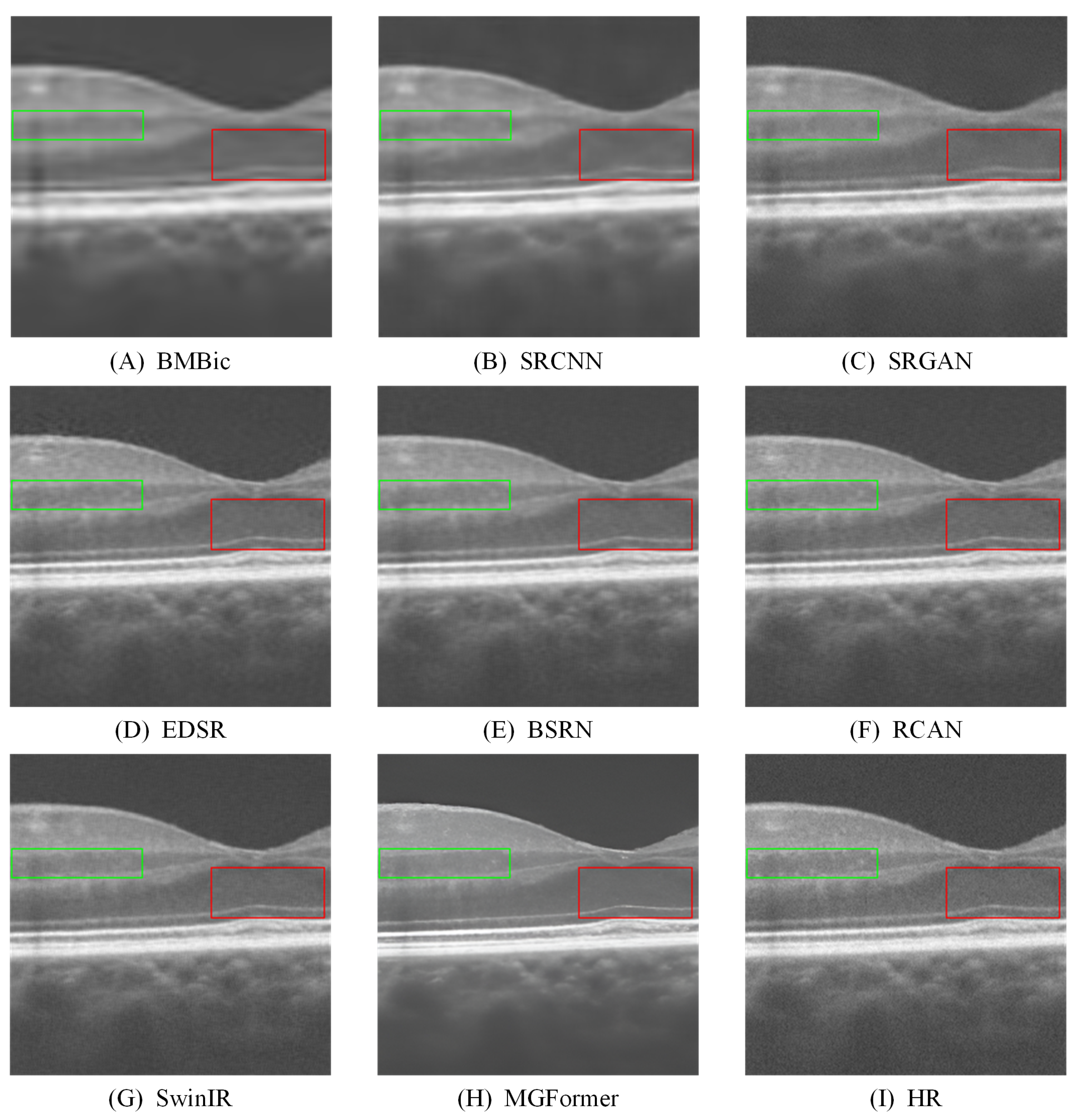
- Extensive experiments on both benchmark and clinical OCT datasets demonstrate that MGFormer consistently outperforms state-of-the-art SR models, including SRCNN, SRGAN, EDSR, BSRN, RCAN, and SwinIR, in terms of both quantitative metrics (PSNR, SSIM, and LPIPS) and qualitative visual assessment.
- The high-fidelity SR outputs generated by MGFormer hold significant clinical relevance by enhancing diagnostic confidence and providing superior inputs for downstream OCT image analysis tasks, such as automated segmentation and disease classification.
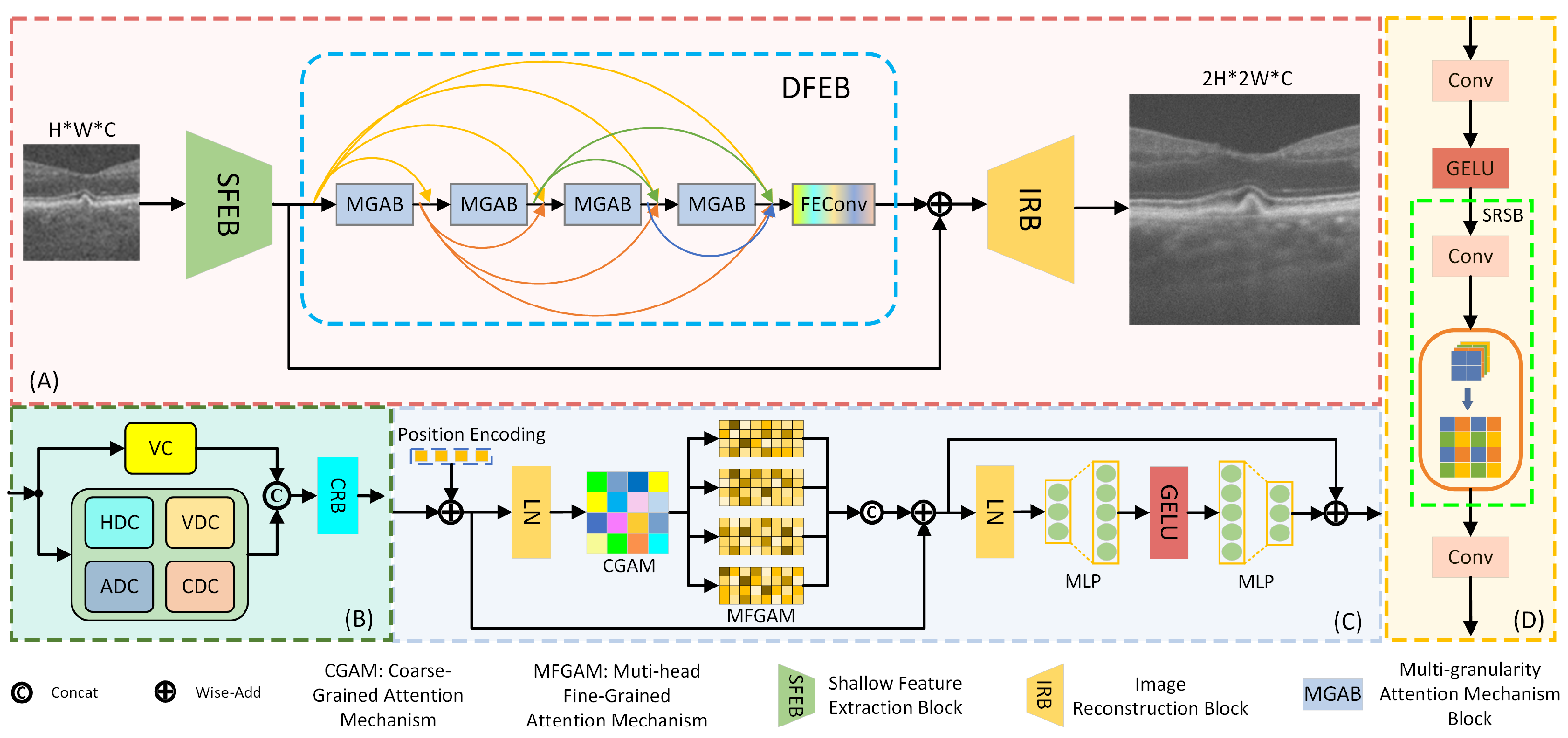
2. Method
2.1. Shallow Feature Extraction Module
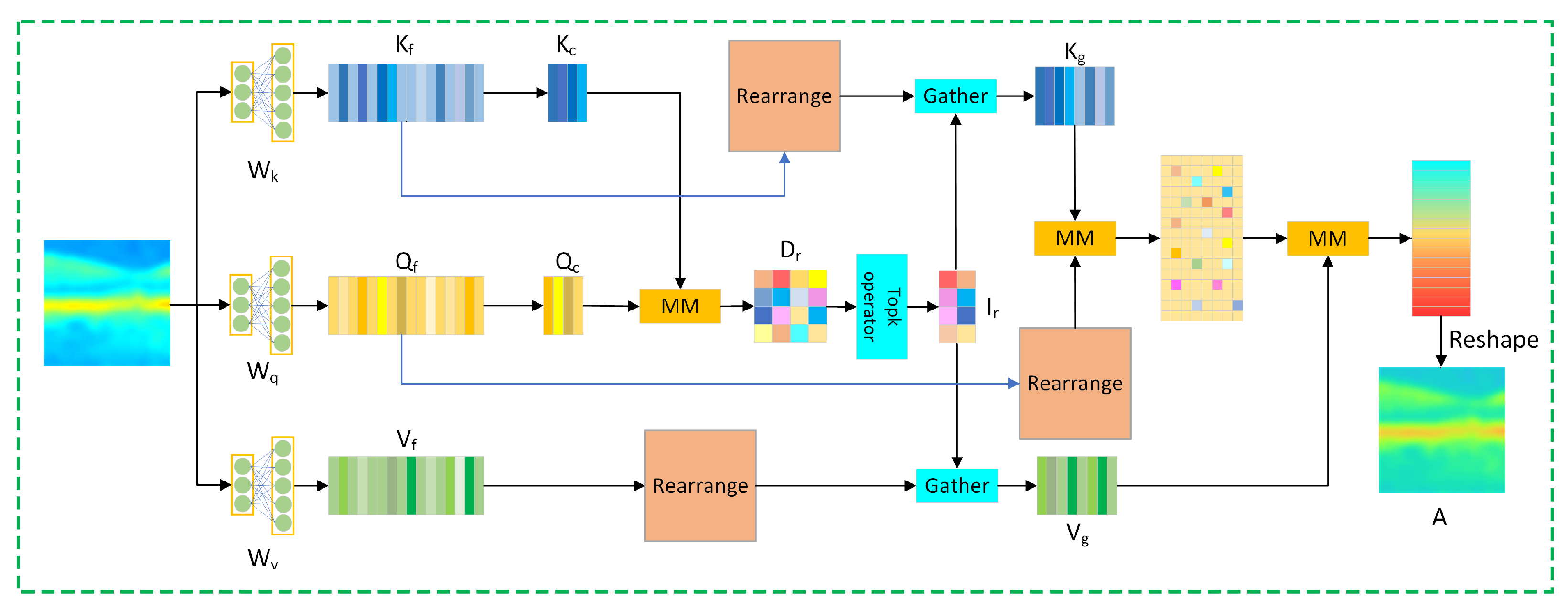
2.2. Deep Feature Extraction Module
2.3. Image Reconstruction Module
2.4. Loss Function
3. Experiments
4. Results and Ablation Study
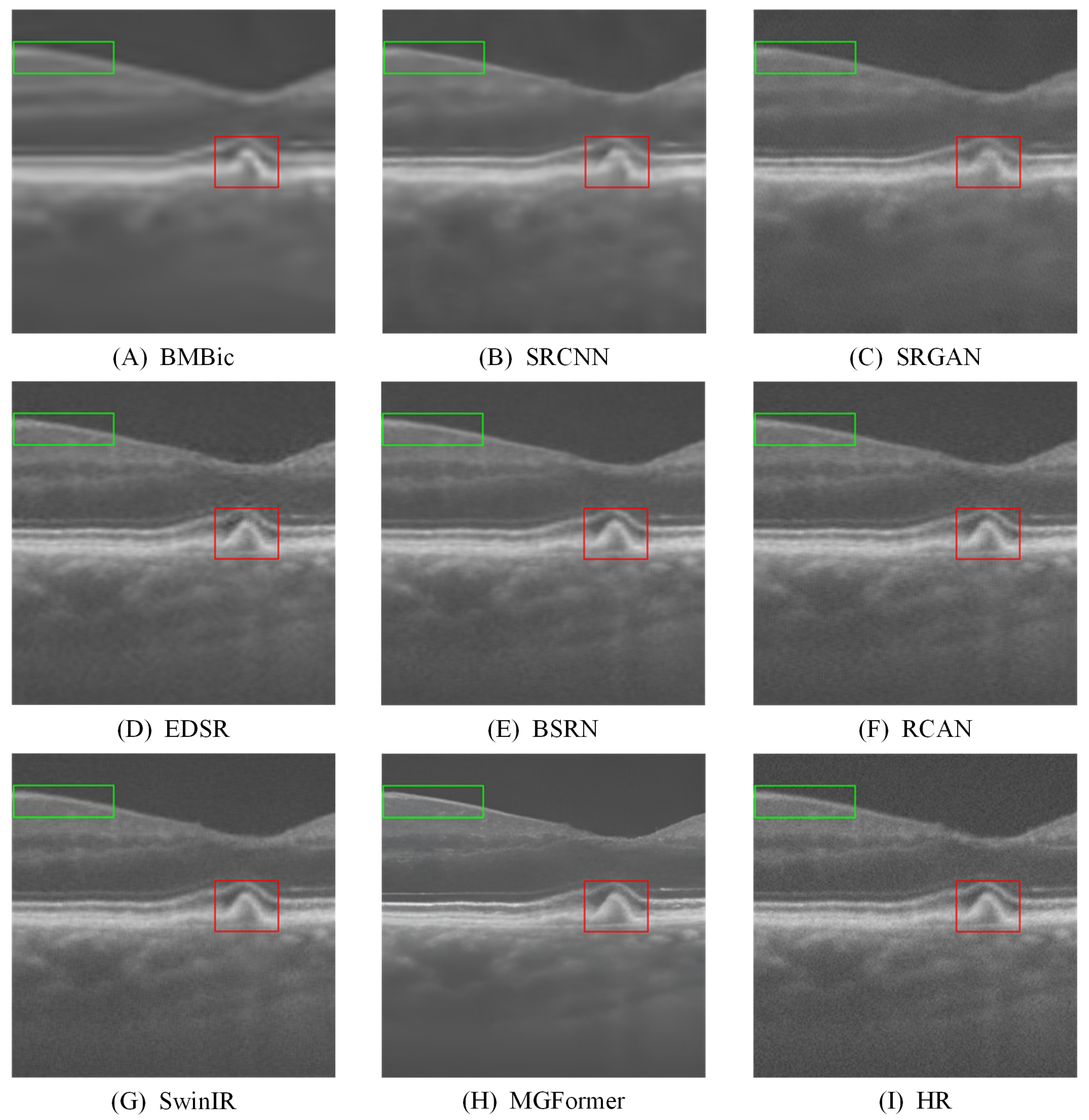
4.1. Results
4.2. Ablation Study
- Effect of MGABs_Number (Patch_Size = 8, K = 8). MGABs_Number has the strongest overall impact, especially on LPIPS and SSIM. Increasing MGABs from 4→8→16 improves PSNR from 33.4988 to 33.7156 to 34.3898 (+2.66% from 4 to 16). SSIM rises from 0.7828 to 0.7979 to 0.8399 (+7.29%). LPIPS decreases from 0.1441 to 0.1395 to 0.1246 (−13.53%). The largest relative gain is in LPIPS, followed by SSIM, with PSNR improving the least in percentage terms (percentages computed relative to the 4-MGAB setting).
- Effect of Patch_Size (MGABs = 16, K = 8). The benefit peaks at a moderate window of 8. Increasing Patch from 4→8→→16 yields PSNR 34.0782→34.3898→34.1530 (+0.91% at 8, +0.22% at 16 vs. 4), SSIM 0.8165→0.8399→0.8213 (+2.87%, +0.59%), and LPIPS 0.1327→0.1246→0.1281 (−6.10% at 8, −3.47% at 16). With a shallower network (MGABs = 4), larger patches provide small monotonic gains (PSNR 33.4571→33.5156→33.5483, SSIM 0.7815→0.7835→0.7855) with modest LPIPS reductions. These comparisons indicate that gains peak at Patch_Size = 8 and diminish at 16, suggesting an optimal receptive-field span around 8 (percentages relative to Patch = 4).
- Effect of K_Value (MGABs = 16, Patch_Size = 8). PSNR increases from 33.9913 (K = 2) to 34.2501 (K = 4) and 34.3898 (K = 8) (+1.17% vs. K = 2), then drops to 34.1452 at K = 16 (−0.71% vs. K = 8). SSIM rises 0.8137→0.8325→0.8399 (+3.22% vs. K = 2) and declines to 0.8207 at K = 16. LPIPS decreases 0.1304→0.1279→0.1246 (−4.45% vs. K = 2) and slightly increases to 0.1248 at K = 16. These results indicate an optimum near K = 8 (percentages relative to K = 2).
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiu, D.; Cheng, Y.; Wang, X. Medical image super-resolution reconstruction algorithms based on deep learning: A survey. Comput. Methods Programs Biomed. 2023, 238, 107590. [Google Scholar] [CrossRef]
- Umirzakova, S.; Ahmad, S.; Khan, L.U.; Whangbo, T. Medical image super-resolution for smart healthcare applications: A comprehensive survey. Inf. Fusion 2024, 103, 102075. [Google Scholar] [CrossRef]
- Leingang, O.; Riedl, S.; Mai, J.; Reiter, G.S.; Faustmann, G.; Fuchs, P.; Scholl, H.P.N.; Sivaprasad, S.; Rueckert, D.; Lotery, A.; et al. Automated deep learning-based AMD detection and staging in real-world OCT datasets (PINNACLE study report 5). Sci. Rep. 2023, 13, 19545. [Google Scholar] [CrossRef] [PubMed]
- Le Blay, H.; Raynaud, E.; Bouayadi, S.; Rieux, E.; Rolland, G.; Saussine, A.; Jachiet, M.; Bouaziz, J.; Lynch, B. Epidermal renewal during the treatment of atopic dermatitis lesions: A study coupling line-field confocal optical coherence tomography with artificial intelligence quantifications. Ski. Res. Technol. 2024, 30, e13891. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Wu, Y.; Li, Y.; Zhou, Y. Optical coherence tomography (OCT)—Versus angiography-guided strategy for percutaneous coronary intervention: A meta-analysis of randomized trials. BMC Cardiovasc. Disord. 2024, 24, 262. [Google Scholar] [CrossRef]
- Ge, C.; Yu, X.; Yuan, M.; Fan, Z.; Chen, J.; Shum, P.P.; Liu, L. Self-supervised Self2Self denoising strategy for OCT speckle reduction with a single noisy image. Biomed. Opt. Express 2024, 15, 1233–1252. [Google Scholar] [CrossRef]
- Li, S.; Azam, M.A.; Gunalan, A.; Mattos, L.S. One-Step Enhancer: Deblurring and Denoising of OCT Images. Appl. Sci. 2022, 12, 10092. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, H.; Wang, S.; He, B.; Cao, L.; Li, M.; Jiang, M.; Li, Q. Subpixel motion artifacts correction and motion estimation for 3D-OCT. J. Biophotonics 2024, 17, e202400104. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, Z. Hybrid attention structure preserving network for reconstruction of under-sampled OCT images. Sci. Rep. 2025, 15, 7405. [Google Scholar] [CrossRef]
- Sampson, D.M.; M.Dubis, A.; K.Chen, F.; J.Zawadzki, R.; D.Sampson, D. Towards standardizing retinal optical coherence tomography angiography: A review. Light (Sci. Appl.) 2022, 11, 520–541. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Zhang, Y.; Wang, M.; Yao, J.; Tang, J. Boundary-Repairing Dual-Path Network for Retinal Layer Segmentation in OCT Image with Pigment Epithelial Detachment. J. Imaging Inform. Med. 2024, 37, 3101–3130. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.; Jin, L.; Hu, J.; Liu, Y.; Yan, Y.; Li, Q.; Lu, Y. PSCAT: A lightweight transformer for simultaneous denoising and super-resolution of OCT images. Biomed. Opt. Express 2024, 15, 2958–2976. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Mauricio, J.; Domingues, I.; Bernardino, J. Comparing Vision Transformers and Convolutional Neural Networks for Image Classification: A Literature Review. Appl. Sci. 2023, 13, 5521. [Google Scholar] [CrossRef]
- Rangel, G.; CuevasTello, J.C.; NunezVarela, J.; Puente, C.; SilvaTrujillo, A.G. A Survey on Convolutional Neural Networks and Their Performance Limitations in Image Recognition Tasks. J. Sens. 2024, 2024, 2797320. [Google Scholar] [CrossRef]
- Hassanin, M.; Anwar, S.; Radwan, I.; Khan, F.S.; Mian, A. Visual attention methods in deep learning: An in-depth survey. Inf. Fusion 2024, 108, 102417. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, Z.; Shao, Z.; Ran, M.; Zhou, J.; Fang, L.; Zhang, Y. Simultaneous denoising and super-resolution of optical coherence tomography images based on a generative adversarial network. Opt. Express 2019, 27, 12289–12307. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.; You, Y.; Huang, Z.; Meng, X.; Jiang, Z.; Zhou, C.; Liu, G.; Yang, K.; Ren, Q.; Lu, Y. N2NSR-OCT: Simultaneous denoising and super-resolution in optical coherence tomography images using semisupervised deep learning. J. Biophotonics 2021, 14, e202000282. [Google Scholar] [CrossRef]
- Das, V.; Dandapat, S.; Bora, P.K. Unsupervised Super-Resolution of OCT Images Using Generative Adversarial Network for Improved Age-Related Macular Degeneration Diagnosis. IEEE Sens. J. 2020, 20, 8746–8756. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 12294–12305. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2021, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. TransUNet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar] [CrossRef]
- Huang, W.; Huang, D. Local feature enhancement transformer for image super-resolution. Sci. Rep. 2025, 15, 20792. [Google Scholar] [CrossRef]
- Wang, J.; Hao, Y.; Bai, H.; Yan, L. Parallel attention recursive generalization transformer for image super-resolution. Sci. Rep. 2025, 15, 8669. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Chen, Z.; He, Z.; Lu, Z. DEA-Net: Single Image Dehazing Based on Detail-Enhanced Convolution and Content-Guided Attention. IEEE Trans. Image Process. 2024, 33, 1002–1015. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, C.; Wang, Z.; Qin, Y.; Su, Z.; Li, X.; Zhou, F.; Zhao, G. Searching central difference convolutional networks for face anti-spoofing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5295–5305. [Google Scholar] [CrossRef]
- Su, Z.; Liu, W.; Yu, Z.; Hu, D.; Liao, Q.; Tian, Q.; Pietikäinen, M.; Liu, L. Pixel Difference Networks for Efficient Edge Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 5117–5127. [Google Scholar] [CrossRef]
- Ren, S.; Zhou, D.; He, S.; Feng, J.; Wang, X. Shunted Self-Attention via Multi-Scale Token Aggregation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10843–10852. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 8–16 October 2016; pp. 694–711. [Google Scholar] [CrossRef]
- Terven, J.; CordovaEsparza, D.; RomeroGonzalez, J.; RamirezPedraza, A.; ChavezUrbiola, E.A. A comprehensive survey of loss functions and metrics in deep learning. Artif. Intell. Rev. 2025, 58, 195. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, X.; Yuan, K. Medical image super-resolution using a generative adversarial network. arXiv 2019, arXiv:1902.00369. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; McNabb, R.P.; Nie, Q.; Kuo, A.N.; Toth, C.A.; Izatt, J.A.; Farsiu, S. Fast Acquisition and Reconstruction of Optical Coherence Tomography Images via Sparse Representation. IEEE Trans. Med. Imaging 2013, 32, 2034–2049. [Google Scholar] [CrossRef]


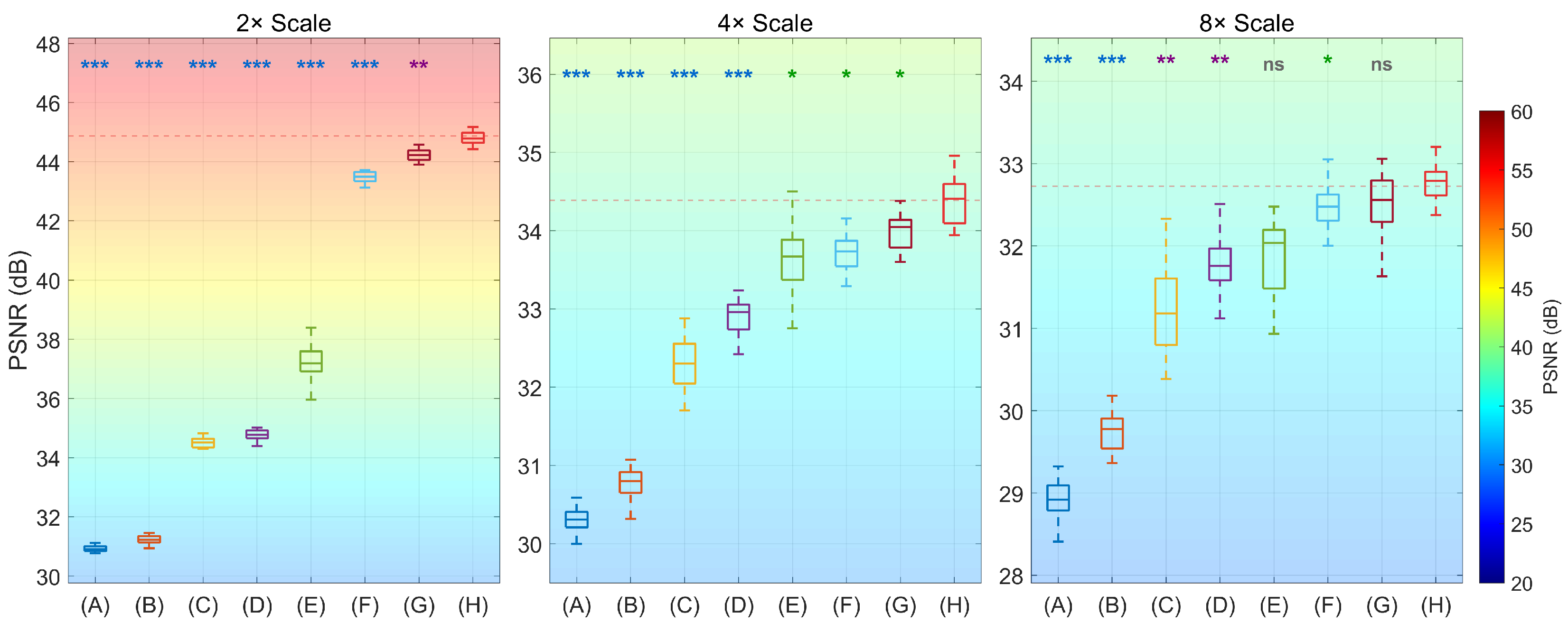


| Method | Scale | PSNR(dB) ↑ | SSIM ↑ | LPIPS ↓ (Mean) | Paired-t (PSNR) | p-Value (vs. Ours) |
|---|---|---|---|---|---|---|
| Bicubic | 2× | 30.9125 ± 0.11 | 0.7182 ± 0.0032 | 0.3430 | 142.04 | 0.001 *** |
| SRCNN | 2× | 31.2335 ± 0.13 | 0.7295 ± 0.0028 | 0.3428 | 132.30 | 0.001 *** |
| SRGAN | 2× | 34.5648 ± 0.25 | 0.8098 ± 0.0095 | 0.2676 | 73.32 | 0.001 *** |
| EDSR | 2× | 34.7313 ± 0.14 | 0.8138 ± 0.0023 | 0.2639 | 95.93 | 0.001 *** |
| BSRN | 2× | 37.1367 ± 0.43 | 0.9056 ± 0.0137 | 0.2095 | 36.73 | 0.001 *** |
| RCAN | 2× | 43.5013 ± 0.22 | 0.9709 ± 0.0015 | 0.0661 | 10.45 | 0.001 *** |
| SwinIR | 2× | 44.2302 ± 0.21 | 0.9765 ± 0.0018 | 0.0837 | 4.97 | 0.008 ** |
| Ours | 2× | 44.8601 ± 0.19 | 0.9813 ± 0.0014 | 0.0652 | / | / |
| Bicubic | 4× | 30.3403 ± 0.16 | 0.7054 ± 0.0053 | 0.4211 | 30.51 | 0.001 *** |
| SRCNN | 4× | 30.8068 ± 0.21 | 0.7166 ± 0.0049 | 0.3857 | 24.54 | 0.001 *** |
| SRGAN | 4× | 32.3078 ± 0.36 | 0.7469 ± 0.0132 | 0.2746 | 10.62 | 0.001 *** |
| EDSR | 4× | 32.9225 ± 0.23 | 0.7602 ± 0.0038 | 0.2288 | 9.65 | 0.001 *** |
| BSRN | 4× | 33.4146 ± 0.57 | 0.7769 ± 0.0184 | 0.1926 | 3.50 | 0.025 * |
| RCAN | 4× | 33.7580 ± 0.28 | 0.8131 ± 0.0028 | 0.1675 | 3.76 | 0.020 * |
| SwinIR | 4× | 33.8748 ± 0.26 | 0.8135 ± 0.0037 | 0.1585 | 3.19 | 0.033 * |
| Ours | 4× | 34.3898 ± 0.25 | 0.8399 ± 0.0023 | 0.1246 | / | / |
| Bicubic | 8× | 28.9156 ± 0.19 | 0.6657 ± 0.0076 | 0.4583 | 23.43 | 0.001 *** |
| SRCNN | 8× | 29.7402 ± 0.23 | 0.6884 ± 0.0091 | 0.3916 | 17.29 | 0.001 *** |
| SRGAN | 8× | 31.3958 ± 0.47 | 0.7285 ± 0.0185 | 0.2748 | 5.28 | 0.006 ** |
| EDSR | 8× | 31.7366 ± 0.26 | 0.7318 ± 0.0072 | 0.2502 | 5.46 | 0.005 ** |
| BSRN | 8× | 32.0317 ± 0.58 | 0.7315 ± 0.0233 | 0.2291 | 2.36 | 0.078 |
| RCAN | 8× | 32.4033 ± 0.34 | 0.7378 ± 0.0053 | 0.2033 | 2.99 | 0.030 * |
| SwinIR | 8× | 32.5387 ± 0.28 | 0.7454 ± 0.0064 | 0.1931 | 1.70 | 0.163 |
| Ours | 8× | 32.7257 ± 0.31 | 0.7482 ± 0.0038 | 0.1875 | / | / |
| Model | BS (Mean ± SD) | PD (Mean ± SD) | DC (Mean ± SD) |
|---|---|---|---|
| BMBic | 2.5 ± 0.3 | 2.3 ± 0.3 | 2.4 ± 0.2 |
| SRGAN | 3.4 ± 0.5 | 3.2 ± 0.6 | 3.3 ± 0.5 |
| SwinIR | 3.9 ± 0.4 | 3.7 ± 0.3 | 3.8 ± 0.3 |
| MGFormer | 4.2 ± 0.3 | 4.1 ± 0.3 | 4.3 ± 0.2 |
| MGABs_Number | Patch_Size | K_Value | PSNR (dB) ↑ | SSIM ↑ | LPIPS ↓ |
|---|---|---|---|---|---|
| 4 | 4 | 2 | 33.3247 | 0.7761 | 0.1487 |
| 4 | 33.4152 | 0.7794 | 0.1459 | ||
| 8 | 33.4571 | 0.7815 | 0.1446 | ||
| 16 | / | / | / | ||
| 8 | 2 | 33.3562 | 0.7779 | 0.1477 | |
| 4 | 33.4489 | 0.7808 | 0.1452 | ||
| 8 | 33.4988 | 0.7828 | 0.1441 | ||
| 16 | 33.5156 | 0.7835 | 0.1436 | ||
| 16 | 8 | 33.4322 | 0.7802 | 0.1465 | |
| 16 | 33.4646 | 0.7818 | 0.1443 | ||
| 32 | 33.5192 | 0.7846 | 0.1438 | ||
| 64 | 33.5483 | 0.7855 | 0.1427 | ||
| 8 | 4 | 2 | 33.4371 | 0.7836 | 0.1448 |
| 4 | 33.6653 | 0.7957 | 0.1432 | ||
| 8 | 33.7243 | 0.7972 | 0.1426 | ||
| 16 | / | / | / | ||
| 8 | 2 | 33.6447 | 0.7960 | 0.1412 | |
| 4 | 33.6916 | 0.7968 | 0.1407 | ||
| 8 | 33.7156 | 0.7979 | 0.1395 | ||
| 16 | 33.7416 | 0.7995 | 0.1386 | ||
| 16 | 8 | 33.7025 | 0.7983 | 0.1406 | |
| 16 | 33.7375 | 0.7992 | 0.1387 | ||
| 32 | 33.7831 | 0.8006 | 0.1362 | ||
| 64 | – | – | – | ||
| 16 | 4 | 2 | 33.9088 | 0.8112 | 0.1368 |
| 4 | 34.0189 | 0.8146 | 0.1345 | ||
| 8 | 34.0782 | 0.8165 | 0.1327 | ||
| 16 | / | / | / | ||
| 8 | 2 | 33.9913 | 0.8137 | 0.1304 | |
| 4 | 34.2501 | 0.8325 | 0.1279 | ||
| 8 | 34.3898 | 0.8399 | 0.1246 | ||
| 16 | 34.1452 | 0.8207 | 0.1248 | ||
| 16 | 8 | 34.153 | 0.8213 | 0.1281 | |
| 16 | – | – | – | ||
| 32 | – | – | – | ||
| 64 | – | – | – |
| Convolution Method | PSNR (dB) ↑ | SSIM ↑ | LPIPS ↓ |
|---|---|---|---|
| VC (in SFEM) + VC (in DFEM) | 34.1734 | 0.8256 | 0.1274 |
| VC (in SFEM) + FEConv (in DFEM) | 34.3178 | 0.8364 | 0.1253 |
| FEConv (in SFEM) + VC (in DFEM) | 34.2770 | 0.8336 | 0.1268 |
| FEConv (in SFEM) + FEConv (in DFEM) | 34.3898 | 0.8399 | 0.1246 |
| Model | FLOPs | Inference Time (ms) ↓ | PSNR (dB) ↑ | SSIM ↑ | LPIPS ↓ |
|---|---|---|---|---|---|
| TD | 233 G | 98.17 | 34.3898 | 0.8399 | 0.1246 |
| w/o TD | 289 G | 166.43 | 34.5342 | 0.8427 | 0.1241 |
| Approach | PSNR (dB) ↑ | SSIM ↑ | LPIPS ↓ |
|---|---|---|---|
| NIA | 34.3898 | 0.8399 | 0.1244 |
| w/o NIA | 34.3771 | 0.8406 | 0.1246 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, J.; Jiao, Z.; Li, Y.; Si, Y.; Liu, J.; Yu, Y.; Yang, D.; Sun, J.; Wei, Z.; Ma, Z. MGFormer: Super-Resolution Reconstruction of Retinal OCT Images Based on a Multi-Granularity Transformer. Photonics 2025, 12, 850. https://doi.org/10.3390/photonics12090850
Luan J, Jiao Z, Li Y, Si Y, Liu J, Yu Y, Yang D, Sun J, Wei Z, Ma Z. MGFormer: Super-Resolution Reconstruction of Retinal OCT Images Based on a Multi-Granularity Transformer. Photonics. 2025; 12(9):850. https://doi.org/10.3390/photonics12090850
Chicago/Turabian StyleLuan, Jingmin, Zhe Jiao, Yutian Li, Yanru Si, Jian Liu, Yao Yu, Dongni Yang, Jia Sun, Zehao Wei, and Zhenhe Ma. 2025. "MGFormer: Super-Resolution Reconstruction of Retinal OCT Images Based on a Multi-Granularity Transformer" Photonics 12, no. 9: 850. https://doi.org/10.3390/photonics12090850
APA StyleLuan, J., Jiao, Z., Li, Y., Si, Y., Liu, J., Yu, Y., Yang, D., Sun, J., Wei, Z., & Ma, Z. (2025). MGFormer: Super-Resolution Reconstruction of Retinal OCT Images Based on a Multi-Granularity Transformer. Photonics, 12(9), 850. https://doi.org/10.3390/photonics12090850






