Low Loss and High Polarization-Maintaining Single-Mode Hollow-Core Anti-Resonant Fibers with S+C+L+U Communication Bands
Abstract
1. Introduction
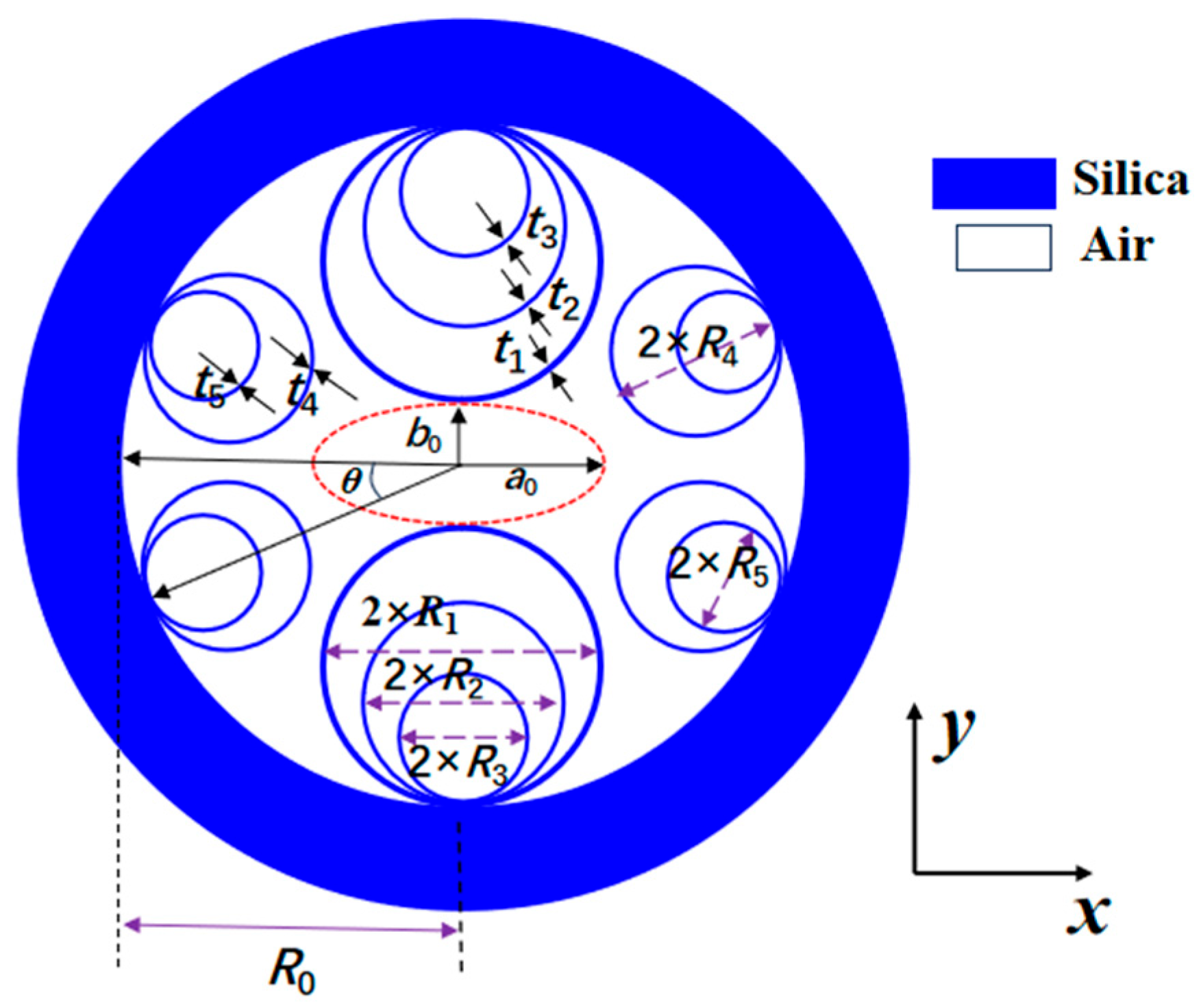
2. Structure Design and Principle
3. Results
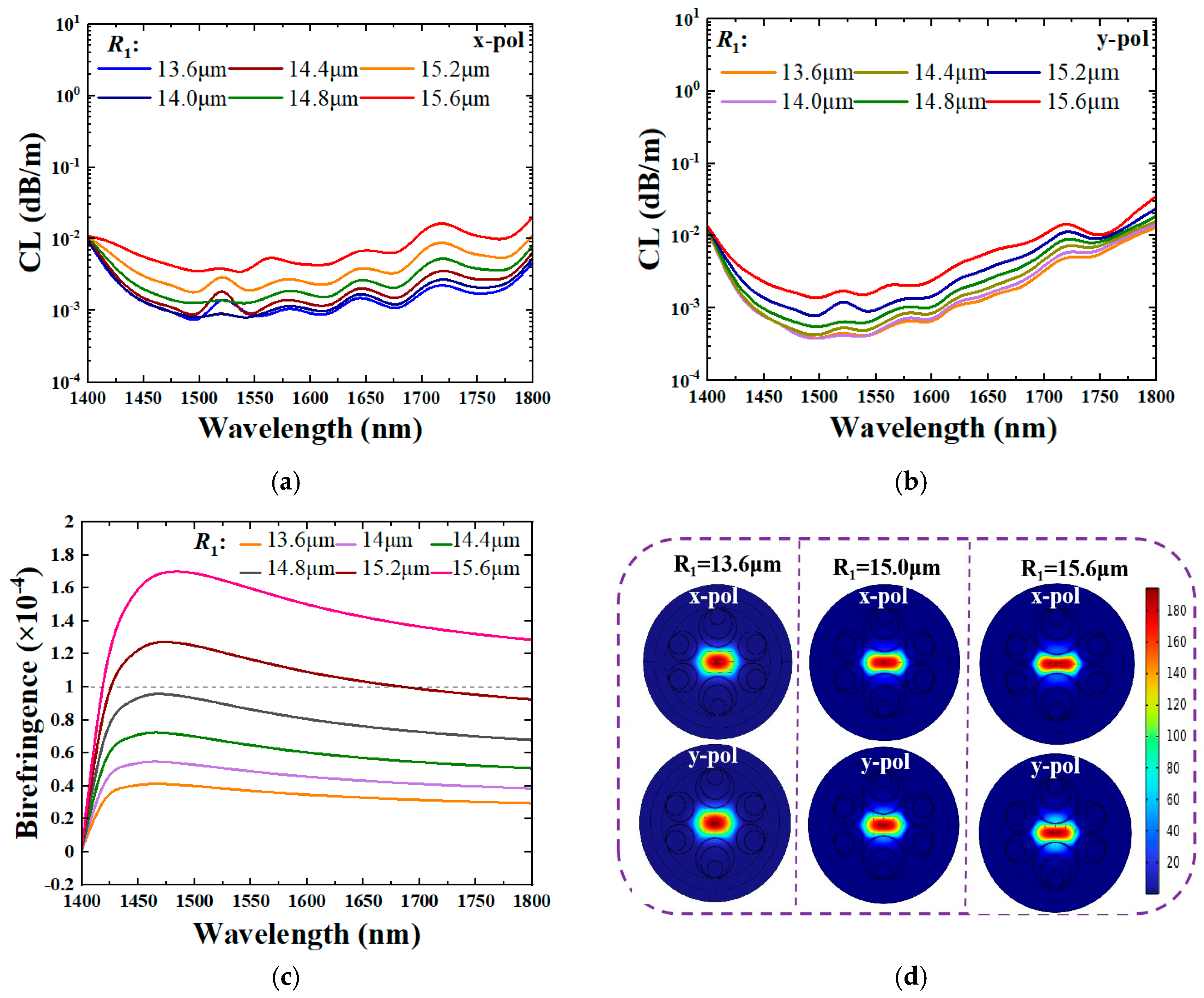
3.1. Effect of R1 on Performance
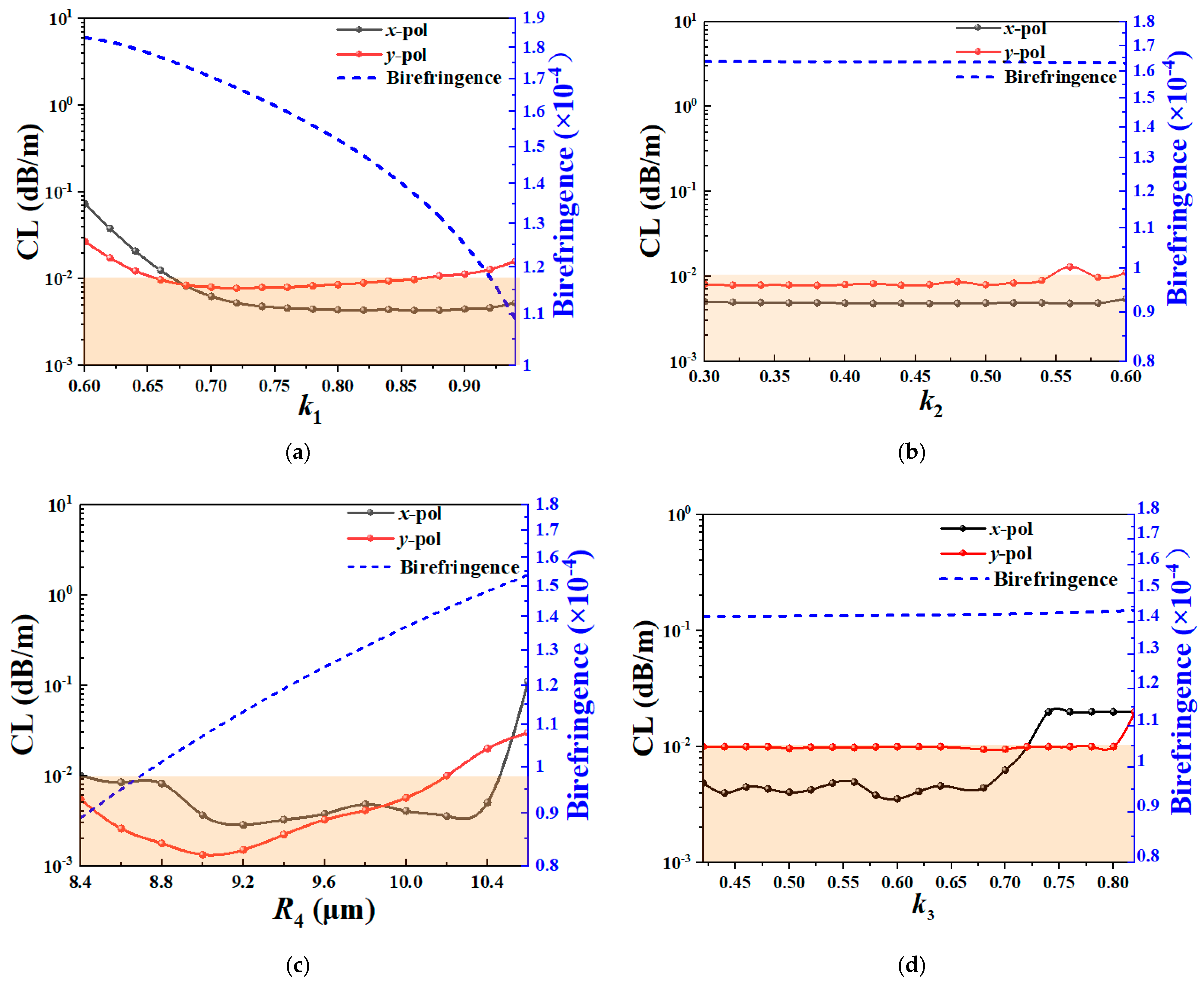
3.2. Effects of k1, k2, k3 and R4 on Performance
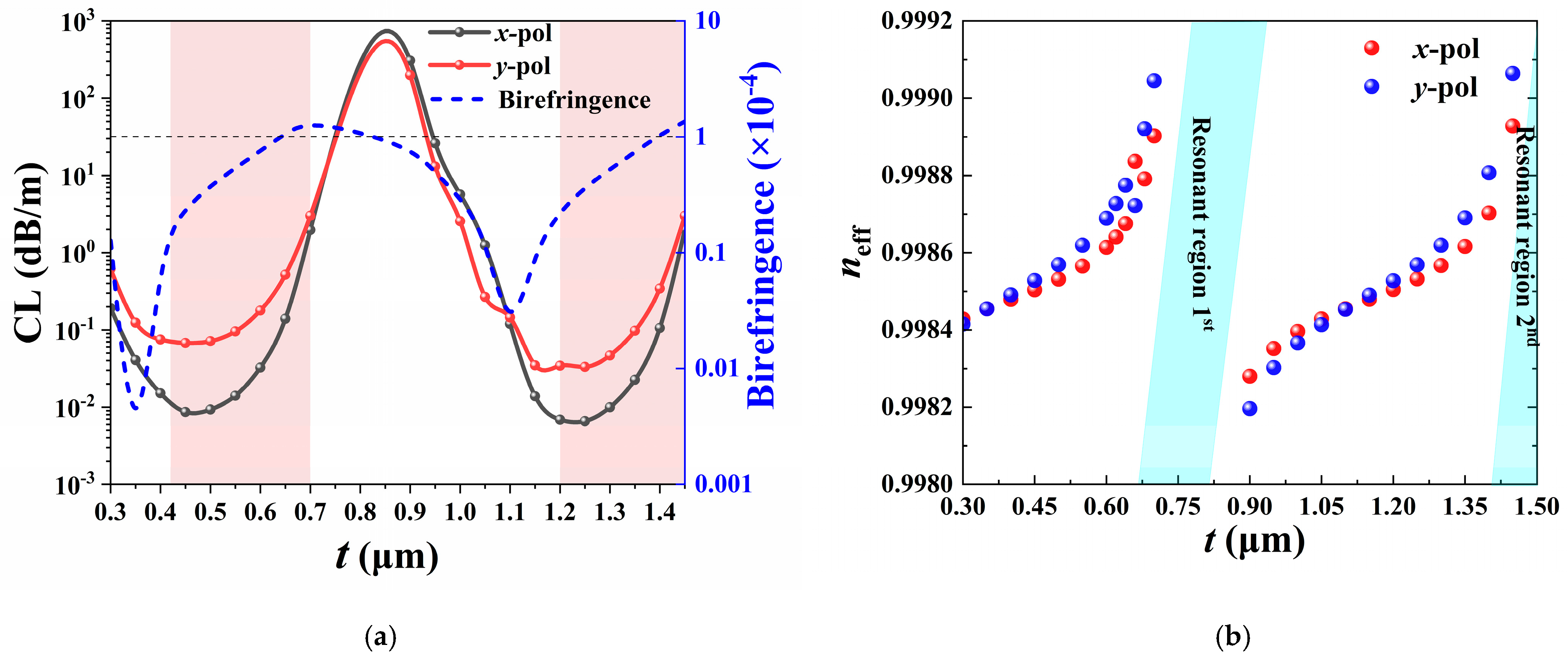
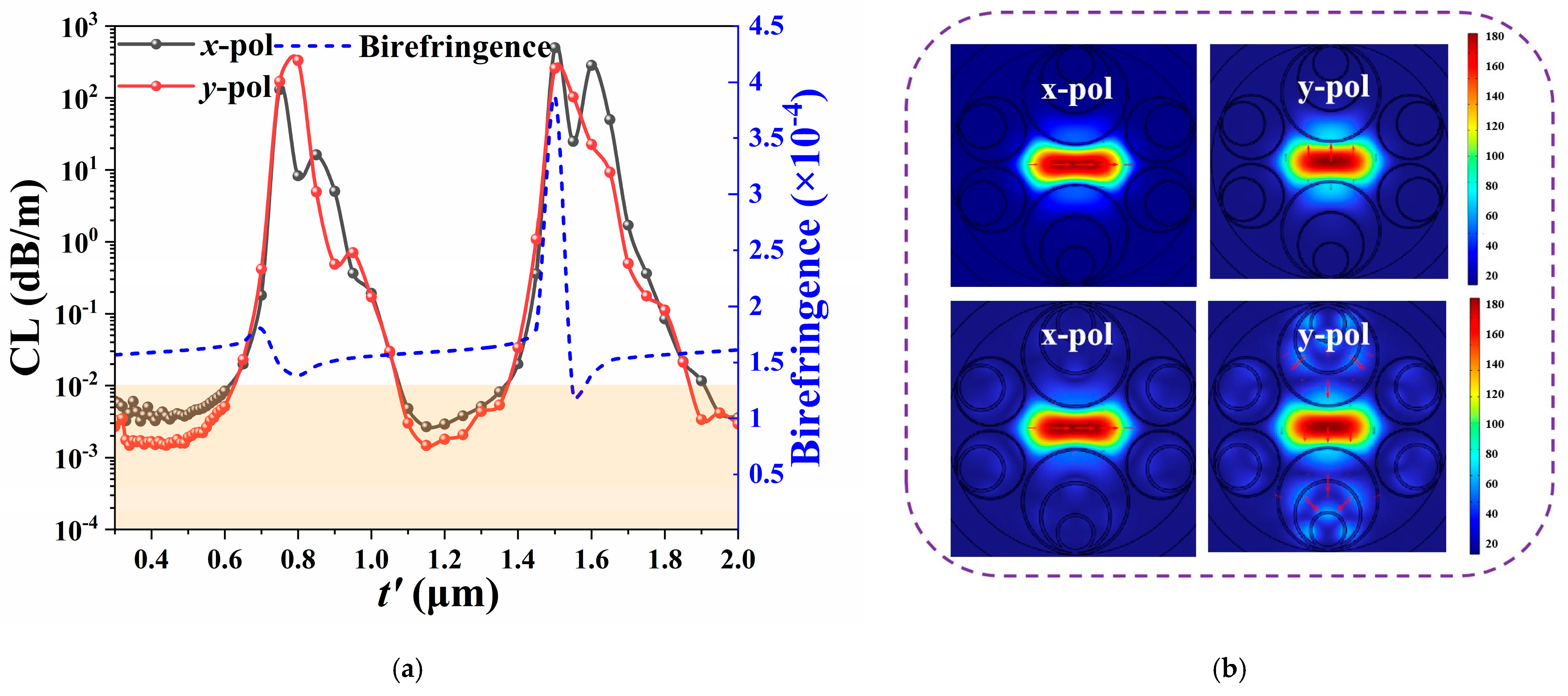
3.3. Influence of t on Performance
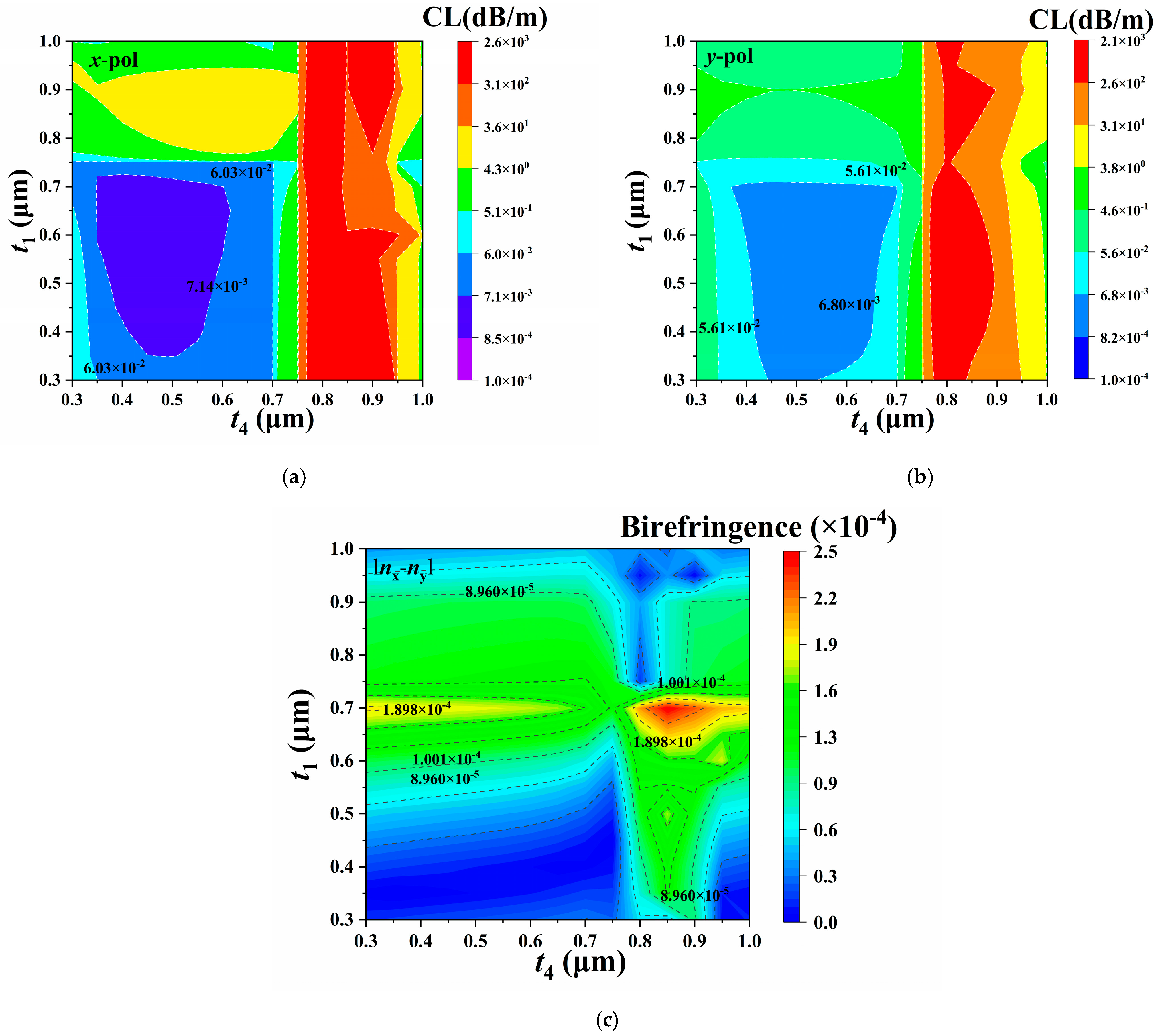
3.4. Orthogonal Differentiated Wall Thickness of t4, t1, and t
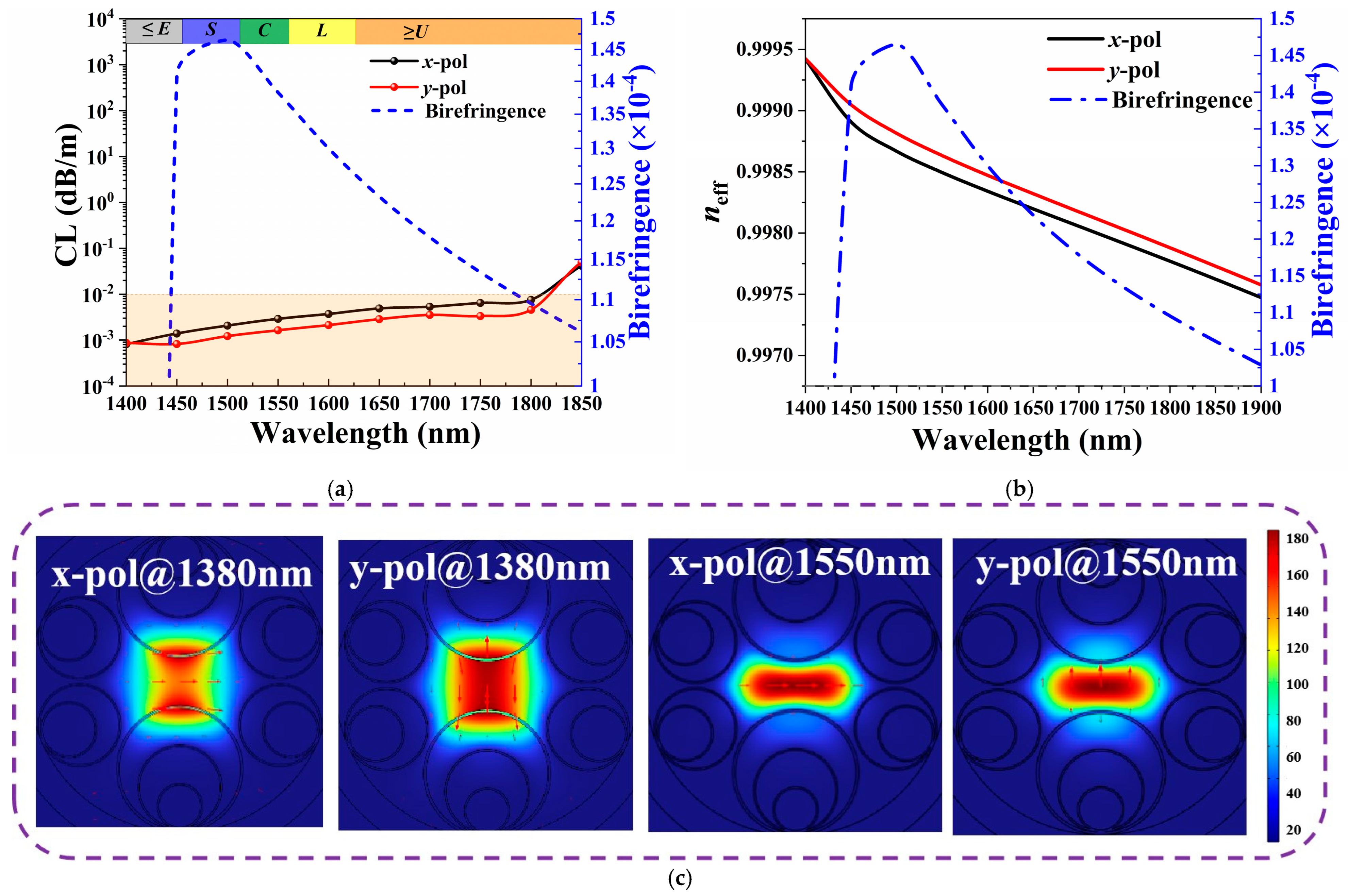
3.5. Transmission Performance
3.6. Bending Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korkishko, Y.N.; Fedorov, V.A.; Prilutskii, V.E.; Ponomarev, V.G.; Morev, I.V.; Skripnikov, S.F.; Khmelevskaya, M.I.; Buravlev, A.S.; Kostritskii, S.M.; Fedorov, I.V.; et al. Strapdown inertial navigation systems based on fiber-optic gyroscopes. Gyroscopy Navig. 2014, 5, 195–204. [Google Scholar] [CrossRef]
- Yao, X.S.; Xuan, H.; Chen, X.; Zou, H.; Liu, X.; Zhao, X. Polarimetry fiber optic gyroscope. Opt. Express 2019, 27, 19984–19995. [Google Scholar] [CrossRef] [PubMed]
- Song, N.; Xu, X.; Zhang, Z.; Gao, F.; Wang, X. Advanced interferometric fiber optic gyroscope for inertial sensing: A review. J. Light. Technol. 2023, 41, 4023–4034. [Google Scholar] [CrossRef]
- Chen, S.; Han, L.; Schülzgen, A.; Li, H.; Li, L.; Moloney, J.V.; Peyghambarian, N. Local electric field enhancement and polarization effects in a surface-enhanced Raman scattering fiber sensor with chessboard nanostructure. Opt. Express 2008, 16, 13016–13023. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Liu, Y.; Mou, C. Polarization-maintaining fiber long-period grating based vector curvature sensor. IEEE Photonics Technol. Lett. 2021, 33, 358–361. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Adamu, A.I.; Dasa, M.K.; Antonio-Lopez, J.E.; Amezcua-Correa, R. Mid-infrared photoacoustic gas monitoring driven by a gas-filled hollow-core fiber laser. Sci. Rep. 2021, 11, 3512. [Google Scholar] [CrossRef]
- Adamu, A.I.; Wang, Y.; Habib, M.S.; Dasa, M.K.; Antonio-Lopez, J.E.; Amezcua-Correa, R.; Bang, O.; Markos, C. Multi-wavelength high-energy gas-filled fiber Raman laser spanning from 1.53 µm to 2.4 µm. Opt. Lett. 2021, 46, 452–455. [Google Scholar] [CrossRef]
- Liu, X.; Li, Q.; Pan, D.; Ye, F.; Malomed, B.A.; Fu, H. A robust and novel linear fiber laser mode-locked by nonlinear polarization evolution in all-polarization-maintaining fibers. J. Light. Technol. 2021, 39, 7509–7516. [Google Scholar] [CrossRef]
- Hosaka, T.; Okamoto, K.; Miya, T.; Sasaki, Y.; Edahiro, T. Low-loss single polarization fibres with asymmetrical strain birefringence. Electron. Lett. 1981, 17, 530–531. [Google Scholar] [CrossRef]
- Girard, S.; Keurinck, J.; Ouerdane, Y.; Meunier, J.-P.; Boukenter, A. Gamma-rays and pulsed X-ray radiation responses of germane silicate single-mode optical fibers: Influence of cladding co-dopants. J. Light. Technol. 2004, 22, 1915–1922. [Google Scholar] [CrossRef]
- Noda, J.; Okamoto, K.; Sasaki, Y. Polarization-maintaining fibers and their applications. J. Light. Technol. 1986, LT-4, 1071–1089. [Google Scholar] [CrossRef]
- Monerie, M.; Jeunhomme, L. Polarization mode coupling in long single-mode fibres. Opt. Quantum Electron. 1980, 12, 449–461. [Google Scholar] [CrossRef]
- Birks, T.A.; Roberts, P.J.; Russell, P.S.J.; Atkin, D.M.; Shepherd, T.J. Full 2-D photonic bandgaps in silica/air structures. Electron. Lett. 1995, 31, 1941–1943. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Abeeluck, A.K.; Headley, C.; Eggleton, B.J. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594. [Google Scholar] [CrossRef]
- Fini, J.M.; Nicholson, J.W.; Mangan, B.; Meng, L.; Windeler, R.S.; Monberg, E.M.; DeSantolo, A.; DiMarcello, F.V. PM single-mode low-loss hollow-core fibres. Nat. Commun. 2014, 5, 5085. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, K.; Koshiba, M. Photonic bandgap fibers with high birefringence. IEEE Photonics Technol. Lett. 2002, 14, 1291–1293. [Google Scholar] [CrossRef]
- Lyngsø, J.; Jakobsen, C.; Simonsen, H.; Broeng, J. Truly single-mode polarization maintaining hollow core PCF. In Proceedings of the OFS2012 22nd International Conference on Optical Fiber Sensors, Proceedings of the OFS2012 22nd International Conference on Optical Fiber Sensors, Beijing, China, 15–19 October 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8421, pp. 100–103. [Google Scholar]
- Michieletto, M.; Lyngsø, J.; Læ gsgaard, J.; Bang, O. Cladding defects in hollow core fibers for surface mode suppression and improved birefringence. Opt. Express 2014, 22, 23324–23332. [Google Scholar] [CrossRef]
- Zhao, X.; Xiang, J.; Wu, X.; Li, Z. High birefringence, single-polarization, low loss hollow-core antiresonant fibers. Opt. Express 2021, 29, 36273–36286. [Google Scholar] [CrossRef]
- Ding, W.; Wang, Y.-Y. Hybrid transmission bands and large birefringence in hollow-core anti-resonant fibers. Opt. Express 2015, 23, 21165–21174. [Google Scholar] [CrossRef]
- Kumar, A.; Varshney, R.; Thyagarajan, K. Birefringence calculations in elliptical-core optical fibres. Electron. Lett. 1984, 20, 112–113. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Sandoghchi, S.R.; Richardson, D.J.; Poletti, F. Broadband high birefringence and polarizing hollow core antiresonant fibers. Opt. Express 2016, 24, 22943–22958. [Google Scholar] [CrossRef]
- Vincetti, L.; Setti, V. Elliptical hollow core tube lattice fibers for terahertz applications. Opt. Fiber Technol. 2013, 19, 31–34. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, Y.; Wu, T.; Hou, Z.; Xia, C.; Liu, J.; Zhou, G. Broadband birefringence hollow-core anti-resonant optical fiber with elliptical air holes. Opt. Commun. 2023, 527, 128976. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, H.; Hong, Y.; Gao, S.; Ding, W. Crescent-Shaped Anti-Resonant Hollow Core Fiber. IEEE J. Sel. Top. Quantum Electron. 2023, 30, 4300508. [Google Scholar] [CrossRef]
- Ran, J.; Meng, Y. Broadband high birefringence and single-polarization hollow-core anti-resonant fibers with an elliptical-like core. Opt. Commun. 2025, 575, 131251. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Richardson, D.J.; Sandoghchi, S.R.; Poletti, F. First design of high birefringence and polarising hollow core anti-resonant fibre. In Proceedings of the 2015 European Conference on Optical Communication, ECOC, Valencia, Spain, 27 September–1 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–3. [Google Scholar]
- Wei, C.L.; Menyuk, C.R.; Hu, J. Polarization-filtering and polarization-maintaining low loss negative curvature fibers. Opt. Express 2018, 26, 9528–9540. [Google Scholar] [CrossRef]
- Yerolatsitis, S.; Shurvinton, R.; Song, P.; Zhang, Y.; Francis-Jones, R.J.A.; Rusimova, K.R. Birefringent anti-resonant hollow-core fiber. J. Light. Technol. 2020, 38, 5157–5162. [Google Scholar] [CrossRef]
- Hong, Y.; Jia, A.; Gao, S.; Sheng, Y.; Lu, X.; Liang, Z.; Zhang, Z.; Ding, W.; Wang, Y. Birefringent, low loss, and broadband semi-tube anti-resonant hollow-core fiber. Opt. Lett. 2023, 48, 163–166. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Chen, W.; Zhang, Q.; Yang, Y.; Li, M.; Yan, M.; Wang, T. Highly birefringent anti-resonant hollow-core fiber with meniscoid nested structure. Opt. Express 2024, 32, 25292–25302. [Google Scholar] [CrossRef]
- Qiu, S.; Yuan, J.; Zhou, X.; Li, F.; Wang, Q.; Qu, Y.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; et al. Hollow-core negative curvature fiber with high birefringence for low refractive index sensing based on surface plasmon resonance effect. Sensors 2020, 20, 6539. [Google Scholar] [CrossRef]
- Saitoh, K.; Koshiba, M. Single-polarization single-mode photonic crystal fibers. IEEE Photon. Technol. Lett. 2003, 15, 1384–1386. [Google Scholar] [CrossRef]
- Zheng, W.; Qin, Y.; Xu, O.; Xiang, M.; Peng, D.; Fu, S.; Li, J. Wideband low confinement loss anti-resonant hollow core fiber with nested U-shape tube. Opt. Express 2021, 29, 24182–24192. [Google Scholar] [CrossRef] [PubMed]
- Murphy, L.R.; Yerolatsitis, S.; Birks, T.A.; Stone, J.M. Stack, seal, evacuate, draw: A method for drawing hollow-core fiber stacks under positive and negative pressure. Opt. Express 2022, 30, 37303–37313. [Google Scholar] [CrossRef]
- Ma, M.; Chen, K.; Ma, Y.; Bi, R.; She, X.; Shu, X. Highly birefringent anti-resonant hollow-core fiber with a low loss. IEEE Photonics Technol. Lett. 2023, 35, 1106–1109. [Google Scholar] [CrossRef]
- Velamuri, A.V.; Patel, K.; Sharma, I.; Gupta, S.S.; Gaikwad, S.; Krishnamurthy, P.K. Investigation of planar and helical bend losses in single-and few-mode optical fibers. J. Light. Technol. 2019, 37, 3544–3556. [Google Scholar] [CrossRef]



| Ref. | CL | Birefringence | Bandwidth | Bending Resistance | HOMER |
|---|---|---|---|---|---|
| [22] | 6 dB/km @1.57 μm | >1 × 10−4 | 300 nm (<103 dB/km) | ------ | No report |
| [24] | 30 dB/km @1.55 μm; | >1 × 10−4 | 460 nm (<103 dB/km) | >4 cm | No report |
| [20] | 340 dB/km @1.55 μm | ~10−4 | ~60 nm | ------ | No report |
| [36] | 6.1 dB/km@ 1.55 μm | >1 × 10−4 | 40 nm | >12 cm | 127 |
| [31] | 8.5 dB/km@1.06 μm; 204.1 dB/km@1.55 μm | 3.62 × 10−5; 9.83 × 10−5 | 172 nm; 216 nm | >10 cm | No report |
| This work | 1.5 dB/km@1.55 μm; 0.82 dB/km@1.45 μm | >1.45 × 10−4 | >1.05 × 10−4, ~380 nm | >3 cm (4.25 dB/km) | 32,070 (>241) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Yang, Y.; Yuan, J.; Wu, D.; Huang, Y.; Luo, S.; Ren, Z.; Xia, C.; Liu, J.; Zhou, G.; et al. Low Loss and High Polarization-Maintaining Single-Mode Hollow-Core Anti-Resonant Fibers with S+C+L+U Communication Bands. Photonics 2025, 12, 846. https://doi.org/10.3390/photonics12090846
Xu H, Yang Y, Yuan J, Wu D, Huang Y, Luo S, Ren Z, Xia C, Liu J, Zhou G, et al. Low Loss and High Polarization-Maintaining Single-Mode Hollow-Core Anti-Resonant Fibers with S+C+L+U Communication Bands. Photonics. 2025; 12(9):846. https://doi.org/10.3390/photonics12090846
Chicago/Turabian StyleXu, Hongxiang, Yuan Yang, Jinhui Yuan, Dongxin Wu, Yilin Huang, Shengbao Luo, Zhiyong Ren, Changming Xia, Jiantao Liu, Guiyao Zhou, and et al. 2025. "Low Loss and High Polarization-Maintaining Single-Mode Hollow-Core Anti-Resonant Fibers with S+C+L+U Communication Bands" Photonics 12, no. 9: 846. https://doi.org/10.3390/photonics12090846
APA StyleXu, H., Yang, Y., Yuan, J., Wu, D., Huang, Y., Luo, S., Ren, Z., Xia, C., Liu, J., Zhou, G., & Hou, Z. (2025). Low Loss and High Polarization-Maintaining Single-Mode Hollow-Core Anti-Resonant Fibers with S+C+L+U Communication Bands. Photonics, 12(9), 846. https://doi.org/10.3390/photonics12090846





