1. Introduction
The light quantum (photon) is one of the foundational concepts of modern physics. First proposed by Einstein in 1905 [
1], the concept gained acceptance following confirmation via experiments identifying the photoelectric effect [
2] and Compton scattering [
3]. Today, photon physics plays a critical role in diverse areas, such as particle physics [
4], the detection of the mass of a photon at rest [
5], phenomena like photon bunching and antibunching [
6,
7], photon-by-photon scattering [
8,
9], photon coherent absorption [
10], two-photon spontaneous emission [
11], the generation of entangled photon pairs [
12,
13], quantum entanglement [
14,
15], many-body quantum and ultracold atomic physics [
16,
17,
18,
19,
20], and other optical processes.
According to Einstein’s theory, the energy of a photon is given by
This is a well-known formula in optoelectronics [
21] and spectroscopy [
22] and is elegantly used for the fundamental process of energy exchange between light and matter. Applying the light quantum to the photoelectric effect, Einstein gave his equation
[
1], where
is the maximum kinetic energy of the photoelectrons (
m and
are the mass and maximum speed of photoelectrons, respectively).
We now consider the stopping voltage
V, which can be derived from the Einstein equation
The photon energy
in this expression still needs further exploration. The question is: Does the
here represent the frequency of a monochromatic light wave, or does it represent the center frequency of a wave train spectrum? If
is interpreted as the frequency of monochromatic light, according to Equation (
2), for non-monochromatic incident light with a wider bandwidth, the measured value of the stopping voltage (see its measurement and definition below) should correspond to the side frequency of the maximum value, since when the spectrum of incident light is broader, the light involves many monochromatic frequency components. Each photon independently excites a photoelectron, resulting in a distribution of photoelectron kinetic energies
, excited by multiple monochromatic frequency components in this case. And the maximum kinetic energy of these photoelectrons
should be excited by the maximum frequency component, and therefore the maximum frequency should determine the stopping voltage, i.e.,
. However, is this assumption valid? If
is the center frequency of a wave train spectrum, then how can it be determined when the incident light is non-monochromatic? What is the spectral bandwidth corresponding to the center frequency
? Is there an upper bound for the bandwidth? These questions need to be answered and justified by experiment. Our experiments demonstrate that the stopping voltage is determined by the maximum center frequency among wave train components (with different center frequencies), not the maximum frequency component of the incident light, determines the stopping voltage. That is to say, in Equation (
2),
represents the center frequency of a wave train spectrum but not the frequency of monochromatic light. The experiment also reveals that in the visible and near-infrared regions, the spectral bandwidth of a wave train component can be as large as 122 nm. These findings may enable applications such as detecting wave train components in an incoherent light, generating entangled photon pairs [
12,
13] or ultracold atoms [
16,
17,
18,
19,
20] with non-monochromatic light.
The experiment was carried out in three steps:
- (1)
First, discrete quasi-monochromatic light sources with wavelengths of 365 nm, 404.7 nm, 435.8 nm, 546.1 nm, 577 nm, 589.3 nm, and 632.8 nm were employed (see
Figure 1). The stopping voltage followed Equation (
2) and was determined by the highest-frequency component when multiple quasi-monochromatic beams were simultaneously incident on the photoelectric tube.
- (2)
Next, non-monochromatic light sources with center wavelengths
and the bandwidth
—specifically (
nm,
nm), (
nm,
nm), (
nm,
nm), (
nm,
nm), (
nm,
nm), and (
nm,
nm)—were tested (see
Figure 2). The stopping voltage was consistently governed by the center wavelength of the incident light.
- (3)
Finally, the non-monochromatic light shown in
Figure 2a (
nm,
nm) was combined with quasi-monochromatic light of 589.3 nm from a sodium lamp and 577 nm and 546.1 nm from a mercury lamp, respectively. It was found that the stopping voltage was determined by each added quasi-monochromatic light wavelength. A similar phenomenon was found by combining non-monochromatic light (
nm,
nm) with quasi-monochromatic light of 365 nm, 404.7 nm, and 435.8 nm from a mercury lamp, respectively.
2. Experimental Procedures and Results
In the first step of the experiment, we used a He-Ne laser, a sodium lamp, and a mercury lamp as light sources, and a ZKY-GD-4 experimental setup (see
Section S1 and Figure S1 in Supplement Material) for the photoelectric effect (the wavelength response is from 340 nm to 700 nm) as a detector to detect the stopping voltage. The anode of the photoelectric tube in the ZKY-GD-4 setup is with a ring structure (diameter 30 mm) made of nickel filament (diameter 0.2 mm). The structure can remarkably reduce the shielding effect of space charge created by the slow photoelectrons (that cannot reach the anode). The spectral lines used are 365, 404.7, 435.8, 546.1, 577, 589.3, and 632.8 nm, respectively. The stopping voltage is measured by (1) adjusting the galvanometer to a value of zero under the condition of no incident light; and (2) letting the light be incident onto the photoelectric tube and adding a smaller reverse voltage to the photoelectric tube (a larger positive photocurrent will be observed at this time). Then, this reverse voltage is slowly increased, and the current is observed, which will decrease continuously with the increase in the reverse voltage; (3) when the photocurrent decreases to zero, the observed reverse voltage at this moment is just the stopping voltage. The experimental result is shown in
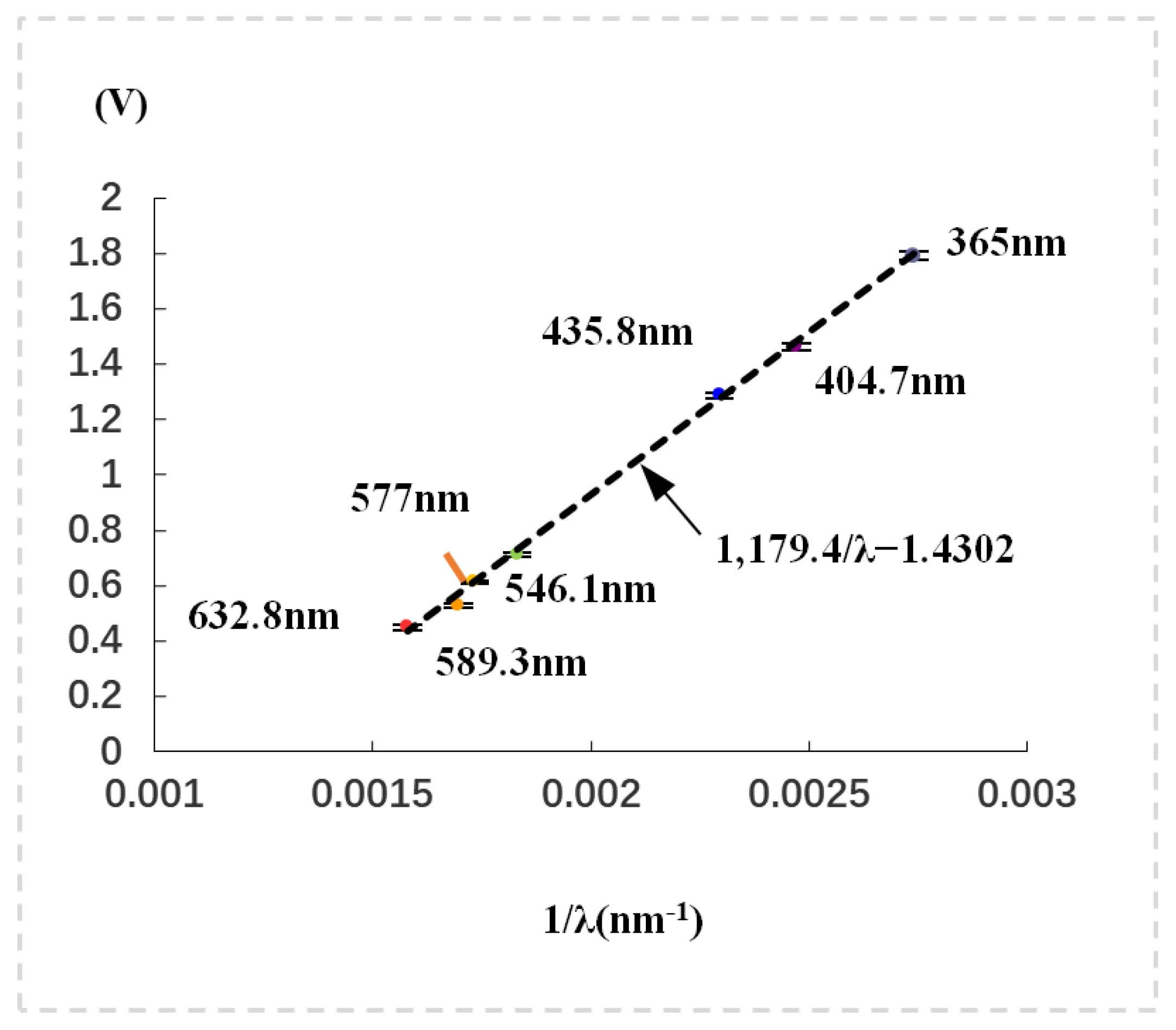
Figure 1, where the points with wavelength are the experimental data, and the dashed straight line is the result obtained by fitting the experimental data with the deformation function of Equation (
2), i.e.,
where
,
is the wavelength in nm. The fitting parameters are
Vnm and
V, respectively. The experimental points are almost on the straight line, which confirms that the experimental device works normally and reliably. We then let the light involving all the spectral lines (≥365 nm) of the mercury lamp be incident onto the photoelectric tube simultaneously. The stopping voltage is found to be 1.7805 V, which is close to 1.7912 V, measured by using single spectral line 365 nm, but slightly lower. The slightly lower value of 1.7912 V is due to the shielding effect of some slow electrons produced by the long-wavelength lights. In order to reduce the shielding effect, we minimized the entrance aperture of the photoelectric tube. An aperture of 2 mm diameter was used. Note that the aggregate of multiple quasi-monochromatic lights can be taken as a non-monochromatic light, in which besides the 365 nm light, there are four long-wavelength lights of 404.7, 435.8, 546.1, and 577 nm, respectively. So, the experiment indicates that the ZKY-GD-4 experimental setup is not only suitable for the monochromatic light, but also suitable for the non-monochromatic light. In addition, this experiment seems to prove that the
in Equation (
2) represents the frequency of a monochromatic light, since the stopping voltage is really determined by the maximum frequency component of the incident light, although the incident light involves many quasi-monochromatic components.
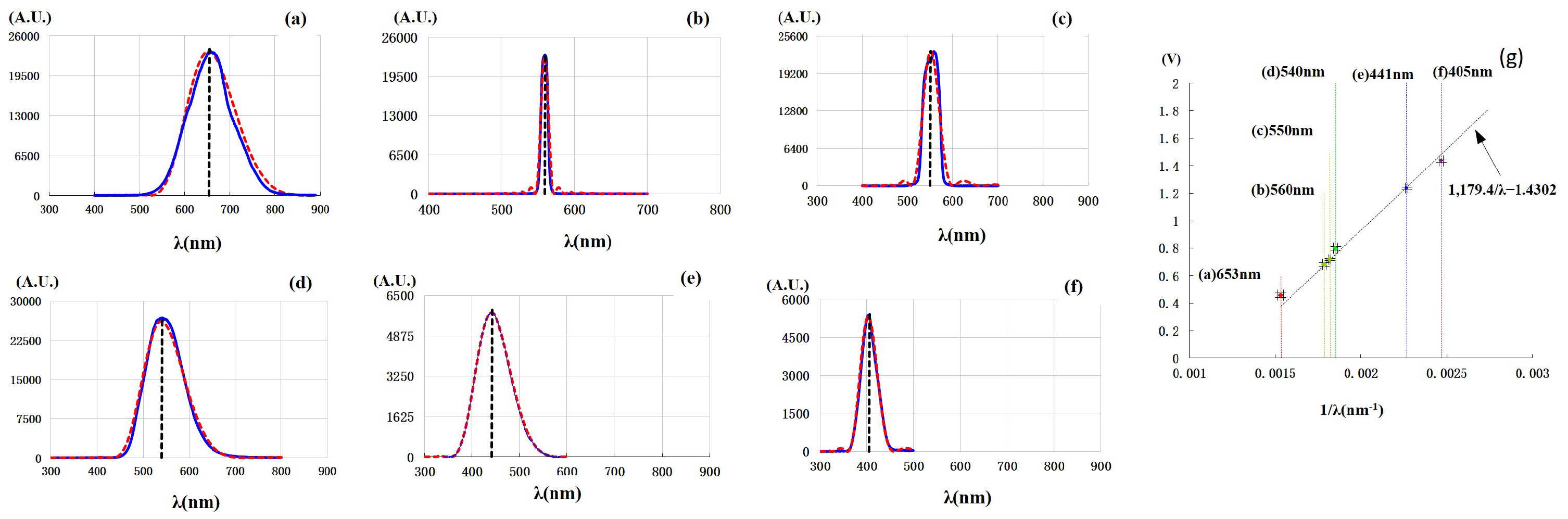
A critical question arises: for non-monochromatic incident light with a broad continuous spectrum, is the stopping voltage determined by the shortest-wavelength component? To address this question, we conducted the second experiment using a bromine tungsten lamp as the light source with six filters to generate non-monochromatic lights. The results are shown in
Figure 2 (see also
Section S2 and Figure S2 in the Supplementary Materials).
The solid blue lines of (a)–(f) are the spectra of non-monochromatic lights, in which the center wavelengths and bandwidths are, respectively, (a)
nm,
nm, (b)
nm,
nm, (c)
nm,
nm, (d)
nm,
nm, (e)
nm,
nm, and (f)
nm,
nm. The red dashed lines in the figure are the fitting ones. The results uncover that the stopping voltage is determined by the center wavelength rather than the shortest one, though the spectral bandwidths of incident lights vary greatly, ranging from 10 nm to 108 nm.
Figure 2g shows the stopping voltages observed. The black dashed straight line in
Figure 2g is from the function
. The vertically dashed lines marked with the wavelength correspond to the black dashed lines in
Figure 2a–f.
These two experimental series (particularly the second) confirm that
in Equation (
2) represents the center wavelength of the incident light spectrum rather than the component of the shortest wavelength involved. The spectral bandwidth of incident light can be very narrow, like that of a He-Ne laser, or very wide, like those shown in
Figure 2, and especially in
Figure 2a, being 108 nm.
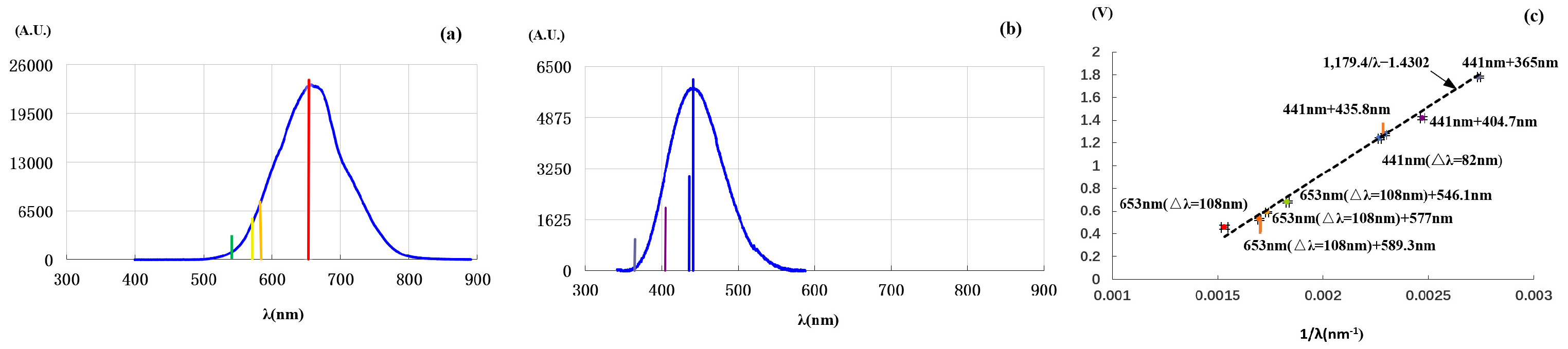
In the third experiment, we superimposed the non-monochromatic light of
Figure 2a (
nm,
nm), respectively, with 589.3 nm quasi-monochromatic light from a sodium lamp, and 577 nm and 546.1 nm from a mercury lamp. The light combination is done by using a splitting prism of no polarization selectivity. Each quasi-monochromatic light goes through the prism and the non-monochromatic light is reflected by the prism; then, they go together to the photoelectric tube (see
Section S1 and Figure S1 in the Supplementary Materials).
Figure 3a shows the spectra of non-monochromatic light and the added quasi-monochromatic lights. The colored vertical lines indicate the positions of quasi-monochromatic light [the red one indicates the center wavelength of
Figure 2a].
Figure 3c shows the relationship between stopping voltage and photon wavelength [see also
Section S3 and Figure S3a in the Supplementary Materials]. One sees that each stopping voltage is determined by the added quasi-monochromatic light and is slightly lower than that when the quasi-monochromatic light is used alone (this is also due to the shielding effect of the slow electrons produced by the long-wavelength light). It should be pointed out that when the added light is removed, the stopping voltage comes back to that corresponding to the center wavelength of
Figure 2a. Notably, while the light in
Figure 2a contained three spectral components (589.3, 577, and 546.1 nm), these components had a negligible effect on the stopping voltage in the second experiment. And in the third experiment, an addition of any of the quasi-monochromatic lights shifted the stopping voltage.
We further carried out another experiment by superimposing the non-monochromatic light of
Figure 2e (
nm,
nm), respectively, with a quasi-monochromatic light at 365, 404.7, and 435.8 nm from a mercury lamp.
Figure 3b shows the spectra of the complex lights. As shown in
Figure 3c, each stopping voltage is also determined by the added quasi-monochromatic light [see also
Section S3 and Figure S3b in the Supplementary Materials]. Although the light used in
Figure 2e contains three components, 365, 404.7, and 435.8 nm, the stopping voltage reflects negligible impact of these light components. It should be mentioned that the stopping voltage for 365nm added light is 1.7806 V, which is close to 1.7912 V, measured by using quasi-monochromatic light at 365 nm alone. We also observed that, when the added quasi-monochromatic light wavelength is longer than 441 nm, for example, the 577 nm light from the mercury lamp, the stopping voltage is determined by the center wavelength of the non-monochromatic light, as well.
3. Discussion
For a monochromatic light, the stopping voltage strictly correlates with the incident wavelength, as predicted by Einstein’s photoelectric equation. Remarkably, for non-monochromatic light (
Figure 2), the stopping voltage is governed by the spectral center wavelength, even when many shorter-wavelength components are present. And the introduction of any quasi-monochromatic component shorter than the center wavelength immediately dominates its impact on stopping voltage. As demonstrated in
Figure 2a, the native spectrum containing 589.3, 577, and 546.1 nm components produces no distinct stopping voltage. However, introducing any of these wavelengths as discrete quasi-monochromatic components immediately establishes a measurable stopping voltage (
Figure 3a,c). These observations can be understood through the finite bandwidth characteristics of the light sources (
Figure 2). According to Born and Wolf [
23], a light with finite bandwidth can be described using a wave train model, i.e., the light can be taken as the superposition of a series of basic wave trains. For example, a light (not needing to be from a pulse laser), whose spectrum is a Gaussian line profile
, can be taken as that composed of a large number of basic wave trains, one of which is a Gaussian wave packet (or wave train) of temporal form
, where
and
are the wave packet duration and center angular frequency of the wave train, respectively. While wave train models for spectral origins are extensively treated in spectroscopy [
22], we adopt the discrete wavelet structure model [
24] for our analysis based on two key considerations: (1) excellent agreement with our experimental spectra, and (2) consistency with the coherent state theory of quantized fields [
25] (
Appendix A), including its discrete energy representation. The discrete wavelet structure theory [
24] indicates that a basic light wave train with finite bandwidth can be described as
Here,
c is the speed of light under vacuum,
is a constant,
is the center wavelength, and
,
,
, which is a parameter for decomposing the wave train as a series of discrete wavelets [
24] (see
Appendix B). Note that with a large
n, Equation (
4) can also describe quasi-monochromatic light waves, like those used in the first step of the experiment. The energy of this wave train is discrete [
24]. Along
and through a cross-section
, the energy that can be devolved to a medium is also discrete, being
, with
being a constant. The spectral distribution of the wave train is
If
is taken as one unit and the spectrum is represented in wavelength, it becomes
Note that the smaller the value of
n, the shorter the wave train is (the wider the spectrum is). The maximum bandwidth
of a wave train (that can devolve discrete energy to a medium or an electron) is the spectrum of Equation (
6), with
[
24].
Now we can explain the experiment shown in
Figure 2. We used Equation (
6) to fit the spectra in
Figure 2. The results are as follows: (a)
,
nm,
nm; (b)
,
nm,
nm; (c)
,
nm,
nm; (d)
,
nm,
nm; (e)
,
nm,
nm; and (f)
,
nm,
nm. The broken red lines are fitting curves, shown in
Figure 2. Each spectrum is that of the single wave train in Equation (
4). One can see that as long as taking the
in Equation (
2) as the center frequency
of the wave train in Equation (
4), and assuming that each photoelectron is excited by one portion of the discrete energy
, it is easy to understand the result shown in
Figure 2, since each stopping voltage corresponds to the center wavelength of the spectrum of each incident light. Importantly, the discrete wavelet theory reveals that
represents a fundamental energy quantum transferable from wave train to photoelectron—not an averaged energy, but a global property of the entire wave train spectrum. In other words, for a wave train spectrum of Equation (
5), there exists only one kind of photon with energy
.
Figure 3a is the experimental spectrum of
Figure 2a combined with 589.3 nm, 577 nm, and 546.1 nm lines. The stopping voltage is completely determined by any of the added quasi-monochromatic lights (see
Figure 3c) though the spectrum in
Figure 2a involves three components: 589.3 nm, 577 nm, and 546.1 nm. This can be understood, since the spectrum
Figure 2a can be described by a single wave train of Equation (
4) of
, and the photon energy of the wave train is
, so the stopping voltage corresponds to
(i.e., for the photoelectric effect, the light with the spectrum in
Figure 2a behaves like a monochromatic light with wavelength
). And the spectrum in
Figure 3a is different to that of
Figure 2a. In each combination experiment, there are two incident lights, i.e., a non-monochromatic light (
nm,
nm) and an added quasi-monochromatic light. These two lights can be equivalent to a monochromatic light of wavelength
and an added quasi-monochromatic light. The wavelength of the added quasi-monochromatic light is shorter than
. The maximum kinetic energy of photoelectrons excited by the added quasi-monochromatic light is larger than that excited by the non-monochromatic light. Therefore, the stopping voltage is determined by the added quasi-monochromatic light. The experiment shown in
Figure 3b,c can be understood analogously.
Figure 3 shows clearly that the stopping voltage is determined by the smallest center wavelength when the incident light involves multiple wave train components with different center wavelengths. Following this law, it is easy to understand the first experiment above when multiple quasi-monochromatic lights are incident onto the photoelectric tube simultaneously, and the light of maximum frequency determines the stopping voltage.
Experimental results show that if a non-monochromatic light can be described by a single wave train of Equation (
4) (as shown in
Figure 2), then the non-monochromatic light behaves like a monochromatic one with a wavelength
. The
corresponds to the stopping voltage. When
[for example, shown in
Figure 2a,d,e], the non-monochromatic components reach the largest spread. In this case, the spectrum width
can be rather large, as large as 122 nm, as shown in
Figure 2a. And if a non-monochromatic light can be described by the superposition of a series of wave trains with different center wavelengths
and integers
(as shown in
Figure 3, where
in each combination experiment), then each of the wave trains behaves separately like a monochromatic component with wavelength
and the stopping voltage is determined by the
. When
are all very large, these wave trains become quasi-monochromatic (for example, the situation when multiple quasi-monochromatic lights are simultaneously incident onto the photoelectric tube in the first experiment, where
).