Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy
Abstract
1. Introduction
2. Principles of Digital Holographic Microscopy
2.1. Theoretical Foundations of Digital Holographic Microscopy
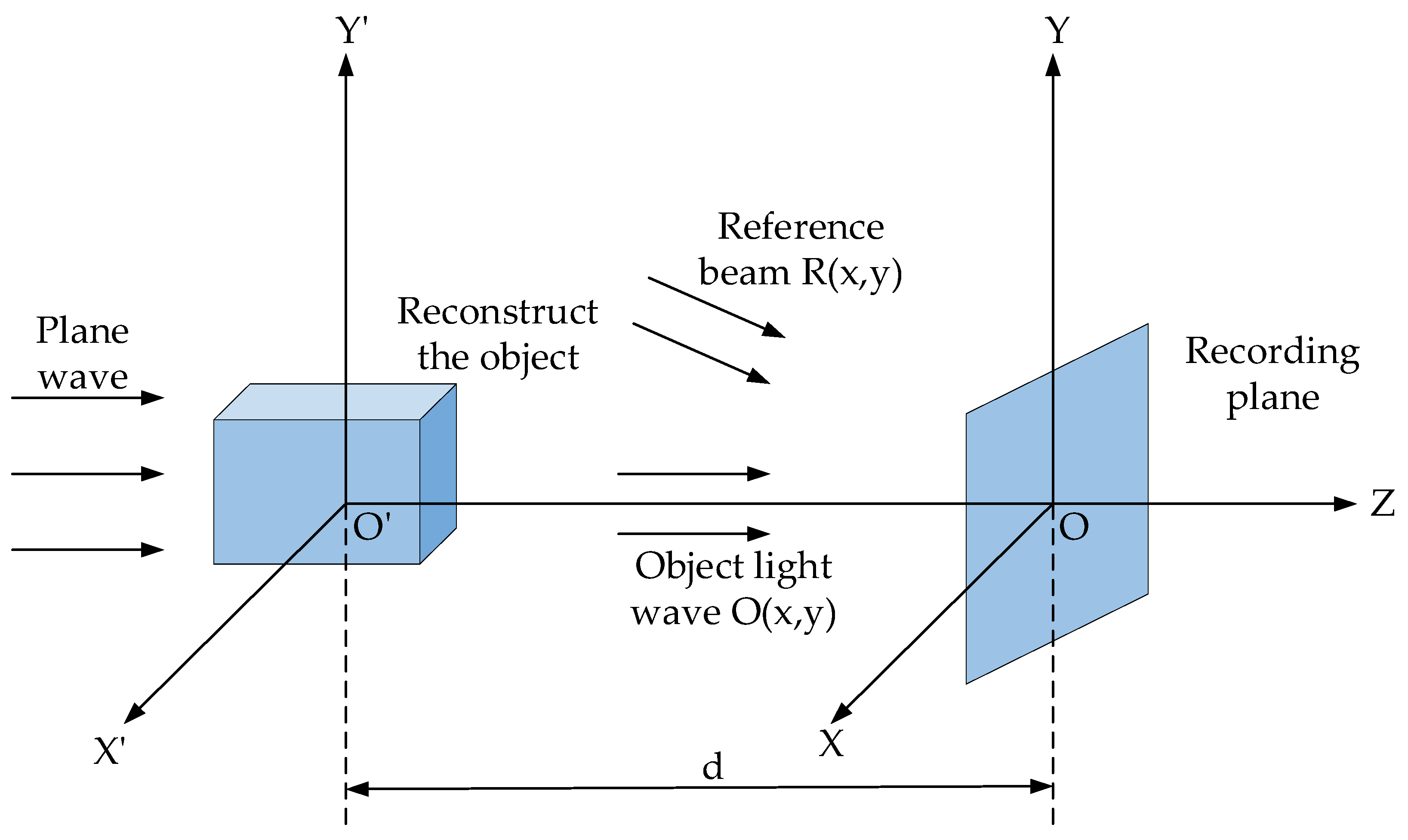
2.1.1. Digital Holographic Microscopy Recording
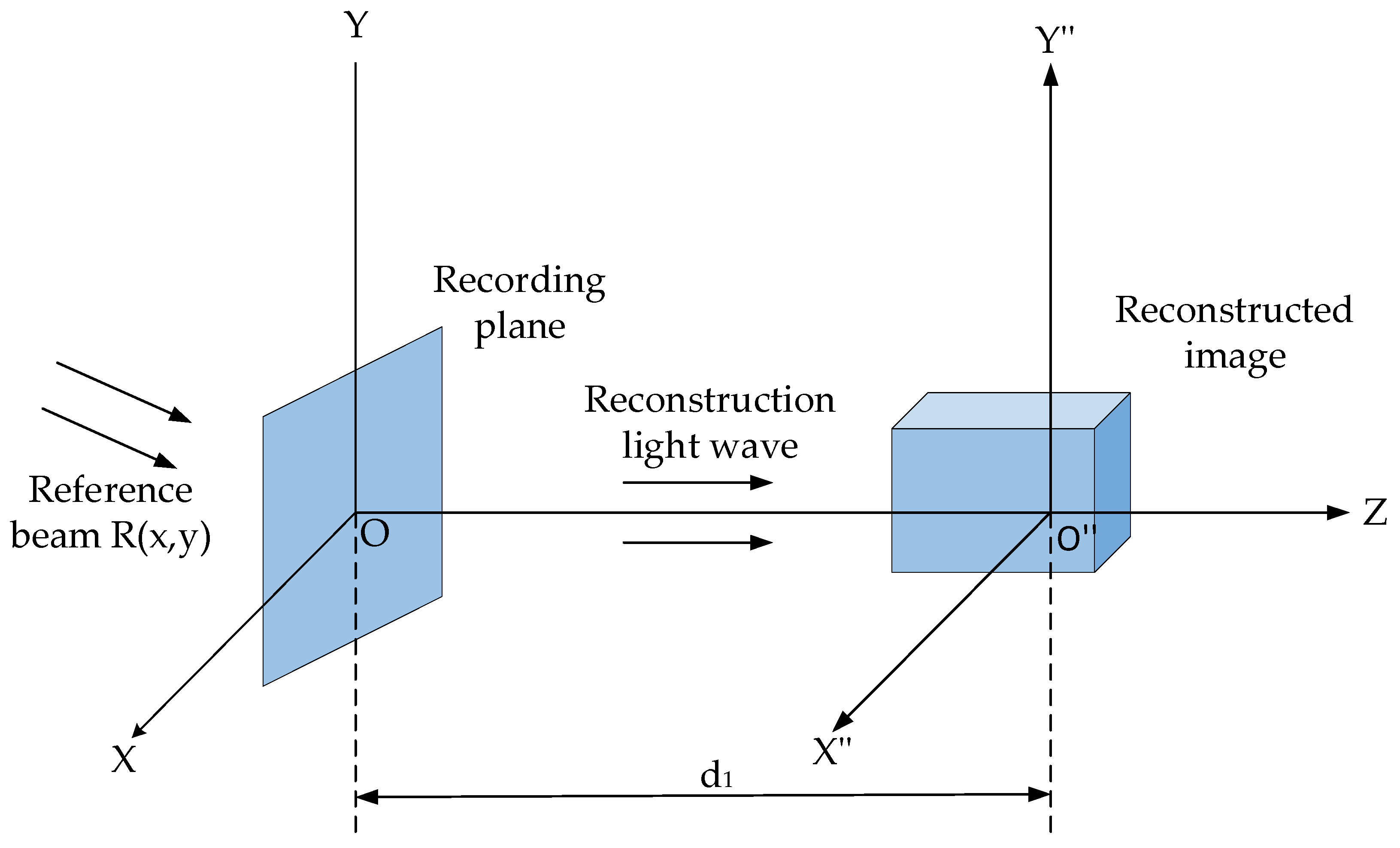
2.1.2. Digital Holographic Microscopy Reconstruction
2.2. Signal Changes in Phase Processing
2.3. Theoretical Framework for Phase Processing in Deep Learning
2.3.1. Application Scenario Dimension
2.3.2. Technical Principle Dimension
2.3.3. Learning Paradigm Dimension
3. Application of Deep Learning in Phase Recovery of Digital Holographic Microscopy
- (1)
- They rely on iterative calculations, which are time-consuming and inefficient.
- (2)
- The complex operational processes lead to lower-quality reconstructed images.
- (3)
- They require that the intensity and phase be processed separately in sequential steps, as they lack an integrated framework for efficient joint reconstruction.
4. Application of Deep Learning in Phase Extraction for Digital Holographic Microscopy
4.1. Application of Deep Learning in Phase Filtering
- (1)
- Difficulty in obtaining noise-free phase maps for labeling.
- (2)
- Unclear feature representation.
- (3)
- Inefficient in denoising.
4.2. Application of Deep Learning in Phase Unwrapping
- (1)
- Prolonged phase unwrapping time;
- (2)
- Limited robustness;
- (3)
- Poor generalization;
- (4)
- Low accuracy.
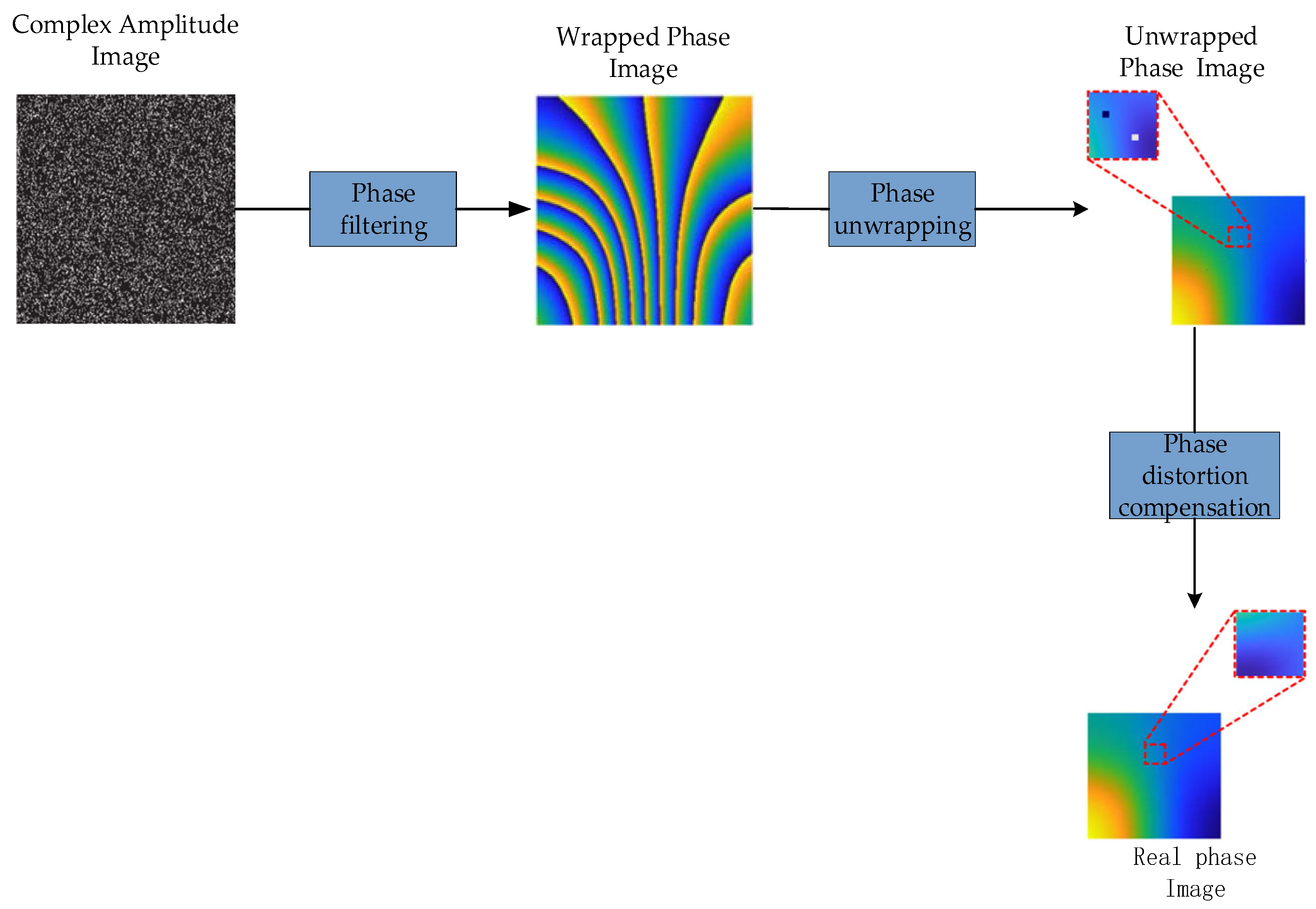
4.3. Application of Deep Learning in Phase Distortion Compensation
- (1)
- They require extensive preprocessing.
- (2)
- They are constrained by perturbation assumptions.
- (3)
- They often require manual intervention.
4.4. Evaluation Metrics for Phase Processing Results
5. Summary and Outlook
- (1)
- Ultrafast 3D Holographic Reconstruction: Current 3D reconstruction in DHM relies on time-consuming iterative algorithms. Future work could focus on deep learning-based fast inversion algorithms, such as Bayesian–physical joint modeling [59] or a 3D reconstruction method based on unpaired data learning [60]. By training on a large dataset of paired holographic interference patterns and their 3D reconstructions, these models can be trained to learn the direct mapping. This pattern enables the rapid conversion of interference patterns into 3D reconstructions, significantly improving real-time imaging—particularly for capturing dynamic processes, such as cell movement.
- (2)
- High-Throughput Holographic Data Analysis: DHM generates vast amounts of data in high-throughput experiments (such as drug screening). Automating data analysis using deep learning pipelines, such as few-shot learning and transfer learning, could improve classification, segmentation, and feature extraction. In practice, the model can first be pre-trained on a large-scale general holographic dataset to learn a broad feature representation of the data. Subsequently, few-shot learning can be applied to quickly adapt the model to specific high-throughput experimental data, enabling accurate analysis and enhancing the efficiency and automation of these experiments.
- (3)
- Precise Quantification of Phase Analysis: In biomedical applications, accurate phase analysis is crucial for the non-destructive measurement of optical thickness and refractive index in cells and tissues. Deep learning could help develop more precise phase recovery algorithms. A CNN-based architecture can be tailored to effectively extract phase information from holograms. By introducing an attention mechanism, the network can prioritize key regions with significant phase features, enabling automatic extraction of quantitative data for complex biological analysis.
- (4)
- Multimodal Data Fusion: Combining DHM with other imaging techniques (e.g., electron or fluorescence microscopy) could significantly enhance the information gathered from images. Deep learning could integrate these modalities. A multimodal fusion network is specifically designed to extract features from each modality separately. These features are then combined through the fusion layer to reveal deeper structural and biological information, enhancing resolution, contrasts, and the diversity of biological markers in biomedical research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodman, J.W. Digital image formation from electronically detected holograms. Proc. SPIE-Int. Soc. Opt. Eng. 1967, 10, 176–181. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light Sci. Appl. 2022, 11, 39. [Google Scholar] [CrossRef]
- Shen, X.; Wang, L.; Li, W.; Wang, H.; Zhou, H.; Zhu, Y.; Yan, W.; Qu, J. Ultralow laser power three-dimensional superresolution microscopy based on digitally enhanced STED. Biosensors 2022, 12, 539. [Google Scholar] [CrossRef]
- Kim, M.K. Applications of digital holography in biomedical microscopy. J. Opt. Soc. Korea 2010, 14, 77–89. [Google Scholar] [CrossRef]
- Potter, J.C.; Xiong, Z.; McLeod, E. Clinical and biomedical applications of lensless holographic microscopy. Laser Photonics Rev. 2024, 18, 2400197. [Google Scholar] [CrossRef]
- Mann, C.J.; Yu, L.; Kim, M.K. Movies of cellular and sub-cellular motion by digital holographic microscopy. Biomed. Eng. OnLine 2006, 5, 21. [Google Scholar] [CrossRef]
- Wu, Y.; Ozcan, A. Lensless digital holographic microscopy and its applications in biomedicine and environmental monitoring. Methods 2017, 136, 4–16. [Google Scholar] [CrossRef]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep learning in holography and coherent imaging. Light Sci. Appl. 2019, 8, 85. [Google Scholar] [CrossRef]
- Wang, K.; Song, L.; Wang, C.; Ren, Z.; Zhao, G.; Dou, J.; Di, J.; Barbastathis, G.; Zhou, R.; Zhao, J.; et al. On the use of deep learning for phase recovery. Light Sci. Appl. 2024, 13, 4. [Google Scholar] [CrossRef]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Wang, L.; Yan, W.; Li, R.; Weng, X.; Zhang, J.; Yang, Z.; Liu, L.; Ye, T.; Qu, J. Aberration correction for improving the image quality in STED microscopy using the genetic algorithm. Nanophotonics 2018, 7, 1971–1980. [Google Scholar] [CrossRef]
- Zeng, T.; Zhu, Y.; Lam, E.Y. Deep learning for digital holography: A review. Opt. Express 2021, 29, 40572–40593. [Google Scholar] [CrossRef]
- Park, Y.K.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Kim, M.K. Principles and techniques of digital holographic microscopy. J. Photonics Energy 2009, 1, 8005. [Google Scholar] [CrossRef]
- Liu, K.; He, Z.; Cao, L. Double amplitude freedom Gerchberg-Saxton algorithm for generation of phase-only hologram with speckle suppression. Appl. Phys. Lett. 2022, 120, 061103. [Google Scholar] [CrossRef]
- Pauwels, E.J.R.; Beck, A.; Eldar, Y.C.; Sabach, S. On Fienup methods for sparse phase retrieval. IEEE Trans. Signal Process. 2018, 66, 982–991. [Google Scholar] [CrossRef]
- Zhang, G.; Guan, T.; Shen, Z.; Wang, X.; Hu, T.; Wang, D.; He, Y.; Xie, N. Fast phase retrieval in off-axis digital holographic microscopy through deep learning. Opt. Express 2018, 26, 19388–19405. [Google Scholar] [CrossRef]
- Nagahama, Y. Phase retrieval using hologram transformation with U-Net in digital holography. Opt. Contin. 2022, 1, 1506–1515. [Google Scholar] [CrossRef]
- Wang, K.; Dou, J.; Kemao, Q.; Di, J.; Zhao, J. Y-Net: A one-to-two deep learning framework for digital holographic reconstruction. Opt. Lett. 2019, 44, 4765–4768. [Google Scholar] [CrossRef]
- Chen, B.; Li, Z.; Zhou, Y.; Zhang, Y.; Jia, J.; Wang, Y. Deep-learning multiscale digital holographic intensity and phase reconstruction. Appl. Sci. 2023, 13, 9806. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, C. An improved median filtering algorithm for image noise reduction. Phys. Procedia 2012, 25, 609–616. [Google Scholar] [CrossRef]
- Rakshit, S.; Ghosh, A.; Shankar, B.U. Fast mean filtering technique (FMFT). Pattern Recognit. 2007, 40, 890–897. [Google Scholar] [CrossRef]
- Kundur, D.; Hatzinakos, D. Blind image deconvolution. IEEE Signal Process. Mag. 1996, 13, 43–64. [Google Scholar] [CrossRef]
- Barjatya, A. Block matching algorithms for motion estimation. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising with Block-Matching and 3D Filtering. In Image Processing: Algorithms and Systems, Neural Networks, and Machine Learning, Proceedings of the Electronic Imaging 2006, 15–19 January 2006, San Jose, CA, USA; SPIE: Bellingham, WA, USA, 2006; Volume 6064, pp. 354–365. [Google Scholar]
- Chen, J.; Benesty, J.; Huang, Y.; Doclo, S. New insights into the noise reduction Wiener filter. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1218–1234. [Google Scholar] [CrossRef]
- Huang, L.; Kemao, Q.; Pan, B.; Asundi, A.K. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase extraction from a single fringe pattern in fringe projection profilometry. Opt. Lasers Eng. 2010, 48, 141–148. [Google Scholar] [CrossRef]
- Villasenor, J.D.; Belzer, B.; Liao, J. Wavelet filter evaluation for image compression. IEEE Trans. Image Process. 1995, 4, 1053–1060. [Google Scholar] [CrossRef]
- Wu, J.; Tang, J.; Zhang, J.; Di, J. Coherent noise suppression in digital holographic microscopy based on label-free deep learning. Front. Phys. 2022, 10, 880403. [Google Scholar] [CrossRef]
- Tang, J.; Chen, B.; Yan, L.; Huang, L. Continuous phase denoising via deep learning based on Perlin noise similarity in digital holographic microscopy. IEEE Trans. Ind. Inform. 2024, 20, 8707–8716. [Google Scholar] [CrossRef]
- Awais, M.; Kim, Y.; Yoon, T.; Choi, W.; Lee, B. A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry. Appl. Sci. 2025, 15, 5514. [Google Scholar] [CrossRef]
- Fang, Q.; Xia, H.-T.; Song, Q.; Zhang, M.; Guo, R.; Montresor, S.; Picart, P. Speckle denoising based on deep learning via a conditional generative adversarial network in digital holographic interferometry. Opt. Express 2022, 30, 20666–20683. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Li, Q.; Song, Q.; Montresor, S.; Picart, P.; Xia, H. Convolutional and Fourier neural networks for speckle denoising of wrapped phase in digital holographic Interferometry. Opt. Commun. 2024, 550, 129955. [Google Scholar] [CrossRef]
- Yu, H.B.; Fang, Q.; Song, Q.H.; Montresor, S.; Picart, P.; Xia, H. Unsupervised speckle denoising in digital holographic interferometry based on 4-f optical simulation integrated cycle-consistent generative adversarial network. Appl. Opt. 2024, 63, 3557–3569. [Google Scholar] [CrossRef] [PubMed]
- Demer, D.A.; Soule, M.A.; Hewitt, R.P. A multiple-frequency method for potentially improving the accuracy and precision of in situ target strength measurements. J. Acoust. Soc. Am. 1999, 105, 2359–2376. [Google Scholar] [CrossRef]
- Belenguer, J.-M.; Benavent, E.; Prins, C.; Prodhon, C.; Calvo, R.W. A branch-and-cut method for the capacitated location-routing problem. Comput. Oper. Res. 2011, 38, 931–941. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zhang, Q.; Su, X.; Asundi, A.; Kemao, Q. Quality-guided phase unwrapping technique: Comparison of quality maps and guiding strategies. Appl. Opt. 2011, 50, 6214–6224. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, J. Improved region growing method for image segmentation of three-phase materials. Powder Technol. 2020, 368, 80–89. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.; Moon, I. Automated phase unwrapping in digital holography with deep learning. Biomed. Opt. Express 2021, 12, 7064–7081. [Google Scholar] [CrossRef]
- Wang, B.; Cao, X.; Lan, M.; Wu, C.; Wang, Y. An Anti-noise-designed residual phase unwrapping neural network for digital speckle pattern interferometry. Optics 2024, 5, 44–55. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, S.; Zhao, Z.; Dixit, K.; Zhou, X.; Hou, J.; Zhang, Y.; Yan, C. Rapid and robust two-dimensional phase unwrapping via deep learning. Opt. Express 2019, 27, 23173–23185. [Google Scholar] [CrossRef]
- Spoorthi, G.E.; Gorthi, R.K.S.S.; Gorthi, S. PhaseNet 2.0: Phase unwrapping of noisy data based on deep learning approach. IEEE Trans. Image Process. 2020, 29, 4862–4872. [Google Scholar] [CrossRef]
- Spoorthi, G.E.; Gorthi, S.; Gorthi, R.K.S.S. PhaseNet: A deep convolutional neural network for two-dimensional phase unwrapping. IEEE Signal Process. Lett. 2018, 26, 54–58. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Liu, C.; Han, Z.; Xiao, Q.; Zhang, Z.; Feng, W.; Liu, M.; Lu, Q. Efficient and robust phase unwrapping method based on SFNet. Opt. Express 2024, 32, 15410–15432. [Google Scholar] [CrossRef]
- Awais, M.; Yoon, T.; Hwang, C.O.; Lee, B. DenSFA-PU: Learning to unwrap phase in severe noisy conditions. Opt. Laser Technol. 2025, 187, 112757. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, L.; Wang, T.; Wang, X.; Du, X.; Hao, R.; Liu, J.; Liu, Y.; Zhang, J. VDE-Net: A two-stage deep learning method for phase unwrapping. Opt. Express 2022, 30, 39794–39815. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Wan, S.; Wan, Y.; Weng, J.; Liu, W.; Gong, Q. Direct and accurate phase unwrapping with deep neural network. Appl. Opt. 2020, 59, 7258–7267. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Kong, Y.; Zhang, D.; Fu, Y.; Zhuang, S. Two-dimensional phase unwrapping based on U2-Net in complex noise environment. Opt. Express 2023, 31, 29792–29812. [Google Scholar] [CrossRef]
- Li, Y.; Meng, L.; Zhang, K.; Zhang, Y.; Xie, Y.; Yuan, L. PUDCN: Two-dimensional phase unwrapping with a deformable convolutional network. Opt. Express 2024, 32, 27206–27220. [Google Scholar] [CrossRef]
- Jiaying, L. Central difference information filtering phase unwrapping algorithm based on deep learning. Opt. Lasers Eng. 2023, 163, 107484. [Google Scholar] [CrossRef]
- Zhao, W.; Yan, J.; Jin, D.; Ling, J. C-HRNet: High resolution network based on contexts for single-frame phase unwrapping. IEEE Photonics J. 2024, 16, 5100210. [Google Scholar] [CrossRef]
- Xiao, W.; Xin, L.; Cao, R.; Wu, X.; Tian, R.; Che, L.; Sun, L.; Ferraro, P.; Pan, F. Sensing morphogenesis of bone cells under microfluidic shear stress by holographic microscopy and automatic aberration compensation with deep learning. Lab A Chip 2021, 21, 1385–1394. [Google Scholar] [CrossRef]
- Li, Z.; Wang, F.; Jin, P.; Zhang, H.; Feng, B.; Guo, R. Accurate phase aberration compensation with convolutional neural network PACUnet3+ in digital holographic microscopy. Opt. Lasers Eng. 2023, 171, 107829. [Google Scholar] [CrossRef]
- Yin, M.; Wang, P.; Ni, C.; Hao, W. Cloud and snow detection of remote sensing images based on improved Unet3+. Sci. Rep. 2022, 12, 14415. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Zhang, J.; Zhang, S.; Mao, S.; Ren, Z.; Di, J.; Zhao, J. Phase aberration compensation via a self-supervised sparse constraint network in digital holographic microscopy. Opt. Lasers Eng. 2023, 168, 107671. [Google Scholar] [CrossRef]
- Nguyen, T.; Bui, V.; Lam, V.; Raub, C.B.; Chang, L.-C.; Nehmetallah, G. AutAomatic phase aberration compensation for digital holographic microscopy based on deep learning background detection. Opt. Express 2017, 25, 15043–15057. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Liu, Q.; Yu, Y.; Luo, Y.; Wang, S. Quantitative phase imaging in digital holographic microscopy based on image inpainting using a two-stage generative adversarial network. Opt. Express 2021, 29, 24928–24946. [Google Scholar] [CrossRef]
- Tan, J.; Niu, H.; Su, W.; He, Z. Structured light 3D shape measurement for translucent media base on deep Bayesian inference. Opt. Laser Technol. 2025, 181, 111758. [Google Scholar] [CrossRef]
- Tan, J.; Liu, J.; Wang, X.; He, Z.; Su, W.; Huang, T.; Xie, S. Large depth range binary-focusing projection 3D shape reconstruction via unpaired data learning. Opt. Lasers Eng. 2024, 181, 108442. [Google Scholar] [CrossRef]










| Method | Application Scenario Dimension | Technical Principle Dimension | Learning Paradigm Dimension |
|---|---|---|---|
| U-Net [18] | Biomedicine (off-axis DHM). | Data-driven (end-to-end mapping from defocused holograms to focused phases using U-Net). | Supervised learning (L2 Loss + high-frequency weighting for phase reconstruction accuracy). |
| U-Net [19] | Biomedicine/materials science (in-line DHM). | Data-driven (multi-scale feature fusion via U-Net for separating object waves and conjugate images in single holograms). | Supervised learning (using MAE loss function for optimizing the mapping relationship between complex amplitude and light intensity). |
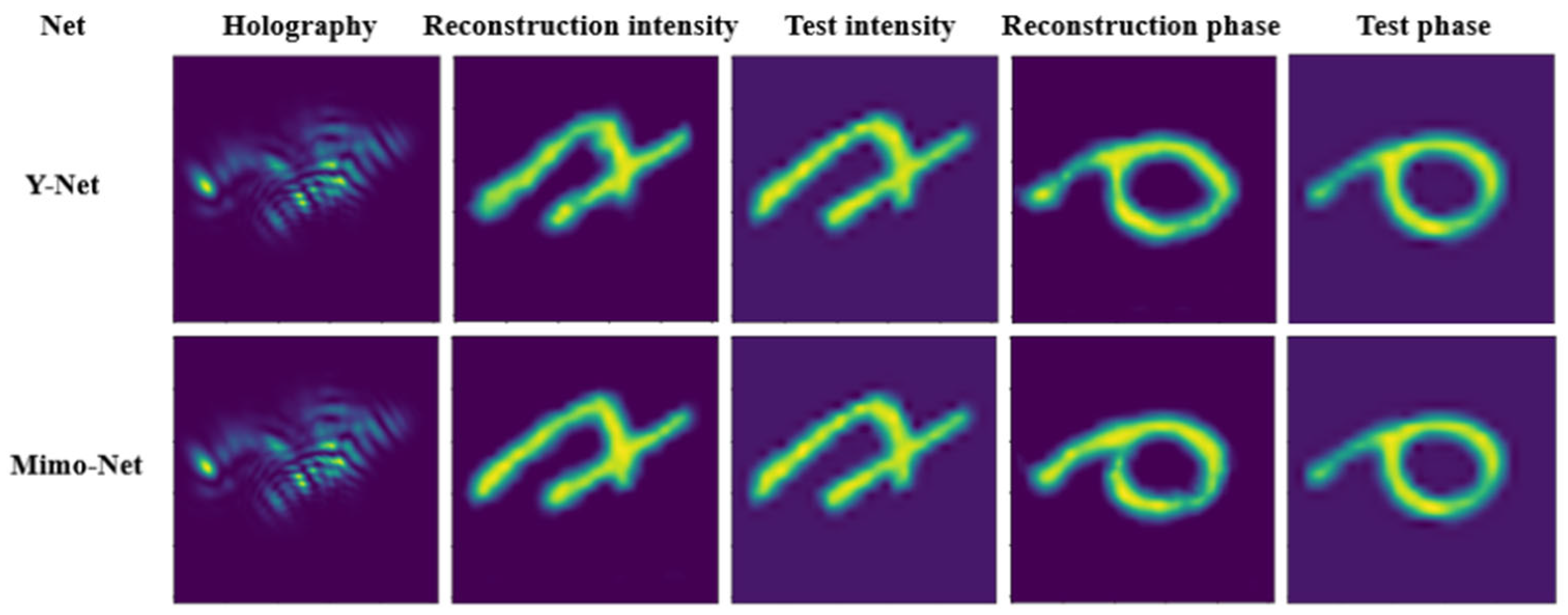
| Y-Net [20] | Real-time biomedical imaging; simultaneous intensity and phase reconstruction (off-axis DHM). | Dual-branch U-Net with single/double/triple convolutional kernels for multi-scale feature extraction. | Supervised learning. |
| Mimo-Net [21] | Multi-scale holographic reconstruction (off-axis DHM). | Multi-branch input with multi-scale feature extraction modules and cross-layer fusion. | Supervised learning. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| Gerchberg–Saxton iterative algorithm [16], Fienup iterative algorithm [17] | Alternating projections between spatial and frequency domains to iteratively approximate the true phase using known amplitude. | High interpretability and low data dependency. | Low computational efficiency, sub-optimal noise resistance, and limited adaptability to complex scenes. | Traditional algorithms offer strong physical interpretability in simple and low-noise settings but are constrained by limited real-time performance and scalability in complex scenarios. |
| U-Net [18] | Extracts multi-level features from defocused holograms via multi-layer convolutions, retains structural details through skip connections, and directly outputs the focused phase. | High real-time performance, strong noise resistance, detail preservation, and good adaptability to complex scenarios. | Dependent on simulated data and sensitive to parameter tuning. | Well-suited for real-time dynamic applications, such as rapid phase monitoring of living cells in biomedical imaging. |
| U-Net [19] | The U-Net encoder captures noise patterns from holograms, while the decoder separates object waves and conjugates images via a nonlinear transformation to output pure phases. | High efficiency in single-image processing, targeted noise reduction, and a simplified workflow. | Limited generalization to diverse noise types and high computational resource demands. | Optimized for single-image noise reduction, making it suitable for high-throughput hologram analysis in materials science. |
| Y-Net [20] | Utilizes a dual-branch U-Net to integrate multi-scale convolutional features for concurrent intensity and phase reconstruction from digital holograms. | Symmetrical structure with 30% fewer parameters than U-Net; achieves SSIM > 0.96 for simultaneous intensity and phase reconstruction. | Limited generalization to complex noise environments and multi-scale scenarios. | Well-suited for real-time biomedical imaging with a reduced parameter count; generalization to complex and multi-scale conditions requires enhancement. |
| Mimo-Net [21] | Applies a multi-branch network to extract global and local features at multiple scales, enabling phase reconstruction through cross-layer fusion. | Supports three scales within a single model; delivers 62% faster reconstruction with superior PSNR and SSIM compared to Y-Net. | Higher computational overhead for multi-scale training; slightly reduced phase reconstruction accuracy. | Effective for high-throughput tasks via multi-branch, multi-scale feature extraction; however, phase accuracy lags behind intensity reconstruction. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| References [22,23,24,25,26,27,28,29] | Signal processing based on prior models, including spatial filtering, frequency-domain filtering, and statistical models. | Strong physical interpretability and low dependency on training data. | Poor adaptability to complex or structured noise, sensitivity to parameters, and potential for structural distortion. | Traditional algorithms retain advantages in physical interpretability for simple and low-noise scenarios, but they are limited in real-time performance and effectiveness under complex scenarios. |
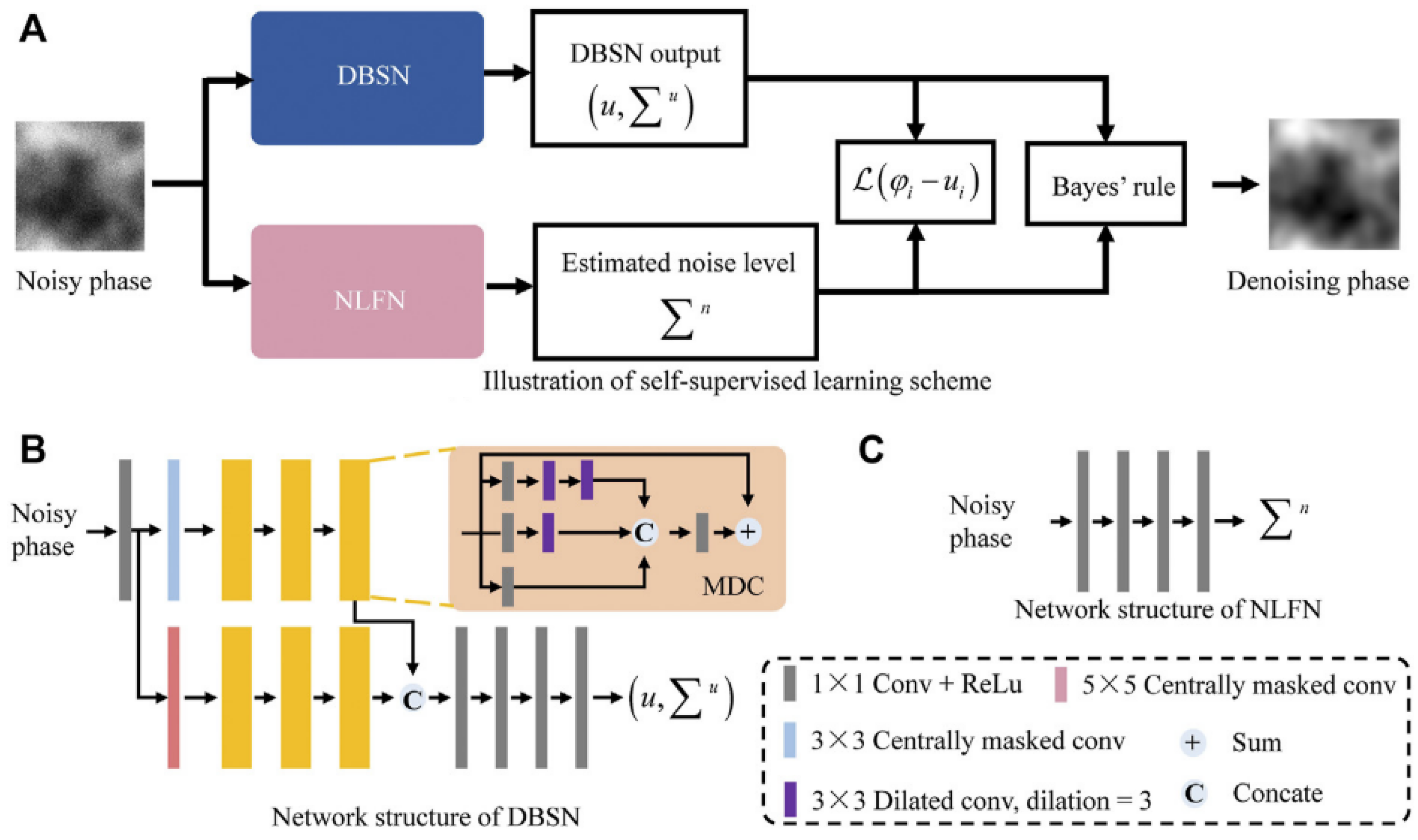
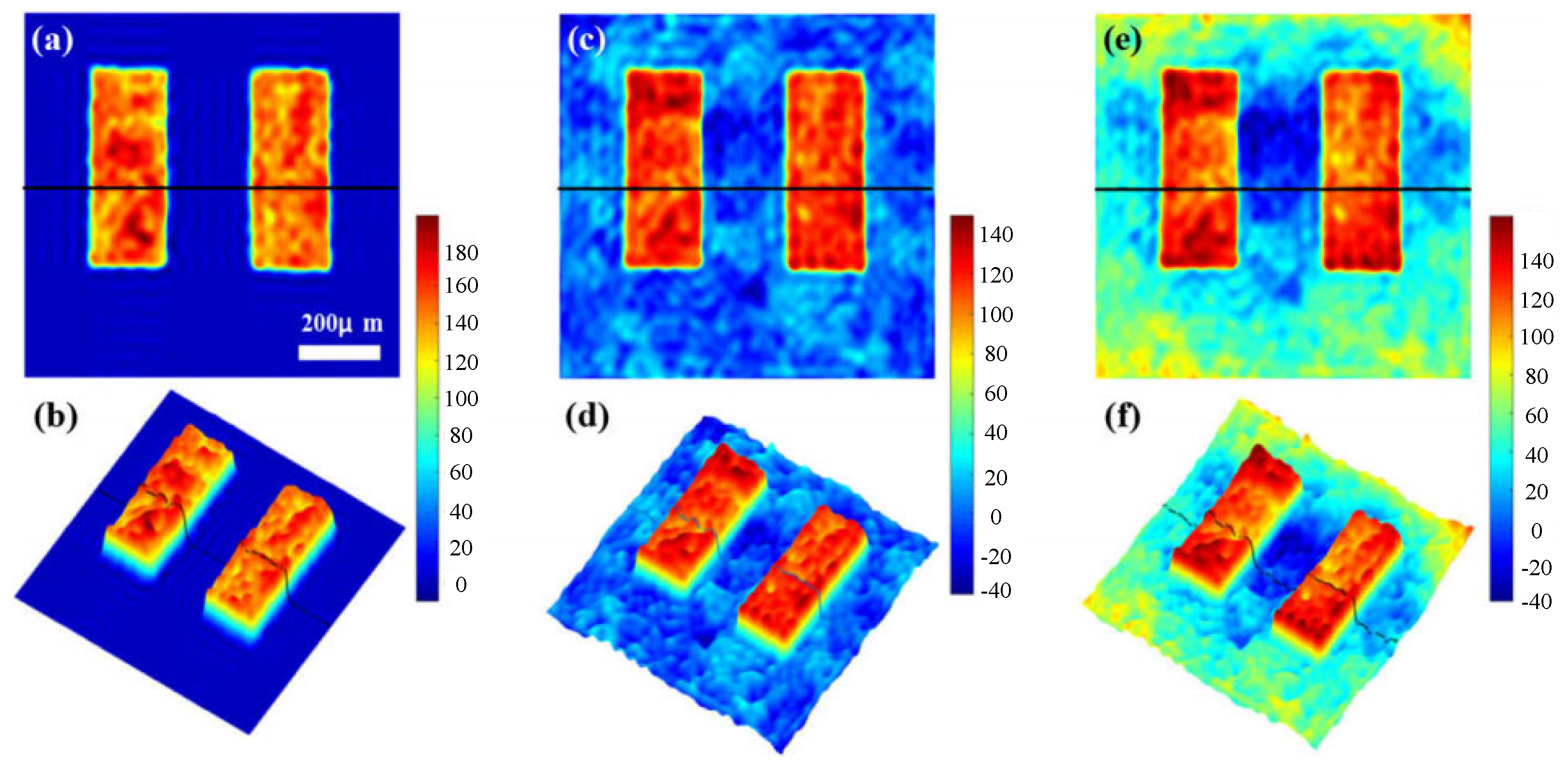
| DBSN and NLFN [30] | Joint training of a denoising network (DBSN) and a noise level estimation network (NLFN) using Bayesian rules and negative log-likelihood loss, eliminating the need for clean labels. | No requirement for labels and dynamic noise estimation capability of noise levels. | Model assumption limitations, high computational complexity. | Designed for biomedical scenarios where label acquisition is difficult; however, generalizability is limited when noise deviates from Gaussian distributions. |
| DHHPN [31] | Observes that holographic noise resembles Perlin noise, which is then used to simulate and generate training data. | Accurate noise simulation and low labeling cost. | Simulation bias and absence of frequency-domain feature representation. | Enhances denoising accuracy through physically inspired noise modeling, but its effectiveness depends on how closely simulated noise matches real noise and the absence of frequency-domain feature representation. |
| WPD-Net [32] | Residual dense attention blocks (RDABs) + dense feature fusion (DFF) with a dynamic hybrid loss function | Lightweight model with strong mixed noise suppression and excellent real-time performance | Performance degrades under extreme noise conditions (SNR < 0 dB) | Suitable for high-noise scenarios in biomedicine and materials science imaging |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| cGAN [33] | The generator (U-Net+DenseNet) maps holograms to clean phases, and the discriminator enforces the generated images to match optical physical characteristics by combining PSNR loss. | High-fidelity reconstruction and strong generalizability. | High data dependency and unstable training. | Enables high-fidelity reconstruction of phase images under strong speckle noise, but requires high-quality labels and is susceptible to generative adversarial network (GAN) mode collapse. |
| Fourier-Unet [34] | Combines CNN for local spatial feature extraction with a Fourier neural operator to capture global frequency information. | Multi-domain complementarity and physically informed design. | High computational cost and complex architecture. | Enhances denoising accuracy and subsequent phase unwrapping effects through joint spatial-frequency processing, but demands significant computational complexity and careful architectural parameters. |
| 4-fCycleGAN [35] | Integrates a 4-f optical system to simulate a speckle noise generator (F) and employs CycleGAN with cyclic consistency loss (Lcyc) to ensure phase reversibility before and after denoising. | Fully unsupervised; accommodates diverse noise patterns. | Limited by fixed simulation parameters; potential performance bottlenecks. | Designed for label-free industrial optical inspection with fixed simulation parameters and tasks, but its generalizability to complex real-world noise is lower than that of supervised methods. |
| Method | Application Scenario Dimension | Technical Principle Dimension | Learning Paradigm Dimension |
|---|---|---|---|
| DBSN and NLFN [30] | Biomedicine, materials science (Off-axis DHM). | Physical noise modeling with self-supervised learning structure. | Unsupervised learning (trained solely on noisy data). |
| DHHPN [31] | Precision measurement, biomedicine (in-line DHM). | Supervised learning with physical noise simulation based on the Perlin noise model. | Supervised learning (paired training with simulated datasets). |
| WPD-Net [32] | Biomedicine, materials science (in-line DHM). | Data-driven (RDAB + DFF) + attention mechanisms | Supervised learning (dynamic hybrid loss) |
| cGAN [33] | Industrial inspection, optical metrology (in-line DHM). | Generative adversarial networks (GANs) with optical simulation datasets. | Supervised learning with noise-clean image pairing. |
| Fourier-Unet [34] | Phase denoising in holographic interferometry, 3D topography measurement (in-line DHM). | Hybrid approach: CNN for spatial features combined with Fourier frequency-domain features. | Supervised learning (using both simulated and experimental data). |
| 4-fCycleGAN [35] | Industrial optical inspection, holographic metrology (in-line DHM). | Unsupervised learning combined with speckle noise simulation via 4-f optical system. | Unsupervised learning (trained on unpaired data). |
| Year | Method | MAE | PSNR | SSIM | SF | Suggestions for Improvement |
|---|---|---|---|---|---|---|
| 2025 | WPD-Net [32] | 0.0068 | 26.586 | 0.987 | / | Enhance WPD-Net’s performance under extreme noise conditions (SNR < 0 dB) by integrating temporal dynamics into the training process |
| 2022 | cGAN [33] | 0.0055 | 25.25 | 0.9974 | 1.3567 | Improve adaptability to dynamic scenes and enhance overall denoising performance. |
| 2023 | Fourier-Unet [34] | 0.0039 | 43.28 | 0.9999 | / | Strengthen denoising capabilities under complex backgrounds and improve phase unwrapping accuracy. |
| 2024 | 4-fCycleGAN [35] | 0.09549 | 16.1647 | / | 0.03614 | Improve generalization to non-Gaussian noise and enhance real-time processing efficiency. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| References [36,37,38,39] | The path tracking method utilizes a phase quality map to guide integration paths. The minimum norm method performs global optimization to minimize phase gradient errors. | High physical interpretability; low dependence on training data. | Sensitive to noise; low computational efficiency; fails in complex phase scenarios. | These traditional methods offer clarity in physical principles and require no training data; however, they are sensitive to noise and phase mutations and are best suited for simple scenarios with low noise and continuous-phase settings. |
| UnwrapGAN [40] | Generative adversarial learning (GAN) improves the authenticity of phase structures through discriminators. | Good real-time performance and strong generalization ability. | Requires high-quality paired data; unstable training. | Enables automatic focusing and phase unwrapping, at over twice the speed of traditional algorithms, but depends heavily on high-quality paired data and is vulnerable to mode collapse during training. |
| Res-Unet [41] | Incorporates residual blocks and attention mechanisms to enhance edge feature extraction and structural detail. | Strong noise resistance; robust in the presence of phase discontinuities. | High model complexity; large parameter count; significant computational demands. | Demonstrates strong robustness to complex noise and undersampling conditions. However, its practical deployment is constrained by high computing resources. |
| Year | Method | SSIM | Time (Seconds) | Suggestions for Improvement |
|---|---|---|---|---|
| 2021 | UnwrapGAN [40] | 0.9000 | 0.5021 | Enhance generalization by expanding the training dataset to cover more diverse cell types and complex phase structures; explore lightweight network designs to reduce computational latency in real-time applications. |
| 2024 | Res-Unet [41] | 0.9936 | 1.087 | Incorporate physics-based constraints into the loss function to improve handling of phase discontinuities under extreme noise scenarios; implement a multi-scale network architecture to enhance performance on high-resolution images without image stitching. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| DeepLabV3+ [42] | Utilizes the encoder-decoder architecture for semantic segmentation. Multi-scale features are extracted through atrous spatial pyramid pooling (ASPP), and high- and low-level features are fused through skip connections to predict wrap counts in phase unwrapping. | Enables multi-scale feature fusion, suitable for unwrapping complex phase structures. | Limited performance on small-target details; requires additional post-processing optimization. | Effectively addresses accuracy and efficiency issues in low-noise, regular-structure scenarios. However, performance on large-sized images requires downsampling, and training depends on high-quality paired datasets. |
| PhaseNet2.0 [43] | Utilizes a fully convolutional DenseNet architecture, framing phase unwrapping as a dense classification problem. A novel loss function combining gradient difference minimization and L1 loss is employed to mitigate class imbalance, directly and predict wrap counts. | Strong resistance to noise; supports high-dynamic range phase recovery; end-to-end training reduces manual intervention. | High reliance on simulated data; limited generalization to unseen noise types. | Effectively addresses the insufficient robustness against complex noise and high-dynamic-range phase conditions. However, it exhibits a large parameter volume and limited generalization to highly complex or geometric structures. |
| SFNet [45] | Builds on a lightweight variant of SegFormer using a hierarchical transformer encoder without positional encoding to capture global phase dependencies, combines an MLP decoder to fuse multi-scale features, and enhances phase unwrapping accuracy in complex noise and discontinuous scenarios via self-attention mechanisms. | Demonstrates strong global feature modeling capability with low parameter count; facilitates real-time inference. | Limited handling of fine local details; relying on the Transformer structure results in slightly higher computational complexity. | This approach addresses the limitations of traditional methods in global feature modeling and real-time performance. However, tile-based processing is needed for extremely high-resolution images, with edge detail accuracy left to be improved. |
| DenSFA-PU [46] | Densely connected encoder + SFA module (Bi-LSTM + BAM) | High robustness to strong noise; fast unwrapping speed | Requires optimization of initial conditions under extreme noise | Suitable for real-time holographic imaging and unwrapping |
| Year | Method | SSIM | RMSE | PSNR | Suggestions for Improvement |
|---|---|---|---|---|---|
| 2019 | DeepLabV3+ [42] | / | 1.2325 | / | Explore multi-scale training strategies to improve performance on high-resolution images, and integrate physics-informed constraints into the network to enhance noise suppression in extreme scenarios. |
| 2020 | PhaseNet2.0 [43] | 0.9200 | 0.035 | 40.5 | Develop an adaptive loss function capable of handling diverse noise types, and explore lightweight network architectures to improve real-time processing efficiency. |
| 2024 | SFNet [45] | 0.9963 | 0.5268 | 101.22 | Include dynamic attention mechanisms to better capture local phase discontinuities, and expand the training dataset to include more complex real-world noise patterns. |
| 2025 | DenSFA-PU [46] | 0.999 | / | / | Improve stability under extreme noise conditions (e.g., SNR < 0 dB) and enhance the network’s ability to capture long-range dependencies. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| VDE-Net [47] | Utilizes a two-stage architecture that emphasizes phase jump regions through a weighted jump-edge attention mechanism; applies dilated convolutions to expand the receptive field and achieves robust phase unwrapping to noise and undersampling. | Enhances edge feature enhancement; robust to noise and undersampling; incorporates physical priors in the preprocessing stage to improve interpretability. | Increased computational complexity due to attention modules; reduced stability under extreme noise environments. | Effectively addresses the shortcomings of traditional methods in edge detail processing and noise robustness. |
| U2-Net [49] | Constructs an encoder–decoder architecture using nested U-shaped residual blocks, enabling multi-scale feature fusion and deep supervision to improve phase unwrapping accuracy and structural stability in complex noise environments. | Provides strong multi-resolution feature extraction capability, superior noise robustness over traditional U-Net, and supports wide dynamic range. | High parameter count and extended training time; performance degrades in extremely low signal-to-noise ratio. | Strikes a balance between parameter scale and noise resilience than traditional deep learning models. |
| PUDCN [50] | Incorporates deformable convolutions to dynamically capture irregular phase edges, combining a pyramid feature dynamic selection module and fusion feature dynamic selection module for multi-scale feature extraction and detail-optimized phase unwrapping via a coarse-to-fine strategy. | Deformable convolutions adapt to phase jumps of arbitrary shapes; lightweight design with only 1.16 M parameters, suitable for deployment on edge devices. | The two-stage training process is complex; inference speed decreases significantly for extremely high-resolution images. | Effectively addresses the limitations of traditional CNNs in handling irregular edges. |
| Year | Method | SSIM | RMSE | PSNR | Suggestions for Improvement |
|---|---|---|---|---|---|
| 2022 | VDE-Net [47] | 0.9984 | / | / | Dynamically adjust the weighted factors in the jump-edge attention mechanism to improve the adaptability to various noise distributions and phase discontinuities. |
| 2023 | U2-Net [49] | 0.9989 | / | 63.6289 | Incorporate lightweight attention modules into U2-Net to reduce computational overhead while preserving its multi-scale feature extraction capability for real-time applications. |
| 2024 | PUDCN [50] | 0.9986 | 0.2625 | / | Employ self-adaptive deformable convolution kernels to effectively extract irregular phase edges and enhance generalization under extreme noise conditions. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| DLCDIFPU [51] | Utilizes a deep learning-based region segmentation model to divide wrapped phase maps into irregular regions along fringe edges; integrates CDIF with a heap-sort path-tracking strategy to unwrap each region independently, merging the results via phase consistency and achieving noise-resistant, and localized phase unwrapping. | Integrates data-driven learning with physical models; achieves an RMSE of only 0.24π under strong noise. Regional segmentation effectively suppresses cross-edge error propagation. | Depends on a dual-network architecture and necessitates high-precision annotated data, increasing implementation complexity. | Enhances phase unwrapping accuracy and efficiency by leveraging regional processing and physical prior, such as fringe edge detection, to guide localized unwrapping. |
| C-HRNet [52] | Extends HRNet by adding a fifth stage for enhanced multi-resolution feature fusion and incorporates the OCR module to aggregate pixel-object relationships. Treats phase unwrapping as a semantic segmentation task, predicting fringe order maps directly from single-frame wrapped phases, thereby improving unwrapping accuracy in complex noise and isolated regions. | Supports multi-scale feature fusion and contextual mechanisms; enables attention, and end-to-end learning for improved phase unwrapping accuracy. | Relies heavily on large-scale, data; lacks clear physical interpretability; incurs high computational cost. | Enhances the robustness of phase unwrapping in complex scenarios through multi-scale feature extraction and contextual semantic modeling. |
| Year | Method | RMSE | Suggestions for Improvement |
|---|---|---|---|
| 2023 | DLCDIFPU [51] | / | Incorporate adaptive noise suppression mechanisms into the central difference information filter to enhance the robustness of complex fringe structures and under severe noise variations. |
| 2024 | C-HRNet [52] | 1.76 | Establish a dynamic context aggregation mechanism in the object contextual representation module to effectively extract diverse phase discontinuities in isolated regions. |
| Method | Application Domain | Technical Principle Dimension | Learning Paradigm |
|---|---|---|---|
| UnwrapGAN [40] | Biomedicine (off-axis DHM). | Pix2Pix-based GAN with an encoder-decoder structure; incorporates adversarial and L1 loss functions. | Supervised learning (paired data). |
| Res-Unet [41] | Digital holographic interferometry; industrial inspection (off-axis DHM). | Residual U-Net architecture enhanced with weighted skip-edge attention mechanisms. | Supervised learning (training on simulated data). |
| DeepLabV3+ [42] | Optical metrology under complex noise conditions (off-axis DHM). | Semantic segmentation framework using dilated convolutions and spatial pyramid pooling. | Supervised learning (augmented noisy data). |
| PhaseNet2.0 [43] | Optical metrology; SAR interferometry (off-axis DHM). | Fully convolutional DenseNet architecture; utilizes composite loss functions (cross-entropy, L1, and residual loss). | Supervised learning (multimodal noisy data). |
| SFNet [45] | Industrial optical inspection; 3D shape reconstruction (off-axis DHM). | Transformer-based encoder with MLP decoder and self-attention mechanism. | Supervised learning (combined simulated and real data). |
| DenSFA-PU [46] | Digital holographic interferometry (off-axis DHM). | Densely connected network + spatial feature aggregator (SFA) | Supervised learning (composite loss function) |
| VDE-Net [47] | Biomedical imaging (off-axis DHM). | Two-stage deep architecture incorporating dilated convolutions and weighted edge attention mechanism. | Supervised learning (attention-guided learning strategy). |
| U2-Net [49] | Dynamic flame imaging; complex surface structure measurement (in-line DHM). | Nested U-shaped residual blocks with deep supervision loss for multi-scale feature extraction. | Supervised learning (multi-scale fusion). |
| PUDCN [50] | Fiber optic interferometry, industrial defect detection (off-axis DHM). | Deformable convolution layers with a pyramid feature selection module for dynamic representation. | Supervised learning (coarse-to-fine two-stage training). |
| DLCDIFPU [51] | Industrial inspection (in-line DHM). | Deep region segmentation combined with central difference information filtering (CDIF) and path tracking. | Supervised learning (simulated phase maps with real phase labels). |
| C-HRNet [52] | Precision metrology, biomedical imaging, industrial inspection (off-axis DHM). | High-resolution network (HRNet) with object-contextual representation (OCR) module for semantic segmentation. | Supervised learning (mixed simulated dataset and real data using cross-entropy loss). |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| CNN+ZPF [53] | Employs a CNN to automatically identify background regions in DHM, fitting phase aberrations via Zernike polynomial expression. | High-accuracy background detection with automated compensation. | Limited generalizability and dependency on annotated datasets. | Enables long-term phase distortion correction without manual intervention by integrating automatic segmentation with model-based phase fitting. |
| PACUnet3+ [54] | Constructs an encoder-decoder architecture based on Unet3+ to learn the mapping between object holograms and sample-free references, enabling data-driven background subtraction for phase correction. | Eliminates reliance on physical modeling while maintaining high accuracy. | Computationally intensive and requires large-scale training data. | Achieves accurate PAC using data-driven hologram reconstruction, bypassing explicit physical model assumptions. |
| SSCNet [56] | Combines a Zernike polynomial-constrained phase model with self-supervised learning and sparse optimization to estimate phase aberration coefficients using a single hologram input. | Capable of compensating for dynamic phase distortions without reference data. | Sensitive to initial conditions and exhibits slow convergence. | Enables adaptive correction of phase errors in dynamically varying systems through self-supervised optimization aligned with physical constraints. |
| Method | Core Mechanism | Advantages | Limitations | Conclusion |
|---|---|---|---|---|
| CNN+ZPF [57] | Utilizes a CNN to segment background regions in the phase image, followed by Zernike polynomial fitting to decouple sample-induced phase from system aberrations, enabling fully automated compensation. | Enables high-throughput processing with simple operation. | Limited robustness under complex background textures or high noise. | Facilitates rapid and automated background identification, making it particularly effective for high-throughput applications, such as cell morphology analysis. |
| Two-stage GAN [58] | Implements a two-step generative adversarial network: the first network reconstructs structural edges of occluded regions, while the second completes the missing content, thereby generating sample-independent reference holograms for phase correction. | Strong capability for large-area restoration with realistic details. | Training is unstable; performance degrades when occlusion exceeds 40%. | Applies unsupervised adversarial learning to restore phase data in highly occluded conditions, outperforming traditional methods in challenging scenarios. |
| Method | Application Scenario Dimension | Technical Principle Dimension | Learning Paradigm Dimension |
|---|---|---|---|
| CNN+ZPF [53] | Biomedical applications and real-time phase analysis (off-axis DHM). | Data-driven + physical model fitting. | Supervised learning. |
| PACUnet3+ [54] | High-precision reconstruction of microstructures (off-axis DHM). | Data-driven (end-to-end hologram generation). | Supervised learning. |
| SSCNet [56] | Adaptive phase correction in dynamic environments (off-axis DHM). | Physical model + self-supervised sparse constraints. | Self-supervised learning. |
| CNN+ZPF [57] | Restoration in complex and large-field-of-view samples. (off-axis DHM). | Data-driven (GAN-generated restoration) + edge priors. | Unsupervised learning. |
| Two-stage GAN [58] | Single-frame unwrapping in noise-intensive conditions (off-axis DHM). | Multi-scale feature fusion + contextual semantic enhancement. | Supervised learning. |
| Year | Method | SSIM | MAE | RMSE | PV | Suggestions for Improvement |
|---|---|---|---|---|---|---|
| 2021 | CNN+ZPF [53] | 0.943 | 0.021 | / | / | Enhance generalization capabilities to accommodate complex cell morphologies or dynamic noise environments. |
| 2023 | PACUnet3+ [54] | 0.93 | / | 0.0963 | 0.6308 | Optimize the network architectures to minimize computational complexity and enhance real-time performance. |
| 2023 | SSCNet [56] | 0.9924 | 0.012 | 0.441 | 5.490 | Investigate more robust sparsity-constrained optimization strategies to accelerate convergence and improve stability. |
| 2017 | CNN+ZPF [57] | 0.927 | 0.028 | / | / | Enhance the precision of background segmentation in scenarios for complex backgrounds or low-contrast sample features. |
| 2021 | Two-stage GAN [58] | 0.9885 | 0.0029 | / | / | Optimize GAN training strategies to ensure repair consistency and detail fidelity for high-occlusion-rate samples. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Liu, L.; Bu, Y. Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy. Photonics 2025, 12, 810. https://doi.org/10.3390/photonics12080810
Jiang W, Liu L, Bu Y. Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy. Photonics. 2025; 12(8):810. https://doi.org/10.3390/photonics12080810
Chicago/Turabian StyleJiang, Wenbo, Lirui Liu, and Yun Bu. 2025. "Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy" Photonics 12, no. 8: 810. https://doi.org/10.3390/photonics12080810
APA StyleJiang, W., Liu, L., & Bu, Y. (2025). Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy. Photonics, 12(8), 810. https://doi.org/10.3390/photonics12080810





