Enhancement of Self-Collimation via Nonlinear Symmetry Breaking in Hexagonal Photonic Crystals

Abstract

This study proposes the use of a low-symmetry hexagonal photonic crystal (LSHPC) incorporating Kerr-type nonlinearity to enhance self-collimation. The equifrequency contours (EFCs) of a C₂-symmetric LSHPC composed of nonlinear LiNbO₃ rods are analyzed as a function of the nonlinear refractive index. The self-collimation characteristics, transmission spectrum, group velocity dispersion (GVD), and third-order dispersion (TOD) are investigated using the Plane Wave Expansion (PWE) and Finite Difference Time Domain (FDTD) methods. The results demonstrate that increasing the nonlinear index leads to a significant flattening of the EFCs, which enhances self-collimation performance. Furthermore, symmetry-lowering perturbations improve beam confinement and enable all-angle self-collimation. These findings highlight the potential of Kerr-type nonlinear photonic crystals for integrated photonic circuits requiring precise control over light propagation.

1. Introduction

Photonic crystals (PCs) are periodic dielectric structures that exhibit photonic band gaps (PBGs), which prohibit the propagation of electromagnetic waves within specific frequency ranges. The formation and properties of these band gaps are predominantly determined by key structural and material parameters, including refractive index contrast, lattice symmetry, lattice constant, and filling fraction. These factors govern not only the existence of the PBG but also its spectral width and position. Additional influences such as dielectric geometry, mode polarization (TE/TM), and material dispersion further refine the photonic band structure. Structural symmetry breaking introduces anisotropy in the photonic band diagram, enabling phenomena such as directional propagation and modal asymmetry. Meanwhile, Kerr-type optical nonlinearities provide dynamic reconfigurability by enabling intensity-dependent modulation of the refractive index, thus offering real-time tunability of photonic behaviors. Computational modeling in both the frequency domain (e.g., Plane-Wave Expansion, PWE) and time domain (e.g., Finite-Difference Time-Domain, FDTD) offers a robust framework for investigating these effects. Of particular interest is the coupling between structural parameters such as unit cell geometry, lattice configuration, index profile, and photonic performance metrics, including group velocity, group index, bandwidth, and transmission efficiency. These interdependencies have become central to the design of functional photonic devices, including optical filters, switches, modulators, sensors, beam splitters, and photonic crystal fibers. Such devices facilitate precise manipulation of light propagation characteristics, including phase, directionality, and dispersion properties [1,2,3,4,5].

The propagation of electromagnetic waves in photonic crystal structures is directly related to the symmetry of the structure. The isotropic propagation and wide bandgaps that occur in crystal structures with high symmetry provide some advantages in terms of application. However, phenomena such as anisotropic propagation, slow light effect, mode decomposition, and spectral narrowing occur when this symmetry is distorted or deliberately reduced. These phenomena allow a more sensitive and controlled optical response to be obtained. In this context, optimization problems such as maximizing the group index-bandwidth and the slow light-high transmission trade-off are frequently addressed in the literature [6,7,8,9]. The ability of light beams at certain frequencies to be guided through a photonic crystal without dispersion is known as self-collimation (SC). In recent years, the SC effect in photonic crystals has enabled the development of compact and low-loss photonic devices or functions by allowing diffraction-free propagation of light without needing a waveguide [1,10,11]. The SC is observed in a region where the equifrequency contours (EFCs) derived from the photonic band structure flatten at a certain frequency. 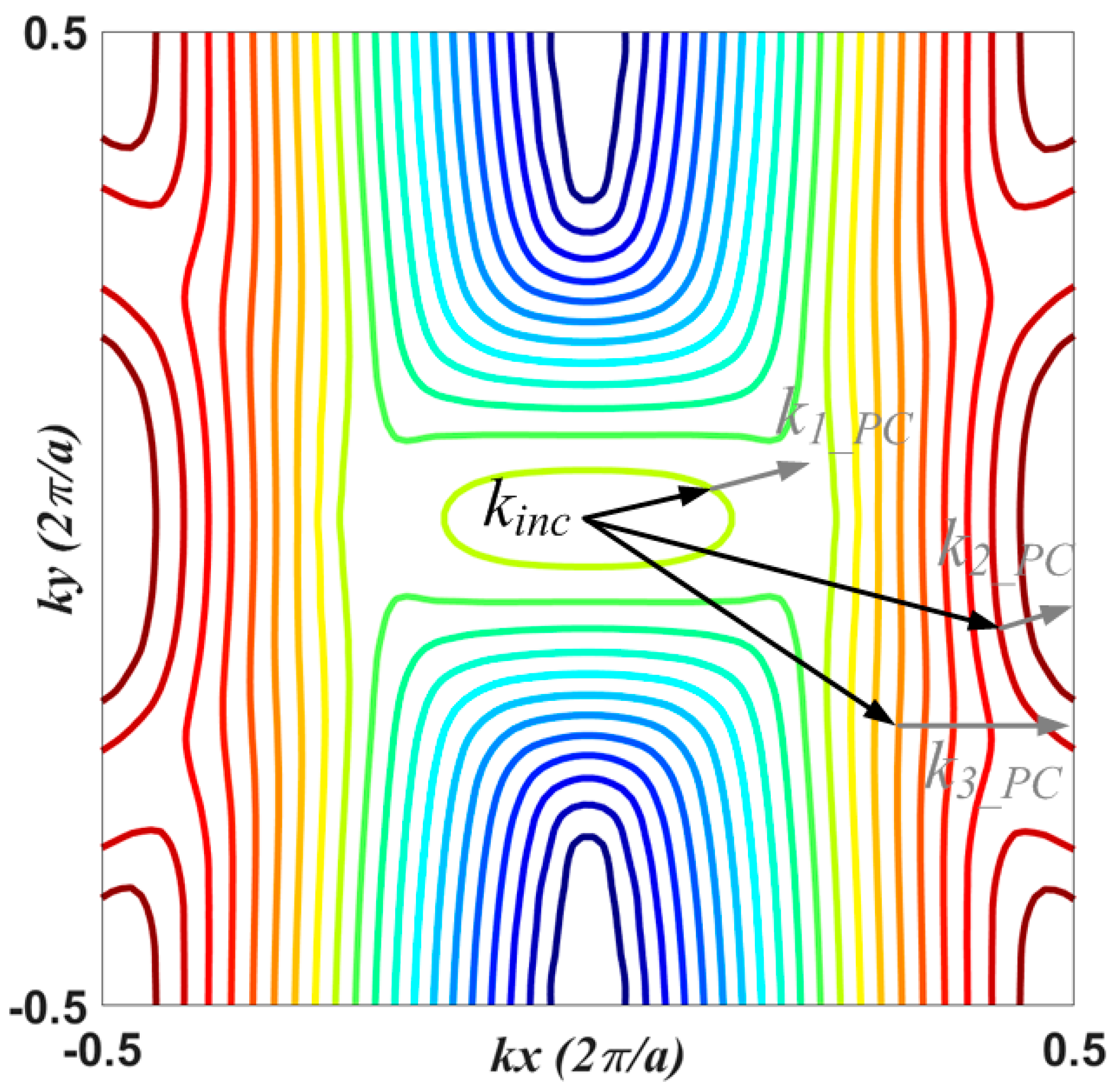The propagation direction is in the direction of the normal of the EFC line as depicted in Figure 1. In these flat parts, the group velocity exhibits a constant orientation, which causes the light to propagate without dispersion [1,10]. Otherwise, the wave will disperse in regions where the EFC curve is not flat (see Figure 1). This allows the creation of steerable optical components with higher manufacturing tolerances compared to conventional imperfect waveguides [11,12,13]. Additionally, self-collimation can be improved through symmetry reduction and the use of materials with a high refractive index [10,14,15]. While conventional photonic crystals are typically designed with high-symmetry unit cells, structures with low rotational symmetry break this symmetry. Symmetrical reduction can be achieved by perturbation in the unit cell. Geometric variations make low-symmetry structures more susceptible to light manipulation, allowing greater control and flexibility over light [1,10,14,16,17,18].

PCs, which show a refractive index change depending on the intensity of the incident light, provide new functionalities by controlling and directing the light propagation inside the crystal as light-matter interactions become stronger [9,10,11,12,13,14,15,16,17,18,19]. Second-order (electro-optical) or third-order (Kerr-type) nonlinearity is used in various applications, such as frequency conversion, phase modulation, bistability, and light-controlled switching [9,19,20,21]. III–V semiconductors like AlGaAs and GaAs possess extremely high nonlinear coefficients, making them excellent candidates for efficient nonlinear frequency conversion. However, several factors motivated our use of LiNbO₃ rods in the current study [9]. The refractive index of LiNbO₃ (n~2.2) is significantly lower than that of GaAs or AlGaAs (n > 3.3). As a result, the index contrast between the rods and air is reduced, leading to narrower photonic bandgaps and smoother EFCs. This condition is advantageous for achieving self-collimation outside the bandgap region, where flat EFCs are more easily engineered in lower-contrast systems. The nonlinear response of LiNbO₃ extends well into the visible and near-infrared ranges, making it compatible with high-frequency applications. LiNbO₃ offers additional physical mechanisms (electro-optic, acousto-optic, and photorefractive effects) and is widely used in commercial photonic systems. Its integration technology is mature, and it has lower optical losses and a broader transparency window (visible to mid-IR).

Since nonlinear photonic crystals allow the propagation characteristics to be changed depending on the strength of the light, this leads to fundamental optical information processes such as the control of light by light [19,22,23,24,25,26,27]. When combined with Kerr-type nonlinearity, the SC is dynamically tunable and gives precise control over the propagation path of the beam by adjusting the light intensity. This tunability is particularly useful for designing reconfigurable photonic devices, where light can be guided or redirected without the need for physical changes to the crystal structure [28,29]. EFCs provide information on the allowed propagation modes and associated group velocities in linear PCs. However, the EFCs become intensity dependent in photonic crystals with Kerr-type nonlinearity. In such systems, the geometry of the equifrequency curve and, consequently, the light propagation vary depending on the light intensity, providing SC behaviors that are controlled by nonlinearity [28,30]. For instance, an increase in the input light intensity can disrupt SC. As the light intensity increases, the nonlinear refractive index variation changes the shape of EFCs, and these interactions, working together with the mutual feedback of photonic crystal cavity resonance, optical density distribution, and material refractive index, can produce unique optical responses, leading to the emergence of complex light behaviors such as beam self-trapping in propagation modes or self-locking of beam width and spatial solitons [29,30,31,32]. Moreover, small spectral variations at the frequency-sensitive super-collimation (FSSC) point can dramatically impact wave propagation, resulting in effects such as bistability and multistability [29].

While conventional strategies such as adjusting the lattice geometry, modifying material composition, or engineering refractive index contrast are effective for tailoring the EFC topology and enhancing SC effects, these approaches inherently result in static dispersion properties that are fixed upon fabrication. Once a specific structural configuration is selected, any subsequent tuning of the beam dynamics typically requires external modulation mechanisms, which introduce additional complexity and latency. In contrast, Kerr nonlinearity provides a reconfigurable and all-optical modulation pathway in which the local refractive index dynamically responds to the optical intensity. This nonlinear response enables SC phenomena wherein the signal beam modifies its own propagation conditions, leading to a continuously evolving index.

As a result, the EFCs, and consequently, the SC axis can be tuned dynamically in situ. Such self-adaptive SC behavior can be attractive for ultrafast and compact integrated photonic systems because it enables directional control, beam steering, and switching functions without the need for physical reconfiguration. Moreover, when Kerr nonlinearity is employed in a low-symmetry photonic crystal, the intensity-dependent index perturbation interacts with the intrinsic anisotropy of the structure. This interplay amplifies directional asymmetries in the dispersion surfaces, allowing for power-sensitive beam steering, splitting, or routing. The resulting propagation regimes become strongly dependent on the input field amplitude, opening avenues for implementing tunable and reconfigurable photonic functionalities within a single physical platform.

The common point of all these studies is the numerical presentation of the determining effects of topology, symmetry, and coupling properties on photonic band structure, group velocity, and light propagation in photonic crystal structures. In this paper, the use of a hexagonal photonic crystal with low symmetry and nonlinearity is proposed to enhance self-collimation. EFCs of a C₂-type low-symmetry hexagonal photonic crystal (LSHPC) structure consisting of Kerr-type nonlinear LiNbO₃ materials are extracted according to the nonlinear index variation, and the GVD and TOD variations, as well as the self-collimation behavior and transmission spectrum, are obtained. Simulation results were obtained with open-source programs MPB and MEEP using Plane-Wave Expansion (PWE) and Finite-Difference Time-Domain (FDTD) methods [33].

As a result of my literature search, to the best of my knowledge, there is no study on the effect of a low-symmetry hexagonal structure in combination with Kerr-type nonlinearity on self-collimation. In reference [30], it is investigated that nonlinearity in a one-dimensional curved waveguide structure destroys the SC. Unlike this study, the effect of nonlinearity contributed to improving the SC rather than destroying it in this paper. In reference [28], a highly symmetric square lattice PC structure and the EFC, incorporating the first band, were investigated in the low-frequency region. In this study, the hexagonal structure is used with low symmetry. Moreover, the SC is enhanced by perturbation of the low symmetry in the hexagonal PC once more. Also, all-angle self-collimation was obtained. Low-index material was preferred, and the upper bands were studied.

In this study, it is shown that Kerr-type nonlinearities arising in low-symmetry hexagonal photonic crystals can enhance the self-collimation effect and change the operational bandwidth by improving the confinement of light inside the photonic crystal. This study reveals that Kerr-type nonlinear photonic crystals are suitable for photonic circuit applications where precise control of light propagation is required, offering potential applications in advanced applications such as TE/TM polarization division multiplexing or frequency-sensitive self-collimation.

2. Mathematical Framework

Due to the inherent complexity of analytical approaches, numerical techniques are predominantly adopted for the analysis and design of photonic structures. A variety of computational methods are available for examining the dispersion relations and transmission characteristics of photonic crystals, including the transfer matrix method (TMM) [34], finite-difference time-domain (FDTD) method [35], plane wave expansion (PWE) method [36], and finite element method (FEM) [37], among others. These approaches are typically categorized into frequency-domain and time-domain methods. Frequency-domain techniques are primarily employed to determine photonic band structures, whereas time-domain methods are more appropriate for investigating wave propagation, resonance behavior, decay times, and transmission phenomena.

Among the available methods, PWE and FDTD are particularly prominent due to their robustness and suitability for the analysis of photonic crystal-based optical devices. Each technique offers distinct advantages and limitations, but PWE and FDTD have become widely favored due to their reliability and versatility. The PWE method addresses the eigenvalue problem for photonic crystals by representing both the electromagnetic fields and the dielectric function through a Fourier series. This approach is ideally suited for the theoretical analysis of periodic structures, relying on the principle that the eigenmodes of a periodic medium can be expressed as a linear combination of plane waves. It is especially effective for generating photonic band diagrams and characterizing mode profiles. In scenarios where the crystal symmetry is perturbed, such as through point or line defects, the supercell technique must be employed to preserve periodicity in the computational model [33].

In this study, the nonlinear photonic crystal is treated using a quasi-static approximation to incorporate Kerr-type optical nonlinearity into the eigenmode-based PWE. Although the PWE method is formally applicable only to linear, periodic systems with intensity-independent permittivity distributions, I extend its use by introducing a static, intensity-dependent modification of the refractive index. Specifically, the Kerr nonlinearity is modeled as a fixed perturbation in the dielectric constant, corresponding to a given optical intensity. This allows us to approximate the nonlinear photonic crystal as an effective linear structure with a modified permittivity profile. This approach, though approximate, enables a first-order evaluation of how nonlinearity perturbs the photonic band structure and modifies EFC topologies. I also emphasize that this method neglects dynamic nonlinear processes, such as self-phase modulation or four-wave mixing, assumes an instantaneous Kerr response without temporal delay, and considers the nonlinear index shift to be spatially uniform within high-field regions. These assumptions constrain the validity of the results to quasi-static, steady-state regimes. Nevertheless, in my case, where the focus is on self-collimation behavior under elevated intensity levels and where the Kerr response time is ultrafast compared to the optical period, the approximation remains physically meaningful. The EFCs computed under this model, therefore, represent the modified dispersion surfaces of the perturbed system and offer valuable insight into the impact of nonlinearity on self-collimation conditions.

Despite its precision in evaluating dispersion relations and identifying photonic band gaps, the PWE method is inherently limited to the study of propagating modes and does not directly yield information about transmission spectra, spatial field distributions, or reflections. To overcome these limitations, time-domain approaches like FDTD are commonly utilized. The FDTD method directly solves Maxwell’s equations in the time domain, enabling the analysis of dynamic phenomena, including transmission and reflection spectra, field evolution, and localized resonances. Simulations typically incorporate absorbing boundary conditions such as Perfectly Matched Layers (PMLs) to eliminate spurious reflections. Consequently, a common modeling strategy involves using PWE to extract band structure data, while FDTD simulations are applied to investigate transmission properties and field dynamics [38].

To ensure a consistent basis for comparison between the two computational approaches utilized in this study, namely, the PWE and the FDTD simulations, a unified quasi-static treatment of Kerr nonlinearity is employed across both frameworks. In the PWE calculations, the Kerr-induced modification is incorporated as a spatially confined, static shift in the dielectric permittivity profile, representing an effective nonlinear index change. Band structures and equifrequency contours (EFCs) are computed for this statically altered medium, thereby capturing the modified dispersion under fixed nonlinear conditions. In the FDTD simulations, a comparable static refractive index perturbation is introduced directly into the simulation grid. This index profile mimics the spatial distribution of field localization expected at the operational frequency, yet remains invariant in time to maintain equivalence with the quasi-static assumption used in PWE. This modeling strategy deliberately excludes dynamic nonlinear phenomena such as self-phase modulation (SPM), cross-phase modulation (XPM), four-wave mixing (FWM), and third-harmonic generation (THG), all of which would necessitate a time-resolved nonlinear formalism. However, the primary objective of the present study is to elucidate how Kerr-induced index changes influence steady-state beam propagation characteristics, particularly with regard to modifications in SC behavior, rather than to investigate ultrafast or transient nonlinear interactions. While this approximation inherently limits the scope to static or slowly varying nonlinear regimes, it remains a widely adopted and validated approach for early-stage studies of nonlinear photonic crystal systems. To confirm the internal consistency of this model, the EFC deformations obtained via PWE were compared with the steady-state field distributions produced by FDTD under identical nonlinear index shifts. The observed self-collimation features show qualitative agreement between both methods, thereby validating the quasi-static nonlinear treatment as a reliable predictor within the parameter space considered. Although higher-order nonlinear effects such as THG fall outside the scope of this paper, an auxiliary analysis of EFCs at the third harmonic frequency revealed no SC-related features in that regime.

In the present study, the open-source software MPB v1.11, implementing the plane-wave expansion (PWE) algorithm, is employed to compute the dispersion properties of the investigated structures. This frequency-domain analysis is complemented by time-domain simulations performed using the freely available MEEP v1.17 package, which is based on the finite-difference time-domain (FDTD) method. This combined approach enables a comprehensive investigation of self-collimation phenomena through complementary spectral and temporal perspectives.

2.1. Self-Collimation in Photonic Crystals

Self-collimation in photonic crystals refers to the ability of the crystal to guide light beams without divergence, typically arising from specific conditions in the photonic band structure. The key to understanding self-collimation lies in analyzing the EFCs in the reciprocal lattice, where ω(k) is the frequency as a function of the wave vector k. k is the wave vector in the photonic crystal. For self-collimation to occur, the EFCs must be flat in certain directions, as shown in Figure 1 [39]. In such cases, the group velocity ${\mathit{v}}_g$ which is given by the following equation:

$$v_g={\nabla }_{\mathit{k}}\omega \left(\mathit{k}\right)$$

(1)

remains constant across the EFC, leading to non-divergent beam propagation. The photonic band structure can be described by solving Maxwell’s equations in a periodic dielectric medium:

$$\nabla \times \left({\displaystyle \frac{1}{ϵ(\mathit{r})}}\nabla \times \mathbf{H}(\mathit{r})\right)={\left({\displaystyle \frac{\omega }{c}}\right)}^2\mathbf{H}(\mathit{r})$$

(2)

where ϵ(r) is the spatially varying dielectric function and H(r) is the magnetic field. For a specific direction, say along the x-axis, the condition for self-collimation is that the curvature of the EFC is close to zero:

$${\displaystyle \frac{{\partial }^2\omega }{\partial k_x^2}}\approx 0$$

(3)

If this condition is met over a range of frequencies, light beams can propagate through the photonic crystal without spreading.

2.2. Low-Symmetry in Photonic Crystals

Hexagonal photonic crystals are characterized by C_6v symmetry, where the subscript “6” indicates that the structure remains geometrically invariant under a rotation of 2π/6 radians (i.e., 60°) about the central axis of a cavity. Similarly, square lattice photonic crystals possess C_4v symmetry, implying invariance under 2π/4 (i.e., 90°) rotations [40]. This rotational symmetry ensures that the structural geometry remains unchanged under discrete angular transformations.

Symmetry reduction can be systematically induced by incorporating perturbations in the horizontal plane, such as directional deformations or controlled defects. These perturbations disrupt the pristine symmetry of the lattice, leading to anisotropic, or directionally biased, photonic responses.

Photonic crystals with high rotational symmetry exhibit highly ordered and isotropic geometries, which simplify their theoretical treatment and fabrication. However, such symmetry can restrict the degree of freedom in tailoring optical functionalities. In contrast, lowering the symmetry of the unit cell, resulting in what are known as low-symmetry photonic crystals (LSPCs), enables more extensive geometrical tunability. This enhanced tunability enables refined control over light–matter interactions by allowing for the selective manipulation of photonic modes.

Achieving this flexibility typically involves the strategic addition of structural elements or the deliberate reconfiguration of existing features within the unit cell. Breaking the original high symmetry unlocks new design possibilities and offers a versatile platform for engineering the optical response of photonic crystals in a manner tailored to specific functional requirements or device applications.

2.3. Kerr-Type Nonlinearity

In a medium exhibiting Kerr-type nonlinearity, the evolution of the optical field E(z,t) can be described by the following equation [41]:

$${\nabla }^2\overrightarrow{E}-{\displaystyle \frac{1}{c_0^2}}{\displaystyle \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}}={\mu }_0{\displaystyle \frac{{\partial }^2{\overrightarrow{P}}_{NL}}{\partial t^2}}$$

(4)

where polarization must be defined as the form of convolution integral as follows:

$${\overrightarrow{P}}_{Kerr}\left(t\right)={\epsilon }_0{\chi }^{\left(3\right)}{\overrightarrow{E}(t){\int }_{-\infty }^{\infty }\delta (t-t^{\prime })E}^2(t\prime )dt\prime$$

(5)

Kerr-type nonlinearity describes the phenomenon where the refractive index of a material varies with the intensity (I) of the light passing through it. This relationship is given by the following equation:

$$n\left(I\right)=n_0+n_{2}I$$

(6)

where I is the optical intensity, $n_0$ denotes the linear refractive index, and $n_2$ represents as

$$n_2={\displaystyle \frac{3{\chi }^{\left(3\right)}}{4n_0^2{c\epsilon }_0}}$$

(7)

related to the Kerr (third-order nonlinear susceptibility) coefficient. Thus, the variation in the effective refractive index induces modifications in the photonic band structure, thereby influencing light propagation.

In practical implementations of Kerr-type optical nonlinearity, two primary configurations are typically employed: one based on pump–probe interactions, and the other relying on self-induced nonlinear effects. In this study, the latter approach is adopted, wherein the signal beam itself induces the nonlinear index modulation during its propagation. This self-modulation mechanism eliminates the need for an external pump and enables passive, self-regulating control over beam dynamics. Such an approach is particularly advantageous for integrated photonic applications where system compactness, low latency, and energy efficiency are critical, including optical switching, logic gates, and reconfigurable photonic circuits.

In the self-induced regime, the refractive index of the medium dynamically varies as a function of the local intensity of the propagating beam, thereby inducing a self-adaptive refractive index. This mechanism facilitates functionalities such as self-steering and self-modulated SC within photonic crystal architectures, without requiring any externally applied control fields. However, several practical considerations govern the viability of this approach. To achieve a measurable index change, the medium must exhibit a sufficiently large third-order nonlinear coefficient n₂ ~ 10⁻¹⁸ − 10⁻¹⁷ m²/W. At the same time, the operating optical intensity must be carefully managed to remain below the material damage threshold, typically around ~10 GW/cm², to prevent deleterious effects such as multiphoton absorption, thermal degradation, or irreversible structural modification. A notable advantage of the self-induced configuration is its intrinsic spatial selectivity; unlike externally pumped schemes that necessitate strict phase-matching and mode-coupling strategies, the nonlinear modulation here occurs naturally along the beam’s inherent propagation path within the medium, thereby simplifying implementation and enhancing design flexibility.

3. Simulation Results

In this study, a low-symmetry unit cell with C₂ symmetry is selected [42]. The low-symmetry configuration is created by adding two auxiliary rods at a 0° and 180° orientation to a photonic crystal structure consisting of circular cross-section rods arranged in a hexagonal lattice on an air substrate. So, the high symmetry of the unit cell is broken, and the C₂ symmetry is obtained. All rods were selected as Kerr-type nonlinear LiNbO₃ with $n_0=2.24$ and $n_2=5.1\times {10}^{-15}{\mathrm{c}\mathrm{m}}^2/\mathrm{W}$. The radius of the rods and auxiliary rods was determined as r = 0.2a and rs = 0.1a, respectively. The low-symmetry rods are positioned at a distance of 0.35a from the lattice rods, as shown in Figure 2. Here “a” denotes the lattice constant, with all dimensions and operating frequencies of the photonic crystal normalized accordingly in MPB and MEEP. For example, if a = 1 μm, then a normalized frequency of 0.743 corresponds to 223 THz. A Gaussian-type source with tunable frequency and bandwidth was employed to analyze the self-propagation behavior. To extract the transmission spectrum, a monitor was placed within the simulation region to record the electromagnetic field components. These data were subsequently used to calculate physical quantities such as intensity, the Poynting vector, and power. The FDTD simulation domain was enclosed by perfectly matched layers (PMLs) to suppress boundary reflections. Additionally, group velocity dispersion (GVD), third-order dispersion (TOD), and the relationship between the NL index change in LSHPCs are presented.

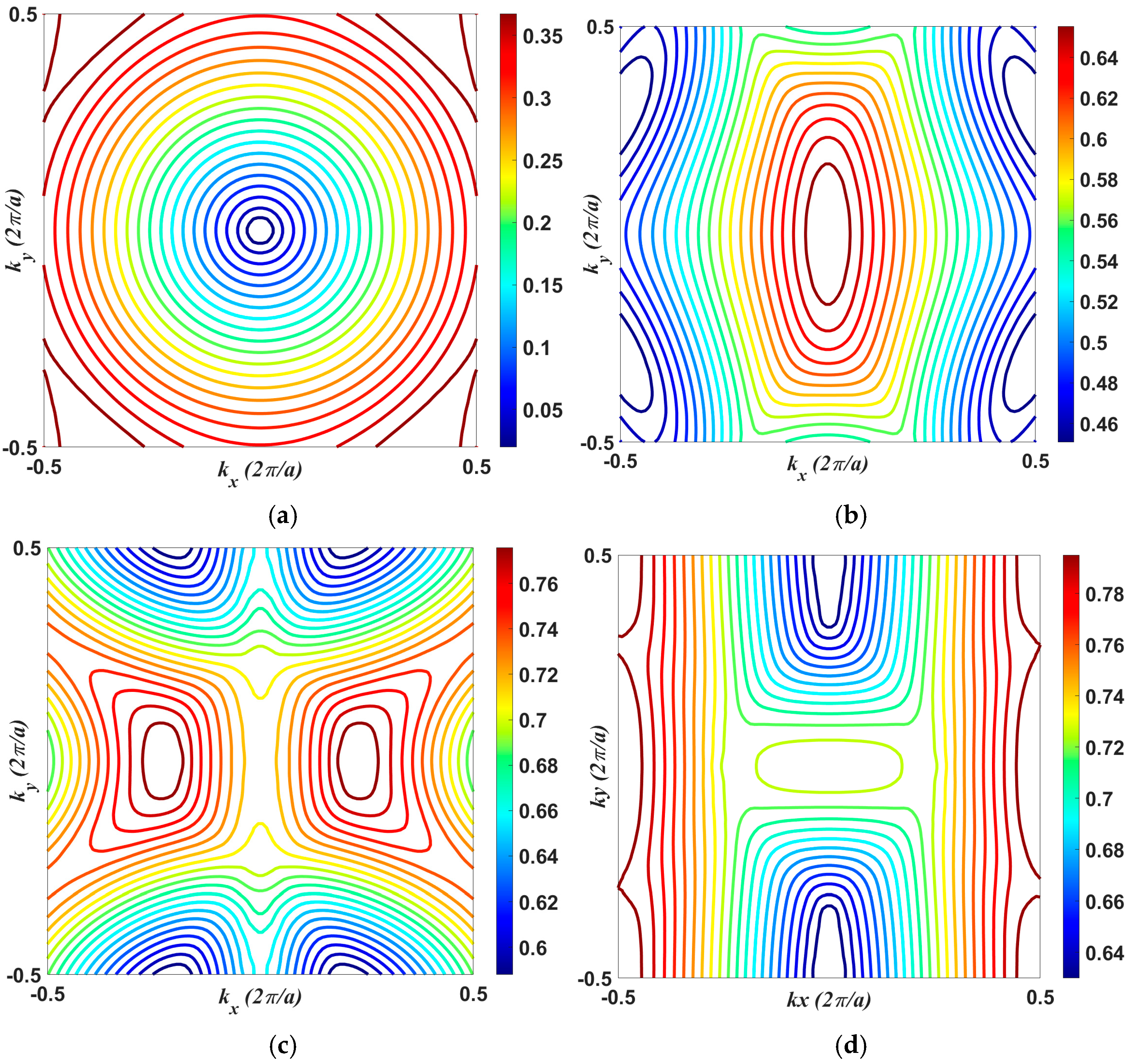
Examining the EFC of the LSHPC structure shown in Figure 3 reveals that the lines are not straight in the absence of nonlinearity. The electromagnetic wave propagation entering the structure will show a dispersion like that in Figure 1 when I examine the EFC frequencies of the 1st band of LSHPC shown in Figure 3a. Figure 3c shows that the EFC is flat in a limited region at the normalized frequency of 0.74. In this case, self-collimation of the electromagnetic wave occurs, but only at a limited angle of incidence and with high dispersion.

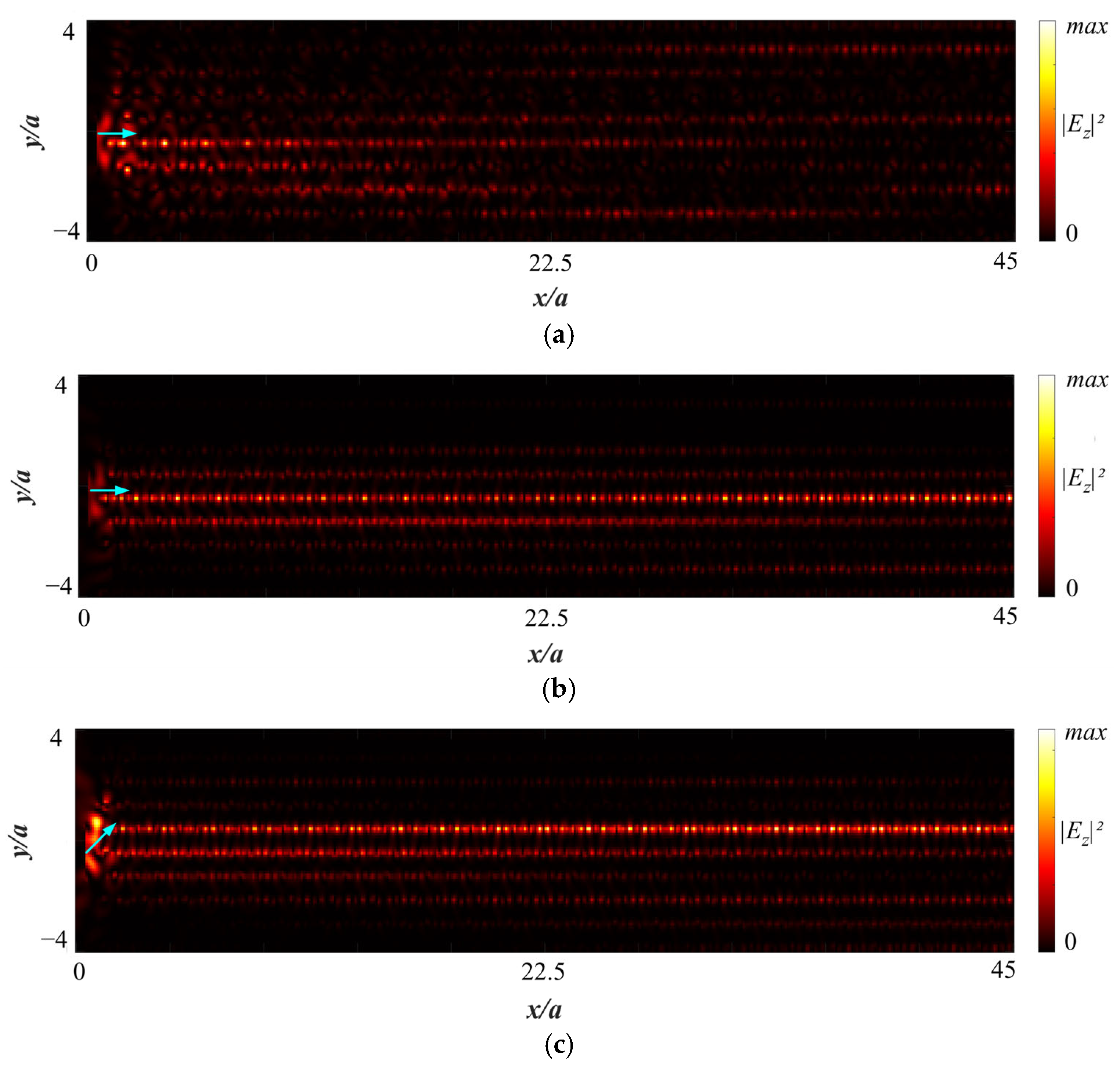
To demonstrate and validate the emergence of self-collimation (SC) within the proposed photonic crystal architecture, the spatial electric field distributions computed via FDTD simulations are analyzed. These simulations were conducted under transverse magnetic (TM) plane-wave excitation, where the electric field is polarized along the out-of-plane Ez direction. The results, corresponding to instantaneous snapshots of the electric field component E_z(r,t) at a single time frame, are presented in Figure 4. These field maps visually reveal the characteristic non-diffracting beam propagation along specific directions, thereby confirming the occurrence of SC under the specified excitation conditions. The simulations were carried out at a fixed normalized frequency situated within the SC regime as predicted by EFC analysis. The observed beam propagation directions are consistent with the flat regions of the equifrequency contours (EFCs), providing further evidence in support of the theoretical predictions concerning anisotropic group velocity and directional energy confinement.

In the FDTD simulations of self-collimation propagation shown in Figure 4, the lattice constant was set to 1 µm, and a TM mode source was applied at a real frequency of 223 THz, which corresponds to a normalized frequency of 0.743. As can be seen in Figure 4a, the dispersion is very high when the propagation of the wave at frequency 0.743 is simulated by the FDTD method. With the introduction of the nonlinearity effect, the EFC is significantly affected by the index change (Δn = 0.3), and the EFC line flattens around the frequency of 0.74, as shown in Figure 3d. Upon examination of the SC propagation at the normalized frequency of 0.743 in Figure 4b, the SC of the wave is enhanced, in accordance with the EFC result. 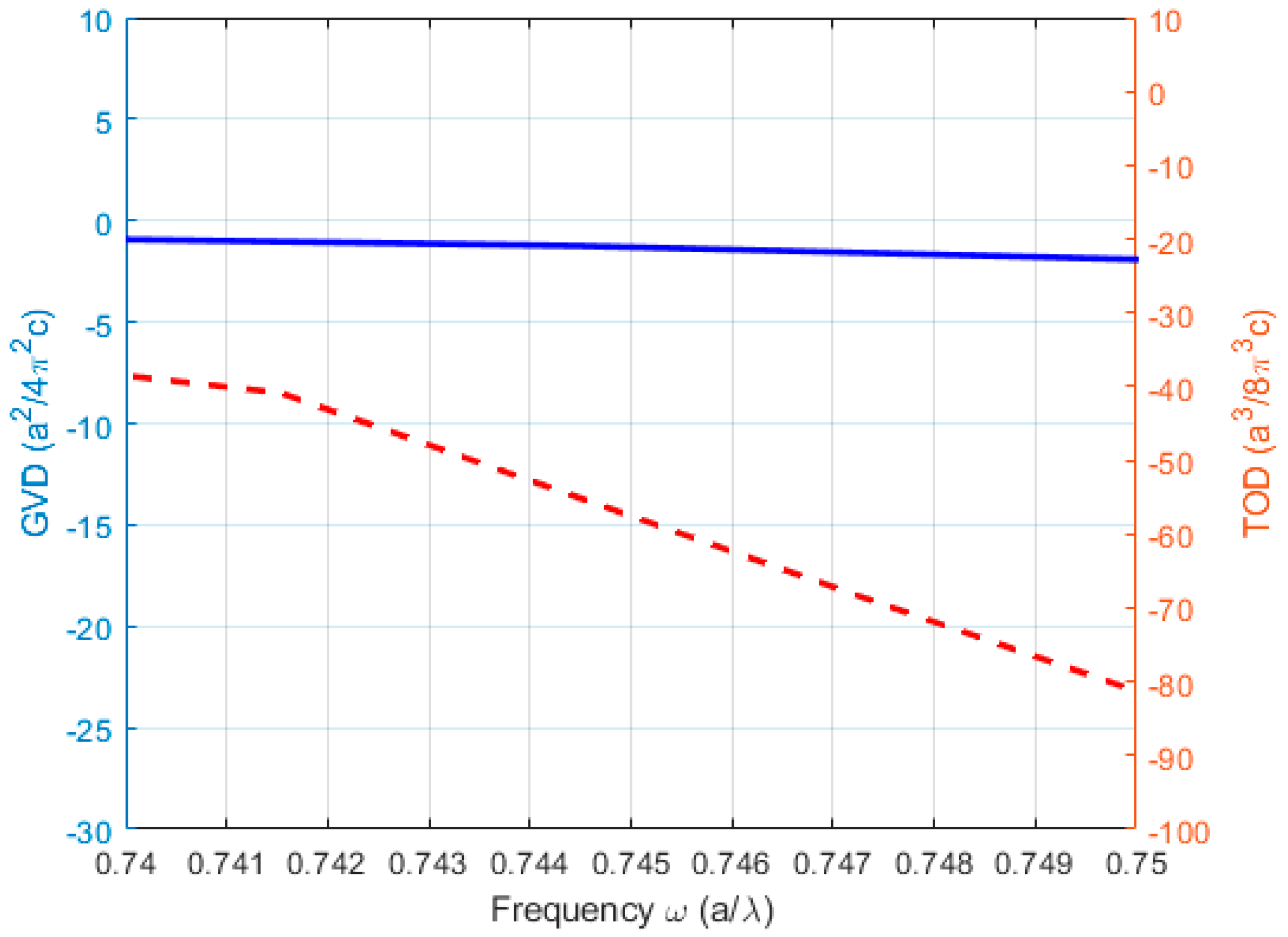Moreover, the EFC line is straight in all k_y directions in Figure 4c, which means that self-collimation will be achieved even when the entrance angle is non-zero. In this case, the GVD shown in Figure 5 is nearly zero. Another parameter examined in dispersion engineering is the third-order dispersion (TOD) value, which shows the frequency dependence of the group delay. It is also necessary to provide dispersion compensation, especially for pulses of about femtoseconds. 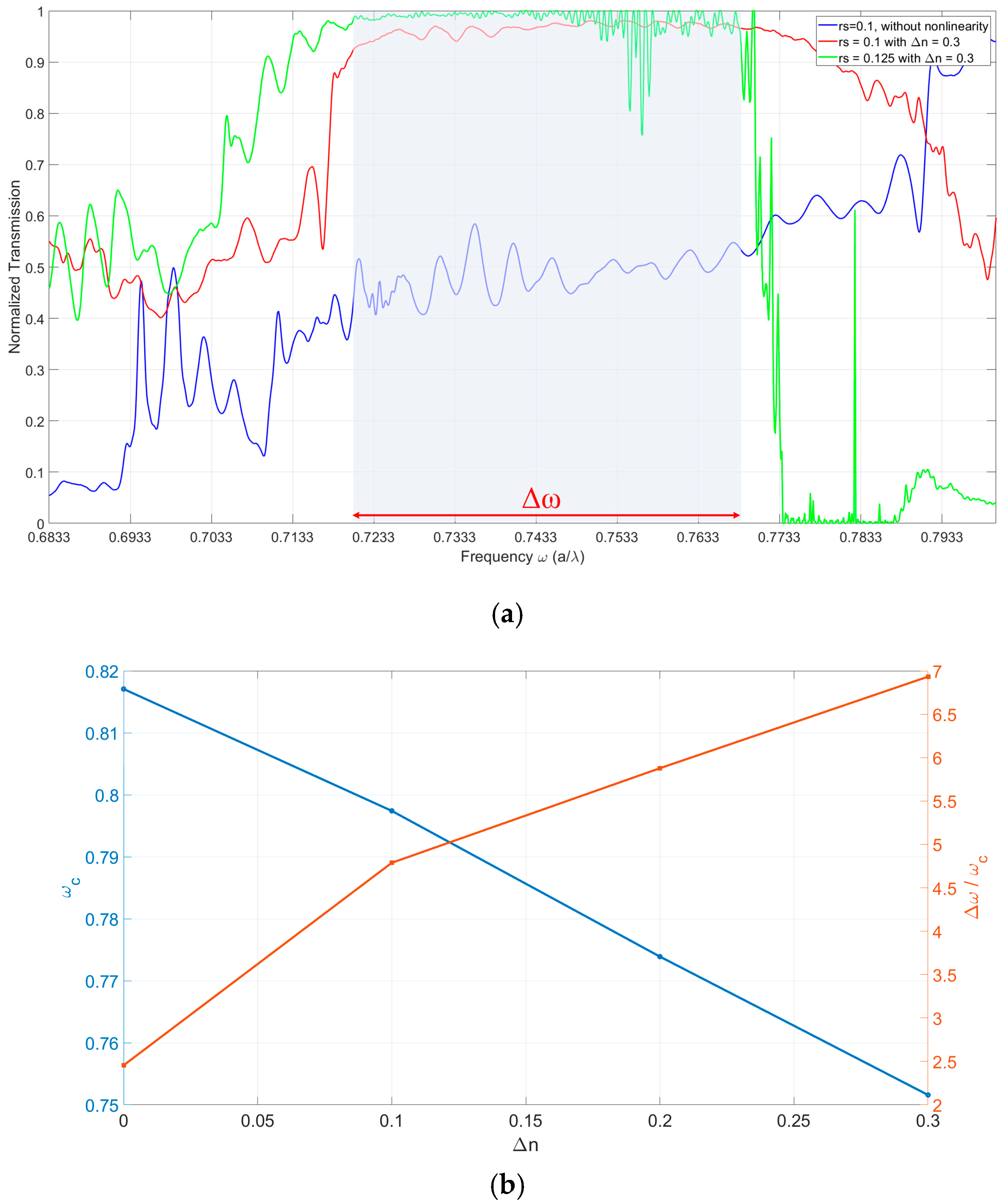The normalized self-collimation bandwidth ($∆\omega$) is defined as the range of frequencies between the starting and ending points of the flat region in the EFC plot, as shown in Figure 6b. In the case of nonlinear variation, bandwidth ($∆\omega$) and the relative bandwidth ($∆\omega /{\omega }_c$) are calculated as 0.052 and 6.9%, respectively.

To further improve self-collimation in the case of nonlinearity, the auxiliary rod radius at 180 degrees is increased and decreased by 25%. The other rod radius at zero degrees remains unchanged. When the radius is reduced (rs = 0.075a), the EFC graph in Figure 6a shows that the bandwidth of the self-collimation increases slightly around the normalized frequency of 0.74, but the EFC lines are distorted. The non-flatness of the EFC lines affects the dispersion of the wave. In other words, the amount of variation in all k-values corresponding to the k-values affects the dispersion of the wave. This amount of fluctuation is symbolized as Δk and shown in Figure 6a. If we define Δk as the difference between the largest and smallest value of k_x in the respective self-collimation frequency line, it can be calculated as 0.024. Increasing the radius (rs = 0.125a) decreases the self-collimation bandwidth ($∆\omega =0.048$) and the relative bandwidth ($∆\omega /{\omega }_c=6.5\%$), but the ripple disappears, and the EFC lines become flatter. 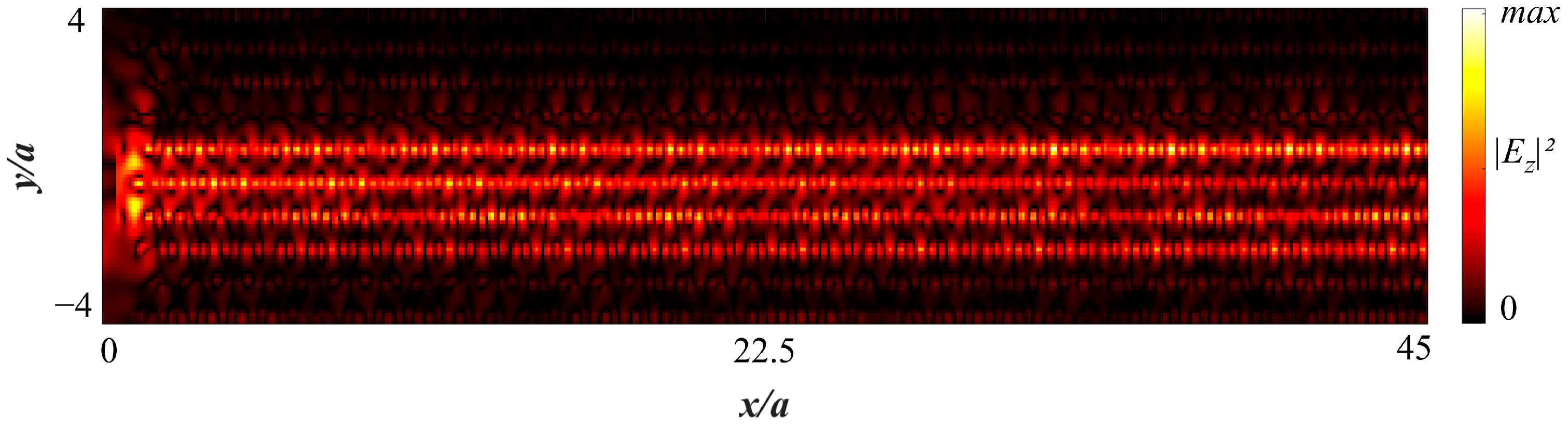As shown in Figure 7, the optimized case reveals that the dispersion decreases and the beamwidth increases when we look at the self-collimation field propagation. Finally, the transmission spectrum shows that over 90% of light is transmitted within the self-collimation band, as shown in Figure 8a. As a result, when the nonlinear index increases, the central frequency of the self-collimation region shifts toward lower frequencies, the EFCs become flatter, the ripples diminish, self-collimation improves, and the bandwidth expands, as shown in Figure 8b. Also, the GVD value remains at zero, as shown in Figure 9.

4. Discussion on the Role of Symmetry and Nonlinearity: Results, Constraints, and Future Outlook

Traditional dispersion engineering methods, such as modifications in lattice symmetry, refractive index contrast, or unit cell topology, enable precise control over equifrequency contour (EFC) curvature and self-collimation (SC) behavior. However, these techniques impose static structural constraints that limit post-fabrication tunability. In this study, Kerr-type nonlinearity is exploited to achieve self-induced, intensity-dependent index modulation, modeled as a steady-state spatial perturbation derived from representative field profiles. While complete photonic bandgap (PBG) engineering remains a foundational strategy for controlling light propagation in periodic dielectric structures, the present study prioritizes beam steering and self-collimation (SC) phenomena, which are more directly dictated by the anisotropy of the equifrequency contours (EFCs). The EFCs, being iso-frequency surfaces projected in the reciprocal lattice, effectively capture the local dispersion characteristics and directional group velocity behavior, providing a more practical and intuitive representation for analyzing beam propagation and collimation effects. In the context of SC, the presence or absence of a full photonic bandgap is not a primary constraint. Instead, the flatness and directionality of EFCs within a single photonic band determine the beam confinement characteristics. Consequently, while we acknowledge that symmetry-lowering perturbations can potentially narrow or segment the PBG, this is not detrimental to SC applications. In contrast, reducing lattice symmetry serves as a deliberate design mechanism to enhance the flexibility of EFC shaping. Specifically, breaking symmetry permits additional degrees of control over the orientation and curvature of the EFCs, enabling tunable SC axes at a fixed operating frequency—a feature not readily achievable in high-symmetry photonic crystal (PC) lattices. This flexibility is further augmented by the incorporation of Kerr-type optical nonlinearity, which introduces an intensity-dependent refractive index modulation. Such nonlinearity enables SC effects, where the propagating signal dynamically alters its own dispersion. As a result, the EFC topology, and thus the SC behavior, becomes a function of the input beam intensity, facilitating real-time, all-optical control over propagation characteristics without requiring structural reconfiguration.

In combination, these two mechanisms, structural symmetry reduction and nonlinear refractive index modulation, establish a dual control for SC behavior: one passive and geometric, the other active and field-responsive. This synergy is particularly valuable in integrated photonic circuits where dynamic tunability, miniaturization, and functionality reconfiguration are essential. Moreover, the observed effects are conceptually similar to nonlinear lensing or self-focusing phenomena but realized here within a spatially periodic and engineered photonic environment.

The reported 6.5% relative group index bandwidth was obtained by analyzing the flat region of the EFCs and validated through FDTD simulations. This bandwidth lies at the upper end of typical values reported for self-collimating photonic crystals, as summarized in [39]. While some studies have demonstrated slightly broader bandwidths, extending up to 7–8%, these often employ high refractive index contrast materials, such as air–silicon configurations and complex multilayer heterostructures. In contrast, the structure presented here achieves competitive bandwidth performance using only passive symmetry-breaking and Kerr-type optical nonlinearity. This combination enables dynamically reconfigurable self-collimation while preserving structural simplicity and fabrication feasibility, making it particularly suitable for compact, integrated photonic applications where tunability and bandwidth must be balanced against material and design constraints.

Although this study is conducted under idealized, noise-free conditions, it is important to note that symmetrical breaking in nonlinear photonic structures may enhance susceptibility to noise-induced effects such as modulation instability, thermal index fluctuations, or amplified spontaneous emission. In our model, the Kerr-type nonlinearity is implemented deterministically, without incorporating stochastic noise sources. Thus, the analysis focuses on the stationary modification of dispersion surfaces and its impact on self-collimation. Future experimental implementations will need to address noise-related dynamics and beam stability to ensure practical applicability of the proposed design.

In contrast to harmonic generation processes (e.g., second-harmonic generation, SHG, and third-harmonic generation, THG) that convert optical energy to higher frequencies (2ω and 3ω) through χ⁽²⁾ and χ⁽³⁾ nonlinear interactions, the Kerr-type nonlinearity investigated in this study induces intensity-dependent refractive index modulation at the fundamental frequency. Although this approach neglects dynamic nonlinear feedback and transient effects such as third-harmonic generation or self-phase modulation, it provides a tractable framework to assess the quasi-static impact of nonlinearity on SC behavior. While SHG and THG play crucial roles in spectral conversion, these mechanisms predominantly influence harmonic frequencies without substantially altering spatial dispersion characteristics at the fundamental frequency. Numerical simulations conducted at the third-harmonic frequency confirmed the absence of sufficient equifrequency contour (EFC) flattening or anisotropy to support self-collimation phenomena.

To evaluate the robustness of the proposed structure against structural fluctuations, we examined the system’s optical response under variations in the radius of the symmetry-lowering perturbation rods. Despite the inherent nonlinearity and broken symmetry of the design, the field propagation patterns and self-collimation characteristics remained qualitatively stable across moderate changes in the perturbation geometry. This observation suggests that the system exhibits a degree of resilience to fabrication-induced imperfections. Nevertheless, due to the potential for nonlinear mode coupling and phase sensitivity in such configurations, future studies should pursue a more rigorous assessment of phase fluctuations and modal instabilities using phase-resolved FDTD analysis or eigenmode perturbation. Such investigations would be particularly relevant for the development of phase-sensitive photonic logic or coherent beam steering in nonlinear photonic crystal platforms.

Moreover, I note that although experimental validation has not yet been performed due to infrastructure limitations, all structural and material parameters were carefully chosen to fall within the capabilities of contemporary nanofabrication techniques. The observed self-collimation and Kerr-type nonlinear effects are consistent with phenomena previously demonstrated in experimentally realized photonic crystal systems. The findings presented herein are intended to provide a theoretical basis for future experimental implementation and optical characterization.”

Compared to conventional high-index contrast or multilayer structures, the proposed approach offers a compact and scalable solution for integrated photonic applications that demand reconfigurability and dynamic control. Although the current modeling framework neglects fully dynamic nonlinear effects, the results establish a theoretical basis for future experimental implementation. Subsequent studies should incorporate time-resolved nonlinear dynamics and assess the impact of noise and phase instabilities, particularly in contexts such as coherent beam steering or nonlinear photonic logic. Overall, Kerr-type low-symmetry nonlinear photonic crystals (LSNLHPCs) represent a promising platform for next-generation adaptive photonic systems.

5. Conclusions

In this study, it is demonstrated that the integration of Kerr-type optical nonlinearity into low-symmetry hexagonal photonic crystals substantially enhances the self-collimation (SC) effect through engineered modulation of equifrequency contours (EFC). The symmetry-breaking perturbations introduced by the lattice asymmetry led to a pronounced flattening of the EFC profile with minimal wavevector fluctuation (∆k ≈ 0), thereby significantly broadening the operational bandwidth (Δω = 0.48) and achieving a relative bandwidth ($∆\omega /{\omega }_c=6.5\%$) at high frequencies. The dynamic modulation of the effective refractive index, governed by the nonlinear relationship $n\left(I\right)=n_0+n_{2}I$ results in tunable photonic band structures that support robust, broadband self-collimated light propagation. To assess robustness, the structure’s optical response was evaluated under variations in the radius of the symmetry-breaking perturbation rods. Despite the presence of nonlinearity and broken symmetry, both the field propagation profiles and SC performance remained qualitatively stable under moderate perturbations, indicating resilience to fabrication tolerances. Future research focused on nonlinear dynamics, optimizing the structure, and exploring their integration into photonic circuits will further expand their applicability in adaptive and high-performance optical systems.