Learnable Priors Support Reconstruction in Diffuse Optical Tomography
Abstract
1. Introduction
2. Materials and Methods
2.1. General Setting
2.2. Forward Model
Graph Neural Network Solvers
- Lifting layer: The input states are lifted to some higher dimensional space using multi-layer perceptrons (MLPs) as follows:
- Kernel integration layer: The processing step consists of several message passing layers with residual connections:where is an activation function applied element-wise, is a tunable tensor, and is a tensor kernel function that is modeled by a Neural Network with learnable parameters .
- Projection layer: In the final decoding step, an MLP transforms the latent node features into the output features :
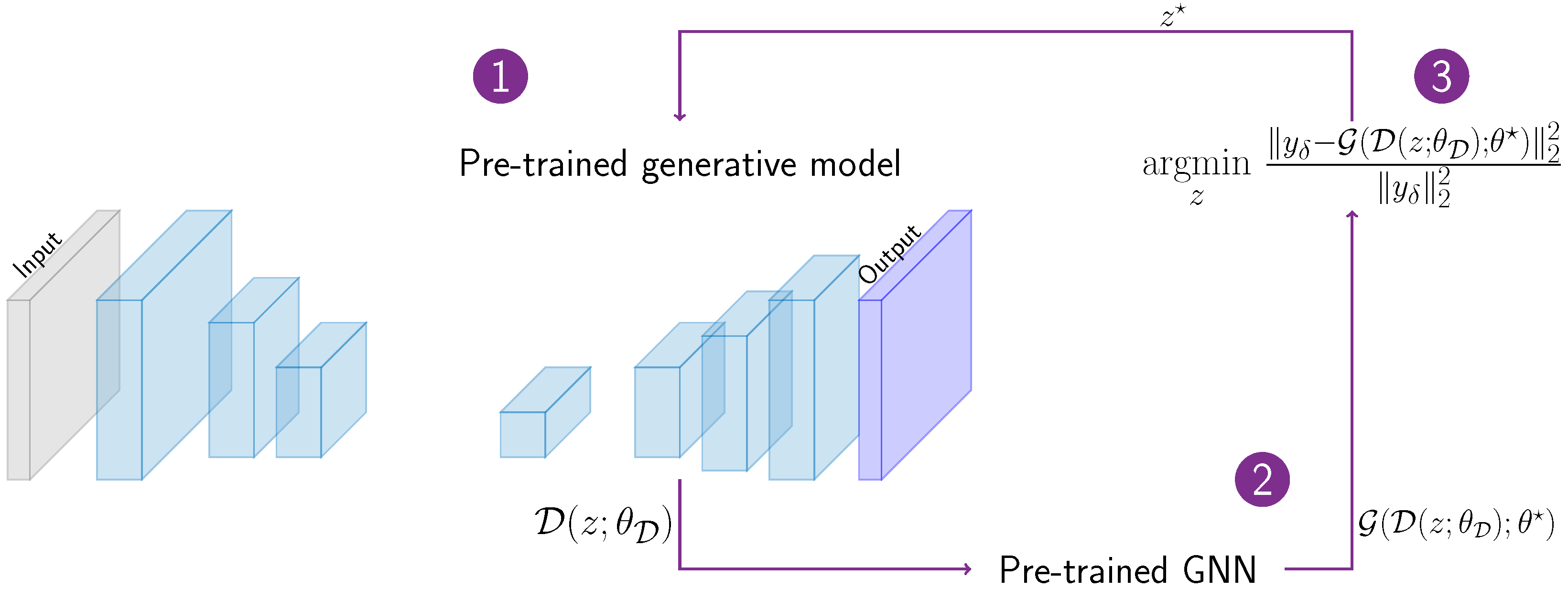
2.3. Learnable Prior
2.4. Learning the Inverse Problem Solution
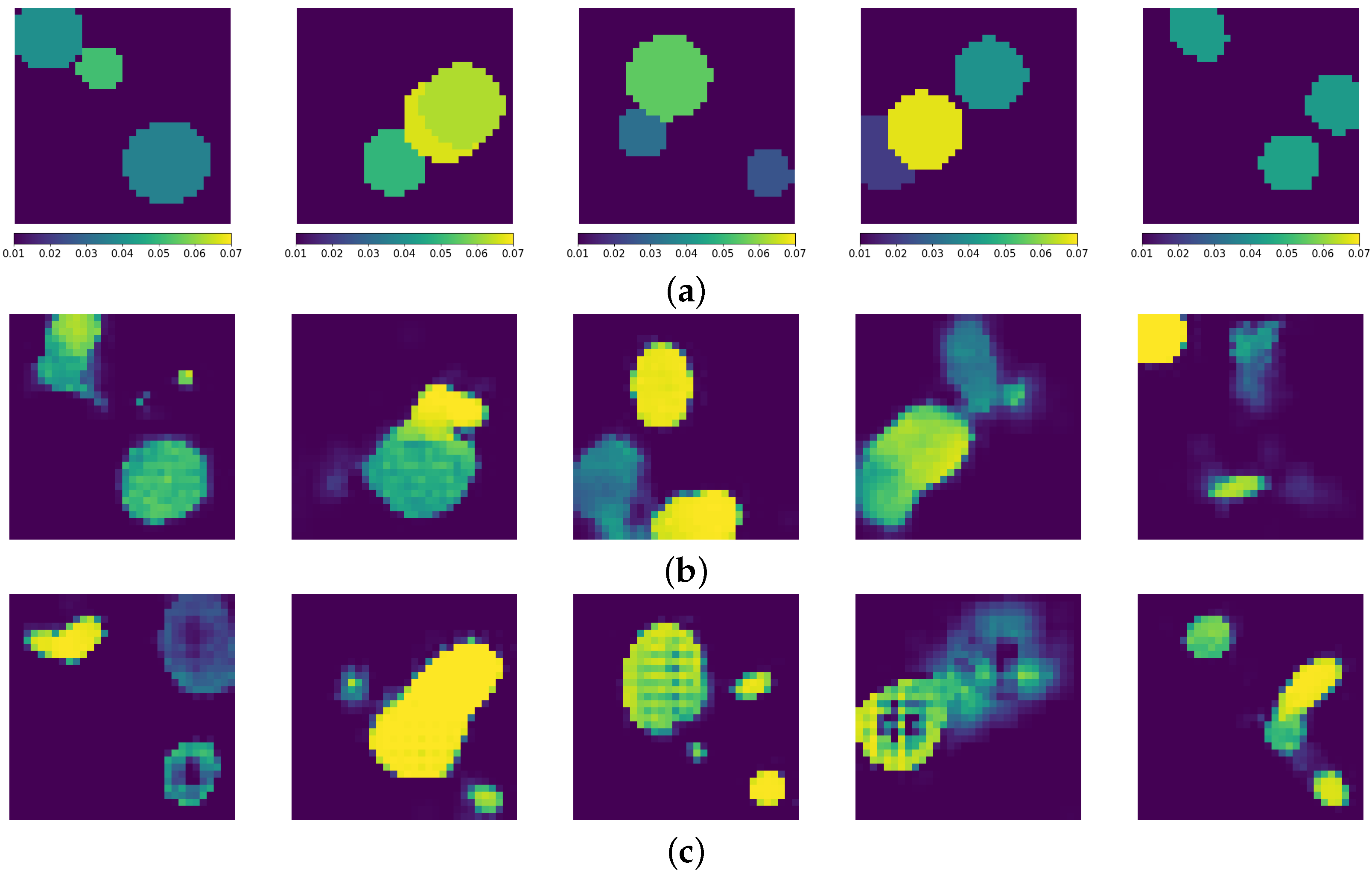
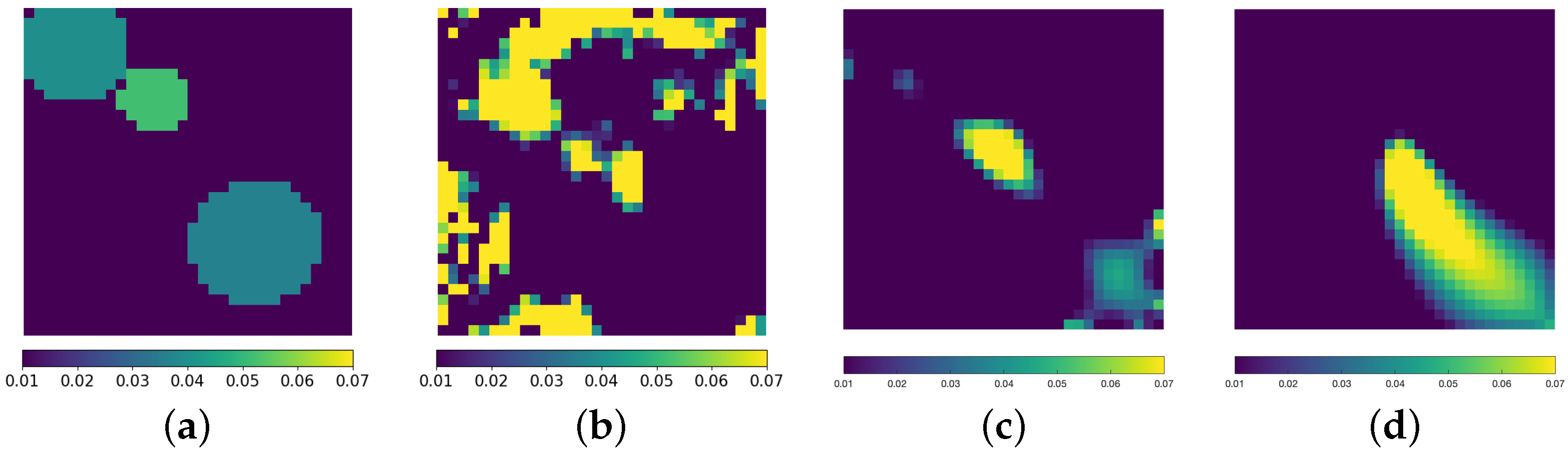
3. Results
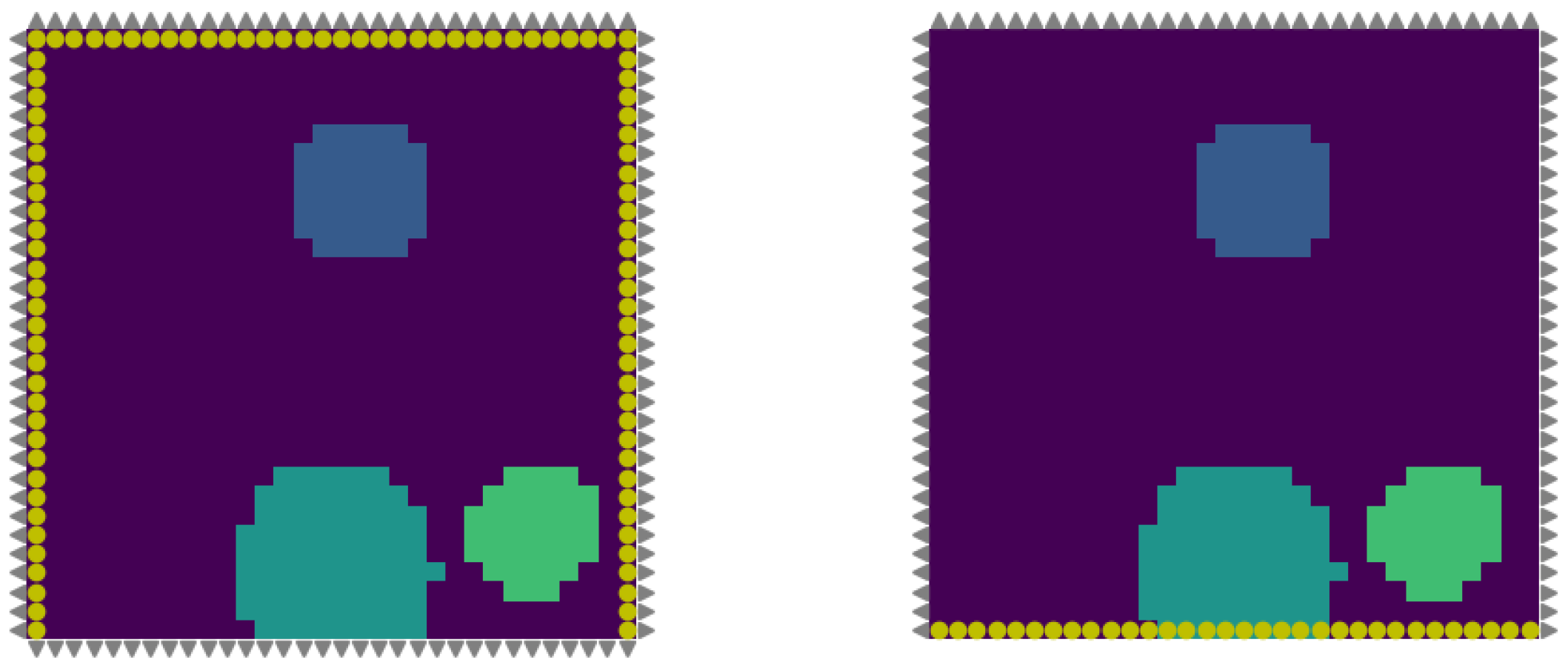
3.1. Generation of Synthetic Data
3.2. Neural Architectures
3.2.1. Graph Neural Network Design
3.2.2. Autoencoder Design
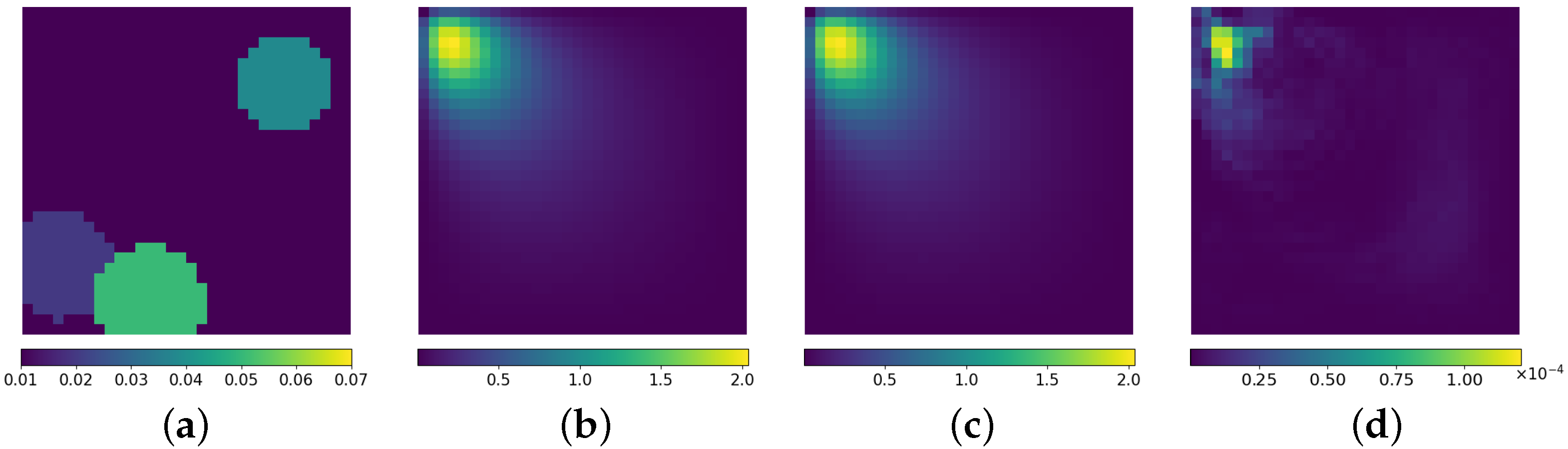
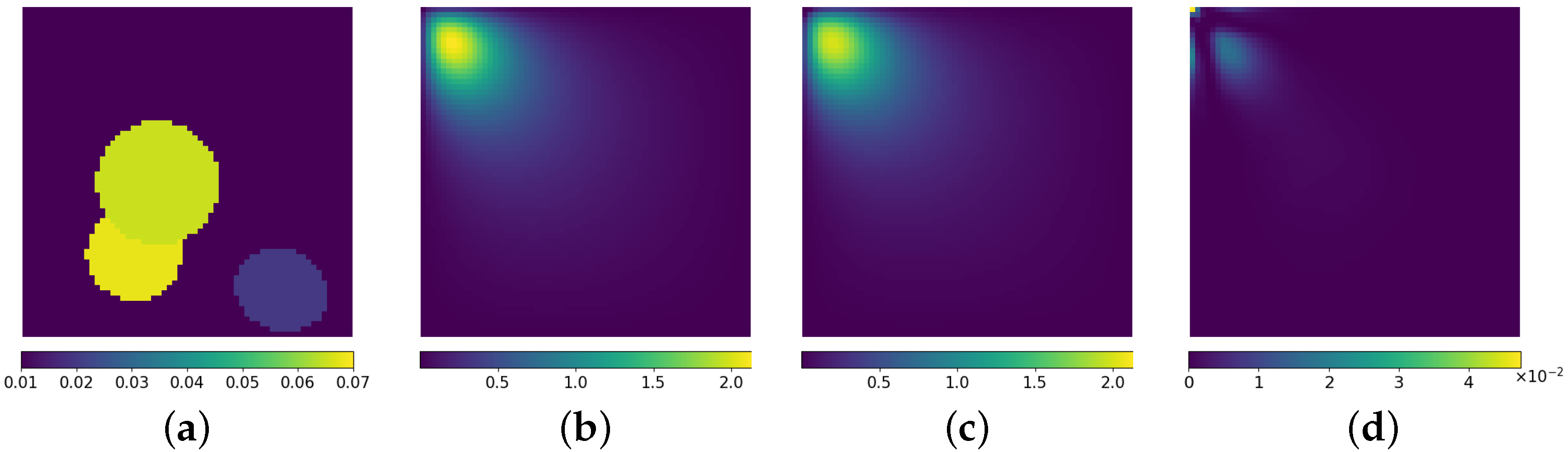
3.3. Inverse Problem
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOT | Diffuse Optical Tomography |
| NIR | Near-Infrared |
| HBO2 | Oxy-Hemoglobin |
| Hb | Deoxy-Hemoglobin |
| H2O | Water |
| CW | Continuous Wave |
| CW-DOT | Continuous Wave Diffuse Optical Tomography |
| LED | Light Emitting Diode |
| MRI | Magnetic Resonance Imaging |
| CT | Computed Tomography |
| DGN | Deep Gauss-Newton |
| Mod-DOT | Modular-Diffuse Optical Tomography |
| RTE | Radiative Transfer Equation |
| DA | Diffusion Approximation |
| GNN | Graph Neural Network |
| PDE | Partial Differential Equation |
| MLP | Multilayer Perceptron |
| MSE | Mean Squared Error |
| HPC | High Performance Computing |
| GPU | Graphics Processing Unit |
| GHz | GigaHertz |
| GB | Gigabyte |
| RAM | Random Access Memory |
| COULE | Contrasted Overlapping Uniform Lines and Ellipses |
| ReLU | Rectified Linear Unit |
| Adam | Adaptive Moment Estimation |
| SSIM | Structural Similarity Index Measure |
| MAE | Mean Absolute Error |
References
- Hoshi, Y.; Yamada, Y. Overview of diffuse optical tomography and its clinical applications. J. Biomed. Opt. 2016, 21, 091312. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H. Diffuse Optical Tomography: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, L.; Wu, H.I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Azar, F.S.; Lee, K.; Khamene, A.; Choe, R.; Corlu, A.; Konecky, S.D.; Sauer, F.; Yodh, A.G. Standardized platform for coregistration of nonconcurrent diffuse optical and magnetic resonance breast images obtained in different geometries. J. Biomed. Opt. 2007, 12, 051902. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.; Maass, P.; Öktem, O.; Schönlieb, C.B. Solving inverse problems using data-driven models. Acta Numer. 2019, 28, 1–174. [Google Scholar] [CrossRef]
- Benning, M.; Burger, M. Modern regularization methods for inverse problems. Acta Numer. 2018, 27, 1–111. [Google Scholar] [CrossRef]
- Arridge, S.R.; Schotland, J.C. Optical tomography: Forward and inverse problems. Inverse Probl. 2009, 25, 123010. [Google Scholar] [CrossRef]
- Lee, O.; Kim, J.M.; Bresler, Y.; Ye, J.C. Compressive diffuse optical tomography: Noniterative exact reconstruction using joint sparsity. IEEE Trans. Med. Imaging 2011, 30, 1129–1142. [Google Scholar] [CrossRef] [PubMed]
- Egger, H.; Schlottbom, M. Analysis and regularization of problems in diffuse optical tomography. SIAM J. Math. Anal. 2010, 42, 1934–1948. [Google Scholar] [CrossRef]
- Kazanci, H.O.; Jacques, S.L. Diffuse Light Tomography to Detect Blood Vessels Using Tikhonov Regularization. Proc. SPIE 2016, 9917, 99170S. [Google Scholar] [CrossRef]
- Aspri, A.; Benfenati, A.; Causin, P.; Cavaterra, C.; Naldi, G. Mathematical and numerical challenges in diffuse optical tomography inverse problems. Discret. Contin. Dyn. Syst. S 2023, 17, 421–461. [Google Scholar] [CrossRef]
- Benfenati, A.; Lupieri, M.; Naldi, G.; Causin, P. Regularization Techniques for Inverse Problem in DOT Applications. J. Phys. Conf. Ser. 2020, 1476, 012007. [Google Scholar] [CrossRef]
- McCann, M.T.; Jin, K.H.; Unser, M. Convolutional Neural Networks for Inverse Problems in Imaging: A Review. In IEEE Signal Process. Mag. 2017, 34, 85–95. [Google Scholar] [CrossRef]
- Zheng, B.; Andrei, S.; Sarker, M.K.; Gupta, K.D. Data Driven Approaches on Medical Imaging; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Patra, R.; Dutta, P.K. Improved DOT reconstruction by estimating the inclusion location using artificial neural network. Med. Imaging 2013 Phys. Med. Imaging 2013, 8668, 86684C. [Google Scholar] [CrossRef]
- Sun, Y.; Xia, Z.; Kamilov, U.S. Efficient and accurate inversion of multiple scattering with deep learning. Opt. Express 2018, 26, 14678–14688. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Sun, Q.; Li, Z.; Sun, Z.; Jia, K. Back-propagation neural network-based reconstruction algorithm for diffuse optical tomography. J. Biomed. Opt. 2018, 24, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.; Sabir, S.; Heo, D.; Kim, K.H.; Wahab, A.; Choi, Y.; Lee, S.-I.; Chae, E.Y.; Kim, H.H.; Bae, Y.M.; et al. Deep Learning Diffuse Optical Tomography. IEEE Trans. Med. Imaging 2020, 39, 877–887. [Google Scholar] [CrossRef] [PubMed]
- Deng, B.; Gu, H.; Carp, S.A. Deep learning enabled high-speed image reconstruction for breast diffuse optical tomography. Opt. Tomogr. Spectrosc. Tissue XIV 2021, 11639, 116390B. [Google Scholar] [CrossRef]
- Mozumder, M.; Hauptmann, A.; Nissila, I.; Arridge, S.R.; Tarvainen, T. A Model-Based Iterative Learning Approach for Diffuse Optical Tomography. IEEE Trans. Med. Imaging 2022, 41, 1289–1299. [Google Scholar] [CrossRef] [PubMed]
- Benfenati, A.; Causin, P.; Quinteri, M. A Modular Deep Learning-based Approach for Diffuse Optical Tomography Reconstruction. arXiv 2024, arXiv:2402.09277. [Google Scholar]
- Herzberg, W.; Rowe, D.B.; Hauptmann, A.; Hamilton, S.J. Graph Convolutional Networks for Model-Based Learning in Nonlinear Inverse Problems. IEEE Trans. Comput. Imaging 2021, 7, 1341–1353. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Lindell, D.B.; Wetzstein, G. Learning to Solve PDE-Constrained Inverse Problems with Graph Networks. In ICML; 2022; Available online: https://icml.cc/media/icml-2022/Slides/16566.pdf (accessed on 22 July 2025).
- Zhao, Q.; Ma, Y.; Boufounos, P.; Nabi, S.; Mansour, H. Deep Born Operator Learning for Reflection Tomographic Imaging. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse Optics for Tissue Monitoring and Tomography. Rep. Prog. Phys. 2010, 73, 076701. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Haskell, R.C.; Svaasand, L.O.; Tsay, T.T.; Feng, T.C.; McAdams, M.S.; Tromberg, B.J. Boundary conditions for the diffusion equation in radiative transfer. J. Opt. Soc. Am. A 1994, 11, 2727–2741. [Google Scholar] [CrossRef] [PubMed]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 1998. [Google Scholar]
- Roach, G.F. Green’s Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Li, Z.; Kovachki, N.B.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.M.; Anandkumar, A. Neural Operator: Graph Kernel Network for Partial Differential Equations. arXiv 2020, arXiv:2003.03485. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for Quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning (ICML’17), Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Arora, S.; Cohen, N.; Hu, W.; Luo, Y. Implicit regularization in deep matrix factorization. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. Article 666. pp. 7413–7424. [Google Scholar]
- Mazumder, A.; Baruah, T.; Kumar, B.; Sharma, R.; Pattanaik, V.; Rathore, P. Learning Low-Rank Latent Spaces with Simple Deterministic Autoencoder: Theoretical and Empirical Insights. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3 January 2024; pp. 2851–2860. [Google Scholar]
- Jing, L.; Zbontar, J.; LeCun, Y. Implicit rank-minimizing autoencoder. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 1 October 2020. [Google Scholar]
- Mounayer, J.; Rodriguez, S.; Ghnatios, C.; Farhat, C.; Chinesta, F. Rank Reduction Autoencoders—Enhancing interpolation on nonlinear manifolds. arXiv 2024, arXiv:2405.13980. [Google Scholar] [CrossRef]
- COULE Dataset. Available online: www.kaggle.com/loiboresearchgroup/coule-dataset (accessed on 15 April 2025).
- PyG Documentation. Available online: https://pytorch-geometric.readthedocs.io/ (accessed on 5 May 2025).
- You, H.; Yu, Y.; D’Elia, M.; Gao, T.; Silling, S. Nonlocal kernel network (NKN): A stable and resolution-independent deep neural network. J. Comput. Phys. 2022, 469, 111536. [Google Scholar] [CrossRef]
| Layer Type | Output Shape | Kernel Size | Stride | Padding |
|---|---|---|---|---|
| Conv2d | [−1, 32, 16, 16] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 32, 16, 16] | - | - | - |
| Conv2d | [−1, 64, 8, 8] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 64, 8, 8] | - | - | - |
| Conv2d | [−1, 128, 4, 4] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 128, 4, 4] | - | - | - |
| Conv2d | [−1, 256, 2, 2] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 256, 2, 2] | - | - | - |
| Conv2d | [−1, 32, 1, 1] | (2, 2) | (1, 1) | (0, 0) |
| Linear | [−1, 32] | - | - | - |
| Linear | [−1, 32] | - | - | - |
| Linear | [−1, 32] | - | - | - |
| Linear | [−1, 32] | - | - | - |
| ConvTranspose2d | [−1, 256, 2, 2] | (2, 2) | (1, 1) | (0, 0) |
| ReLU | [−1, 256, 2, 2] | - | - | - |
| ConvTranspose2d | [−1, 128, 4, 4] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 128, 4, 4] | - | - | - |
| ConvTranspose2d | [−1, 64, 8, 8] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 64, 8, 8] | - | - | - |
| ConvTranspose2d | [−1, 32, 16, 16] | (4, 4) | (2, 2) | (1, 1) |
| ReLU | [−1, 32, 16, 16] | - | - | - |
| ConvTranspose2d | [−1, 1, 32, 32] | (4, 4) | (2, 2) | (1, 1) |
| Tanh | [−1, 1, 32, 32] | - | - | - |
| SSIM | MAE | |
|---|---|---|
| Reconstruction using 1 light source | 0.305 | 0.023 |
| Reconstruction using 20 light sources | 0.375 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serianni, A.; Benfenati, A.; Causin, P. Learnable Priors Support Reconstruction in Diffuse Optical Tomography. Photonics 2025, 12, 746. https://doi.org/10.3390/photonics12080746
Serianni A, Benfenati A, Causin P. Learnable Priors Support Reconstruction in Diffuse Optical Tomography. Photonics. 2025; 12(8):746. https://doi.org/10.3390/photonics12080746
Chicago/Turabian StyleSerianni, Alessandra, Alessandro Benfenati, and Paola Causin. 2025. "Learnable Priors Support Reconstruction in Diffuse Optical Tomography" Photonics 12, no. 8: 746. https://doi.org/10.3390/photonics12080746
APA StyleSerianni, A., Benfenati, A., & Causin, P. (2025). Learnable Priors Support Reconstruction in Diffuse Optical Tomography. Photonics, 12(8), 746. https://doi.org/10.3390/photonics12080746





