Mie Coefficients

Abstract

We consider the scattering of electromagnetic radiation by a spherical particle, known as Mie scattering. The electric and magnetic fields are represented by multipole fields, and the amplitudes are the Mie scattering coefficients. Properties of the particle are mainly contained in these coefficients. We have studied the dependence of these coefficients on the various parameters, with an emphasis on the dependence on the particle radius. Central to this discussion is what is known as the ‘Mie circle’. Without absorption in the particle or the embedding medium, the Mie scattering coefficients lie on this universal circle in the complex plane. We have studied the location of the Mie scattering coefficients on this circle as a function of the particle radius. The Mie circle also serves as a reference for the case when there is absorption in the particle or the medium. In the limit of a small particle, a peculiar divergence appears in the expression for the Mie coefficients, known as the Fröhlich resonance. We show that this apparent singularity is a consequence of the fact that the limit of a small particle fails in the neighborhood of this resonance, and we derive an expression for the correct small-particle limit in the neighborhood of this resonance.

1. Introduction

The problem of the scattering of a plane wave by a spherical particle was solved more than a century ago by Gustav Mie [1]. This milestone achievement has found numerous applications, ranging from the detection of aerosols in the atmosphere to measurements of the radii of nano-sized particles. More recently, small dielectric Mie particles were considered for the building blocks of metamaterials [2,3,4]. An interesting phenomenon is the appearance of photonic jets in Mie scattering [5,6]. Numerous papers have been devoted to the numerical evaluation of the Mie coefficients [7,8,9,10,11,12,13,14,15,16,17], and comprehensive reviews of Mie scattering can be found in [18,19,20].

Figure 1 schematically shows the setup for Mie scattering. A particle with the radius R is located at the origin of coordinates. It has (relative) permittivity ${\epsilon }_{\mathrm{p}}$ and (relative) permeability ${\mu }_{\mathrm{p}},$ and the particle is embedded in a medium with permittivity ${\epsilon }_1$ and permeability ${\mu }_1.$ A laser beam with angular frequency $\omega ,$ propagating into the positive $z$ direction, irradiates the particle. The wave number in free space is $k_{\mathrm{o}}=\omega /c.$ We set $\overline{R}=k_{\mathrm{o}}R$ for the dimensionless radius of the particle, and we shall simply refer to this as the radius of the particle. On this scale, a distance of $2\pi$ corresponds to an optical wavelength in free space. The incident radiation scatters off the particle, and part of it enters the particle. Mie theory provides the expressions for the electric and magnetic fields, both inside and outside of the particle, and for any values of the parameters.

The parameters $\epsilon$ and $\mu$ are complex, in general, and they depend on the angular frequency $\omega ,$ which is a constant in this problem. For causality reasons, these parameters lie in the upper half of the complex plane, or on the real axis [21] (p. 310), e.g.,

$$\mathrm{Im}\epsilon \ge 0,\hspace{1em}\mathrm{Im}\mu \ge 0.$$

(1)

The index of refraction $n$ is the solution of $n^2=\epsilon \mu .$ This equation has two solutions, and we need the solution for which

$$\mathrm{Im}n\ge 0.$$

(2)

A moment of thought then shows that the correct solution is

$$n=\sqrt{\epsilon }\sqrt{\mu },$$

(3)

both for the embedding medium and the particle. For the square root function, we take the cut in the complex plane just below the negative real axis. It will turn out to be advantageous to introduce the particle parameters relative to the parameters of the embedding medium. We set

$${\widehat{\epsilon }}_{\mathrm{p}}={\displaystyle \frac{{\epsilon }_{\mathrm{p}}}{{\epsilon }_1}},\hspace{1em}{\widehat{\mu }}_{\mathrm{p}}={\displaystyle \frac{{\mu }_{\mathrm{p}}}{{\mu }_1}},\hspace{1em}{\widehat{n}}_{\mathrm{p}}={\displaystyle \frac{n_{\mathrm{p}}}{n_1}}.$$

(4)

2. Incident Field

The incident field is a monochromatic polarized plane wave, with $E_{\mathrm{inc}}(r)$ and $B_{\mathrm{inc}}(r)$ as the complex amplitudes of the electric and magnetic fields, respectively. The electric field itself is

$$E_{\mathrm{inc}}(r,t)=\mathrm{Re}{E}_{\mathrm{inc}}(r)e^{-i\omega \hspace{0.17em}t},$$

(5)

and similarly for the magnetic field. For the electric field, we have

$$E_{\mathrm{inc}}(r)=E_{\mathrm{o}}{u}_{\mathrm{L}}{e}^{i k_{\mathrm{L}}\cdot r}.$$

(6)

Here, $u_{\mathrm{L}}$ is the unit polarization vector, normalized as $u_{\mathrm{L}}^{*}\cdot u_{\mathrm{L}}=1$. This generally complex vector lies in the $xy$ plane. The wave vector is $k_{\mathrm{L}}=k_1{e}_z,$ with $k_1=n_1{k}_{\mathrm{o}}$ as the wave number in the embedding medium. The corresponding magnetic field is

$$B_{\mathrm{inc}}(r)=n_1{\displaystyle \frac{E_{\mathrm{o}}}{c}}(e_z\times u_{\mathrm{L}})e^{i k_{\mathrm{L}}\cdot r}.$$

(7)

We set

$$B_{\mathrm{o}}=n_1{\displaystyle \frac{E_{\mathrm{o}}}{c}},$$

(8)

$${u_{\mathrm{L}}}^{\prime }=e_z\times u_{\mathrm{L}},$$

(9)

so that

$$B_{\mathrm{inc}}(r)=B_{\mathrm{o}}{u_{\mathrm{L}}}^{\prime }{e}^{i k_{\mathrm{L}}\cdot r}.$$

(10)

This notation is particularly useful when studying electric and magnetic dipole radiation, as in Appendix C.

The index of refraction $n_1$ will be complex, in general. We set

$$n_1={n_1}^{\prime }+i{n_1}^{″},\hspace{1em}{n_1}^{\prime } \mathrm{real},\hspace{1em}{n_1}^{″}\ge 0.$$

(11)

With $k_{\mathrm{L}}\cdot r=n_1{k}_{\mathrm{o}}z,$ the time-dependent electric field from Equation (5) becomes

$$E_{\mathrm{inc}}(r,t)=e^{-n_1″k_{\mathrm{o}}z}\mathrm{Re}{E}_{\mathrm{o}}{u}_{\mathrm{L}}{e}^{i({n_1}^{\prime }{k}_{\mathrm{o}}z-\omega \hspace{0.17em}t)}.$$

(12)

Due to the overall exponential, the field decays in amplitude into the positive $z$ direction if ${n_1}^{″}>0$. The exponential factor inside $\mathrm{Re}(...)$ is a traveling plane wave with phase velocity

$$v_{\mathrm{ph}}={\displaystyle \frac{c}{{n_1}^{\prime }}}.$$

(13)

For ${n_1}^{\prime }>0$, the wave pattern moves into the positive $z$ direction, and for ${n_1}^{\prime }<0$, it moves into the negative $z$ direction. It can be shown that the energy always flows into the positive $z$ direction.

In order to eliminate non-essential constants, we introduce dimensionless fields as

$$E(r)=E_{\mathrm{o}}\mathcal{E}(r),$$

(14)

$$B(r)=n{\displaystyle \frac{E_{\mathrm{o}}}{c}}\mathcal{B}(r).$$

(15)

For the magnetic field, we take $n$ as $n_1$ for a field outside the particle and as $n_{\mathrm{p}}$ for a field inside the particle. For the incident fields, this becomes

$${\mathcal{E}}_{\hspace{0.17em}\mathrm{inc}}(r)=u_{\mathrm{L}}{e}^{i k_{1}z},$$

(16)

$${\mathcal{B}}_{\hspace{0.17em}\mathrm{inc}}(r)={u_{\mathrm{L}}}^{\prime }{e}^{i k_{1}z}.$$

(17)

For Mie scattering, it is advantageous to consider circularly polarized incident radiation. We take $u_{\mathrm{L}}$ as a spherical unit vector:

$${\widehat{u}}_{\mathrm{L}}=e_{\tau }=-{\displaystyle \frac{\tau }{\sqrt{2}}}(e_x+i\tau e_y),\hspace{1em}\tau =\pm 1.$$

(18)

For $\tau =1$, this gives a left-polarized plane wave, or a wave with positive helicity. The electric and magnetic field vectors rotate counterclockwise when viewed down the positive $z$ axis, with the magnetic field lagging the electric field by ${90}^{\circ }.$ For the magnetic field, we have

$${u_{\mathrm{L}}}^{\prime }={e_{\tau }}^{\prime }=e_z\times e_{\tau }=-i\tau e_{\tau },$$

(19)

so, the dimensionless incident fields are related as

$${\mathcal{B}}_{\hspace{0.17em}\mathrm{inc}}(r)=-i\tau {\mathcal{E}}_{\mathrm{inc}}(r).$$

(20)

For other polarizations of the incident field, the solution can be obtained by superposition.

3. Fields and Mie Coefficients

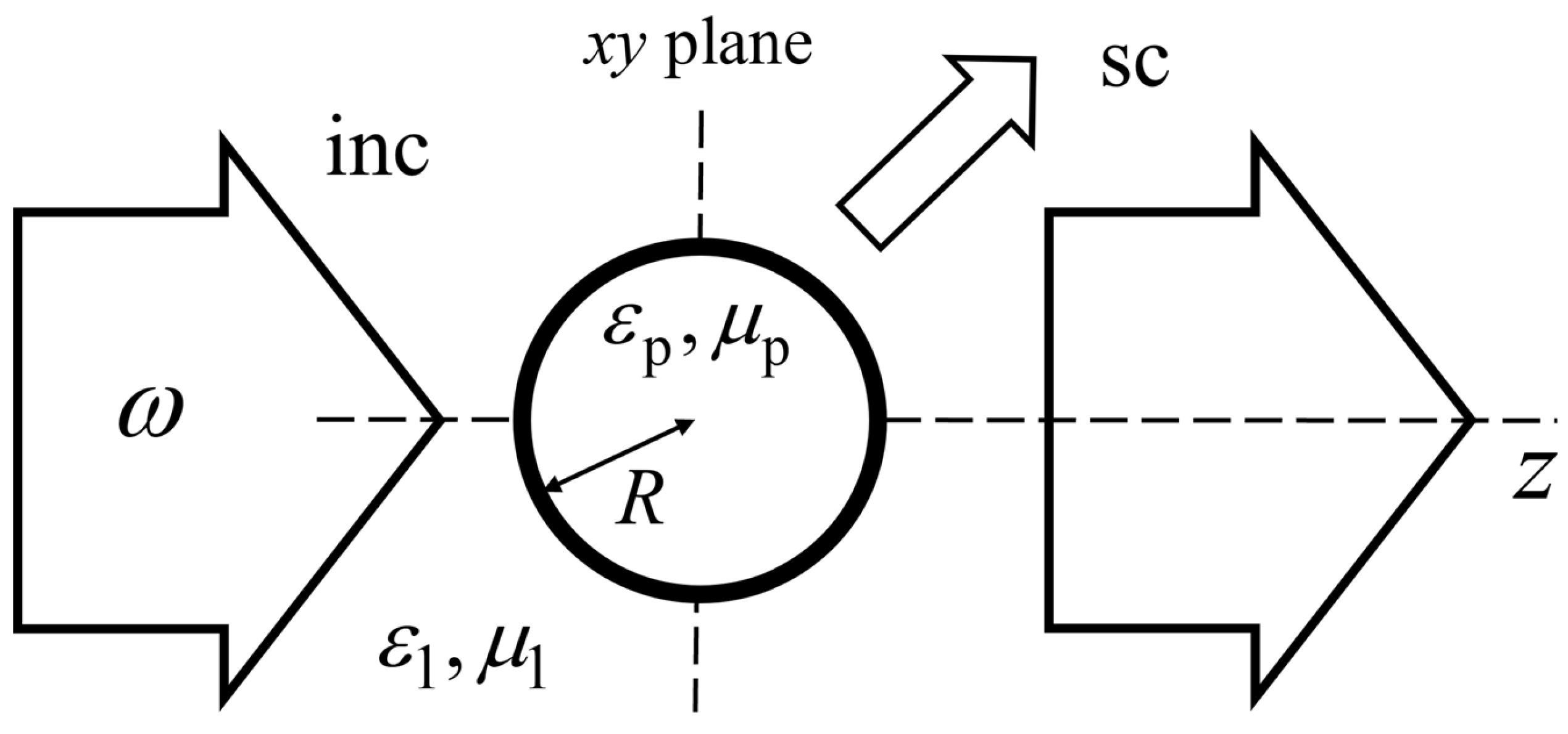
Mie theory provides the exact solution of Maxwell’s equations for the setup depicted in Figure 1. Since Mie’s paper, mathematics has evolved substantially, and the theory has been put on a more solid, and elegant, footing. Now, the fields are expanded onto a complete set of vector functions on the unit sphere, the vector spherical harmonics [22,23]. Each vector spherical harmonic is multiplied by a spherical Bessel function, and this gives a partial wave of the solution. This gives a consistent expansion of the fields in vector multipole fields.

The scattered fields are ${\mathcal{E}}_{\mathrm{sc}}(r)$ and ${\mathcal{B}}_{\mathrm{sc}}(r),$ and the particle fields are ${\mathcal{E}}_{\mathrm{p}}(r)$ and ${\mathcal{B}}_{\mathrm{p}}(r).$ Their explicit expressions in terms of multipole fields are given in Appendix A. We have electric (e) and magnetic (m) multipole fields, and the order of a multipole is indicated by $\mathcal{l}=1,2,...\hspace{0.17em}\hspace{0.17em}.$ The amplitudes of the scattered multipole fields are $a_{\mathcal{l}}(\alpha ),$ with $\alpha =e,m,$ and the amplitudes of the particle multipole fields are $b_{\mathcal{l}}(\alpha ).$ These are the Mie coefficients. It is outlined in Appendix B how these amplitudes are computed from the boundary conditions at the surface of the sphere. In most references, these Mie coefficients are expressed in terms of Riccati–Bessel functions and their derivatives. Although such representations are very compact, they are not very suitable for analysis. Appendix B gives various representations of the Mie coefficients. The Mie scattering coefficients take the form

$$a_{\mathcal{l}}(\alpha )={\displaystyle \frac{P_{\mathcal{l}}(\alpha )}{P_{\mathcal{l}}(\alpha )+i{Q}_{\mathcal{l}}(\alpha )}},\hspace{1em}\alpha =e,m,$$

(21)

and for the Mie particle coefficients, we have

$$b_{\mathcal{l}}(\alpha )=-{\displaystyle \frac{i}{n_1\overline{R}}}{\displaystyle \frac{1}{{\Lambda }_{\mathcal{l}}(\alpha )}},\hspace{1em}\alpha =e,m.$$

(22)

Here,

$${\Lambda }_{\mathcal{l}}(\alpha )=P_{\mathcal{l}}(\alpha )+i{Q}_{\mathcal{l}}(\alpha ).$$

(23)

Equations (A34) and (A35) give the most useful representations for the auxiliary functions $P_{\mathcal{l}}(e)$ and $Q_{\mathcal{l}}(e).$ They only involve the spherical Bessel functions $j_{\mathcal{l}}(z)$ and the spherical Neumann functions $n_{\mathcal{l}}(z).$ The function ${\Lambda }_{\mathcal{l}}(e)$ can then be found from Equation (23). Alternatively, Equation (A36) can be used for ${\Lambda }_{\mathcal{l}}(e),$ which involves the spherical Hankel functions $h_{\mathcal{l}}^{(1)}(z).$ These are the functions for electric multipoles. They contain the parameter ${\widehat{\epsilon }}_{\mathrm{p}}.$ As explained in Appendix B, the corresponding magnetic multipole functions simply follow by replacing ${\widehat{\epsilon }}_{\mathrm{p}}$ by ${\widehat{\mu }}_{\mathrm{p}}.$ This implies that any computation performed (as below) for electric multipoles automatically carries over to magnetic multipoles. Oddly enough, this is never recognized in the literature, to the best of our knowledge. The reason is probably that most authors set ${\mu }_1={\mu }_{\mathrm{p}}=1$. This is a very good approximation for most materials, but it destroys the symmetry between electric and magnetic Mie coefficients. As a result, two sets of equations are presented, one for electric multipoles and one for magnetic multipoles, and all calculations need to be performed twice. Our approach is clearly much more efficient, and elegant.

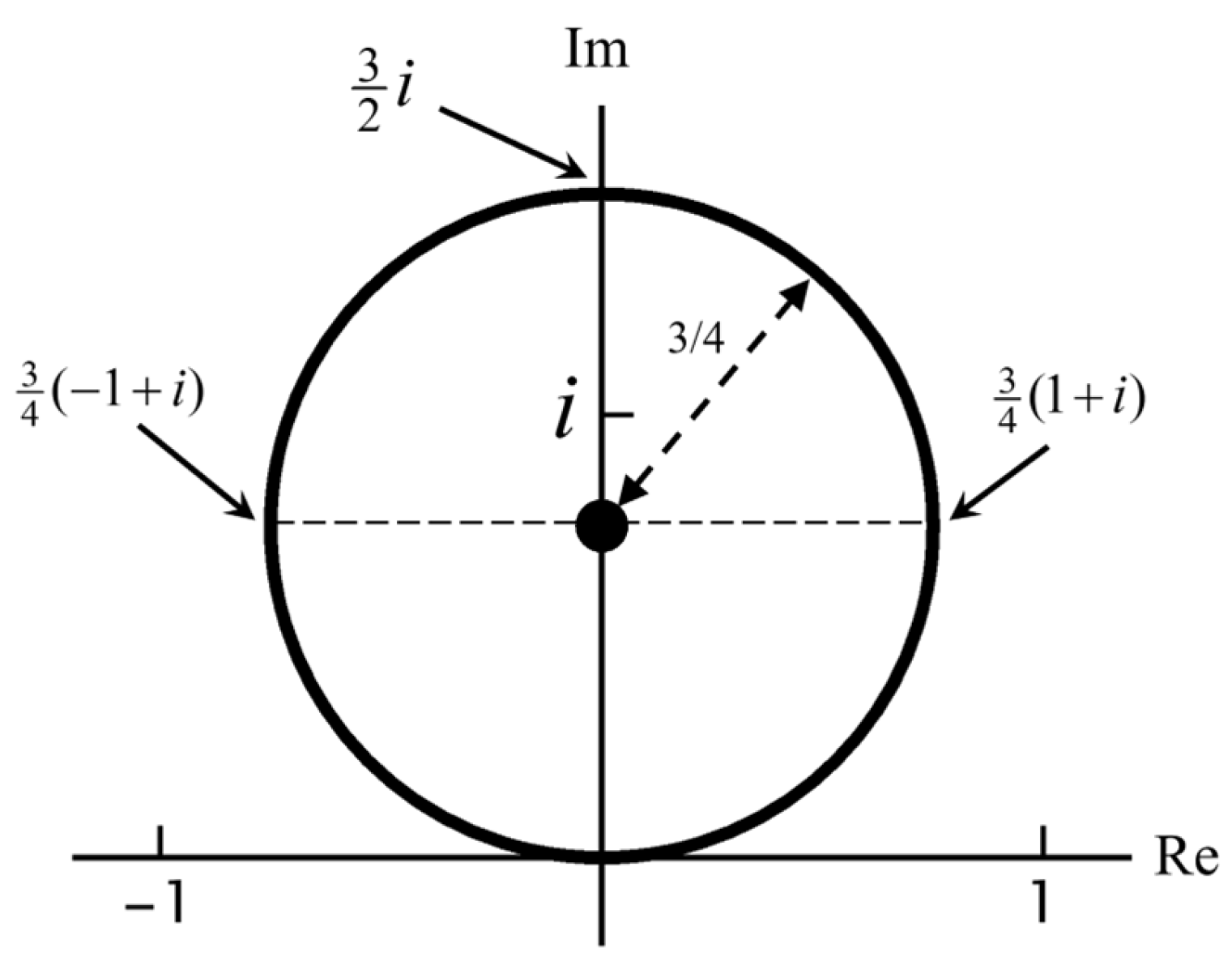
A Mie resonance is defined as a situation where $a_{\mathcal{l}}(\alpha )=1$. It follows from Equation (21) that $Q_{\mathcal{l}}(\alpha )=0$ is a sufficient condition.

The lowest-order multipoles have $\mathcal{l}=1,$ representing electric and magnetic dipole radiation. By far the most studied radiation is electric dipole radiation, both in classical electromagnetism and quantum optics. It is shown in Appendix C that these $\mathcal{l}=1$ multipole fields are identical to the textbook expressions for such radiation, as well as how the dipole moments of the particle can be obtained from the Mie scattering coefficients. For dipoles, the Mie coefficients can be expressed in terms of elementary functions rather than spherical Bessel functions. The explicit results for the dipole Mie coefficients are given in Appendix D.

Of particular interest is the ever-popular perfect conductor. Such material is impenetrable for electromagnetic radiation, and this gives huge simplifications for all types of problems. A perfectly conducting particle is a metallic particle in the limit where the conductivity becomes very large. In Appendix E, we derive the expressions for the Mie coefficients for a perfectly conducting particle.

4. Dielectric Particle

Central to Mie scattering are the Mie coefficients. In this section, we shall restrict the material parameters to

$${\epsilon }_1>0\hspace{1em},\hspace{1em}{\mu }_1>0\hspace{1em},\hspace{1em}{\epsilon }_{\mathrm{p}}>0\hspace{1em},\hspace{1em}{\mu }_{\mathrm{p}}>0.$$

(24)

The conditions ${\epsilon }_{\mathrm{p}}>0$ and ${\mu }_{\mathrm{p}}>0$ represent a typical dielectric particle. None of the parameters has an imaginary part, so there is no absorption, or damping, in the particle or in the embedding medium. Then, the indices of refraction $n_1$ and $n_{\mathrm{p}}$ are positive. The spherical Bessel functions $j_{\mathcal{l}}(z)$ and $n_{\mathcal{l}}(z)$ are real for $z>0$. With Equations (A34) and (A35), we then see that the functions $P_{\mathcal{l}}(\alpha )$ and $Q_{\mathcal{l}}(\alpha )$ are real. Let us now consider a complex number $z$ that can be written as

$$z={\displaystyle \frac{p}{p+iq}}\hspace{1em},\hspace{1em}p,q \mathrm{real}.$$

(25)

It follows immediately that

$$|z-\frac{1}{2}|=\frac{1}{2}.$$

(26)

This represents a circle in the complex plane with radius 1/2 and centered at 1/2. We call this the Mie circle, and this circle is shown in Figure 2.

• In the Mie scattering coefficients, given by Equation (21), the functions $P_{\mathcal{l}}(\alpha )$ and $Q_{\mathcal{l}}(\alpha )$ are real, and therefore they are of the form given in Equation (25). Consequently,

$$|a_{\mathcal{l}}(\alpha )-\frac{1}{2}|=\frac{1}{2},$$

(27)

and we conclude that the Mie scattering coefficients lie on the Mie circle. The location of $a_{\mathcal{l}}(\alpha )$ on the Mie circle depends on the parameters of the system. It should be noted that this conclusion is independent of the detailed forms of $P_{\mathcal{l}}(\alpha )$ and $Q_{\mathcal{l}}(\alpha ).$ We only used the fact that there is no absorption in the system. Moreover, it has been shown [24] that it follows from conservation of energy that the Mie coefficients $a_{\mathcal{l}}(\alpha )$ must lie on the Mie circle when there is no dissipation in the system, without using any assumptions of their explicit form. At a Mie resonance, we have $a_{\mathcal{l}}(\alpha )=1,$ and this is indicated by the white circle in the figure.

From Equation (27), we easily derive

$$\mathrm{Re}{\displaystyle \frac{1}{a_{\mathcal{l}}(\alpha )}},$$

(28)

$$\mathrm{Re}{a}_{\mathcal{l}}(\alpha )\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}|a_{\mathcal{l}}(\alpha ){|}^2.$$

(29)

The Mie particle coefficients $b_{\mathcal{l}}(\alpha )$ do not lie on this circle. A typical example is shown in Figure 3. The black dot on the real axis is the center of the Mie circle. We shall show in Section 8 that $b_{\mathcal{l}}(\alpha )$ rotates around the origin rather than around the Mie circle.

5. Metallic Particle

In this section, we consider the important case of a metallic particle, without dissipation in the particle or the embedding medium. We then have

$${\epsilon }_1>0\hspace{1em},\hspace{1em}{\mu }_1>0\hspace{1em},\hspace{1em}{\epsilon }_{\mathrm{p}}<0\hspace{1em},\hspace{1em}{\mu }_{\mathrm{p}}>0.$$

(30)

The index of refraction $n_1$ of the medium is positive, and the index of refraction of the particle is positive imaginary. We set

$$n_{\mathrm{p}}=i{m}_{\mathrm{p}}\hspace{1em},\hspace{1em}{m}_{\mathrm{p}}>0.$$

(31)

The auxiliary functions $P_{\mathcal{l}}(e),$ $Q_{\mathcal{l}}(e)$ and ${\Lambda }_l(e),$ given by Equations (A34), (A35) and (A36), respectively, contain the spherical Bessel functions $j_{\mathcal{l}}(n_{\mathrm{p}}\overline{R}).$ Since the argument is imaginary, it becomes advantageous to set

$$j_{\mathcal{l}}(n_{\mathrm{p}}\overline{R})=i^{\mathcal{l}}\sqrt{{\displaystyle \frac{\pi }{2m_p\overline{R}}}}{I}_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R}),$$

(32)

with $I_{\mathcal{l}+\frac{1}{2}}(z)$ a modified Bessel function. This function is real for the real argument. We define the functions ${\tilde{P}}_{\mathcal{l}}(e),$ ${\tilde{Q}}_{\mathcal{l}}(e)$ and ${\tilde{\Lambda }}_l(e)$ by

$$P_{\mathcal{l}}(e)=i^{\mathcal{l}}\sqrt{{\displaystyle \frac{\pi }{2m_{\mathrm{p}}\overline{R}}}}{\tilde{P}}_{\mathcal{l}}(e),$$

(33)

$$Q_{\mathcal{l}}(e)=i^{\mathcal{l}}\sqrt{{\displaystyle \frac{\pi }{2m_{\mathrm{p}}\overline{R}}}}{\tilde{Q}}_{\mathcal{l}}(e),$$

(34)

$${\Lambda }_{\mathcal{l}}(e)=i^{\mathcal{l}}\sqrt{{\displaystyle \frac{\pi }{2m_{\mathrm{p}}\overline{R}}}}{\tilde{\Lambda }}_{\mathcal{l}}(e).$$

(35)

The functions ${\tilde{P}}_{\mathcal{l}}(e),$ ${\tilde{Q}}_{\mathcal{l}}(e),$ and ${\tilde{\Lambda }}_l(e)$ then become

$${\tilde{P}}_{\mathcal{l}}(e)=({\widehat{\epsilon }}_{\mathrm{p}}-1)\mathcal{l}{j}_{\mathcal{l}}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R})+m_{\mathrm{p}}\overline{R}\hspace{0.17em}{j}_{\mathcal{l}}(n_1\overline{R})I_{\mathcal{l}-\hspace{0.17em}\frac{1}{2}}(m_{\mathrm{p}}\overline{R})-{\widehat{\epsilon }}_{\mathrm{p}}{n}_1\overline{R}\hspace{0.17em}{j}_{\mathcal{l}-1}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R}),$$

(36)

$${\tilde{Q}}_{\mathcal{l}}(e)=({\widehat{\epsilon }}_{\mathrm{p}}-1)\mathcal{l}{n}_{\mathcal{l}}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R})+m_{\mathrm{p}}\overline{R}\hspace{0.17em}{n}_{\mathcal{l}}(n_1\overline{R})I_{\mathcal{l}-\hspace{0.17em}\frac{1}{2}}(m_{\mathrm{p}}\overline{R})-{\widehat{\epsilon }}_{\mathrm{p}}{n}_1\overline{R}\hspace{0.17em}{n}_{\mathcal{l}-1}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R}),$$

(37)

$${\tilde{\Lambda }}_{\mathcal{l}}(e)=({\widehat{\epsilon }}_{\mathrm{p}}-1)\mathcal{l}{h}_{\mathcal{l}}^{(1)}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R})+m_{\mathrm{p}}\overline{R}\hspace{0.17em}{h}_{\mathcal{l}}^{(1)}(n_1\overline{R})I_{\mathcal{l}-\hspace{0.17em}\frac{1}{2}}(m_{\mathrm{p}}\overline{R})-{\widehat{\epsilon }}_{\mathrm{p}}{n}_1\overline{R}\hspace{0.17em}{h}_{\mathcal{l}-1}^{(1)}(n_1\overline{R})I_{\mathcal{l}+\frac{1}{2}}(m_{\mathrm{p}}\overline{R}).$$

(38)

For magnetic multipoles, we set ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}.$

In terms of these new functions, the Mie scattering coefficients take the form

$$a_{\mathcal{l}}(\alpha )={\displaystyle \frac{{\tilde{P}}_{\mathcal{l}}(\alpha )}{{\tilde{P}}_{\mathcal{l}}(\alpha )+i{\tilde{Q}}_{\mathcal{l}}(\alpha )}},\hspace{1em}\alpha =e,m.$$

(39)

We see from Equations (36) and (37) that ${\tilde{P}}_{\mathcal{l}}(e)$ and ${\tilde{Q}}_{\mathcal{l}}(e)$ are real, and therefore $a_{\mathcal{l}}(\alpha )$ lies on the Mie circle. This reflects again that there is no dissipation in the system. The particle Mie coefficients become

$$b_{\mathcal{l}}(\alpha )={\displaystyle \frac{{(-i)}^{\mathcal{l}+1}}{n_1\overline{R}}}\sqrt{{\displaystyle \frac{2m_{\mathrm{p}}\overline{R}}{\pi }}}{\displaystyle \frac{1}{{\tilde{\Lambda }}_{\mathcal{l}}(\alpha )}}.$$

(40)

The Mie scattering coefficients for a perfect conductor are given by Equations (A86) and (A87). Both for electric and magnetic multipoles, they have the form of $z$ in Equation (25), so if there is no absorption in the embedding medium, then the Mie scattering coefficients for a perfectly conducting particle lie on the Mie circle.

6. Small Particle

Mie theory is particularly important for scattering off small particles. Here, ‘small’ means small in comparison with the wavelength of the radiation. Since we have $\overline{R}=k_{\mathrm{o}}R,$ we consider $\overline{R}<<2\pi .$ The auxiliary functions $P_{\mathcal{l}}(\alpha )$ and $Q_{\mathcal{l}}(\alpha )$ are determined by the spherical Bessel functions $j_{\mathcal{l}}(z)$ and $n_{\mathcal{l}}(z),$ which appear with arguments $n_1\overline{R}$ and $n_{\mathrm{p}}\overline{R}.$ For small $z$, we have

$$j_{\mathcal{l}}(z)={\displaystyle \frac{z^{\mathcal{l}}}{(2\mathcal{l}+1)!!}}\left[1-{\displaystyle \frac{1}{2(2\mathcal{l}+3)}}{z}^2+\mathcal{O}(z^4)\right],$$

(41)

$$n_{\mathcal{l}}(z)=-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{(2\mathcal{l}-1)!!}{z^{\mathcal{l}+1}}}\left[1+{\displaystyle \frac{1}{2(2\mathcal{l}-1)}}{z}^2+\mathcal{O}(z^4)\right].$$

(42)

For $P_{\mathcal{l}}(e)$, we find from Equation (A34)

$$P_{\mathcal{l}}(e)=(1-{\widehat{\epsilon }}_{\mathrm{p}}){\displaystyle \frac{\mathcal{l}}{2\mathcal{l}+1}}{d}_{\mathcal{l}}\hspace{0.17em}{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}}\left[1+\mathcal{O}({\overline{R}}^2)\right].$$

(43)

Here, we have introduced the abbreviation

$$d_{\mathcal{l}}={\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{\displaystyle \frac{\mathcal{l}+1}{{[(2\mathcal{l}+1)!!]}^2}}.$$

(44)

Table 1. Table showing $d_{\mathcal{l}}$ for various values of $\mathcal{l}$.

$\mathcal{l}$	$d_{\mathcal{l}}$
1	0.667
2	0.0333
3	8.47 × 10−4
4	1.26 × 10−5
5	1.22 × 10−7
10	1.22 × 10−19
20	2.50 × 10−49

lists $d_{\mathcal{l}}$ for some $\mathcal{l}$ values. We see that $d_{\mathcal{l}}$ is already very small for moderate $\mathcal{l}$ values. For $Q_{\mathcal{l}}(e)$, we obtain from Equation (A35)

$$Q_{\mathcal{l}}(e)=({\widehat{\epsilon }}_{\mathcal{l}}-{\widehat{\epsilon }}_{\mathrm{p}}){\displaystyle \frac{\mathcal{l}}{2\mathcal{l}+1}}{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}{\displaystyle \frac{1}{n_1\overline{R}}}\left[1+\mathcal{O}({\overline{R}}^2)\right].$$

(45)

The parameter ${\widehat{\epsilon }}_{\mathcal{l}}$ is defined as

$${\widehat{\epsilon }}_{\mathcal{l}}=-{\displaystyle \frac{\mathcal{l}+1}{\mathcal{l}}},$$

(46)

which lies in the range $-2\le {\widehat{\epsilon }}_{\mathcal{l}}<-1$.

The function $P_{\mathcal{l}}(e)$ is $\mathcal{O}({\overline{R}}^{2\mathcal{l}})$ and $Q_{\mathcal{l}}(e)$ is $\mathcal{O}(1/\overline{R}),$ so in ${\Lambda }_{\mathcal{l}}(e)$, we can neglect $P_{\mathcal{l}}(e).$ This yields the results for small $\overline{R}:$

$$a_{\mathcal{l}}(e)=-i{\displaystyle \frac{{\widehat{\epsilon }}_{\mathrm{p}}-1}{{\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}}}{d}_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1}\left[1+\mathcal{O}({\overline{R}}^2)\right],$$

(47)

$$b_{\mathcal{l}}(e)={\displaystyle \frac{1}{{\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}}}{\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{\displaystyle \frac{1}{{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}}}\left[1+\mathcal{O}({\overline{R}}^2)\right].$$

(48)

For $\overline{R}=0$, we have $a_{\mathcal{l}}(e)=0,$ but $b_{\mathcal{l}}(e)$ is finite.

In these expressions, there is a problem when ${\widehat{\epsilon }}_{\mathrm{p}}$ is close to ${\widehat{\epsilon }}_{\mathcal{l}}.$ Since ${\widehat{\epsilon }}_{\mathcal{l}}<0$, this can happen for a metallic particle. We will come back to this issue in Section 11. For magnetic multipoles, we make the replacement ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}.$ Then, $a_{\mathcal{l}}(m)$ becomes proportional to ${\widehat{\mu }}_{\mathrm{p}}-1,$ which presents another problem. For most materials, we have ${\mu }_1\approx 1$ and ${\mu }_{\mathrm{p}}\approx 1$. Then, ${\widehat{\mu }}_{\mathrm{p}}\approx 1,$ and the first term in $a_{\mathcal{l}}(m)$ goes to zero. For this case, we need one more term in the expansion for small $\overline{R}.$ This is found to be

$$a_{\mathcal{l}}(m)={\displaystyle \frac{-i}{{[(2\mathcal{l}+1)!!]}^2}}{\displaystyle \frac{1}{2\mathcal{l}+3}}({\widehat{\epsilon }}_{\mathrm{p}}-1){(n_1\overline{R})}^{2\mathcal{l}+3}\left[1+\mathcal{O}({\overline{R}}^2)\right]\hspace{1em},\hspace{1em}{\widehat{\mu }}_{\mathrm{p}}=1.$$

(49)

For the case of a perfect conductor, we find from Equations (A86) and (A87)

$$a_{\mathcal{l}}(e)=-i{d}_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1}\left[1+\mathcal{O}({\overline{R}}^2)\right],$$

(50)

$$a_{\mathcal{l}}(m)=-i\hspace{0.17em}{\displaystyle \frac{\mathcal{l}}{\mathcal{l}+1}}{d}_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1}\left[1+\mathcal{O}({\overline{R}}^2)\right].$$

(51)

Here, we notice that

$$a_{\mathcal{l}}(e)=-{\displaystyle \frac{\mathcal{l}+1}{\mathcal{l}}}{a}_{\mathcal{l}}(m)+...,$$

(52)

so, the electric and magnetic multipole Mie coefficients have the same order of magnitude [25].

7. Large Particle

We now consider the opposite case of a large particle, so a particle with a radius larger than an optical wavelength. We use the asymptotic formulas for spherical Bessel functions

$$j_{\mathcal{l}}(z)\approx {\displaystyle \frac{1}{z}}\sin (z-\mathcal{l}\pi /2),$$

(53)

$$n_{\mathcal{l}}(z)\approx -{\displaystyle \frac{1}{z}}\cos (z-\mathcal{l}\pi /2).$$

(54)

Rather than considering $a_{\mathcal{l}}(e),$ here it is better to consider

$$2a_{\mathcal{l}}(e)-1={\displaystyle \frac{P_{\mathcal{l}}(e)-i{Q}_{\mathcal{l}}(e)}{P_{\mathcal{l}}(e)+i{Q}_{\mathcal{l}}(e)}}.$$

(55)

When $a_{\mathcal{l}}(e)$ is on the Mie circle, then $2a_{\mathcal{l}}(e)-1$ is on the unit circle, and vice versa. We obtain the following from Equations (A34) and (A35):

$$\begin{array}{l}2a_{\mathcal{l}}(e)-1\approx {(-1)}^{\mathcal{l}+1}{e}^{-2i{n}_1\overline{R}}\\ \times \left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)+i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right]\\ \times {\left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)-i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right]}^{-1}.\end{array}$$

(56)

For the Mie particle coefficients, we find

$$b_{\mathcal{l}}(e)\approx i^{\mathcal{l}}{\widehat{n}}_{\mathrm{p}}{e}^{-i{n}_1\overline{R}}{\left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)-i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right]}^{-1}.$$

(57)

For magnetic multipoles, we replace ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}.$ Figure 4 shows $\mathrm{Re}{a}_3(m)$ and the large-$\overline{R}$ approximation for the parameters given in the caption. We see that, apart from some tiny wiggles, the approximation is excellent for $\overline{R}$ not too small. With increasing $\overline{R},$ the Mie coefficient rotates around the Mie circle, and this gives the oscillations in the figure. At the maxima, we have $\mathrm{Re}{a}_3(m)=1,$ and since this represents a point on the Mie circle, we have $\mathrm{Im}{a}_3(m)=0$. Therefore, $a_3(m)=1$ at a maximum in the graph, and this represents a Mie resonance. The above expressions for large $\overline{R}$ hold for any combination of parameters. Let us now consider a metallic particle, as in Section 5. The index of refraction $n_{\mathrm{p}}$ of the particle is positive imaginary, and we set $n_{\mathrm{p}}=i{m}_{\mathrm{p}},$ with $m_{\mathrm{p}}>0$. We then have for the sines and cosines in Equations (56) and (57)

$$\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\to \frac{1}{2}{i}^{\mathcal{l}}{e}^{m_{\mathrm{p}}\overline{R}},$$

(58)

$$\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\to \frac{1}{2}{i}^{\mathcal{l}+1}{e}^{m_{\mathrm{p}}\overline{R}},$$

(59)

since $\exp (-m_{\mathrm{p}}\overline{R})\to 0$. Equation (56) simplifies to

$$2a_{\mathcal{l}}(e)-1\approx {(-1)}^{\mathcal{l}+1}{e}^{-2i{n}_1\overline{R}}{\displaystyle \frac{m_{\mathrm{p}}+i{n}_1{\widehat{\epsilon }}_{\mathrm{p}}}{m_{\mathrm{p}}-i{n}_1{\widehat{\epsilon }}_{\mathrm{p}}}}.$$

(60)

The right-hand side lies on the unit circle, so $a_{\mathcal{l}}(e)$ lies approximately on the Mie circle. Since for a metallic particle, $a_{\mathcal{l}}(e)$ lies on the Mie circle for all $\overline{R},$ this has to be so. Equation (57) becomes

$$b_{\mathcal{l}}(e)\approx e^{-i{n}_1\overline{R}}{e}^{-m_{\mathrm{p}}\overline{R}}{\displaystyle \frac{2m_{\mathrm{p}}}{m_{\mathrm{p}}-i{n}_1{\widehat{\epsilon }}_{\mathrm{p}}}}.$$

(61)

Rather than circling around the origin, as in Figure 3, $b_{\mathcal{l}}(e)$ spirals into the origin for a metallic particle, due to the overall factor $\exp (-i{m}_{\mathrm{p}}\overline{R}).$ This is illustrated in Figure 5. For magnetic multipoles, we replace ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}$ in Equations (60) and (61). For a perfect conductor, we find the simple result

$$2a_{\mathcal{l}}(e)-1\approx {(-1)}^{\mathcal{l}}{e}^{-2i{n}_1\overline{R}},$$

(62)

$$2a_{\mathcal{l}}(m)-1\approx {(-1)}^{\mathcal{l}+1}{e}^{-2i{n}_1\overline{R}}.$$

(63)

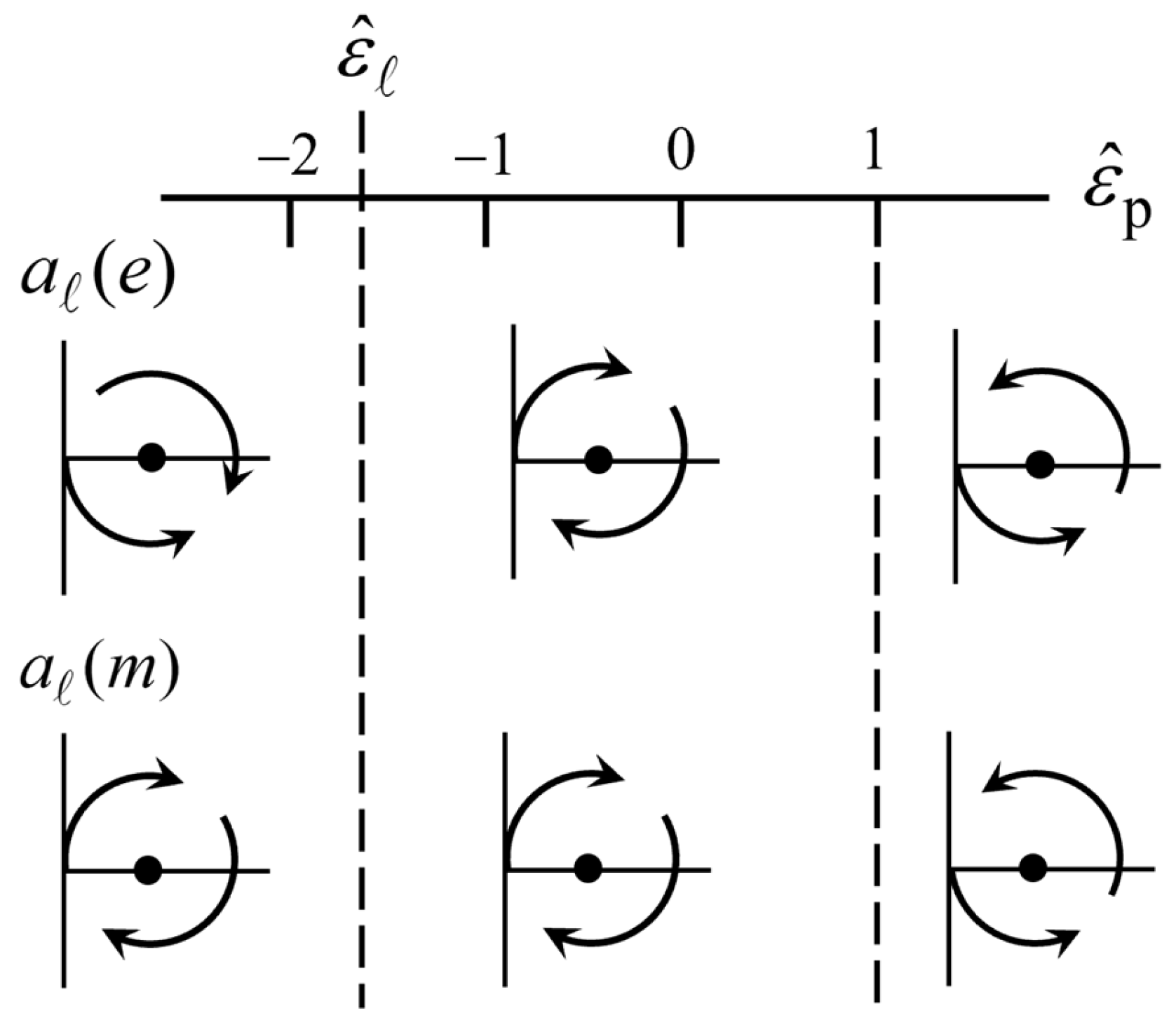
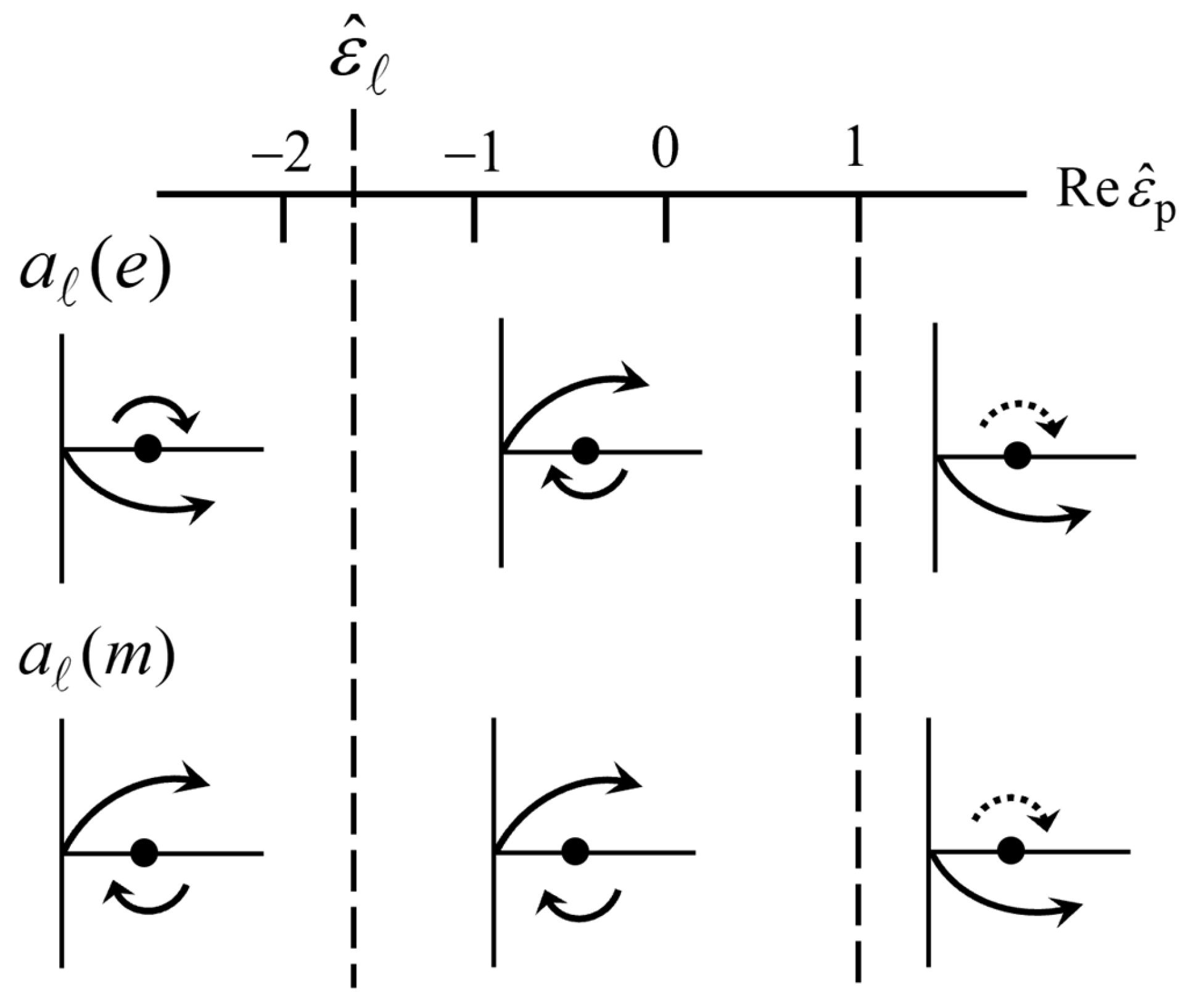
8. Rotation Directions

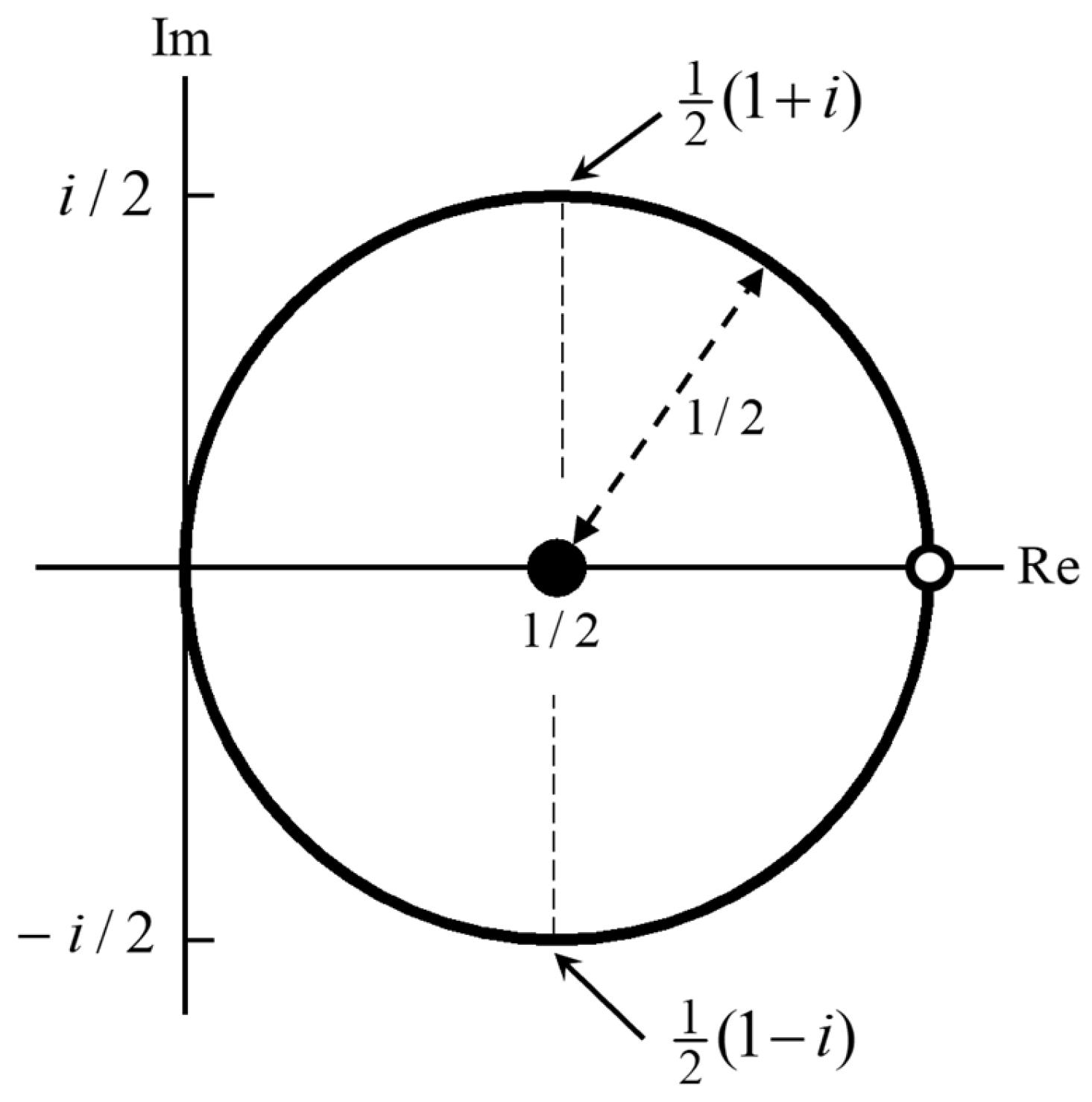
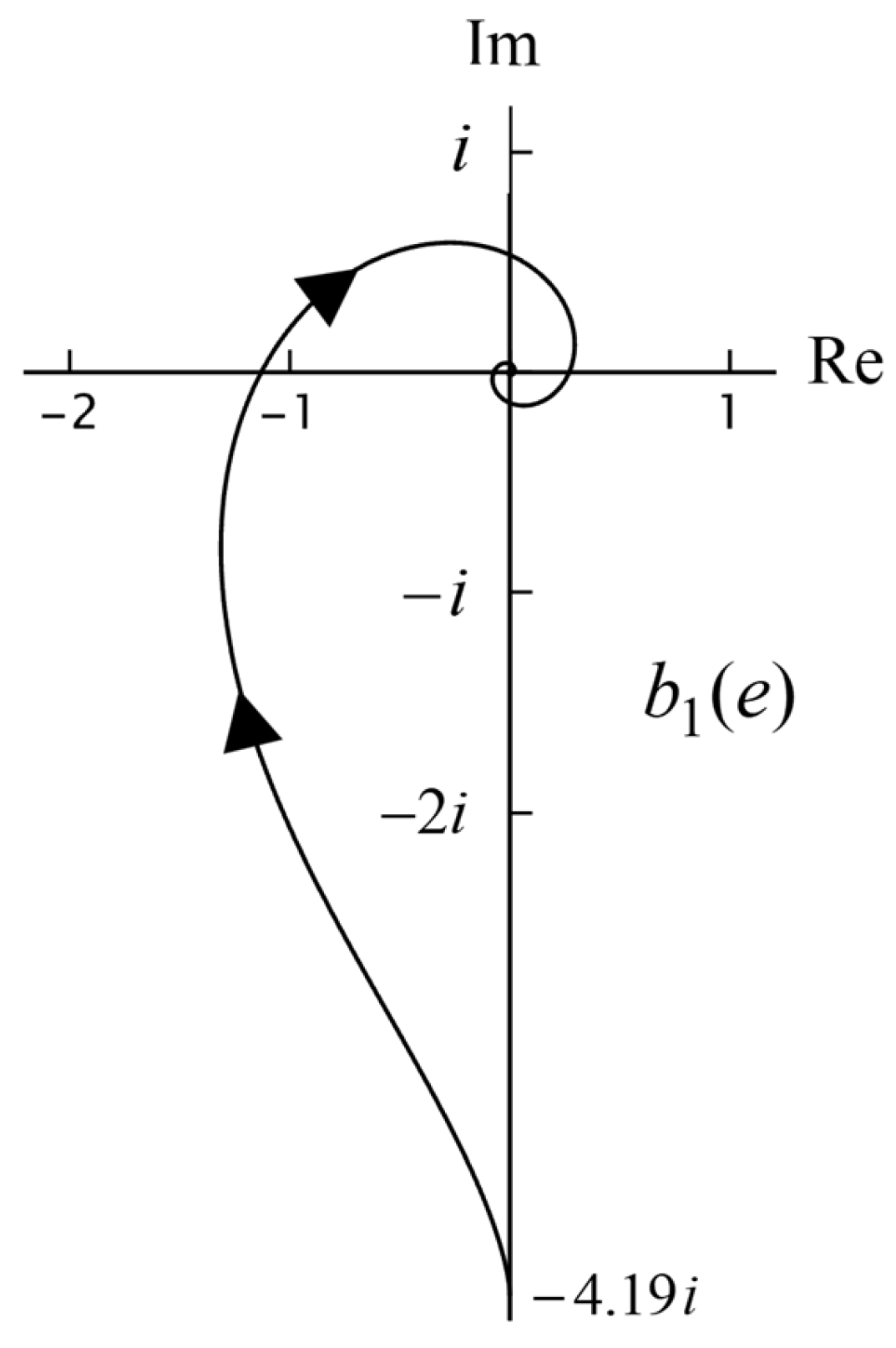
When there is no dissipation in the medium or particle, then $a_{\mathcal{l}}(\alpha )$ lies on the Mie circle. For $\overline{R}=0$, we have $a_{\mathcal{l}}(\alpha )=0,$ and with increasing $\overline{R}$, the particle moves around the Mie circle. We shall now consider this in more detail. In order to simplify the discussion somewhat, we shall assume

$${\epsilon }_1>0\hspace{1em},\hspace{1em}{\mu }_1=1\hspace{1em},\hspace{1em}{\epsilon }_{\mathrm{p}} \mathrm{real}\hspace{1em},\hspace{1em}{\mu }_{\mathrm{p}}=1.$$

(64)

For ${\epsilon }_{\mathrm{p}}$ positive, this corresponds to a dielectric particle, as in Section 4, and for ${\epsilon }_{\mathrm{p}}$ negative, this is a metallic particle, as in Section 5.

For $\overline{R}$ small, $a_{\mathcal{l}}(e)$ is given by Equation (47). We recall that ${\widehat{\epsilon }}_{\mathcal{l}}$ from Equation (46) lies in the range $-2\le {\widehat{\epsilon }}_{\mathcal{l}}<-1$. If ${\widehat{\epsilon }}_{\mathrm{p}}$ is smaller than ${\widehat{\epsilon }}_{\mathcal{l}},$ then ${\widehat{\epsilon }}_{\mathrm{p}}$ is smaller than unity, and the overall factor $({\widehat{\epsilon }}_{\mathrm{p}}-1)/({\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}})$ is positive. This means that $a_{\mathcal{l}}(e)$ is negative imaginary, so the rotation around the Mie circle starts counterclockwise. For ${\widehat{\epsilon }}_{\mathrm{p}}>1$, we also have ${\widehat{\epsilon }}_{\mathrm{p}}>{\widehat{\epsilon }}_{\mathcal{l}},$ and again $({\widehat{\epsilon }}_{\mathrm{p}}-1)/({\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}})>0,$ and so the rotation is initially counterclockwise. For the region in between, e.g., ${\widehat{\epsilon }}_{\mathcal{l}}<{\widehat{\epsilon }}_{\mathrm{p}}<1$, we have $({\widehat{\epsilon }}_{\mathrm{p}}-1)/({\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}})<0,$ so $a_{\mathcal{l}}(e)$ is positive imaginary, and the rotation is clockwise. For $a_{\mathcal{l}}(m)$, we need to consider Equation (49). For ${\widehat{\epsilon }}_{\mathrm{p}}>1,$ $a_{\mathcal{l}}(m)$ is negative imaginary, and the rotation starts counterclockwise. For ${\widehat{\epsilon }}_{\mathrm{p}}<1,$ this becomes clockwise. 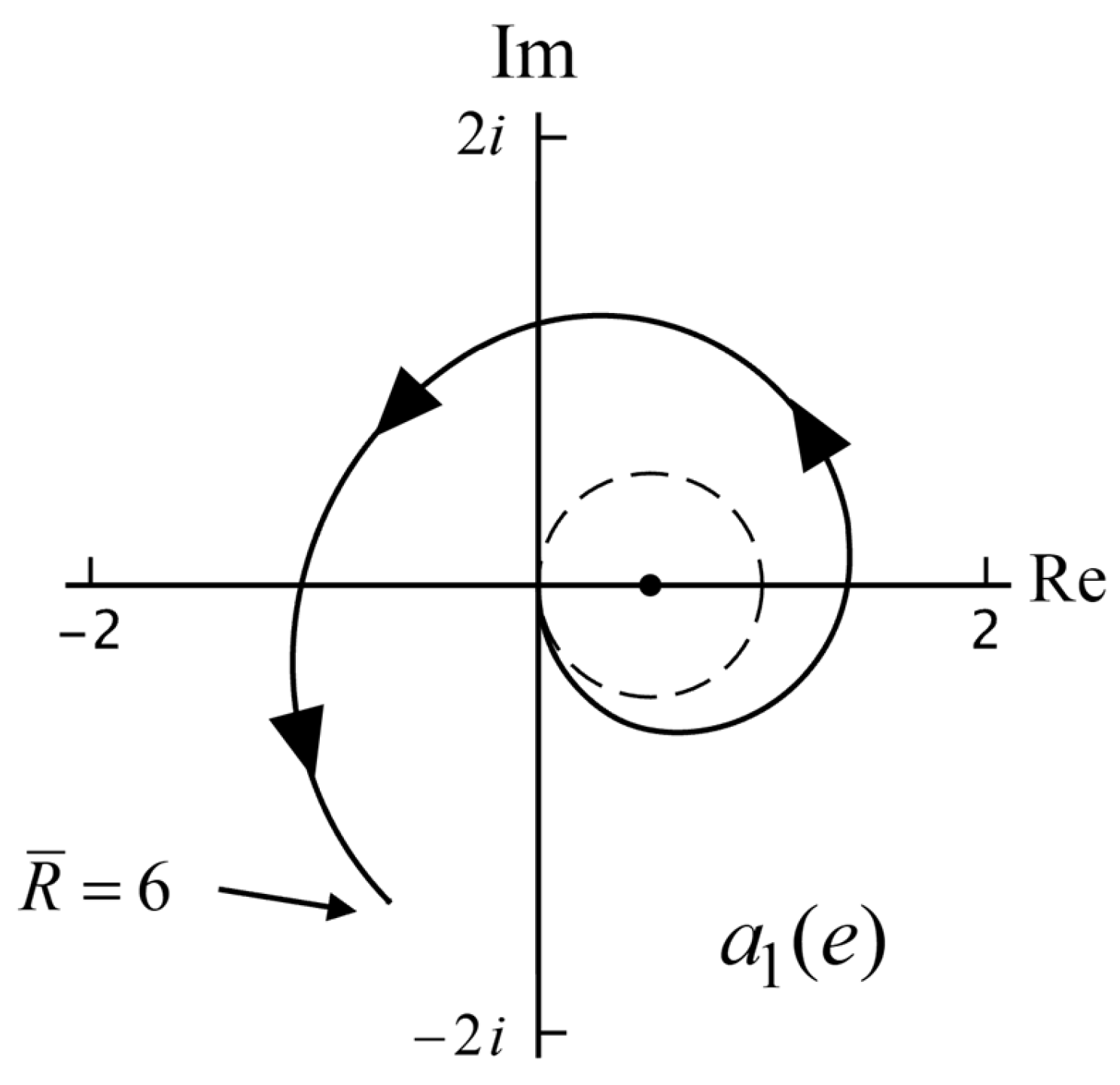This is made much clearer by looking at Figure 6.

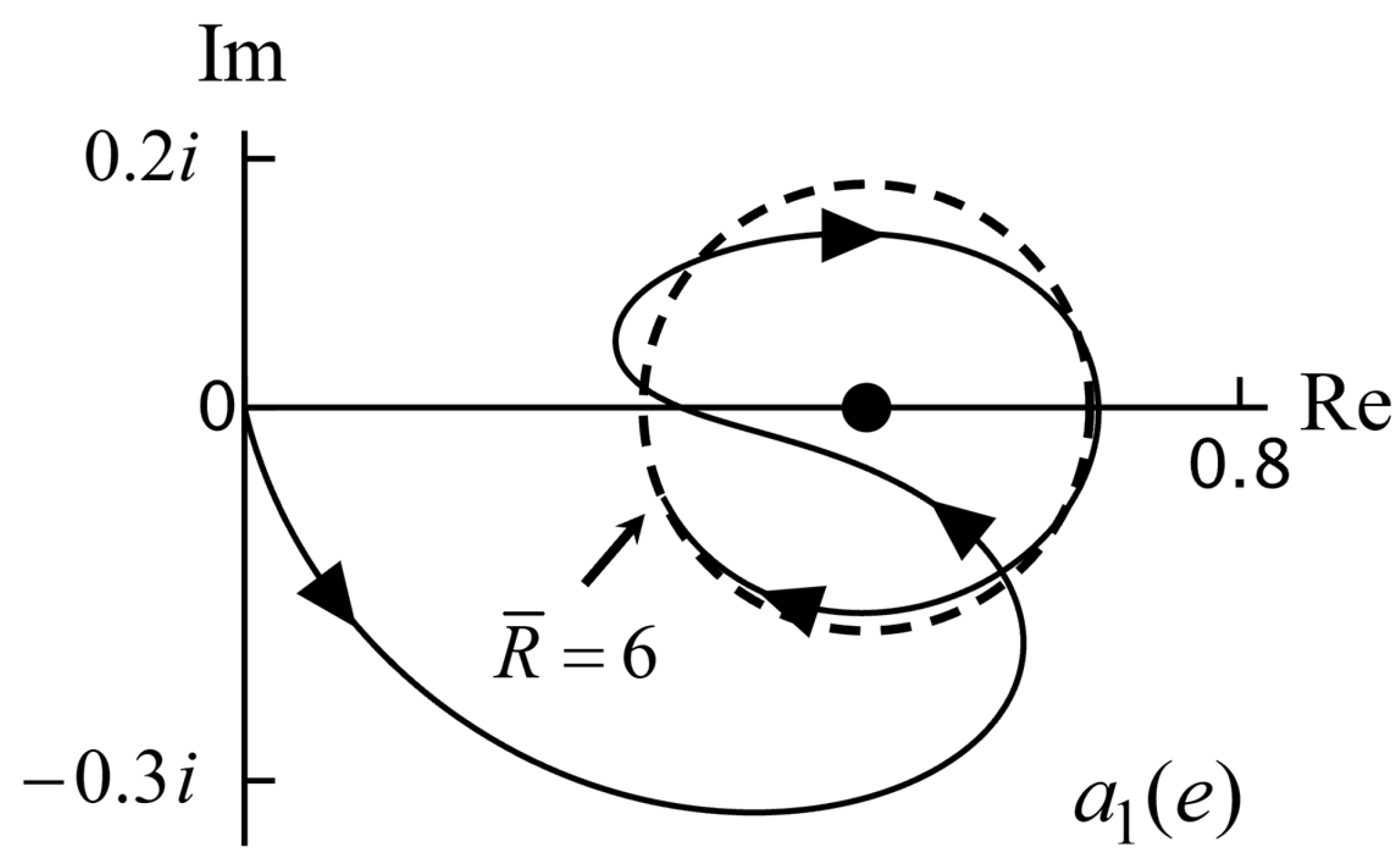
For large $\overline{R}$, we need to consider Equation (56) for ${\widehat{\epsilon }}_{\mathrm{p}}>0$. Then, we also have ${\widehat{n}}_{\mathrm{p}}>0$. With $n_1>0,$ the factor $\exp (-2i{n}_1\overline{R})$ rotates around the unit circle in the clockwise direction with increasing $\overline{R}.$ The period $\Delta \hspace{0.17em}\overline{R}$ for this rotation follows from $2n_1\Delta \hspace{0.17em}\overline{R}=2\pi .$ The first factor in square brackets in Equation (56) is periodic with $\Delta \hspace{0.17em}\overline{R}$ given by $n_{\mathrm{p}}\Delta \hspace{0.17em}\overline{R}=2\pi .$ Due to the factors ${\widehat{n}}_{\mathrm{p}}$ and ${\widehat{\epsilon }}_{\mathrm{p}},$ this factor rotates over an ellipse, and it goes counterclockwise. The factor in square brackets in the denominator also gives a counterclockwise rotation with $n_{\mathrm{p}}\Delta \hspace{0.17em}\overline{R}=2\pi .$ The two factors combined then give a counterclockwise rotation with $2n_{\mathrm{p}}\Delta \hspace{0.17em}\overline{R}=2\pi .$ The period for the rotation of $2a_{\mathcal{l}}(e)-1$ around the unit circle then becomes $2(n_{\mathrm{p}}-n_1)\Delta \hspace{0.17em}\overline{R}=2\pi .$ We conclude that for $n_{\mathrm{p}}>n_1$, the rotation is counterclockwise, and for $n_{\mathrm{p}}<n_1$, the rotation is clockwise. Since we consider ${\mu }_1={\mu }_{\mathrm{p}}=1$ in this section, this is equivalent to ${\widehat{\epsilon }}_{\mathrm{p}}>1$ and ${\widehat{\epsilon }}_{\mathrm{p}}<1,$ respectively, (and ${\widehat{\epsilon }}_{\mathrm{p}}>0$ in this paragraph). For large $\overline{R}$ and ${\widehat{\epsilon }}_{\mathrm{p}}<0$, we have a metallic particle, and the result for $\overline{R}$ large is given by Equation (60). The only rotation is due to the factor $\exp (-2i{n}_1\overline{R}),$ and this rotates clockwise.

For $a_{\mathcal{l}}(m),$ with ${\widehat{\mu }}_{\mathrm{p}}=1,$ we have Equation (49) for $\overline{R}$ small. The rotation direction only depends on ${\widehat{\epsilon }}_{\mathrm{p}}-1,$ so we have counterclockwise for ${\widehat{\epsilon }}_{\mathrm{p}}>1$ and clockwise for ${\widehat{\epsilon }}_{\mathrm{p}}<1$. For $\overline{R}$ large, there is no difference in the rotation direction between $a_{\mathcal{l}}(m)$ and $a_{\mathcal{l}}(e),$ given ${\widehat{\epsilon }}_{\mathrm{p}}.$

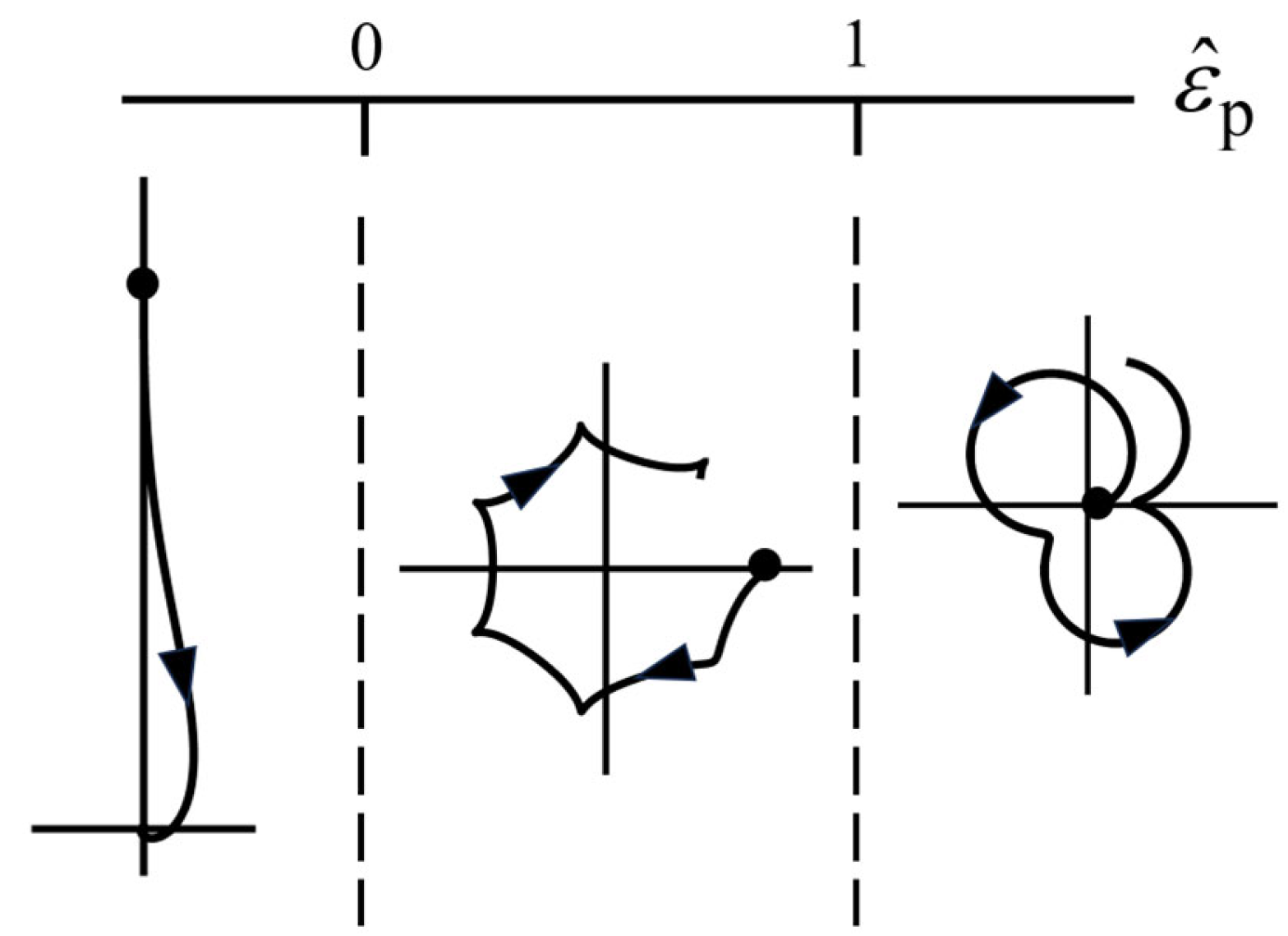
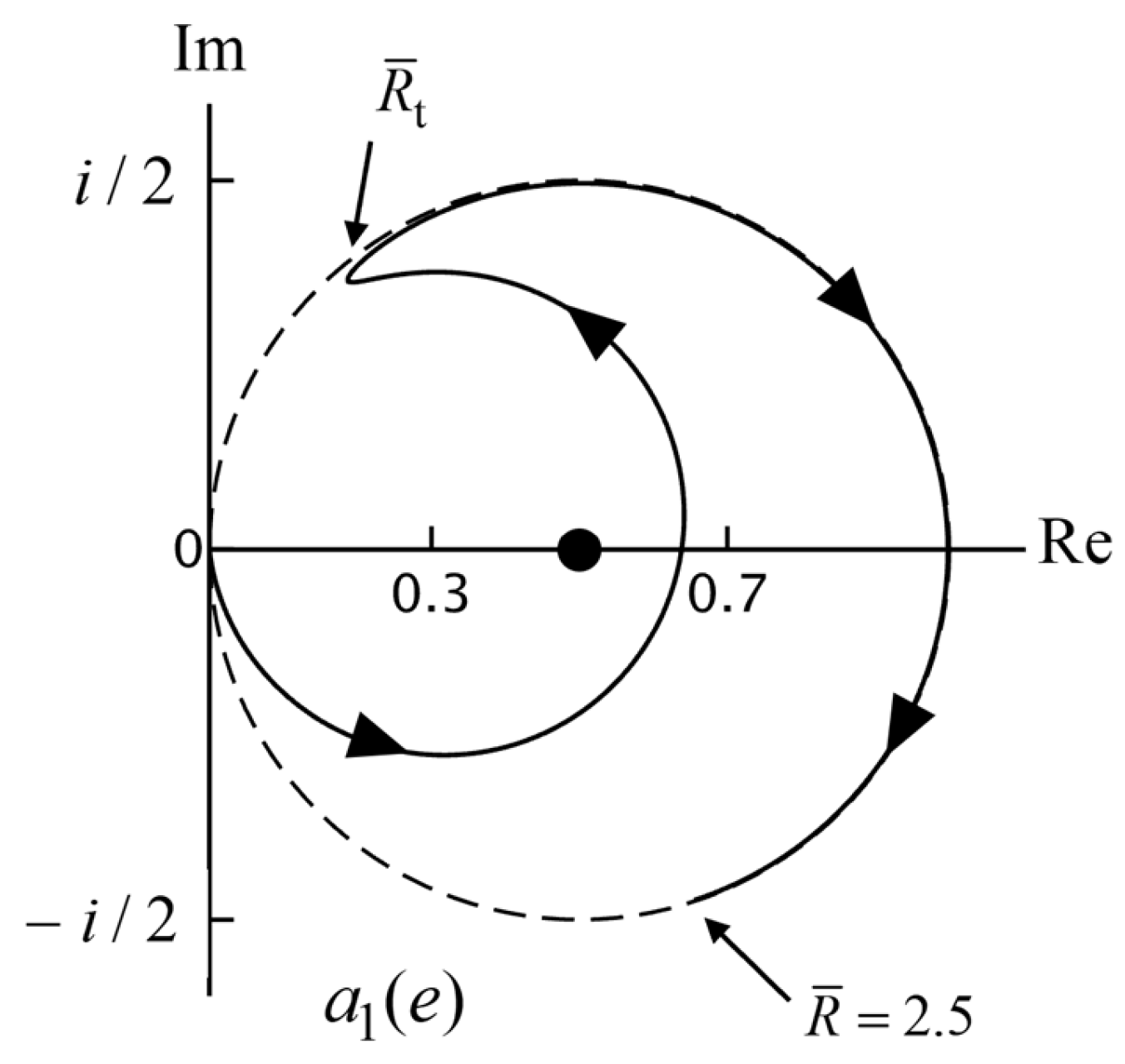
The Mie particle coefficients $b_{\mathcal{l}}(e)$ for small $\overline{R}$ are given by Equation (48), and with ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}=1$, we find the expression for $b_{\mathcal{l}}(m).$ These functions are finite for $\overline{R}=0$. For ${\widehat{\epsilon }}_{\mathrm{p}}$ positive, we have ${\widehat{n}}_{\mathrm{p}}$ positive, and ${\widehat{\epsilon }}_{\mathrm{p}}-{\epsilon }_{\mathcal{l}}>0,$ $1-{\epsilon }_{\mathcal{l}}>0,$ so $b_{\mathcal{l}}(\alpha )$ lies on the positive real axis. For ${\widehat{\epsilon }}_{\mathrm{p}}$ negative, we have ${\widehat{n}}_{\mathrm{p}}=i(m_{\mathrm{p}}/n_1),$ and so $b_{\mathcal{l}}(\alpha )$ is proportional to ${(-i)}^{\mathcal{l}}.$ Therefore, $b_{\mathcal{l}}(\alpha )$ lies on the real or imaginary axis, either at the positive or negative side, and when we increase the value of $\mathcal{l}$ by unity, the picture rotates clockwise over ${90}^{\circ }.$ The Mie particle coefficients do not have a specific rotation direction for $\overline{R}$ small.

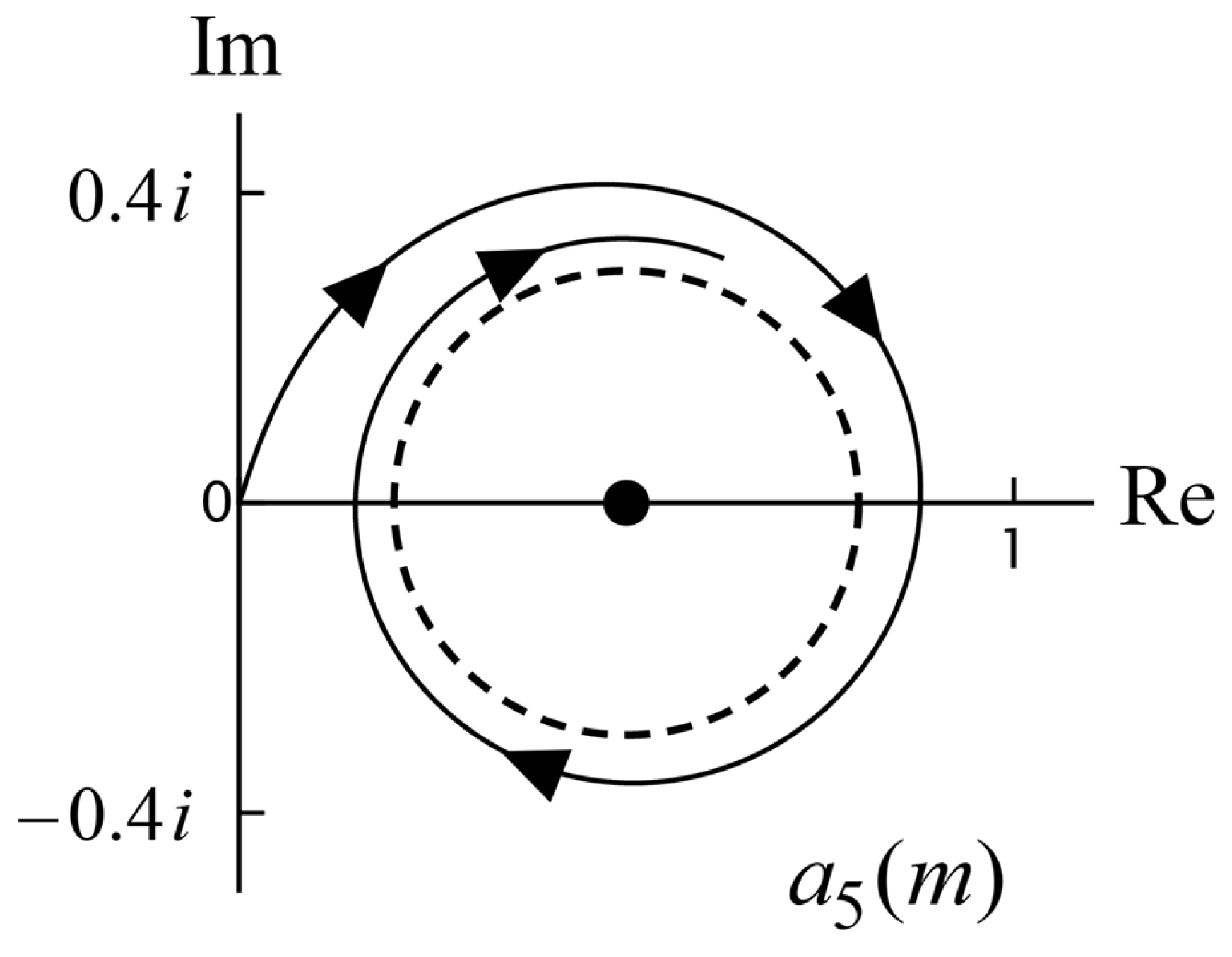
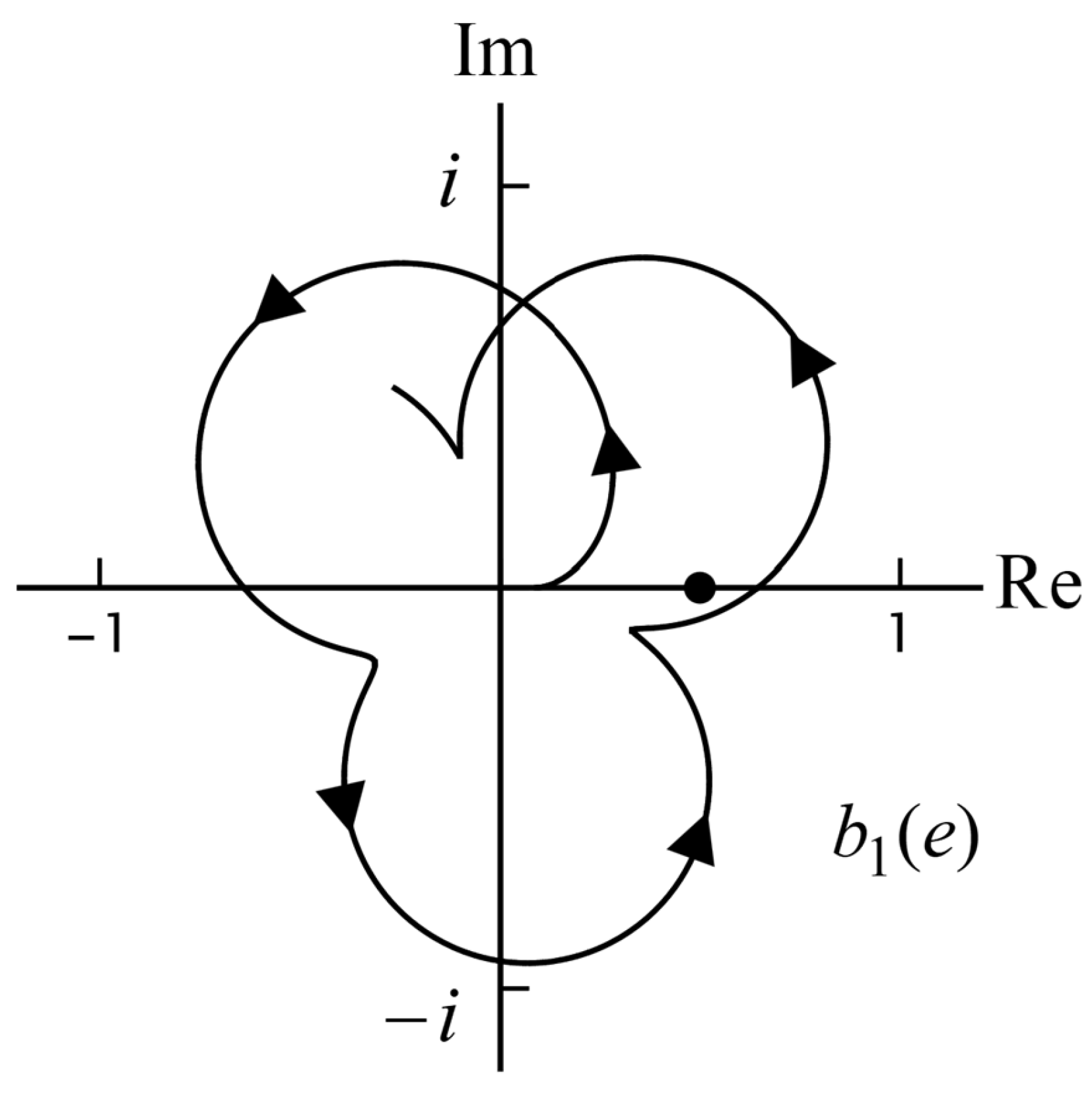
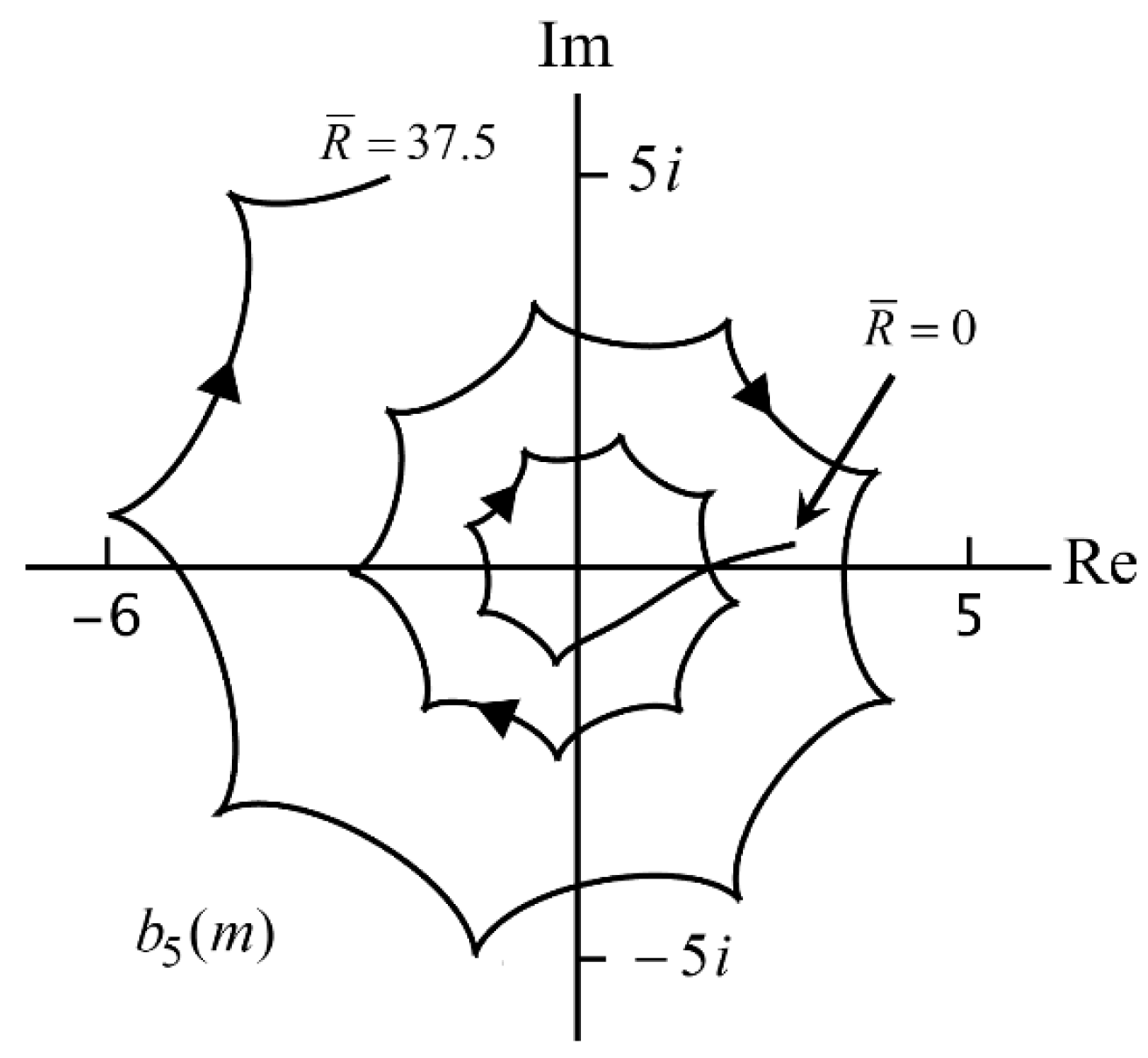
For $\overline{R}$ large, we consider Equation (57), when ${\widehat{\epsilon }}_{\mathrm{p}}>0$. With the same arguments as above for $2a_{\mathcal{l}}(\alpha )-1,$ we now find that $b_{\mathcal{l}}(\alpha )$ rotates clockwise for $0<{\widehat{\epsilon }}_{\mathrm{p}}<1$ and counterclockwise for ${\widehat{\epsilon }}_{\mathrm{p}}>1$. However, the rotation is around the origin and not around the Mie circle, and the path is not circular. 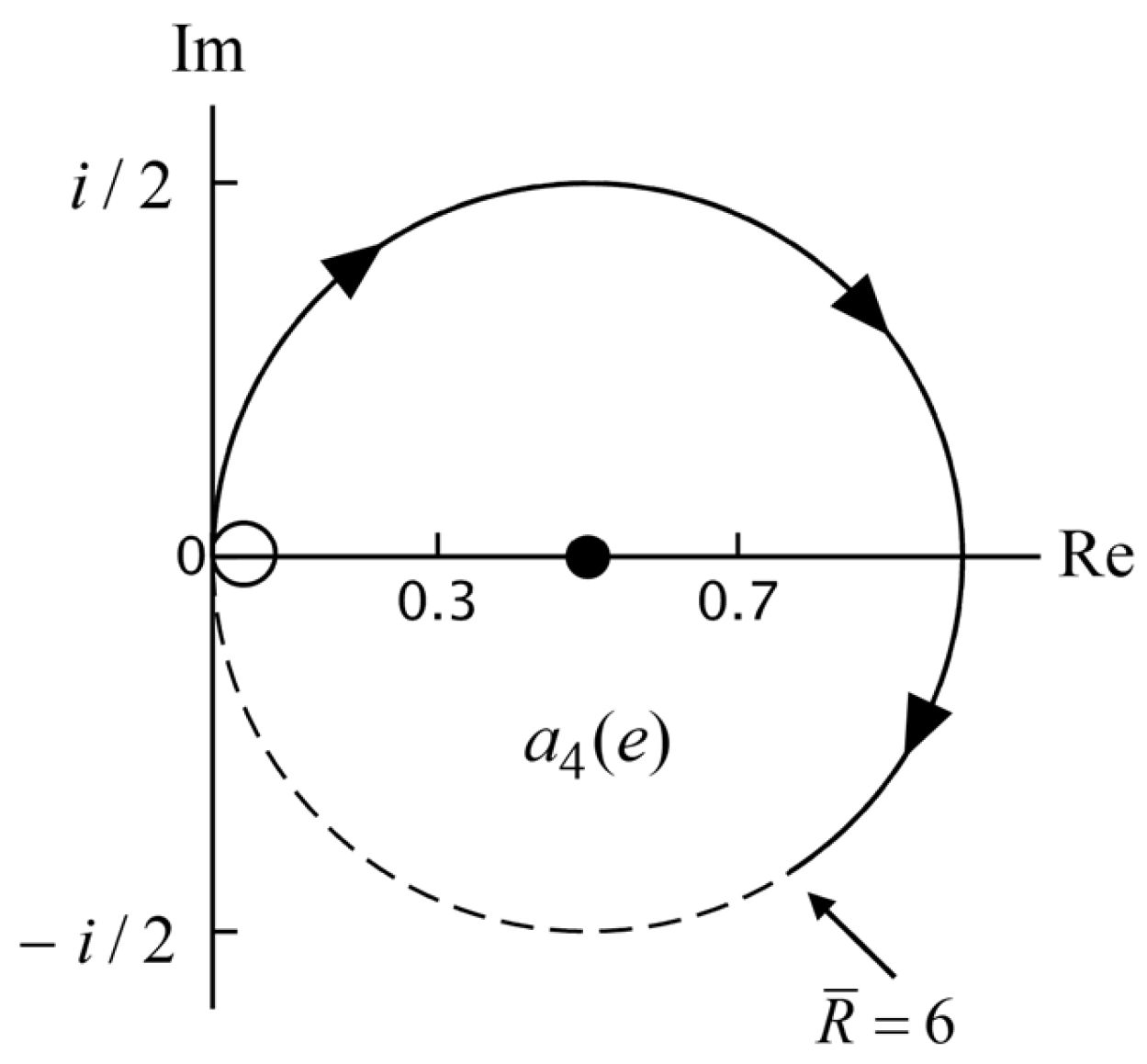An example is shown in Figure 3. 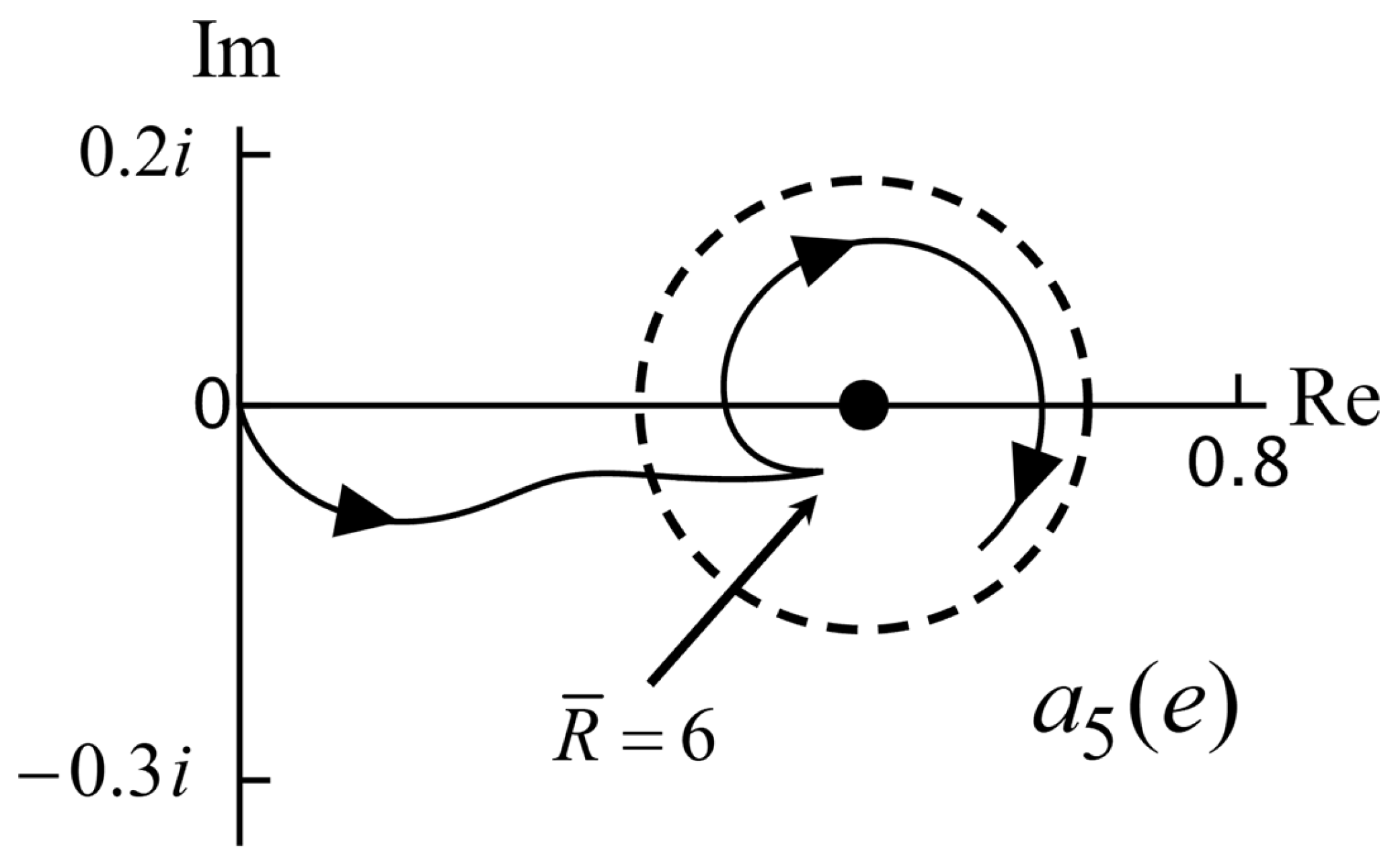For ${\widehat{\epsilon }}_{\mathrm{p}}<0,$ we look at Equation (61). The only rotation comes from $\exp (-i{n}_1\overline{R}),$ and this gives a clockwise rotation. For large $\overline{R}$, we have $b_{\mathcal{l}}(\alpha )\to 0,$ due to the factor $\exp (-m_{\mathrm{p}}\overline{R}).$ An example is show in Figure 5. The three possibilities are illustrated in Figure 7.

For a perfect conductor, the rotation directions of $a_{\mathcal{l}}(\alpha )$ are the same as those in Figure 6 for ${\widehat{\epsilon }}_{\mathrm{p}}<{\epsilon }_{\mathcal{l}}.$

9. Turning Points

The rotation directions of the Mie scattering coefficients $a_{\mathcal{l}}(\alpha )$ around the Mie circle are depicted in Figure 6. We see that the initial rotation directions ($\overline{R}\to 0$) and the final rotation directions ($\overline{R}\to \infty$) are the same, except for $a_{\mathcal{l}}(e)$ when ${\widehat{\epsilon }}_{\mathrm{p}}<{\epsilon }_{\mathcal{l}}.$ In this case, the rotation starts counterclockwise and ends clockwise. Therefore, the curve has a turning point ${\overline{R}}_{\mathrm{t}}$ at which the rotation direction reverses. We shall now examine this in detail. 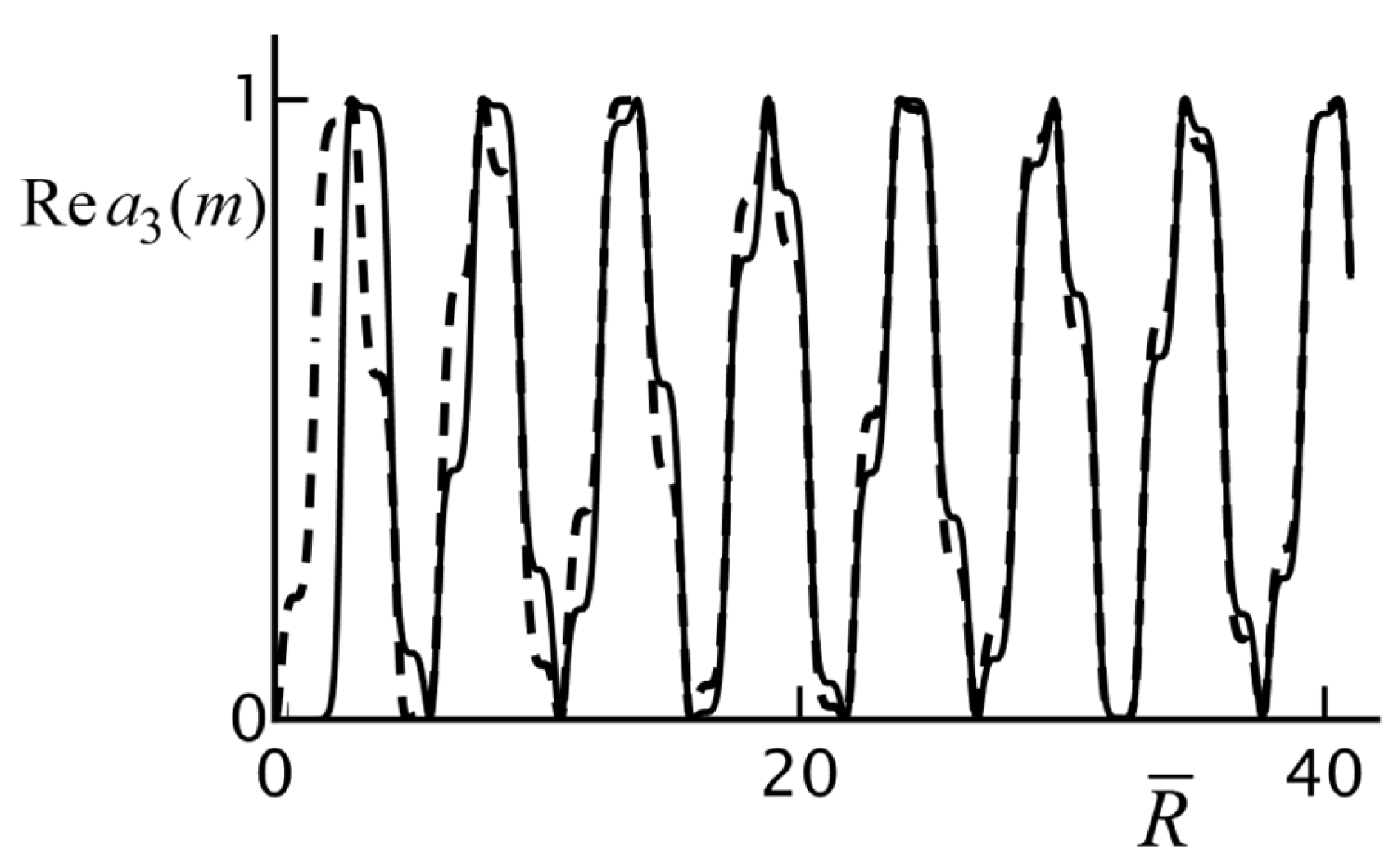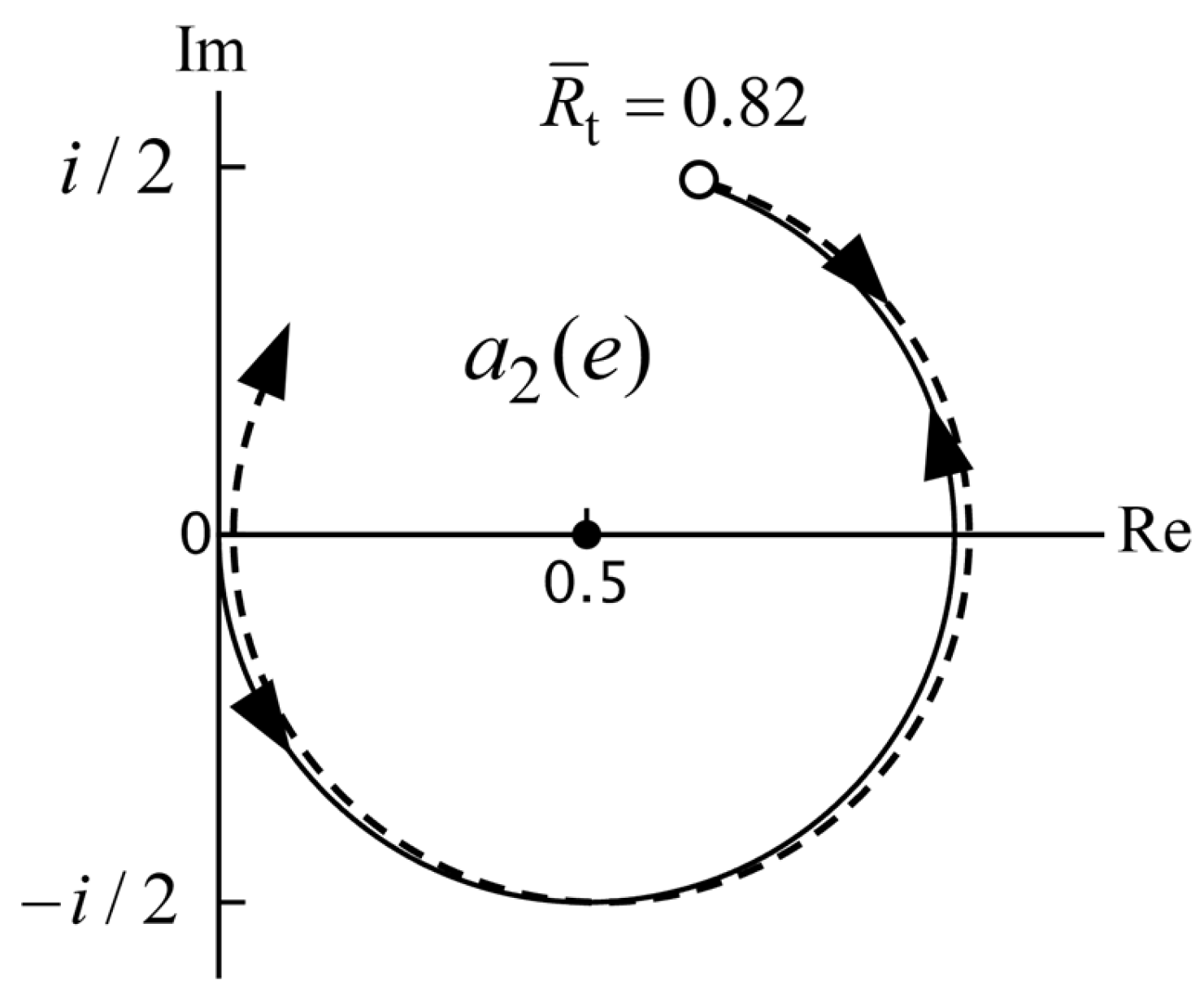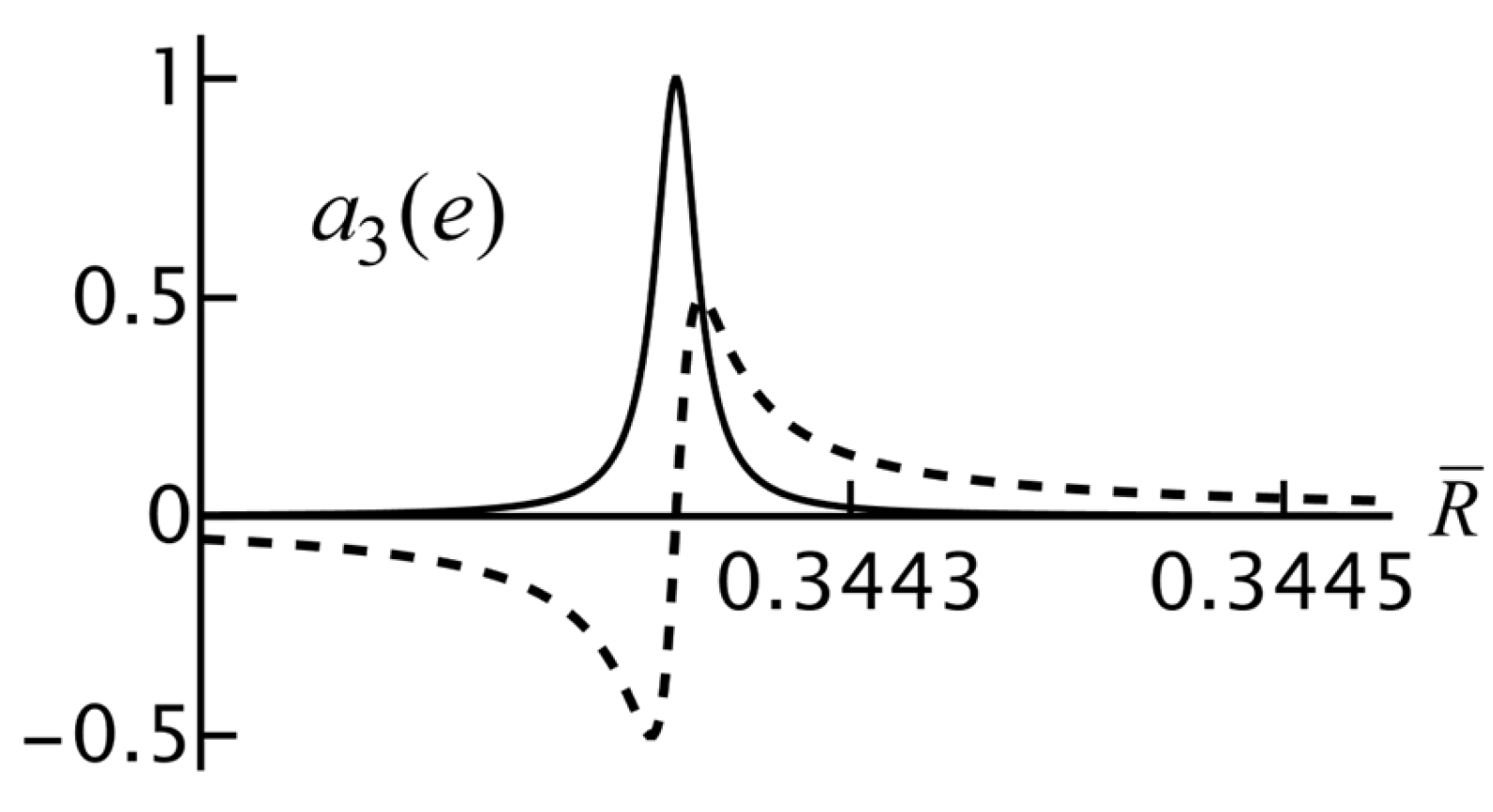Figure 8 shows an example. At a turning point, it has to hold that

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}\overline{R}}}{a}_{\mathcal{l}}(e)=0.$$

(65)

The derivatives of the Mie scattering coefficients with respect to $\overline{R}$ are derived in Appendix F. In this section, we shall assume ${\epsilon }_1>0,$ ${\mu }_1=1,$ ${\mu }_{\mathrm{p}}=1,$ and we have ${\widehat{\epsilon }}_{\mathrm{p}}<0$ for a turning point to occur. Since $a_{\mathcal{l}}(e)$ is complex, Equation (65) has to hold for the real and imaginary parts of $a_{\mathcal{l}}(e)$ simultaneously. 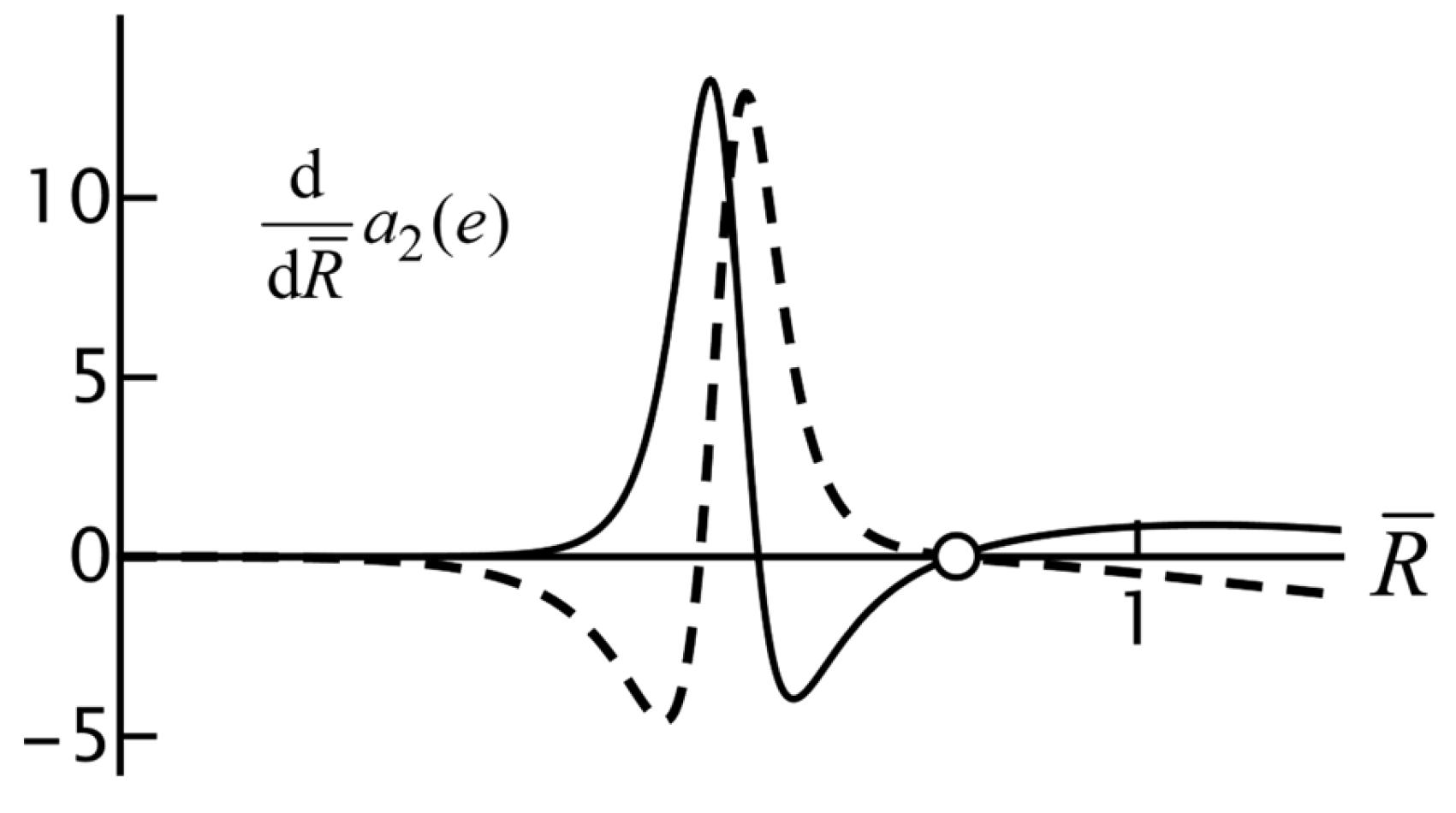Figure 9 shows the real and imaginary parts of the derivative of $a_2(e)$ for the same parameters as in Figure 8. We see that near $\overline{R}=0.82,$ both the real and imaginary parts of $\mathrm{d}{a}_2(e)/\mathrm{d}\overline{R}$ are zero, so this is the turning point ${\overline{R}}_{\mathrm{t}}.$

Near a turning point, $\overline{R}$ is neither small nor large, so we need to consider the exact solution for all $\overline{R}.$ From Equation (A93), we see that for

$${\varsigma }_{\mathcal{l}}{(n_{\mathrm{p}}\overline{R})}^2+{\widehat{\epsilon }}_{\mathrm{p}}\mathcal{l}(\mathcal{l}+1)j_{\mathcal{l}}{(n_{\mathrm{p}}\overline{R})}^2=0,$$

(66)

the derivative of $a_{\mathcal{l}}(e)$ is zero. Under this condition, the real and imaginary parts are simultaneously zero. Here, we have $n_{\mathrm{p}}=i{m}_{\mathrm{p}},$ with $m_{\mathrm{p}}>0,$ so the arguments of ${\varsigma }_{\mathcal{l}}$ and $j_{\mathcal{l}}$ are positive imaginary. Then, it is advantageous to switch to modified Bessel functions, as in Equation (32). Equation (66) becomes

$${\left[m_{\mathrm{p}}\overline{R}\hspace{0.17em}{I}_{\mathcal{l}- \frac{1}{2}}(m_{\mathrm{p}}\overline{R})-\mathcal{l}\hspace{0.17em}{I}_{\mathcal{l}+ \frac{1}{2}}(m_{\mathrm{p}}\overline{R})\right]}^2={\alpha }_{\mathcal{l}}^2{I}_{\mathcal{l}+ \frac{1}{2}}{(m_{\mathrm{p}}\overline{R})}^2.$$

(67)

Here, we have set

$${\alpha }_{\mathcal{l}}={\displaystyle \frac{m_{\mathrm{p}}}{n_1}}\sqrt{\mathcal{l}(\mathcal{l}+1)},$$

(68)

which is positive. Setting $y=m_{\mathrm{p}}\overline{R}$ simplifies the appearance of Equation (67) to

$${\left[y{I}_{\mathcal{l}-\frac{1}{2}}(y)-\mathcal{l}{I}_{\mathcal{l}+\frac{1}{2}}(y)\right]}^2={\alpha }_{\mathcal{l}}^2{I}_{\mathcal{l}+\frac{1}{2}}{(y)}^2.$$

(69)

Both sides of the equation are squares. With recursion relations for modified Bessel functions, it can be shown that

$$y{I}_{\mathcal{l}-\frac{1}{2}}(y)-\mathcal{l}{I}_{\mathcal{l}+\frac{1}{2}}(y)=y{I}_{\mathcal{l}+\frac{1}{2}}{(y)}^{\prime }+\frac{1}{2}{I}_{\mathcal{l}+\frac{1}{2}}(y).$$

(70)

With the known series expansions of the modified Bessel functions, we find easily that $I_{\mathcal{l}+ \frac{1}{2}}(y)$ and its derivative are positive for $y>0$. Therefore, the right-hand side of Equation (70) is positive. Then, the expression in square brackets on the left-hand side of Equation (69) is positive, as is ${\alpha }_{\mathcal{l}}{I}_{\mathcal{l}+ \frac{1}{2}}(y)$ on the right-hand side. Consequently, we can take the square roots of both sides as

$$y{I}_{\mathcal{l}-\frac{1}{2}}(y)-\mathcal{l}{I}_{\mathcal{l}+\frac{1}{2}}(y)={\alpha }_{\mathcal{l}}{I}_{\mathcal{l}+\frac{1}{2}}(y).$$

(71)

We now set

$$H_{\mathcal{l}}(y)=y{I}_{\mathcal{l}-\frac{1}{2}}(y)-(\mathcal{l}+{\alpha }_{\mathcal{l}})I_{\mathcal{l}+\frac{1}{2}}(y).$$

(72)

A turning point then corresponds to a solution of

$$H_{\mathcal{l}}(y)=0.$$

(73)

For a solution $y,$ the turning point is

$${\overline{R}}_{\mathrm{t}}={\displaystyle \frac{y}{m_{\mathrm{p}}}}.$$

(74)

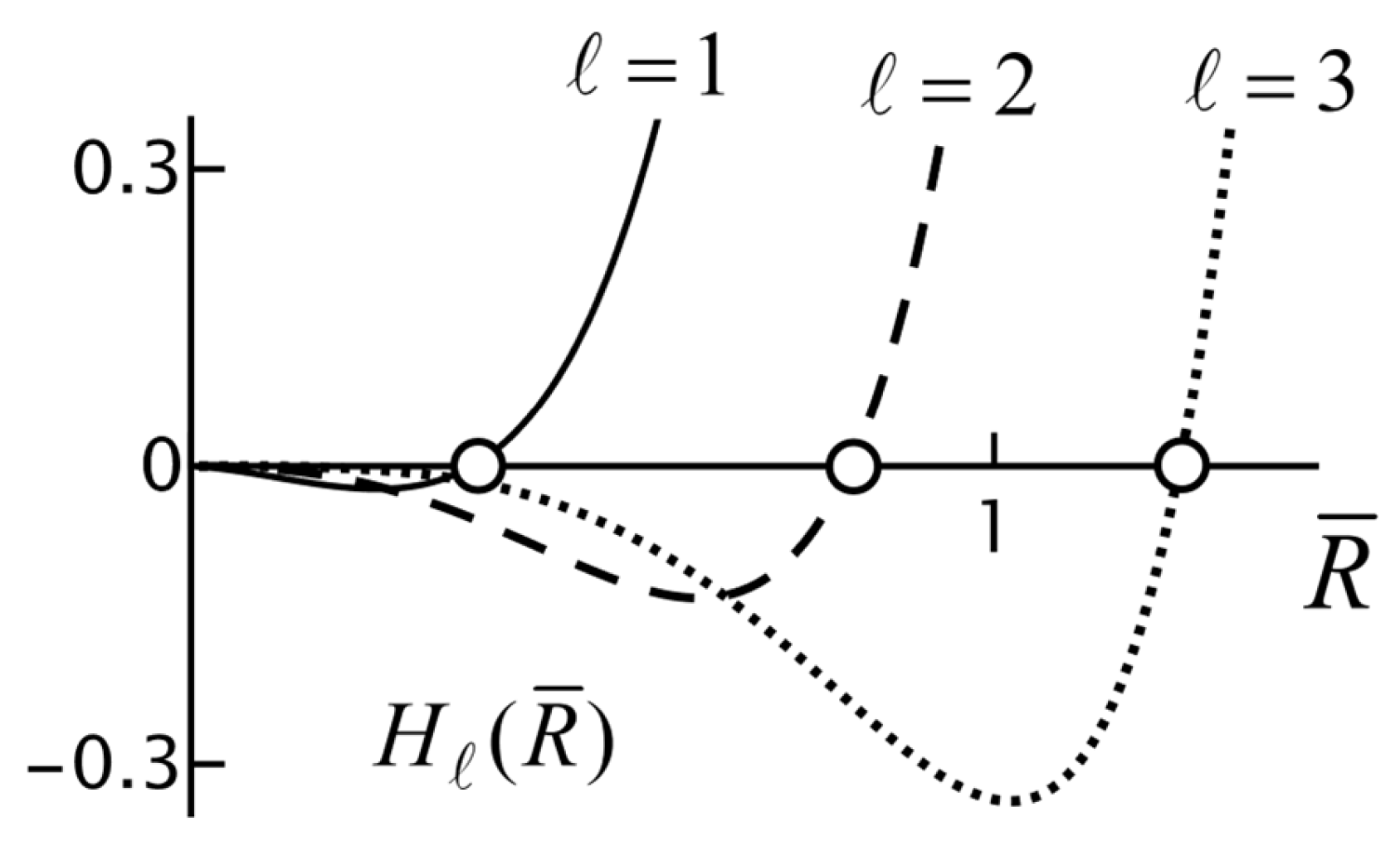
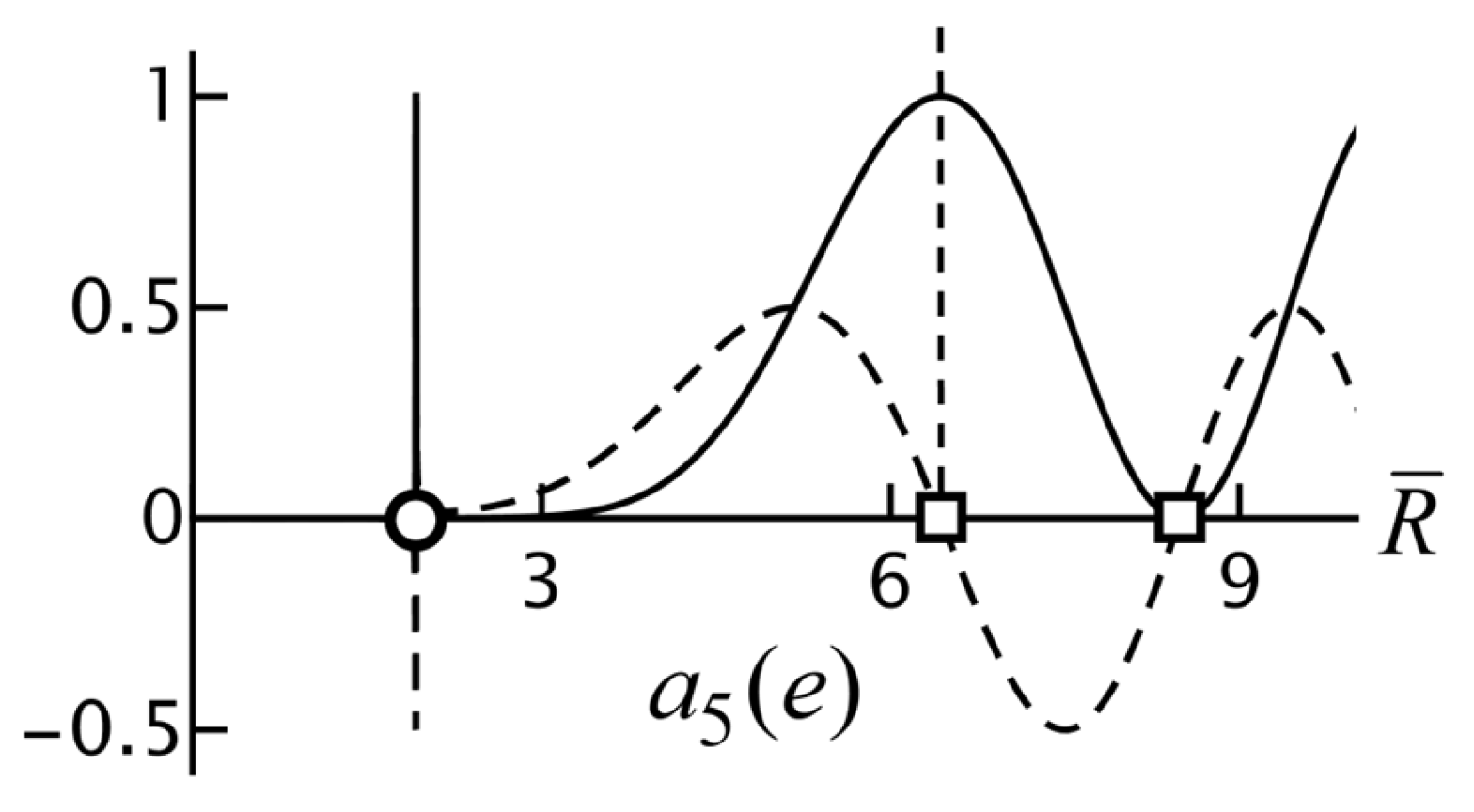
Figure 10 shows the function $H_{\mathcal{l}},$ seen as a function of $\overline{R},$ for $\mathcal{l}=$1, 2 and 3, and for ${\epsilon }_1=4,$ ${\epsilon }_{\mathrm{p}}=-10$. The zeros are found from the graph as ${\overline{R}}_{\mathrm{t}}=0.35,$ $0.82$ and $1.23,$ respectively. Alternatively, Equation (73) can easily be solved numerically, which would give more precise values for ${\overline{R}}_{\mathrm{t}}.$

Equation (73) can be written as

$$y{\displaystyle \frac{I_{\mathcal{l}-\frac{1}{2}}(y)}{I_{\mathcal{l}+\frac{1}{2}}(y)}}=\mathcal{l}+{\alpha }_{\mathcal{l}},$$

(75)

and the parameter $m_{\mathrm{p}}$ is

$$m_{\mathrm{p}}=n_1\sqrt{-{\widehat{\epsilon }}_{\mathrm{p}}}.$$

(76)

For ${\widehat{\epsilon }}_{\mathrm{p}}$ very negative, this parameter becomes large. Then, $y=m_{\mathrm{p}}\overline{R}$ is large, and we can consider the modified Bessel functions for the large argument:

$$I_{\mathcal{l}\pm \frac{1}{2}}(y)\approx {\displaystyle \frac{1}{\sqrt{2\pi y}}}{e}^y.$$

(77)

The right-hand side is independent of $\mathcal{l}$, so Equation (75) becomes

$$y\approx \mathcal{l}+{\alpha }_{\mathcal{l}},$$

(78)

and this is

$$y\approx \mathcal{l}+{\displaystyle \frac{m_{\mathrm{p}}}{n_1}}\sqrt{\mathcal{l}(\mathcal{l}+1)}.$$

(79)

For $m_{\mathrm{p}}$ large, and with

$$\mathcal{l}<\sqrt{\mathcal{l}(\mathcal{l}+1)}<\mathcal{l}+1,$$

(80)

the first $\mathcal{l}$ on the right-hand side of Equation (79) can be neglected. At a turning point, we have $y=m_{\mathrm{p}}{\overline{R}}_{\mathrm{t}},$ so the turning point is approximately

$${\overline{R}}_{\mathrm{t}}\approx {\displaystyle \frac{1}{n_1}}\sqrt{\mathcal{l}(\mathcal{l}+1)},$$

(81)

for $\left|{\widehat{\epsilon }}_{\mathrm{p}}\right|$ large. For the examples in Figure 10, this gives 0.71, 1.22 and 1.73 for $\mathcal{l}=1,$ $\mathcal{l}=2$ and $\mathcal{l}=3,$ respectively. We have verified that the accuracy of this approximation improves considerably with increasing $\left|{\widehat{\epsilon }}_{\mathrm{p}}\right|.$

For $\left|{\widehat{\epsilon }}_{\mathrm{p}}\right|$ very large, the particle approaches the perfect conductor limit. The derivative of $a_{\mathcal{l}}(e)$ is given by Equation (A95). At a turning point, this should be zero, which gives

$$1-{\displaystyle \frac{\mathcal{l}(\mathcal{l}+1)}{{(n_1{\overline{R}}_{\mathrm{t}})}^2}}=0,$$

(82)

and this is

$${\overline{R}}_{\mathrm{t}}={\displaystyle \frac{1}{n_1}}\sqrt{\mathcal{l}(\mathcal{l}+1)}.$$

(83)

Clearly, the approximate value from Equation (81) becomes the exact solution for a perfect conductor.

10. Dissipation in the Particle

When there is no absorption in the particle or the embedding medium, the Mie scattering coefficients $a_{\mathcal{l}}(\alpha )$ lie on the Mie circle, and they rotate around this circle with increasing $\overline{R}.$ We shall now consider the effect of damping in the particle. We set ${\epsilon }_1>0,$ ${\mu }_1>0,$ so that there is no absorption in the surrounding medium. For the particle material, we shall assume $\mathrm{Im}{\epsilon }_{\mathrm{p}}>0,$ and possibly $\mathrm{Im}{\mu }_{\mathrm{p}}>0$.

The coefficients $a_{\mathcal{l}}(\alpha )$ are zero for $\overline{R}=0$. For small $\overline{R},$ the value of $a_{\mathcal{l}}(e)$ is given by Equation (47), and with ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}$, this gives $a_{\mathcal{l}}(m),$ provided that ${\widehat{\mu }}_{\mathrm{p}}\ne 0$. For ${\widehat{\mu }}_{\mathrm{p}}=0,$ we need to consider Equation (49). Without absorption, $a_{\mathcal{l}}(\alpha )$ is pure imaginary, so with increasing $\overline{R},$ the rotation starts either up or down the imaginary axis. This is expected, because the imaginary axis is the tangent line at the Mie circle at $\overline{R}=0$. With absorption, $a_{\mathcal{l}}(\alpha )$ has a real part, and so the initial direction with increasing $\overline{R}$ is under an angle with the imaginary axis. Equation (47) reads

$$a_{\mathcal{l}}(e)=-i{\displaystyle \frac{{\widehat{\epsilon }}_{\mathrm{p}}-1}{{\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}}}\times (\mathrm{positive} \mathrm{factor}).$$

(84)

For ${\widehat{\epsilon }}_{\mathrm{p}}$ real, the shown factor is imaginary. For ${\widehat{\epsilon }}_{\mathrm{p}}$ complex, we set ${\widehat{\epsilon }}_{\mathrm{p}}={{\widehat{\epsilon }}_{\mathrm{p}}}^{\prime }+i{\widehat{\epsilon }}_{\mathrm{p}}".$ Under the assumption that the damping is relatively small, we then find

$$-i{\displaystyle \frac{{\widehat{\epsilon }}_{\mathrm{p}}-1}{{\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}}}=-i{\displaystyle \frac{{{\widehat{\epsilon }}_{\mathrm{p}}}^{\prime }-1}{{{\widehat{\epsilon }}_{\mathrm{p}}}^{\prime }-{\widehat{\epsilon }}_{\mathcal{l}}}}+\eta ,$$

(85)

with

$$\eta ={{\widehat{\epsilon }}_{\mathrm{p}}}^{″}{\displaystyle \frac{1-{\widehat{\epsilon }}_{\mathcal{l}}}{{({{\widehat{\epsilon }}_{\mathrm{p}}}^{\prime }-{\widehat{\epsilon }}_{\mathcal{l}})}^2}},$$

(86)

which is positive. Therefore, $\mathrm{Re}{a}_{\mathcal{l}}(\alpha )>0,$ and the curve in the complex plane bends away from the imaginary axis to the right. From a different point of view, $a_{\mathcal{l}}(\alpha )$ moves to the inside of the Mie circle. The initial direction along the imaginary axis is the same as without absorption, provided we replace ${\widehat{\epsilon }}_{\mathrm{p}}$ by its real part. For $a_{\mathcal{l}}(m)$, we assume ${\widehat{\mu }}_{\mathrm{p}}=1,$ and it then follows immediately from Equation (49) that the same conclusion holds.

For large $\overline{R},$ the general expression is given by Equation (56). We shall now simplify this result for the case that there is damping in the particle. The particle index of refraction $n_{\mathrm{p}}$ is complex, and we write

$$n_{\mathrm{p}}={n_{\mathrm{p}}}^{\prime }+i{n_{\mathrm{p}}}^{″}\hspace{1em},\hspace{1em}{n_{\mathrm{p}}}^{\prime } \mathrm{real},\hspace{1em}{n_{\mathrm{p}}}^{″}>0.$$

(87)

For the sines and cosines in Equation (56), we use $\exp (-{n_{\mathrm{p}}}^{″}\overline{R})\to 0$. This yields

$$\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\to \frac{1}{2}{e}^{-i({n_{\mathrm{p}}}^{\prime }\overline{R}-\mathcal{l}\pi /2)}{e}^{{n_{\mathrm{p}}}^{″}\overline{R}},$$

(88)

$$\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\to \frac{i}{2}{e}^{-i({n_{\mathrm{p}}}^{\prime }\overline{R}-\mathcal{l}\pi /2)}{e}^{{n_{\mathrm{p}}}^{″}\overline{R}}.$$

(89)

Both terms grow exponentially with $\overline{R}$ due to the factors $\exp ({n_{\mathrm{p}}}^{″}\overline{R}).$ Fortunately, these factors appear both in the numerator and denominator, so they cancel. We obtain

$$2a_{\mathcal{l}}(e)-1\approx {(-1)}^{\mathcal{l}+1}{\displaystyle \frac{{\widehat{n}}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\epsilon }}_{\mathrm{p}}}}{e}^{-2i{n}_1\overline{R}},$$

(90)

for $\overline{R}$ large. For magnetic multipoles, we replace ${\widehat{\epsilon }}_{\mathrm{p}}$ by ${\widehat{\mu }}_{\mathrm{p}},$ and we use the identity

$${\displaystyle \frac{{\widehat{n}}_{\mathrm{p}}-{\widehat{\mu }}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\mu }}_{\mathrm{p}}}}=-{\displaystyle \frac{{\widehat{n}}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\epsilon }}_{\mathrm{p}}}}.$$

(91)

This gives

$$2a_{\mathcal{l}}(m)-1\approx {(-1)}^{\mathcal{l}}{\displaystyle \frac{{\widehat{n}}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\epsilon }}_{\mathrm{p}}}}{e}^{-2i{n}_1\overline{R}},$$

(92)

which differs from $2a_{\mathcal{l}}(e)-1$ by only a minus sign.

The only rotation in $2a_{\mathcal{l}}(\alpha )-1$ comes from $\exp (-2i{n}_1\overline{R}),$ which is clockwise, and the path in the complex plane is a circle around the origin. Then, $a_{\mathcal{l}}(\alpha )$ rotates clockwise around the point 1/2, and the radius of the circle is

$$r_{\mathrm{M}}={\displaystyle \frac{1}{2}}\left|{\displaystyle \frac{{\widehat{n}}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\epsilon }}_{\mathrm{p}}}}\right|.$$

(93)

This circle is concentric with the Mie circle, and we shall call this the reduced Mie circle. The radius $r_{\hspace{0.17em}\mathrm{M}}$ is the same for electric and magnetic multipole coefficients. Also interesting to see is that the rotation direction for $\overline{R}$ large is the same for all parameters. This is in contrast to the case without damping, where the rotation is counterclockwise for ${\widehat{\epsilon }}_{\mathrm{p}}>1,$ ${\widehat{\mu }}_{\mathrm{p}}=1$ (Figure 6). We note that the reduced Mie circle does not necessarily go over in the Mie circle in the limit of no damping. We have used $\mathrm{Im}{n}_{\mathrm{p}}>0$ to arrive at Equations (88) and (89), and this excludes the limit $\mathrm{Im}{n}_{\mathrm{p}}=0$.

Figure 11 summarizes the rotation directions for the case when there is damping in the particle. The initial rotation direction is determined by the real part of ${\widehat{\epsilon }}_{\mathrm{p}},$ and the curves start under an angle with the imaginary axis such that the damping gives a deviation to the right. For $a_{\mathcal{l}}(m)$, we assumed ${\widehat{\mu }}_{\mathrm{p}}=1$. The final directions for all cases are clockwise, so this is independent of $\mathrm{Re}{\widehat{\epsilon }}_{\mathrm{p}}.$ As compared to Figure 6, we see that for $\mathrm{Re}{\widehat{\epsilon }}_{\mathrm{p}}>1,$ the rotation direction is opposite to the case without damping, so the dissipation in the particle reverses the final rotation direction. Since this direction is opposite to the initial rotation direction, the Mie coefficients must have a turning point due to the absorption of energy in the particle.

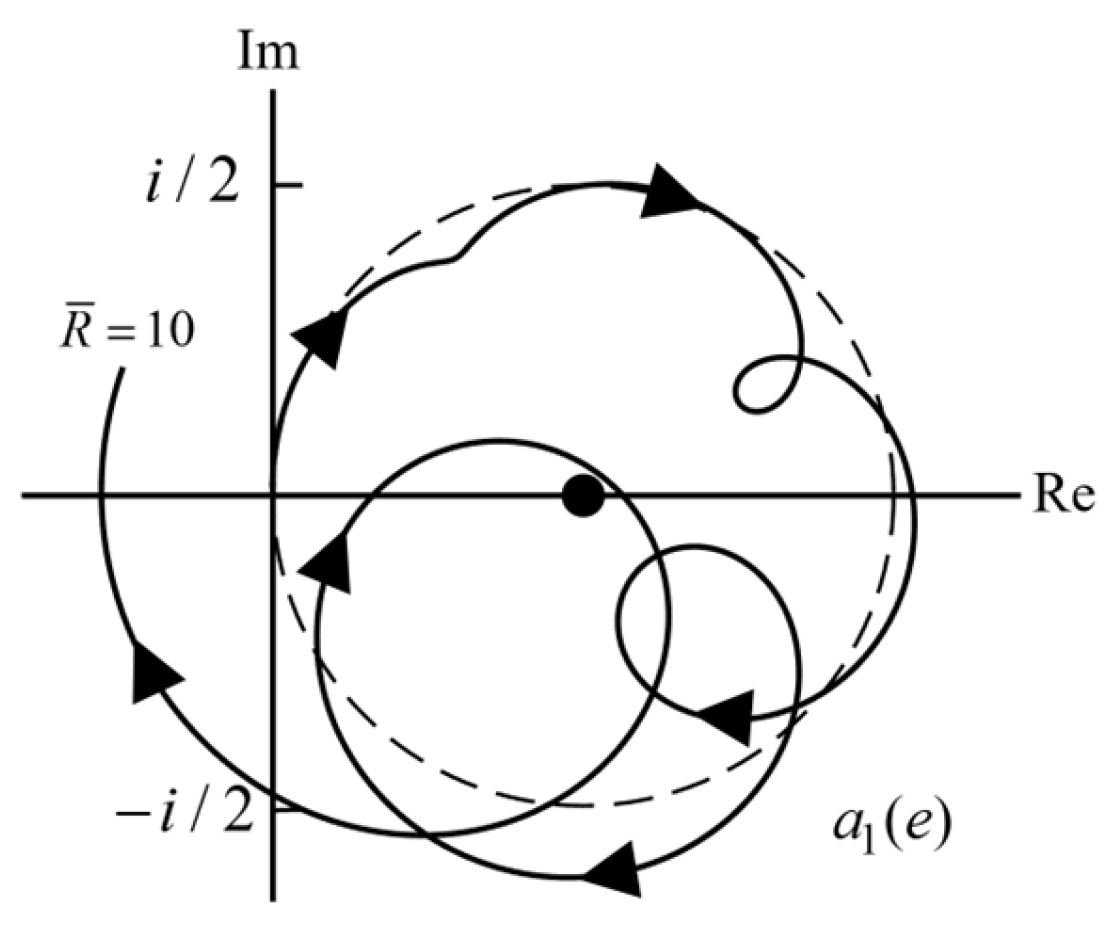
Figure 12 shows a typical curve in the complex plane. The rotation direction is clockwise for all $\overline{R},$ and for $\overline{R}$ large, the curve approaches the reduced Mie circle. Another example is shown in Figure 13. The initial rotation is counterclockwise, but then the direction reverses and becomes clockwise by the time it reaches the reduced Mie circle. A similar case is shown in Figure 14, but now we can clearly see the predicted turning point. Without absorption, the rotation direction would be counterclockwise for all $\overline{R}.$

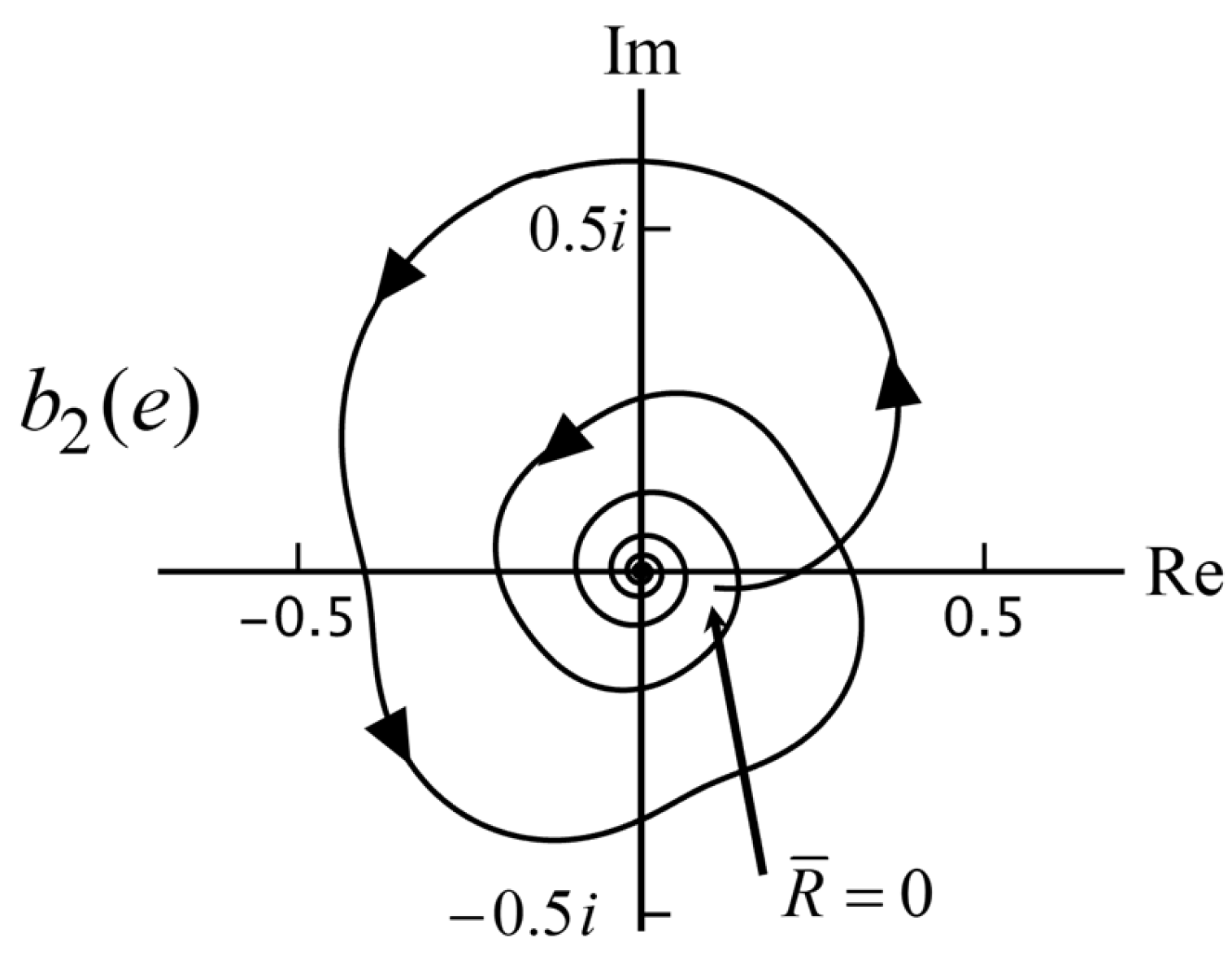
The Mie particle coefficient $b_{\mathcal{l}}(e)$ at $\overline{R}=0$ is given by Equation (48), and the value of $b_{\mathcal{l}}(m)$ at $\overline{R}=0$ follows from ${\widehat{\epsilon }}_p\to {\widehat{\mu }}_{\mathrm{p}}.$ They are finite, but they do not lie on an axis as they do without damping. With a similar calculation as above, we find for $\overline{R}$ large

$$b_{\mathcal{l}}(e)\approx {\displaystyle \frac{2{\widehat{n}}_{\mathrm{p}}}{{\widehat{n}}_{\mathrm{p}}+{\widehat{\epsilon }}_{\mathrm{p}}}}{e}^{-n_{\mathrm{p}}"\overline{R}}{e}^{i({n_{\mathrm{p}}}^{\prime }-\hspace{0.17em}{n}_1)\overline{R}},$$

(94)

and for $b_{\mathcal{l}}(m)$, we replace ${\widehat{\epsilon }}_{\mathrm{p}}$ with ${\widehat{\mu }}_{\mathrm{p}}.$ For large $\overline{R},$ $b_{\mathcal{l}}(\alpha )\to 0$ due to the factor $\exp (-{n_p}^{″}\overline{R}).$ The Mie coefficients spiral into the origin, unlike without damping, where this only happens for ${\widehat{\epsilon }}_{\mathrm{p}}<0$ (Figure 7). The rotation around the origin comes from $\exp [i({n_{\mathrm{p}}}^{\prime }-n_1)].$ The rotation is counterclockwise for ${n_{\mathrm{p}}}^{\prime }>n_1$ and clockwise for ${n_{\mathrm{p}}}^{\prime }<n_1.$ A typical example is shown in Figure 15.

11. Dissipation in the Medium

Let us now consider the effect of damping in the embedding material. We shall assume ${\epsilon }_{\mathrm{p}}>0,$ ${\mu }_{\mathrm{p}}>0,$ so that there is no absorption in the particle, and we set $n_1={n_1}^{\prime }+i{n_1}^{″}$, as in Equation (11). Here, ${n_1}^{\prime }$ is real, and ${n_1}^{″}$ is positive. The behavior of $a_{\mathcal{l}}(e)$ for $\overline{R}$ large follows from Equation (56). We find

$$\begin{gathered} 2a_{\mathcal{l}}(e)-1\approx {(-1)}^{\mathcal{l}+1}{e}^{-2i{n_1}^{\prime }\overline{R}}{e}^{2{n_1}^{″}\overline{R}} \\ \times \left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)+i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right] \\ \times {\left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)-i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right]}^{-1}, \end{gathered}$$

(95)

and for the Mie particle coefficients, we find from Equation (57)

$$b_{\mathcal{l}}(e)\approx i^{\mathcal{l}}{\widehat{n}}_{\mathrm{p}}{e}^{-i{n_1}^{\prime }\overline{R}}{e}^{n_1″\overline{R}}{\left[{\widehat{n}}_{\mathrm{p}}\cos (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)-i{\widehat{\epsilon }}_{\mathrm{p}}\sin (n_{\mathrm{p}}\overline{R}-\mathcal{l}\pi /2)\right]}^{-1}.$$

(96)

For magnetic multipoles, we replace ${\widehat{\epsilon }}_{\mathrm{p}}\to {\widehat{\mu }}_{\mathrm{p}}.$ With the same reasoning as in Section 8, we see that the rotation direction is counterclockwise for $n_{\mathrm{p}}>{n_1}^{\prime }$ and clockwise for $n_{\mathrm{p}}<{n_1}^{\prime }.$ The Mie coefficient $a_{\mathcal{l}}(\alpha )$ rotates around the Mie circle, and $b_{\mathcal{l}}(\alpha )$ rotates around the origin.

The most striking feature is the factors $\exp (2{n_1}^{″}\overline{R})$ in $a_{\mathcal{l}}(\alpha )$ and $\exp ({n_1}^{″}\overline{R})$ in $b_{\mathcal{l}}(\alpha ).$ These factors grow exponentially with the particle radius $\overline{R}.$ When there is damping in the particle, $a_{\mathcal{l}}(\alpha )$ moves to the inside of the Mie circle and eventually starts to rotate around the reduced Mie circle, as illustrated in Figure 13 and Figure 14. The coefficients $b_{\mathcal{l}}(\alpha )$ spiral into the origin with increasing $\overline{R},$ as shown in Figure 15. Due to damping in the surrounding medium, the effect is the opposite. The coefficients $a_{\mathcal{l}}(\alpha )$ spiral away from the Mie circle and continue to grow without bounds with increasing $\overline{R}.$ This is illustrated in Figure 16. Also, $b_{\mathcal{l}}(\alpha )$ grows exponentially, as shown in Figure 17. When there is damping in the particle and in the host medium, it depends on which one ‘wins’. Figure 18 depicts this combined effect. Initially, the curve tends to go to the inside of the Mie circle as a result of the damping in the particle, but eventually it turns to the outside and keeps on growing.

12. The Fröhlich Mode

It was shown in Section 6, Equation (47), that for $\overline{R}$ small we have

$$a_{\mathcal{l}}(e)\approx -i{\displaystyle \frac{{\widehat{\epsilon }}_{\mathrm{p}}-1}{{\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}}}{d}_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1},$$

(97)

with ${\widehat{\epsilon }}_{\mathcal{l}}=-\hspace{0.17em}(\mathcal{l}+1)/\mathcal{l}.$ We notice immediately that there is a problem if ${\widehat{\epsilon }}_{\mathrm{p}}$ is close to ${\widehat{\epsilon }}_{\mathcal{l}},$ and since ${\widehat{\epsilon }}_{\mathcal{l}}$ is negative, this can happen easily for a metallic particle. This situation is referred to as the Fröhlich resonance, or the Fröhlich mode. The Mie particle coefficient $b_{\mathcal{l}}(e)$ from Equation (48) has the same problem. A division by zero would give an infinite Mie coefficient, which is unphysical. Moreover, we know that without damping, $a_{\mathcal{l}}(e)$ lies on the Mie circle. The magnetic multipole Mie coefficients do not have this issue (unless one would consider ${\widehat{\mu }}_{\mathrm{p}}\approx -\hspace{0.17em}(\mathcal{l}+1)/\mathcal{l},$ which is unrealistic), so in this section, we shall only consider electric multipoles. It is often argued in the literature that one should include a small positive imaginary part in ${\epsilon }_{\mathrm{p}}$ in order to keep $a_{\mathcal{l}}(e)$ finite. We shall show below that this gives the wrong result [26]. This issue was also addressed in [27], from a different point of view.

The small-$\overline{R}$ limit of the Mie coefficients was derived in Section 4, starting from the representations (21) and (22). We expanded the functions $P_{\mathcal{l}}(e)$ and $Q_{\mathcal{l}}(e)$ in a Taylor series in $\overline{R},$ with the results given by Equations (43) and (45). In the numerators, we have $P_{\mathcal{l}}(e)+i{Q}_{\mathcal{l}}(e).$ Since $P_{\mathcal{l}}(e)$ is of a much higher order in $\overline{R},$ we neglected $P_{\mathcal{l}}(e)$ in $P_{\mathcal{l}}(e)+i{Q}_{\mathcal{l}}(e),$ and this gave the results shown in Equations (47) and (48). From Equation (45) we see that $Q_{\mathcal{l}}(e)$ is zero at ${\widehat{\epsilon }}_{\mathrm{p}}={\widehat{\epsilon }}_{\mathcal{l}},$ and this is the root of the problem with the approximation (97), and similarly for $b_{\mathcal{l}}(e)$. When $Q_{\mathcal{l}}(e)\to 0,$ we need to retain $P_{\mathcal{l}}(e)$ in $P_{\mathcal{l}}(e)+i{Q}_{\mathcal{l}}(e).$ First, we change to alternative $P’\mathrm{s}$ and $Q’\mathrm{s}:$

$$p_{\mathcal{l}}(e)=-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{\displaystyle \frac{1}{{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}}}{n}_1\overline{R}\hspace{0.17em}{P}_{\mathcal{l}}(e),$$

(98)

$$q_{\mathcal{l}}(e)=-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{\displaystyle \frac{1}{{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}}}{n}_1\overline{R}\hspace{0.17em}{Q}_{\mathcal{l}}(e),$$

(99)

which are more suitable for the study of $\overline{R}$ small. The Mie coefficients are then

$$a_{\mathcal{l}}(e)={\displaystyle \frac{p_{\mathcal{l}}(e)}{p_{\mathcal{l}}(e)+i\hspace{0.17em}{q}_{\mathcal{l}}(e)}},$$

(100)

$$b_{\mathcal{l}}(e)=i{\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{\displaystyle \frac{1}{{\widehat{n}}_{\mathrm{p}}^{\mathcal{l}}}}{\displaystyle \frac{1}{{\lambda }_{\mathcal{l}}(e)}},$$

(101)

with ${\lambda }_{\mathcal{l}}(e)=p_{\mathcal{l}}(e)+i\hspace{0.17em}{q}_{\mathcal{l}}(e).$ From here on, we shall use an equal sign instead of $\approx$ for the small-$\overline{R}$ approximation. For $p_{\mathcal{l}}(e)$, we keep the result from Equation (43):

$$p_{\mathcal{l}}(e)=({\widehat{\epsilon }}_{\mathrm{p}}-1)d_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1},$$

(102)

but for $q_{\mathcal{l}}(e)$, we add one more term in the Taylor expansion for small $\overline{R}.$ This gives

$$q_{\mathcal{l}}(e)={\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}+c_{\mathcal{l}}{(n_1\overline{R})}^2.$$

(103)

Here, we introduced the parameter

$$c_{\mathcal{l}}=-{\displaystyle \frac{1}{2\mathcal{l}}}({\widehat{\epsilon }}_{\mathrm{p}}{\widehat{\mu }}_{\mathrm{p}}-1)-{\displaystyle \frac{1}{2\mathcal{l}}}({\widehat{\epsilon }}_{\mathrm{p}}-1)\left({\displaystyle \frac{\mathcal{l}}{2\mathcal{l}+3}}{\widehat{\epsilon }}_{\mathrm{p}}{\widehat{\mu }}_{\mathrm{p}}-{\displaystyle \frac{\mathcal{l}-2}{2\mathcal{l}-1}}\right).$$

(104)

The new and improved small-$\overline{R}$ approximations to the Mie coefficients are then given by Equations (100) and (101).

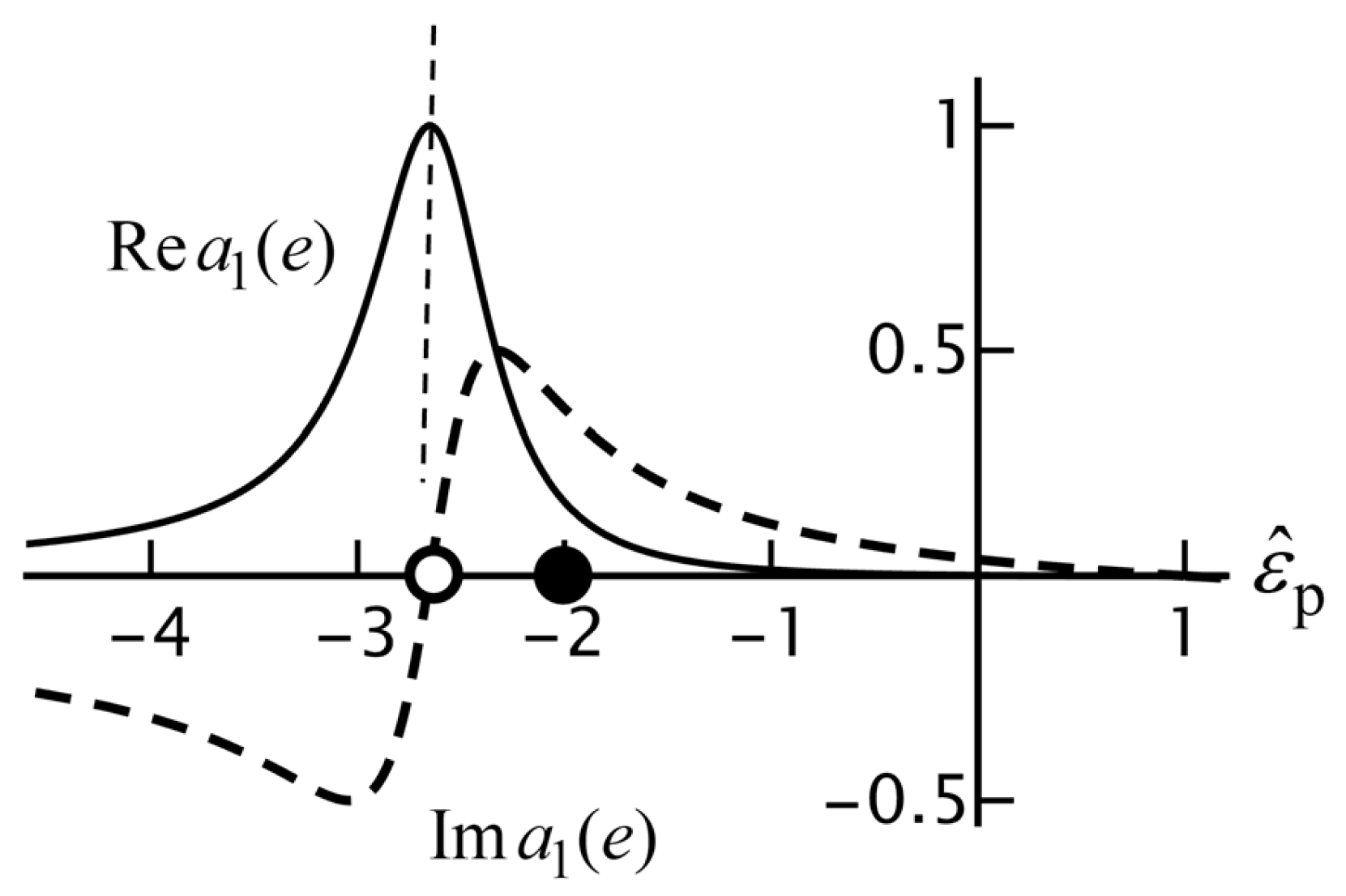
First, we notice that the singularities for ${\widehat{\epsilon }}_{\mathrm{p}}$ near ${\widehat{\epsilon }}_{\mathcal{l}}$ have disappeared. Second, without damping in the particle or the surrounding medium, $p_{\mathcal{l}}(e)$ and $q_{\mathcal{l}}(e)$ are real. So, $a_{\mathcal{l}}(e)$ has the same form as in Equation (25), and therefore the approximation lies on the Mie circle. This reflects conservation of energy, even for the approximate formula. Third, for $q_{\mathcal{l}}(e)=0$ we have $a_{\mathcal{l}}(e)=1,$ and so this resonance is a Mie resonance in the true sense of the meaning. As a consistency check, consider a transparent particle. Then, ${\widehat{\epsilon }}_{\mathrm{p}}=1,$ ${\widehat{\mu }}_{\mathrm{p}}=1,$ and we immediately find $p_{\mathcal{l}}(e)=0$, and so $a_{\mathcal{l}}(e)=0$. From Equation (104), we see that $c_{\mathcal{l}}=0,$ and with $1-{\widehat{\epsilon }}_{\mathcal{l}}=(2\mathcal{l}+1)/\mathcal{l}$, we find $b_{\mathcal{l}}(e)=1$.

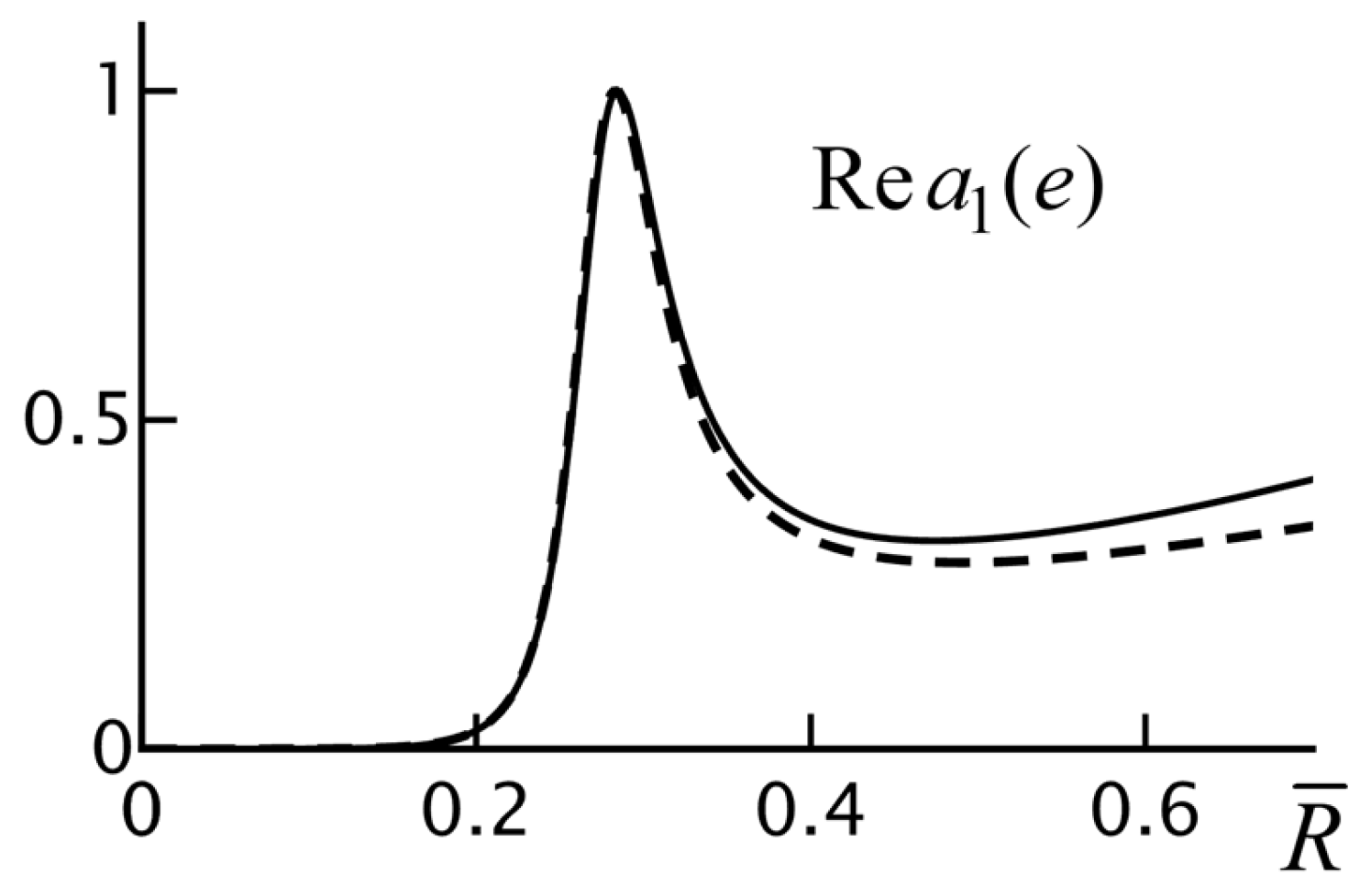
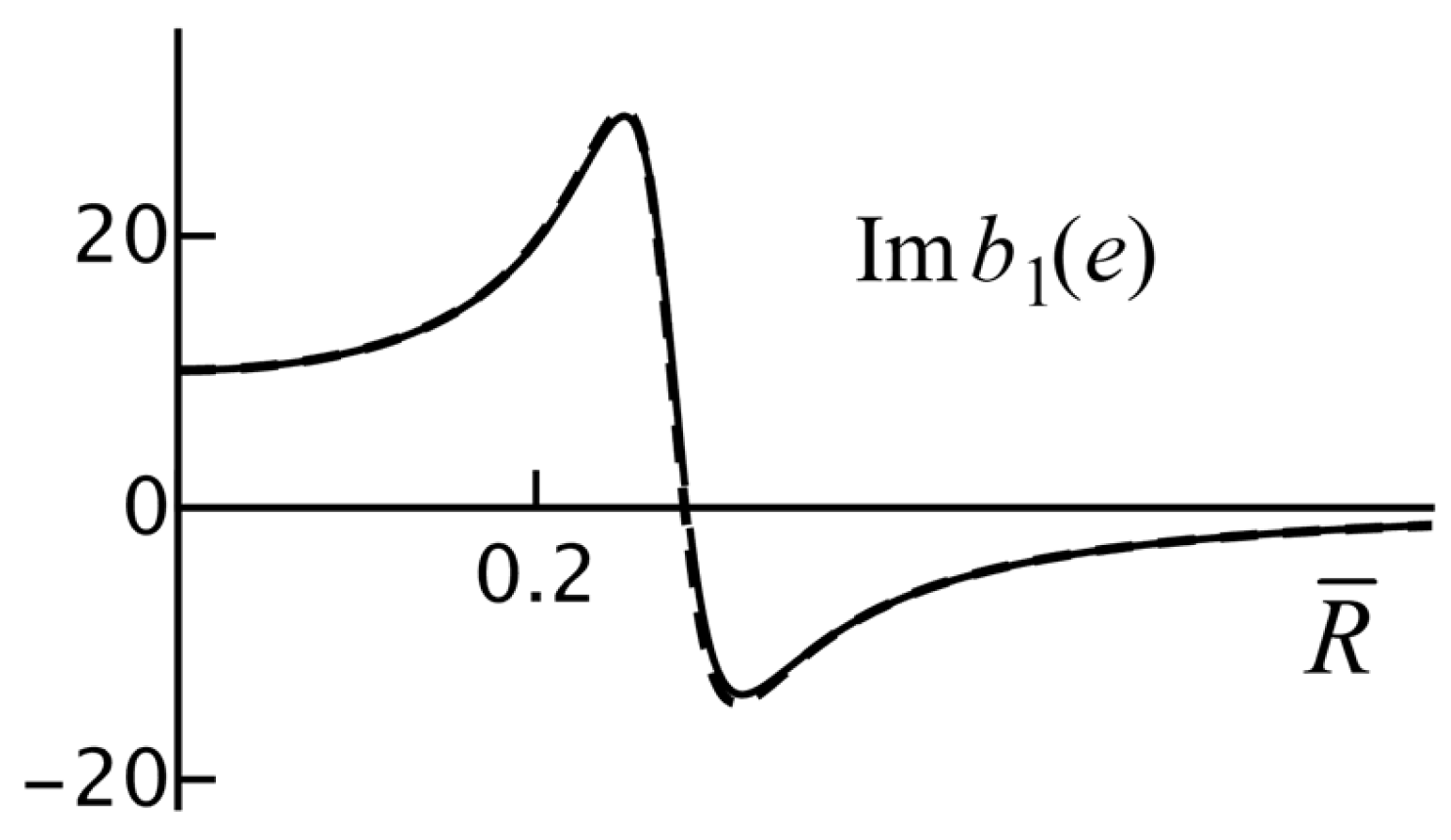
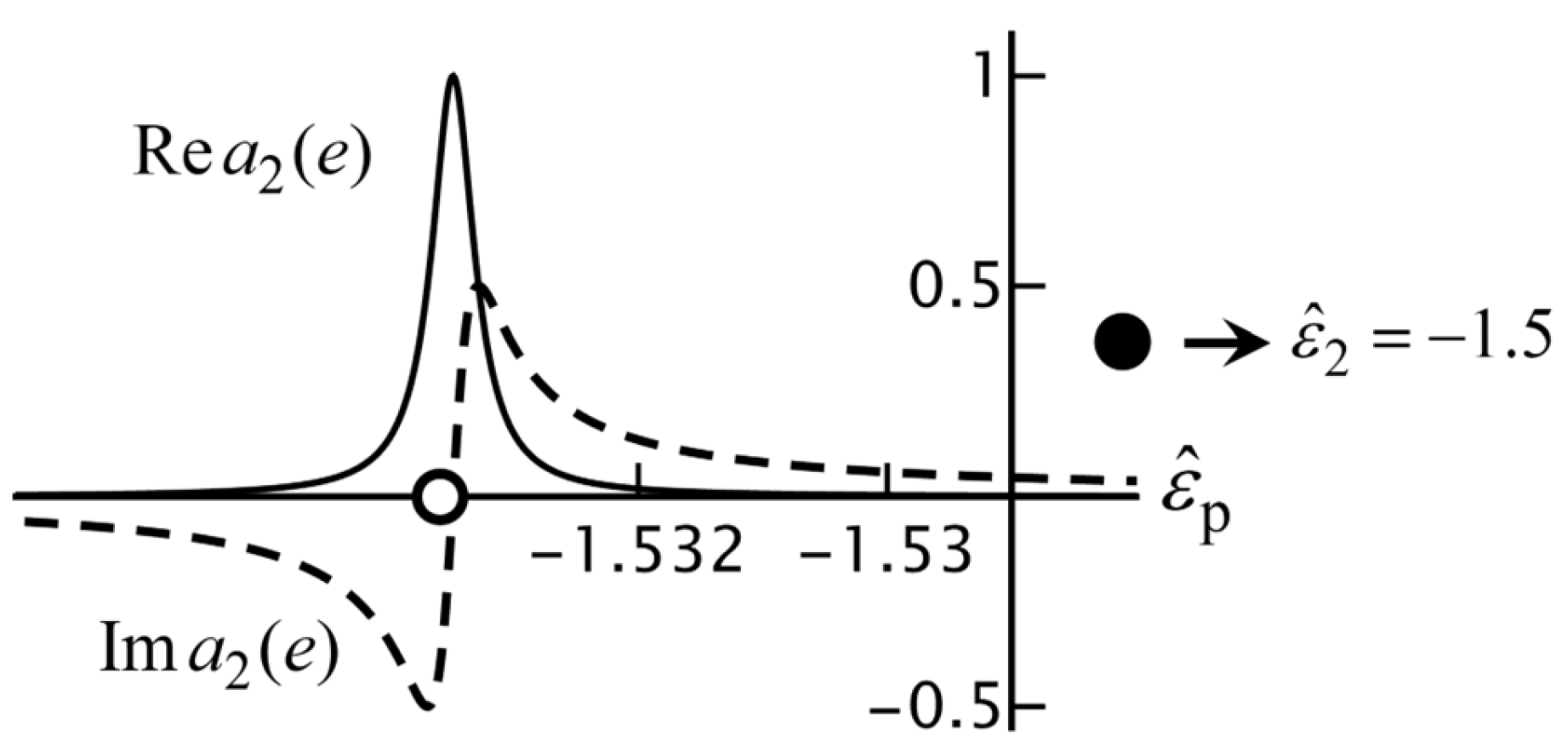
Figure 19 shows $\mathrm{Re}{a}_1(e)$ as a function of $\overline{R},$ and the small-$\overline{R}$ approximation. We have ${\widehat{\epsilon }}_{\mathrm{p}}=-2.2,$ which is close to ${\widehat{\epsilon }}_{\mathcal{l}}=-2$ for $\mathcal{l}=1$. Figure 20 shows $\mathrm{Im}{b}_1(e)$ for the same parameters. We notice that the approximation is excellent. Another thing to see is that the exact curve indeed gives a resonance, where $\mathrm{Re}{a}_1(e)=1$ (and $\mathrm{Im}{a}_1(e)=0,$ not shown in the graph). It can also be verified that for parameters not near the Fröhlich resonance, the new approximation for $\overline{R}$ small is a huge improvement, as compared to Equation (97).

For the remainder of this section, we shall set μ₁ = 1, ${\mu }_{\mathrm{p}}=1$. Then, $c_{\mathcal{l}}$ from Equation (104) simplifies to

$$c_{\mathcal{l}}=-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{1}{2(2\mathcal{l}+3)}}({\widehat{\epsilon }}_{\mathrm{p}}-1)({\widehat{\epsilon }}_{\mathrm{p}}-{{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }),$$

(105)

with

$${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }=-\hspace{0.17em} {\displaystyle \frac{\mathcal{l}+1}{\mathcal{l}}} {\displaystyle \frac{2\mathcal{l}+3}{2\mathcal{l}-1}}.$$

(106)

With Equation (46) we have

$${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }= {\displaystyle \frac{2\mathcal{l}+3}{2\mathcal{l}-1}}{\widehat{\epsilon }}_{\mathcal{l}}.$$

(107)

Since ${\widehat{\epsilon }}_{\mathcal{l}}<0,$ we have ${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }<{\widehat{\epsilon }}_{\mathcal{l}},$ and we also see that ${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }$ lies in the range $-10\le {{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }<-1$. 

Table 2. The table shows ${\widehat{\epsilon }}_{\mathcal{l}}$ and ${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }$ for various values of $\mathcal{l}$.

$\mathcal{l}$	${\widehat{\epsilon }}_{\mathcal{l}}$	${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }$
1	−2.00	−10.0
2	−1.50	−3.50
3	−1.33	−2.40
4	−1.25	−1.96
5	−1.20	−1.73
10	−1.10	−1.33
20	−1.05	−1.16

shows various values of ${\widehat{\epsilon }}_{\mathcal{l}}$ and ${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }.$

Function $q_{\mathcal{l}}(e)$ from Equation (103) is the Fröhlich resonance function. At the resonance, we have $q_{\mathcal{l}}(e)=0,$ so the resonance condition becomes

$${\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}+c_{\mathcal{l}}{(n_1\overline{R})}^2=0.$$

(108)

Under this condition, we have $a_{\mathcal{l}}(e)=1$. Let us now consider the $\overline{R}$ dependence of $a_{\mathcal{l}}(e),$ for a given ${\widehat{\epsilon }}_{\mathrm{p}},$ in more detail. It follows from Equation (108) that a resonance occurs at the radius

$${\overline{R}}_{\mathrm{F}}={\displaystyle \frac{1}{n_1}}\sqrt{{\displaystyle \frac{{\widehat{\epsilon }}_{\mathcal{l}}-{\widehat{\epsilon }}_{\mathrm{p}}}{c_{\mathcal{l}}}}},$$

(109)

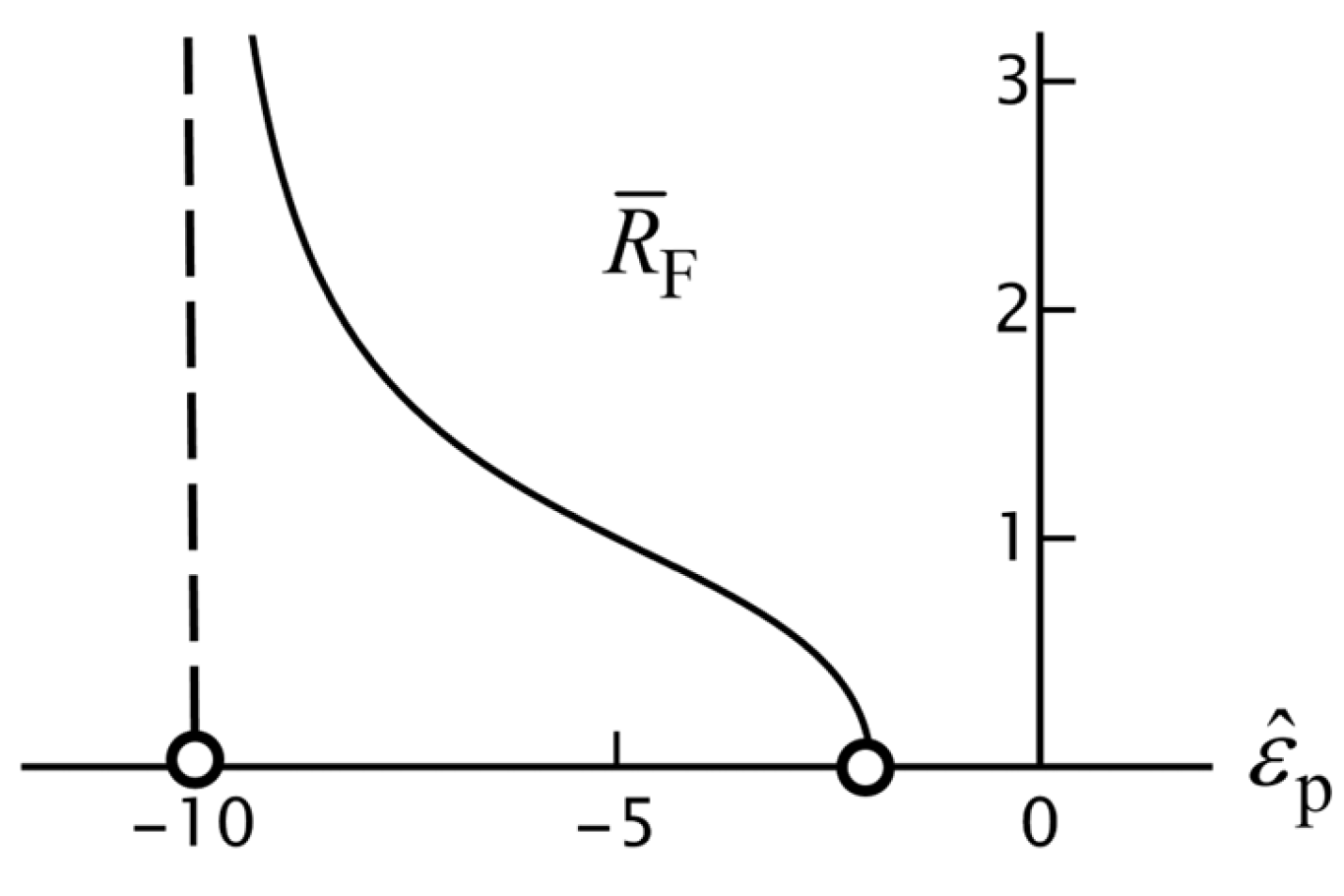
provided that the argument of the square root is positive. We call this the Fröhlich radius. The first condition for ${\overline{R}}_{\mathrm{F}}$ to exist is that ${\widehat{\epsilon }}_{\mathrm{p}}$ must be real. Then, for ${\widehat{\epsilon }}_{\mathrm{p}}>{\widehat{\epsilon }}_{\mathcal{l}}$, we must have $c_{\mathcal{l}}<0,$ and for ${\widehat{\epsilon }}_{\mathrm{p}}<{\widehat{\epsilon }}_{\mathcal{l}}$, we must have $c_{\mathcal{l}}>0$. With Equation (105) for $c_{\mathcal{l}}$ we find that ${\widehat{\epsilon }}_{\mathrm{p}}$ must lie in the range

$${{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime }<{\widehat{\epsilon }}_{\mathrm{p}}<{\widehat{\epsilon }}_{\mathcal{l}}.$$

(110)

In principle, there could also be a solution for ${\widehat{\epsilon }}_{\mathrm{p}}>1,$ but this is too far away from the Fröhlich resonance, and the value of ${\overline{R}}_{\mathrm{F}}$ would be too large to justify the small-$\overline{R}$ approximation. This also brings up the condition that the predicted value of ${\overline{R}}_{\mathrm{F}}$ by Equation (107) must be small enough for the small-$\overline{R}$ approximation to hold. Figure 21 shows the dependence of ${\overline{R}}_{\mathrm{F}}$ on ${\widehat{\epsilon }}_{\mathrm{p}}$ for $\mathcal{l}=1$. For larger $\mathcal{l}$ values, the curve becomes much steeper, thereby increasing the value of ${\overline{R}}_{\mathrm{F}}$ for a given ${\widehat{\epsilon }}_{\mathrm{p}}.$ The Fröhlich resonance function from Equation (103) can be written as

$$q_{\mathcal{l}}(e)=c_{\mathcal{l}}{n}_1^2({\overline{R}}^2-{\overline{R}}_{\mathrm{F}}^2),$$

(111)

which shows more clearly that $q_{\mathcal{l}}(e)=0$ for $\overline{R}={\overline{R}}_{\mathrm{F}}.$ We see from Figure 19 that $\mathrm{Re}{a}_{\mathcal{l}}(e)$ has the appearance of a resonance line. With the above, the width $\Delta \overline{R}$ of the line (half-width at half maximum) can be estimated to be

$$\Delta \overline{R}={\displaystyle \frac{(2\mathcal{l}+3)d_{\mathcal{l}}{(n_1{\overline{R}}_{\mathrm{F}})}^{2\mathcal{l}}}{n_1({\widehat{\epsilon }}_{\mathrm{p}}-{{\widehat{\epsilon }}_{\mathcal{l}}}^{\prime })}}.$$

(112)

For the line in Figure 19, we find ${\overline{R}}_{\mathrm{F}}=0.283$ with Equation (107) and $\Delta \overline{R}=0.0342$ with Equation (112). When measured from the graph, we find ${\overline{R}}_{\mathrm{F}}=0.283$ and $\Delta \overline{R}=0.0451$. The width of the line decreases very rapidly with increasing $\mathcal{l},$ as shown in Figure 22. With Equations (109) and (112), we find ${\overline{R}}_{\mathrm{F}}=0.348$ and $\Delta \overline{R}=1.30*{10}^{-\hspace{0.17em}5},$ respectively, and from the graph, we measure these quantities as ${\overline{R}}_{\mathrm{F}}=0.344$ and $\Delta \overline{R}=1.15*{10}^{-\hspace{0.17em}5}.$ The accuracies of the predicted values with the small-$\overline{R}$ approximation are $1.3\%$ and $13\%,$ respectively. In Figure 23, we have $\mathcal{l}=5,$ and the Fröhlich resonance is extremely narrow. From the graph we find ${\overline{R}}_{\mathrm{F}}=1.9,$ and with Equation (109) we get ${\overline{R}}_{\mathrm{F}}=2.55$. The discrepancy between the two numbers is due to the fact that ${\overline{R}}_{\mathrm{F}}$ is relatively large, so that the small-$\overline{R}$ approximation becomes invalid. Nevertheless, the Fröhlich resonance is still there.

The relative width $\Delta \overline{R}/{\overline{R}}_{\mathrm{F}}$ of the Fröhlich resonance is extremely small. For instance, for the parameters in Figure 19, we have $\Delta \overline{R}/{\overline{R}}_{\mathrm{F}}\sim {10}^{-5}.$ Experimentally, it seems impossible to make a particle with such a precise radius. In an experiment, one would scan the laser (angular) frequency $\omega$ in order to measure the lineshapes. The material parameters ${\epsilon }_1,$ ${\mu }_1,$ ${\epsilon }_{\mathrm{p}}$ and ${\mu }_{\mathrm{p}}$ depend on $\omega ,$ but in a very smooth way. Their variation with $\omega$ over a small frequency range can be neglected. Moreover, $\omega$ only enters the expressions for the Mie coefficients through $k_{\mathrm{o}}=\omega /c,$ and this wave number in free space only comes in through the scale factor in $\overline{R}=k_{\mathrm{o}}R.$ So, we have $\overline{R}=\omega R/c.$ When we consider the particle radius $R$ as fixed, then a graph of a Mie coefficient as a function of $\overline{R}$ is identical to a graph of this coefficient as a function of $\omega ,$ apart from the scale factor $R/c$ on the horizontal axis. Then, a line in the $\overline{R}$ graph becomes a spectral line in the $\omega$ graph. The Fröhlich resonance in an $\omega$ graph appears at

$${\omega }_{\mathrm{F}}={\displaystyle \frac{c}{R}}{\overline{R}}_{\mathrm{F}}.$$

(113)

A change $\Delta \overline{R}$ in $\overline{R}$ then becomes a change $\Delta \omega$ in $\omega ,$ with $\Delta \omega$ the spectral width of the line. We then find

$${\displaystyle \frac{\Delta \overline{R}}{{\overline{R}}_{\mathrm{F}}}}={\displaystyle \frac{\Delta \omega }{{\omega }_{\mathrm{F}}}},$$

(114)

so, the relative widths are the same in both representations. If the resonance ${\overline{R}}_{\mathrm{F}}$ exists, then we have ${\overline{R}}_{\mathrm{F}}\sim 1,$ as follows from Figure 21. Let the particle be a nano-particle with $R\sim 300\hspace{0.17em}\mathrm{nm}.$ With Equation (113), we then find ${\omega }_{\mathrm{F}}\sim {10}^{15}\mathrm{rad}/\mathrm{s}$, which is in the visible region of the spectrum. The width of the line is with Equation (114) $\Delta \omega \sim {10}^{10}\mathrm{rad}/\mathrm{s},$ or about 10 GHz. So, in order to resolve the line experimentally, the laser linewidth has to be somewhat smaller than 10 GHz. This is easily possible with today’s lasers.

The Frölich resonance in the $\overline{R}$ dependence occurs when ${\widehat{\epsilon }}_{\mathrm{p}}$ is real and smaller than ${\widehat{\epsilon }}_{\mathcal{l}}.$ It was shown in Section 9 that under these conditions, $a_{\mathcal{l}}(e)$ must have a turning point on the Mie circle. At this point, the derivative of $a_{\mathcal{l}}(e)$ with respect to $\overline{R}$ vanishes. For the small-$\overline{R}$ approximation, we find

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}\overline{R}}}{a}_{\mathcal{l}}(e)={\displaystyle \frac{i{n}_1}{{\lambda }_{\mathcal{l}}{(e)}^2}}({\widehat{\epsilon }}_{\mathrm{p}}-1)d_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}}\left[(2\mathcal{l}+1)({{\widehat{\epsilon }}_{\mathrm{p}}}^{\prime }{\widehat{\epsilon }}_{\mathcal{l}})+(2\mathcal{l}-1)c_{\mathcal{l}}{(n_1\overline{R})}^2\right].$$

(115)

This is zero for

$${\overline{R}}_{\mathrm{t}}={\displaystyle \frac{1}{n_1}}\sqrt{{\displaystyle \frac{2\mathcal{l}+1}{2\mathcal{l}-1}}{\displaystyle \frac{{\widehat{\epsilon }}_{\mathcal{l}}-{\widehat{\epsilon }}_{\mathrm{p}}}{c_{\mathcal{l}}}}},$$

(116)

provided that the right-hand side is a positive number. This is so under condition (108). A comparison with Equation (109) shows that the turning point is related to the Fröhlich resonance radius as

$${\overline{R}}_{\mathrm{t}}=\sqrt{{\displaystyle \frac{2\mathcal{l}+1}{2\mathcal{l}-1}}}{\overline{R}}_{\mathrm{F}},$$

(117)

in the small-$\overline{R}$ approximation. In Section 9, we presented a method for finding the turning point without any restrictions on the value of $\overline{R}$. As an example, for the turning point of $a_1(e)$ with ${\widehat{\epsilon }}_{\mathrm{p}}=-2.2,$ we find from Equation (116) that ${\overline{R}}_{\mathrm{t}}=0.49,$ whereas the exact solution gives ${\overline{R}}_{\mathrm{t}}=0.47$.

A peculiar phenomenon associated with the Fröhlich mode is shown in Figure 24. When ${\widehat{\epsilon }}_{\mathrm{p}}$ is real, $a_{\mathcal{l}}(e)$ lies on the Mie circle. When ${\widehat{\epsilon }}_{\mathrm{p}}$ has an imaginary part, $a_{\mathcal{l}}(e)$ curves inwards, and for large $\overline{R}$, it rotates around the reduced Mie circle in a clockwise direction, as shown in Section 10. For small $\overline{R},$ the rotation is counterclockwise, so there is a turning point. We now consider the case where the imaginary part of ${\widehat{\epsilon }}_{\mathrm{p}}$ is relatively small. Then, ${\widehat{n}}_{\mathrm{p}}$ is almost positive imaginary, and the radius of the reduced Mie circle is $r_{\mathrm{M}}\approx ½$ with Equation (93), so it almost coincides with the Mie circle. We see from the figure that a circle inside the Mie circle appears for $\overline{R}<{\overline{R}}_{\mathrm{t}}.$ After the turning point, the curve continues along the Mie circle, which is actually the reduced Mie circle. The graph shows the exact $a_1(e)$, but the curve for the small-$\overline{R}$ approximation gives nearly the same graph. This suggests that this circle-in-a-circle has its origin in the Frölich mode. It can also be shown that when ${\widehat{\epsilon }}_{\mathrm{p}}$ is far away from the Fröhlich mode, the small circle disappears. It either becomes bigger, and then coincides with the Mie circle, or it shrinks to a point. Figure 25 illustrates the same phenomenon for different parameters.

The central parameter for the Fröhlich mode is the relative permittivity ${\widehat{\epsilon }}_{\mathrm{p}}$ of the particle. In order for the resonance line to be present, ${\widehat{\epsilon }}_{\mathrm{p}}$ must be close to ${\widehat{\epsilon }}_{\mathcal{l}},$ and somewhat smaller than ${\widehat{\epsilon }}_{\mathcal{l}},$ according to Figure 18. We shall now consider the Mie coefficients as a function of ${\widehat{\epsilon }}_{\mathrm{p}},$ for a fixed value of the particle radius $\overline{R}$. In the resonance function $q_{\mathcal{l}}(e)$ from Equation (103), the parameter $c_{\mathcal{l}}$ depends on ${\widehat{\epsilon }}_{\mathrm{p}}.$ In order to simplify the algebra a little bit, we shall set ${\widehat{\epsilon }}_{\mathrm{p}}={\widehat{\epsilon }}_{\mathcal{l}}$ in $c_{\mathcal{l}},$ and we indicate this approximation by ${c_{\mathcal{l}}}^{\prime }.$ We find from Equation (105)

$${c_{\mathcal{l}}}^{\prime }={\displaystyle \frac{2(\mathcal{l}+1)(2\mathcal{l}+1)}{{\mathcal{l}}^2(2\mathcal{l}-1)(2\mathcal{l}+3)}}.$$

(118)

Table 3. The table shows ${c_{\mathcal{l}}}^{\prime }$ for various values of $\mathcal{l}$.

$\mathcal{l}$	${c_{\mathcal{l}}}^{\prime }$
1	2.40
2	0.357
3	0.138
4	0.0731
5	0.0451
10	0.0106
20	0.00257

shows some values of ${c_{\mathcal{l}}}^{\prime }.$ The resonance condition (108) becomes

$${\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathcal{l}}+{c_{\mathcal{l}}}^{\prime }{(n_1\overline{R})}^2=0.$$

(119)

The solution of this equation is

$${\widehat{\epsilon }}_{\mathrm{F}}={\widehat{\epsilon }}_{\mathcal{l}}-{c_{\mathcal{l}}}^{\prime }{(n_1\overline{R})}^2=0.$$

(120)

We could call this the Fröhlich resonance permittivity. The resonance function becomes

$$q_{\mathcal{l}}(e)={\widehat{\epsilon }}_{\mathrm{p}}-{\widehat{\epsilon }}_{\mathrm{F}},$$

(121)

which shows that the Fröhlich resonance is located at ${\widehat{\epsilon }}_{\mathrm{p}}={\widehat{\epsilon }}_{\mathrm{F}}.$ Since ${c_{\mathcal{l}}}^{\prime }<0,$ we have ${\widehat{\epsilon }}_{\mathrm{F}}<{\widehat{\epsilon }}_{\mathcal{l}}.$ Unlike ${\overline{R}}_{\mathrm{F}}$ from Equation (109), ${\widehat{\epsilon }}_{\mathrm{F}}$ always exists. Figure 26 shows the exact $a_1(e)$ for $\overline{R}=0.5$. The expected peak, according to the old approximation, Equation (97), should be located at ${\widehat{\epsilon }}_{\mathrm{p}}={\widehat{\epsilon }}_1,$ but with the new and improved approximation, it should be located at ${\widehat{\epsilon }}_{\mathrm{p}}={\widehat{\epsilon }}_{\mathrm{F}}.$ So, there is a line shift of

$$\delta {\widehat{\epsilon }}_{\mathrm{p}}=-\hspace{0.17em}{c_{\mathcal{l}}}^{\prime }{(n_1\overline{R})}^2.$$

(122)

This shift is to a lower ${\widehat{\epsilon }}_{\mathrm{p}},$ and it is due to the finite radius $\overline{R}$ of the particle. The shift measured from the graph is $\delta {\widehat{\epsilon }}_{\mathrm{p}}=-\hspace{0.17em}0.65,$ whereas the estimate (122) gives $\delta {\widehat{\epsilon }}_{\mathrm{p}}=-\hspace{0.17em}0.60$. The linewidth is estimated to be

$$\Delta {\widehat{\epsilon }}_{\mathrm{p}}={\displaystyle \frac{2\mathcal{l}+1}{\mathcal{l}}}{d}_{\mathcal{l}}{(n_1\overline{R})}^{2\mathcal{l}+1}.$$

(123)

The linewidth found from the graph is $\Delta {\widehat{\epsilon }}_{\mathrm{p}}=0.34,$ whereas Equation (123) predicts $\Delta {\widehat{\epsilon }}_{\mathrm{p}}=0.25$. The estimates for the shift and the width seem reasonably accurate, especially since the radius $\overline{R}$ of the particle is not really small. The linewidth decreases rapidly with increasing $\mathcal{l},$ as is illustrated in Figure 27. We also see that the original expectation ${\widehat{\epsilon }}_2=-1.5$ of the line position is way outside the graph on the right. This is an example of the serious improvement with the new small-$\overline{R}$ approximation. For the estimated values of the width and the shift, we find that the estimated shift has an error of $0.088\%,$ whereas the linewidth has an error of $3.7\hspace{0.17em}\%.$

13. Conclusions

We have studied the Mie scattering coefficients $a_{\mathcal{l}}(\alpha )$ and the Mie particle coefficients $b_{\mathcal{l}}(\alpha ),$ with a particular emphasis on their dependence on the (dimensionless) particle radius $\overline{R}.$ Central to this discussion is the Mie circle in the complex plane. When there is no dissipation in the particle or the embedding medium, then the scattering coefficients lie on this circle. We have shown this from the explicit expressions for the Mie scattering coefficients, but it can be shown that it is a direct consequence of conservation of energy in the system. For $\overline{R}=0$, we have $a_{\mathcal{l}}(\alpha )=0$. With increasing $\overline{R},$ the Mie coefficients rotate around this circle. This rotation can be clockwise or counterclockwise, depending on the parameters. It is also possible that the rotation starts counterclockwise and ends clockwise. In this case, there has to be a turning point. We have presented a numerical method for the evaluation of this turning point. When there is absorption in the particle and not in the host medium, the curve in the complex plane bends to the inside of the Mie circle, and for large $\overline{R}$, the Mie scattering coefficients rotate clockwise around a smaller circle. We have derived an expression for the radius of this reduced Mie circle. When there is absorption in the host medium and not in the particle, the magnitudes of the Mie coefficients increase exponentially with the particle radius $\overline{R}.$

A particularly interesting phenomenon is the Fröhlich resonance for a small particle. When the relative permittivity ${\widehat{\epsilon }}_{\mathrm{p}}$ of the particle is in the neighborhood of $- (\mathcal{l}+1)/\mathcal{l},$ with $\mathcal{l}$ the order of the multipole, then the electric multipole Mie coefficient $a_{\mathcal{l}}(e)$ has a resonance. In the usual approximation of $a_{\mathcal{l}}(e)$ for small $\overline{R},$ Equation (47), we get a division by zero, which is unphysical. We have shown that a more careful approximation formula for small $\overline{R}$ gives $a_{\mathcal{l}}(e)=1$ at the resonance. Our approximation also puts $a_{\mathcal{l}}(e)$ on the Mie circle, which guarantees conservation of energy. The $\overline{R}$ dependence of $a_{\mathcal{l}}(e)$ has the form of a resonance line. We have derived expressions for the position and width of this line, based on the small-$\overline{R}$ approximation, and this was numerically found to be in excellent agreement with the exact result for the Mie coefficients. Also, the dependence on ${\widehat{\epsilon }}_{\mathrm{p}}$ has the appearance of a resonance line.