Modal Mode Simulation of Near-Unstable Cavities with Realistic Mirror Maps
Abstract
1. Introduction
1.1. Stability Criteria and near Unstable Cavity
1.2. Challenges of Using near Unstable Cavity
2. Model of the Simulation
2.1. Finesse Simulation Framework with Higher-Order Modes
2.2. A Plano-Concave Cavity Model
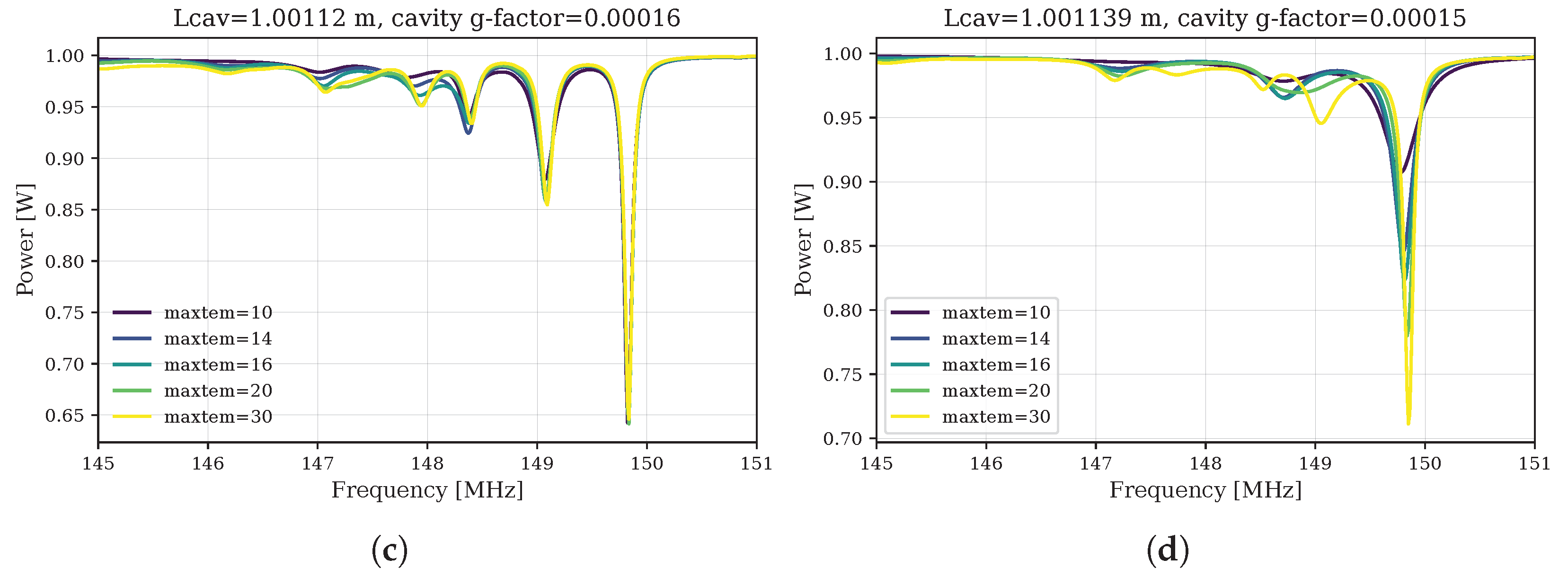
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Rel. 2009, 12, 2. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101, Erratum in: Phys. Rev. Lett. 2018, 121, 129902. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Winkler, W.; Danzmann, K.; Ruediger, A.; Schilling, R. Heating by optical absorption and the performance of interferometric gravitational wave detectors. Phys. Rev. A 1991, 44, 7022–7036. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allem, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Harry, G.M.; Gretarsson, A.M.; Saulson, P.R.; Kittelberger, S.E.; Penn, S.D.; Startin, W.J.; Rowan, S.; Fejer, M.M.; Crooks, D.R.M.; Cagnoli, G.; et al. Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings. Class. Quant. Grav. 2002, 19, 897–918. [Google Scholar] [CrossRef]
- Rowan, S.; Hough, J.; Crooks, D.R.M. Thermal noise and material issues for gravitational wave detectors. Phys. Lett. A 2005, 347, 25–32. [Google Scholar] [CrossRef]
- Hild, S. Future Interferometers. In LIGO Document G1000715; LIGO Scientific Collaboration: Hanford, WA, USA, 2010. [Google Scholar]
- Hild, S. LIGO-3 Overview. In LIGO Document G1300577; LIGO Scientific Collaboration: Hanford, WA, USA, 2013. [Google Scholar]
- Bertet, P.; Osnaghi, S.; Rauschenbeutel, A.; Nogues, G.; Auffeves, A.; Brune, M.; Raimond, J.; Haroche, S. A complementarity experiment with an interferometer at the quantum–classical boundary. Nature 2001, 411, 166–170. [Google Scholar] [CrossRef]
- Durak, K.; Nguyen, C.H.; Leong, V.; Straupe, S.; Kurtsiefer, C. Diffraction-limited Fabry–Perot cavity in the near concentric regime. New J. Phys. 2014, 16, 103002. [Google Scholar] [CrossRef]
- Álvarez, M.D. Fundamental limitations of cavity-assisted atom interferometry. In Optical Cavities for Optical Atomic Clocks, Atom Interferometry and Gravitational-Wave Detection; Springer: Berlin/Heidelberg, Germany, 2019; pp. 141–155. [Google Scholar]
- Nguyen, C.H.; Utama, A.N.; Lewty, N.; Kurtsiefer, C. Operating a near-concentric cavity at the last stable resonance. Phys. Rev. A 2018, 98, 063833. [Google Scholar] [CrossRef]
- Pal, R.; Yadav, V.; Sharma, A. Transportable optical cavity systems for terrestrial and space-borne portable optical atomic clocks. Front. Quantum Sci. Technol. 2024, 3, 1438345. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Li, Z.; Yu, P.; Zhang, G. Stabilization of transverse modes for a high finesse near-unstable cavity. Appl. Sci. 2019, 9, 4580. [Google Scholar] [CrossRef]
- Siegman, A.E. Unstable optical resonators for laser applications. Proc. IEEE 1965, 53, 277–287. [Google Scholar] [CrossRef]
- Siegman, A. Unstable optical resonators. Appl. Opt. 1974, 13, 353–367. [Google Scholar] [CrossRef]
- Siegman, A.; Arrathoon, R. Modes in unstable optical resonators and lens waveguides. IEEE J. Quantum Electron. 1967, 3, 156–163. [Google Scholar] [CrossRef]
- Karman, G.; McDonald, G.; New, G.; Woerdman, J. Fractal modes in unstable resonators. Nature 1999, 402, 138. [Google Scholar] [CrossRef]
- Brown, D.D.; Rowlinson, S.; Leavey, S.; Jones, P.; Freise, A. Finesse 3. 2020. Available online: https://finesse.ifosim.org/ (accessed on 25 March 2025).
- Harry, G.M. Advanced LIGO: The next generation of gravitational wave detectors. Class. Quantum Gravity 2010, 27, 084006. [Google Scholar] [CrossRef]
- Acernese, F.; Adams, T.; Agathos, M.; Agatsuma, K.; Allocca, A.; Astone, P.; Ballardin, G.; Barone, F.; Barsuglia, M.; Basti, A.; et al. The Advanced Virgo detector. J. Physics Conf. Ser. 2015, 610, 012014. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Atsuta, S.; Awai, K.; Barton, M.A.; Cannon, K.; et al. The status of KAGRA underground cryogenic gravitational wave telescope. J. Physics Conf. Ser. 2020, 1342, 012014. [Google Scholar] [CrossRef]
- Somiya, K. Detector configuration of KAGRA - the Japanese cryogenic gravitational-wave detector. Class. Quantum Gravity 2011, 29, 124007–124018. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Wang, H.; Dovale-Álvarez, M.; Collins, C.; Brown, D.D.; Wang, M.; Mow-Lowry, C.M.; Han, S.; Freise, A. Feasibility of near-unstable cavities for future gravitational wave detectors. Phys. Rev. D 2018, 97, 022001. [Google Scholar] [CrossRef]
- Wang, H. Beware of Warped Surfaces: Near-Unstable Cavities for Future Gravitational Wave Detectors. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2017. [Google Scholar]
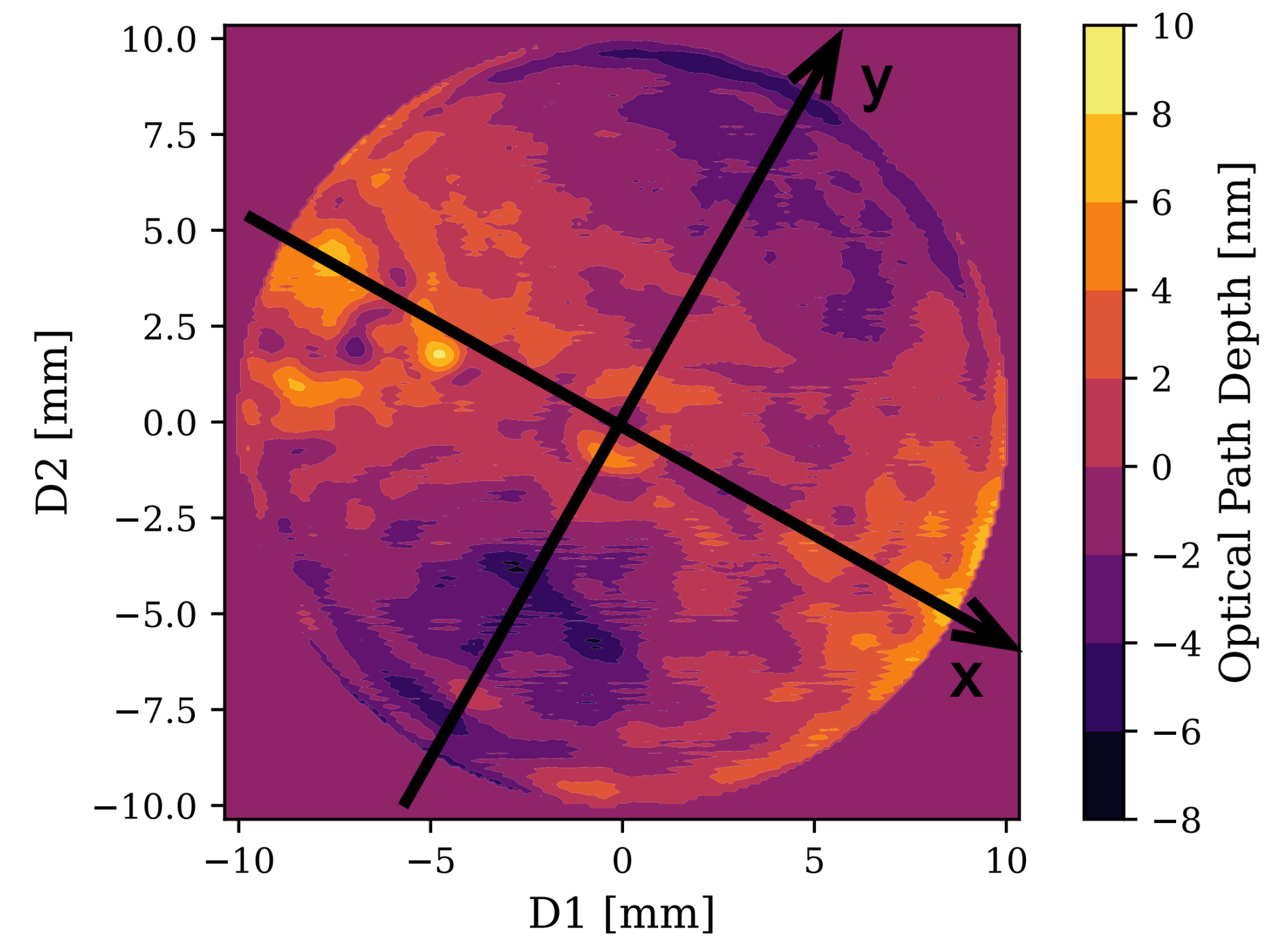
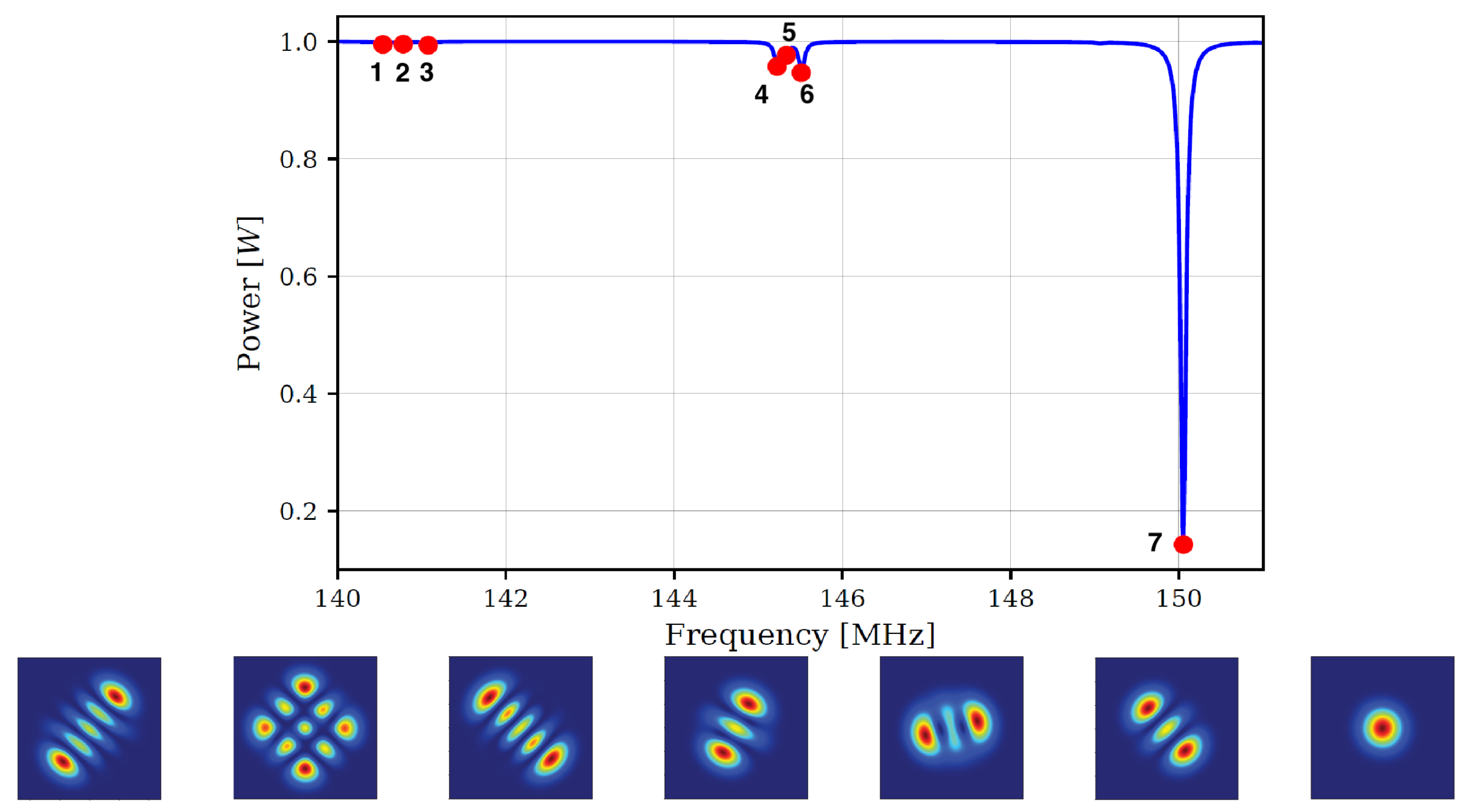
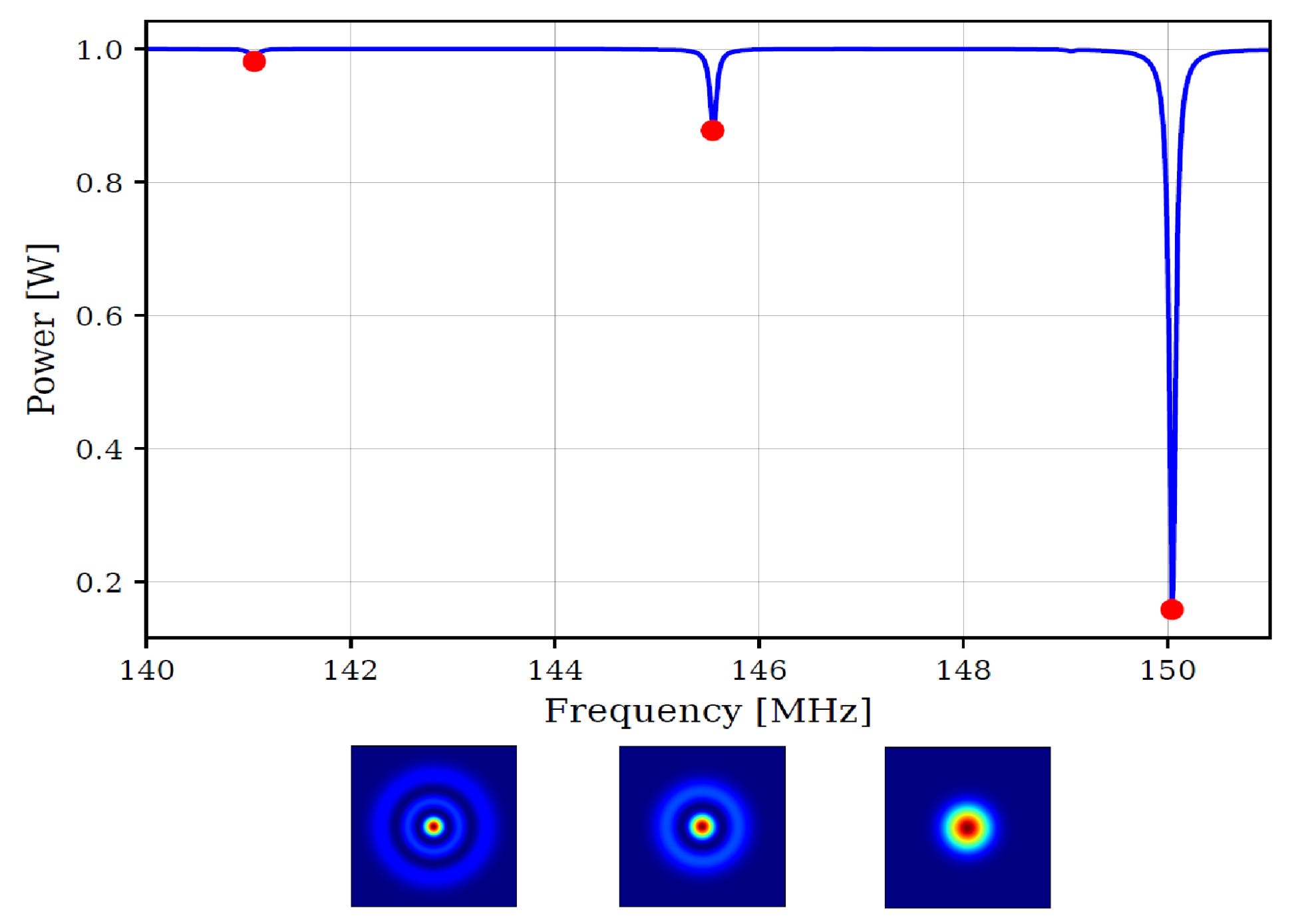
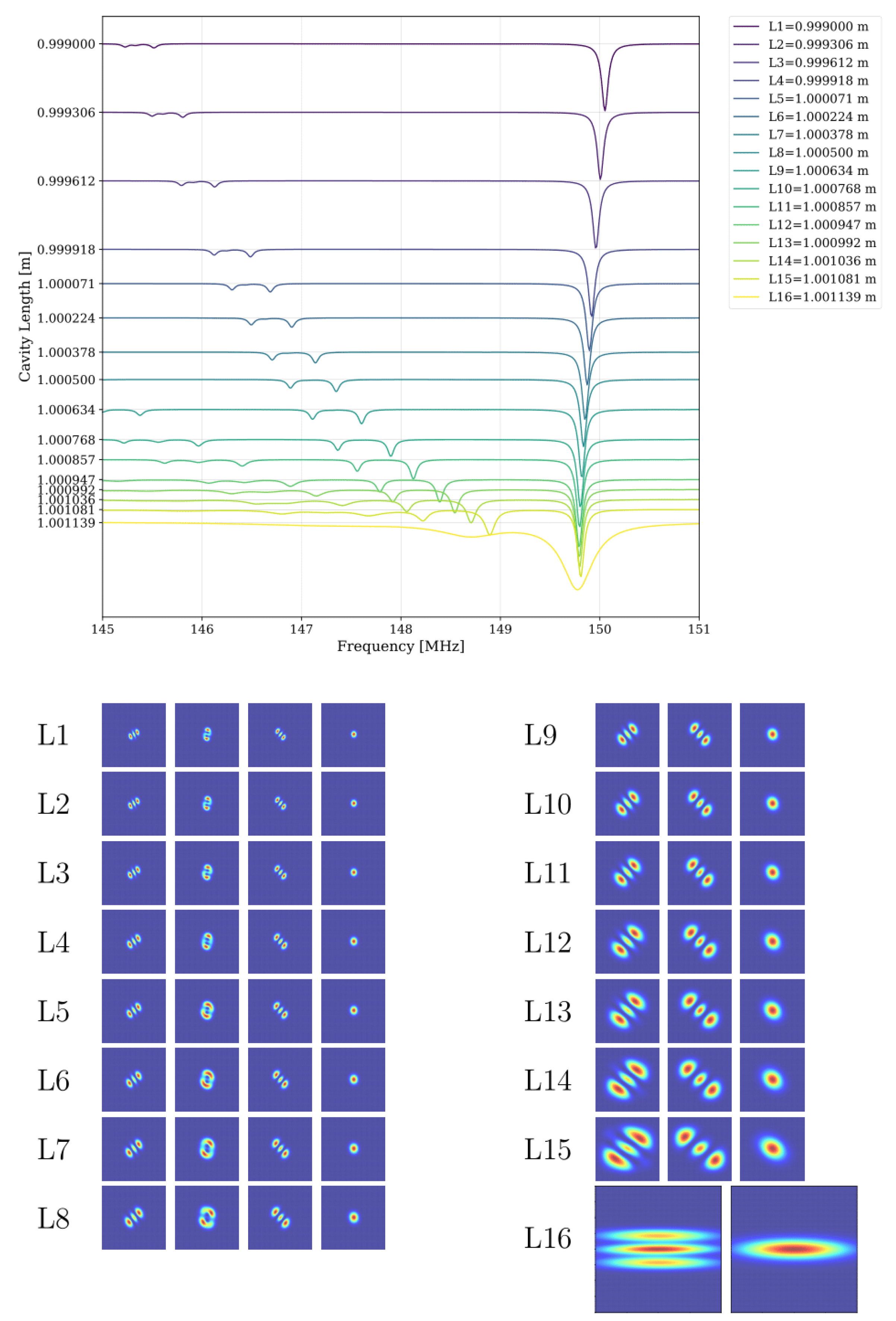
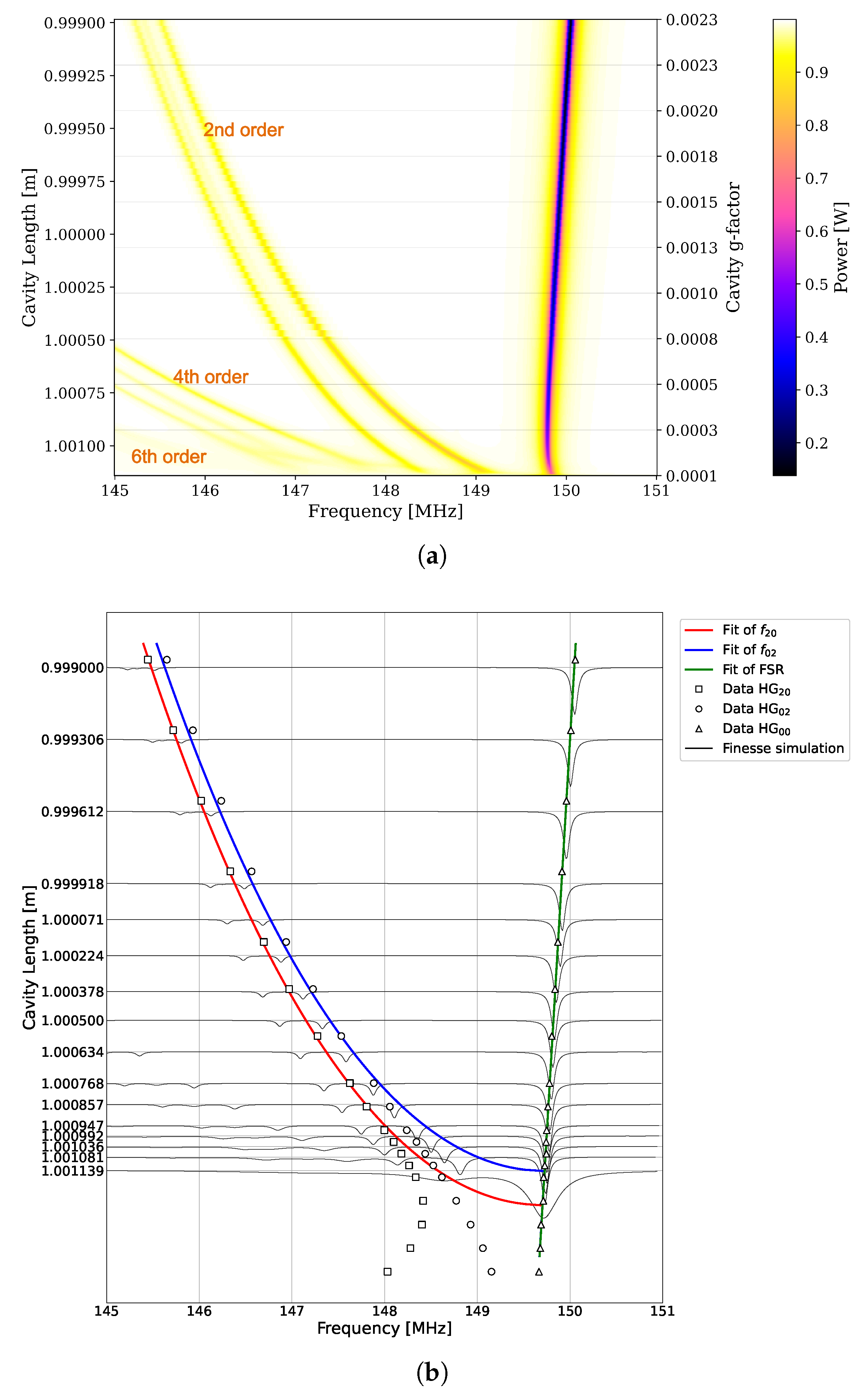
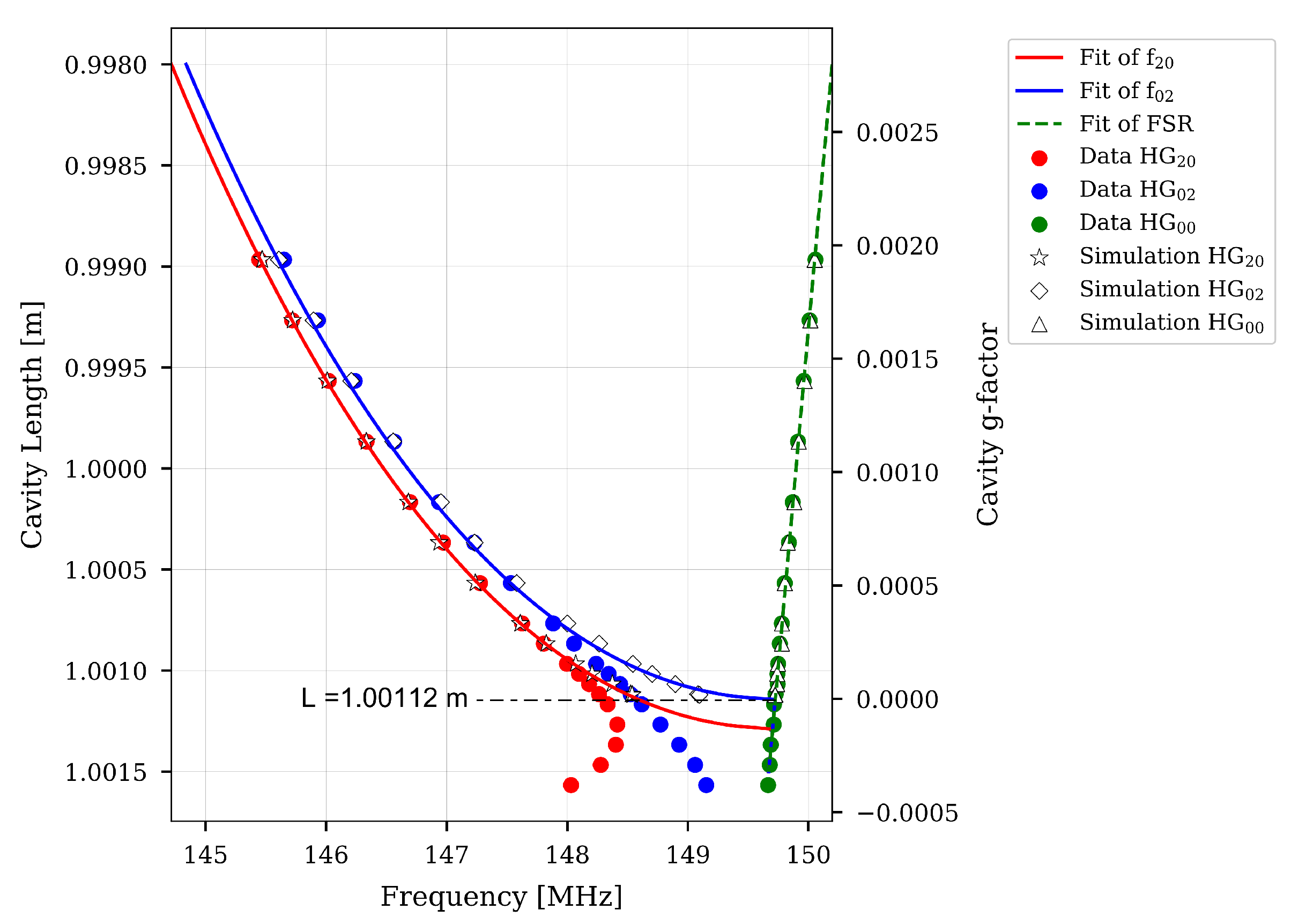
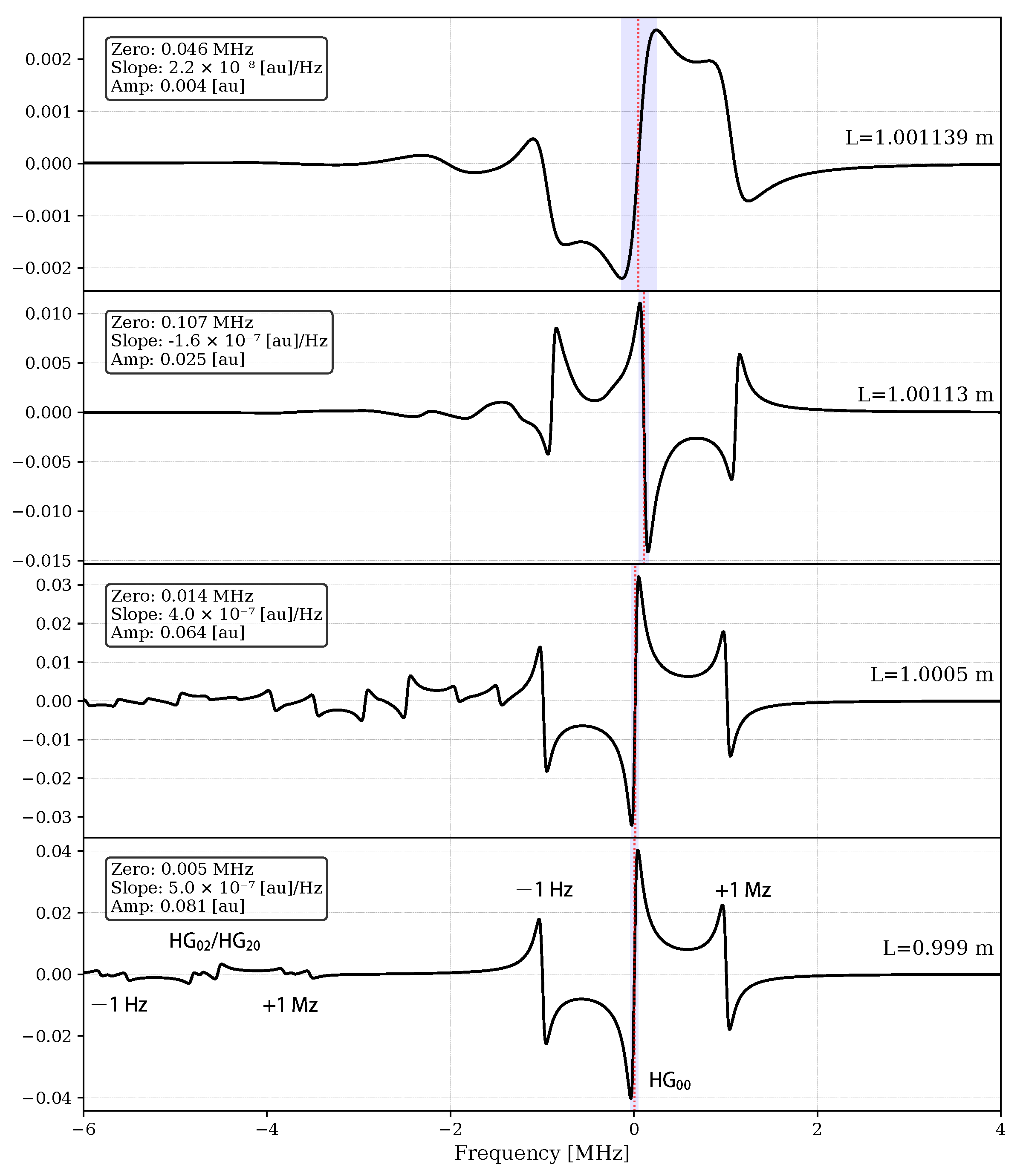
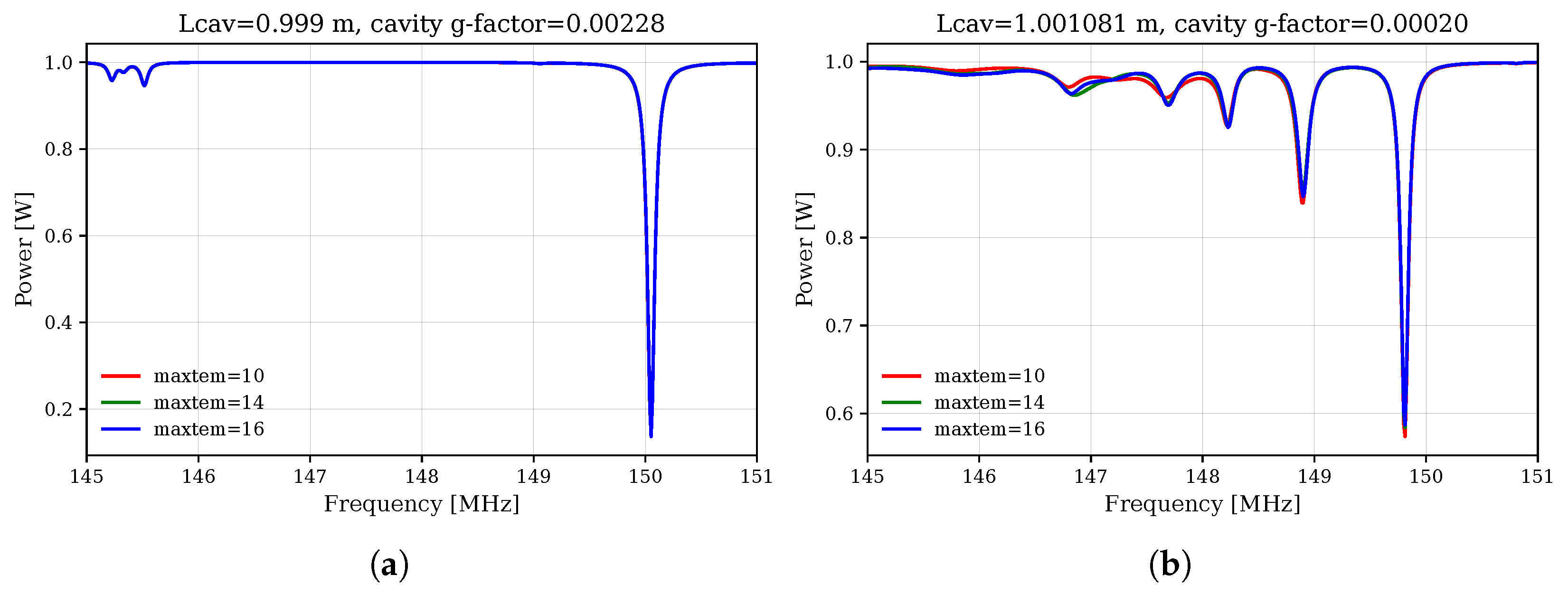
| Parameters | Values |
|---|---|
| Laser Power | 1 W |
| Modulated Frequency | 1 MHz |
| Modulation Type | Phase Modulation |
| Cavity Length | ∼1 m |
| Radius of Curvature of IM | Flat |
| Radius of Curvature of EM | 1.0012849 m |
| Radius of Curvature of EM | 1.00114 m |
| Reflectivity of IM | 0.9985 |
| Reflectivity of EM | 0.9985 |
| FSR | ∼150.05 MHz |
| Finesse | 2092.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Wang, H.; Freise, A.; Brown, D.; Zhu, Z.-H. Modal Mode Simulation of Near-Unstable Cavities with Realistic Mirror Maps. Photonics 2025, 12, 670. https://doi.org/10.3390/photonics12070670
Cao M, Wang H, Freise A, Brown D, Zhu Z-H. Modal Mode Simulation of Near-Unstable Cavities with Realistic Mirror Maps. Photonics. 2025; 12(7):670. https://doi.org/10.3390/photonics12070670
Chicago/Turabian StyleCao, Mengdi, Haoyu Wang, Andreas Freise, Daniel Brown, and Zong-Hong Zhu. 2025. "Modal Mode Simulation of Near-Unstable Cavities with Realistic Mirror Maps" Photonics 12, no. 7: 670. https://doi.org/10.3390/photonics12070670
APA StyleCao, M., Wang, H., Freise, A., Brown, D., & Zhu, Z.-H. (2025). Modal Mode Simulation of Near-Unstable Cavities with Realistic Mirror Maps. Photonics, 12(7), 670. https://doi.org/10.3390/photonics12070670





