Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review
Abstract
1. Introduction
2. Working Principles of OFSs
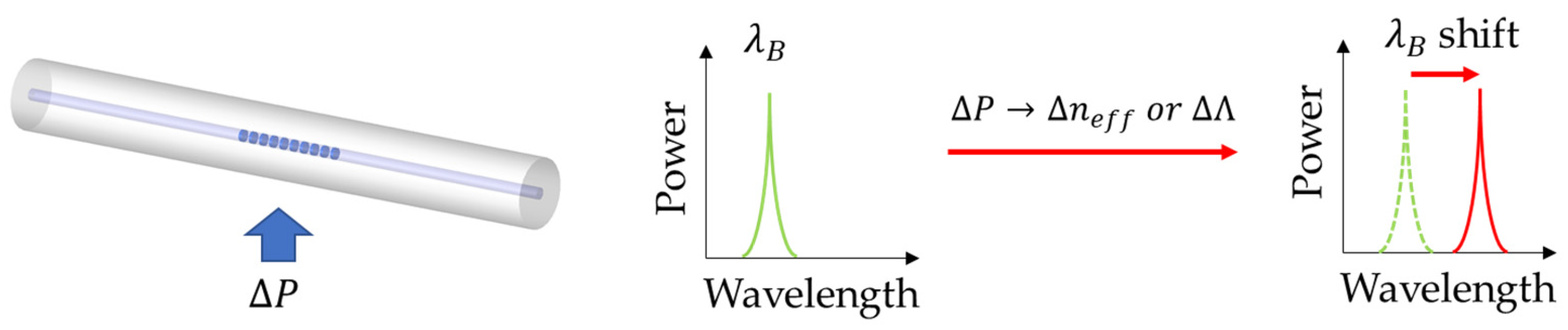
2.1. Fiber Bragg Grating Sensors
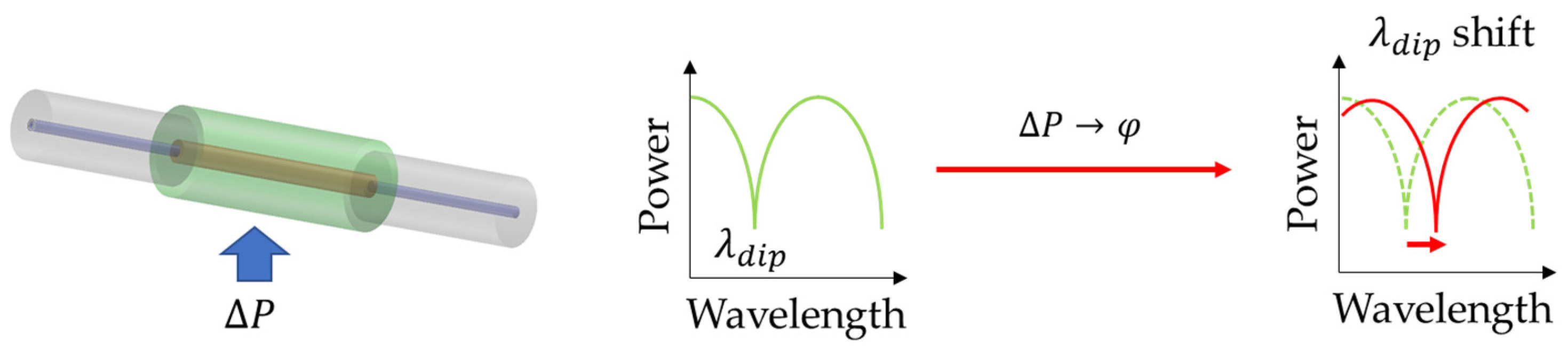
2.2. Fabry–Pérot Interferometer Fiber Sensors
2.3. Cascaded Optical Fiber Sensors
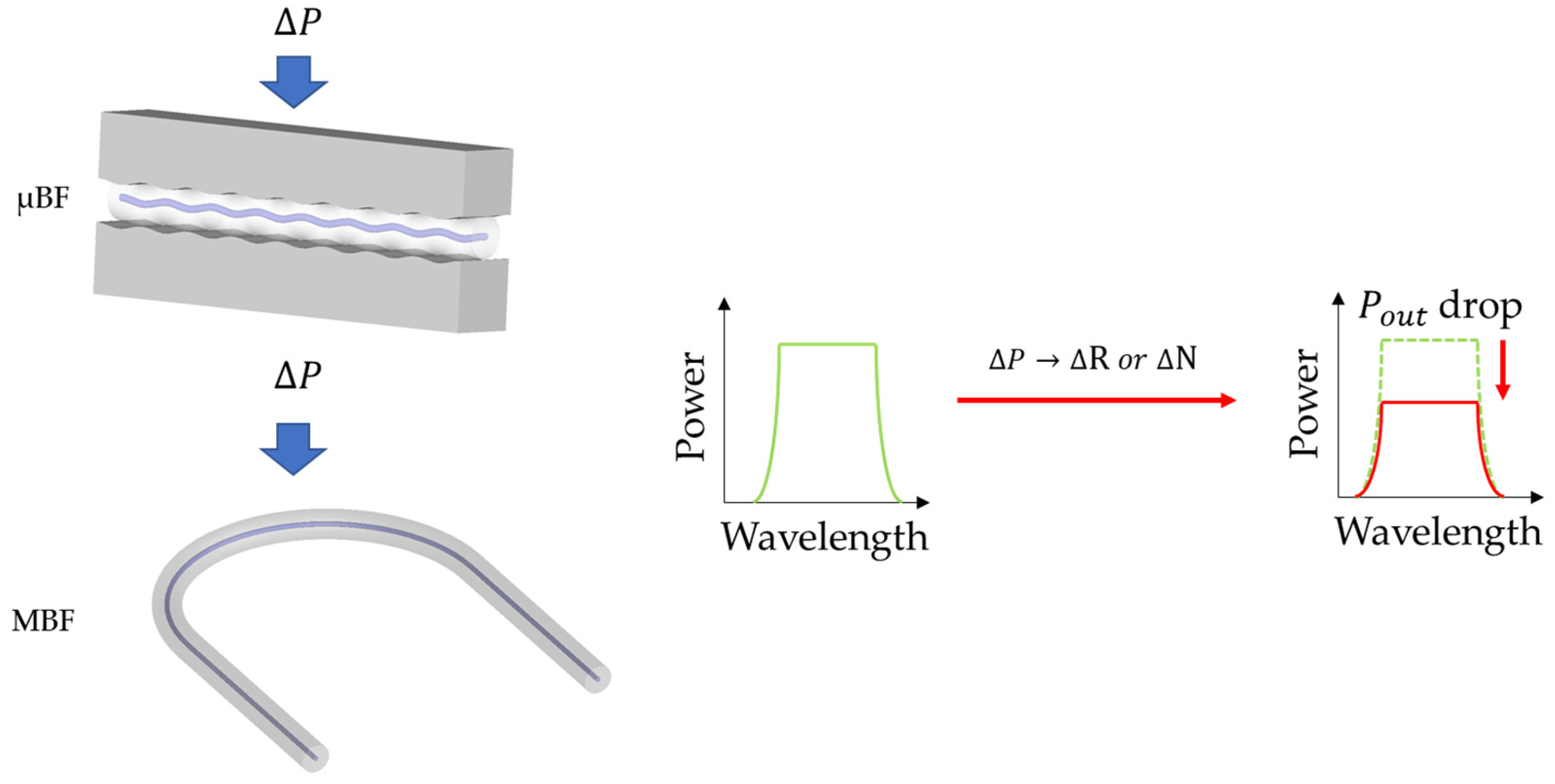
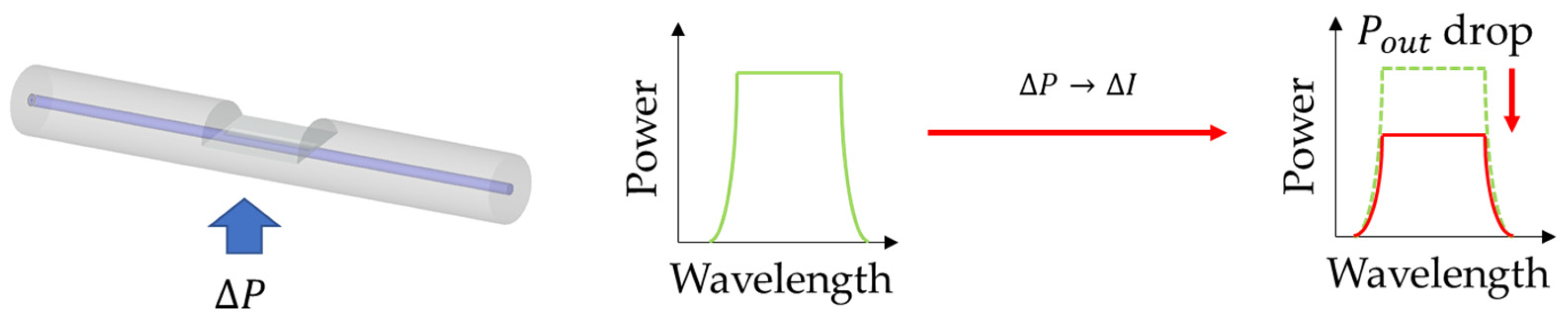
2.4. Macro-/Micro-Bend Fiber Sensors
2.5. Cladding-Removed Fiber Sensors
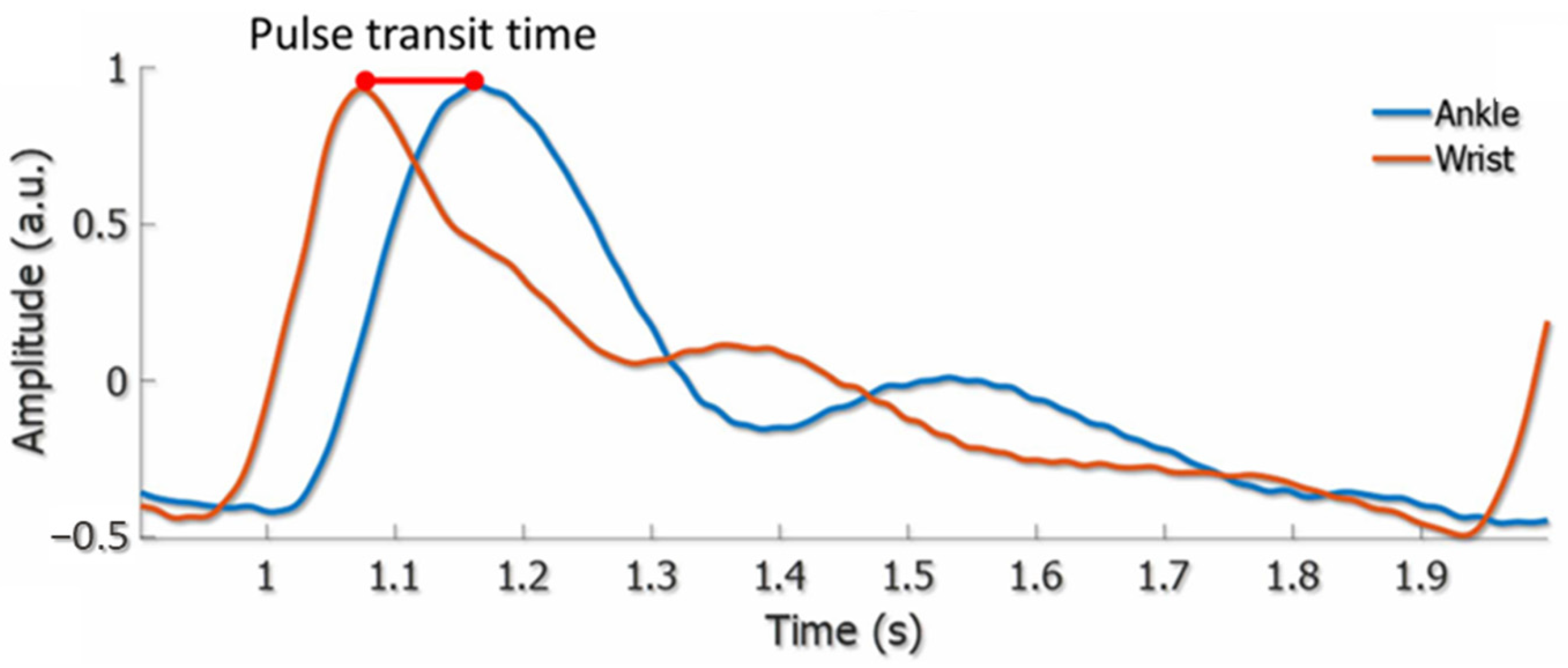
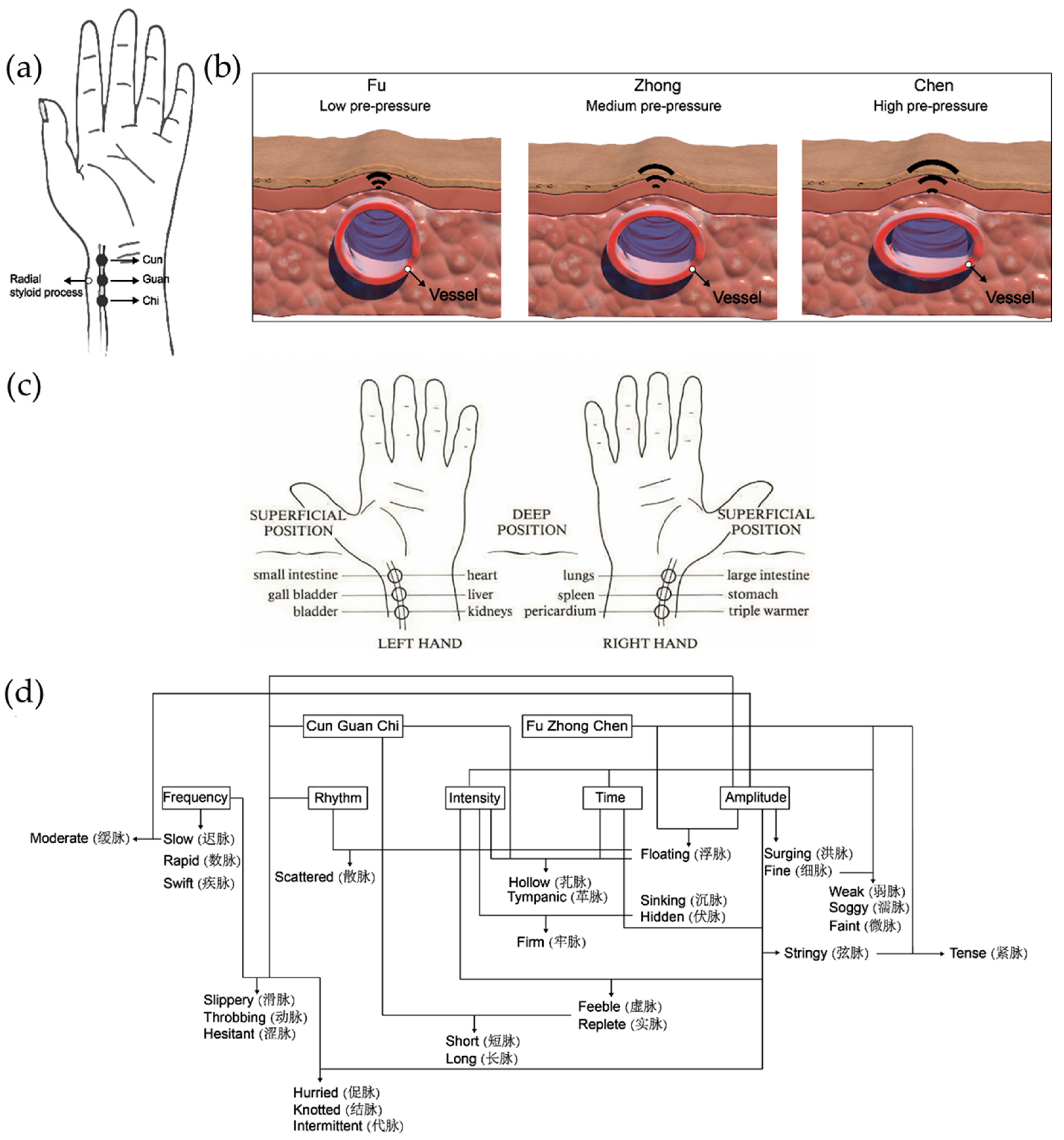
3. Arterial Pulse Wave and Pulse Waveform Analysis
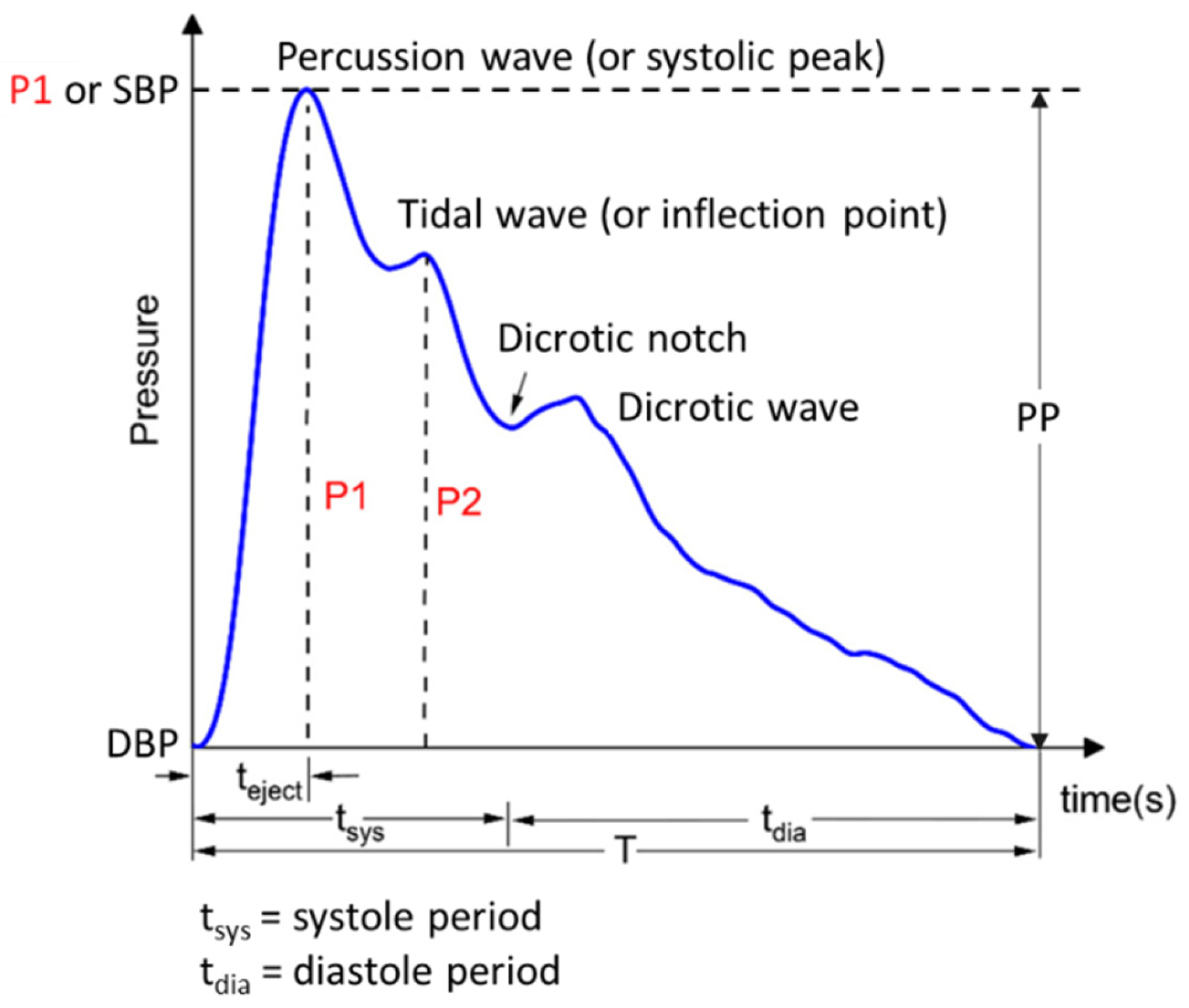
4. OFSs for Pulse Waveform Sensing
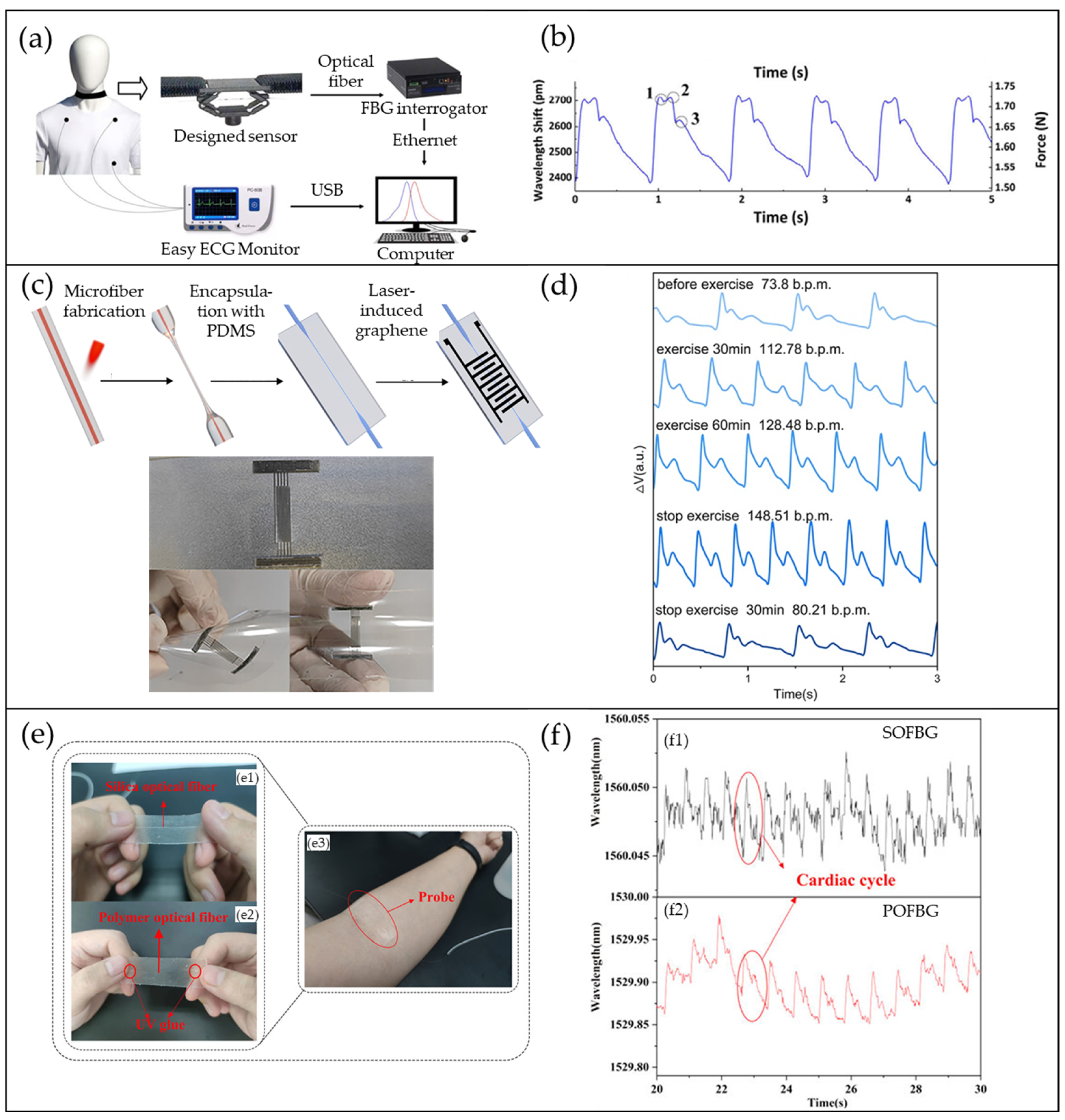
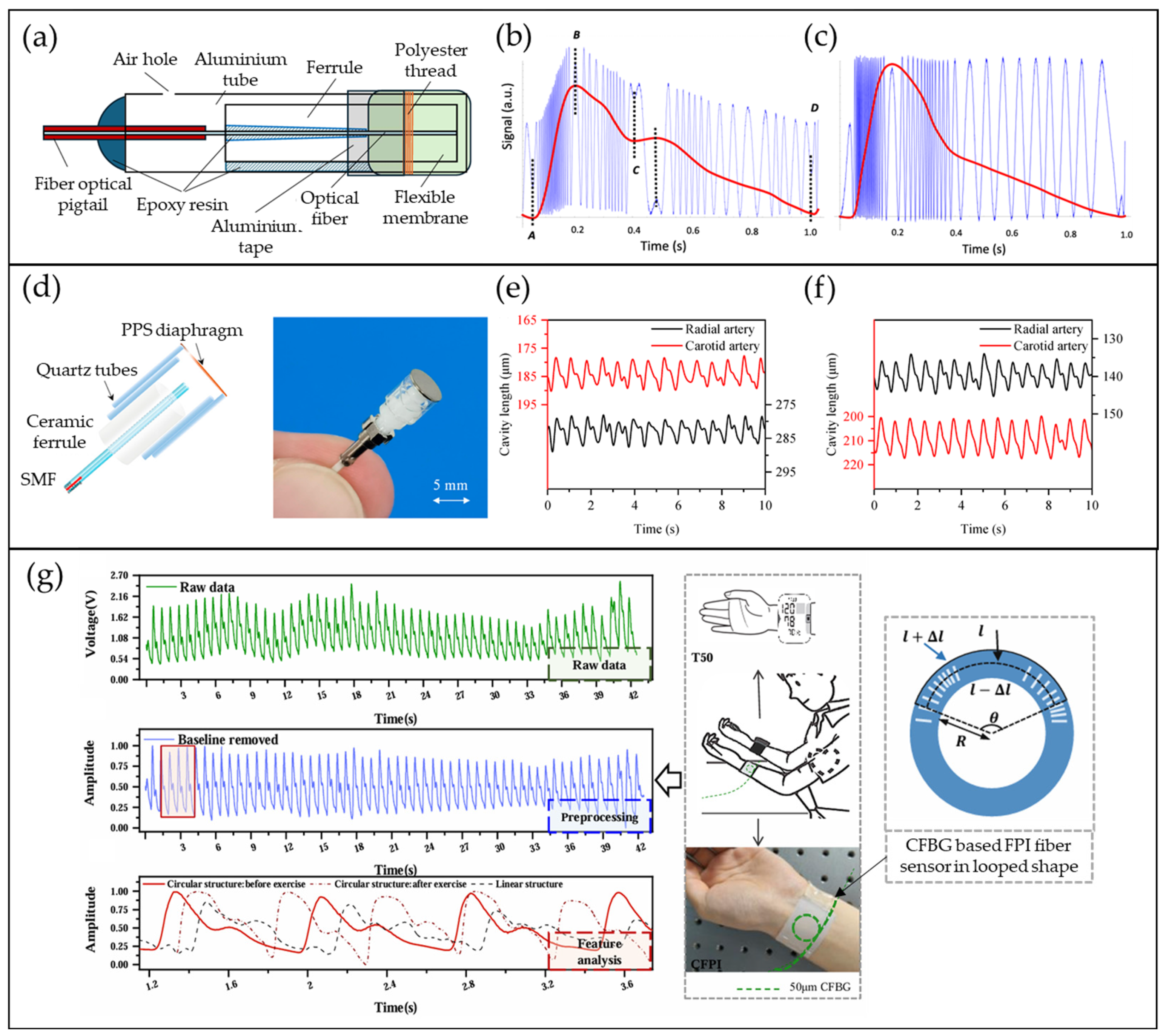
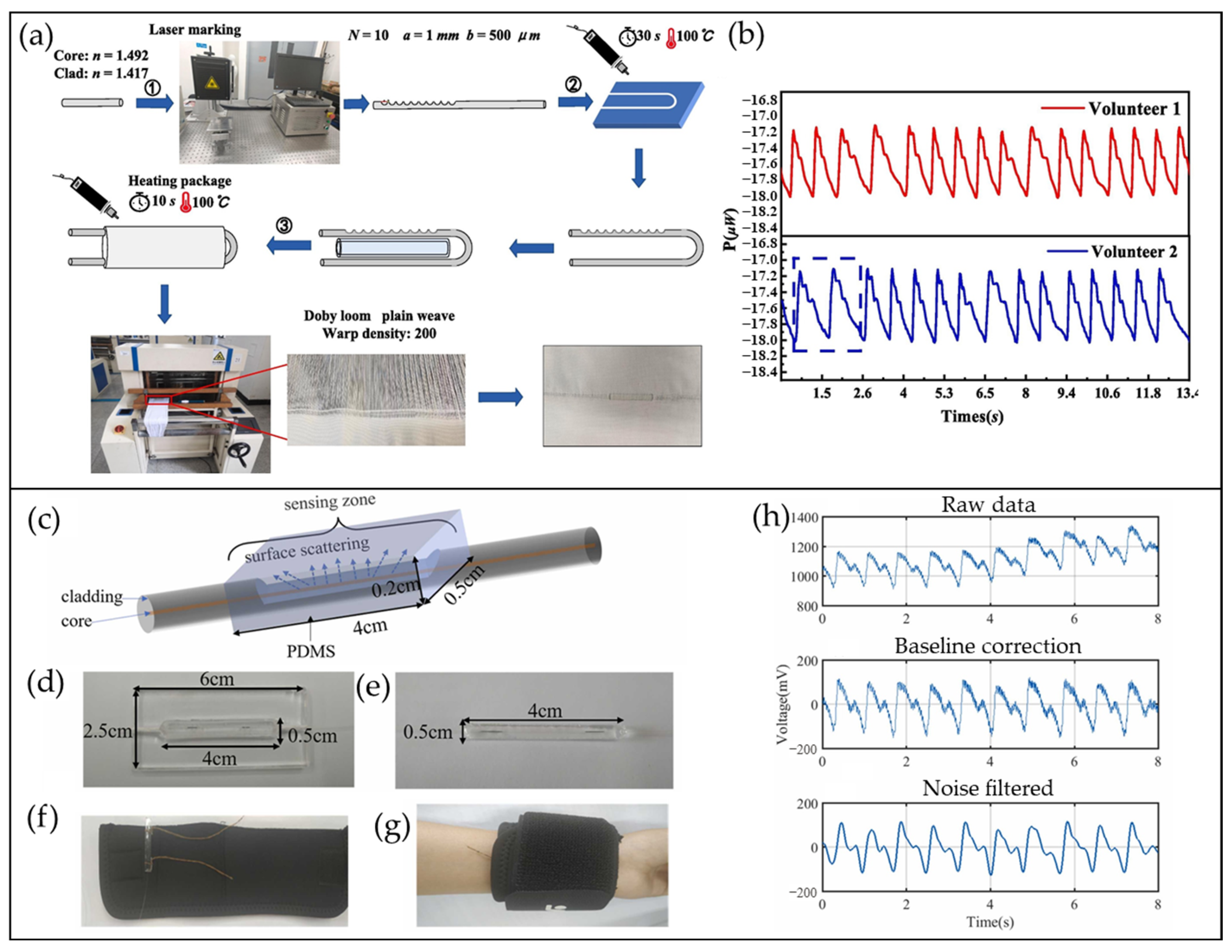
4.1. FBG-Based Pulse Waveform Sensors
4.2. FPI-Based Pulse Waveform Sensors
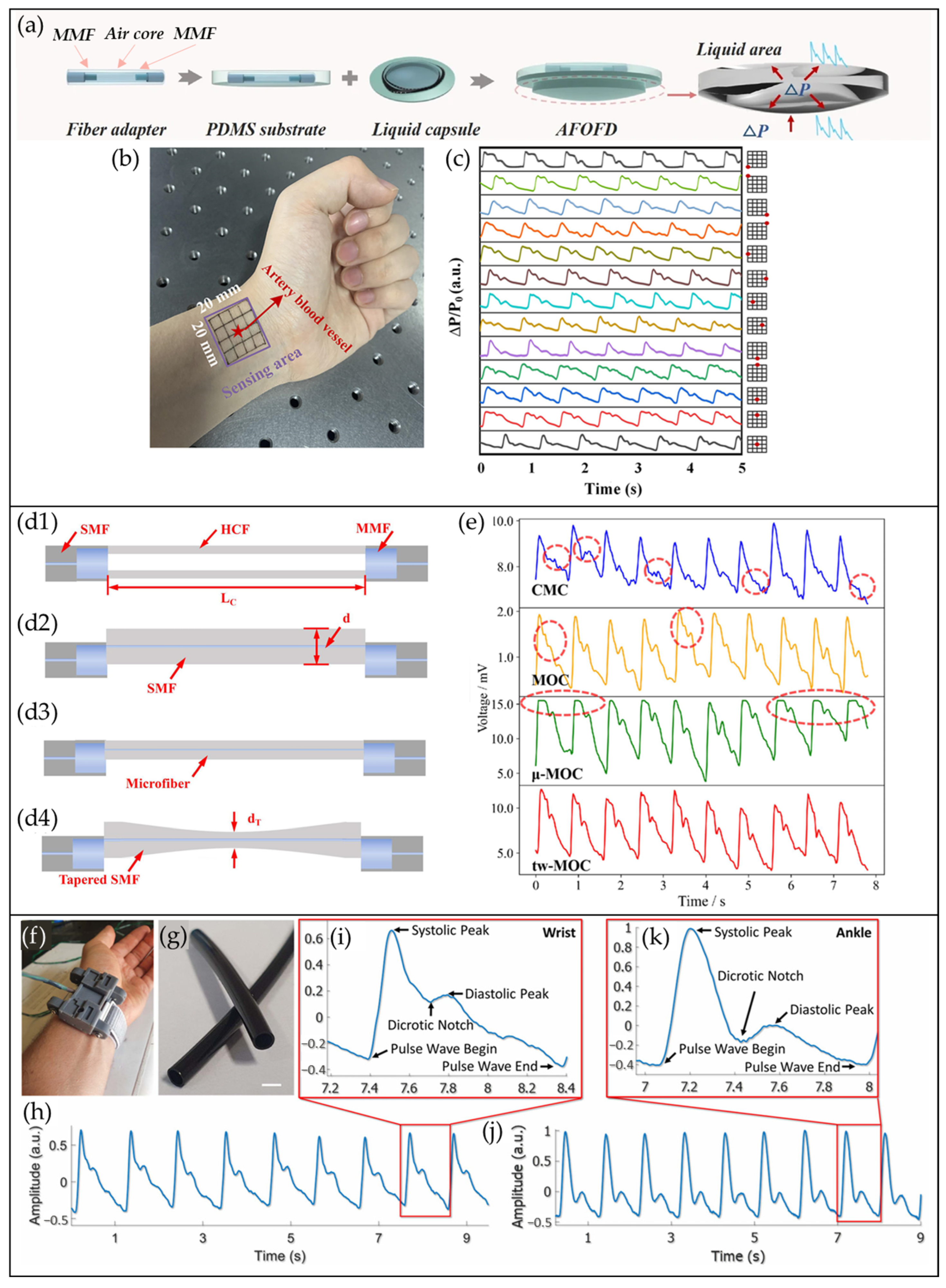
4.3. COF-Based Pulse Waveform Sensors
4.4. MBF/µBF-Based Pulse Waveform Sensors
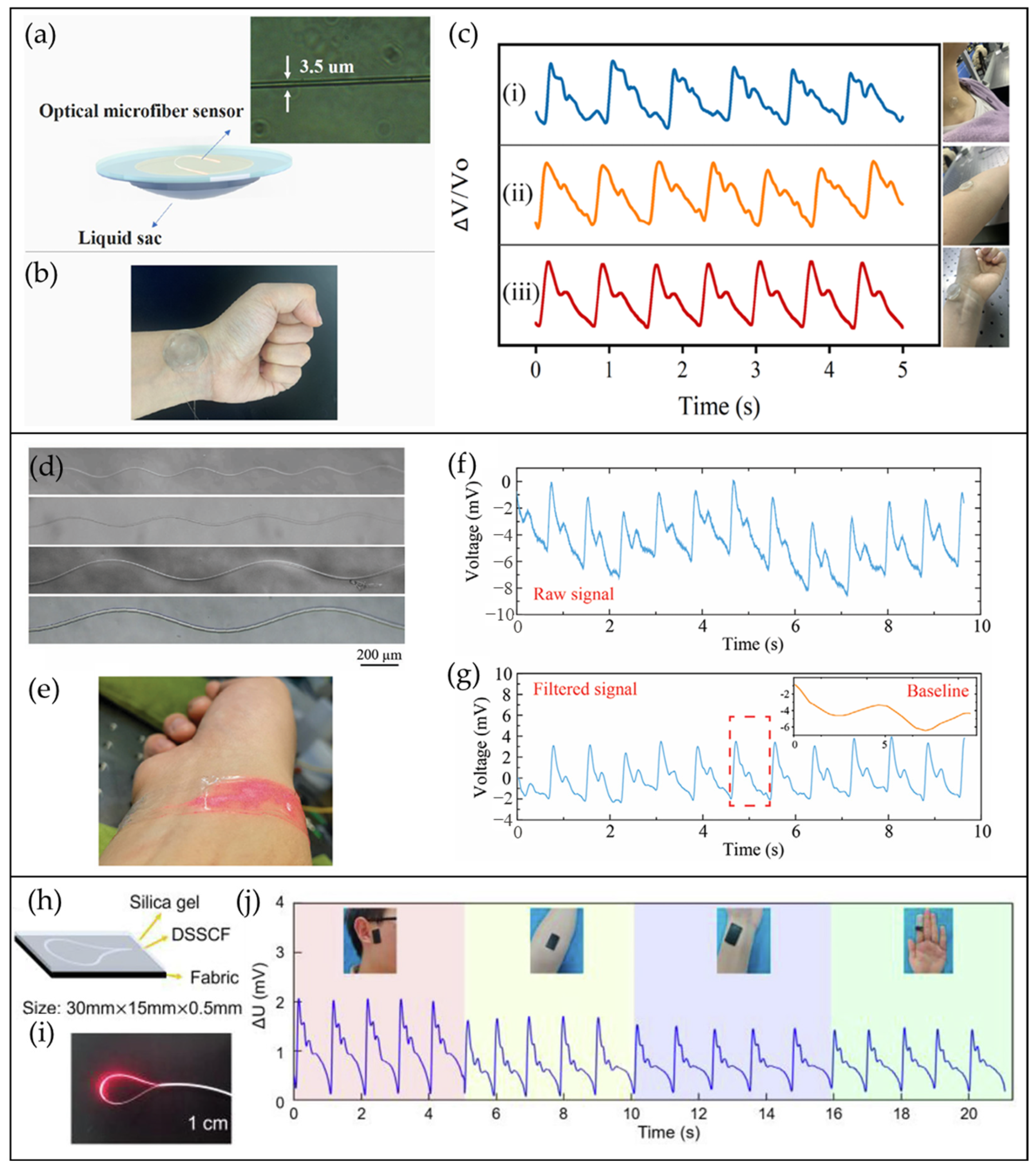
4.5. CRF-Based Pulse Waveform Sensors
4.6. Other Types of OFS for Pulse Waveform Monitoring
5. Challenges and Opportunities
5.1. Environmental Robustness and Signal Integrity
5.2. Wearability
5.3. Miniaturization and Power Efficiency
5.4. Toward Multimodal Diagnostics and Clinical Adoption
5.5. Self-Calibration Measures
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Report on Hypertension: The Race Against a Silent Killer; World Health Organization: Geneva, Switzerland, 2023. [Google Scholar]
- Zhou, B.; Perel, P.; Mensah, G.A.; Ezzati, M. Global epidemiology, health burden and effective interventions for elevated blood pressure and hypertension. Nat. Rev. Cardiol. 2021, 18, 785–802. [Google Scholar] [CrossRef] [PubMed]
- Scardulla, F.; Cosoli, G.; Spinsante, S.; Poli, A.; Iadarola, G.; Pernice, R.; Busacca, A.; Pasta, S.; Scalise, L.; D’Acquisto, L. Photoplethysmograhic sensors, potential and limitations: Is it time for regulation? A comprehensive review. Measurement 2023, 218, 113150. [Google Scholar] [CrossRef]
- Samartkit, P.; Pullteap, S. Non-invasive continuous blood pressure sensors in biomedical engineering research: A review. Sens. Actuators A Phys. 2024, 367, 115084. [Google Scholar] [CrossRef]
- Pang, Y.-N.; Liu, B.; Liu, J.; Wan, S.-P.; Wu, T.; Yuan, J.; Xin, X.; He, X.-D.; Wu, Q. Singlemode-multimode-singlemode optical fiber sensor for accurate blood pressure monitoring. J. Light. Technol. 2022, 40, 4443–4450. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Liu, B.; Liu, J.; Yang, H.; Hu, Y.; Fu, Y.; Wu, Q. Optical microfiber intelligent watchband for cuffless blood pressure monitoring. Sens. Actuators A Phys. 2025, 386, 116325. [Google Scholar] [CrossRef]
- Li, L.; Sheng, S.; Liu, Y.; Wen, J.; Song, C.; Chen, Z.; Xu, W.; Zhang, Z.; Fan, W.; Chen, C. Automatic and continuous blood pressure monitoring via an optical-fiber-sensor-assisted smartwatch. PhotoniX 2023, 4, 21. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, Y.-T. Pulse transit time technique for cuffless unobtrusive blood pressure measurement: From theory to algorithm. Biomed. Eng. Lett. 2019, 9, 37–52. [Google Scholar] [CrossRef]
- Sharma, M.; Barbosa, K.; Ho, V.; Griggs, D.; Ghirmai, T.; Krishnan, S.K.; Hsiai, T.K.; Chiao, J.-C.; Cao, H. Cuff-less and continuous blood pressure monitoring: A methodological review. Technologies 2017, 5, 21. [Google Scholar] [CrossRef]
- Pant, S.; Umesh, S.; Asokan, S. A novel approach to acquire the arterial pulse by finger plethysmography using fiber Bragg grating sensor. IEEE Sens. J. 2020, 20, 5921–5928. [Google Scholar] [CrossRef]
- Leitão, C.S.J.; da Costa Antunes, P.F.; Bastos, J.A.; Pinto, J.; de Brito André, P.S. Plastic optical fiber sensor for noninvasive arterial pulse waveform monitoring. IEEE Sens. J. 2014, 15, 14–18. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Zhang, D.; Zhang, D. Wrist pulse signal diagnosis using modified Gaussian models and Fuzzy C-Means classification. Med. Eng. Phys. 2009, 31, 1283–1289. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, J.C.; Wang, Z.; Zhang, X.; Yao, R.; Li, Y. Application research of pulse signal physiology and pathology feature mining in the field of disease diagnosis. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1111–1124. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, J.; Zhang, B. Computational traditional Chinese medicine diagnosis: A literature survey. Comput. Biol. Med. 2021, 133, 104358. [Google Scholar] [CrossRef]
- World Health Organization. WHO International Standard Terminologies on Traditional Chinese Medicine; World Health Organization: Geneva, Switzerland, 2022; pp. 83–93. [Google Scholar]
- Maciocia, G. The Foundations of Chinese Medicine: A Comprehensive Text; Elsevier Health Sciences: Amsterdam, The Netherlands, 2015; pp. 373–396. [Google Scholar]
- Bing, Z.; Hongcai, W. Diagnostics of Traditional Chinese Medicine; Singing Dragon: London, UK, 2010; pp. 89–112. [Google Scholar]
- Choong, C.L.; Shim, M.B.; Lee, B.S.; Jeon, S.; Ko, D.S.; Kang, T.H.; Bae, J.; Lee, S.H.; Byun, K.E.; Im, J. Highly stretchable resistive pressure sensors using a conductive elastomeric composite on a micropyramid array. Adv. Mater. 2014, 26, 3451–3458. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Hu, J.; Luo, N.; Sun, F.; Venkatesan, H.; Zhao, N.; Zhang, Y. Ultrafast-response/recovery flexible piezoresistive sensors with DNA-like double helix yarns for epidermal pulse monitoring. Adv. Mater. 2022, 34, 2104313. [Google Scholar] [CrossRef]
- Schwartz, G.; Tee, B.C.-K.; Mei, J.; Appleton, A.L.; Kim, D.H.; Wang, H.; Bao, Z. Flexible polymer transistors with high pressure sensitivity for application in electronic skin and health monitoring. Nat. Commun. 2013, 4, 1859. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, S.; Zhu, Z.; Han, Z.; Li, J.; Deng, L.; Zhou, Z.; Zhang, T.; Guan, M.; Wang, H. Low modulus coupling circuits: A feasible strategy for achieving highly sensitive linear pressure sensing in fiber crossbars. Adv. Funct. Mater. 2024, 34, 2405099. [Google Scholar] [CrossRef]
- Lin, Q.; Huang, J.; Yang, J.; Huang, Y.; Zhang, Y.; Wang, Y.; Zhang, J.; Wang, Y.; Yuan, L.; Cai, M. Highly sensitive flexible iontronic pressure sensor for fingertip pulse monitoring. Adv. Healthc. Mater. 2020, 9, 2001023. [Google Scholar] [CrossRef]
- Chu, Y.; Zhong, J.; Liu, H.; Ma, Y.; Liu, N.; Song, Y.; Liang, J.; Shao, Z.; Sun, Y.; Dong, Y. Human pulse diagnosis for medical assessments using a wearable piezoelectret sensing system. Adv. Funct. Mater. 2018, 28, 1803413. [Google Scholar] [CrossRef]
- Nie, J.; Zhang, L.; Liu, J.; Wang, Y. Pulse taking by a piezoelectric film sensor via mode energy ratio analysis helps identify pregnancy status. IEEE J. Biomed. Health Inform. 2021, 26, 2116–2123. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Su, Y.; Joe, P.; Yona, R.; Liu, Y.; Kim, Y.-S.; Huang, Y.; Damadoran, A.R.; Xia, J.; Martin, L.W. Conformable amplified lead zirconate titanate sensors with enhanced piezoelectric response for cutaneous pressure monitoring. Nat. Commun. 2014, 5, 4496. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Meng, K.; He, Q.; Zhang, G.; Zhou, Z.; Tan, X.; Feng, Z.; Sun, C.; Yang, J. Enabling the unconstrained epidermal pulse wave monitoring via finger-touching. Adv. Funct. Mater. 2021, 31, 2102378. [Google Scholar] [CrossRef]
- Kim, J.; Salvatore, G.A.; Araki, H.; Chiarelli, A.M.; Xie, Z.; Banks, A.; Sheng, X.; Liu, Y.; Lee, J.W.; Jang, K.-I. Battery-free, stretchable optoelectronic systems for wireless optical characterization of the skin. Sci. Adv. 2016, 2, e1600418. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, X.; Xu, J.; Fang, Y.; Chen, G.; Song, Y.; Li, S.; Chen, J. Giant magnetoelastic effect in soft systems for bioelectronics. Nat. Mater. 2021, 20, 1670–1676. [Google Scholar] [CrossRef]
- Zhu, H.T.; Zhan, L.W.; Dai, Q.; Xu, B.; Chen, Y.; Lu, Y.Q.; Xu, F. Self-assembled wavy optical microfiber for stretchable wearable sensor. Adv. Opt. Mater. 2021, 9, 2002206. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Song, C.; Sheng, S.; Yang, L.; Yan, Z.; Hu, D.J.J.; Sun, Q. Wearable alignment-free microfiber-based sensor chip for precise vital signs monitoring and cardiovascular assessment. Adv. Fiber Mater. 2022, 4, 475–486. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Sun, Q.; Ni, X.; Ai, F.; Wang, S.; Yan, Z.; Liu, D. Diaphragm-based optical fiber sensor for pulse wave monitoring and cardiovascular diseases diagnosis. J. Biophotonics 2019, 12, e201900084. [Google Scholar] [CrossRef]
- Meng, K.; Xiao, X.; Wei, W.; Chen, G.; Nashalian, A.; Shen, S.; Xiao, X.; Chen, J. Wearable pressure sensors for pulse wave monitoring. Adv. Mater. 2022, 34, 2109357. [Google Scholar] [CrossRef]
- Nedoma, J.; Fajkus, M.; Novak, M.; Strbikova, N.; Vasinek, V.; Nazeran, H.; Vanus, J.; Perecar, F.; Martinek, R. Validation of a novel fiber-optic sensor system for monitoring cardiorespiratory activities during mri examinations. Adv. Electr. Electron. Eng. 2017, 15, 536. [Google Scholar] [CrossRef]
- Silva, A.; Carmo, J.; Mendes, P.; Correia, J. Simultaneous cardiac and respiratory frequency measurement based on a single fiber Bragg grating sensor. Meas. Sci. Technol. 2011, 22, 075801. [Google Scholar] [CrossRef]
- Lu, L.; Cui, J.; Nawarathne, D.D.; Tam, H.-Y. Magnetic field sensing with magnetic shape memory alloy and fiber Bragg grating on silica and polymer optical fibers. IEEE Trans. Instrum. Meas. 2025, 74, 7007008. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.n.; Jiang, L.; Li, L.; Li, X.; Zhao, J. Flexible optical fiber sensor for non-invasive continuous monitoring of human physiological signals. Small Methods 2025, 9, 2401368. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, S.; Sun, Y.; Zhou, N.; Yu, H.; Zhang, H.; Jia, D. Wearable optical sensing in the medical internet of things (MIoT) for pervasive medicine: Opportunities and challenges. ACS Photonics 2022, 9, 2579–2599. [Google Scholar] [CrossRef]
- Jia, D.; Chao, J.; Li, S.; Zhang, H.; Yan, Y.; Liu, T.; Sun, Y. A fiber Bragg grating sensor for radial artery pulse waveform measurement. IEEE Trans. Biomed. Eng. 2017, 65, 839–846. [Google Scholar] [CrossRef]
- Lo Presti, D.; Santucci, F.; Massaroni, C.; Formica, D.; Setola, R.; Schena, E. A multi-point heart rate monitoring using a soft wearable system based on fiber optic technology. Sci. Rep. 2021, 11, 21162. [Google Scholar] [CrossRef]
- Ferraro, D.; D’Alesio, G.; Camboni, D.; Zinno, C.; Costi, L.; Haberbusch, M.; Aigner, P.; Maw, M.; Schlöglhofer, T.; Unger, E. Implantable fiber Bragg grating sensor for continuous heart activity monitoring: Ex-vivo and in-vivo validation. IEEE Sens. J. 2021, 21, 14051–14059. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Ma, L.; Wang, Q.; Wang, H.; Leal-Junior, A.; Li, X.; Marques, C.; Min, R. Optical microfiber intelligent sensor: Wearable cardiorespiratory and behavior monitoring with a flexible wave-shaped polymer optical microfiber. ACS Appl. Mater. Interfaces 2024, 16, 8333–8345. [Google Scholar] [CrossRef]
- Bonefacino, J.; Tam, H.-Y.; Glen, T.S.; Cheng, X.; Pun, C.-F.J.; Wang, J.; Lee, P.-H.; Tse, M.-L.V.; Boles, S.T. Ultra-fast polymer optical fibre Bragg grating inscription for medical devices. Light Sci. Appl. 2018, 7, 17161. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Marques, C. Diaphragm-embedded optical fiber sensors: A review and tutorial. IEEE Sens. J. 2020, 21, 12719–12733. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Zhao, W.; Zhang, M.; Qin, H.; Xie, Y. Flexible, stretchable sensors for wearable health monitoring: Sensing mechanisms, materials, fabrication strategies and features. Sensors 2018, 18, 645. [Google Scholar] [CrossRef]
- Peng, N.; Meng, W.; Wei, Q.; Ai, Q.; Liu, Q.; Xie, S. Wearable optical fiber sensors for biomechanical measurement in medical rehabilitation: A review. IEEE Sens. J. 2023, 23, 12455–12469. [Google Scholar] [CrossRef]
- Zhu, H.; Luo, J.; Dai, Q.; Zhu, S.; Yang, H.; Zhou, K.; Zhan, L.; Xu, B.; Chen, Y.; Lu, Y. Spatiotemporal hemodynamic monitoring via configurable skin-like microfiber Bragg grating group. Opto-Electron. Adv. 2023, 6, 230018. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Z.; Wang, P.; Peng, D.; Liu, Z. Flexible pressure sensor realized by a chirped fiber Bragg grating pair for vital signs monitoring. J. Light. Technol. 2025, 43, 4778–4786. [Google Scholar] [CrossRef]
- Li, Z.; Sun, L.P.; Tan, Y.; Wang, Z.; Yang, X.; Huang, T.; Li, J.; Zhang, Y.; Guan, B.O. Flexible optoelectronic hybrid microfiber long-period grating multimodal sensor. Adv. Sci. 2025, 12, 2501352. [Google Scholar] [CrossRef]
- Cheng, X.; Gunawardena, D.S.; Pun, C.-F.J.; Bonefacino, J.; Tam, H.-Y. Single nanosecond-pulse production of polymeric fiber Bragg gratings for biomedical applications. Opt. Express 2020, 28, 33573–33583. [Google Scholar] [CrossRef]
- Koyama, S.; Haseda, Y.; Ishizawa, H.; Okazaki, F.; Bonefacino, J.; Tam, H.-Y. Measurement of pulsation strain at the fingertip using a plastic FBG sensor. IEEE Sens. J. 2021, 21, 21537–21545. [Google Scholar] [CrossRef]
- Haseda, Y.; Bonefacino, J.; Tam, H.-Y.; Chino, S.; Koyama, S.; Ishizawa, H. Measurement of pulse wave signals and blood pressure by a plastic optical fiber FBG sensor. Sensors 2019, 19, 5088. [Google Scholar] [CrossRef]
- Martincek, I.; Tarjanyiova, G. Optical fiber Fabry-Perot interferometer for arterial pulse waveform measurement. IEEE Sens. J. 2024, 24, 25742–25747. [Google Scholar] [CrossRef]
- Wang, J.; Ai, F.; Sun, Q.; Liu, T.; Li, H.; Yan, Z.; Liu, D. Diaphragm-based optical fiber sensor array for multipoint acoustic detection. Opt. Express 2018, 26, 25293–25304. [Google Scholar] [CrossRef]
- Ma, J.; Xuan, H.; Ho, H.L.; Jin, W.; Yang, Y.; Fan, S. Fiber-optic Fabry–Pérot acoustic sensor with multilayer graphene diaphragm. IEEE Photonics Technol. Lett. 2013, 25, 932–935. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, W.; Shi, G.; Wu, J.; Sun, D.; Ma, J. Optical smart wearable sensor: Pulse waveform and pulse rate monitoring with a flexible loop optic-microfiber. J. Light. Technol. 2024, 43, 1462–1468. [Google Scholar] [CrossRef]
- Jay, J.A. An overview of macrobending and microbending of optical fibers. White Pap. Corning 2010, WP1212, 17792593. [Google Scholar]
- Leal-Junior, A.G.; Diaz, C.R.; Jimenez, M.F.; Leitão, C.; Marques, C.; Pontes, M.J.; Frizera, A. Polymer optical fiber-based sensor system for smart walker instrumentation and health assessment. IEEE Sens. J. 2018, 19, 567–574. [Google Scholar] [CrossRef]
- Hu, H.-F.; Sun, S.-J.; Lv, R.-Q.; Zhao, Y. Design and experiment of an optical fiber micro bend sensor for respiration monitoring. Sens. Actuators A Phys. 2016, 251, 126–133. [Google Scholar] [CrossRef]
- Pollock, C.R. Fundamentals of Optoelectronics; Irwin Publishers: Burr Ridge, IL, USA, 1995; pp. 36–38. [Google Scholar]
- Punjabi, N.; Satija, J.; Mukherji, S. Evanescent Wave Absorption Based Fiber-Optic Sensor-Cascading of Bend and Tapered Geometry for Enhanced Sensitivity. In Sensing Technology: Current Status and Future Trends III; Mason, A., Mukhopadhyay, S.C., Jayasundera, K.P., Eds.; Springer: Cham, Switzerland, 2015; pp. 25–45. [Google Scholar]
- Zhang, C.; Gao, T.; Wen, X.; Li, Y.; Zhang, M.; Xu, J.; Li, H.; Su, H.; Sun, J. Force-sensitive optical fiber fabric based on hollow elastic tube and structural grating. Opt. Laser Technol. 2025, 187, 112792. [Google Scholar] [CrossRef]
- Li, J.; Liu, B.; Liu, J.; Shi, J.-L.; He, X.-D.; Yuan, J.; Wu, Q. Low-cost wearable device based D-shaped single mode fiber curvature sensor for vital signs monitoring. Sens. Actuators A Phys. 2022, 337, 113429. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, J.; Wang, Z.; Zhang, X.; Yao, R.; Li, Y. Research on feature mining algorithm and disease diagnosis of pulse signal based on piezoelectric sensor. Inform. Med. Unlocked 2021, 26, 100717. [Google Scholar] [CrossRef]
- Boron, W.F.; Boulpaep, E.L. Medical Physiology E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2016; pp. 509–513. [Google Scholar]
- Murgo, J.P.; Westerhof, N.; Giolma, J.P.; Altobelli, S.A. Aortic input impedance in normal man: Relationship to pressure wave forms. Circulation 1980, 62, 105–116. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, X.; Zhong, Y.; Zhao, X.; Lin, S.; Li, J.; Li, X.; Xu, J.; Li, Z.; Zhu, H. A wearable and highly sensitive graphene strain sensor for precise home-based pulse wave monitoring. ACS Sens. 2017, 2, 967–974. [Google Scholar] [CrossRef]
- Xie, T.; Chen, H.; Xu, Z.; Huang, W.; Fu, H. High precision strain sensing system based on optoelectronic oscillator for human pulse monitoring. IEEE Sens. J. 2025, 25, 6355–6362. [Google Scholar] [CrossRef]
- Park, J.; Seok, H.S.; Kim, S.-S.; Shin, H. Photoplethysmogram analysis and applications: An integrative review. Front. Physiol. 2022, 12, 808451. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Sun, K.; Zheng, R.; Sun, Y.; Yang, H.; Zhong, Y.; Li, X. Three-dimensional arterial pulse signal acquisition in time domain using flexible pressure-sensor dense arrays. Micromachines 2021, 12, 569. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, G.F.; Conlin, P.R.; Dunlap, M.E.; Lacourcière, Y.; Arnold, J.M.O.; Ogilvie, R.I.; Neutel, J.; Izzo, J.L., Jr.; Pfeffer, M.A. Aortic diameter, wall stiffness, and wave reflection in systolic hypertension. Hypertension 2008, 51, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Gurovich, A.N.; Braith, R.W. Pulse wave analysis and pulse wave velocity techniques: Are they ready for the clinic? Hypertens. Res. 2011, 34, 166–169. [Google Scholar] [CrossRef]
- Stefani, A.; Rukhlenko, I.D.; Runge, A.F.; Large, M.C.; Fleming, S.C. Wearable conformal fiber sensor for high fidelity physiological measurements. IEEE J. Sel. Top. Quantum Electron. 2023, 30, 1–9. [Google Scholar] [CrossRef]
- Zhou, Z.-B.; Cui, T.-R.; Li, D.; Jian, J.-M.; Li, Z.; Ji, S.-R.; Li, X.; Xu, J.-D.; Liu, H.-F.; Yang, Y. Wearable continuous blood pressure monitoring devices based on pulse wave transit time and pulse arrival time: A review. Materials 2023, 16, 2133. [Google Scholar] [CrossRef]
- Dai, P.; Cong, Z.; Sun, Y.; Yan, W.; Chen, P.; Wang, X.; Jiang, C. Bio-inspired flexible optical microfiber sensor with nanohemisphere array microstructure for ultra-sensitive detection of skin signals. Measurement 2024, 235, 114874. [Google Scholar] [CrossRef]
- Xiong, L.; Zhong, H.; Wan, S.; Yu, J. Single-point curved fiber optic pulse sensor for physiological signal prediction based on the genetic algorithm-support vector regression model. Opt. Fiber Technol. 2024, 82, 103583. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, Z.; Zhang, H.; Yang, X.; Yang, J. All-fiber wearable continues blood pressure monitoring via tapered waveguide and machine-learning assistance. IEEE Trans. Instrum. Meas. 2025, 74, 7004212. [Google Scholar] [CrossRef]
- Tang, Y.; Roberts, R.C.; Lam, C.H.M.; Wong, W.S.; Yang, M.; Lao, L.; Lee, W.-N. Design of a barometer-based pulse-taking device with in vivo validation against high-frequency ultrasound pulse wave imaging. IEEE Sens. J. 2022, 22, 7219–7230. [Google Scholar] [CrossRef]
- Wei, M.; Chen, Z.; Chen, G.; Huang, X.; Jin, Y.; Lao, K.; Li, Z.; Li, S.; Zhong, F.; Liang, H. A portable three-channel data collector for Chinese medicine pulses. Sens. Actuators A Phys. 2021, 323, 112669. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, J.; Zhang, B. Graph based multichannel feature fusion for wrist pulse diagnosis. IEEE J. Biomed. Health Inform. 2020, 25, 3732–3743. [Google Scholar] [CrossRef] [PubMed]
- Nandi, M.; Venton, J.; Aston, P.J. A novel method to quantify arterial pulse waveform morphology: Attractor reconstruction for physiologists and clinicians. Physiol. Meas. 2018, 39, 104008. [Google Scholar] [CrossRef] [PubMed]
- Gowda, R.B.; Sharan, P.; Saara, K.; Braim, M.; Alodhayb, A.N. An FBG-based optical pressure sensor for the measurement of radial artery pulse pressure. J. Biophotonics 2024, 17, e202400083. [Google Scholar] [CrossRef]
- Qu, H.; Liang, W.; Cheng, X.; Tam, H.-Y.; Min, R.; Li, P.; Hu, X. Embedded POFBG for respiratory and heart rate measurement. IEEE Sens. J. 2024, 25, 4612–4619. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, H.; Ni, X.; Wang, K. An FBG-based sensor with both wearable and handheld forms for carotid arterial pulse waveform measurement. IEEE Trans. Instrum. Meas. 2023, 72, 7506610. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, S.; Shi, C. Development of a hybrid force-displacement sensor based on fiber Bragg grating for radial artery pulse waveform measurement. IEEE Sens. J. 2021, 21, 20045–20054. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Li, X.; Tan, Y.; Zhou, Z. RSM-based data-driven optimized design of a 3-D-printed building block-type FBG tactile sensor for nursing robots. IEEE Trans. Instrum. Meas. 2023, 72, 4006513. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Z.; Zhang, H.; Liu, Y. Development of an FBG-based wearable sensor for simultaneous respiration and heartbeat measurement. IEEE Trans. Instrum. Meas. 2022, 72, 1–9. [Google Scholar]
- Guo, J.; Wang, W.; Zhang, J.; Chen, H.; Chen, R.; Zhao, B.; Chen, D. Fiber cladding waveguide phase-shifted FBG encapsulated in flexible material for estimating human blood pressure. J. Light. Technol. 2024, 43, 3261–3268. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, J.; Dong, L.; Du, Y.; Guo, Z.; Chen, H.; Chen, D.; Wang, W. Parallel waveguide fiber Bragg gratings–Used for detecting human respiratory rate, trunk status, and pulse. Opt. Laser Technol. 2025, 181, 111960. [Google Scholar] [CrossRef]
- Kumar, N.V.; Pant, S.; Sridhar, S.; Marulasiddappa, V.; Srivatzen, S.; Asokan, S. Fiber Bragg grating-based pulse monitoring device for real-time non-invasive blood pressure measurement—A feasibility study. IEEE Sens. J. 2021, 21, 9179–9185. [Google Scholar] [CrossRef]
- Taoping, S.; Zhichao, L. Design of pulse and respiration monitoring system based on fiber optic sensing and VMD-FPR processing algorithm. Opt. Fiber Technol. 2022, 73, 103033. [Google Scholar] [CrossRef]
- Koyama, S.; Yoda, T.; Yamamoto, M.; Shiokawa, S.; Kane, K.; Martinka, M. Verification of optimal installation point of FBG sensor for pulsation strain measurement. IEEE Sens. J. 2023, 23, 18183–18192. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Zhang, Z.; Li, P.; Pan, H.; Ren, Y.; Hou, T.; Wang, C.; Kwong, C.-F.; Zhang, B. Simultaneous Measurement of Local Pulse Wave Velocities in Radial Arteries Using a Soft Sensor Based on the Fiber Bragg Grating Technique. Micromachines 2024, 15, 507. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Wang, L. Blood pressure and heart rate measurements using fiber Bragg grating sensor with optical power detection scheme. Sensors 2025, 25, 2007. [Google Scholar] [CrossRef]
- Zhao, K.; Ma, G.; Wu, Z.; Wang, Q.; Zhong, S.; Chen, K.P. High resolution wearable FBG-based sensing device for cardiac rate and blood pressure monitoring. In Proceedings of the Optical Fibers and Sensors for Medical Diagnostics, Treatment, and Environmental Applications XXV, San Francisco, CA, USA, 20 March 2025; pp. 158–160. [Google Scholar]
- Xu, Y.; Gao, L.; Qian, C.; Wang, Y.; Liu, W.; Cai, X.; Liu, Q. Multi-channel sparse-frequency-scanning white-light interferometry with adaptive mode locking for pulse wave velocity measurement. Photonics 2025, 12, 316. [Google Scholar] [CrossRef]
- Ratanapanya, N.; Pullteap, S. A blood pressure measurement system using fiber optic-based Fabry-Perot interferometer. Opt. Lasers Eng. 2025, 184, 108667. [Google Scholar] [CrossRef]
- Takayama, R.; Nishiyama, M.; Koyama, Y. Wearable Textile Sensor Using Hetero-Core Optical Fiber for Blood Pressure Measurement. In Proceedings of the 2024 IEEE SENSORS, Kobe, Japan, 20–23 October 2024; pp. 1–4. [Google Scholar]
- Koyama, Y.; Kamada, H.; Watanabe, K.; Nishiyama, M. Cuff-less blood pressure estimation using hetero-core optical fibers. Electron. Commun. Jpn. 2024, 107, e12438. [Google Scholar] [CrossRef]
- Li, Z.; Tang, X.; Zhao, T.; Chen, K.; Zhang, T. Highly sensitive skin-like wearable optical sensor for human physiological signals monitoring. Opt. Fiber Technol. 2024, 82, 103652. [Google Scholar] [CrossRef]
- Mishra, P.; Sahu, P.K.; Kumar, H.; Jha, R. Human pulse and respiration monitoring: Reconfigurable and scalable balloon-shaped fiber wearables. Adv. Mater. Technol. 2023, 8, 2300429. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, H.; Chen, M.; He, Y.; Zhang, Z.; Gan, J.; Yang, Z. Highly sensitive strain sensor based on microfiber coupler for wearable photonics healthcare. Adv. Intell. Syst. 2023, 5, 2200344. [Google Scholar] [CrossRef]
- Liang, H.; Wang, Y.; Kan, L.; Xu, K.; Dong, T.; Wang, W.; Gao, B.; Jiang, C. Wearable and multifunctional self-mixing microfiber sensor for human health monitoring. IEEE Sens. J. 2022, 23, 2122–2127. [Google Scholar] [CrossRef]
- Guo, J.; Tuo, J.; Sun, J.; Li, Z.; Guo, X.; Chen, Y.; Cai, R.; Zhong, J.; Xu, L. Stretchable multimodal photonic sensor for wearable multiparameter health monitoring. Adv. Mater. 2025, 37, 2412322. [Google Scholar] [CrossRef]
- Kuang, R.; Wang, Z.; Ma, L.; Wang, H.; Chen, Q.; Junior, A.L.; Kumar, S.; Li, X.; Marques, C.; Min, R. Smart photonic wristband for pulse wave monitoring. Opto-Electron. Sci. 2024, 3, 240009-1–240009-16. [Google Scholar] [CrossRef]
- Gunwant, D. Interfacial strengthening in bio-inspired materials: A review. Compos. Interfaces 2025, 32, 509–585. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, Y.; Jiao, Y.; Yang, L.; Sheng, Z.; He, S.; Dai, D. Compact arrayed waveguide grating devices based on small SU-8 strip waveguides. J. Light. Technol. 2011, 29, 2009–2014. [Google Scholar] [CrossRef]
- Sahoo, H.K.; Ansbæk, T.; Ottaviano, L.; Semenova, E.; Zubov, F.; Hansen, O.; Yvind, K. Tunable MEMS VCSEL on silicon substrate. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1700707. [Google Scholar] [CrossRef]

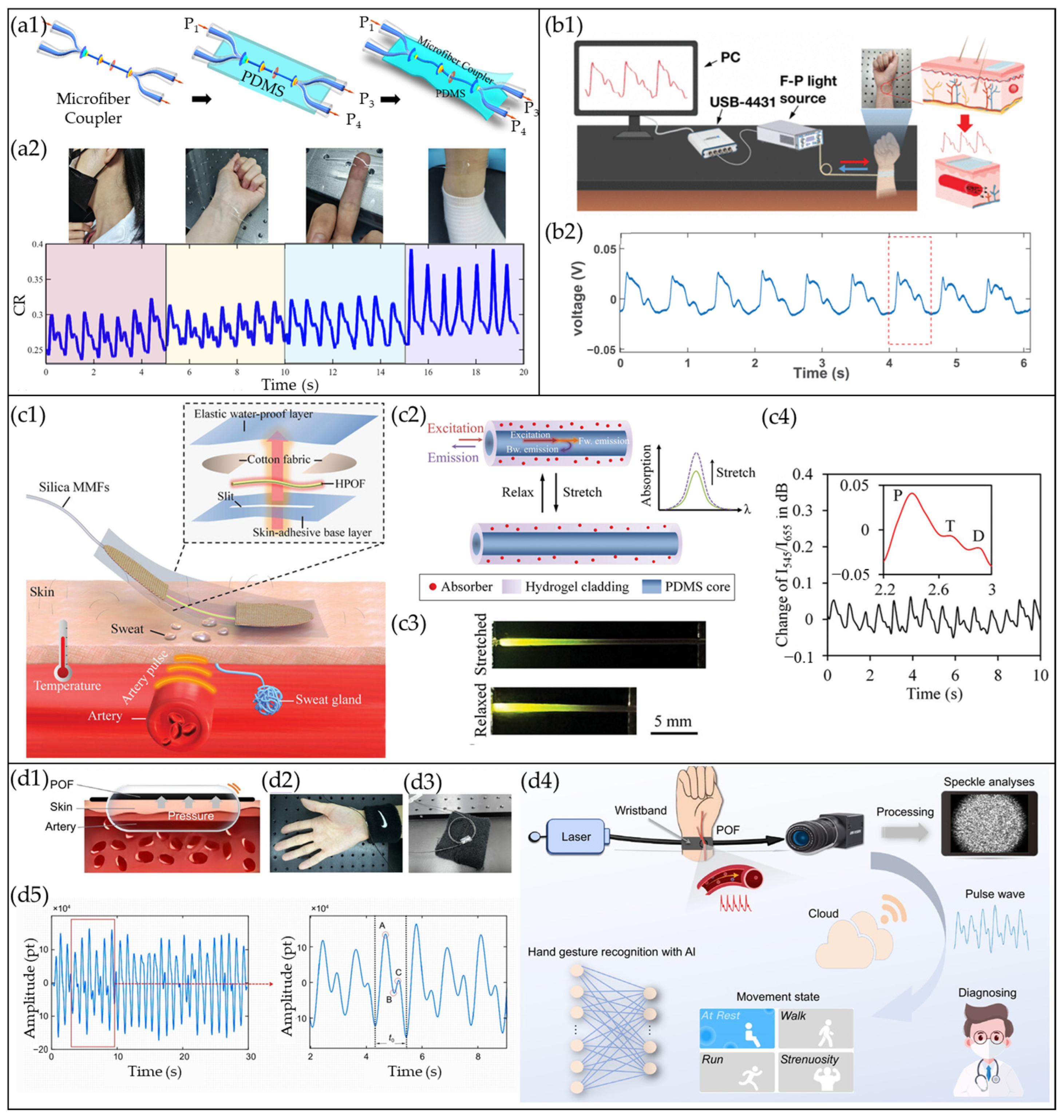
| Type of Sensor | Working Principle | Advantages | Disadvantages |
|---|---|---|---|
| Piezoresistive | Convert into a change in resistance () | Low cost | Low sensitivity |
| Large response range | Large hysteresis | ||
| Capacitive | Convert into a change in capacitance () | Good dynamic response | High parasitic capacitance effect |
| High sensitivity at low | |||
| Piezoelectric | Convert into a change in voltage () | Simple fabrication | Low sensitivity at high ΔP |
| High signal-to-noise ratio | |||
| Triboelectric | Convert into a change in electrical charge () | High dynamic response | Low sensitivity at high ΔP |
| High sensitivity at low | |||
| Magnetoelastic | Convert into a change in magnetic flux density () | High stretchability | Magnetic field interference |
| Intrinsic waterproofness | |||
| Optical fiber | Convert into a change in light intensity ( or wavelength () | High spatial resolution | Bulky detection system |
| Anti-electromagnetic interference |
| English Term Defined by WHO [15] | Description of Level of Feeling | Alternative Term |
|---|---|---|
| Floating | Light pressure | Fu, superficial pressure |
| Medium | Moderate pressure | Zhong, medium pressure |
| Deep | Deep pressure | Chen, heavy pressure |
| Ref. | Device Configuration | Diagnostic Type | Sensitivity | Size | Waveform Resolution | Deployment Type |
|---|---|---|---|---|---|---|
| [83] | SOFBG suspended on a rigid-body flexure | Pulse waveform, HR | 1547.3 pm/N | 35 mm × 29 mm × 20 mm (75 mm for handheld) | High | Wearable, handheld |
| [84] | SOFBG suspended on an orthogonal–planar spring structure | Pulse waveform, HR | 2143.7 pm/N | 57 mm (length) 30 mm (diameter) | High | Tabletop |
| [85] | SOFBG suspended in a 3-D printed bellows elastomer | Pulse waveform, HR | 225.04 pm/N | 8 mm × 8 mm × 22.28 mm | High | Tabletop |
| [86] | SOFBG in silicone membrane on an arc-shaped curved structure | Pulse waveform, HR, RR * | 748.86 pm/N (simulation) | 106 mm × 45 mm × 15 mm | High | Wearable |
| [40] | SOFBG in Dragon Skin 30 with housing | HR, RR, BP | 1.21 pm/µε | 41 mm × 3 mm × 15 mm | High | Implantable |
| [48] | Laser-induced graphene-microfiber LPG in PDMS | Pulse waveform, HR, glucose | 2.06 nm/kPa | Not reported | High | Wearable |
| [46] | Microfiber FBG in PDMS | Pulse waveform, HR, RR, BP | 2.86 nm/N for stress 0.05–0.45 N | Not reported | High | Wearable |
| [87] | Parallel waveguide SOFBG in PDMS | Pulse waveform, BP | 1.33 nm/m−1 | 40 mm × 10 mm × 0.6 mm | High | Wearable |
| [88] | Parallel waveguide SOFBG in PDMS | Pulse waveform, RR, trunk bending | Not reported | 50 mm × 20 mm × 2 mm | High | Wearable |
| [10] | SOFBG on silicone diaphragm, finger plethysmograph sensor | Pulse waveform | 1.20 pm/µε | 25 mm (length) 16 mm (slit width) | Moderate | Wearable |
| [89] | SOFBGs on a neoprene rubber sheet | Pulse waveform, BP | 1.20 pm/µε | 30 mm × 140 mm × 5 mm | Moderate | Table-top |
| [90] | FBG † in nylon bandage | Pulse waveform, HR, RR | Not reported | Not reported | High | Wearable |
| [91] | SOFBG arrays on bubble wrap cushioning | Pulse waveform, HR | Not reported | Not reported | High | Wearable |
| [92] | FBG † arrays on PDMS | Pulse waveform | Not reported | Not reported | Moderate | Wearable |
| [81] | SOFBG on a 3-D-printed flat platform | Pulse waveform | Not reported | Not reported | Low | Handheld |
| [93] | FBGs † in silicone sheet | Pulse waveform, BP | Not reported | 3 mm (thickness) | High | Wearable |
| [94] | SOFBG array in medical tape | Pulse waveform, BP | Not reported | Not reported | High | Wearable |
| [82] | POFBG in PDMS | Pulse waveform, HR, RR | Not reported | 70 mm × 20 mm × 1 mm | High | Wearable |
| [50] | POFBG on gel sheet on a 3-D-printed platform | HR | Not reported | 40 mm × 50 mm × 10 mm | Moderate | Tabletop |
| Ref. | Device Configuration | Diagnostic Type | Sensitivity | Size | Waveform Resolution | Deployment Type |
|---|---|---|---|---|---|---|
| [52] | Probe-like, flexible condom membrane | Pulse waveform | Not reported | Sensing diameter 3 cm | High | Handheld |
| [95] | Probe-like, nickel-coated PPS membrane | Pulse waveform, HR | Not reported | Sensing diameter 5 mm | Moderate | Handheld |
| [96] | Probe-like, aluminum-coated latex membrane | Pulse waveform, HR, and BP | 56.88 nm/mmHg | Sensing diameter 10 mm | Low | Handheld |
| [47] | All-fiber-based, chirped FBGs as mirrors | Pulse waveform, BP | 0.612 nm/N (loop structure) | 30 mm × 20 mm × 1 mm | High | Wearable |
| [67] | All-fiber based, COF with capillary fiber as cavity | Pulse waveform, HR | 47.96 Hz/µε | Not reported | High | Wearable |
| Ref. | Device configuration | Diagnostic type | Sensitivity | Size | Waveform Resolution | Deployment Type |
|---|---|---|---|---|---|---|
| [7] | MMF-capillary-MMF sealed in a PE tube, embedded in PDMS, on a liquid capsule | Pulse waveform, BP | −213 µW/kPa | 25 mm diameter of the liquid capsule | High | Wearable |
| [76] | Tapered-waveguide assisted microcavity structure in PDMS | Pulse waveform, BP | 264.97 µW/kPa | 50 mm × 10 mm × 3 mm | High | Wearable |
| [72] | PU capillary fiber coupled between two PMMA optical waveguides | Pulse waveform, HR, RR | Not reported | Not reported | High | Wearable |
| [5] | SM-MM-SM fiber in PDMS, on an elastic belt | Pulse waveform, BP | Not reported | 3 mm thickness (PDMS), 2 mm thickness (belt) | High | Wearable |
| [55] | SM-microfiber-SM fiber in PDMS, loop shape | Pulse waveform, HR | 5.85 V/kPa | 500 µm thickness (PDMS) | Low | Wearable |
| [97] | 5-µm core SMF spliced with common SMFs in textile, assisted by PU rod | Pulse waveform, BP | Not reported | 70 mm × 60 mm × 6 mm | Low | Wearable |
| [98] | 5-µm core SMF spliced with common SMFs in PU, assisted by a PU rod | Pulse waveform, BP | Not reported | 50 mm × 50 mm × 1 mm | Moderate | Wearable |
| Ref. | Device Configuration | Diagnostic Type | Sensitivity | Size | Waveform Resolution | Deployment Type |
|---|---|---|---|---|---|---|
| [30] | U-shaped microfiber in PDMS on liquid sac # | Pulse waveform, HR | −0.22 kPa−1 (for 0–2 kPa), −0.02 kPa−1 (for 2–10 kPa) | 3 mm thickness, 20 mm diameter | High | Wearable |
| [75] | U-shaped SMF in silicone # | Pulse waveform, BP | Not reported | 15 mm × 10 mm × 10 mm | High | Wearable |
| [29] | Wavy microfiber in PDMS film ‡ | Pulse waveform, BP | 257 (gauge factor) or 85.7 mm−1 | ≈21 mm sensing length | High | Wearable |
| [74] | Microfiber fiber in nano-hemispherical microstructure PDMS ‡ | Pulse waveform, HR, BP | 0.0138 mV/kPa | 20 mm × 20 mm × 0.15 mm | Moderate | Wearable |
| [41] | Wavy polymer optical microfiber in PDMS ‡ | RR, HR, behaviour detection | Not reported | 15 mm × 50 mm × 0.20 mm | Low | Wearable |
| [99] | Loop structure small core fiber in silica gel # | Pulse waveform, HR | 2.2 kPa−1 (for <200 Pa), 0.91 kPa−1 (for 200–600 Pa) | 30 mm × 15 mm × 0.5 mm | High | Wearable |
| [100] | Loop structure SMF in PDMS # | Pulse waveform, HR, RR | 27.4 pm/µm (longitudinal), 11.6 pm/µm (lateral) | 500 µm (thickness of PDMS) | High | Wearable |
| [6] | Loop structure microfiber in silicone # | Pulse waveform, BP | Not reported | 25 mm × 30 mm × 35 mm | High | Wearable |
| Ref. | Device Configuration | Diagnostic Type | Sensitivity | Size | Waveform Resolution | Deployment Type |
|---|---|---|---|---|---|---|
| [61] | Cladding removed grating PMMA fiber in U-shaped structure, supported by a PVC hollow tube | Pulse waveform, hand motion detection | 50.294 N−1 (0.201 kPa−1) | 15 cm × 10 cm, with 20 mm × 2 mm force-sensitive area | High | Wearable |
| [62] | D-shaped fiber in PDMS | Pulse waveform, HR, RR | 7.208%/m−1 | 40 mm × 5 mm × 2 mm | Moderate | Wearable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chew, J.W.; Gan, S.X.; Cui, J.; Chan, W.D.; Chu, S.T.; Tam, H.-Y. Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review. Photonics 2025, 12, 662. https://doi.org/10.3390/photonics12070662
Chew JW, Gan SX, Cui J, Chan WD, Chu ST, Tam H-Y. Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review. Photonics. 2025; 12(7):662. https://doi.org/10.3390/photonics12070662
Chicago/Turabian StyleChew, Jing Wen, Soon Xin Gan, Jingxian Cui, Wen Di Chan, Sai T. Chu, and Hwa-Yaw Tam. 2025. "Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review" Photonics 12, no. 7: 662. https://doi.org/10.3390/photonics12070662
APA StyleChew, J. W., Gan, S. X., Cui, J., Chan, W. D., Chu, S. T., & Tam, H.-Y. (2025). Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review. Photonics, 12(7), 662. https://doi.org/10.3390/photonics12070662





