Role of Diffuser Autocorrelation and Spatial Translation in Computational Ghost Imaging
Abstract
1. Introduction
2. Heuristic Analysis and Theoretical Results
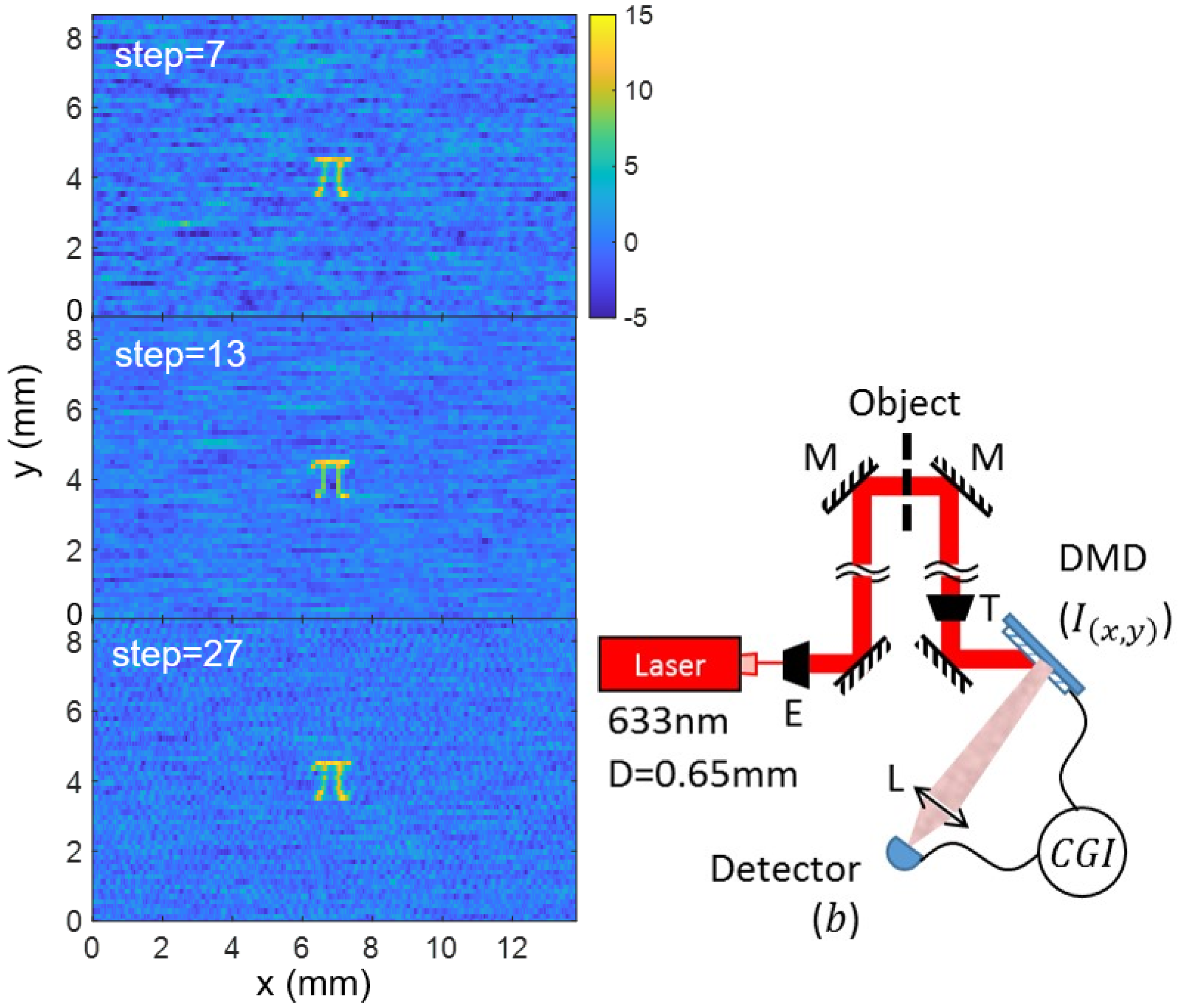
3. Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pittman, T.B.; Shih, Y.; Strekalov, D.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429. [Google Scholar] [CrossRef] [PubMed]
- Bennink, R.S.; Bentley, S.J.; Boyd, R.W. “Two-photon” coincidence imaging with a classical source. Phys. Rev. Lett. 2002, 89, 113601. [Google Scholar] [CrossRef]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: Comparing entanglement and classicalcorrelation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [PubMed]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Chan, W.L.; Charan, K.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G.; Mittleman, D.M. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93, 121105. [Google Scholar] [CrossRef]
- Bromberg, Y.; Katz, O.; Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 2009, 79, 053840. [Google Scholar]
- Erkmen, B.I. Computational ghost imaging for remote sensing. J. Opt. Soc. Am. A 2012, 29, 782–789. [Google Scholar] [CrossRef]
- Devaux, F.; Moreau, P.A.; Denis, S.; Lantz, E. Computational temporal ghost imaging. Optica 2016, 3, 698–701. [Google Scholar]
- Le, M.; Wang, G.; Zheng, H.; Liu, J.; Zhou, Y.; Xu, Z. Underwater computational ghost imaging. Opt. Express 2017, 25, 22859–22868. [Google Scholar] [CrossRef]
- Zhou, C.; Tian, T.; Gao, C.; Gong, W.; Song, L. Multi-resolution progressive computational ghost imaging. J. Opt. 2019, 21, 055702. [Google Scholar]
- Huang, J.; Shi, D.; Meng, W.; Zha, L.; Yuan, K.; Hu, S.; Wang, Y. Spectral encoded computational ghost imaging. Opt. Commun. 2020, 474, 126105. [Google Scholar] [CrossRef]
- Shimobaba, T.; Endo, Y.; Nishitsuji, T.; Takahashi, T.; Nagahama, Y.; Hasegawa, S.; Sano, M.; Hirayama, R.; Kakue, T.; Shiraki, A.; et al. Computational ghost imaging using deep learning. Opt. Commun. 2018, 413, 147–151. [Google Scholar] [CrossRef]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef]
- Rizvi, S.; Cao, J.; Zhang, K.; Hao, Q. DeepGhost: Real-time computational ghost imaging via deep learning. Sci. Rep. 2020, 10, 11400. [Google Scholar] [CrossRef] [PubMed]
- Pelliccia, D.; Rack, A.; Scheel, M.; Cantelli, V.; Paganin, D.M. Experimental X-ray ghost imaging. Phys. Rev. Lett. 2016, 117, 113902. [Google Scholar] [CrossRef]
- Schori, A.; Shwartz, S. X-ray ghost imaging with a laboratory source. Opt. Express 2017, 25, 14822–14828. [Google Scholar] [CrossRef]
- Klein, Y.; Schori, A.; Dolbnya, I.; Sawhney, K.; Shwartz, S. X-ray computational ghost imaging with single-pixel detector. Opt. Express 2019, 27, 3284–3293. [Google Scholar] [CrossRef] [PubMed]
- Sefi, O.; Ben Yehuda, A.; Klein, Y.; Sobol, Z.; Bloch, S.; Schwartz, H.; Cohen, E.; Shwartz, S. 20 μm resolution multipixel ghost imaging with high-energy X-rays. Opt. Express 2024, 32, 37001–37010. [Google Scholar] [CrossRef] [PubMed]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef]
- Katkovnik, V.; Astola, J. Compressive sensing computational ghost imaging. J. Opt. Soc. Am. A 2012, 29, 1556–1567. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light Sci. Appl. 2022, 11, 1. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.X.; He, Y.H.; Wu, L.A.; Chen, L.M.; Wang, B.B. Tabletop X-ray ghost imaging with ultra-low radiation. Optica 2018, 5, 374–377. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Zhang, Y. User’s guide for TVAL3: TV minimization by augmented lagrangian and alternating direction algorithms. CAAM Rep. 2009, 20, 4. [Google Scholar]
- Ferri, F.; Magatti, D.; Lugiato, L.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]


| Jump | ||||||||
|---|---|---|---|---|---|---|---|---|
| ACL | 2 | 4 | 7 | 13 | 27 | 40 | 70 | 100 |
| 2 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 |
| 4 | 2 | 1 | 4 | 4 | 4 | 1 | 2 | 1 |
| 7 | 7 | 7 | 1 | 7 | 7 | 7 | 1 | 7 |
| 10 | 5 | 5 | 10 | 10 | 10 | 1 | 1 | 1 |
| 13 | 13 | 13 | 13 | 1 | 13 | 13 | 13 | 13 |
| 20 | 10 | 5 | 20 | 20 | 20 | 1 | 2 | 1 |
| Jump | ||||||||
|---|---|---|---|---|---|---|---|---|
| ACL | 2 | 4 | 7 | 13 | 27 | 40 | 70 | 100 |
| 2 | 14.2 | 16.1 | 17.0 | 17.0 | 17.0 | 16.8 | 16.8 | 16.8 |
| 4 | 14.3 | 18.5 | 18.8 | 18.7 | 18.7 | 19.2 | 18.6 | 19.2 |
| 7 | 14.9 | 19.5 | 20.2 | 20.2 | 20.2 | 21.2 | 21.2 | 21.2 |
| 10 | 20.3 | 20.6 | 20.2 | 20.2 | 20.3 | 18.6 | 18.6 | 18.6 |
| 13 | 19.8 | 19.9 | 20.0 | 17.9 | 20.0 | 20.0 | 20.0 | 20.0 |
| 20 | 19.0 | 18.7 | 19.1 | 19.1 | 19.1 | 17.1 | 17.9 | 17.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albeck, Y.; Sukholuski, S.; Herman, O.; Arusi-Parpar, T.; Shwartz, S.; Cohen, E. Role of Diffuser Autocorrelation and Spatial Translation in Computational Ghost Imaging. Photonics 2025, 12, 650. https://doi.org/10.3390/photonics12070650
Albeck Y, Sukholuski S, Herman O, Arusi-Parpar T, Shwartz S, Cohen E. Role of Diffuser Autocorrelation and Spatial Translation in Computational Ghost Imaging. Photonics. 2025; 12(7):650. https://doi.org/10.3390/photonics12070650
Chicago/Turabian StyleAlbeck, Yishai, Shimon Sukholuski, Orit Herman, Talya Arusi-Parpar, Sharon Shwartz, and Eliahu Cohen. 2025. "Role of Diffuser Autocorrelation and Spatial Translation in Computational Ghost Imaging" Photonics 12, no. 7: 650. https://doi.org/10.3390/photonics12070650
APA StyleAlbeck, Y., Sukholuski, S., Herman, O., Arusi-Parpar, T., Shwartz, S., & Cohen, E. (2025). Role of Diffuser Autocorrelation and Spatial Translation in Computational Ghost Imaging. Photonics, 12(7), 650. https://doi.org/10.3390/photonics12070650






