Abstract
The photon blockade effect, as a quantum behavior in cavity optomechanics, has certain limitations, including stringent requirements for system parameters and technical difficulties in achieving strong nonlinear interactions. This paper proposes a novel scheme that aims to achieve strong nonlinear effects through introducing the degenerate optical parametric amplifier (OPA) and mechanical squeezing. These enhanced nonlinear effects can significantly improve the photon blockade effect, effectively overcoming the limitations of weak coupling. Our theoretical analysis demonstrates the successful realization of an ideal single-photon blockade (1PB) state through optimized parameter conditions. Additionally, this joint approach significantly enhances the two-photon blockade (2PB) effect and broadens the region where 2PB occurs. This finding helps us identify the optimal system parameters to maximize two-photon emission efficiency. By precisely controlling these parameters, a new pathway is opened for more flexible manipulation and utilization of the photon blockade effect in experiments.
1. Introduction
Cavity optomechanics, originally employed for the observation of gravitational waves, have recently received significant attention and undergone considerable advancement due to their exceptional sensitivity to weak signals [1,2,3,4]. As a macroscopic system, significant progress has been made in the study of quantum effects, including quantum entanglement [5,6,7,8], optomechanically induced transparency [9,10,11,12], the photon blockade effect [13,14,15,16,17], and so on. In this type of system, various typical experimental platforms can be realized so far, including Fabry–Perot cavity optomechanical systems [9,18], microwave optomechanical systems utilizing movable capacitor plates [19,20], whispering gallery-mode optomechanical systems [21], photonic crystal cavity optomechanical systems [22,23,24], and nano-waveguide systems [25,26]. In order to study the quantum effects of macroscopic mechanical oscillators in cavity optomechanical systems, it is necessary to reduce the effect of environmental thermal noise on the system. In light of this, a variety of ground-state cooling schemes have been proposed, including feedback control [27,28,29,30], tuning coupling strength [31,32], and sideband cooling [33,34,35,36,37].
Since the discovery of the photon blockade effect in cavity optomechanical systems, realizing strong optical nonlinearities at the single-photon level has become an essential target for quantum optics researchers, which is of great significance in the fields of quantum computation [38], quantum information processing [39,40], and optical quantum simulation [41,42,43]. A photon blockade relies on the anharmonicity of the energy-level structure of the system, which is caused by nonlinear effects [44,45,46,47]. Nonlinear quantum optomechanics describes the strong interaction between photons and other degrees of freedom in a system, leading to photon–photon interactions mediated by the system’s anharmonic energy spectrum. This interaction enables a single photon to significantly modify the system’s optical response, making it less likely for additional photons to be absorbed, thereby suppressing the absorption of subsequent photons [48,49,50,51]. By studying and exploiting these nonlinear effects, the behavior of photons can be precisely controlled, playing a key role in the development of single-photon sources [52,53,54,55,56].
In order to gain insight into the intrinsic nonlinearity of optomechanical systems, a lot of efforts have been devoted to enhancing single-photon coupling strength. A promising approach is to use a parametric driving field to squeeze the cavity mode [57,58,59,60,61,62,63,64]. In this instance, the single-photon state within the squeezed cavity mode is equivalent to an exponential increase in the number of photons within the original cavity mode. Consequently, the optomechanical interaction induced by the photons in the squeezed mode is exponentially enhanced. On the other hand, the squeezing of the mechanical modes has the potential to amplify the effective mechanical zero-point fluctuations, thereby further enhancing the nonlinear optomechanical interactions [65,66,67,68,69].
Here, we put forward a new scheme to improve the photon blockade effect in cavity optomechanical systems. The cavity mode traps a nonlinear medium and is coupled to a mechanical squeezed mode by radiation pressure. This squeezing is achieved through Coulomb interaction between a charged mechanical oscillator and another charged body. We analytically derive the optimal conditions for 1PB in the steady state and obtain the analytical solution of the system under the joint effects of mechanical squeezing and degenerate OPA, which is consistent with the numerical simulation results. It is found that the initial weak coupling coefficients can be dramatically amplified by introducing degenerate OPA and adjusting the squeezing parameters.
The rest of this paper is organized as follows. In Section 2, we describe the physical model of the system and derive the effective Hamiltonian. The coherence correlation function and the master equation of the system are presented in Section 3. In Section 4, we give the analysis of the enhancement effect on 1PB in the system. In Section 5, we further present a discussion of the enhancement effect on 2PB. Finally, we give the conclusion in Section 6.
2. Model and System Hamiltonian
Firstly, we construct the model diagram of the system and the anharmonic eigenenergy spectrum corresponding to different photon excitation numbers in Figure 1a and Figure 1b, respectively. The latter will be explained in greater detail later in the text. As shown in Figure 1a, the system consists of an optical cavity with the moving charged plate and an externally charged body, where a nonlinear medium is placed in the cavity. The model comprises an optical cavity confined by a nonlinear medium and subjected to an externally charged body. The moving charged plate is coupled to the cavity field through the radiation pressure of the mechanical oscillator and is connected to a gate voltage of with electrodes having a quantity of electric charge . The fixed charged plate interacts with the charged plate through the Coulomb force, and its voltage is connected to the gate voltage of , with the electrode carrying a charge of . The optical cavity is driven by a classical laser field with frequency and amplitude E, while the nonlinear medium is driven by a pump field with frequency and amplitude . In a rotating frame with frequency , the Hamiltonian of system can be written as follows:
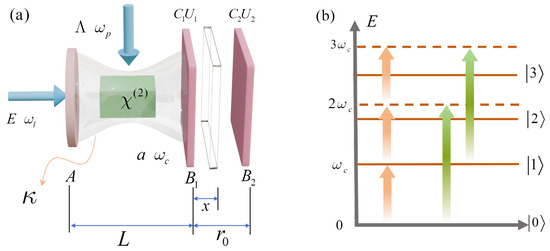
Figure 1.
(a) Schematic diagram of a cavity optomechanical system containing a nonlinear medium, where the cavity is driven by a classical laser and the nonlinear medium is driven by another pumping field. The optomechanical cavity is coupled to a charged plate via Coulomb force. The optical cavity is driven by a classical laser field with frequency and amplitude E, while the nonlinear medium is driven by a pump field with frequency and amplitude . (b) Anharmonic eigenenergy spectrum corresponding to different photon excitation numbers. The yellow arrows indicate that 1PB when single-photon resonance condition (i.e., ) is satisfied. The green arrows indicate that 2PB occurs when two-photon resonance condition (i.e., ) is satisfied.
The first three terms represent the free Hamiltonian operators of the cavity field and the resonator, while is the annihilation (creation) operator of the cavity field; represents the detuning between the cavity mode and the laser field, while denotes the frequency of the oscillator. The fourth term signifies the optomechanical interaction between the cavity field and the mechanical oscillator; represents the single-photon optomechanical coupling strength, whereas L denotes the distance between the mirror A and the oscillator in the absence of radiation pressure and Coulomb interaction. The fifth term represents the Coulomb interaction between the two charged plates, and . Here, is the Coulomb constant.
Since the displacement of the oscillator from its equilibrium position is much smaller than the equilibrium distance between them, i.e., , the Coulomb interaction term can be expanded up to the second order:
The linear term of this equation can be ignored by redefining the equilibrium position of the mechanical oscillator, and the constant term can be further eliminated. At this juncture, the fifth term in Equation (1) can be expressed as . After introducing the position and momentum operators, and , the Hamiltonian in Equation (1) can be written as
where and denote the mechanical coupling constant and the effective optomechanical coupling strength, respectively. By employing the squeezing transformation under , the Hamiltonian of the strong optomechanical coupling is obtained
where , the squeezing parameter ( is determined by requiring the coefficient of the non-diagonal term to vanish, denotes the mechanical squeezing frequency, and is the squeezing-enhanced optomechanical coupling rate. For simplicity, we choose .
As shown in Figure 2a, we first display the mechanical squeezing coupling strength versus the mechanical coupling constant with different mechanical frequency . Furthermore, as illustrated in Figure 2b, we show the variation of the squeezing parameter r with the mechanical frequency and the mechanical coupling constant . It can be demonstrated that a large squeezing parameter can be achieved by setting to be approximately four times the size of . One can see that a large squeezing parameter r can be obtained by choosing a suitable system parameter or G, which enables strong optomechanical coupling. In other words, our system enters the nonlinear quantum region even if the original system is weakly coupled.
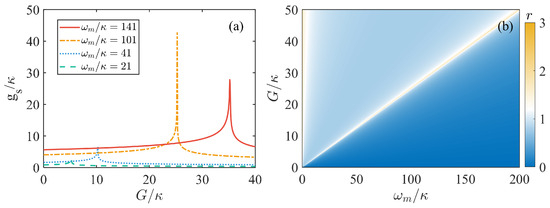
Figure 2.
(a) Mechanical squeezing coupling strength versus mechanical coupling constant for different mechanical frequencies , and 21. The parameter of effective optomechanical coupling strength is . (b) The variation of the squeezing parameter r with the mechanical frequency and mechanical coupling constant .
To more intuitively observe the effect of nonlinear optomechanical coupling on the anharmonicity of the system’s eigenenergy spectrum, we make a polaron transformation as , where . Under the condition that , we can ignore the small exponential factor, which could be effectively decoupled from the Hamiltonian of the system. Therefore, when we are interested only in optical properties, the Hamiltonian is rewritten as
The process of the n-photon blockade described by this Hamiltonian is shown in Figure 1b, where the optical cavity in the system exhibits an anharmonic character, which is induced by a shift in the optical eigenenergy spectrum due to nonlinear optomechanical coupling with the eigenvalues of .
In our proposal, even if the system initially operates in the weak coupling regime, the optomechanical coupling can be exponentially enhanced to the single-photon strong coupling regime via mechanical squeezing. Specifically, based on the contemporary experimental technique [70], the frequency of the mechanical oscillator is assumed as and the system decay rate is set to . The experiment has demonstrated cavity dissipation at , validating the feasibility of cavity dissipation [71]. The mechanical oscillator frequency can be calculated to yield , . Pirkkalainen et al. utilized in a system coupling superconducting qubits to nanomechanical oscillators, validating the feasibility of capacitance [72]. An experiment applied microwave pulses with an equivalent voltage to control qubit energy levels, confirming the feasibility of voltage modulation [73]. Based on the mechanical coupling via the Coulomb interaction in the cavity optomechanical system (array), many fascinating physical phenomena have been investigated in previous studies [74,75,76,77]. Therefore, utilizing the Coulomb interaction to realize mechanical coupling has been a popular manipulation method and mature technology in cavity optomechanics.
However, despite the feasibility of the individual components, implementing the full scheme in a practical experiment still faces notable challenges. Our scheme relies on precisely setting the parametric driving phase to to fully suppress effective thermal noise, as shown in Equation (10). While theoretically sound, maintaining such exact phase control is experimentally challenging, due to inevitable phase drift and noise in degenerate OPA and mechanical squeezing, which can reintroduce decoherence and weaken the blockade effect. Additionally, the fabrication of the proposed device in Figure 1 is technically demanding. Integrating a nonlinear medium, a movable charged mechanical oscillator, and a fixed charged plate () within an optical cavity requires nanoscale precision to preserve system symmetry and ensure effective Coulomb coupling. This demands advanced MEMS fabrication techniques and careful electrostatic design. Moreover, precise control of small capacitances (∼) and low voltages (∼) adds further complexity. Addressing these challenges is essential for realizing the proposed scheme in practice.
Next, we analyze the stability of the system. From the Hamiltonian of the system, via the Heisenberg–Langevin approach, we separate the steady-state terms and fluctuation terms. Substituting the orthogonal fluctuation operators, the drift matrix of the system is derived as
where , , and represent the steady-state mean values of the cavity mode and mechanical mode, respectively. Both can be treated as real numbers by adjusting the phase of the laser drive. According to the Routh–Hurwitz criterion, the system is stable if and only if all eigenvalues of the drift matrix A have negative real parts [78]. Through calculation, the Routh–Hurwitz criterion can be simplified to the following inequalities:
Since condition Equation (7c) is a common factor of condition Equation (7b), we only need to ensure condition Equation (7a) and condition Equation (7b) are positive to prove the validity of the Routh–Hurwitz criterion. Through calculation, the Routh–Hurwitz criterion can be simplified to the following inequalities:
The sufficient condition for the solution is that if both and , based on the chosen numerical parameter , then it is straightforward to verify that the system satisfies the Routh–Hurwitz criterion, thereby ensuring the stability of our system. In this system, the potential instability mainly arises from two competing mechanisms. On the one hand, degenerate OPA leads to exponential growth of the optical field, and when exceeds the cavity loss rate it can trigger optical parametric oscillation. On the other hand, mechanical squeezing introduces an effective anti-damping effect, causing the mechanical resonator to exhibit negative stiffness when . Under the parameters used in this work (with and ≈ 0.002), the system’s stability is primarily limited by G, as it more readily approaches the negative stiffness threshold.
3. System Dynamics
In general, the quantum master equation approach is commonly used to study the photon blockade effect in open quantum systems. Under the Born–Markov approximation, the quantum master equation of the system can be written as
Here, is the mechanical thermal excitation number, while and represent the decay rate of the optical mode and the damping rate of the mechanical mode, respectively. In this work, the system undergoes a squeezing transformation, and the master equation is correspondingly transformed, taking the form
where represents the system density operator after the squeezing transformation, and and corresponds to the effective thermal noise and the strength of the two-phonon correlation for the squeezed mechanical mode [79]. Within the squeezed-state framework of the master equation, the strength of the two phonon correlations of the effective thermal noise and the squeezed mechanical mode (quantified by and ) can be fully suppressed when the ideal parameter condition is satisfied. Specifically, this condition leads to [80]. Here, depends on the phase difference between the squeezed vacuum reference phase and the parametric driving phase. Therefore, adjusting the phase of the parametric drive can directly control . In our work, we strictly adhere to this ideal parameter regime (), ensuring complete suppression of thermal noise and correlated phonon dynamics.
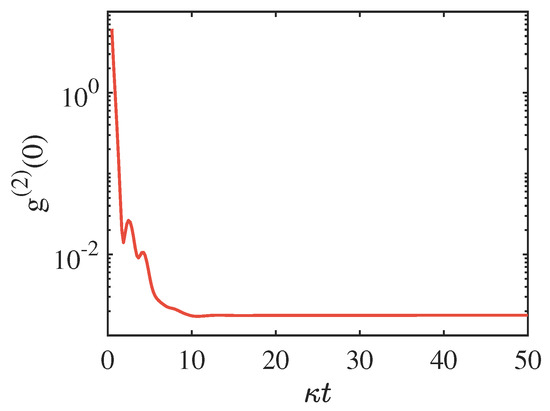
To calculate the relaxation time required to reach the steady state, in Figure 3 we plot the evolution of the correlation function . It clearly shows that the correlation approaches a steady value at 10. For , the relaxation time of the system is about 47.6 .
When the system reaches steady state, the density operator is expressed as . In this case, the equal-time second-order and third-order correlation functions of the photons in the cavity can be expressed as
On the other hand, the analytical solution of the system can be obtained by solving the Schrödinger equation , where . Under the condition of weak driving, and , the system state function can be expressed as , where the photon number is truncated to 3. Therefore, we obtain the following equations of motion for the probability amplitudes:
We assume and obtain an approximate steady-state solution by neglecting higher-order terms:
where . In general, 1PB can be measured by the delayed second-order correlation function of the photons in the cavity,
which represents the probability of detecting two photons with a delay time . When , it is reduced as the equal-time second-order correlation function, which indicates the probability of detecting two photons simultaneously. When , it indicates that the photons in the cavity are in a sub-Poisson statistics regime, meaning that photon blockade has occurred. The analytical result for the equal-time second-order correlation function can be obtained from Equation (14) as follows:
As to the 2PB, the analytical result of the correlation function can be simplified as
4. Enhancement of Single-Photon Blockade Effect
In order to achieve the perfect 1PB, we set and correspondingly obtain
Based on the condition of Equation (18), the delayed second-order correlation functions in the presence or absence of degenerate OPA and mechanical squeezing are plotted in Figure 4a. From Figure 4a, we can clearly see that the squeezed mechanical mode is a great improvement on the 1PB (). Figure 4a clearly shows that the squeezed mechanical mode has a greater effect than no operation. Furthermore, the photon blockade effect of the squeezed cavity mode is greater than that of the squeezed mechanical mode. Meanwhile, the blockade effect is best when both the cavity mode and mechanical mode are squeezed at the same time. This is because the system at the beginning belongs to the weak coupling region and does not have sufficient anharmonicity. However, based on the joint effect between the degenerate OPA and mechanical squeezing, the obtained optomechanical coupling is sufficient to achieve strong enough anharmonicity, breaking the weak coupling limitation of optomechanical systems. Therefore, the optimal blockade effect occurs. The size of the suppressed region is governed by the effective nonlinear coupling strength of the system. When mechanical squeezing and degenerate OPA act jointly, the nonlinear interaction is enhanced, resulting in a stronger photon blockade effect and a broader suppression range. Additionally, the magnitude of the mechanical squeezing parameter r influences this region: a larger r indicates stronger squeezing, which further extends the suppression range. Figure 4a dynamically reveals the relaxation process of the system from a non-equilibrium state to equilibrium. On the other hand, we quantified the purity of single-photon emission by analyzing the static metric of the photon blockade. In Figure 4b, we further show the variation of equal-time second-order correlation function versus detuning . By varying the mechanical frequency , we identified the optimal photon blockade. As shown in Figure 4b, a better blockade effect () can be achieved when the degenerate OPA and mechanical squeezing are simultaneously performed. Figure 4 integrates both the transient characteristics and steady-state behavior of the photon blockade, providing key insights for optimizing single-photon source performance.
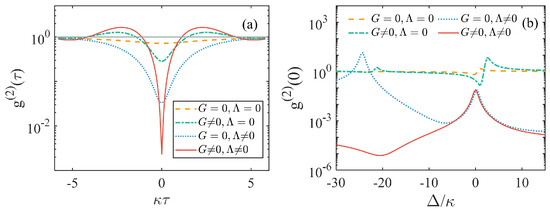
Figure 4.
(a) The delayed second-order correlation functions in the presence or absence of degenerate OPA and mechanical squeezing. (b) The equal-time second-order correlation functions versus mechanical frequency and detuning in the presence or absence of degenerate OPA and mechanical squeezing. The parameters of mechanical frequency are , and 19, respectively. Mechanical coupling constant , and is the optimal condition; the other parameters are the same as given in Figure 3.
Based on the optimal blockade position shown in Figure 4b, and , we investigate the thermal excitation number on the 1PB and plot the variation with the thermal excitation number . As displayed in Figure 5, the yellow curve represents the without mechanical squeezing or degenerate OPA. The green curve corresponds to the case with mechanical squeezing added. By comparing these two curves, it is observed that the inclusion of mechanical squeezing slows the rise of , demonstrating that mechanical squeezing suppresses thermal noise. The blue curve represents the with degenerate OPA added. When comparing the yellow and blue curves, the blockade effect is enhanced with degenerate OPA, but thermal noise is not fully suppressed. The red curve corresponds to the case where both degenerate OPA and mechanical squeezing are applied. A comparison between the red and blue curves reveals that the combined use of degenerate OPA and mechanical squeezing not only improves the blockade effect but also completely suppresses thermal noise. This aligns with our earlier theoretical assumption under ideal conditions (i.e., , ), where the effective thermal noise approaches zero when the squeezing phase .
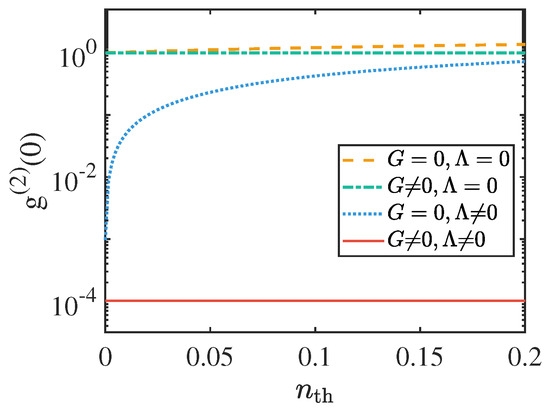
Figure 5.
Second-order correlation function versus mean photon thermal occupation . The other parameters are the same as given in Figure 3.
Subsequently, in Figure 6a, we further analyze the variation of the equal-time second-order correlation function with the detuning and the gain rate of degenerate OPA . And in Figure 6b, we analyze the variation of with the effective mechanical coupling constant and the gain rate of degenerate OPA . The optimal parameter relationship of the 1PB, indicated by the white dashed curves, is consistent with the results of the numerical simulation. This not only corroborates the optimal parametric relationship for 1PB generation previously identified, but also demonstrates the optimal range of values for the degenerate OPA and mechanical squeezing parameters.
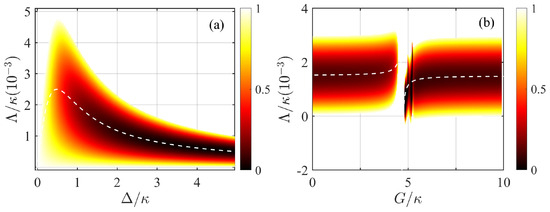
Figure 6.
(a) The equal-time second-order correlation function versus the detuning and the gain rate of degenerate OPA . (b) The equal-time second-order correlation function versus the effective mechanical coupling constant and the gain rate of degenerate OPA . The other parameters are , , , , , and . The white dashed curves in both (a) and (b) correspond to the optimal parameter condition in Equation (14).
On the other hand, when preparing the single-photon source, we also need to consider the emission efficiency of the single-photon source. The study reveals that the peak position of the single-photon occupation probability satisfies the relation . This occurs because the driving laser is precisely tuned to the system’s single-excitation resonance frequency. Therefore, the optimal position for 1PB is not arbitrary but corresponds to the single-excitation resonance of the system. To achieve the best 1PB, one should first determine the position of maximum single-photon occupation by analyzing the system’s single-excitation spectrum and then select the optimal degenerate OPA parameters based on this position. The results are shown in Figure 7, where the red curve represents the equal-time second-order correlation function and the black curve represents the single-photon occupation probability . The solid lines correspond to a driving field amplitude = 0.05, while the dashed lines correspond to = 0.1. From the figure, it is evident that although the single-photon occupation probability increases with the driving field amplitude, the photon blockade effect deteriorates due to the weak driving condition. When = 0.05, the maximum single-photon occupation probability reaches approximately . For an optical cavity with a decay rate MHz, this corresponds to a single-photon emission efficiency in the order of per second.
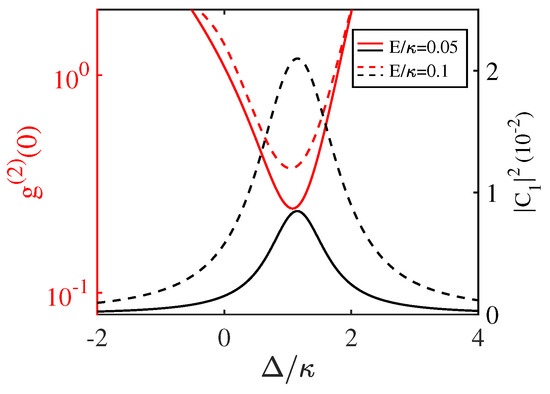
Figure 7.
Effect of different pump field amplification = 0.05 and 0.1 on 1PB (red solid line, red dashed line) and single-photon occupancy probability (black solid line, black dashed line) versus cavity pump field detuning. The other parameters are the same as given in Figure 3.
5. Enhancement of Two-Photon Blockade Effect
In order to further investigate the effects of degenerate OPA and mechanical squeezing on the 2PB in the cavity, we calculate both the second- and third-order correlation functions of the system. The system would realize the 2PB effect when and . In order to realize the 2PB, the system parameters must satisfy the following condition:
where . We first discuss the situation where there is no degenerate OPA and mechanical squeezing in the system (i.e., ). Through numerical calculation, the obtained correlation functions and versus the detuning are shown in Figure 8. In Figure 8a, the red solid curve represents the equal-time second-order correlation function, while the blue dashed curve represents the equal-time third-order correlation function. According to the conditions for the occurrence of 2PB, the pink area indicates the region where 2PB is achieved. However, at this point, the blockade result is not ideal. When we apply squeezing to the mechanical oscillator, as shown in Figure 8b, it can broaden the region of 2PB. At this time, . When we further consider the degenerate OPA to the system, i.e., , as shown in Figure 8c, the 2PB region is significantly broadened and . This indicates that under the joint effect of mechanical squeezing and degenerate OPA, the 2PB is greatly enhanced. This is because in a system without the degenerate OPA and mechanical squeezing, the single-photon coupling strength is small and there is not enough anharmonicity. The eigenenergy spectrum at this time is not sufficient to produce strong 2PB. However, once the degenerate OPA and mechanical squeezing are simultaneously applied on the system, it generates a sufficiently large anharmonic eigenenergy spectrum. In general, a stronger nonlinearity leads to a broader photon blockade region, since enhanced nonlinearity results in larger energy level shifts, making multiphoton transitions more difficult to occur. In the present optomechanical system, the nonlinearity arises from the photon–phonon interaction. Specifically, the optomechanical coupling strength modifies the energy level structure of the system, such that the energy spacing between the single-photon and two-photon states becomes unequal. This alteration affects the condition under which two-photon blockade (2PB) occurs.
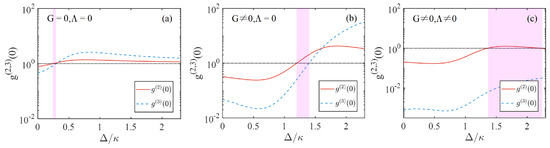
Figure 8.
(a) The equal-time second-order correlation function and equal-time third-order correlation function versus the detuning without degenerate OPA and mechanical squeezing (). (b) and versus the detuning without degenerate OPA (). (c) and versus the detuning with mechanical squeezing (). Here, we choose , , , , . The value of adopts the optimal 2PB condition given by Equation (19). The pink area corresponds to the region where the 2PB effect is achieved.
6. Conclusions
In conclusion, we have studied the photon blockade effect enhanced by the degenerate OPA and mechanical squeezing in an optomechanical system consisting of a nonlinear medium cavity field coupled to a charged mechanical oscillator. We found that even if the original anharmonicity is relatively weak, it can still achieve strong anharmonicity through the joint effect of above two operations and realize a better 1PB in the system. Furthermore, the 2PB in the system has been observed to exhibit enhanced blockade effect and a broadened region of occurrence. The coupling strength required for the photon blockade studied in this paper has been significantly reduced compared to the standard cavity-mechanical systems, making it more promising for experimental realization of the photon blockade effect. This scheme offers a theoretical framework for the realization of photon blockade in cavity optomechanical systems, provides a theoretical foundation for the development of high-efficiency and high-quality single-photon sources, and it will also contribute to the study of multi-photon blockade in the system.
Author Contributions
Conceptualization, Y.H. and J.-L.T.; methodology and investigation, Y.H. and J.-L.T.; software, Y.H. and J.-L.T.; validation, Y.H., J.-L.T. and S.B.; formal analysis, Y.H., J.-L.T. and S.B.; resources and data curation, S.-X.W. and C.-H.B.; writing—original draft preparation, Y.H.; writing—review and editing, S.-X.W. and C.-H.B.; visualization, Y.H. and J.-L.T.; supervision, S.-X.W. and C.-H.B.; project administration, S.B., S.-X.W. and C.-H.B.; funding acquisition, S.B. and C.-H.B. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (NSFC) (12204440, 12204292); Fundamental Research Program of Shanxi Province (202203021212405).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dorsel, A.; McCullen, J.D.; Meystre, P.; Vignes, E.; Walther, H. Optical Bistability and Mirror Confinement Induced by Radiation Pressure. Phys. Rev. Lett. 1983, 51, 1550–1553. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Metcalfe, M. Applications of cavity optomechanics. Appl. Phys. Rev. 2014, 1, 031105. [Google Scholar] [CrossRef]
- Favero, I.; Karrai, K. Optomechanics of deformable optical cavities. Nat. Photon. 2009, 3, 201–205. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565–582. [Google Scholar] [CrossRef]
- Wu, S.X.; Bai, C.H.; Li, G.; Yu, C.S.; Zhang, T. Quantum squeezing-induced quantum entanglement and EPR steering in a coupled optomechanical system. Opt. Express 2024, 32, 260–274. [Google Scholar] [CrossRef] [PubMed]
- Asjad, M.; Zippilli, S.; Vitali, D. Mechanical Einstein-Podolsky-Rosen entanglement with a finite-bandwidth squeezed reservoir. Phys. Rev. A 2016, 93, 062307. [Google Scholar] [CrossRef]
- Weis, S.; Rivière, R.; Deléglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 330, 1520–1523. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Y. Fundamentals and applications of optomechanically induced transparency. Appl. Phys. Rev. 2018, 5, 031305. [Google Scholar] [CrossRef]
- Karuza, M.; Biancofiore, C.; Bawaj, M.; Molinelli, C.; Galassi, M.; Natali, R.; Tombesi, P.; Di Giuseppe, G.; Vitali, D. Optomechanically induced transparency in a membrane-in-the-middle setup at room temperature. Phys. Rev. A 2013, 88, 013804. [Google Scholar] [CrossRef]
- Koppenhöfer, M.; Padgett, C.; Cady, J.V.; Dharod, V.; Oh, H.; Bleszynski Jayich, A.C.; Clerk, A.A. Single-Spin Readout and Quantum Sensing Using Optomechanically Induced Transparency. Phys. Rev. Lett. 2023, 130, 093603. [Google Scholar] [CrossRef]
- Imamoḡlu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly Interacting Photons in a Nonlinear Cavity. Phys. Rev. Lett. 1997, 79, 1467–1470. [Google Scholar] [CrossRef]
- Rebić, S.; Parkins, A.S.; Tan, S.M. Photon statistics of a single-atom intracavity system involving electromagnetically induced transparency. Phys. Rev. A 2002, 65, 063804. [Google Scholar] [CrossRef]
- Gao, X.C.; Wu, X.J.; Bai, C.H.; Wu, S.X.; Yu, C.S. Photon blockade with a trapped Λ-type three-level atom in asymmetrical cavity. Opt. Express 2023, 31, 36796–36809. [Google Scholar] [CrossRef]
- Wu, S.X.; Gao, X.C.; Cheng, H.H.; Bai, C.H. Nonreciprocal photon blockade induced by parametric amplification in an asymmetrical cavity. Phys. Rev. A 2025, 111, 043714. [Google Scholar] [CrossRef]
- Huang, B.; Li, C.; Fan, B.; Duan, Z. Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model. Photonics 2024, 11, 369. [Google Scholar] [CrossRef]
- Rempe, G.; Thompson, R.J.; Kimble, H.J.; Lalezari, R. Measurement of ultralow losses in an optical interferometer. Opt. Lett. 1992, 17, 363–365. [Google Scholar] [CrossRef]
- Tian, L.; Zoller, P. Coupled Ion-Nanomechanical Systems. Phys. Rev. Lett. 2004, 93, 266403. [Google Scholar] [CrossRef]
- Hensinger, W.K.; Utami, D.W.; Goan, H.S.; Schwab, K.; Monroe, C.; Milburn, G.J. Ion trap transducers for quantum electromechanical oscillators. Phys. Rev. A 2005, 72, 041405. [Google Scholar] [CrossRef]
- Vernooy, D.W.; Furusawa, A.; Georgiades, N.P.; Ilchenko, V.S.; Kimble, H.J. Cavity QED with high-Q whispering gallery modes. Phys. Rev. A 1998, 57, R2293–R2296. [Google Scholar] [CrossRef]
- Vučković, J.; Lončar, M.; Mabuchi, H.; Scherer, A. Design of photonic crystal microcavities for cavity QED. Phys. Rev. E 2001, 65, 016608. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Camacho, R.; Chan, J.; Vahala, K.J.; Painter, O. A picogram-and nanometre-scale photonic-crystal optomechanical cavity. Nature 2009, 459, 550–555. [Google Scholar] [CrossRef]
- Chan, J.; Eichenfield, M.; Camacho, R.; Painter, O. Optical and mechanical design of a “zipper” photonic crystal optomechanical cavity. Opt. Express 2009, 17, 3802–3817. [Google Scholar] [CrossRef]
- Mitatha, S.; Pornsuwancharoen, N.; Yupapin, P.P. A Simultaneous Short-Wave and Millimeter-Wave Generation Using a Soliton Pulse Within a Nano-Waveguide. IEEE Photonics Technol. Lett. 2009, 21, 932–934. [Google Scholar] [CrossRef]
- Noual, A.; Pennec, Y.; Akjouj, A.; Djafari-Rouhani, B.; Dobrzynski, L. Nanoscale plasmon waveguide including cavity resonator. J. Phys. Condens. Mat. 2009, 21, 375301. [Google Scholar] [CrossRef] [PubMed]
- Genes, C.; Vitali, D.; Tombesi, P.; Gigan, S.; Aspelmeyer, M. Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes. Phys. Rev. A 2008, 77, 033804. [Google Scholar] [CrossRef]
- Mansouri, D.; Rezaie, B.; Ranjbar N, A.; Daeichian, A. Cavity-assisted coherent feedback cooling of a mechanical resonator to the ground-state in the unresolved sideband regime. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 165501. [Google Scholar] [CrossRef]
- Cohadon, P.F.; Heidmann, A.; Pinard, M. Cooling of a Mirror by Radiation Pressure. Phys. Rev. Lett. 1999, 83, 3174–3177. [Google Scholar] [CrossRef]
- Guo, J.; Norte, R.; Gröblacher, S. Feedback Cooling of a Room Temperature Mechanical Oscillator close to its Motional Ground State. Phys. Rev. Lett. 2019, 123, 223602. [Google Scholar] [CrossRef]
- Wang, X.; Vinjanampathy, S.; Strauch, F.W.; Jacobs, K. Ultraefficient Cooling of Resonators: Beating Sideband Cooling with Quantum Control. Phys. Rev. Lett. 2011, 107, 177204. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.L.; Otten, M.; Gray, S.K. Ground-state cooling enabled by critical coupling and dark entangled states. Phys. Rev. B 2019, 99, 014107. [Google Scholar] [CrossRef]
- Neuhauser, W.; Hohenstatt, M.; Toschek, P.; Dehmelt, H. Optical-Sideband Cooling of Visible Atom Cloud Confined in Parabolic Well. Phys. Rev. Lett. 1978, 41, 233–236. [Google Scholar] [CrossRef]
- Leibrandt, D.R.; Labaziewicz, J.; Vuletić, V.; Chuang, I.L. Cavity Sideband Cooling of a Single Trapped Ion. Phys. Rev. Lett. 2009, 103, 103001. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef]
- Marquardt, F.; Chen, J.P.; Clerk, A.A.; Girvin, S.M. Quantum Theory of Cavity-Assisted Sideband Cooling of Mechanical Motion. Phys. Rev. Lett. 2007, 99, 093902. [Google Scholar] [CrossRef]
- Asjad, M.; Abari, N.E.; Zippilli, S.; Vitali, D. Optomechanical cooling with intracavity squeezed light. Opt. Express 2019, 27, 32427–32444. [Google Scholar] [CrossRef]
- Kiraz, A.; Atatüre, M.; Imamoğlu, A. Quantum-dot single-photon sources: Prospects for applications in linear optics quantum-information processing. Phys. Rev. A 2004, 69, 032305. [Google Scholar] [CrossRef]
- An, J.H.; Feng, M.; Oh, C.H. Quantum-information processing with a single photon by an input-output process with respect to low-Q cavities. Phys. Rev. A 2009, 79, 032303. [Google Scholar] [CrossRef]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2018, 82, 016001. [Google Scholar] [CrossRef]
- Jennewein, T.; Barbieri, M.; White, A.G. Single-photon device requirements for operating linear optics quantum computing outside the post-selection basis. J. Mod. Opt. 2011, 58, 276–287. [Google Scholar] [CrossRef]
- Hartmann, M.J. Quantum simulation with interacting photons. J. Opt. 2016, 18, 104005. [Google Scholar] [CrossRef]
- Cerf, N.J.; Adami, C.; Kwiat, P.G. Optical simulation of quantum logic. Phys. Rev. A 1998, 57, R1477–R1480. [Google Scholar] [CrossRef]
- Hamsen, C.; Tolazzi, K.N.; Wilk, T.; Rempe, G. Two-Photon Blockade in an Atom-Driven Cavity QED System. Phys. Rev. Lett. 2017, 118, 133604. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.J.; Gong, S.Q. Two-photon blockade generated and enhanced by mechanical squeezing. Phys. Rev. A 2021, 103, 043509. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Shen, H.Z.; Yi, X.X. Unconventional photon blockade with second-order nonlinearity. Phys. Rev. A 2015, 92, 023838. [Google Scholar] [CrossRef]
- Wu, Q.C.; Zhang, X.Y.; Wang, Y.M.; Liu, T.; Zhou, Y.H.; Shen, H.Z.; Yang, C.P. Two-photon blockade with second-order nonlinearity in cavity systems. Int. J. Theor. Phys. 2022, 61, 21. [Google Scholar] [CrossRef]
- Ferretti, S.; Gerace, D. Single-photon nonlinear optics with Kerr-type nanostructured materials. Phys. Rev. B 2012, 85, 033303. [Google Scholar] [CrossRef]
- Peyronel, T.; Firstenberg, O.; Liang, Q.Y.; Hofferberth, S.; Gorshkov, A.V.; Pohl, T.; Lukin, M.D.; Vuletić, V. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 2012, 488, 57–60. [Google Scholar] [CrossRef]
- Javadi, A.; Söllner, I.; Arcari, M.; Hansen, S.L.; Midolo, L.; Mahmoodian, S.; Kiršanskė, G.; Pregnolato, T.; Lee, E.; Song, J.; et al. Single-photon non-linear optics with a quantum dot in a waveguide. Nat. Commun. 2015, 6, 8655. [Google Scholar] [CrossRef]
- Ren, Y.; Duan, S.; Xie, W.; Shao, Y.; Duan, Z. Antibunched photon-pair source based on photon blockade in a nondegenerate optical parametric oscillator. Phys. Rev. A 2021, 103, 053710. [Google Scholar] [CrossRef]
- Claudon, J.; Bleuse, J.; Malik, N.S.; Bazin, M.; Jaffrennou, P.; Gregersen, N.; Sauvan, C.; Lalanne, P.; Gérard, J.M. A highly efficient single-photon source based on a quantum dot in a photonic nanowire. Nat. Photon. 2010, 4, 174–177. [Google Scholar] [CrossRef]
- Husko, C.A.; Clark, A.S.; Collins, M.J.; De Rossi, A.; Combrié, S.; Lehoucq, G.; Rey, I.H.; Krauss, T.F.; Xiong, C.; Eggleton, B.J. Multi-photon absorption limits to heralded single photon sources. Sci. Rep. 2013, 3, 3087. [Google Scholar] [CrossRef] [PubMed]
- Zasedatelev, A.V.; Baranikov, A.V.; Sannikov, D.; Urbonas, D.; Scafirimuto, F.; Shishkov, V.Y.; Andrianov, E.S.; Lozovik, Y.E.; Scherf, U.; Stöferle, T.; et al. Single-photon nonlinearity at room temperature. Nature 2021, 597, 493–497. [Google Scholar] [CrossRef]
- Hloušek, J.; Straka, I.; Ježek, M. Experimental observation of anomalous supralinear response of single-photon detectors. Appl. Phys. Rev. 2023, 10, 011412. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Liu, T.; Su, Q.P.; Zhang, X.Y.; Wu, Q.C.; Chen, D.X.; Shi, Z.C.; Shen, H.Z.; Yang, C.P. Universal Photon Blockade. Phys. Rev. Lett. 2025, 134, 183601. [Google Scholar] [CrossRef]
- Collett, M.J.; Gardiner, C.W. Squeezing of intracavity and traveling-wave light fields produced in parametric amplification. Phys. Rev. A 1984, 30, 1386–1391. [Google Scholar] [CrossRef]
- Wu, L.A.; Xiao, M.; Kimble, H.J. Squeezed states of light from an optical parametric oscillator. J. Opt. Soc. Am. B 1987, 4, 1465–1475. [Google Scholar] [CrossRef]
- Lü, X.Y.; Wu, Y.; Johansson, J.R.; Jing, H.; Zhang, J.; Nori, F. Squeezed Optomechanics with Phase-Matched Amplification and Dissipation. Phys. Rev. Lett. 2015, 114, 093602. [Google Scholar] [CrossRef]
- Wang, D.Y.; Yan, L.L.; Su, S.L.; Bai, C.H.; Wang, H.F.; Liang, E. Squeezing-induced nonreciprocal photon blockade in an optomechanical microresonator. Opt. Express 2023, 31, 22343–22357. [Google Scholar] [CrossRef]
- Shen, H.Z.; Wang, Q.; Wang, J.; Yi, X.X. Nonreciprocal unconventional photon blockade in a driven dissipative cavity with parametric amplification. Phys. Rev. A 2020, 101, 013826. [Google Scholar] [CrossRef]
- Bai, C.H.; Wang, D.Y.; Zhang, S.; Liu, S.; Wang, H.F. Engineering of strong mechanical squeezing via the joint effect between Duffing nonlinearity and parametric pump driving. Photon. Res. 2019, 7, 1229–1239. [Google Scholar] [CrossRef]
- Wu, S.X.; Bai, C.H.; Li, G.; Yu, C.S.; Zhang, T. Enhancing the quantum entanglement and EPR steering of a coupled optomechanical system with a squeezed vacuum field. J. Opt. Soc. Am. B 2023, 40, 2885–2893. [Google Scholar] [CrossRef]
- Gan, J.H.; Liu, Y.C.; Lu, C.; Wang, X.; Tey, M.K.; You, L. Intracavity-Squeezed Optomechanical Cooling. Laser Photonics Rev. 2019, 13, 1900120. [Google Scholar] [CrossRef]
- Xie, H.; He, L.W.; Shang, X.; Lin, X.M. Photon Blockade in Cavity Optomechanics via Parametric Amplification. Adv. Quantum Technol. 2024, 7, 2400065. [Google Scholar] [CrossRef]
- Xie, H.; He, L.W.; Shang, X.; Lin, X.M. Phonon Blockade in A Squeezed Cavity Optomechanical System. Adv. Quantum Technol. 2024, 7, 2300239. [Google Scholar] [CrossRef]
- Lemonde, M.A.; Didier, N.; Clerk, A.A. Enhanced nonlinear interactions in quantum optomechanics via mechanical amplification. Nat. Commun. 2016, 7, 11338. [Google Scholar] [CrossRef]
- Peano, V.; Schwefel, H.G.L.; Marquardt, C.; Marquardt, F. Intracavity Squeezing Can Enhance Quantum-Limited Optomechanical Position Detection through Deamplification. Phys. Rev. Lett. 2015, 115, 243603. [Google Scholar] [CrossRef]
- Lau, H.K.; Clerk, A.A. Ground-State Cooling and High-Fidelity Quantum Transduction via Parametrically Driven Bad-Cavity Optomechanics. Phys. Rev. Lett. 2020, 124, 103602. [Google Scholar] [CrossRef]
- Li, M.; Pernice, W.H.P.; Tang, H.X. Reactive Cavity Optical Force on Microdisk-Coupled Nanomechanical Beam Waveguides. Phys. Rev. Lett. 2009, 103, 223901. [Google Scholar] [CrossRef]
- Yang, P.; Xia, X.; He, H.; Li, S.; Han, X.; Zhang, P.; Li, G.; Zhang, P.; Xu, J.; Yang, Y.; et al. Realization of Nonlinear Optical Nonreciprocity on a Few-Photon Level Based on Atoms Strongly Coupled to an Asymmetric Cavity. Phys. Rev. Lett. 2019, 123, 233604. [Google Scholar] [CrossRef] [PubMed]
- Pirkkalainen, J.M.; Cho, S.; Massel, F.; Tuorila, J.; Heikkilä, T.; Hakonen, P.; Sillanpää, M. Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 2015, 6, 6981. [Google Scholar] [CrossRef] [PubMed]
- Mi, X.; Benito, M.; Putz, S.; Zajac, D.M.; Taylor, J.M.; Burkard, G.; Petta, J.R. A coherent spin–photon interface in silicon. Nature 2018, 555, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.C.; Zhang, J.Q.; Xiao, Y.; Feng, M.; Zhang, Z.M. Tunable double optomechanically induced transparency in an optomechanical system. Phys. Rev. A 2014, 90, 043825. [Google Scholar] [CrossRef]
- Ullah, K.; Jing, H.; Saif, F. Multiple electromechanically-induced-transparency windows and Fano resonances in hybrid nano-electro-optomechanics. Phys. Rev. A 2018, 97, 033812. [Google Scholar] [CrossRef]
- Bai, C.H.; Wang, D.Y.; Zhang, S.; Liu, S.; Wang, H.F. Double-mechanical-oscillator cooling by breaking the restrictions of quantum backaction and frequency ratio via dynamical modulation. Phys. Rev. A 2021, 103, 033508. [Google Scholar] [CrossRef]
- Sarma, B.; Sarma, A.K. Tunable phonon blockade in weakly nonlinear coupled mechanical resonators via Coulomb interaction. Sci. Rep. 2018, 8, 14583. [Google Scholar] [CrossRef]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288–5290. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Wang, Y.; Wu, J.L.; Han, J.X.; Xia, Y.; Jiang, Y.Y.; Song, J. Enhanced Phonon Blockade in a Weakly Coupled Hybrid System via Mechanical Parametric Amplification. Phys. Rev. Appl. 2022, 17, 024009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).