Some Insights on Kerr Lensing Effects
Abstract
1. Introduction
2. Kerr Lensing Effect (KLE)
2.1. Kerr Lens Effect Induced by a Gaussian Beam
- (i)
- the minimum value of , denoted
- (ii)
- the longitudinal position, denoted , where the diffracted beam has a shrinkage which is maximum, i.e., .
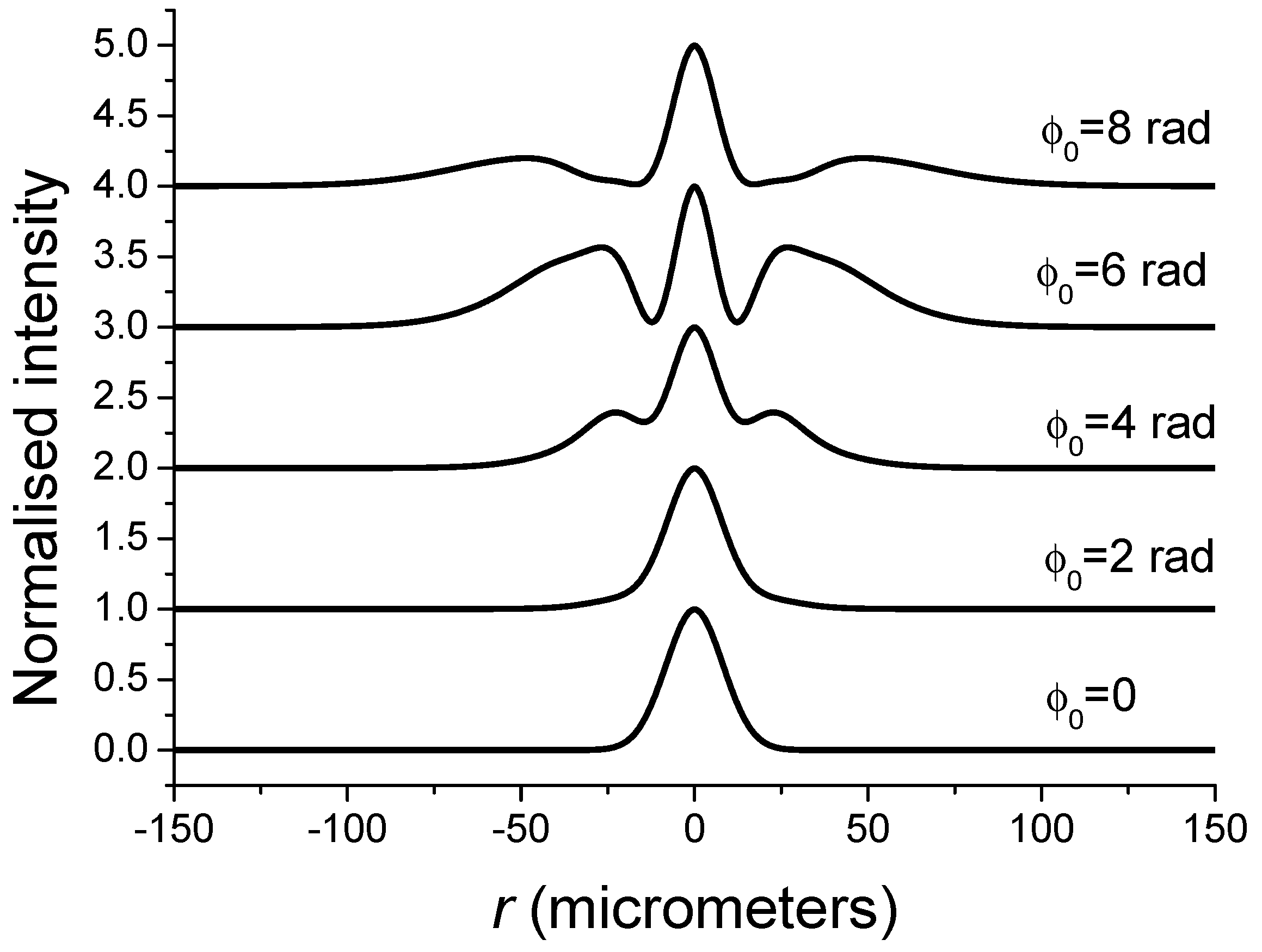
2.2. Kerr Lens Effect Induced by a LGp0 Beam
3. LGp0 Beams Subject to OKE: Applications
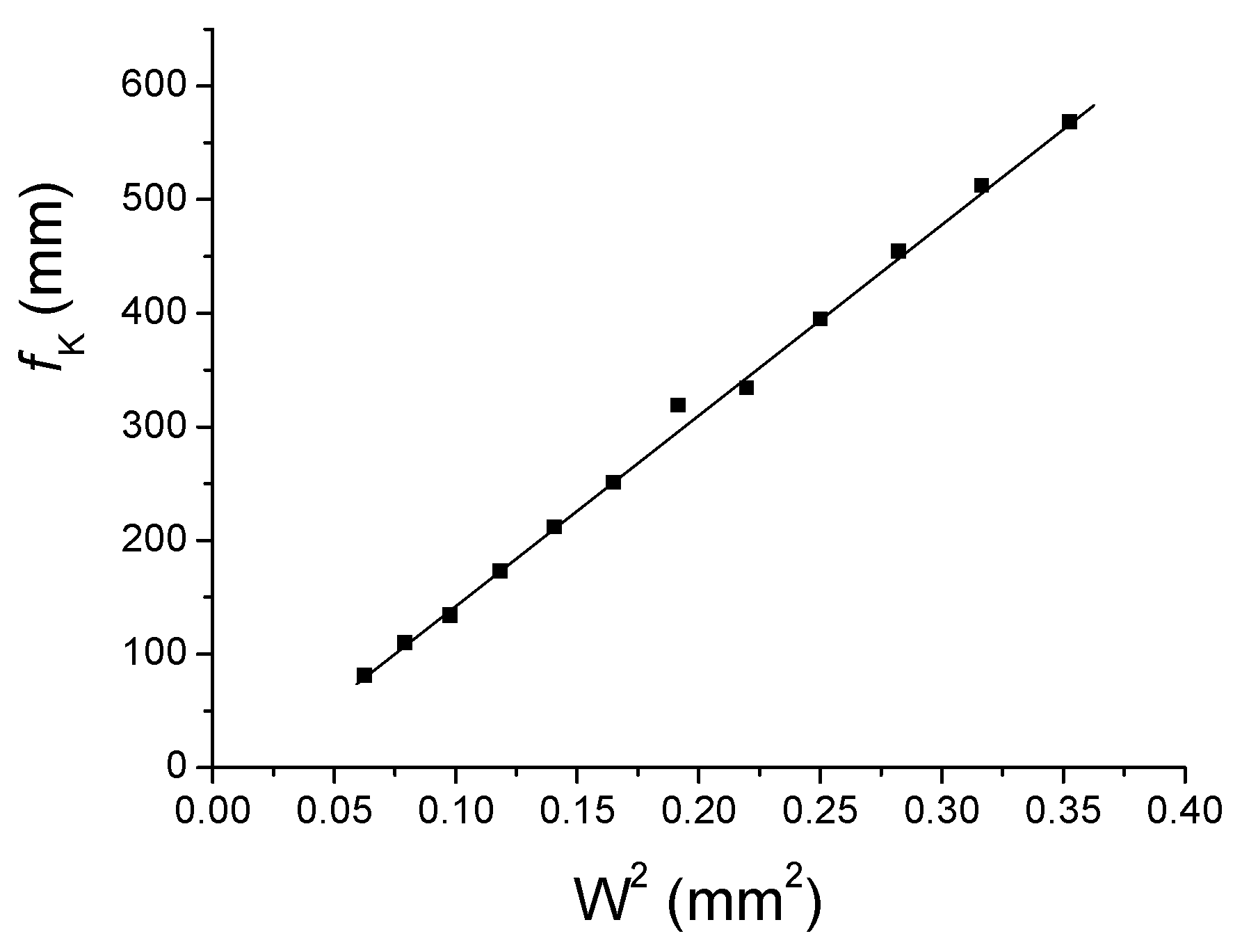
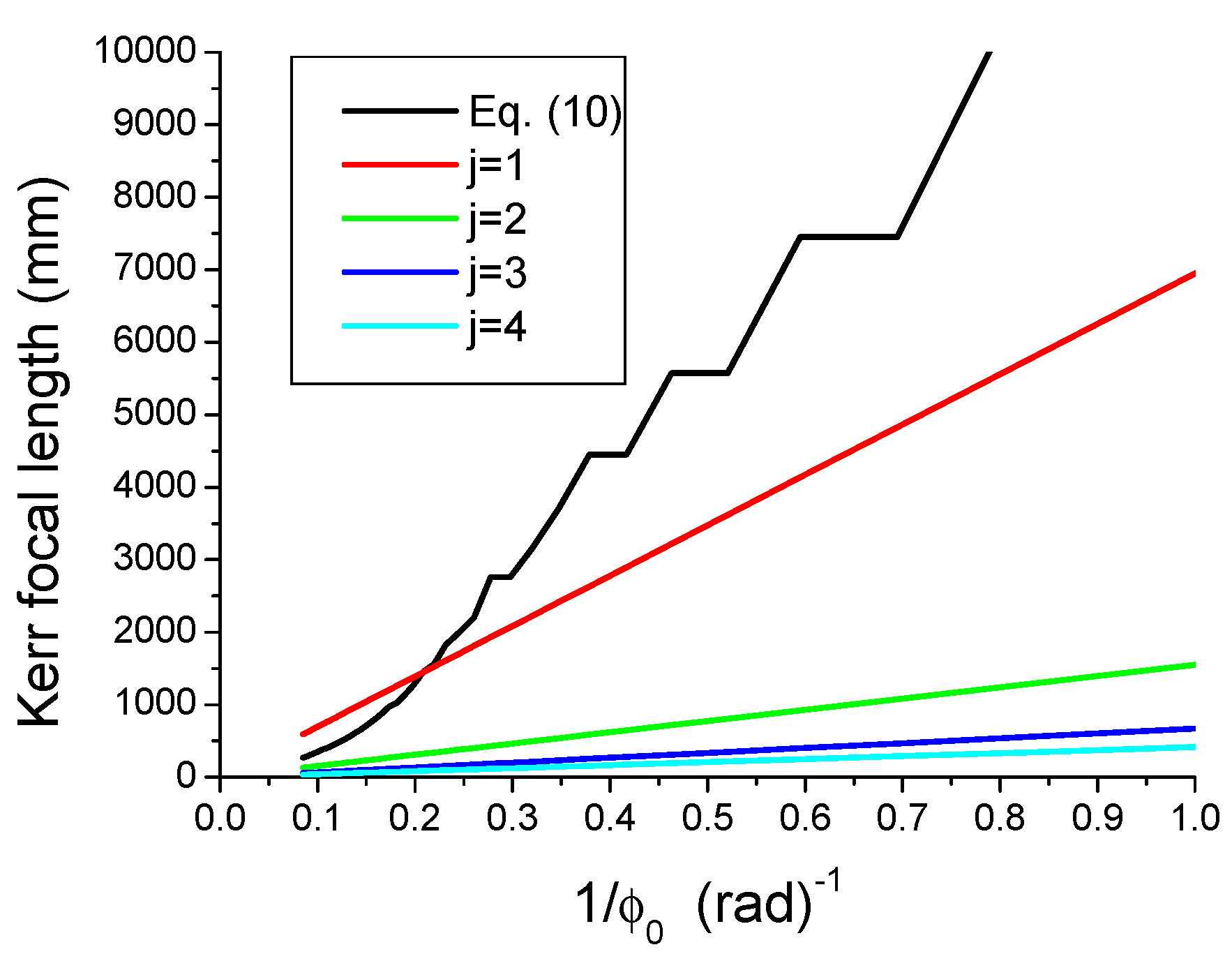
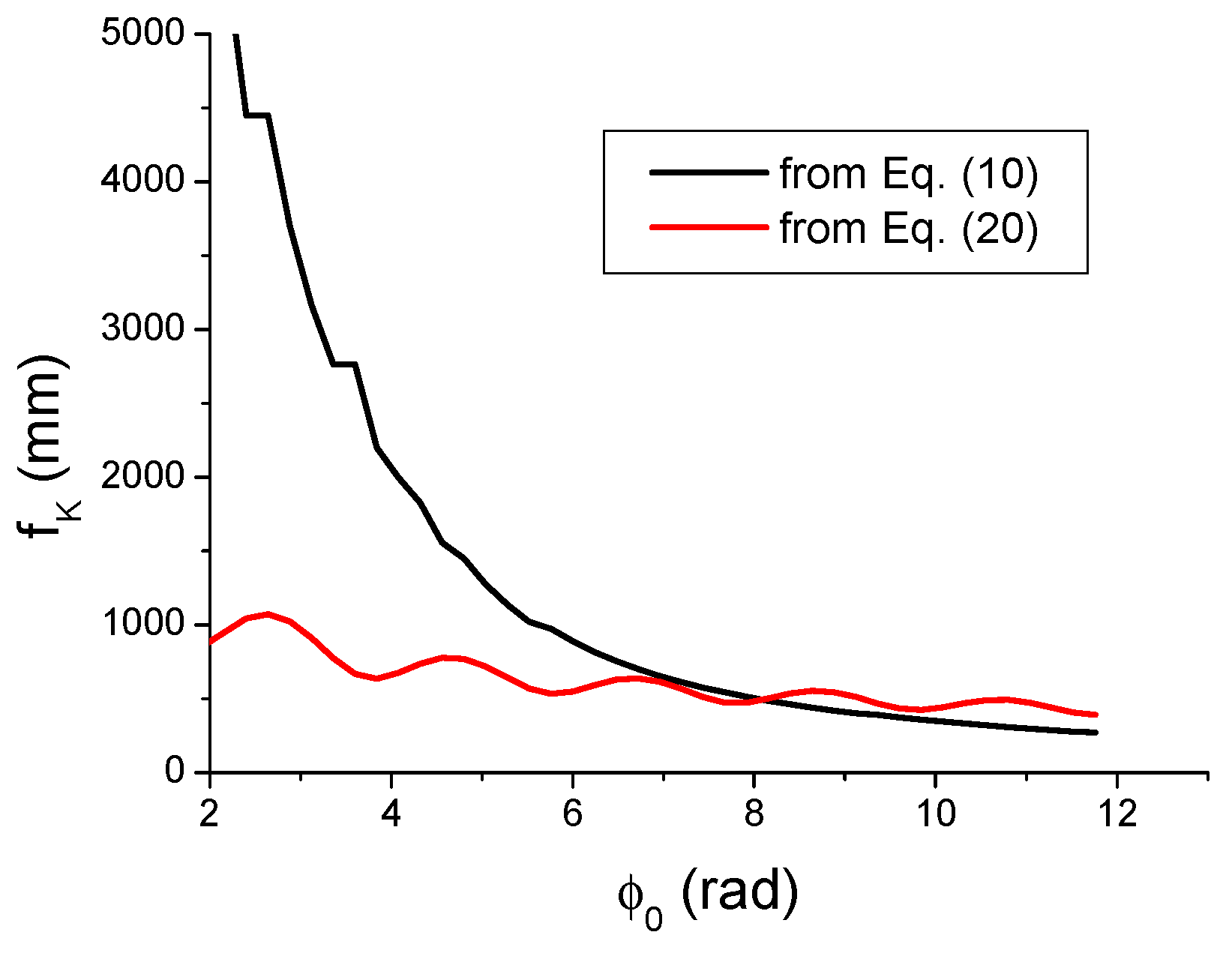
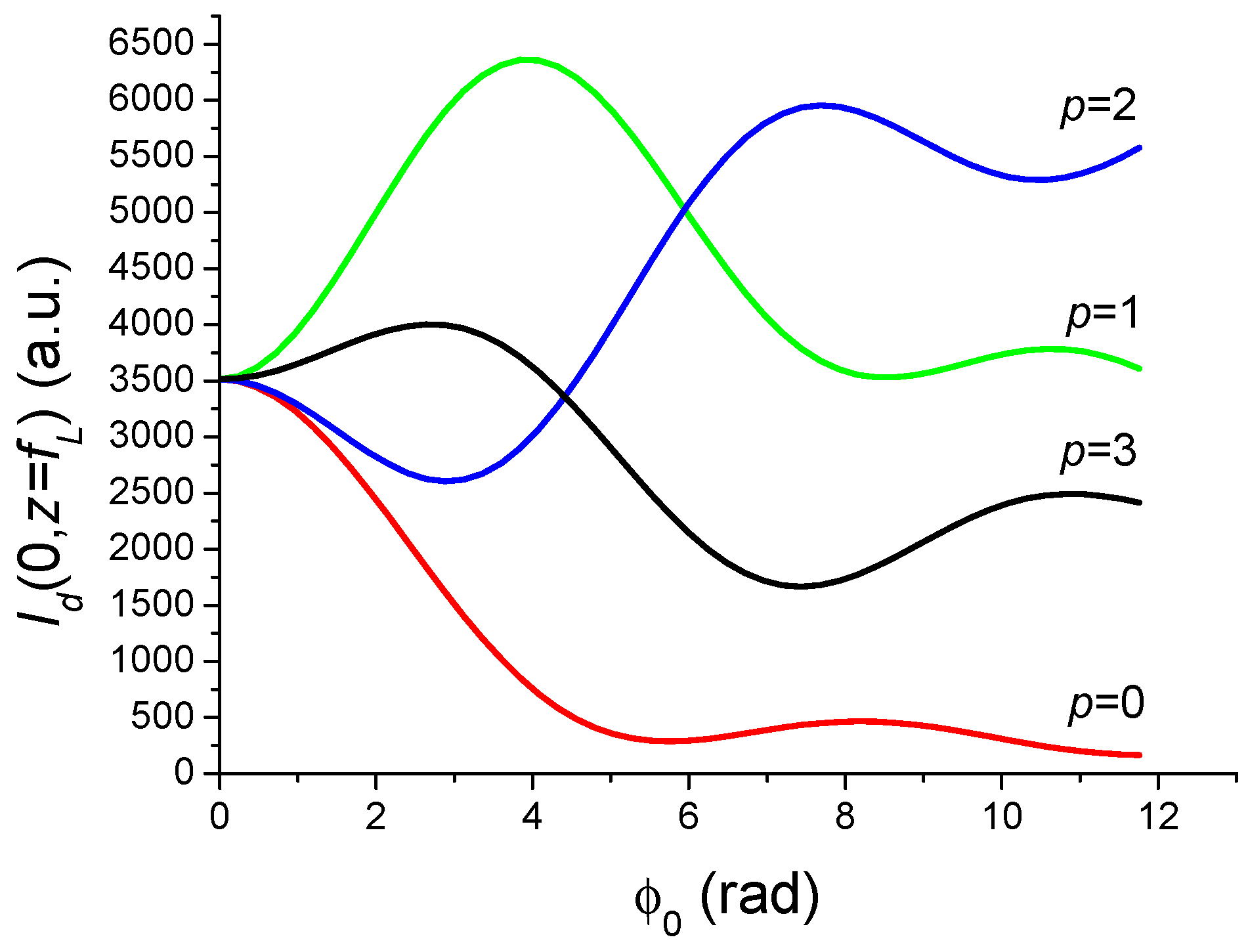
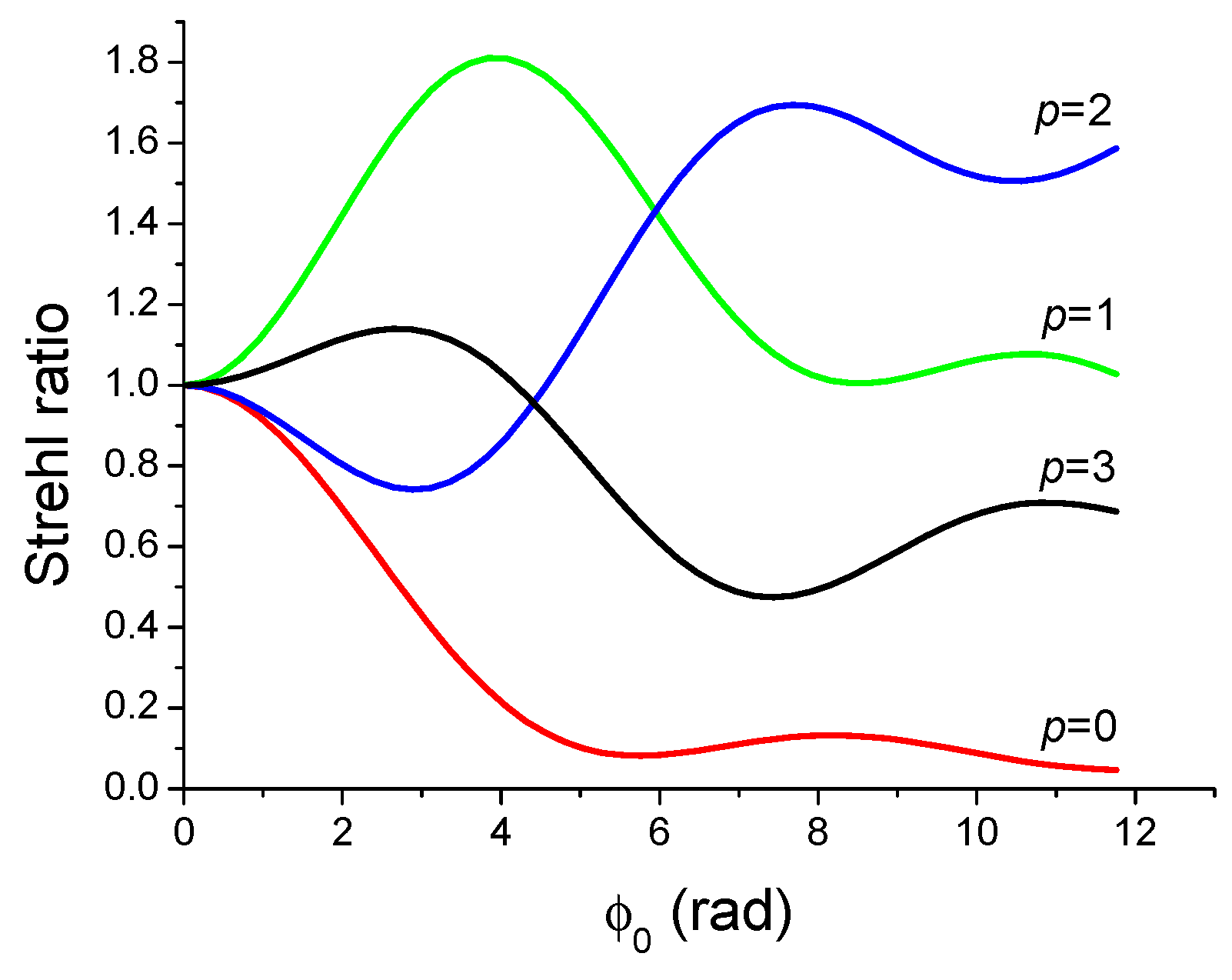
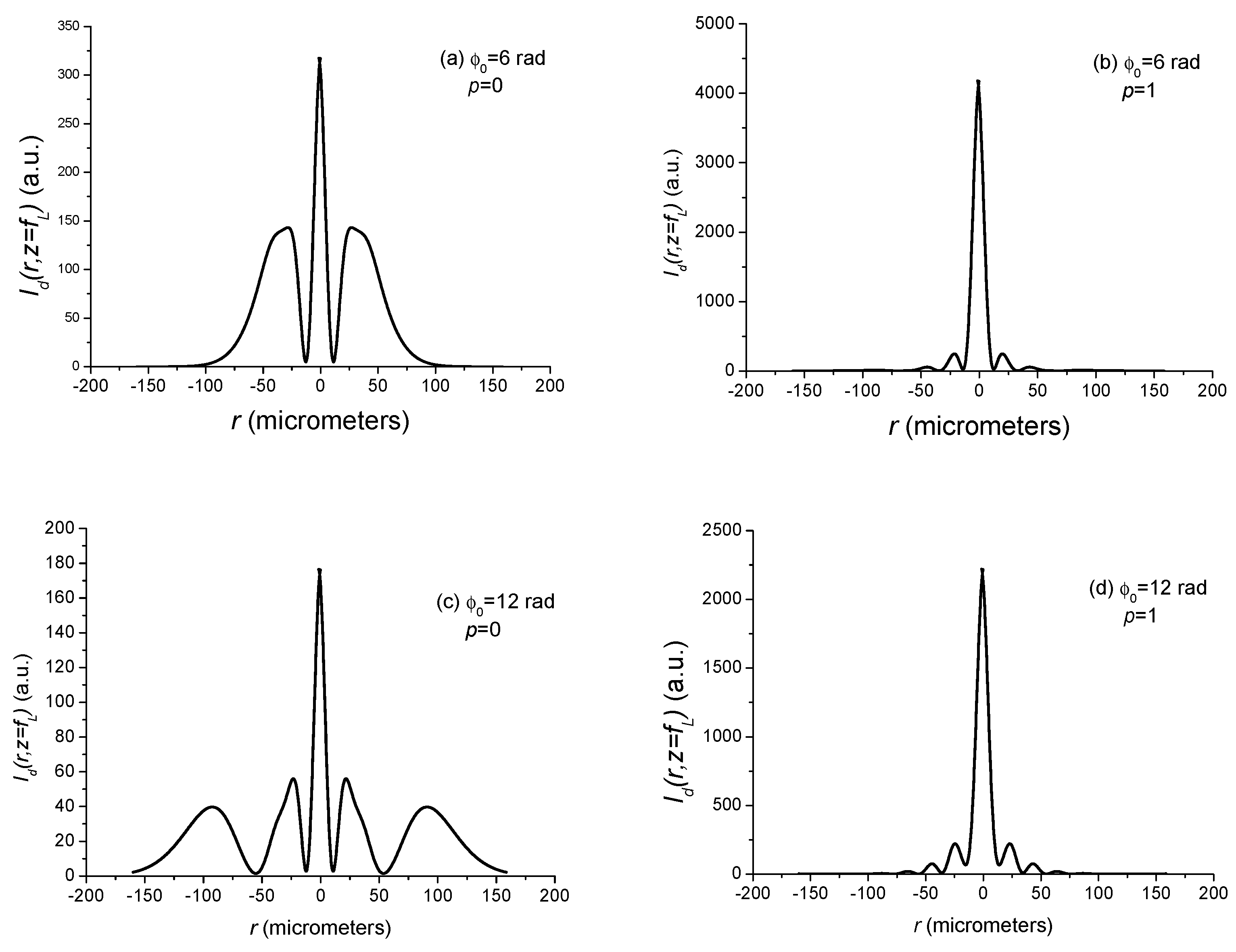
3.1. Improving the Focusing Properties of a Laser Beam Subject to OKE
- (i)
- Small-scale self-focusing: The “small-scale self-focusing” is a phenomenon leading to an exponential growth [27] of spatial irregularities present in the laser pulse which can result in a beam breakup (self-focusing filamentation), i.e., very hot spots in the section of the laser beam. These hot spots, in extreme cases, can destroy the amplifying medium, and must be suppressed using spatial filters [45]. No more attention is given in this paper to small-scale self-focusing.
- (ii)
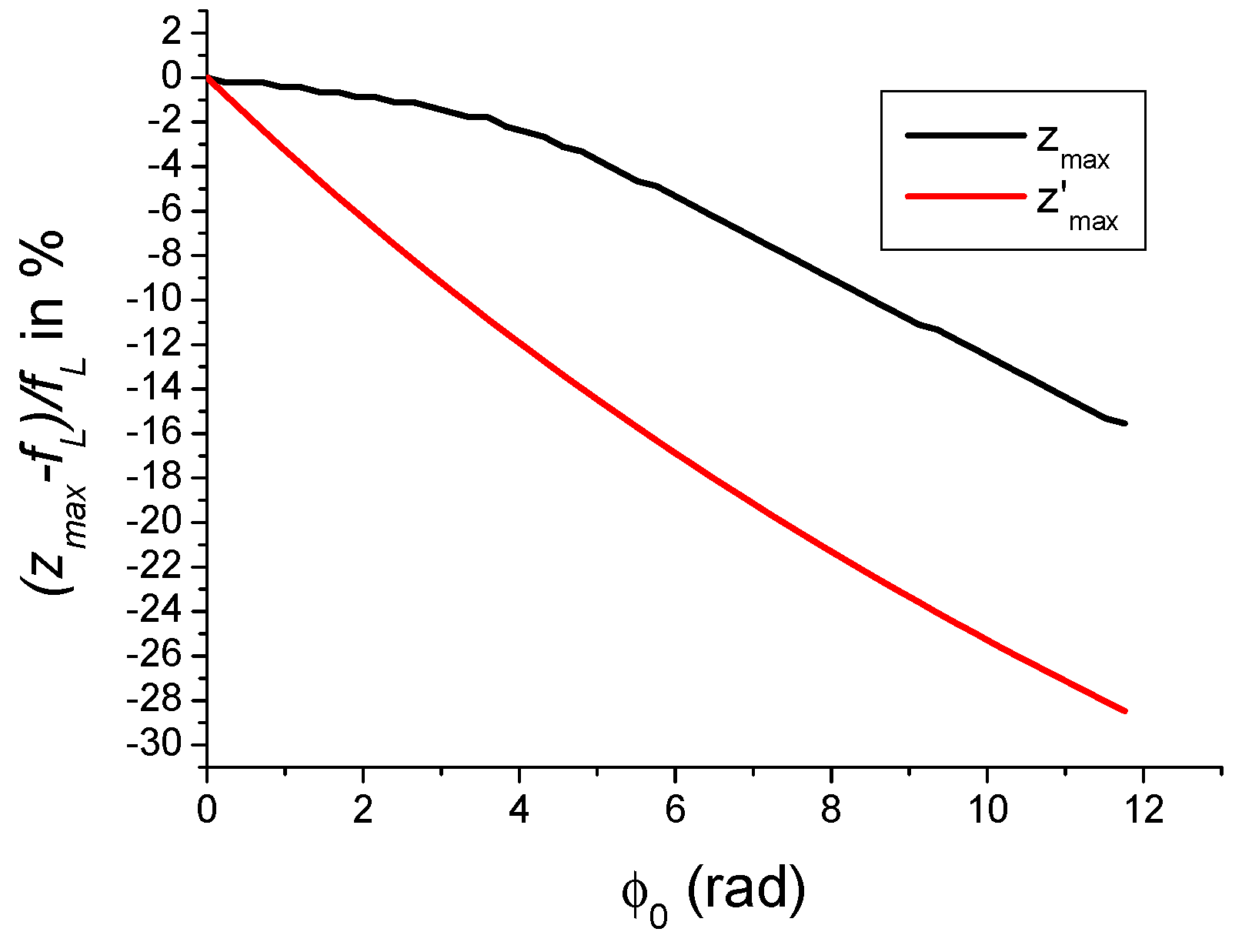
- Large-scale self-focusing: The “large-scale self-focusing” is linked directly to the Kerr lensing effect having the tendency to focus the laser pulse more and more as it propagates inside the amplifying medium. In the extreme case, the large scale self-focusing leads to a collapse of the laser beam inside the amplifying medium, thus leading to its damage. It is then important to limit the length of the amplifying medium in order that the beam collapse will never occur. With no further detail, we can expect from the plots in Figure 14 that the amplification of a beam instead of the usual Gaussian beam could be envisaged with a long amplifying medium.
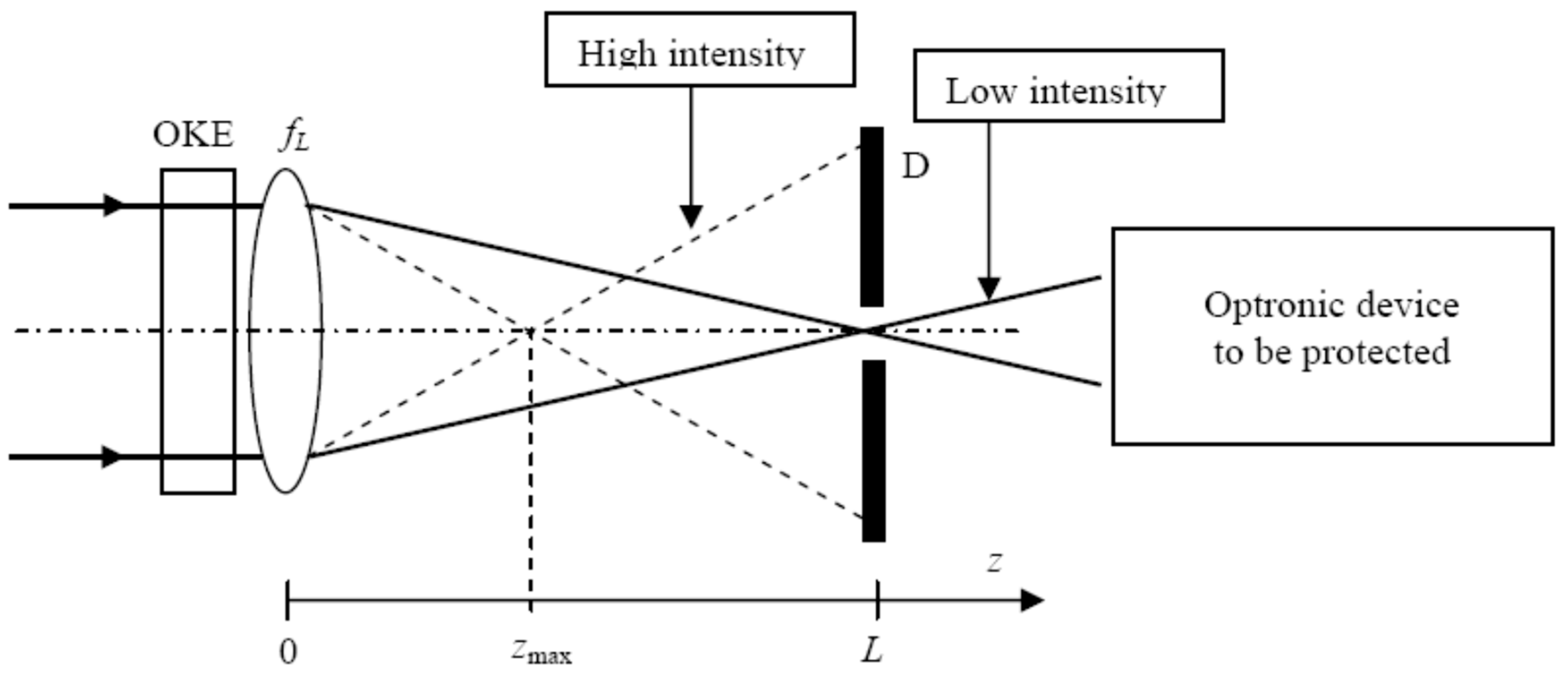
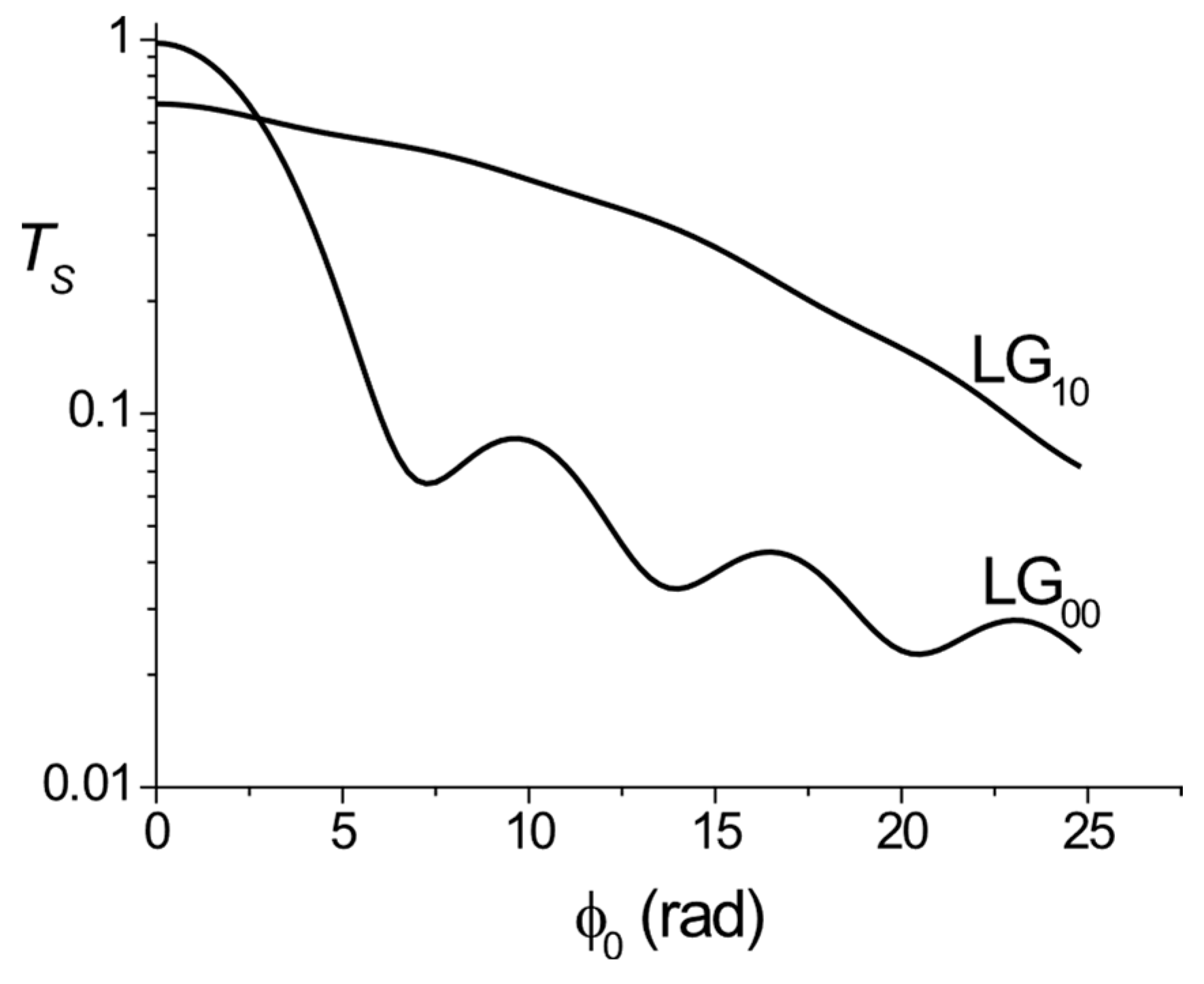
3.2. An LG10 Beam for Weakening of the Optical Limiters Protection
- -
- The protecting device has to be almost transparent in the visible and the near-infrared.
- -
- The response time of the limiter has to be in the picosecond (or less) range.
- -
- The spectral response of the limiter has to be large.
- -
- The nonlinear material used in the limiter must be resistant to permanent optical damage.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| j | Type of Aberration | |
|---|---|---|
| 4 | Defocus | |
| 11 | Primary spherical | |
| 22 | Secondary spherical | |
| 37 | Tertiary spherical |
| Incident wave | ||||
| Plane wave | ||||
| Gaussian beam |
References
- Campillo, A.; Shapiro, S.; Suydam, B. Periodic breakup of optical beams due to self-focusing. Appl. Phys. Lett. 1973, 23, 628–630. [Google Scholar] [CrossRef]
- Feit, M.; Fleck, J. Beam nonparaxiality, filament formation, and beam breakup in the self-focusing of optical beams. JOSA B 1988, 5, 633–640. [Google Scholar] [CrossRef]
- Magni, V.; Cerullo, S.; DeSilvestri, S. ABCD matrix analysis of propagation of Gaussian beams through Kerr media. Opt. Commun. 1993, 96, 348–355. [Google Scholar] [CrossRef]
- Hermann, J. Theory of Kerr-Lens mode locking: Role of self-focusing and radially varying gain. JOSA B 1994, 11, 498–512. [Google Scholar] [CrossRef]
- Yefet, S.; Pe’er, A. A review of cavity design for Kerr Lens mode-locked solid-state lasers. Appl. Sci. 2013, 3, 694–724. [Google Scholar] [CrossRef]
- Akbari, R.; Major, A. Kerr-lens mode locking of a diode-pumped Yb:KGW laser using an additional intracavity Kerr medium. Las. Phys. Lett. 2018, 15, 085001. [Google Scholar] [CrossRef]
- Levine, Z.H.; Du, Z. Semiclassical calculation of the power saturation of the Kerr effect in Rb vapor. JOSA B 2023, 40, 3190–3195. [Google Scholar] [CrossRef]
- Robertson, S. Optical Kerr effect in vacuum. Phys. Rev. A 2019, 100, 063831. [Google Scholar] [CrossRef]
- Hsieh, T.; Lee, D.S.; Lin, C.Y. Throat effects on strong gravitational lensing in Kerr-like wormholes. Phys. Rev. D 2025, 111, 044051. [Google Scholar] [CrossRef]
- Gralla, S.E.; Lupsasca, A. Lensing by Kerr black holes. Phys. Rev. D 2020, 101, 044031. [Google Scholar] [CrossRef]
- Siegman, A. Analysis of laser beam quality degradation caused by quartic phase aberrations. Appl. Opt. 1993, 32, 5893–5901. [Google Scholar] [CrossRef] [PubMed]
- Ruff, J.A.; Siegman, A.E. Measurement of beam quality degradation due to spherical aberration in a simple lens. Opt. Quantum Electron. 1994, 26, 629–632. [Google Scholar] [CrossRef]
- Pu, J.; Zhang, H. Intensity distribution of Gaussian beams focused by a lens with spherical aberration. Opt. Commun. 1998, 151, 331–338. [Google Scholar] [CrossRef]
- Karman, G.P.; Van Duijl, A.; Woerdman, J.P. Observation of a stronger focus due to spherical aberration. J. Mod. Opt. 1998, 45, 2513–2517. [Google Scholar] [CrossRef]
- Ji, X.; Lü, B. Focal shift of flattened Gaussian beams passing through a spherically aberrated lens. Optik 2002, 113, 201–204. [Google Scholar] [CrossRef]
- Escobar, I.; Saavedra, G.; Martinez-Corral, M. Reduction of the spherical aberration effect in high-numerical-aperture optical scanning instruments. JOSA A 2006, 23, 3150–3155. [Google Scholar] [CrossRef]
- Alkelly, A. Spot size and radial intensity distribution of focused Gaussian beams in spherical and non-spherical aberration lenses. Opt. Commun. 2007, 277, 397–405. [Google Scholar] [CrossRef]
- Singh, R.; Senthilkumaran, P.; Singh, K. Focusing of a singular beam in the presence of spherical aberration and defocusing. Optik 2008, 119, 459–464. [Google Scholar] [CrossRef]
- George, J.; Seihgal, R.; Oak, S.M.; Mehendale, S.C. Beam quality degradation of a higher order transverse mode beam due to spherical aberration of a lens. Appl. Opt. 2009, 48, 6202–6206. [Google Scholar] [CrossRef]
- Soileau, M.; Williams, W.; Van Stryland, E. Optical power limiter with picosecond response time. IEEE J. Quant. Electron. 1983, 19, 731–735. [Google Scholar] [CrossRef]
- Hermann, J. Beam propagation and optical power limiting with nonlinear media. JOSA B 1984, 1, 729–736. [Google Scholar] [CrossRef]
- Hermann, J. Simple model for a passive optical power limiter. Opt. Acta 1985, 32, 541–547. [Google Scholar] [CrossRef]
- Hermann, J. External self-focusing, self-bending and optical limiting with thin non-linear media. Opt. Quant. Electron. 1987, 19, 169–178. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.; Hagan, D.; Soileau, M.; Van Stryland, E. Simple analysis and geometric optimization of a passive optical limiter based on internal sel-action. Proc. SPIE 1989, 1105, 146–153. [Google Scholar]
- Bliss, E.S.; Hunt, J.T.; Renard, P.A.; Sommargren, G.E.; Weaver, H.J. Effects of nonlinear propagation on laser focusing properties. IEEE J. Quantum Electron. 1976, 12, 402–406. [Google Scholar] [CrossRef]
- Glaze, J.A. High energy glass lasers. Opt. Eng. 1976, 15, 152136. [Google Scholar] [CrossRef]
- Yu, B.; Chen, X.; Qiu, W.; Pu, J. Impact of nonlinear Kerr effect on the focusing performance of optical lens with high-intensity laser incidence. Appl. Sci. 2020, 10, 1945. [Google Scholar] [CrossRef]
- Kogelnik, H. Imaging of optical modes-resonators with internal lenses. Bell Syst. Tech. J. 1965, 44, 455–494. [Google Scholar] [CrossRef]
- Guo, P.; Schaller, R.D.; Ocola, L.E.; Diroll, B.T.; Ketterson, J.B.; Chang, R. Large optical nonlinearity of ITO nanorods for subpicosecond all-optical modulation of the full-visible spectrum. Nat. Commun. 2016, 7, 12892. [Google Scholar] [CrossRef]
- Pinçon-Roetzinger, N.; Prot, D.; Palpant, B.; Charron, E.; Debrus, S. Large optical Kerr effect in matrix-embedded metal nanoparticles. Mat. Sci. Eng. C 2002, 19, 51–54. [Google Scholar] [CrossRef]
- Genchi, D.; Dodici, F.; Cesca, T.; Mattei, G. Design of optical Kerr effect in multilayer hyperbolic metamaterials. Nanophotonics 2024, 13, 4523–4536. [Google Scholar] [CrossRef]
- Alam, M.Z.; Schulz, S.A.; Upham, J.; De Leon, I.; Boyd, R.W. Large optical nonlinearity of nanoantennas coupled to an epsilon-near-zero material. Nat. Photonics 2018, 12, 79–83. [Google Scholar] [CrossRef]
- Mafusire, C.; Forbes, A. Mean focal length of an aberrated lens. JOSA A 2011, 28, 1403–1409. [Google Scholar] [CrossRef]
- Leghmizi, S.; Hasnaoui, A.; Boubaha, B.; Aissani, A.; Ait-Ameur, K. On the effective ways for defining the effective focal length of a Kerr lens effect. Laser. Phys. 2017, 27, 106201. [Google Scholar] [CrossRef]
- Hall, D.R.; Jackson, P.E. The Physics and Technology of Laser Resonators; Institute of Physics Publishing: Bristol, UK, 1989; Chapter 9. [Google Scholar]
- Haddadi, S.; Bouzid, O.; Fromager, M.; Hasnaoui, A.; Harfouche, A.; Cagniot, E.; Forbes, A.; Aït-Ameur, K. Structured Laguerre-Gaussian beams for mitigation of spherical aberration in tightly focused regimes. J. Opt. 2018, 20, 045602. [Google Scholar] [CrossRef]
- Ait-Ameur, K.; Hasnaoui, A. Improving the longitudinal and radial forces of optical tweezers: A numerical study. Opt. Commun. 2024, 551, 130033. [Google Scholar] [CrossRef]
- Yoshida, A.; Asakura, T. Propagation and focusing of Gaussian laser beams beyond conventional diffraction limit. Opt. Commun. 1996, 123, 694–704. [Google Scholar] [CrossRef]
- Caumes, J.; Videau, L.; Rouyer, C.; Freysz, E. Direct measurement of wave-front distortion induced during secon-harmonic generation: Application to breakup-integral compensation. Opt. Lett. 2004, 29, 899–901. [Google Scholar] [CrossRef]
- Khoo, I.C.; Hou, J.Y.; Yan, T.H.; Michael, R.R.; Finn, G.M. Transverse self-phase modulation and bistability in the transmission of a laser beam through a nonlinear thin film. JOSA B 1987, 4, 886–891. [Google Scholar] [CrossRef]
- Marburger, J.H. Self-focusing: Theory. Prog. Quantum Electron. 1975, 4, 35–110. [Google Scholar] [CrossRef]
- Simmons, W.W.; Hunt, J.T.; Warren, W.E. Light propagation through large laser systems. IEEE J. Quantum Electron. 1981, 17, 1727–1744. [Google Scholar] [CrossRef]
- Simmons, W.; Speck, D.; Hunt, J. Argus laser system: Performance summary. Appl. Opt. 1978, 17, 999–1005. [Google Scholar] [CrossRef]
- Simmons, W.; Godwin, R. Nova laser fusion facility design, engineering, and assembly overview. Nucl. Technol. Fusion 1983, 4, 8–24. [Google Scholar] [CrossRef]
- Kuz’mina, N.B.; Rozanov, N.N.; Smirnov, V.A. On spatial filtration of apodized laser beams. Opt. Spectro. 1981, 51, 509–514. [Google Scholar]
- Deng, J.; Ji, X. Influence of atmospheric turbulence on the energy focusability of Gaussian beams with spherical aberration. J. Opt. 2014, 16, 055705. [Google Scholar] [CrossRef]
- Weberpais, J.; Dausinger, F.; Göbel, G.; Brener, B. The role of strong focusability on the welding process. In Proceedings of the ICALEO 2006: 25th International Congress on Laser Materials Processing and Laser Microfabrication, Scottsdale, AR, USA, 30 October–2 November 2006; paper#905. pp. 553–560. [Google Scholar] [CrossRef]
- Mahajan, V.N. Strehl ratio of a Gaussian beam. JOSA A 2005, 22, 1824–1833. [Google Scholar] [CrossRef]
- Jabczynski, J.K.; Kaskow, M.; Gorajek, L.; Kopczynski, K.; Zendzian, W. Modeling of the laser beam shape for high-poer applications. Opt. Eng. 2018, 57, 046107. [Google Scholar] [CrossRef]
- Aït-Ameur, K. The advantages and disadvantages of using structured high-order but single Laguerre-Gauss LGp0 laser beams. Photonics 2024, 11, 217. [Google Scholar] [CrossRef]
- Boyd, R.W.; Lukishova, S.G.; Shen, Y.R. Self-Focusing: Past and Present, Fundamentals and Prospects; Topics in Applied Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 114, Chapter 8. [Google Scholar]
- Campillo, A.J.; Fisher, R.A.; Hyer, R.C.; Shapiro, L. Streak camera investigation of the self-focusing onset in glass. Appl. Phys. Lett. 1974, 25, 408–410. [Google Scholar] [CrossRef]
- Maine, P.; Strickland, D.; Bado, P.; Pessot, M.; Mourou, G. Generation of ultrahigh peak power pulses by chirped pulse amplification. IEEE J. Quantum Electron. 1988, 24, 398–403. [Google Scholar] [CrossRef]
- Mourou, G. The ultrahigh-peak-power laser: Present and future. Appl. Phys. B 1997, 65, 205–211. [Google Scholar] [CrossRef]
- Mourou, G.; Fish, N.J.; Malkin, V.N.; Toroker, Z.; Khazanov, E.A.; Sergeev, A.M.; Tajima, T.; Le Garrec, B. Exawatt-Zettawatt pulse gerenation and applications. Opt. Commun. 2012, 285, 720–724. [Google Scholar] [CrossRef]
- Tutt, L.W.; Boggess, T.F. A review of optical limiting mechanisms and devices using organic, fullerenes, semiconductors and other materials. Prog. Quant. Electron. 1993, 17, 299–338. [Google Scholar] [CrossRef]
- Hasnaoui, A.; Ait-Ameur, K. Simple modelling of nonlinear losses induced by Kerr lensing effect. Appl. Phys. B 2021, 127, 100. [Google Scholar] [CrossRef]
- Hermann, J. Self-focusing effects and applications using thin nonlinear media. Int. J. Nonlinear Opt. Phys. Mat. 1992, 1, 541–561. [Google Scholar] [CrossRef]
- Hermann, J.; Wilson, P. Factors affecting optical limiting and scanning with thin nonlinear samples. Int. J. Nonlinear Opt. Phys. Mat. 1993, 2, 613–629. [Google Scholar] [CrossRef]
- Aït-Ameur, K.; Fromager, M.; Hasnaoui, A. Numerical simulation of an optical resonator for the generation of radial Laguerre-Gauss LGp0 modes. Appl. Sci. 2025, 15, 3331. [Google Scholar] [CrossRef]
- Mahajan, V.N. Optical Imaging and Aberrations; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Mahajan, V.N. Zernike circle polynomials and optical aberrations of system with circular pupils. Appl. Opt. 1994, 33, 8121–8124. [Google Scholar] [CrossRef]
- Mahajan, V.N. Zernike-Gauss polynomials and optical aberrations of systems with Gaussian pupils. Appl. Opt. 1995, 34, 8057–8059. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aït-Ameur, K.; Hasnaoui, A. Some Insights on Kerr Lensing Effects. Photonics 2025, 12, 596. https://doi.org/10.3390/photonics12060596
Aït-Ameur K, Hasnaoui A. Some Insights on Kerr Lensing Effects. Photonics. 2025; 12(6):596. https://doi.org/10.3390/photonics12060596
Chicago/Turabian StyleAït-Ameur, Kamel, and Abdelkrim Hasnaoui. 2025. "Some Insights on Kerr Lensing Effects" Photonics 12, no. 6: 596. https://doi.org/10.3390/photonics12060596
APA StyleAït-Ameur, K., & Hasnaoui, A. (2025). Some Insights on Kerr Lensing Effects. Photonics, 12(6), 596. https://doi.org/10.3390/photonics12060596





