Parametric Interaction-Induced Asymmetric Behaviors in a Coupled-Cavities Quantum Electrodynamics System
Abstract
1. Introduction
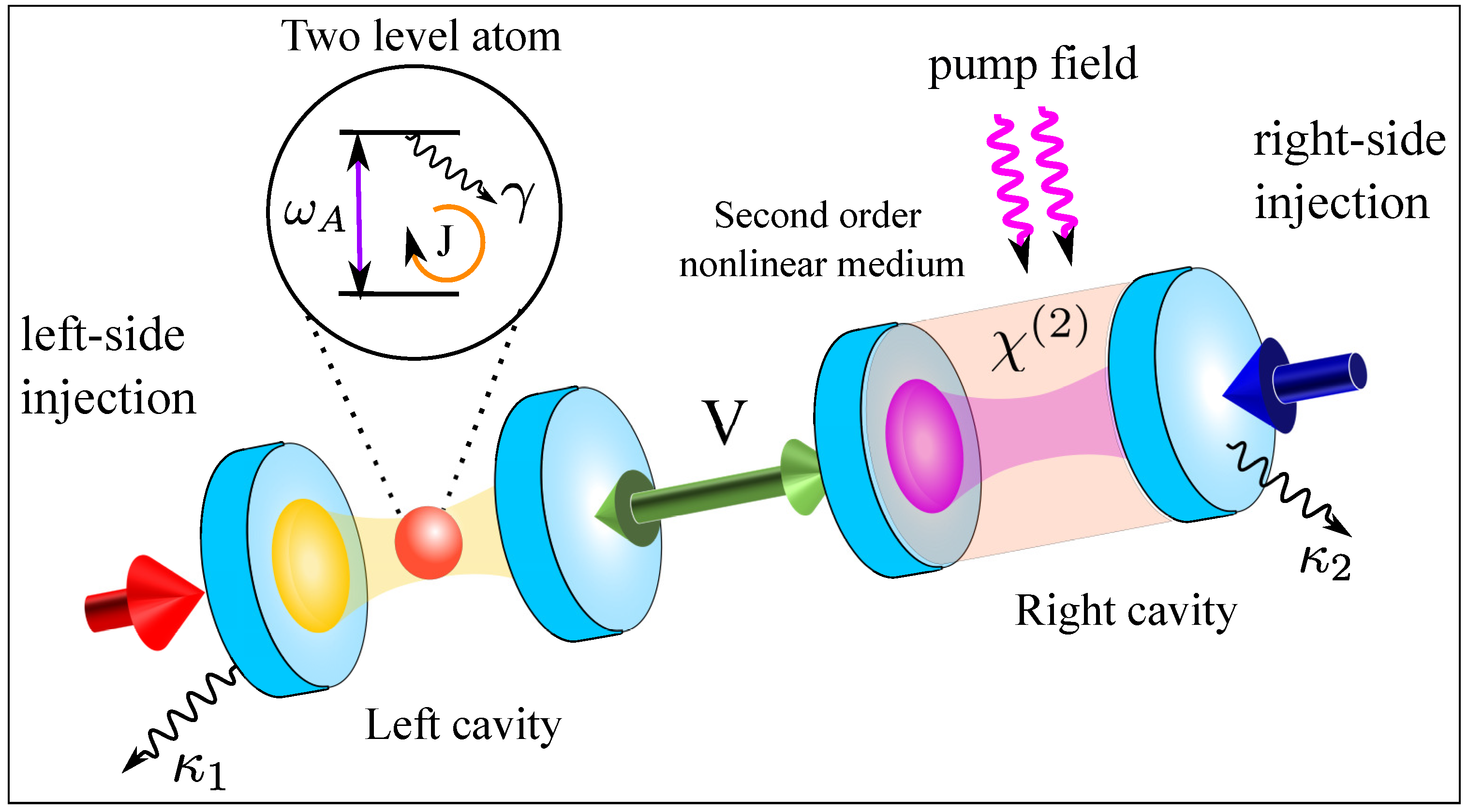
2. Model
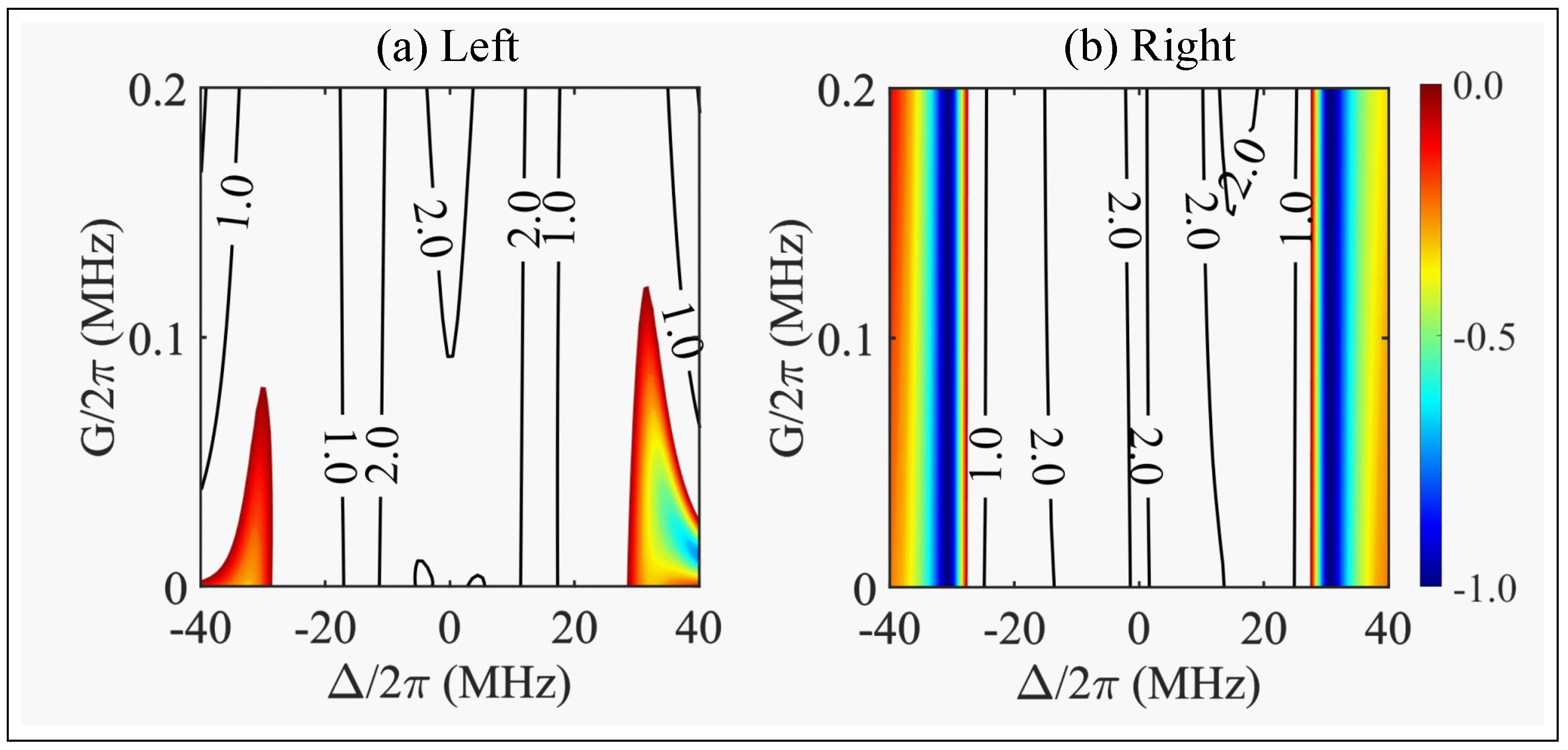
3. Classical Asymmetric Behavior
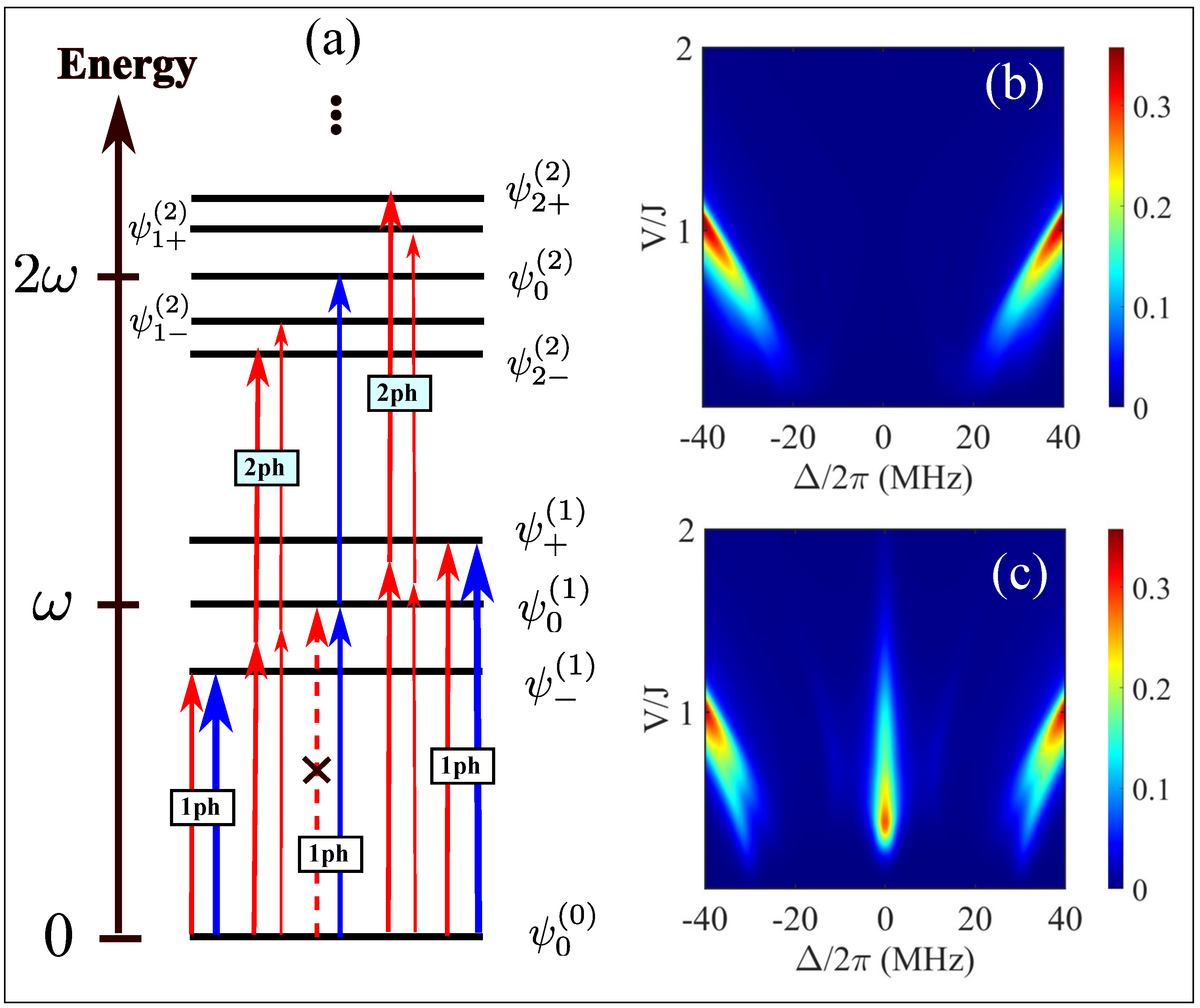
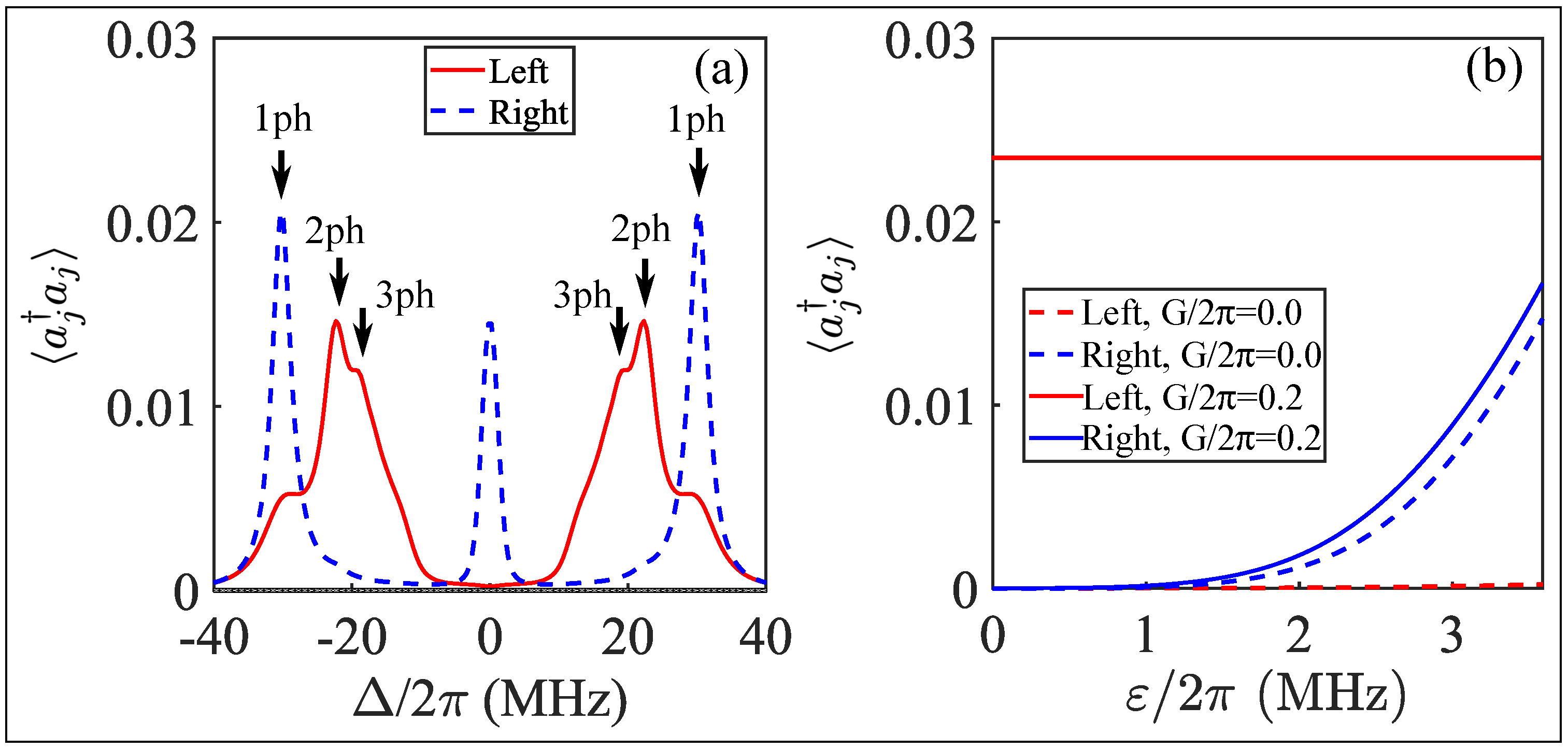
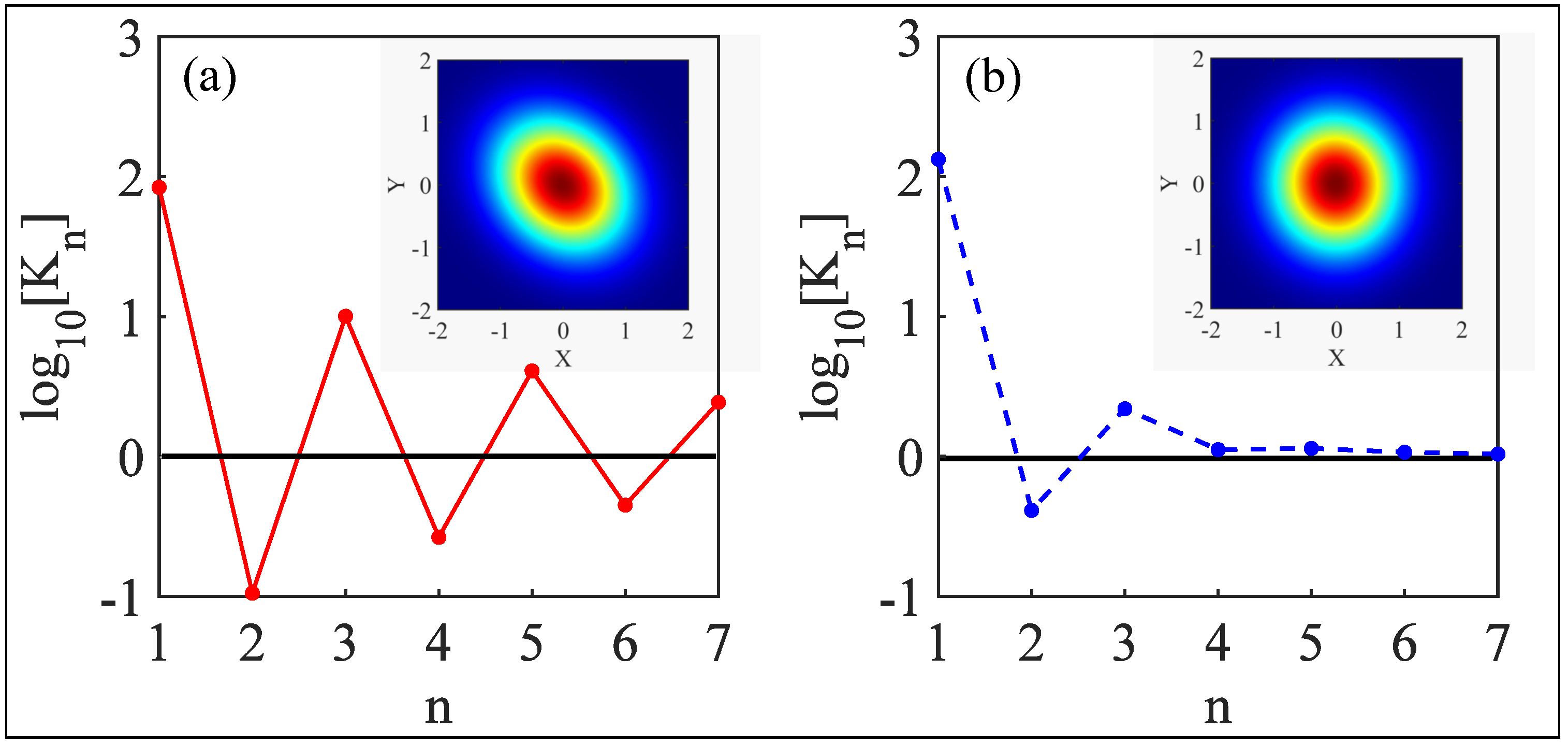
4. Quantum Asymmetric Behavior
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—And what is not—An optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Hu, Y.; Lin, G.; Niu, Y.; Xia, K.; Gong, J.; Gong, S. Thermal-motion-induced non-reciprocal quantum optical system. Nat. Photonics 2018, 12, 744–748. [Google Scholar] [CrossRef]
- Dong, M.; Xia, K.; Zhang, W.; Yu, Y.; Ye, Y.; Li, E.; Zeng, L.; Ding, D.; Shi, B.; Guo, G.; et al. All-optical reversible single-photon isolation at room temperature. Sci. Adv. 2021, 7, eabe8924. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, G.; Hu, Y.; Qi, Y.; Niu, Y.; Gong, S. Cavity-free circulator with low insertion loss using hot atoms. Phys. Rev. Appl. 2020, 14, 024032. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Y.C. Perfect nonreciprocity by loss engineering. Phys. Rev. A 2023, 107, 023703. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, J.; Zhu, Y. All-optical switching in a coupled cavity-atom system. Phys. Rev. A 2010, 82, 033808. [Google Scholar] [CrossRef]
- Zou, B.; Tan, Z.; Musa, M.; Zhu, Y. Interaction-free all-optical switching at low light intensities in a multiatom cavity-QED system. Phys. Rev. A 2014, 89, 023806. [Google Scholar] [CrossRef]
- Sohn, D.B.; Kim, S.; Bahl, G. Time-reversal symmetry breaking with acoustic pumping of nanophotonic circuits. Nat. Photonics 2018, 12, 91–97. [Google Scholar] [CrossRef]
- Sohn, D.B.; Bahl, G. Direction reconfigurable nonreciprocal acousto-optic modulator on chip. APL Photonics 2019, 4, 126103. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P.; Kimble, H.J.; Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 1997, 78, 3221. [Google Scholar] [CrossRef]
- Xia, K.; Lu, G.; Lin, G.; Cheng, Y.; Niu, Y.; Gong, S.; Twamley, J. Reversible nonmagnetic single-photon isolation using unbalanced quantum coupling. Phys. Rev. A 2014, 90, 043802. [Google Scholar] [CrossRef]
- Lu, J.; Zhou, L.; Kuang, L.M.; Nori, F. Single-photon router: Coherent control of multichannel scattering for single photons with quantum interferences. Phys. Rev. A 2014, 89, 013805. [Google Scholar] [CrossRef]
- Scheucher, M.; Hilico, A.; Will, E.; Volz, J.; Rauschenbeutel, A. Quantum optical circulator controlled by a single chirally coupled atom. Science 2016, 354, 1577–1580. [Google Scholar] [CrossRef]
- Gao, X.; Du, L.; Ma, N.; Zhou, X.; Wang, C.; Gao, P.P. Magneto-optical imaging characteristics of weld defects under alternating and rotating magnetic field excitation. Opt. Laser Technol. 2019, 112, 188–197. [Google Scholar] [CrossRef]
- Dong, C.; Shen, Z.; Zou, C.; Zhang, Y.; Fu, W.; Guo, G. Brillouin-scattering-induced transparency and non-reciprocal light storage. Nat. Commun. 2015, 6, 6193. [Google Scholar] [CrossRef]
- Merklein, M.; Stiller, B.; Vu, K.; Ma, P.; Madden, S.J.; Eggleton, B.J. On-chip broadband nonreciprocal light storage. Nanophotonics 2020, 10, 75–82. [Google Scholar] [CrossRef]
- Lau, H.; Clerk, A.A. Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing. Nat. Commun. 2018, 9, 4320. [Google Scholar] [CrossRef]
- Bao, L.; Qi, B.; Dong, D.; Nori, F. Fundamental limits for reciprocal and nonreciprocal non-Hermitian quantum sensing. Phys. Rev. A 2021, 103, 042418. [Google Scholar] [CrossRef]
- Aplet, L.; Carson, J.W. A Faraday effect optical isolator. Appl. Opt. 1964, 3, 544–545. [Google Scholar] [CrossRef]
- Chen, R.; Jiang, G.; Hao, Y.; Yang, J.; Wang, M.; Jiang, X. Enhancement of nonreciprocal phase shift by using nanoscale air gap. Opt. Lett. 2010, 35, 1335–1337. [Google Scholar] [CrossRef] [PubMed]
- Bi, L.; Hu, J.; Jiang, P.; Kim, D.H.; Dionne, G.F.; Kimerling, L.C.; Ross, C. On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat. Photonics 2011, 5, 758–762. [Google Scholar] [CrossRef]
- Yu, Z.; Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photonics 2009, 3, 91–94. [Google Scholar] [CrossRef]
- Yu, Z.; Fan, S. Optical isolation based on nonreciprocal phase shift induced by interband photonic transitions. Appl. Phys. Lett. 2009, 94, 171116. [Google Scholar] [CrossRef]
- Estep, N.A.; Sounas, D.L.; Soric, J.; Alu, A. Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nat. Phys. 2014, 10, 923–927. [Google Scholar] [CrossRef]
- Sounas, D.L.; Alù, A. Non-reciprocal photonics based on time modulation. Nat. Photonics 2017, 11, 774–783. [Google Scholar] [CrossRef]
- Fan, L.; Wang, J.; Varghese, L.T.; Shen, H.; Niu, B.; Xuan, Y.; Weiner, A.M.; Qi, M. An all-silicon passive optical diode. Science 2012, 335, 447–450. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators. Nat. Photonics 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Xia, K.; Nori, F.; Xiao, M. Cavity-free optical isolators and circulators using a chiral cross-Kerr nonlinearity. Phys. Rev. Lett. 2018, 121, 203602. [Google Scholar] [CrossRef]
- Li, E.; Ding, D.; Yu, Y.; Dong, M.; Zeng, L.; Zhang, W.; Ye, Y.; Wu, H.; Zhu, Z.; Gao, W.; et al. Experimental demonstration of cavity-free optical isolators and optical circulators. Phys. Rev. Res. 2020, 2, 033517. [Google Scholar] [CrossRef]
- Caloz, C.; Alu, A.; Tretyakov, S.; Sounas, D.; Achouri, K.; Deck-Léger, Z.L. Electromagnetic nonreciprocity. Phys. Rev. Appl. 2018, 10, 047001. [Google Scholar] [CrossRef]
- Schuster, I.; Kubanek, A.; Fuhrmanek, A.; Puppe, T.; Pinkse, P.W.; Murr, K.; Rempe, G. Nonlinear spectroscopy of photons bound to one atom. Nat. Phys. 2008, 4, 382–385. [Google Scholar] [CrossRef]
- Kato, S.; Aoki, T. Strong coupling between a trapped single atom and an all-fiber cavity. Phys. Rev. Lett. 2015, 115, 093603. [Google Scholar] [CrossRef] [PubMed]
- Hamsen, C.; Tolazzi, K.N.; Wilk, T.; Rempe, G. Two-photon blockade in an atom-driven cavity QED system. Phys. Rev. Lett. 2017, 118, 133604. [Google Scholar] [CrossRef]
- Yang, P.; Li, M.; Han, X.; He, H.; Li, G.; Zou, C.L.; Zhang, P.; Qian, Y.; Zhang, T. Non-Reciprocal Cavity Polariton with Atoms Strongly Coupled to Optical Cavity. Laser Photonics Rev. 2023, 17, 2200574. [Google Scholar] [CrossRef]
- Xia, X.; Xu, J.; Yang, Y. Controllable optical bistability of an asymmetric cavity containing a single two-level atom. Phys. Rev. A 2014, 90, 043857. [Google Scholar] [CrossRef]
- Yang, P.; Xia, X.; He, H.; Li, S.; Han, X.; Zhang, P.; Li, G.; Zhang, P.; Xu, J.; Yang, Y.; et al. Realization of nonlinear optical nonreciprocity on a few-photon level based on atoms strongly coupled to an asymmetric cavity. Phys. Rev. Lett. 2019, 123, 233604. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y. Optical nonreciprocity and optomechanical circulator in three-mode optomechanical systems. Phys. Rev. A 2015, 91, 053854. [Google Scholar] [CrossRef]
- Ruesink, F.; Miri, M.A.; Alu, A.; Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 2016, 7, 13662. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Y.; Chen, Y.; Zou, C.; Xiao, Y.; Zou, X.; Sun, F.; Guo, G.; Dong, C. Experimental realization of optomechanically induced non-reciprocity. Nat. Photonics 2016, 10, 657–661. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Wulf, M.; Peruzzo, M.; Kalaee, M.; Dieterle, P.; Painter, O.; Fink, J.M. Mechanical on-chip microwave circulator. Nat. Commun. 2017, 8, 953. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Miranowicz, A.; Liao, J.; Nori, F.; Jing, H. Nonreciprocal photon blockade. Phys. Rev. Lett. 2018, 121, 153601. [Google Scholar] [CrossRef]
- Li, B.; Huang, R.; Xu, X.; Miranowicz, A.; Jing, H. Nonreciprocal unconventional photon blockade in a spinning optomechanical system. Photonics Res. 2019, 7, 630–641. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, C.; Wang, H.; Qin, W.; Lü, X.Y.; Nori, F. Nonreciprocal Superradiant Phase Transitions and Multicriticality in a Cavity QED System. Phys. Rev. Lett. 2024, 132, 193602. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.; Zhang, X.; Xu, J.; Li, H.; Fu, Z.; Yang, Y. Giant nonreciprocal unconventional photon blockade with a single atom in an asymmetric cavity. Phys. Rev. A 2021, 104, 063713. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, X.; Xu, J.; Li, H.; Fu, Z.; Yang, Y. Improvement of nonreciprocal unconventional photon blockade by two asymmetrical arranged atoms embedded in a cavity. Opt. Express 2022, 30, 7907–7917. [Google Scholar] [CrossRef]
- White, D.H.; Kato, S.; Német, N.; Parkins, S.; Aoki, T. Cavity dark mode of distant coupled atom-cavity systems. Phys. Rev. Lett. 2019, 122, 253603. [Google Scholar] [CrossRef]
- Kato, S.; Német, N.; Senga, K.; Mizukami, S.; Huang, X.; Parkins, S.; Aoki, T. Observation of dressed states of distant atoms with delocalized photons in coupled-cavities quantum electrodynamics. Nat. Commun. 2019, 10, 1160. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Wu, Y.; Johansson, J.R.; Jing, H.; Zhang, J.; Nori, F. Squeezed optomechanics with phase-matched amplification and dissipation. Phys. Rev. Lett. 2015, 114, 093602. [Google Scholar] [CrossRef]
- Tang, L.; Tang, J.; Chen, M.; Nori, F.; Xiao, M.; Xia, K. Quantum squeezing induced optical nonreciprocity. Phys. Rev. Lett. 2022, 128, 083604. [Google Scholar] [CrossRef]
- Shen, C.P.; Chen, J.Q.; Pan, X.F.; Ren, Y.M.; Dong, X.L.; Hei, X.L.; Qiao, Y.F.; Li, P.B. Tunable nonreciprocal photon correlations induced by directional quantum squeezing. Phys. Rev. A 2023, 108, 023716. [Google Scholar] [CrossRef]
- Wu, S.-X.; Bai, C.-H.; Li, G.; Yu, C.-S.; Zhang, T. Quantum squeezing-induced quantum entanglement and EPR steering in a coupled optomechanical system. Opt. Express 2024, 32, 260–274. [Google Scholar] [CrossRef]
- Qin, W.; Miranowicz, A.; Li, P.B.; Lu, X.Y.; You, J.Q.; Nori, F. Exponentially enhanced light-matter interaction, cooperativities, and steady-state entanglement using parametric amplification. Phys. Rev. Lett. 2018, 120, 093601. [Google Scholar] [CrossRef] [PubMed]
- Azuma, K.; Economou, S.E.; Elkouss, D.; Hilaire, P.; Jiang, L.; Lo, H.-K.; Tzitrin, I. Quantum repeaters: From quantum networks to the quantum internet. Rev. Mod. Phys. 2023, 95, 045006. [Google Scholar] [CrossRef]
- Li, C.L.; Yin, H.L.; Chen, Z.B. Asynchronous quantum repeater using multiple quantum memory. Rep. Prog. Phys. 2024, 87, 127901. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.J.; Ping, L.L.; Yang, Y.P.; Agarwal, G.S. Squeezed light induced symmetry breaking superradiant phase transition. Phys. Rev. Lett. 2020, 124, 073602. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Kono, S.; Masuyama, Y.; Ishikawa, T.; Tabuchi, Y.; Yamazaki, R.; Usami, K.; Koshino, K.; Nakamura, Y. Nonclassical photon number distribution in a superconducting cavity under a squeezed drive. Phys. Rev. Lett. 2017, 119, 023602. [Google Scholar] [CrossRef]
- Innocenti, L.; Lachman, L.; Filip, R. Nonclassicality detection from few Fock-state probabilities. NPJ Quantum Inf. 2022, 8, 30. [Google Scholar] [CrossRef]
- Kelly, J.F.; Samoc, A.; Samoc, M.; Krausz, E.R.; Willis, A.C. Anisotropy of second-order nonlinear optical susceptibilities of arsenic triiodide–sulfur addition complex: AsI3·3S8. Opt. Commun. 2006, 264, 49–54. [Google Scholar] [CrossRef]
- Xue, B.; Lin, J.; Hou, J.; Zhu, Y.; Ma, R.; Chen, X.; Cheng, Y.; Ge, L.; Wan, W. Dual-color coherent perfect absorber. Phys. Rev. Lett. 2025, 134, 013802. [Google Scholar] [CrossRef]
- Hou, J.; Zhu, J.; Ma, R.; Xue, B.; Zhu, Y.; Lin, J.; Jiang, X.; Zheng, Y.; Chen, X. Enhanced frequency conversion in parity-time symmetry line. Phys. Rev. Lett. 2024, 132, 256902. [Google Scholar] [CrossRef] [PubMed]
- He, G.S. Second-order nonlinear (three-wave) frequency mixing. In Nonlinear Optics and Photonics; Oxford Academic: Oxford, UK, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Guo, D.; Zhu, C.; Xu, J. Parametric Interaction-Induced Asymmetric Behaviors in a Coupled-Cavities Quantum Electrodynamics System. Photonics 2025, 12, 563. https://doi.org/10.3390/photonics12060563
Ma X, Guo D, Zhu C, Xu J. Parametric Interaction-Induced Asymmetric Behaviors in a Coupled-Cavities Quantum Electrodynamics System. Photonics. 2025; 12(6):563. https://doi.org/10.3390/photonics12060563
Chicago/Turabian StyleMa, Xu, Dexi Guo, Chengjie Zhu, and Jingping Xu. 2025. "Parametric Interaction-Induced Asymmetric Behaviors in a Coupled-Cavities Quantum Electrodynamics System" Photonics 12, no. 6: 563. https://doi.org/10.3390/photonics12060563
APA StyleMa, X., Guo, D., Zhu, C., & Xu, J. (2025). Parametric Interaction-Induced Asymmetric Behaviors in a Coupled-Cavities Quantum Electrodynamics System. Photonics, 12(6), 563. https://doi.org/10.3390/photonics12060563



