Complete Dispersion Measurement for Few-Mode Fibers with Large Mode Numbers Enabled by Multiplexer-Assisted S2
Abstract
1. Introduction
2. Principle of MMUX-Assisted S2 Technique
3. Alignment for Optical Paths of MMUX’s Pigtails
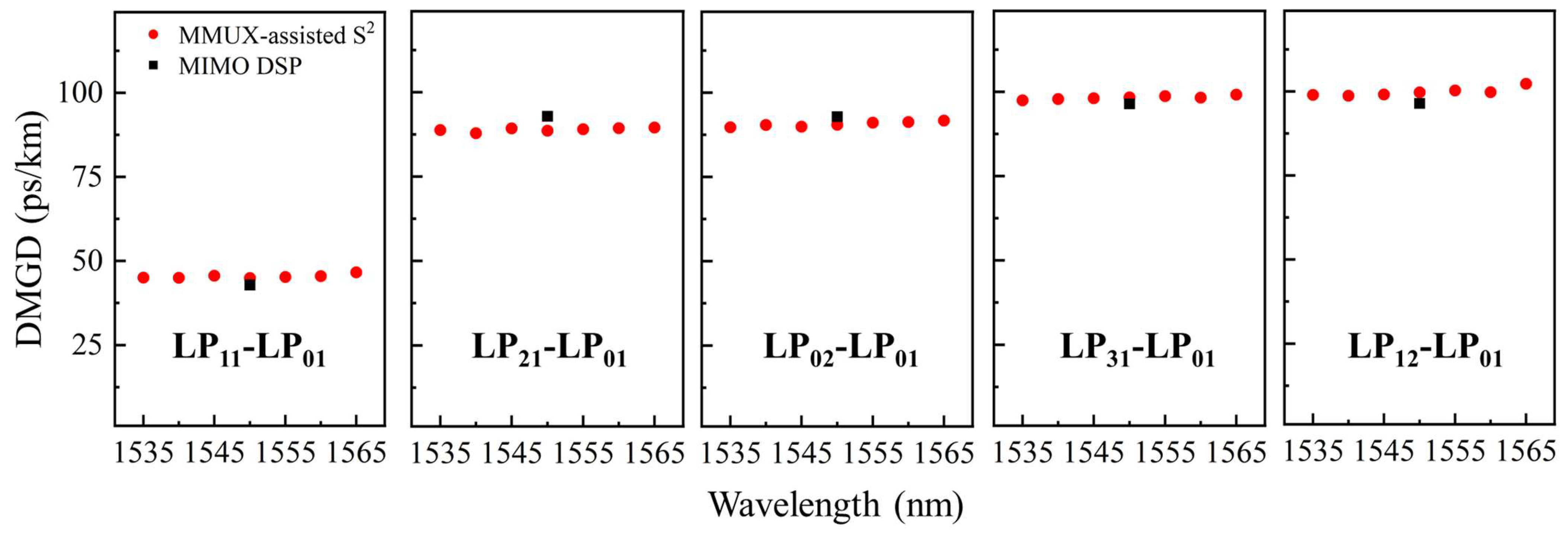
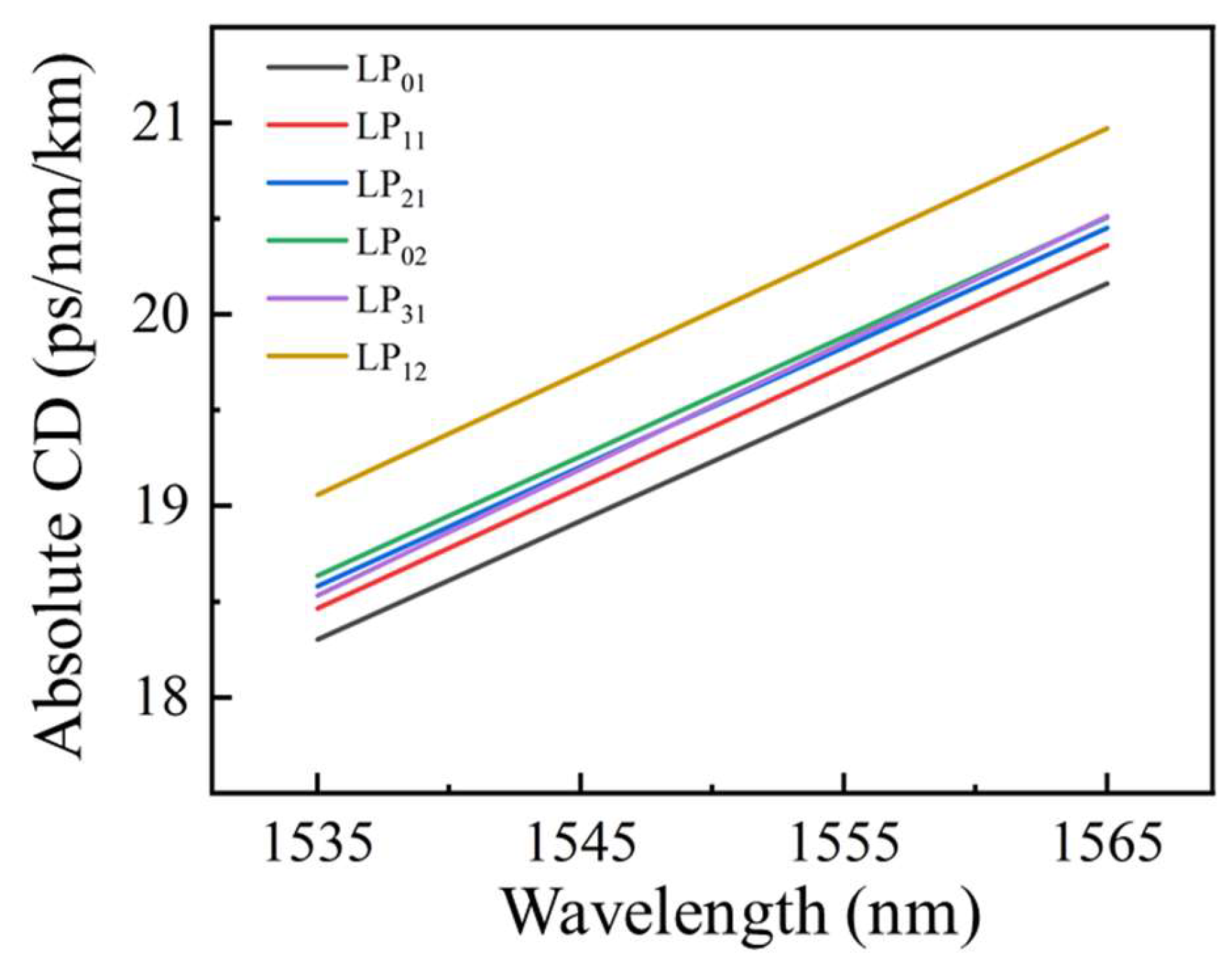
4. Measurement for the DMGDs and Absolute CDs of a 6-LP FMF
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-Division Multiplexing in Optical Fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-Division Multiplexing: The next Frontier in Optical Communication. Adv. Opt. Photonics 2014, 6, 413–487. [Google Scholar] [CrossRef]
- Van Uden, R.G.H.; Correa, R.A.; Lopez, E.A.; Huijskens, F.M.; Xia, C.; Li, G.; Schülzgen, A.; De Waardt, H.; Koonen, A.M.J.; Okonkwo, C.M. Ultra-High-Density Spatial Division Multiplexing with a Few-Mode Multicore Fibre. Nat. Photonics 2014, 8, 865–870. [Google Scholar] [CrossRef]
- Li, A.; Chen, X.; Al Amin, A.; Ye, J.; Shieh, W. Space-Division Multiplexed High-Speed Superchannel Transmission Over Few-Mode Fiber. J. Light. Technol. 2012, 30, 3953–3964. [Google Scholar] [CrossRef]
- Beppu, S.; Igarashi, K.; Kikuta, M.; Soma, D.; Nagai, T.; Saito, Y.; Takahashi, H.; Tsuritani, T.; Morita, I.; Suzuki, M. Weakly Coupled 10-Mode-Division Multiplexed Transmission over 48-Km Few-Mode Fibers with Real-Time Coherent MIMO Receivers. Opt. Express 2020, 28, 19655–19668. [Google Scholar] [CrossRef]
- Shibahara, K.; Hoshi, M.; Miyamoto, Y. 10-Spatial-Mode 1300-Km Transmission Over 6-LP Graded Index Few-Mode Fiber With 36-Ns Modal Dispersion. J. Light. Technol. 2024, 42, 1257–1264. [Google Scholar] [CrossRef]
- Rademacher, G.; Puttnam, B.J.; Luis, R.S.; Galdino, L.; Maruyama, R.; Aikawa, K.; Awaji, Y.; Furukawa, H. Space-Division Multiplexed Transmission in the S-Band over 55 Km Few-Mode Fibers. Opt. Express 2020, 28, 27037–27043. [Google Scholar] [CrossRef]
- Dehdashti Jahromi, H. Performance Analysis of Transmissive Modified Cladding Optical Fibre Sensors. IET Optoelectron. 2022, 16, 63–71. [Google Scholar] [CrossRef]
- Ho, K.-P.; Kahn, J.M. Linear Propagation Effects in Mode-Division Multiplexing Systems. J. Light. Technol. 2014, 32, 614–628. [Google Scholar] [CrossRef]
- Liu, H.; Wen, H.; Huang, B.; Correa, R.A.; Sillard, P.; Chen, H.; Li, Z.; Li, G. Reducing Group Delay Spread Using Uniform Long-Period Gratings. Sci. Rep. 2018, 8, 3882. [Google Scholar] [CrossRef]
- Zhou, X.; Urata, R.; Liu, H. Beyond 1 Tb/s Intra-Data Center Interconnect Technology: IM-DD OR Coherent? J. Light. Technol. 2020, 38, 475–484. [Google Scholar] [CrossRef]
- Tauber, D.; Smith, B.; Lewis, D.; Muhigana, E.; Nissov, M.; Govan, D.; Hu, J.; Zhou, Y.; Wang, J.; Jiang, W.-J.; et al. Role of Coherent Systems in the Next DCI Generation. J. Light. Technol. 2023, 41, 1139–1151. [Google Scholar] [CrossRef]
- Cheng, J.; Pedersen, M.E.V.; Wang, K.; Xu, C.; Grüner-Nielsen, L.; Jakobsen, D. Time-Domain Multimode Dispersion Measurement in a Higher-Order-Mode Fiber. Opt. Lett. 2012, 37, 347–349. [Google Scholar] [CrossRef]
- Gabet, R.; Hamel, P.; Jaouen, Y.; Obaton, A.-F.; Lanticq, V.; Debarge, G. Versatile Characterization of Specialty Fibers Using the Phase-Sensitive Optical Low-Coherence Reflectometry Technique. J. Light. Technol. 2009, 27, 3021–3033. [Google Scholar] [CrossRef]
- Gabet, R.; Le Cren, E.; Jin, C.; Gadonna, M.; Ung, B.; Sillard, P.; Nguyen, H.G.; Jaouen, Y.; Thual, M.; LaRochelle, S. Complete Dispersion Characterization of Few Mode Fibers by OLCI Technique. J. Light. Technol. 2015, 33, 1155–1160. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Feng, Y.; Li, Z. Modal Dispersion Characterization of Few-Mode Fiber Based on Electrical Spectral Interferometry with Optical Frequency Comb. Opt. Fiber Technol. 2017, 38, 75–79. [Google Scholar] [CrossRef]
- Yang, Z.; Mi, R.; Zhao, N.; Zhang, L.; Li, G. Simultaneous Measurement of Chromatic and Modal Dispersion in FMFs Using Microwave Photonic Techniques. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Veronese, R.; Galtarossa, A.; Palmieri, L. Distributed Characterization of Few-Mode Fibers Based on Optical Frequency Domain Reflectometry. J. Light. Technol. 2020, 38, 4843–4849. [Google Scholar] [CrossRef]
- Veronese, R.; Cappelletti, M.; Fontaine, N.K.; Chen, H.; Mazur, M.; Ryf, R.; Santagiustina, M.; Galtarossa, A.; Palmieri, L. Mode Selective Distributed Characterization of Few-Mode Fibers. J. Light. Technol. 2025, 43, 3982–3988. [Google Scholar] [CrossRef]
- Nicholson, J.W.; Yablon, A.D.; Ramachandran, S.; Ghalmi, S. Spatially and Spectrally Resolved Imaging of Modal Content in Large-Mode-Area Fibers. Opt. Express 2008, 16, 7233–7243. [Google Scholar] [CrossRef]
- Blin, S.; Nguyen, D.M.; Nguyen, T.M.; Provino, L.; Thual, M.; Chartier, T. Simple Modal Analysis Method for Multi-Mode Fibers. In Proceedings of the 2009 35th European Conference on Optical Communication, Vienna, Austria; 2009. [Google Scholar]
- Sillard, P.; Molin, D.; Bigot-Astruc, M.; De Jongh, K.; Achten, F.; Velazquez-Benitez, A.M.; Amezcua-Correa, R.; Okonkwo, C.M. Low-Differential-Mode-Group-Delay 9-LP-Mode Fiber. J. Light. Technol. 2016, 34, 425–430. [Google Scholar] [CrossRef]
- Boccuzzi, K.A.; Marciante, J.R. Limitations of the S2 (Spatially and Spectrally Resolved) Imaging Technique. OSA Contin. 2021, 4, 3276–3286. [Google Scholar] [CrossRef]
- Rubio, E.A.L. Modified S2 Imaging Modal Decomposition Technique in Few Mode Fibers. Matemática 2020, 18. Available online: https://www.revistas.espol.edu.ec/index.php/matematica/article/view/694 (accessed on 23 May 2025).
- Yu, J.; Tan, F.; Yu, C. Few-Mode Fiber Characterization System Based on the Spatially and Spectrally Imaging Technique. Sensors 2022, 22, 1809. [Google Scholar] [CrossRef]
- Yu, J.; Tan, F.; Yu, C. Mode Dispersion Measurement of Few-Mode Fiber Utilizing S2 Technique. In Proceedings of the 2021 Opto-Electronics and Communications Conference (OECC), Hong Kong, China, 3–7 July 2021; pp. 1–3. [Google Scholar]
- Gray, D.R.; Petrovich, M.N.; Sandoghchi, S.R.; Wheeler, N.V.; Baddela, N.K.; Jasion, G.T.; Bradley, T.; Richardson, D.J.; Poletti, F. Real-Time Modal Analysis via Wavelength-Swept Spatial and Spectral (S2) Imaging. IEEE Photonics Technol. Lett. 2016, 28, 1034–1037. [Google Scholar] [CrossRef]
- Newkirk, A.V.; Antonio-Lopez, J.E.; Anderson, J.; Alvarez-Aguirre, R.; Eznaveh, Z.S.; Lopez-Galmiche, G.; Amezcua-Correa, R.; Schülzgen, A. Modal Analysis of Antiresonant Hollow Core Fibers Using S2 Imaging. Opt. Lett. 2016, 41, 3277–3280. [Google Scholar] [CrossRef]
- Leandro, L.; Grüner-Nielsen, L.; Rottwitt, K. Mode Resolved Bend-Loss Analysis in Few-Mode Fibers Using Spatially and Spectrally Resolved Imaging. Opt. Lett. 2015, 40, 4583–4586. [Google Scholar] [CrossRef]
- Gausmann, S.; Antonio-Lopez, J.E.; Anderson, J.; Wittek, S.; Eznaveh, S.E.; Jang, H.-J.; Habib, M.S.; Cook, J.; Richardson, M.C.; Correa, R.A.; et al. S2 Measurements Showing Suppression of Higher Order Modes in Confined Rare Earth Doped Large Core Fibers. J. Light. Technol. 2020, 38, 1953–1958. [Google Scholar] [CrossRef]
- Huang, B.; Chen, H.; Fontaine, N.K.; Jin, C.; Shang, K.; Ryf, R.; Essiambre, R.-J.; Ung, B.; Messaddeq, Y.; LaRochelle, S.; et al. Spatially and Spectrally Resolved Gain Characterization of Space-Division Multiplexing Amplifiers With Coherent Swept-Wavelength Reflectometry. J. Light. Technol. 2017, 35, 741–747. [Google Scholar] [CrossRef]
- Nicholson, J.W.; Meng, L.; Fini, J.M.; Windeler, R.S.; DeSantolo, A.; Monberg, E.; DiMarcello, F.; Dulashko, Y.; Hassan, M.; Ortiz, R. Measuring Higher-Order Modes in a Low-Loss, Hollow-Core, Photonic-Bandgap Fiber. Opt. Express 2012, 20, 20494–20505. [Google Scholar] [CrossRef]
- Jensen, R.V.; Grüner-Nielsen, L.; Wong, N.H.L.; Sun, Y.; Jung, Y.; Richardson, D.J. Demonstration of a 9 LP-Mode Transmission Fiber with Low DMD and Loss. In Proceedings of the Optical Fiber Communication Conference; OSA: Los Angeles, CA, USA, 2015; p. W2A.34. [Google Scholar]
- Nguyen, D.M.; Blin, S.; Nguyen, T.N.; Le, S.D.; Provino, L.; Thual, M.; Chartier, T. Modal Decomposition Technique for Multimode Fibers. Appl. Opt. 2012, 51, 450–456. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, L.; Jin, C.; Messaddeq, Y.; LaRochelle, S. Microwave Interferometric Technique for Characterizing Few Mode Fibers. IEEE Photonics Technol. Lett. 2014, 26, 1695–1698. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Yang, Z.; Lv, Z.; Wang, H.; Liu, Y.; Huang, Z.; Zhang, L. Complete Dispersion Measurement for Few-Mode Fibers with Large Mode Numbers Enabled by Multiplexer-Assisted S2. Photonics 2025, 12, 561. https://doi.org/10.3390/photonics12060561
Zhao B, Yang Z, Lv Z, Wang H, Liu Y, Huang Z, Zhang L. Complete Dispersion Measurement for Few-Mode Fibers with Large Mode Numbers Enabled by Multiplexer-Assisted S2. Photonics. 2025; 12(6):561. https://doi.org/10.3390/photonics12060561
Chicago/Turabian StyleZhao, Bingyi, Zhiqun Yang, Zhongze Lv, Huihui Wang, Yaping Liu, Zhanhua Huang, and Lin Zhang. 2025. "Complete Dispersion Measurement for Few-Mode Fibers with Large Mode Numbers Enabled by Multiplexer-Assisted S2" Photonics 12, no. 6: 561. https://doi.org/10.3390/photonics12060561
APA StyleZhao, B., Yang, Z., Lv, Z., Wang, H., Liu, Y., Huang, Z., & Zhang, L. (2025). Complete Dispersion Measurement for Few-Mode Fibers with Large Mode Numbers Enabled by Multiplexer-Assisted S2. Photonics, 12(6), 561. https://doi.org/10.3390/photonics12060561





