High-Capacity Near-Infrared Optical Vortex Sorting and Detection by Nonlinear Dammann Vortex Grating
Abstract
1. Introduction
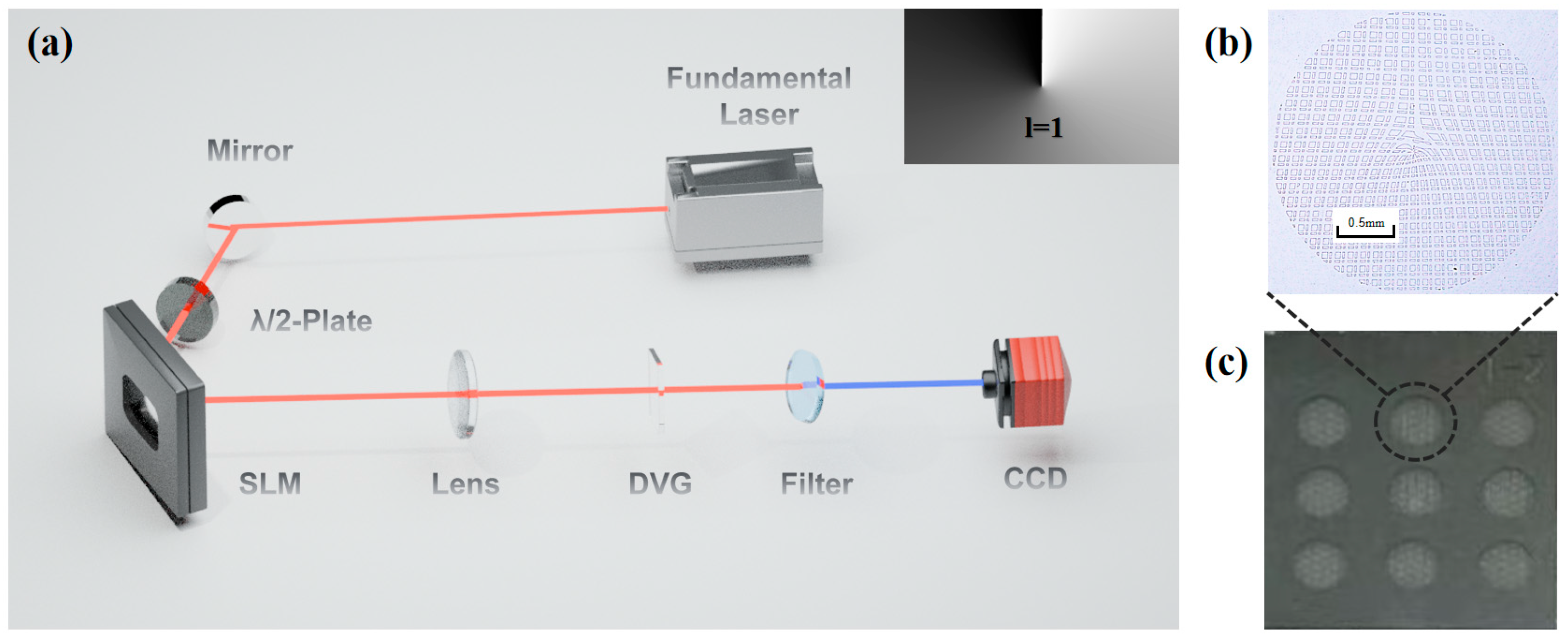
2. Materials and Methods
3. Experiment
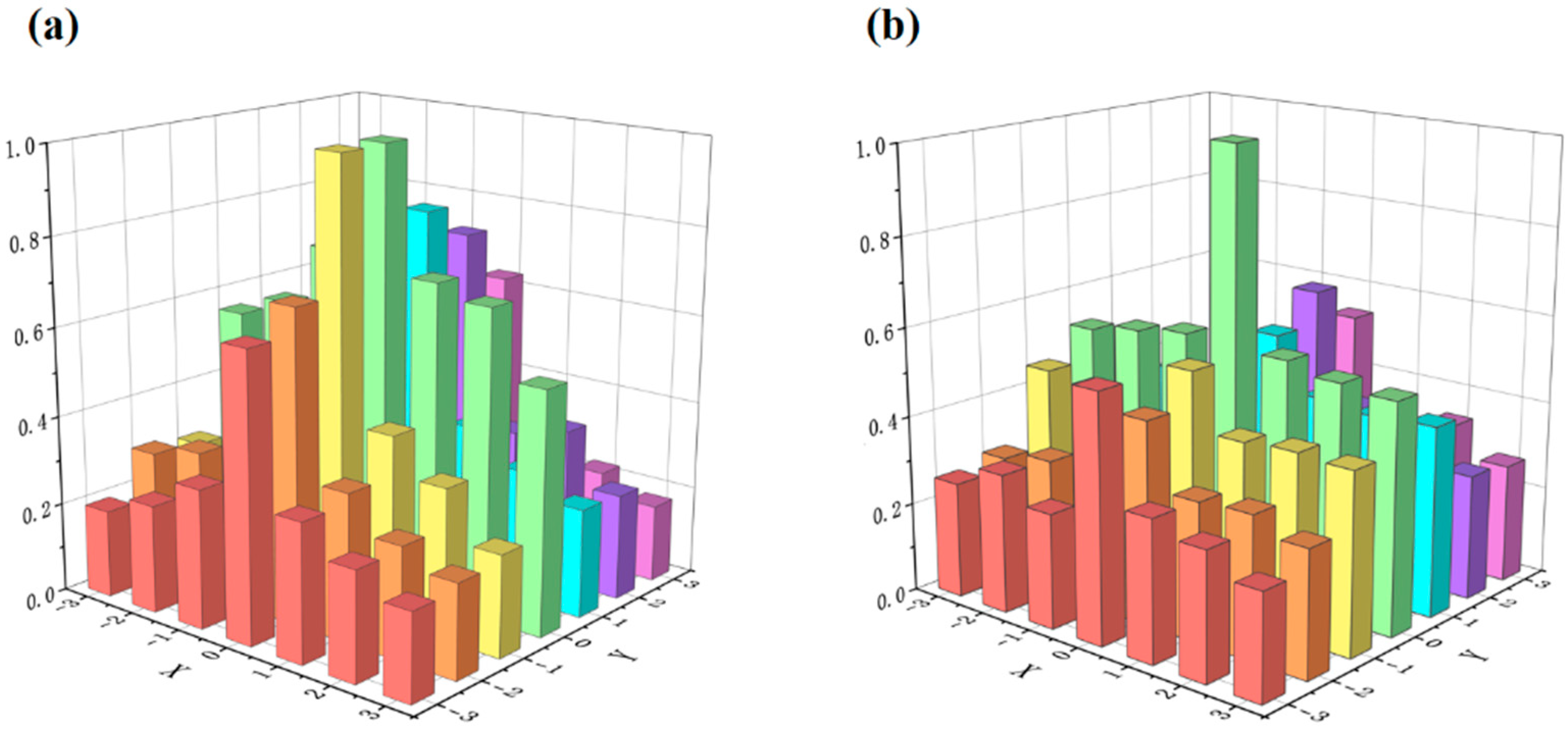
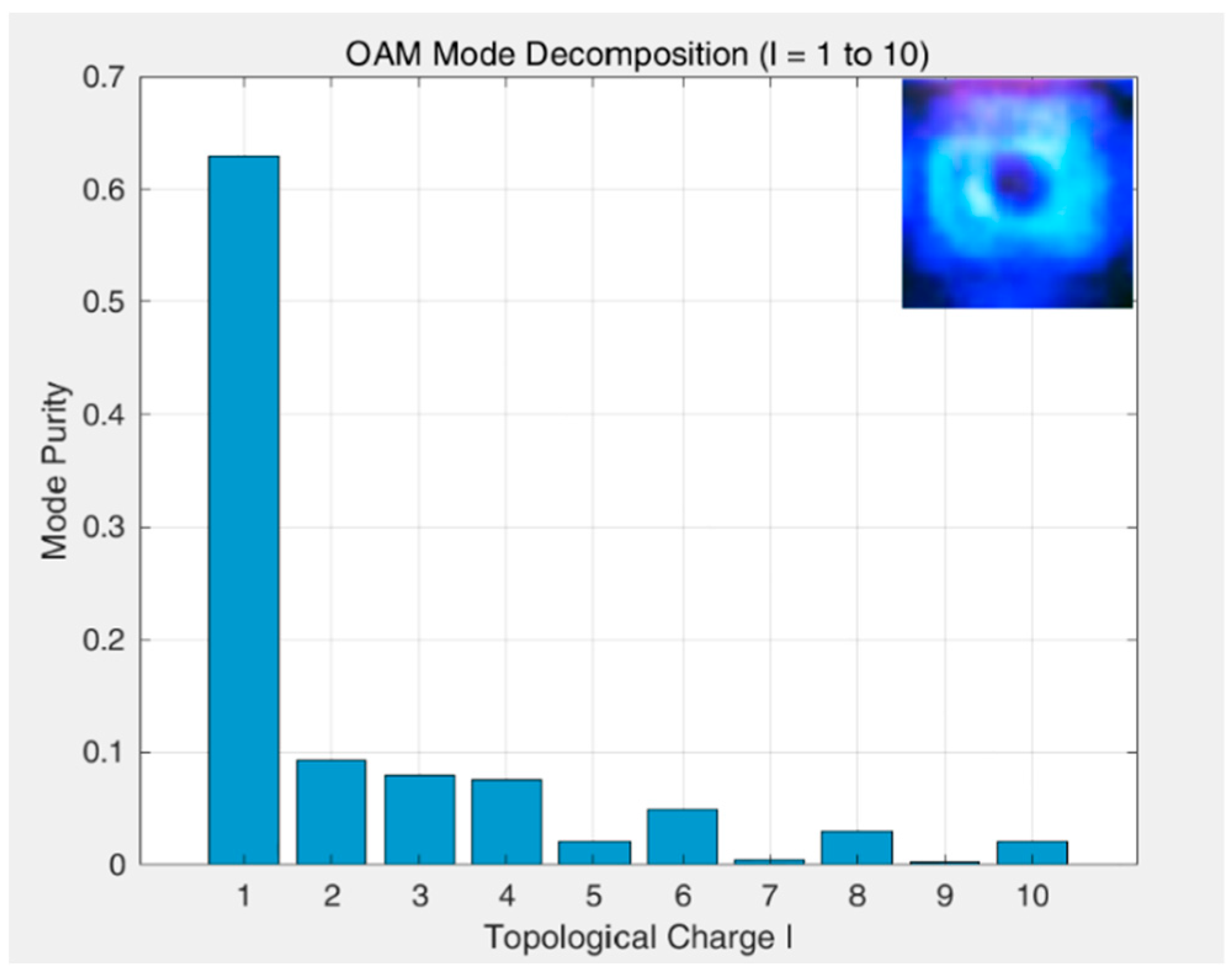
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Mei, H.; Gao, J.; Xu, L.; Jiang, H.; Liu, Y. Optical free induction decay emission carrying orbit angular momentum from ionic nitrogen enabled by multiple-photon resonance. Chin. Opt. Lett. 2024, 22, 063201. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Gbur, G.; Tyson, R.K. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J. Opt. Soc. Am. A 2007, 25, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: Generation and detection of orbital angular momentum. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Du, J.; Quan, Z.; Li, K.; Wang, J. Optical vortex array: Generation and applications. Chin. Opt. Lett. 2024, 22, 020011. [Google Scholar] [CrossRef]
- Wang, X.-L.; Luo, Y.-H.; Huang, H.-L.; Chen, M.-C.; Su, Z.-E.; Liu, C.; Chen, C.; Li, W.; Fang, Y.-Q.; Jiang, X. 18-qubit entanglement with six photons’ three degrees of freedom. Phys. Rev. Lett. 2018, 120, 260502. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Cao, H.; Yuan, R.; Xu, C.; Zhang, Y.; Hu, W. Broadband decoupled spin and orbital angular momentum detection via programming dual-twist reactive mesogens. Opt. Lett. 2021, 46, 5751–5754. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Parkin, S.; Knüner, G.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Measurement of the total optical angular momentum transfer in optical tweezers. Opt. Express 2006, 14, 6963–6970. [Google Scholar] [CrossRef]
- Pang, F.; Xiang, L.; Liu, H.; Zhang, L.; Wen, J.; Zeng, X.; Wang, T. Review on fiber-optic vortices and their sensing applications. J. Light. Technol. 2021, 39, 3740–3750. [Google Scholar] [CrossRef]
- Saitoh, K.; Hasegawa, Y.; Hirakawa, K.; Tanaka, N.; Uchida, M. Measuring the orbital angular momentum of electron vortex beams using a forked grating. Phys. Rev. Lett. 2013, 111, 074801. [Google Scholar] [CrossRef]
- Mohagheghian, M.; Ghavami Sabouri, S. Switching the sign of the topological charge of vortex beams via changing the fork grating resolution. Opt. Laser Technol. 2023, 157, 108641. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, C.; Lu, Y.; Wu, J.; Zhu, L.; Jia, W. Square lattices of quasi-perfect optical vortices generated by two-dimensional encoding continuous-phase gratings. Opt. Lett. 2015, 40, 2513–2516. [Google Scholar] [CrossRef]
- Ren, Y.; Qiu, S.; Liu, T.; Liu, Z. Compound motion detection based on OAM interferometry. Nanophotonics 2022, 11, 1127–1135. [Google Scholar] [CrossRef]
- Gavril’Eva, K.; Mermoul, A.; Sevryugin, A.; Shubenkova, E.; Touil, M.; Tursunov, I.; Efremova, E.; Venediktov, V.Y. Detection of optical vortices using cyclic, rotational and reversal shearing interferometers. Opt. Laser Technol. 2019, 113, 374–378. [Google Scholar] [CrossRef]
- Shao, G.-H.; Wu, Z.-J.; Chen, J.-H.; Xu, F.; Lu, Y.-Q. Nonlinear frequency conversion of fields with orbital angular momentum using quasi-phase-matching. Phys. Rev. A 2013, 88, 063827. [Google Scholar] [CrossRef]
- Jiang, H.; Liang, H.; Luo, R.; Chen, X.; Chen, Y.; Lin, Q. Nonlinear frequency conversion in one dimensional lithium niobate photonic crystal nanocavities. Appl. Phys. Lett. 2018, 113, 5039948. [Google Scholar] [CrossRef]
- Liu, H.; Li, H.; Zheng, Y.; Chen, X. Nonlinear frequency conversion and manipulation of vector beams. Opt. Lett. 2018, 43, 5981–5984. [Google Scholar] [CrossRef] [PubMed]
- Fang, B.; Li, H.; Zhu, S.; Li, T. Second-harmonic generation and manipulation in lithium niobate slab waveguides by grating metasurfaces. Photonics Res. 2020, 8, 391850. [Google Scholar] [CrossRef]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photonics 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Bloch, N.V.; Shemer, K.; Shapira, A.; Shiloh, R.; Juwiler, I.; Arie, A. Twisting light by nonlinear photonic crystals. Phys. Rev. Lett. 2012, 108, 233902. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, L. Numerical study of Dammann array illuminators. Appl. Opt. 1995, 34, 5961–5969. [Google Scholar] [CrossRef]
- Zhang, N.; Yuan, X.; Burge, R. Extending the detection range of optical vortices by Dammann vortex gratings. Opt. Lett. 2010, 35, 3495–3497. [Google Scholar] [CrossRef]
- Wang, H.; Wei, D.; Xu, X.; Wang, M.; Cui, G.; Lu, Y.; Zhang, Y.; Xiao, M. Controllable generation of second-harmonic vortex beams through nonlinear supercell grating. Appl. Phys. Lett. 2018, 113, 5050423. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.; Zhang, W.; Ma, C.Q.; Chen, H.X.; Xiong, Y.F.; Yuan, R.; Tang, J.; Chen, P.; Hu, W. Visible and Online Detection of Near-Infrared Optical Vortices via Nonlinear Photonic Crystals. Adv. Opt. Mater. 2022, 10, 2101098. [Google Scholar] [CrossRef]
- Ge, S.-J.; Chen, P.; Ma, L.-L.; Liu, Z.; Zheng, Z.-G.; Shen, D.; Hu, W.; Lu, Y.-Q. Optical array generator based on blue phase liquid crystal Dammann grating. Opt. Mater. Express 2016, 6, 001087. [Google Scholar] [CrossRef]
- Mendlovic, D.; Ouzieli, I.; Kiryuschev, I.; Marom, E. Two-dimensional wavelet transform achieved by computer-generated multireference matched filter and Dammann grating. Appl. Opt. 1995, 34, 8213–8219. [Google Scholar] [CrossRef]
- Glickman, Y.; Winebrand, E.; Arie, A.; Rosenman, G. Electron-beam-induced domain poling in LiNbO3 for two-dimensional nonlinear frequency conversion. Appl. Phys. Lett. 2006, 88, 2159089. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, R.; Liu, Q.; Hu, X.; Xu, T.; Sheng, Y. Direct detection of near-infrared fractional vortex beam. Infrared Phys. Technol. 2025, 148, 105893. [Google Scholar] [CrossRef]
- Saltiel, S.M.; Neshev, D.N.; Krolikowski, W.; Arie, A.; Bang, O.; Kivshar, Y.S. Multiorder nonlinear diffraction in frequency doubling processes. Opt. Lett. 2009, 34, 848–850. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.; Kong, Q.; Wang, W.; Kalinowski, K.; Krolikowski, W. Theoretical investigations of nonlinear Raman–Nath diffraction in the frequency doubling process. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 055401. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhao, R.; Liu, Q.; Sheng, Y.; Xu, T. High-Capacity Near-Infrared Optical Vortex Sorting and Detection by Nonlinear Dammann Vortex Grating. Photonics 2025, 12, 532. https://doi.org/10.3390/photonics12060532
Zhao H, Zhao R, Liu Q, Sheng Y, Xu T. High-Capacity Near-Infrared Optical Vortex Sorting and Detection by Nonlinear Dammann Vortex Grating. Photonics. 2025; 12(6):532. https://doi.org/10.3390/photonics12060532
Chicago/Turabian StyleZhao, Hui, Ruwei Zhao, Qilu Liu, Yan Sheng, and Tianxiang Xu. 2025. "High-Capacity Near-Infrared Optical Vortex Sorting and Detection by Nonlinear Dammann Vortex Grating" Photonics 12, no. 6: 532. https://doi.org/10.3390/photonics12060532
APA StyleZhao, H., Zhao, R., Liu, Q., Sheng, Y., & Xu, T. (2025). High-Capacity Near-Infrared Optical Vortex Sorting and Detection by Nonlinear Dammann Vortex Grating. Photonics, 12(6), 532. https://doi.org/10.3390/photonics12060532




