Electrically Stimulated and Frequency-Tunable Photonic Tonic Spiking Neuron Based on a DFB-LD Under Optical Feedback
Abstract
1. Introduction
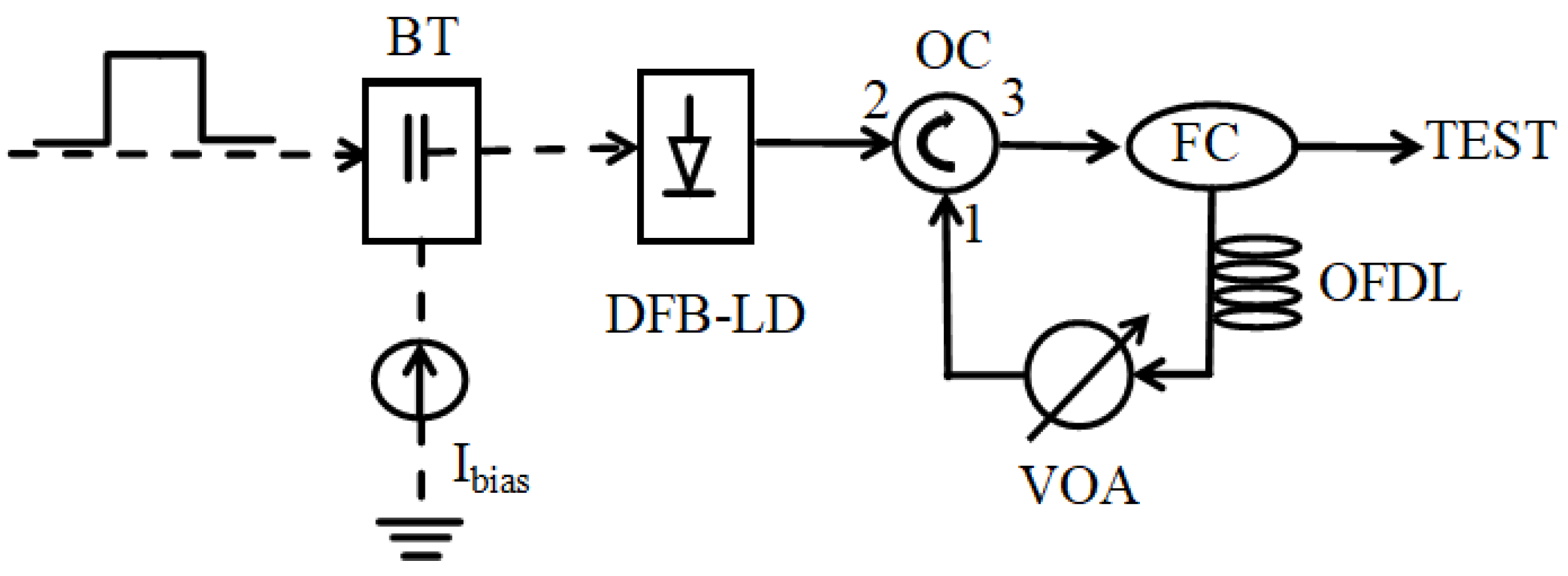
2. Methods and Theory
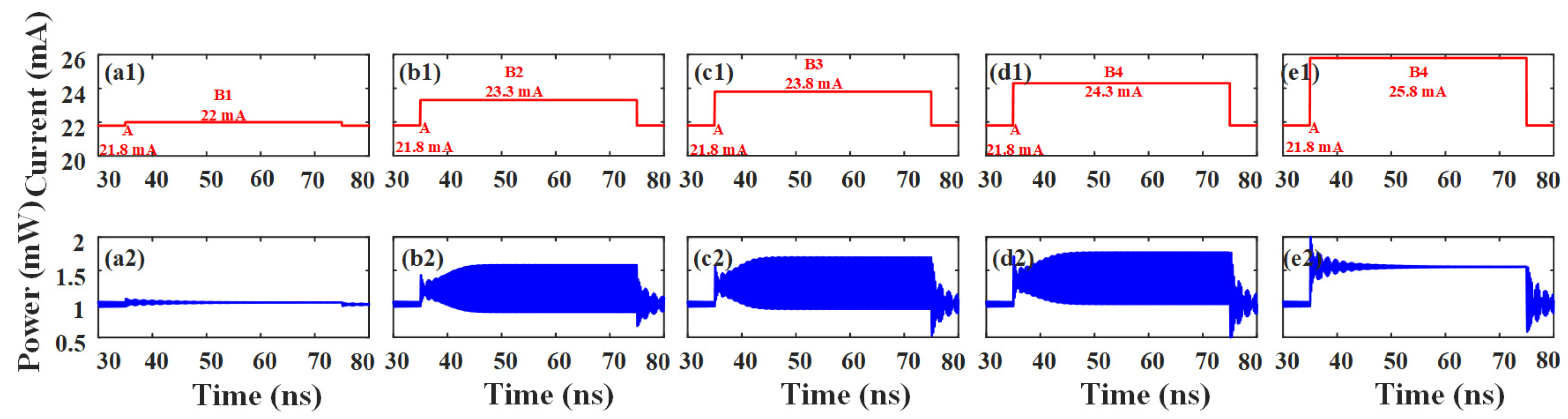
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashtiani, F.; Geers, A.J.; Aflatouni, F. An on-chip photonic deep neural network for image classification. Nature 2022, 606, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Shastri, B.J.; Tait, A.N.; Ferreira De Lima, T.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Wei, C.; Yu, Y.; Wang, Z.; Jiang, L.; Zeng, Z.; Ye, J.; Zou, X.; Pan, W.; Xie, X.; Yan, L. Ultra-wideband waveguide-coupled photodiodes heterogeneously integrated on a thin-film lithium niobate platform. Light Adv. Manuf. 2023, 4, 30. [Google Scholar] [CrossRef]
- Brunner, D.; Soriano, M.C.; Mirasso, C.R.; Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 2013, 4, 1364. [Google Scholar] [CrossRef]
- Shen, Y.W.; Li, R.Q.; Liu, G.T.; Yu, J.; He, X.; Yi, L.; Wang, C. Deep photonic reservoir computing recurrent network. Optica 2023, 10, 1745–1751. [Google Scholar] [CrossRef]
- Robertson, J.; Wade, E.; Kopp, Y.; Bueno, J.; Hurtado, A. Toward neuromorphic photonic networks of ultrafast spiking laser neurons. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 7700715. [Google Scholar] [CrossRef]
- Ni, M.; Lin, X.; Tang, X.; Gao, Z.; Xiao, L.; Wang, J.; Ma, F.; Zheng, Q.; Deng, T. Image transmission based on spiking dynamics of electrically controlled VCSEL-SA neuron. Photonics 2021, 8, 238. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Cui, C.; Li, R.; Li, Y.; Liu, B.; Wu, C. Simulating the spiking response of VCSEL-based optical spiking neuron. Opt. Commun. 2018, 407, 327–332. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, W.; Fu, B.; He, Z. Frequency-switched photonic spiking neurons. Opt. Express 2022, 30, 21599–21608. [Google Scholar] [CrossRef]
- Temgoua, L.P.G.; Mbe, J.H.T.; Woafo, P. Dynamical behaviors of vertical cavity surface-emitting lasers with an embedded saturable absorber subjected to an on-off keying (OOK) current modulation. Phys. Scr. 2023, 98, 085250. [Google Scholar] [CrossRef]
- Hejda, M.; Vaughan, M.; Henning, I.; Al-Seyab, R.; Hurtado, A.; Adams, M. Spiking behaviour in laterally-coupled pairs of VCSELs with applications in neuromorphic photonics. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1700210. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Zhang, Y.H.; Guo, X.X.; Wen, A.J.; Hao, Y. Photonic Generation of Neuron-Like Dynamics Using VCSELs Subject to Double Polarized Optical Injection. J. Light. Technol. 2018, 36, 4227–4234. [Google Scholar] [CrossRef]
- Auge, D.; Hille, J.; Mueller, E.; Knoll, A. A survey of encoding techniques for signal processing in spiking neural networks. Neural Process. Lett. 2021, 53, 4693–4710. [Google Scholar] [CrossRef]
- Li, J.; Peng, L.; Li, S.S.; Zhang, L.; Ding, X.; Jiang, L.; Zou, X.; Pan, W.; Yan, L. Photonic spiking neuron based on a single VCSEL with optical feedback. Opt. Laser Technol. 2025, 181, 111941. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Wen, A.; Pan, W. Emulation of spiking response and spiking frequency property in VCSEL-based photonic neuron. IEEE Photonics J. 2016, 8, 1504109. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Shi, Y.; Guo, X.; Zhang, Y.; Wang, H.; Zheng, D.; Song, Z.; Han, Y.; Gao, S.; Zhao, S.; et al. Hardware-algorithm collaborative computing with photonic spiking neuron chip based on an integrated Fabry-Perot laser with a saturable absorber. Optica 2023, 10, 162–171. [Google Scholar] [CrossRef]
- Zheng, D.Z.; Xiang, S.Y.; Li, N.Q.; Zhang, Y.H.; Guo, X.X.; Zhu, X.J. The hybrid photonic convolutional neural networks based on SOA and FP-SA. J. Light. Technol. 2024, 42, 8819–8825. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, N.; Zhang, Y.; Li, A.; Xiong, H.; Hu, G.; Cao, Y.; Qiu, K. On-chip spiking neural networks based on add-drop ring microresonators and electrically reconfigurable phase-change material photonic switches. Photonics Res. 2024, 12, 755–766. [Google Scholar] [CrossRef]
- Gouda, M.; Abreu, S.; Bienstman, P. Surrogate gradient learning in spiking networks trained on event-based cytometry dataset. Opt. Express 2024, 32, 16260–16272. [Google Scholar] [CrossRef]
- Peng, H.T.; Nahmias, M.A.; de Lima, T.F.; Tait, A.N.; Shastri, B.J. Neuromorphic photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 6101715. [Google Scholar] [CrossRef]
- Peng, H.T.; Angelatos, G.; De Lima, T.F.; Nahmias, M.A.; Tait, A.N.; Abbaslou, S.; Shastri, B.J.; Prucnal, P.R. Temporal information processing with an integrated laser neuron. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 5100209. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Shi, Y.C.; Zhang, Y.H.; Guo, X.X.; Zheng, L. Photonic integrated neuro-synaptic core for convolutional spiking neural network. Opto-Electron. Adv. 2023, 6, 230140. [Google Scholar] [CrossRef]
- Selmi, F.; Braive, R.; Beaudoin, G.; Sagnes, I.; Kuszelewicz, R.; Erneux, T.; Barbay, S. Spike latency and response properties of an excitable micropillar laser. Phys. Rev. E 2016, 94, 042219. [Google Scholar] [CrossRef] [PubMed]
- Pammi, V.A.; Alfaro-Bittner, K.; Clerc, M.G.; Barbay, S. Photonic computing with single and coupled spiking micropillar lasers. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500307. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Rosado, A.; Esquivias, I. Complete optical field reconstruction and determination of linewidth enhancement factor in gain-switched semiconductor lasers using the Gerchberg-Saxton algorithm. Opt. Laser Technol. 2025, 181, 111731. [Google Scholar] [CrossRef]
- Hamedi, S.; Jahromi, H.D.; Lotfiani, A. Artificial intelligence-aided nanoplasmonic biosensor modeling. Eng. Appl. Artif. Intell. 2023, 118, 105646. [Google Scholar] [CrossRef]
- Jahromi, H.D.; Hamedi, S. Artificial intelligence approach for calculating electronic and optical properties of nanocomposites. Mater. Res. Bull. 2021, 141, 111371. [Google Scholar] [CrossRef]
- Hamedi, S.; Jahromi, H.D. Performance analysis of all-optical logical gate using artificial neural network. Expert Syst. Appl. 2021, 178, 115029. [Google Scholar] [CrossRef]



| Parameters | Descriptions | Values | Units |
|---|---|---|---|
| Γ | Optical confinement factor | 0.06 | - |
| Transparency carrier density | 1.3 × 1024 | m−3 | |
| Volume of active region | 1.53 × 10−17 | m3 | |
| A | Non-radiative recombination coefficient | 2.8 × 108 | s−1 |
| B | Spontaneous recombination coefficient | 1.5 × 10−16 | m3s−1 |
| C | Auger recombination coefficient | 9.0 × 10−41 | m6s−1 |
| Differential gain | 4.38 × 10−20 | m2 | |
| Photon lifetime | 2.17 | ps | |
| Linewidth enhancement factor | 3 | - | |
| Nonlinear gain coefficient | 1.97 × 10−23 | m3 | |
| Product of the differential quantum efficiency and coupling efficiency | 0.17 | - |
| Refs. | Years | Photonic Spiking Neurons | Control Methods | Tuning Ranges (GHz) |
|---|---|---|---|---|
| [15] | 2016 | VCSELs | pump current and optical injection | ~4 |
| [12] | 2018 | VCSELs | optical injection | ~1 |
| [22] | 2023 | DFB-SA | gain current | ~2 |
| [14] | 2025 | VCSELs | optical feedback | ~2 |
| This work | 2025 | DFB-LD | optical feedback and electrical pulse | ~5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; He, C.; Wang, Q.; Ou, P.; Wu, Z.; Xia, G. Electrically Stimulated and Frequency-Tunable Photonic Tonic Spiking Neuron Based on a DFB-LD Under Optical Feedback. Photonics 2025, 12, 510. https://doi.org/10.3390/photonics12050510
Lei Z, He C, Wang Q, Ou P, Wu Z, Xia G. Electrically Stimulated and Frequency-Tunable Photonic Tonic Spiking Neuron Based on a DFB-LD Under Optical Feedback. Photonics. 2025; 12(5):510. https://doi.org/10.3390/photonics12050510
Chicago/Turabian StyleLei, Zhiqiang, Chaotao He, Qiupin Wang, Pu Ou, Zhengmao Wu, and Guangqiong Xia. 2025. "Electrically Stimulated and Frequency-Tunable Photonic Tonic Spiking Neuron Based on a DFB-LD Under Optical Feedback" Photonics 12, no. 5: 510. https://doi.org/10.3390/photonics12050510
APA StyleLei, Z., He, C., Wang, Q., Ou, P., Wu, Z., & Xia, G. (2025). Electrically Stimulated and Frequency-Tunable Photonic Tonic Spiking Neuron Based on a DFB-LD Under Optical Feedback. Photonics, 12(5), 510. https://doi.org/10.3390/photonics12050510





