Strong Coupling Based on Quasibound States in the Continuum of Nanograting Metasurfaces in Near-Infrared Region
Abstract
1. Introduction
2. Results and Discussion
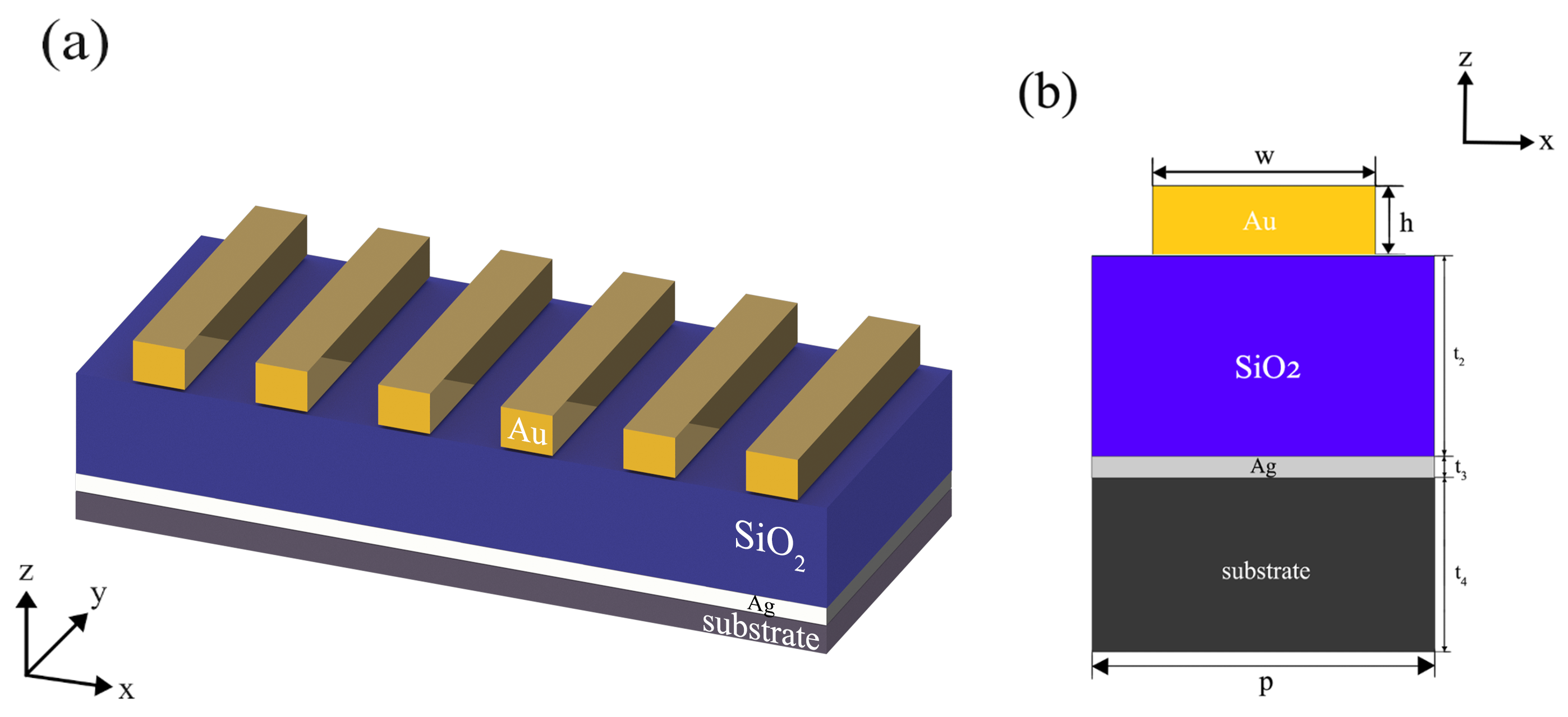
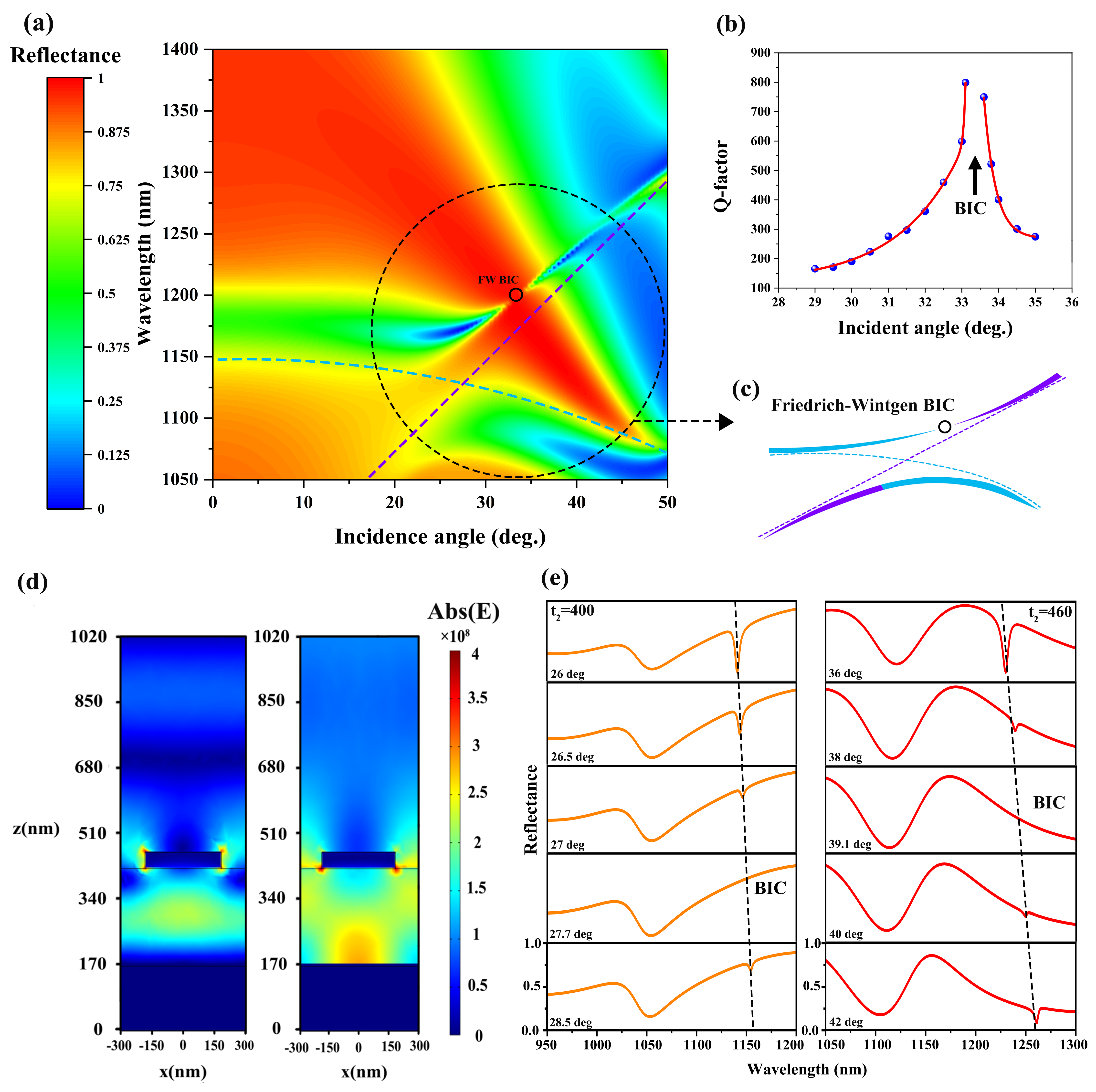
2.1. Friedrich–Wintgen Bound States in the Continuum in Nanograting Metasurfaces
2.2. Near-Infrared Strong Coupling Between qBICs Nanograting Metasurface and MoTe2
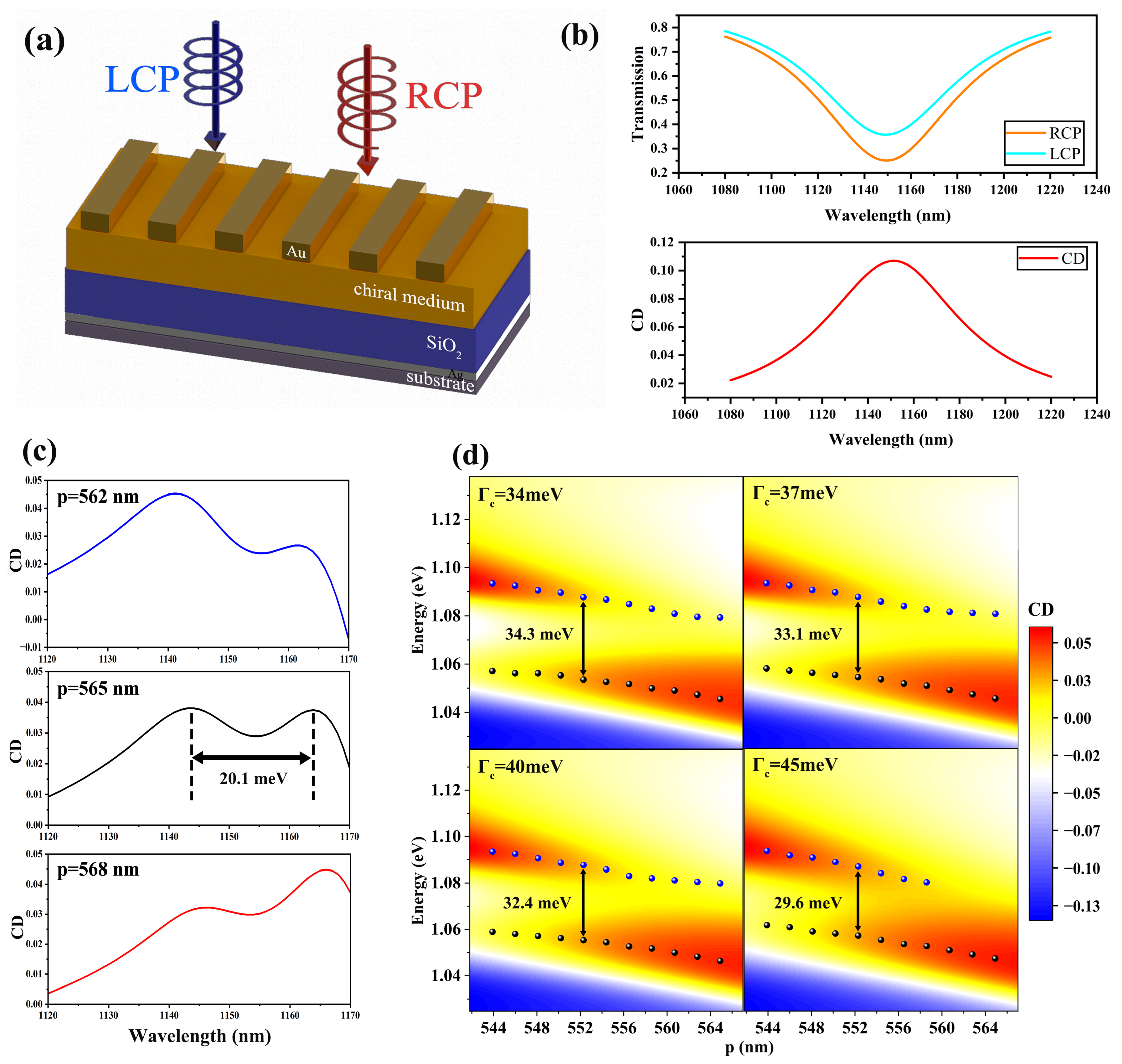
2.3. Near-Infrared Chiral Strong Coupling Between qBIC and Chiral Medium
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santhosh, K.; Bitton, O.; Chuntonov, L.; Haran, G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 2016, 7, ncomms11823. [Google Scholar] [CrossRef] [PubMed]
- Törmä, P.; Barnes, W.L. Strong coupling between surface plasmon polaritons and emitters: A review. Rep. Prog. Phys. 2014, 78, 013901. [Google Scholar] [CrossRef]
- Li, S.; Fang, Y.; Wang, J. Control of light–matter interactions in two-dimensional materials with nanoparticle-on-mirror structures. Opto-Electron. Sci. 2024, 3, 240011. [Google Scholar] [CrossRef]
- Kasprzak, J.; Richard, M.; Kundermann, S.; Baas, A.; Jeambrun, P.; Keeling, J.M.J.; Marchetti, F.; Szymańska, M.; André, R.; Staehli, J.; et al. Bose–Einstein condensation of exciton polaritons. Nature 2006, 443, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Lerario, G.; Fieramosca, A.; Barachati, F.; Ballarini, D.; Daskalakis, K.S.; Dominici, L.; De Giorgi, M.; Maier, S.A.; Gigli, G.; Kéna-Cohen, S.; et al. Room-temperature superfluidity in a polariton condensate. Nat. Phys. 2017, 13, 837–841. [Google Scholar] [CrossRef]
- Ghosh, S.; Liew, T.C. Quantum computing with exciton-polariton condensates. Npj Quantum Inf. 2020, 6, 16–21. [Google Scholar] [CrossRef]
- Kleemann, M.E.; Chikkaraddy, R.; Alexeev, E.M.; Kos, D.; Carnegie, C.; Deacon, W.; de Pury, A.C.; Große, C.; de Nijs, B.; Mertens, J.; et al. Strong-coupling of WSe2 in ultra-compact plasmonic nanocavities at room temperature. Nat. Commun. 2017, 8, 1296–1302. [Google Scholar] [CrossRef]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 86, 115409. [Google Scholar] [CrossRef]
- Qin, M.; Duan, J.; Xiao, S.; Liu, W.; Yu, T.; Wang, T.; Liao, Q. Strong coupling between excitons and quasibound states in the continuum in bulk transition metal dichalcogenides. Phys. Rev. B 2023, 107, 045417. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, M.; Xu, H.; Wei, G.; Li, H.; Gao, W.; Liu, J.; Wu, F. Photonic spin-controlled self-hybridized exciton-polaritons in WS 2 metasurfaces driven by chiral quasibound states in the continuum. Phys. Rev. B 2024, 109, 125201. [Google Scholar] [CrossRef]
- Xie, P.; Ding, Q.; Liang, Z.; Shen, S.; Yue, L.; Zhang, H.; Wang, W. Cavity-assisted boosting of self-hybridization between excitons and photonic bound states in the continuum in multilayers of transition metal dichalcogenides. Phys. Rev. B 2023, 107, 075415. [Google Scholar] [CrossRef]
- Al-Ani, I.A.; As’ Ham, K.; Huang, L.; Miroshnichenko, A.E.; Hattori, H.T. Enhanced strong coupling of TMDC monolayers by bound state in the continuum. Laser Photonics Rev. 2021, 15, 2100240. [Google Scholar] [CrossRef]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 2019, 1, 016001. [Google Scholar] [CrossRef]
- Huang, L.; Xu, L.; Rahmani, M.; Neshev, D.; Miroshnichenko, A.E. Pushing the limit of high-Q mode of a single dielectric nanocavity. Adv. Photonics 2021, 3, 016004. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- von Neumann, J.; Wigner, E.P. Über merkwürdige diskrete Eigenwerte. In The Collected Works of Eugene Paul Wigner: Part A: The Scientific Papers; Springer: Berlin/Heidelberg, Germany, 1993; pp. 291–293. [Google Scholar]
- Longhi, S. Bound states in the continuum in a single-level Fano-Anderson model. Eur. Phys. J. B 2007, 57, 45–51. [Google Scholar] [CrossRef]
- Marinica, D.; Borisov, A.; Shabanov, S. Bound states in the continuum in photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F. Bound states in the continuum in photonic waveguides inspired by defects. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 78, 075105. [Google Scholar] [CrossRef]
- Yamanouchi, K.; Shibayama, K. Propagation and amplification of Rayleigh waves and piezoelectric leaky surface waves in LiNbO3. J. Appl. Phys. 1972, 43, 856–862. [Google Scholar] [CrossRef]
- Lyapina, A.; Maksimov, D.; Pilipchuk, A.; Sadreev, A. Bound states in the continuum in open acoustic resonators. J. Fluid Mech. 2015, 780, 370–387. [Google Scholar] [CrossRef]
- McIver, M. An example of non-uniqueness in the two-dimensional linear water wave problem. J. Fluid Mech. 1996, 315, 257–266. [Google Scholar] [CrossRef]
- McIver, M. Trapped modes supported by submerged obstacles. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2000, 456, 1851–1860. [Google Scholar] [CrossRef]
- Benabid, F.; Knight, J.C.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 2002, 298, 399–402. [Google Scholar] [CrossRef]
- Couny, F.; Benabid, F.; Roberts, P.; Light, P.; Raymer, M. Generation and photonic guidance of multi-octave optical-frequency combs. Science 2007, 318, 1118–1121. [Google Scholar] [CrossRef]
- Jahani, Y.; Arvelo, E.R.; Yesilkoy, F.; Koshelev, K.; Cianciaruso, C.; De Palma, M.; Kivshar, Y.; Altug, H. Imaging-based spectrometer-less optofluidic biosensors based on dielectric metasurfaces for detecting extracellular vesicles. Nat. Commun. 2021, 12, 3246–3255. [Google Scholar] [CrossRef] [PubMed]
- Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photonics 2019, 13, 390–396. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- Hwang, M.S.; Lee, H.C.; Kim, K.H.; Jeong, K.Y.; Kwon, S.H.; Koshelev, K.; Kivshar, Y.; Park, H.G. Ultralow-threshold laser using super-bound states in the continuum. Nat. Commun. 2021, 12, 4135–4143. [Google Scholar] [CrossRef]
- Vabishchevich, P.; Kivshar, Y. Nonlinear photonics with metasurfaces. Photonics Res. 2023, 11, B50–B64. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Barreda, Á.; Moreno, F.; Litman, A.; Geffrin, J.M.; Sánchez-Gil, J.A. High-Q transparency band in all-dielectric metasurfaces induced by a quasi bound state in the continuum. Laser Photonics Rev. 2021, 15, 2000263. [Google Scholar] [CrossRef]
- Koshelev, K.; Kruk, S.; Melik-Gaykazyan, E.; Choi, J.H.; Bogdanov, A.; Park, H.G.; Kivshar, Y. Subwavelength dielectric resonators for nonlinear nanophotonics. Science 2020, 367, 288–292. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Deng, X.; Liang, X.; He, C.; Zhou, P.; Wang, T.; Liang, K.; Yu, L. Second Harmonic Generation from exciton-polaritons: Strong coupling between monolayer WS2 and multilayer WSe2 metasurfaces Quasibound states in the continuum. Opt. Commun. 2024, 570, 130935. [Google Scholar] [CrossRef]
- Luo, Z.; Ding, Y.; Peng, F.; Wei, G.; Wang, Y.; Wu, S.T. Ultracompact and high-efficiency liquid-crystal-on-silicon light engines for augmented reality glasses. Opto-Electron. Adv. 2024, 7, 240039. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Q.; Shen, B.; Tao, Y.; Zhang, X.; Tao, Z.; Xing, L.; Ge, Z.; Li, T.; Bai, B.; et al. Multifunctional mixed analog/digital signal processor based on integrated photonics. Opto-Electron. Sci. 2024, 3, 240012. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, T.; Zhu, Q.; Gu, M. Ultrahigh performance passive radiative cooling by hybrid polar dielectric metasurface thermal emitters. Opto-Electron. Adv. 2024, 7, 230194. [Google Scholar] [CrossRef]
- Jing, X.; Tang, X.; Tian, Y.; Kong, Z.; Li, C.; Shen, C.; Hong, Z. Enhancement of diffraction efficiency based on the addition principle of coded digital gratings. J. Light. Technol. 2022, 40, 136–142. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Tian, Y.; Li, C.; Huang, W.; Liu, Y.; Jin, Y.; Fang, B.; Hong, Z.; Jing, X. Focus control of wide-angle metalens based on digitally encoded metasurface. Opto-Electron. Adv. 2024, 7, 240095. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Fan, K.; Shadrivov, I.V.; Padilla, W.J. Dynamic bound states in the continuum. Optica 2019, 6, 169–173. [Google Scholar] [CrossRef]
- Chern, R.L.; Yang, H.C.; Chang, J.C. Bound states in the continuum in asymmetric dual-patch metasurfaces. Opt. Express 2023, 31, 16570–16581. [Google Scholar] [CrossRef]
- Azzam, S.I.; Shalaev, V.M.; Boltasseva, A.; Kildishev, A.V. Formation of bound states in the continuum in hybrid plasmonic-photonic systems. Phys. Rev. Lett. 2018, 121, 253901. [Google Scholar] [CrossRef]
- Deng, X.; Liang, X.; He, C.; Li, J.; Zhou, P.; Liang, K.; Yu, L. Realization of exciton-polariton optical chirality based on strong coupling between intrinsic chiral quasibound states in the continuum and monolayer WS2. Opt. Express 2024, 32, 11522–11533. [Google Scholar] [CrossRef] [PubMed]
- Sapunova, A.A.; Yandybaeva, Y.I.; Zakoldaev, R.A.; Afanasjeva, A.V.; Andreeva, O.V.; Gladskikh, I.A.; Vartanyan, T.A.; Dadadzhanov, D.R. Laser-induced chirality of plasmonic nanoparticles embedded in porous matrix. Nanomaterials 2023, 13, 1634. [Google Scholar] [CrossRef]
- Gladskikh, I.A.; Toropov, N.A.; Dadadzhanov, D.R.; Baranov, M.A.; Gladskikh, A.A.; Mirzoyan, G.; Markovich, G.; Vartanyan, T.A. Laser-Based Reshaping of Self-Organized Metasurfaces of Supported Ag Nanoparticles for Encoding Tunable Linear Dichroism Patterns. ACS Appl. Nano Mater. 2024, 7, 11342–11349. [Google Scholar] [CrossRef]
- Abdel-Megied, A.M.; Hanafi, R.S.; Aboul-Enein, H.Y. A chiral enantioseparation generic strategy for anti-Alzheimer and antifungal drugs by short end injection capillary electrophoresis using an experimental design approach. Chirality 2018, 30, 165–176. [Google Scholar] [CrossRef]
- Brenna, E.; Fuganti, C.; Serra, S. Enantioselective perception of chiral odorants. Tetrahedron Asymmetry 2003, 14, 1–42. [Google Scholar] [CrossRef]
- Baranov, D.G.; Munkhbat, B.; Länk, N.O.; Verre, R.; Käll, M.; Shegai, T. Circular dichroism mode splitting and bounds to its enhancement with cavity-plasmon-polaritons. Nanophotonics 2020, 9, 283–293. [Google Scholar] [CrossRef]
- Wu, F.; Guo, J.; Huang, Y.; Liang, K.; Jin, L.; Li, J.; Deng, X.; Jiao, R.; Liu, Y.; Zhang, J.; et al. Plexcitonic optical chirality: Strong exciton–plasmon coupling in chiral j-aggregate-metal nanoparticle complexes. ACS Nano 2020, 15, 2292–2300. [Google Scholar] [CrossRef]
- Wu, F.; Li, N.; Ding, B.; Zhang, W. Plasmon–exciton strong coupling effects of the chiral hybrid nanostructures based on the plexcitonic born–kuhn model. ACS Photonics 2023, 10, 1356–1366. [Google Scholar] [CrossRef]
- Deng, X.; Li, J.; Jin, L.; Wang, Y.; Liang, K.; Yu, L. Plexcitonic optical chirality in the chiral plasmonic structure-microcavity-exciton strong coupling system. Opt. Express 2023, 31, 32082–32092. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef]
- Gao, C.; You, S.; Zhang, Y.; Wang, L.; Duan, H.; He, H.; Xie, Q.; Zhou, C. Strong coupling between excitons and quasi-bound states in the continuum mode with stable resonance wavelength in the near-infrared region. Appl. Phys. Lett. 2024, 124, 051701. [Google Scholar] [CrossRef]
- Li, H.; Qin, M.; Ren, Y.; Hu, J. Angle-independent strong coupling between plasmonic magnetic resonances and excitons in monolayer WS2. Opt. Express 2019, 27, 22951–22959. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V.; Zabkov, I.; Pavlov, A.; Guzatov, D. Eigen oscillations of a chiral sphere and their influence on radiation of chiral molecules. Opt. Express 2014, 22, 18564–18578. [Google Scholar] [CrossRef]
- Zhang, Y.; Birgisson, B.; Lytton, R.L. Weak form equation–based finite-element modeling of viscoelastic asphalt mixtures. J. Mater. Civ. Eng. 2016, 28, 04015115. [Google Scholar] [CrossRef]
- Lv, S.; Hu, F.; Luo, W.; Xu, H.; An, L. Design of tunable selective light-absorbing metasurfaces driven by intrinsically chiral quasi-bound states in the continuum. Opt. Express 2024, 32, 30053–30064. [Google Scholar] [CrossRef]
- Xie, S.; Chen, J.; Sun, M.; Sun, S.; Zeng, Z.; Guan, X.; Yang, S. Strong coupling between excitons and chiral quasibound states in the continuum of the bulk WS2 metasurface. Opt. Express 2024, 32, 32523–32537. [Google Scholar] [CrossRef]
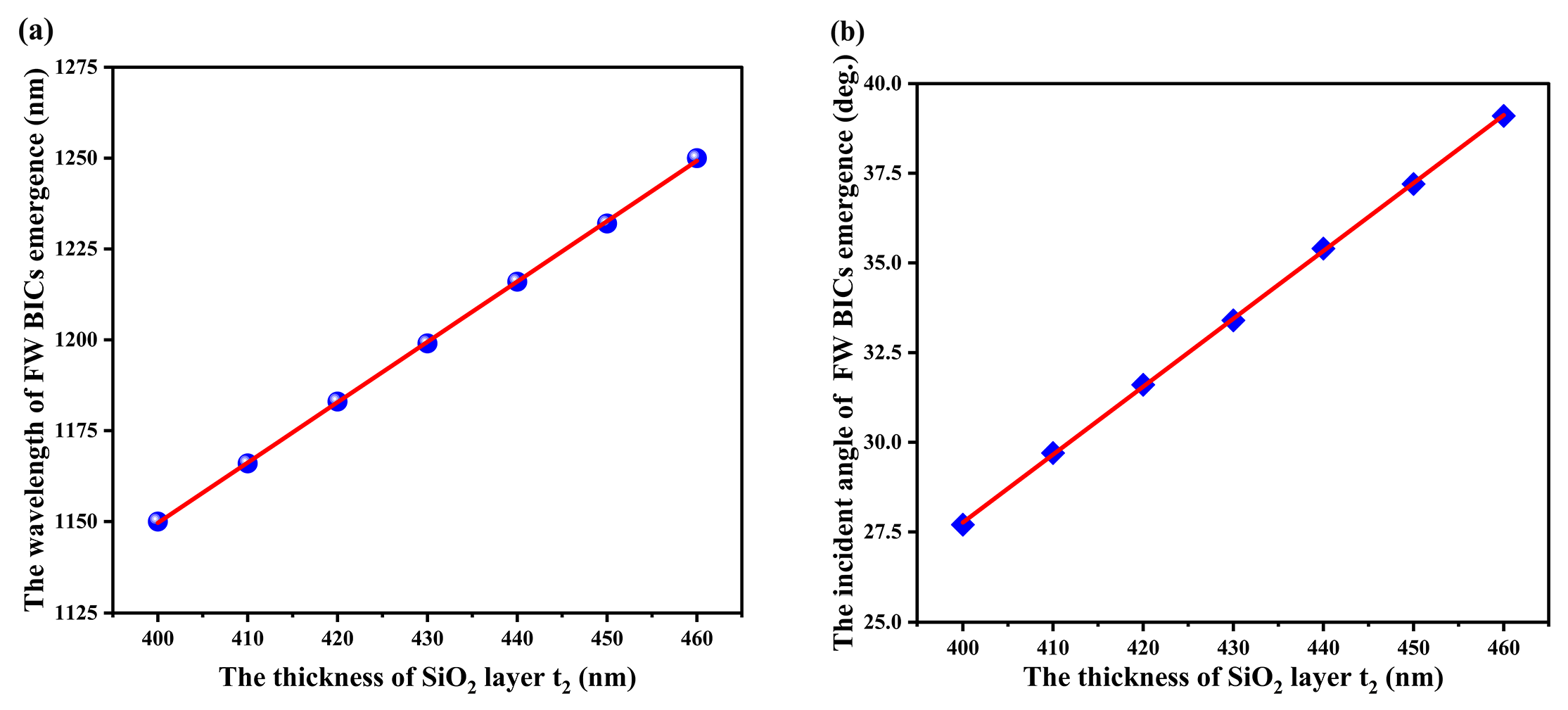

| The Thickness of SiO2 Layer | The Wavelength when FW BICs Emerge | The Incident Angle when FW BICs Emerge |
|---|---|---|
| 400 nm | 1150 nm | 27.7° |
| 410 nm | 1166 nm | 29.7° |
| 420 nm | 1183 nm | 31.6° |
| 430 nm | 1199 nm | 33.4° |
| 440 nm | 1216 nm | 35.4° |
| 450 nm | 1232 nm | 37.2° |
| 460 nm | 1250 nm | 39.1° |
| The Source of Chirality in Coupling Systems | The Pasteur Parameter Amplitude | Ref. | |
|---|---|---|---|
| Symmetry-breaking nanodisk metasurface (SC) | N/A | 0.3 | [43] |
| Symmetry-breaking bulk WS2 metasurface (SC) | N/A | 0.203 | [60] |
| 20 nm chiral medium layer (MC) | 0.03 | 0.007 | [48] |
| 10 nm chiral medium layer (MC) | 0.03 | 0.003 | [51] |
| 10 nm chiral medium layer (MC) | 0.03 | 0.05 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, J.; Liu, Y.; Yue, Y.; Dang, Y.; Wang, Y.; Liang, K.; Yu, L. Strong Coupling Based on Quasibound States in the Continuum of Nanograting Metasurfaces in Near-Infrared Region. Photonics 2025, 12, 508. https://doi.org/10.3390/photonics12050508
Zhao Y, Li J, Liu Y, Yue Y, Dang Y, Wang Y, Liang K, Yu L. Strong Coupling Based on Quasibound States in the Continuum of Nanograting Metasurfaces in Near-Infrared Region. Photonics. 2025; 12(5):508. https://doi.org/10.3390/photonics12050508
Chicago/Turabian StyleZhao, Yulun, Junqiang Li, Yuchang Liu, Yadong Yue, Yongchuan Dang, Yilin Wang, Kun Liang, and Li Yu. 2025. "Strong Coupling Based on Quasibound States in the Continuum of Nanograting Metasurfaces in Near-Infrared Region" Photonics 12, no. 5: 508. https://doi.org/10.3390/photonics12050508
APA StyleZhao, Y., Li, J., Liu, Y., Yue, Y., Dang, Y., Wang, Y., Liang, K., & Yu, L. (2025). Strong Coupling Based on Quasibound States in the Continuum of Nanograting Metasurfaces in Near-Infrared Region. Photonics, 12(5), 508. https://doi.org/10.3390/photonics12050508





