Efficient Testing Light Path for Aspherical Surfaces Based on Secondary Imaging
Abstract
1. Introduction
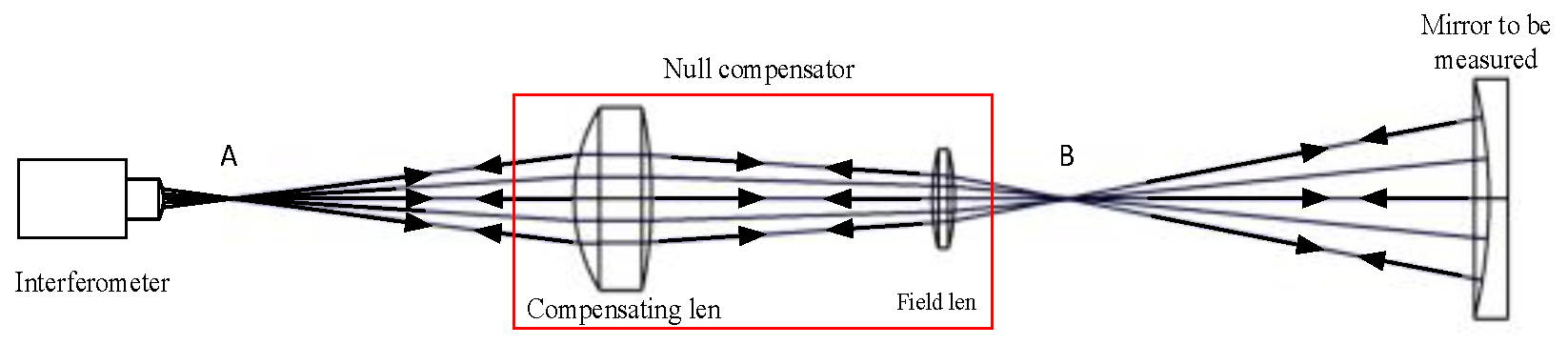
2. Design Principle of the Testing Light Path
3. Design of the Testing Light Path
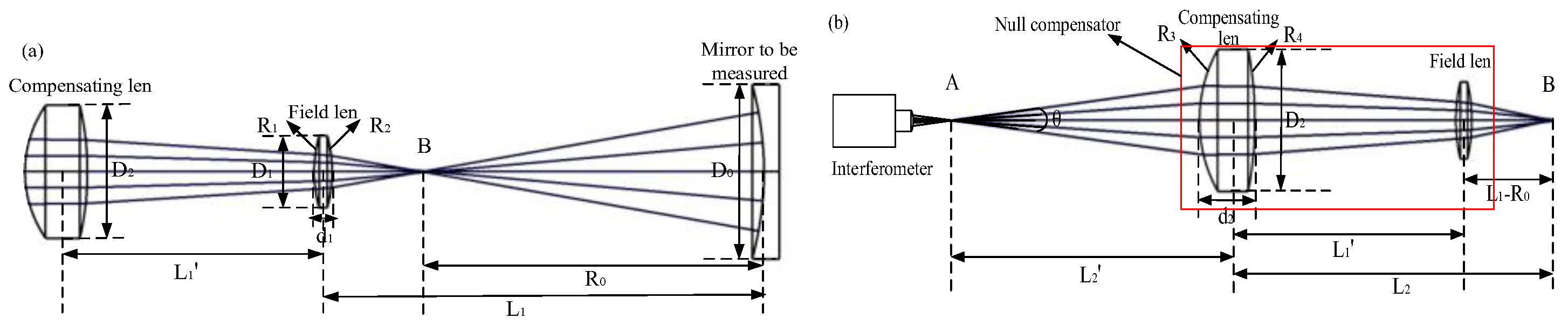
3.1. Compensator Design
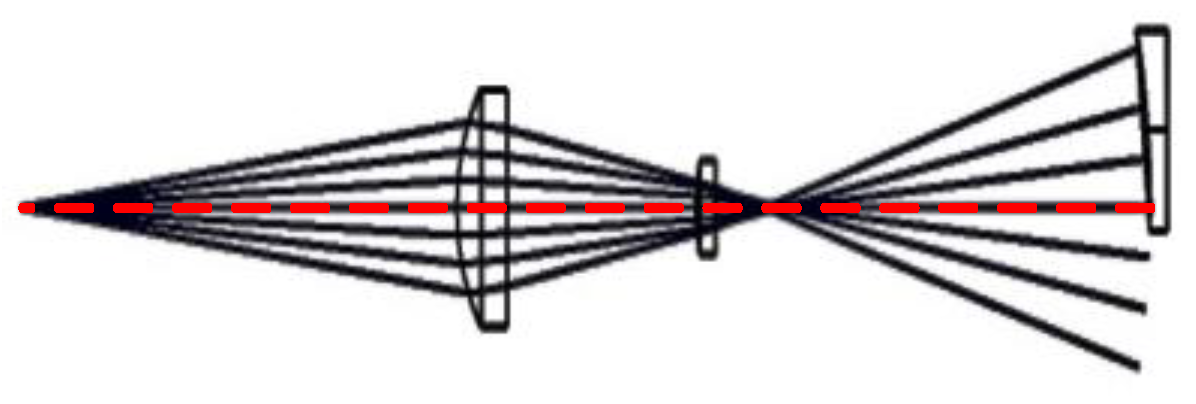
3.2. Design Results and Tolerance Analysis
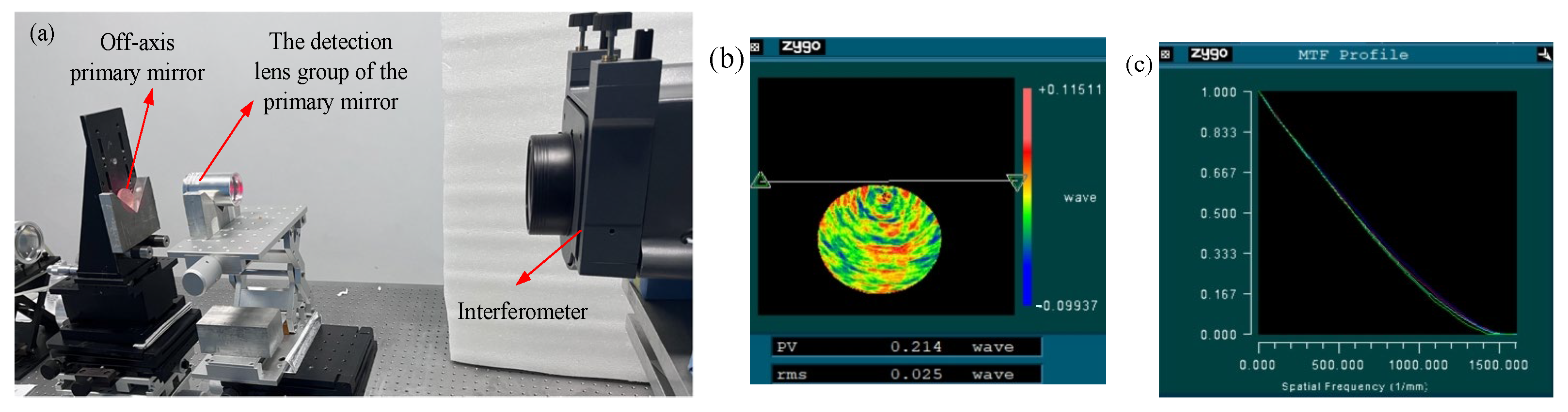
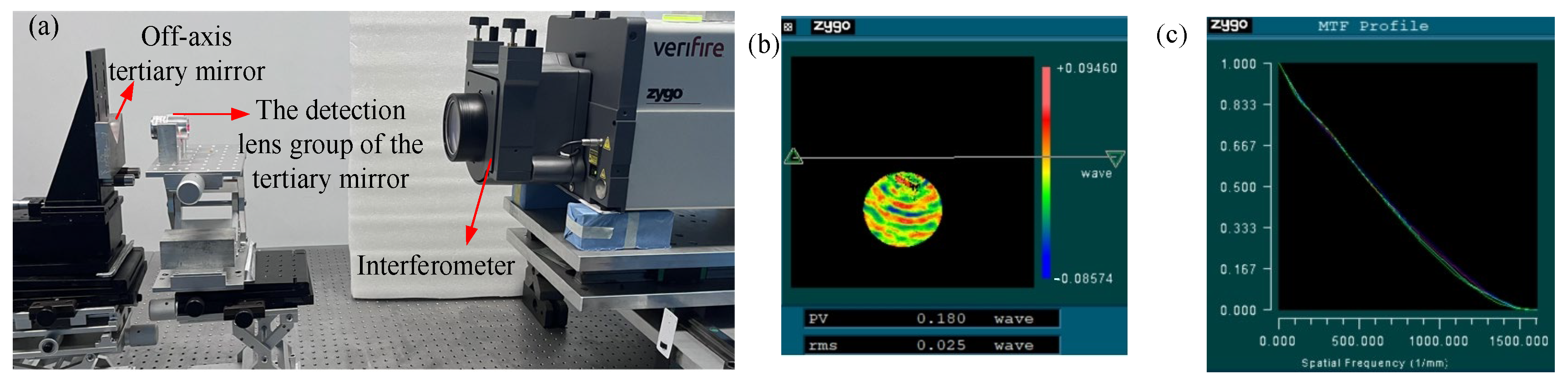
4. Light Path Construction and Detection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, L.; He, Z.; Lv, G.; Wang, Y.; Li, C.; Xie, J.N.; Wang, J. Optical design, laboratory test, and calibration of airborne long wave infrared imaging spectrometer. Opt. Express 2017, 25, 22440–22454. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Xie, J.; Tang, X.; Chen, W.; Li, Q. On-orbit radiometric performance of GF-7 satellite multispectral imagery. Remote Sens. 2022, 14, 886. [Google Scholar] [CrossRef]
- Tang, X.M.; Zhou, P.; Zhang, G.; Wang, X.; Jiang, Y.H.; Guo, L.; Liu, S.H. Verification of ZY-3 satellite imagery geometric accuracy without ground control points. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2100–2104. [Google Scholar] [CrossRef]
- Ungar, S.; Pearlman, J.S.; Mendenhall, J.A.; Reuter, D. Overview of the Earth Observing One (EO-1) mission. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1149–1159. [Google Scholar] [CrossRef]
- Collin, A.; Lambert, N.; Etienne, S. Satellite-based salt marsh elevation, vegetation height, and species composition mapping using the superspectral WorldView-3 imagery. Int. J. Remote Sens. 2018, 39, 5619–5637. [Google Scholar] [CrossRef]
- Blechinger, F.; Charlton, D.E.; Davancens, R.; Harnisch, B.; Kunkel, B.P.; Meynart, R.; Novi, A.; O’Mongain, E.; Schwarzer, H.H.; Slater, P.N. High-resolution imaging spectrometer (HRIS): Optics, focal plane, and calibration. In Proceedings of the Optical Engineering and Photonics in Aerospace Sensing, Orlando, FL, USA, 11–16 April 1993. [Google Scholar] [CrossRef]
- Giremus, A.; Grussenmeyer, P. Design of the high resolution optical instrument for the Pleiades HR Earth observation satellites. Int. J. Remote Sens. 2012, 33, 1234–1256. [Google Scholar] [CrossRef]
- Zhang, X.J. Progress on space optics manufacturing: From aspheres to freeforms. Acta Opt. Sin. 2023, 43, 0822009. [Google Scholar]
- Wang, T.; Huang, L.; Vescovi, M.; Kuhne, D.; Tayabaly, K.; Bouet, N.; Idir, M. Study on an effective one-dimensional ion-beam figuring method. Opt. Express 2019, 27, 15368–15381. [Google Scholar] [CrossRef] [PubMed]
- Sidpara, M.A. Magnetorheological finishing: A perfect solution to nanofinishing requirements. Opt. Eng. 2014, 53, 092002. [Google Scholar] [CrossRef]
- Ghozeil, I. Hartmann and other screen tests. In Optical Shop Testing; Malacara, D., Ed.; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Zhao, W.C.; Fan, B.; Wu, F. Experimental analysis of reflector test based on phase measuring deflectometry. Acta Opt. Sin. 2013, 33, 98–101. (In Chinese) [Google Scholar]
- Zhao, C.; Hu, M.; Zhang, S.; Li, X.; Li, Z. Research on Compensation Detection Method for Large Aperture High-order Aspheric Surfaces. Laser Optoelectron. Prog. 2020, 57, 270–276. [Google Scholar]
- Zhang, L.; Hu, W.; Zheng, L.; Hao, P. Catadioptric null compensating test. Acta Photonica Sin. 2016, 45, 0722002. [Google Scholar]
- Zhou, P.; Burge, J.H. Fabrication error analysis and experimental demonstration for computer generated holograms. Appl. Opt. 2006, 46, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, C.; Huang, X.; Zhang, Y.; Zhou, S.; Li, J.; Yu, B. Compact adaptive interferometer for unknown freeform surfaces with large departure. Opt. Express 2020, 82, 1897–1913. [Google Scholar] [CrossRef] [PubMed]
- Gappinger, R.O.; Greivenkamp, J.E. Iterative reverseoptimization procedure for calibration of aspheric wave-front measurements on a nonnull interferometer. Appl. Opt. 2004, 43, 5152–5161. [Google Scholar] [CrossRef] [PubMed]
- Offner, A. A null corrector for paraboloidal mirrors. Appl. Opt. 1963, 2, 153–155. [Google Scholar] [CrossRef]
- Pan, J. Optical Aspheric Design, Processing and Testing; Suzhou University Press: Suzhou, China, 2004. [Google Scholar]
- Wang, X.; Li, X.; Zhang, Q.; Shi, Y.; Wei, W.; Liu, E. Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer. Photonics 2024, 11, 1072. [Google Scholar] [CrossRef]
- Yu, D.Y.; Tan, H.Y. Engineering Optics, 4th ed.; China Machine Press: Beijing, China, 2016. [Google Scholar]
- Cui, H.B.; Li, Y.P.; Kang, X.L. Optics, 2nd ed.; Science Press: Beijing, China, 2015; pp. 33–34. [Google Scholar]
- MIL-0-13830 A/B; Standard for Surface Imperfections of Optical Components. United States Department of Defense Standardization Bureau: Washington, DC, USA, 1994.
- GB 1185-1989; China Machinery Industry Federation. Surface Imperfections of Optical Components; China Standards Press: Beijing, China, 1989.
- GB/T 1185-2006; Standardization Administration of the People’s Republic of China. Surface Imperfections of Optical Components; China Standards Press: Beijing, China, 2007.



| D0 The Aperture of the Test Mirror | R0 The Radius of Test Mirror | n Compensator Lens Refractive Index | e02 Conic Coefficients of Test Mirror | Obscuration Ratio | Magnification | Aberration Sharing Factor | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1 Compensating Lens | α2 Field Lens | β1 Compensating Lens | β2 Field Lens | t1 Compensating Lens | t2 Field Lens | |||||
| Third-order aberration | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Secondary imaging | √ | √ | √ | × | × | × | × | × | × | × |
| Title | Radius of Curvature/mm | Diameter/mm | Off-Axis Amount/mm | The Aperture of the Off-Axis Mirror/mm | Conic |
|---|---|---|---|---|---|
| Primary mirror | −106.736 | 58 | 13 | 32 | −2.394 |
| Tertiary mirror | −69.432 | 42 | 6 | 30 | −1.294 |
| Op# | Type | Surf1 | Surf2 | Target | Weight | Value | ||
|---|---|---|---|---|---|---|---|---|
| Control the length of the optical path | 1 | TTHI | A | Compensating lens | OPGT | 35 | 1 | 129.445 |
| OPLT | 200 | 1 | ||||||
| 2 | TTHI | Compensating lens | Field lens | OPGT | 20 | 1 | 56.349 | |
| OPLT | 100 | 1 | ||||||
| 3 | TTHI | Field lens | Primary mirror | OPGT | 50 | 1 | 129.296 | |
| OPLT | 135 | 1 | ||||||
| Control the system aberration | 4 | Field | Freq | Target | Weight | Value | ||
| 5 | GMTS | 1 | 40 | 1 | 1 | 0.851 | ||
| 6 | GMTT | 1 | 40 | 1 | 1 | 0.851 | ||
| 7 | Term | Field | Target | Weight | Value | |||
| 8 | ZERN | Astigmatism X | 1 | 0 | 1 | 7.27 × 10−18 | ||
| 9 | ZERN | Astigmatism Y | 1 | 0 | 1 | −1.59 × 10−19 | ||
| 10 | ZERN | Coma X | 1 | 0 | 1 | 6.23 × 10−19 | ||
| 11 | ZERN | Coma Y | 1 | 0 | 1 | 5.85 × 10−18 | ||
| 12 | ZERN | Primary Spherical | 1 | 0 | 1 | −2.23 × 10−7 | ||
| 13 | ZERN | Trefoil X | 1 | 0 | 1 | −1.80 × 10−19 | ||
| 14 | ZERN | Trefoil Y | 1 | 0 | 1 | −9.25 × 10−18 | ||
| D1/mm | D2/mm | L1/mm | L1′/mm | L2/mm | L2′/mm | R1/mm | R2/mm | R3/mm | R4/mm | d1/mm | d2/mm | Mirror Material | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Primary mirror | 16 | 40 | 129.296 | 56.349 | 78.909 | 129.445 | 28.152 | ∞ | 31.603 | ∞ | 5.623 | 14.705 | H-K9L |
| Tertiary mirror | 20 | 30 | 78.193 | 37.858 | 46.619 | 177.192 | 19.482 | ∞ | 24.857 | ∞ | 7.794 | 9.813 | H-K9L |
| Type | Suf | Value | Criterion | Change | |
|---|---|---|---|---|---|
| Primary mirror | TEDX | R3 of compensating lens | ±5 × 10−3 | 0.8709 | −0.0169 |
| TEDY | |||||
| TEDX | R1 of field lens | ±5 × 10−3 | 0.8748 | −0.0129 | |
| TEDY | |||||
| TIND | Compensating lens | 5 × 10−3 | 0.8736 | −0.0141 | |
| −5 × 10−3 | 0.8739 | −0.0138 | |||
| Tertiary mirror | TEDX | R3 of compensating lens | ±5 × 10−3 | 0.7810 | −0.0247 |
| TEDY | |||||
| TEDX | R1 of field lens | ±5 × 10−3 | 0.7887 | −0.0171 | |
| TEDY | |||||
| TIND | Compensating lens | 5 × 10−3 | 0.7912 | −0.0146 | |
| TRAD | R3 of compensating lens | −5 × 10−3 | 0.7929 | −0.0129 |
| Primary Mirror | Tertiary Mirror | |
|---|---|---|
| Nominal MTF | 0.8878 (40 lp/mm) | 0.8058 (40 lp/mm) |
| Simulation result | 10% > 0.8833 | 10% > 0.7991 |
| 50% > 0.8714 | 50% > 0.7870 | |
| 90% > 0.8451 | 90% > 0.7564 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, X.; Zhang, Q.; Wei, W.; Liu, E. Efficient Testing Light Path for Aspherical Surfaces Based on Secondary Imaging. Photonics 2025, 12, 485. https://doi.org/10.3390/photonics12050485
Wang X, Li X, Zhang Q, Wei W, Liu E. Efficient Testing Light Path for Aspherical Surfaces Based on Secondary Imaging. Photonics. 2025; 12(5):485. https://doi.org/10.3390/photonics12050485
Chicago/Turabian StyleWang, Xinrui, Xin Li, Quan Zhang, Wei Wei, and Enchao Liu. 2025. "Efficient Testing Light Path for Aspherical Surfaces Based on Secondary Imaging" Photonics 12, no. 5: 485. https://doi.org/10.3390/photonics12050485
APA StyleWang, X., Li, X., Zhang, Q., Wei, W., & Liu, E. (2025). Efficient Testing Light Path for Aspherical Surfaces Based on Secondary Imaging. Photonics, 12(5), 485. https://doi.org/10.3390/photonics12050485





