Abstract
This study investigates a laser ranging technology scheme featuring a large divergence angle for both the emitted and received laser beams, focusing on applications where both the measured target and the ranging carrier are high-mobility platforms. A dual-concave beam-reducing lens design is adopted to reshape the original beam divergence angle of 10 mrad from the erbium glass laser into a ranging output beam divergence angle of 26 mrad, while maintaining the Gaussian energy distribution of the original laser beam. A φ500 μm photosensitive surface APD detector is used, and a combination of aspherical and spherical elements is employed in the receiving optical system to achieve a 30 mrad large field-of-view echo reception within the small photosensitive surface. This laser ranging system addresses the challenge of aiming and tracking for laser ranging between relatively high-speed moving objects and reduces the stability precision requirements for the ranging carrier platform.
1. Introduction
As of 19 February 2025, there are 13,810 operational satellites in orbit globally—a dramatic increase from just 4852 satellites recorded at the end of 2021. According to a report by Euroconsult, the number of satellites in orbit is projected to grow by 17,000 by 2030, representing a fourfold increase compared to the past decade. Additionally, ABI Research, a global technology intelligence firm, estimates that the total number of active low Earth orbit (LEO) satellites will surge from 7473 in 2023 to approximately 42,600 by 2032. The surge in on-orbit satellites heralds the rapid development of applications such as satellite networking, navigation, exploration, remote sensing, and countermeasures. This growth is shifting the demand for spaceborne ranging from traditional long-distance satellite-to-ground measurement to close-range inter-satellite ranging.
As a high-precision measurement tool, laser rangefinders play an indispensable role in the aerospace field. The characteristics of high precision, high speed, and non-contact measurement make it a crucial device for precise distance measurement, navigation, detection, and monitoring in aerospace missions. The application of aerospace laser rangefinders is significant in enhancing the navigation accuracy of spacecraft and ensuring the safety of aerospace missions.
Unlike common applications such as vehicle-mounted, ground-based, or individual use scenarios, laser ranging equipment for aerospace applications often measures targets that are in high-speed motion and have extremely small reflective cross-sections, with a considerable relative velocity between the measuring platform and the target, reaching up to 15 km/s. The entire satellite not only moves around the Earth under the action of the Earth’s gravitational force, but its orbit will also be affected by other disturbing forces [1]. The high relative motion between the platform and the target makes alignment challenging during the ranging process. Therefore, how to observe and track targets under such conditions of relatively high-speed motion is a key technical issue that needs to be addressed in the future development of space-based satellites.
The relationship between the true value of the probability of laser ranging and the illumination probability and detection probability is represented as
In the equation, represents the true probability, which is the probability of accurately measuring the real distance to the target. denotes the illumination probability, which is the probability that the entire target cross-section is illuminated by the laser when aimed and fired at the target. is the detection probability, which is the probability of detecting the target when the entire cross-section is illuminated by the laser. The illumination probability is dependent on the aiming error, which includes both random errors and systematic errors [2]. Detection probability relies on the detection capability of the laser rangefinder and its signal processing performance, while illumination probability is directly related to the system’s aiming performance or the size of the laser spot on the target. High-precision aiming and tracking systems tend to be heavier and bulkier; thus, increasing the size of the laser spot on the target and enhancing the divergence angle of the laser beam emitted by the rangefinder is a more cost-effective solution.
2. Overall Solution
To achieve a >1 km ranging performance on small targets, the solution adopts the time-of-flight (TOF) ranging methodology, which calculates the distance between the rangefinder and target by measuring the round-trip propagation time of laser pulses. The principle of pulse laser ranging is similar to that of radar ranging. It involves emitting a single laser pulse or a series of laser pulses toward the target using a pulsed laser. A counter measures the round-trip time of the laser pulse from the emitter to the target and back to the receiver, allowing for the calculation of the target’s distance. The principle of pulse laser ranging is illustrated in Figure 1, and the ranging formula is as follows:
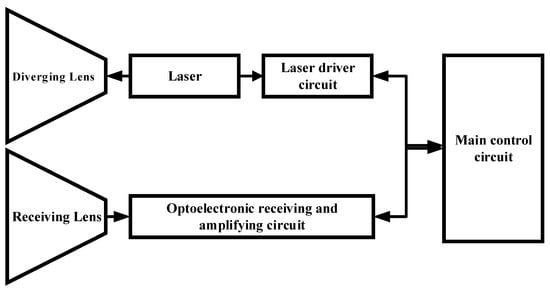
Figure 1.
Composition diagram of a laser ranging system.
In the equation, d represents the measurement distance, c denotes the speed of light, and t refers to the round-trip time of the ranging signal [3].
Compared to conventional laser rangefinders with a divergence angle generally less than 1 mrad, the divergence angle of the laser designed in this system is approximately 26 mrad. Additionally, the optical system’s receiving field of view is designed to be approximately 30 mrad, which can meet the requirements for effective echo reception under conditions of large divergence angle emission.
3. Design of Large-Divergence Transmitter and Wide-Field-of-View (WFOV) Receiver Systems
3.1. Selection of Laser Source
The requirements for the weight of spaceborne payloads are extremely strict, involving various aspects such as launch vehicle capability, fuel efficiency, maneuverability, structural strength, thermal control systems, scientific instruments, redundancy design, mission objectives, as well as international competition and cooperation. To meet these demands, aerospace engineers must perform comprehensive optimization and trade-offs in areas such as design, material selection, manufacturing processes, and mission planning. Reducing payload weight not only lowers mission costs but also enhances the success rate and scientific returns of the mission, making it one of the key factors for the success of aerospace missions. Therefore, choosing erbium glass lasers with high peak energy and low volume and weight as the ranging light source is critical.
The project employs a passive Q-switched Er-glass laser; passive Q-switching technology is simple in principle, easy to operate, reliable in system performance, and low in cost. It is particularly suitable for various miniaturized laser systems and, therefore, has been widely used [4]. The laser used in this project has an emission wavelength of 1535 nm, as the light energy at this wavelength is strongly absorbed by water. When it enters the human eye, it is almost completely absorbed by the cornea and does not reach the retina, thus posing no harm to the eyes. The core parameters of the Er-glass laser adopted in the project are shown in Table 1. The appearance of the laser is shown in Figure 2.

Table 1.
Laser core parameters.

Figure 2.
Outline drawing of Er-glass laser.
3.2. Diverging Lens
At present, there are various methods to collimate beam divergence angles, such as collimation using telescope systems [5] or binary optical astigmatism-correcting collimating devices [6]. However, most of these methods have complex structures and are not conducive to modularization. Since laser ranging requires the system to be as compact and lightweight as possible, the emission collimation system should be as simple as possible while meeting the ranging performance requirements [7].
As mentioned above, the divergence angle directly output by the laser is 12.2 mrad. In order to meet the requirement of a divergence angle greater than 26 mrad, it is necessary to design a collimation system that converts the laser’s divergence angle from 12.2 mrad to above 26 mrad. A single double-concave lens can effectively increase the divergence angle of the laser. The principle is to utilize the divergence characteristics of the double-concave lens to convert a collimated laser beam into a diverging beam. The processing diagram of the double-concave lens is shown in Figure 3.
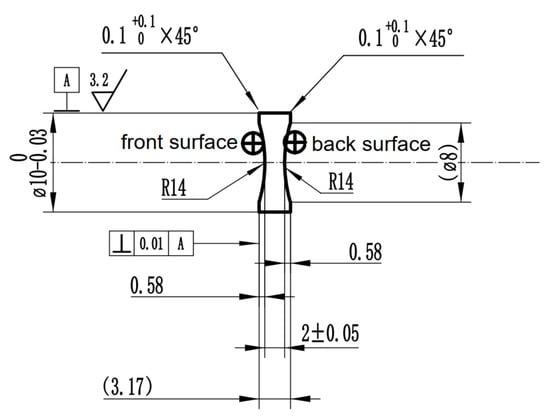
Figure 3.
Parameters of a biconcave lens.
For a biconcave lens, given the front surface curvature radius R1 and the back surface curvature radius R2. The focal length of the lens can be calculated by the following formula:
In this case, n refers to the refractive index of the lens material. For the above biconcave lens, R1 = −14 mm, R2 = 14 mm.
The biconcave lens is made of HK9 material, which has a refractive index of 1.51. The focal length f of this biconcave lens, calculated from the figure above, is −13.7 mm.
Given the laser divergence angle θ1 = 12.2 mrad ≈ 0.012 rad, and the laser wavelength λ = 1535 nm = 1.535 × 10−3 mm.
Calculate the waist radius of the laser according to the following formula:
Substituting λ = 1.535 × 10−3 mm and θ1 = 0.012 rad into the formula yields the following:
At the waist position, the wavefront curvature radius R = ∞, and the formula for the complex curvature radius is q1 = i.
Substituting w1 = 0.04 mm and λ = 1.55 × 10−3 mm yields the following:
The focal length of the biconcave lens is f = −13.7 mm, and its ABCD matrix is (
), where A = 1, B = 0, C = mm−1, D = 1.
According to the ABCD law, ; substituting A = 1, B = 0, C = mm−1, D = 1, q1 = i3.37 mm into the formula, we can obtain the following:
According to this formula, it can be calculated that q2 ≈ i0.713 mm.
At the waist of the output laser beam, q2 = i, it is known that Im (q2) = 0.713 mm, λ = 1.535 × 10−3 mm. Substitute in the formula to obtain = ≈ 0.0186 mm.
According to the relationship between laser divergence angle and beam waist radius, θ = , it can be obtained that
To sum up, the divergence angle of the laser beam through the biconcave lens is about 26.4 mrad. The Diverging Lens Ray Diagram is shown in Figure 4.
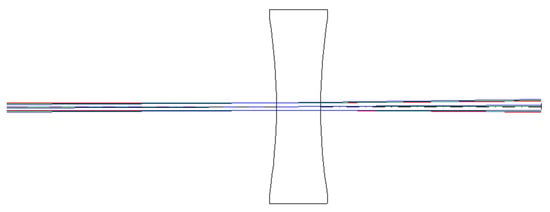
Figure 4.
Diverging Lens Ray Diagram [8].
The real ray tracing analysis of the design results of the optical system can be obtained as shown in Figure 5:
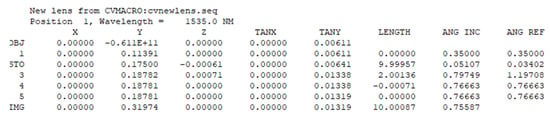
Figure 5.
Real ray tracing data.
The simulation results show that the incident laser divergence angle is 0.35 × 17.45 × 2 = 12.2 mrad, and the outgoing laser divergence angle is 0.755 × 17.45 × 2 = 26.35 mrad, which is almost the same as the calculation results.
3.3. Beam Quality Simulation of Diverging Lens Optical System
The light incident on the paraxial sphere at a small angle with the optical axis (Z axis) is called paraxial light. Let the angle between the paraxial ray and the optical axis be θ, then sin θ ≈ θ is satisfied, tan θ ≈ θ, and cos θ ≈ 1.
The original divergence angle of the laser is 12.2 mrad, so it can be obtained that the angle between the light and the laser optical axis is about θ = 6.1 mrad ≈ 0.006 rad, then sin () = 0.00598, tan () ≈ 0.006 and cos () = 0.999982 meet paraxial optical conditions. When the paraxial optical conditions are satisfied, the beam conversion can be regarded as not affecting the beam quality.
The laser spot, after passing through the divergent lens, is simulated at a distance of 100 mm and 1000 m from the lens. The results are shown in Figure 6 and Figure 7 below. It can be seen from the simulation results that the Gaussian distribution of power is ensured for the spot after beam reduction at both short and long distances.
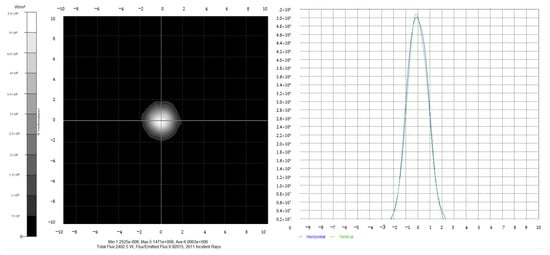
Figure 6.
Illuminance simulation diagram at 100 mm.
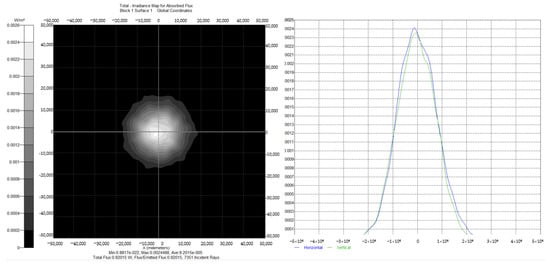
Figure 7.
Illuminance simulation diagram at 1000 mm.
3.4. Design of Wide Field-of-View (WFOV) Optical Reception System for Laser Echo Detection
The laser receiving the optical system collects the laser energy reflected from the target and focuses it onto the light-sensitive surface of an avalanche photodiode (APD) [9]. When designing the receiving system, it is necessary to both enhance the ranging capability for small targets by increasing the receiving field of view and to balance the need for suppressing background stray light (especially from close-range backgrounds) [10]. According to the requirements of the receiving FOV, the APD with a photosensitive surface size of 500 μm is selected as the receiving detector. The main parameters of the receiving detector are shown in Table 2 below:

Table 2.
APD core parameters.
The receiving optical system is composed of spherical lenses, which are mainly made of Radiation-resistant glass, and the numerical aperture F# is 0.54. The optical path diagram is shown in Figure 8. Lens 1 in the figure is a narrow-band filter, which can filter out the background light clutter beyond 1535 nm in the ambient light. Lenses 2, 3, and 4 are laser convergence optical systems, and lens 5 is the APD optical window.
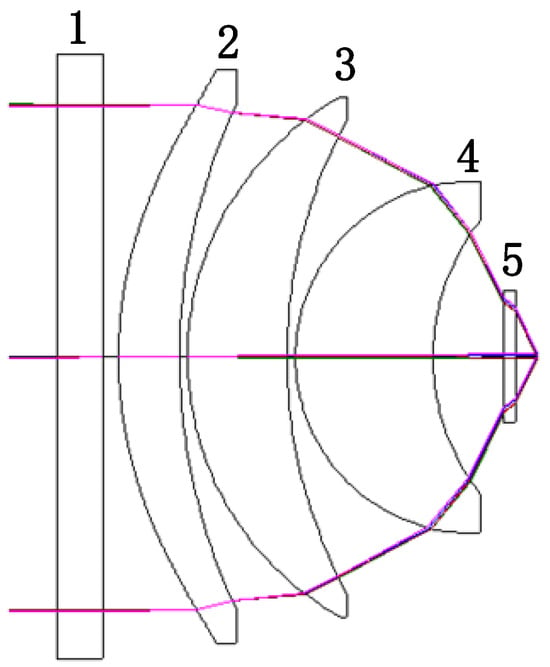
Figure 8.
Receiving optical system light path diagram [8].
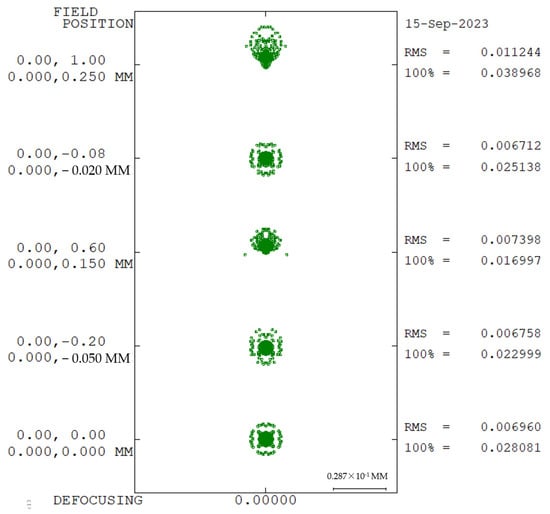
Figure 9.
Spot diagram at room temperature.
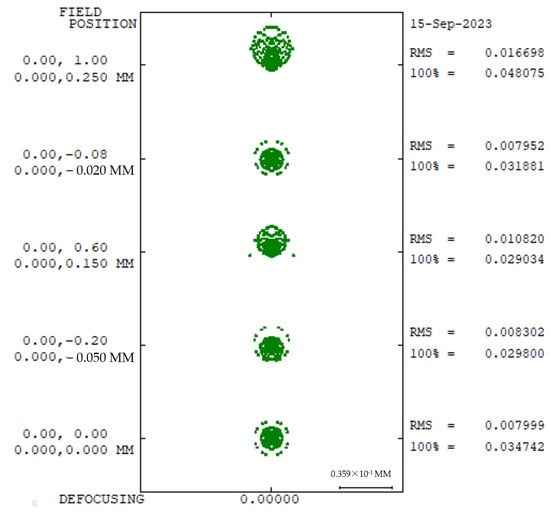
Figure 10.
Spot diagram at −40 °C.
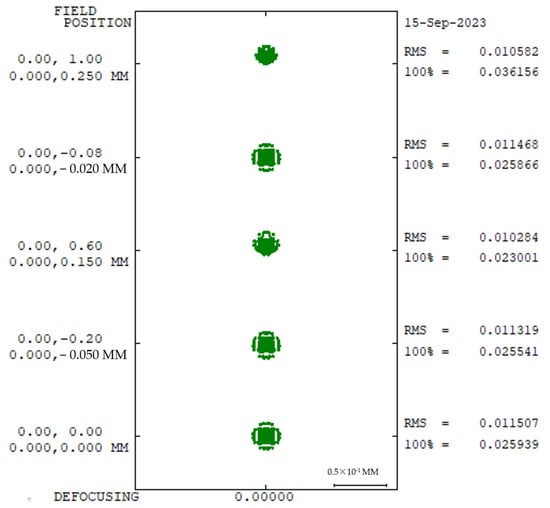
Figure 11.
Spot diagram at +60 °C.
In the whole temperature range of −40 °C~60 °C, the receiving optical system has good energy distribution and spot size, which can meet the requirements of a large field of view reception.
4. Experimental Results and Discussion
4.1. Laser Beam Divergence Angle Test
The divergence angle of the collimated laser is tested using the Aperture Method. During the experiment, the test pinhole plate is placed at the focal length of the reflector. The divergence angle of the rangefinder can be calculated using the following formula:
In the formula, θ: divergence angle of the multimode beam;
ds: The diameter of the multimode spot at a distance S from the beam waist, in mm. During actual measurement, it is the diameter of the pinhole aperture placed on the focal plane of the reflector. In this test system, it is 52 mm.
S: The distance from the beam waist to the measured spot, in mm. In actual measurement, it is the focal length f of the reflector, in mm. For this test system, it is 2000 mm.
During the experiment, the laser energy needs to be tested both in front of and behind the pinhole. Let the laser energy in front of the pinhole be E1, and the laser energy behind the pinhole be E2. If the ratio of the energy behind the pinhole to that in front of the pinhole, E2/E1 is less than 86.5%, then it can be considered that the pinhole aperture meets the testing requirements, and the measured laser divergence angle is greater than 26 mrad. The laser beam divergence angle test diagram is shown in Figure 12. The pinhole plate in the test is shown in Figure 13. The laser energy before and after the pinhole is shown in Figure 14.
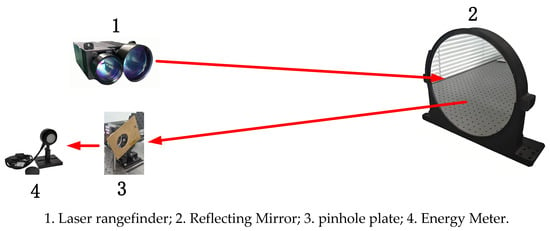
Figure 12.
Laser beam divergence angle test diagram.

Figure 13.
Pinhole plate in the test.

Figure 14.
Laser energy before and after the pinhole: (a) laser energy before the pinhole E1. (b) Laser energy behind the pinhole E2.
Based on the test results, the energy in front of the pinhol·e E1 is 391 μJ, and the energy behind the pinhole E2 is 331 μJ. = 84.65%, which is close to the ISO11146-1:2021 standard [11] requirement of 86.5%. Therefore, the calculated laser divergence angle is greater than 26 mrad, which meets the design specifications.
4.2. Ranging Capability Test
To verify the ranging capability of the laser rangefinder, especially under conditions where the target is not precisely aimed at, field verification testing was conducted to validate the rangefinder’s performance. A slender and tall signal tower was selected as the test target, the shape of which is shown in Figure 15 below.

Figure 15.
Target—signal tower.
During the test, ranging measurements were conducted on the signal tower at distances of 1011 m and 709 m, respectively, with the precise distances being calibrated by differential GPS equipment.
The range data are shown in Figure 16 and Figure 17. The range data at 1011 m corresponds to the test conducted when the rangefinder was perfectly aligned with the target. The test distance of 709 m corresponds to the data obtained when there was a deviation of 0.6° between the aiming axis and the target. Test images under different aiming conditions is shown in Figure 18.
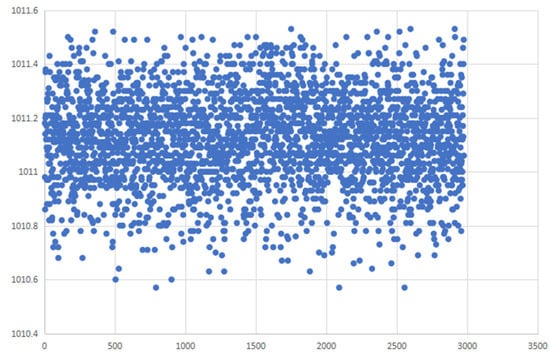
Figure 16.
Test data for 1011 m with full aim.
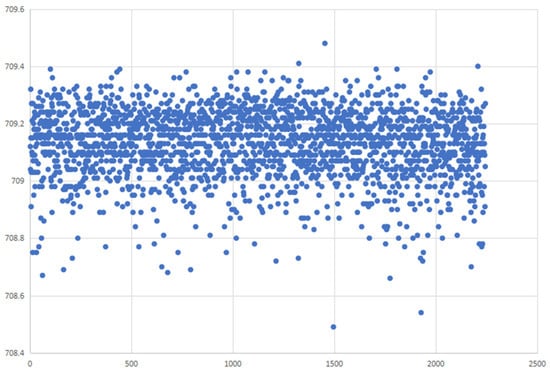
Figure 17.
Test data for 709 m with 0.6° aiming deviation.

Figure 18.
Aiming deviation 0.6° test image: (a) aim with a rightward deviation of 0.6°. (b) Fully aim. (c) Aim with a leftward deviation of 0.6°.
In Figure 16 and Figure 17, the abscissa (x-axis) denotes the number of ranging cycles, while the ordinate (y-axis) represents the measured distance. Each circular marker in the plot corresponds to a discrete ranging measurement. At the 1011 m range, 3000 discrete data points were acquired, while 2250 measurements were recorded at the 709 m distance. For the 1011 m range testing, all measured data points fell within the interval of 1010.5 to 1011.6 m, demonstrating absolute errors ranging from −0.5 to +0.6 m relative to the ground truth distance. For the 709 m range testing, all measured data points fell within the range of 708.5 to 709.5 m, demonstrating absolute errors strictly bounded by ±0.5 m relative to ground truth.
Given distinct application scenarios and objectives, the technical approach adopted in this study differs significantly from conventional long-range inter-satellite detection methods. Traditional long-distance laser ranging typically employs interferometric techniques, as exemplified by the LISA mission, where a laser beam divergence of 1.43 μrad and sophisticated Acquisition, Tracking, and Pointing (ATP) systems are required to achieve μrad-level alignment precision for successful inter-satellite ranging [12].
In contrast, this work utilizes a large-divergence-angle laser ranging technique that achieves stable, high-precision measurements even with a pointing deviation of 0.6° (10.47 mrad). This approach dramatically reduces the required tracking and alignment precision—a breakthrough with no comparable published research to date. The proposed method offers a novel solution for close-range, low-cost, and miniaturized inter-satellite laser ranging applications.
5. Results
Inter-satellite distance measurement is a primary focus in applications such as formation flying of small satellites and satellite constellations. Since both the ranging platform and the target are in high-speed motion, it is challenging to achieve high-precision tracking and aiming, which makes reliable distance measurement difficult. To address this issue, this paper proposes a technical solution that simultaneously increases the laser divergence angle of the laser rangefinder and the field of view (FOV) of the receiving optical system. The design of the Er-glass laser’s beam-shrinking emission optical system and the wide-FOV receiving optical system is detailed in the paper, achieving a laser divergence angle of 26 mrad and a receiving FOV of 30 mrad. Field tests of the ranging prototype demonstrate that the rangefinder can stably measure the distance to a signal tower target at 709 m with an aiming axis deviation of 0.6°, and under this test condition, a ranging accuracy of ±0.5 m can also be achieved. This demonstrates that increasing both the laser rangefinder’s beam divergence angle and receiver field of view enables precise target ranging without requiring full optical alignment. Field testing confirms that the design of the ranging system reduces the requirement for aiming precision of the target and can reliably measure distances in scenarios where both the ranging platform and the target are in high-speed motion.
Author Contributions
Conceptualization, S.Y.; methodology, J.J.; validation, J.J. and Y.F.; editing, J.J.; visualization, J.J. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, W.-B.; Wang, T.-F.; Guo, J. Analysis for opto-electrical acquisition tracking and pointing control technology on satellite. Chin. Opt. 2014, 7, 6. [Google Scholar]
- Jiang, H.-B. Selecting Optimum of Signal-to-Noise Ratio and Laser Beam Divergence for Laser Range-Finder. Opt. Optoelectron. Technol. 2023, 1, 1. [Google Scholar]
- Xiao, B. Methods for Laser Distance Measurement. Geospat. Inf. 2010, 4, 8. [Google Scholar]
- Chen, B.; Chen, Y.; Wang, G.-C. Recent Advance in Passive Q-switch of l.54 μm Er: Glass Laser. Opt. Optoelectron. Technol. 2004, 1, 2. [Google Scholar]
- Zhang, J.-J. Design of transmitting and receiving system for long-distance pulse laser ranging. Laser J. 2024, 11, 45. [Google Scholar]
- Yagiu, Y.; Kumazawa, T. New collimating lens systems for laser diode package. In Proceedings of the IEEE 43rd Electronic Components and Technology Conference, Orlando, FL, USA, 1–4 June 1993; Volume 43, pp. 1135–1138. [Google Scholar]
- Yan, Y.-B.; Wang, C.; Wu, M.-X.; Jin, G.-F. A binary optical element of laser diode for compensating astigmation and enhancing collimation. Infrared Laser Eng. 1996, 25, 5. [Google Scholar]
- Ji, J.-W.; Yang, S.-H. Research on Large Divergence Angle Laser Ranging System. In Proceedings of the 10th Symposium on Novel Optoelectronic Detection Technonlogy and Application, Taiyuan, China, 1–3 November 2024. [Google Scholar]
- Zhang, C.; Wang, X.-X.; Yan, G.-S. Optimum Design to a Single Lens Transmitted Collimating Module of Laser Ranging Finders. Laser Binfrared 2009, 39, 4. [Google Scholar]
- Wang, G. Design and study about field diaphragm of receiving optical system in a laser rangefinder. Laser Technol. 2014, 38, 5. [Google Scholar]
- ISO11146-1:2021; Lasers and laser-related equipment—Test methods for laser beam widths, divergence angles and beam propagation ratios. ISO: Geneva, Switzerland, 2021.
- Duan, H.-Z.; Luo, Y.-X.; Zhang, J.-Y. Inter-satellite laser interferometry. Acta Sci. Nat. Univ. Sunyatseni 2021, 60, 1–2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).