1. Introduction
Due to their unique long-range interactions and long coherence times, Rydberg atoms have emerged as pivotal systems in quantum information science and quantum computing research [
1,
2]. These atoms exhibit remarkably strong van der Waals interactions that stem from their huge dipole moments [
3,
4,
5,
6]. Such distinctive interactions provide unprecedented capabilities for quantum control and entanglement generation. In particular, the Rydberg blockade effect, where strong interatomic interactions prevent the simultaneous excitation of multiple atoms to Rydberg states, enables the creation of collective excitations known as “superatoms” [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. The superatom paradigm provides a platform for quantum information applications such as quantum simulation, quantum computing, and quantum communication [
18,
19]. Beyond facilitating coherent quantum state manipulation, the tunability of Rydberg superatoms across physical configurations reveals new opportunities in emerging domains. It shows promising prospects in cutting-edge applications such as non-linear quantum optical phenomena and photonic quantum devices [
20,
21,
22,
23,
24,
25].
Recently, the manipulation of quantum effects and the preparation of entanglements in cavity optomechanical systems have also attracted significant attention [
26]. A typical optomechanical system involves coupling between the optical field within the cavity and the mechanical motion of a moving mirror, where radiation pressure drives the movable mirror to vibrate, leading to the formation of quantum vibrational modes [
27]. When the coupling strength between the cavity mode and mechanical mode is precisely tuned, the optical field and the mechanical motion of the mirror can achieve a highly quantized coupling state, ultimately generating entangled states. Cavity optomechanical systems are of critical importance for applications in quantum precision measurement, quantum sensing, and quantum communication [
28,
29,
30,
31,
32]. In addition, optomechanical systems provide a unique platform for the study of macroscopic objects in the quantum regime, opening new possibilities for the exploration of macroscopic quantum effects [
33]. Notably, in studies of quantum sensing and fundamental quantum mechanics, cavity optomechanical systems are an ideal tool for quantum manipulation and show potential to realize other fundamental quantum properties in macroscopic moving objects [
34,
35].
Cavity optomechanical systems demonstrate exceptional compatibility, with the unique capability to interface with degrees of freedom that remain largely inaccessible in alternative physical systems. This capability enables the construction of novel hybrid quantum devices and the realization of new quantum interfaces [
36]. The confinement of atomic ensembles within cavity optomechanical architectures enables the generation of steady-state continuous-variable (CV) entanglement between arbitrary pairwise combinations of atomic ensembles, optical modes, and moving mirrors [
37,
38,
39,
40,
41]. Building on the dipole blockade effect and preceding advances, this study proposes a hybrid system combining a Rydberg superatom with a single-mode optomechanical cavity to investigate entanglement sustainability under weak-excitation conditions.
Within parameter regimes where the atomic transition frequency matches the Stokes sideband frequency, continuous-variable steady-state bipartite entanglement is established among the Rydberg superatom, the cavity field, and the movable mirrors. Specifically, the cavity–mirror entanglement (
) and cavity–superatom entanglement (
) originate from direct coupling mechanisms, while the superatom–mirror entanglement (
) emerges through indirect Stokes-mediated coupling. Recent breakthroughs have demonstrated the direct generation of W-class tripartite entanglement through spontaneous six-wave mixing (SSWM) in atomic vapor [
42]. In this pioneering work, the authors employed the novel SSWM technique to achieve a critical milestone: the observation of genuine continuous-mode time-energy-entangled W-class triphotons, rigorously verified by different bipartite entanglements. By enabling direct tripartite entanglement generation via a fundamentally distinct nonlinear interaction mechanism, this groundbreaking study marks a historic advancement in multiphoton entanglement research over the past three decades. Notably, it transcends conventional methodologies that rely on spontaneous parametric down-conversion (SPDC) or spontaneous four-wave mixing (SFWM) with biphoton sources.. In our work, we demonstrate that the exceptional longevity of Rydberg states (manifested through suppressed decay rates at high principal quantum numbers) fundamentally reshapes the entanglement hierarchy. As the atomic decay rate decreases (corresponding to increasing principal quantum numbers), we observe the redistribution of
: a small fraction transfers to (
), while the dominant portion migrates to
. Strikingly, under optimized resonance matching, both direct coupling entanglements (
and
) vanish entirely, leaving only the indirect coupling entanglement (
) persistent. This entanglement redistribution and transfer mechanism is systematically investigated through parameter adjustments. Finally, we quantify the thermal robustness of the surviving entanglement, demonstrating its resilience against environmental decoherence up to experimentally accessible temperatures. These results not only elucidate fundamental aspects of quantum entanglement in macroscopic hybrid systems but also provide a practical framework for the engineering of robust matter-based entanglement in quantum technologies.
2. Model and Equations
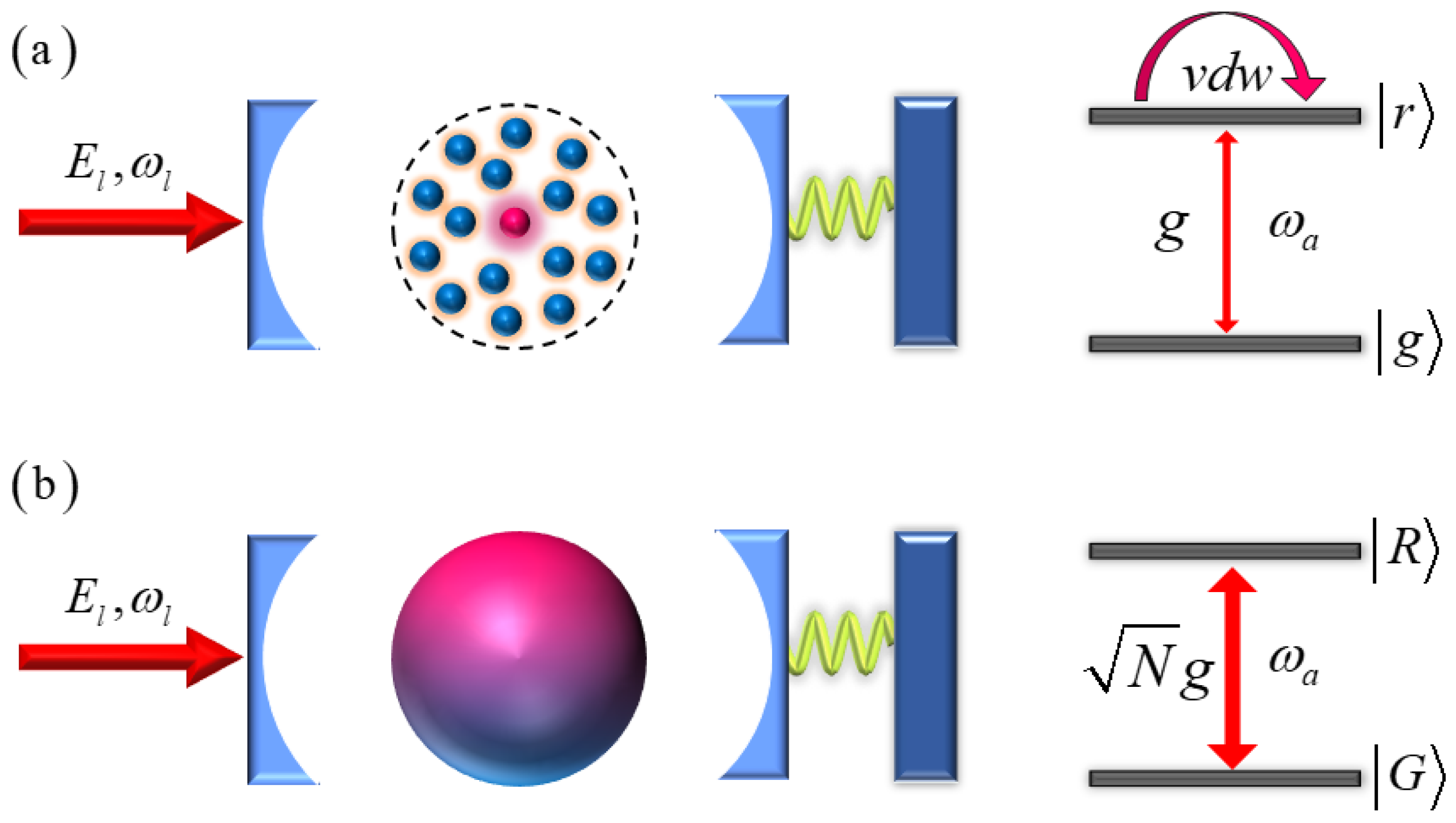
We consider in
Figure 1a a hybrid cavity optomechanical system: an external driving field with frequency
and amplitude
is incident from one side of the fixed cavity mirror, and a single-mode field with frequency
is excited inside the cavity, with a length of
L. The single-mode cavity field drives a movable mirror (we use “mirror” instead of “movable mirror” hereafter) with mass
m and frequency
, causing slight vibrations that exhibit typical optomechanical behavior. Meanwhile,
N two-level Rydberg atoms with a resonant frequency of
are trapped with the same blockade region inside the cavity, where
denotes the ground state and
represents the Rydberg state. When the atoms are excited to the Rydberg state by the single-mode cavity field, a strong van der Waals (vdW) interaction emerges between the atoms. The entire Hamiltonian of the system is given by
In Equation (
1), the first four terms represent the free Hamiltonian of the cavity, the Hamiltonian of the movable mirror, the Hamiltonian of the optomechanical interaction, and the Hamiltonian describing the cavity mode excitation driven by an external driving field, respectively. The operators
a and
are the annihilation and creation operators of the single-mode cavity field, obeying the commutation relation
. The position and momentum operators
p and
q satisfy the commutation relation
. The optomechanical coupling constant is defined as
and the external driving field amplitude is given by
, where
is the field power and
is the cavity decay rate. The fifth and sixth terms represent the free Hamiltonian of the atoms and the interacting Hamiltonian between the atoms and the cavity field, respectively, with
g denoting the atom–cavity coupling constant. The operator
represents the transition operator
or projection operator
for the
j-th atom. Finally, the last term accounts for the van der Waals interaction, where the coupling strength between atoms
j and
k (when excited to a Rydberg state) is
. Here,
is the van der Waals coefficient and
denotes the interatomic distance.
Due to the Rydberg blockade effect, which inhibits the simultaneous excitation of multiple Rydberg atoms within the ensemble, only a single Rydberg excitation is shared collectively by the entire ensemble in a blockade region. Consequently, the atomic ensemble behaves as a two-level Rydberg superatom (we use “superatom” instead of “Rydberg superatom” hereafter), as illustrated in
Figure 1b. The collective ground state of the superatom is defined as
, and its collective excited state is
[
7,
8,
9,
10,
11,
12,
13,
14,
15]. Based on this description, the spin operators of the superatom are defined as
,
and
, satisfying the commutation relations
,
. By replacing the atomic operators in Equation (
1) with the superatom operators, and in the rotating frame at the frequency
of the external driving field, the effective Hamiltonian is obtained as [
8,
14,
16,
17]
where
and
. Clearly, the coupling strength between the superatom and the cavity exhibits a
enhancement. This scaling arises because the superatom model inherently satisfies the low-excitation (single-atom excitation) approximation by construction. For systems with a large number of atoms, the superatom operators can be bosonized as
. When nearly all atoms populate the ground state, this simplifies to
, which satisfies the standard bosonic commutation relation
. With these formalisms, the quantum Langevin equations for the system can be expressed as follows (with
):
where
is the collective coupling coefficient between a single superatom and the cavity field, and
is the decay rate of the Rydberg state. The Hermitian Brownian noise operator
satisfies the correlation function
where
, with
denoting the Boltzmann constant and
T the temperature of the mechanical oscillator’s thermal reservoir. The other two noise operators satisfy the following nonvanishing correlation functions:
Subsequently, each operator is decomposed into its mean value and a small fluctuation, like
,
,
,
. Given that the external laser acts as a strong driving field, the steady-state cavity field amplitude satisfies
. Substituting these operators into Equation (
3), we obtain two sets of coupled dynamical equations. By solving the equations for the operator’s mean values, the steady-state solutions are obtained as
where
is the effective cavity detuning, with
denoting the effective optomechanical coupling strength.
To characterize the steady-state quantum correlations among the superatom, cavity, and mirror, we analyze the dynamics of quantum fluctuations around the steady-state solution. The quadrature fluctuation operators are defined as
,
,
, and
. By combining the dynamical equations for the fluctuation operators (governed by Equation (
3)) with the steady-state conditions in Equation (
6), we derive the dynamical equation for the quadrature fluctuation vector as
,
where the transfer matrix
A satisfies
with the vector of noise
. Here,
,
,
, and
[
37].
In this system, the steady state of the quantum fluctuation is a continuous-variable tripartite Gaussian state, fully characterized by the
correlation matrix
. Under the Markovian approximation, the steady-state correlation matrix
V is determined by solving the Lyapunov equation:
where
is the diffusion matrix originating from noise correlations. Here,
represents the mean phonon occupation number. To quantify the steady-state bipartite entanglement among the superatom, cavity, and mirror, we extract a reduced
correlation matrix from
V:
where blocks
A,
B, and
C encode subsystem correlations.
Subsequently, to quantify the steady-state bipartite entanglement between the subsystems, we calculate the logarithmic negativity [
43]:
where
with
. The indices
label the cavity (c), mirror (m), and superatom (s), respectively. For clarity, we define the logarithmic negativities for the cavity–mirror, cavity–superatom, and superatom–mirror bipartitions as
,
, and
, respectively.
3. Discussion and Analysis of Numerical Results
In this section, we numerically evaluate the steady-state bipartite entanglements. The parameters are chosen to be experimentally feasible, with most values adopted from [
37,
44,
45], except for the following specific cases: the mass of the movable mirror
and its frequency
; the length of the optomechanical cavity
, the quality factor
, and the finesse
; the power of the external driving field
; and the optomechanical coupling strength
. Other parameters are provided in the figure captions and main text.
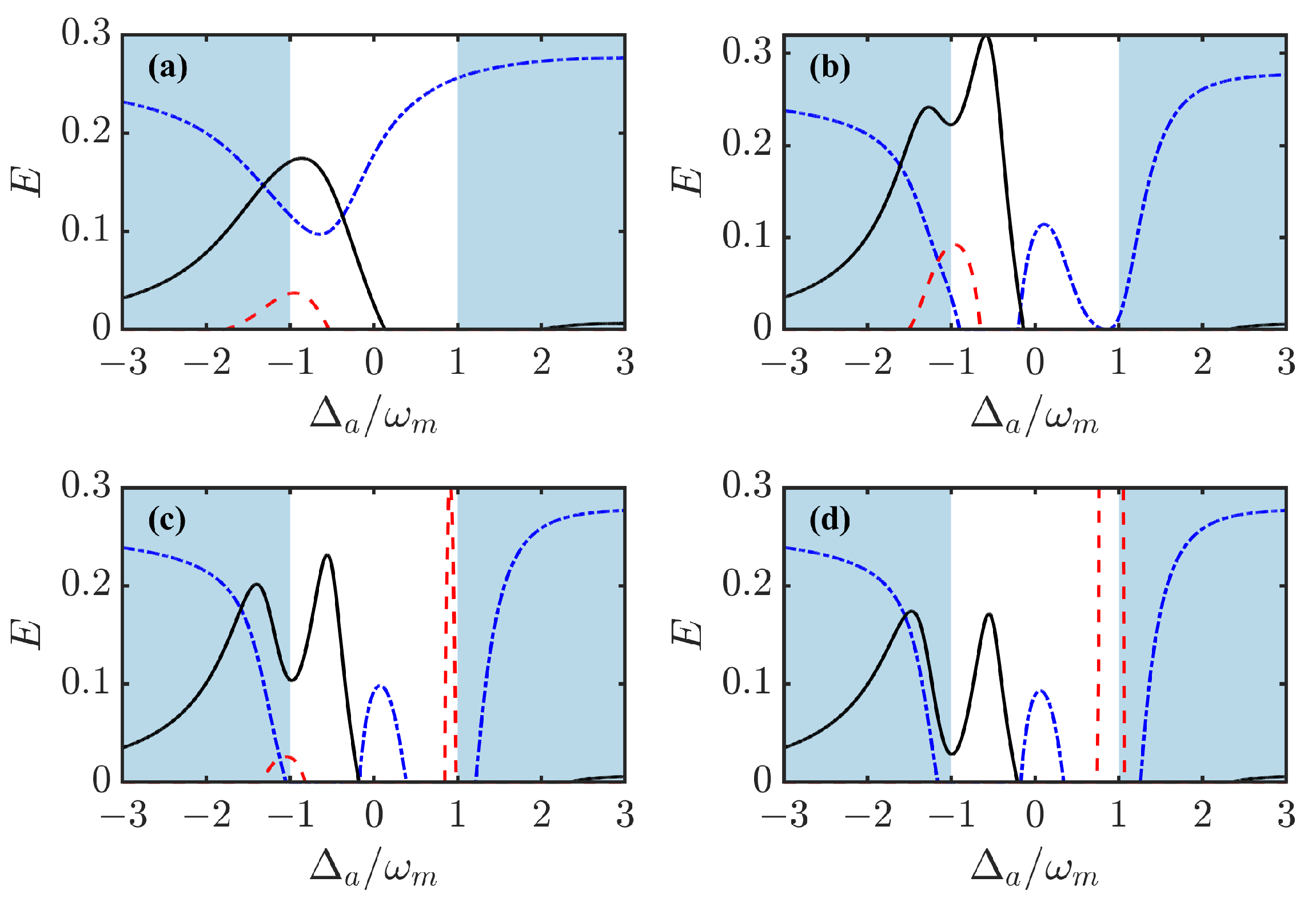
To better characterize the impact of the long lifetime of Rydberg atoms, we first consider the case of noninteracting atoms. As shown in
Figure 2a, when
, the direct optomechanical coupling between the cavity and the mirror generates the entanglement
. The atomic detuning significantly affects the system’s entanglement, leading to the redistribution and transfer of the cavity–mirror entanglement
to both the cavity–superatom entanglement
and the superatom–mirror entanglement
. When
, i.e., the atomic frequency is resonant with the Stokes sideband,
reaches its maximum. In contrast, no superatom–mirror entanglement
is observed when the atomic frequency is resonant with the anti-Stokes sideband
. This is because a resonant indirect coupling between the atoms and mirror mediated by the cavity field is established, resulting in the atom–mirror entanglement predominantly localized in the Stokes sideband, while the recycling of anti-Stokes photons by the absorbing atoms disrupts the mirror–cavity cooling process, i.e., the physical foundation of bipartite optomechanical entanglement [
37].
When
Rydberg atoms with principal quantum numbers
are selected, the atomic decay rate decreases significantly, i.e.,
[
46]. For
, as shown in
Figure 2b, the tripartite atom–mirror–cavity is established at
with
,
, and
. In contrast to noninteracting atoms, both the direct cavity–superatom coupling entanglement and the indirect superatom–mirror coupling entanglement are enhanced, as nearly all direct cavity–mirror coupling entanglement is redistributed to these two channels. Due to the complexity of the dynamical evolution, the total system entanglement is not conserved during this redistribution and transfer process. Notably, the superatom–mirror entanglement
exhibits a characteristic dip at
, flanked by asymmetric peaks on both sides. This feature originates from destructive interference between the cavity–superatom coupling channel and the cavity–mirror coupling channel, which is directly imprinted on the superatom–mirror entanglement dynamics. At
,
, with only a negligible residual cavity–mirror entanglement (
). For
, as shown in
Figure 2c, the cavity–mirror entanglement
vanishes at
, indicating complete optomechanical entanglement redistribution. An electromagnetically induced transparency (EIT)-like phenomenon emerges in the superatom–mirror entanglement
as the destructive interference strengthens. At
,
. Meanwhile, the cavity–superatom entanglement
emerges near
, with a stronger anti-Stokes sideband peak than the Stokes sideband. For
, as shown in
Figure 2d, a counterintuitive phenomenon occurs: at
, both direct coupling entanglements (
and
) vanish, while the indirect coupling superatom–mirror entanglement
persists. This signifies a complete entanglement transfer from direct to indirect coupling channels. The underlying mechanism involves photons released via relaxation, which partially leak from the cavity (proportional to
) and partially strengthen the cavity–superatom coupling. As
decreases, the weakened optomechanical coupling suppresses
, while the redistributed
diminishes, shifting the entanglement to the anti-Stokes sideband (
at
). Below a critical decay rate, the EIT mechanism suppresses direct coupling entanglement, leaving only
.
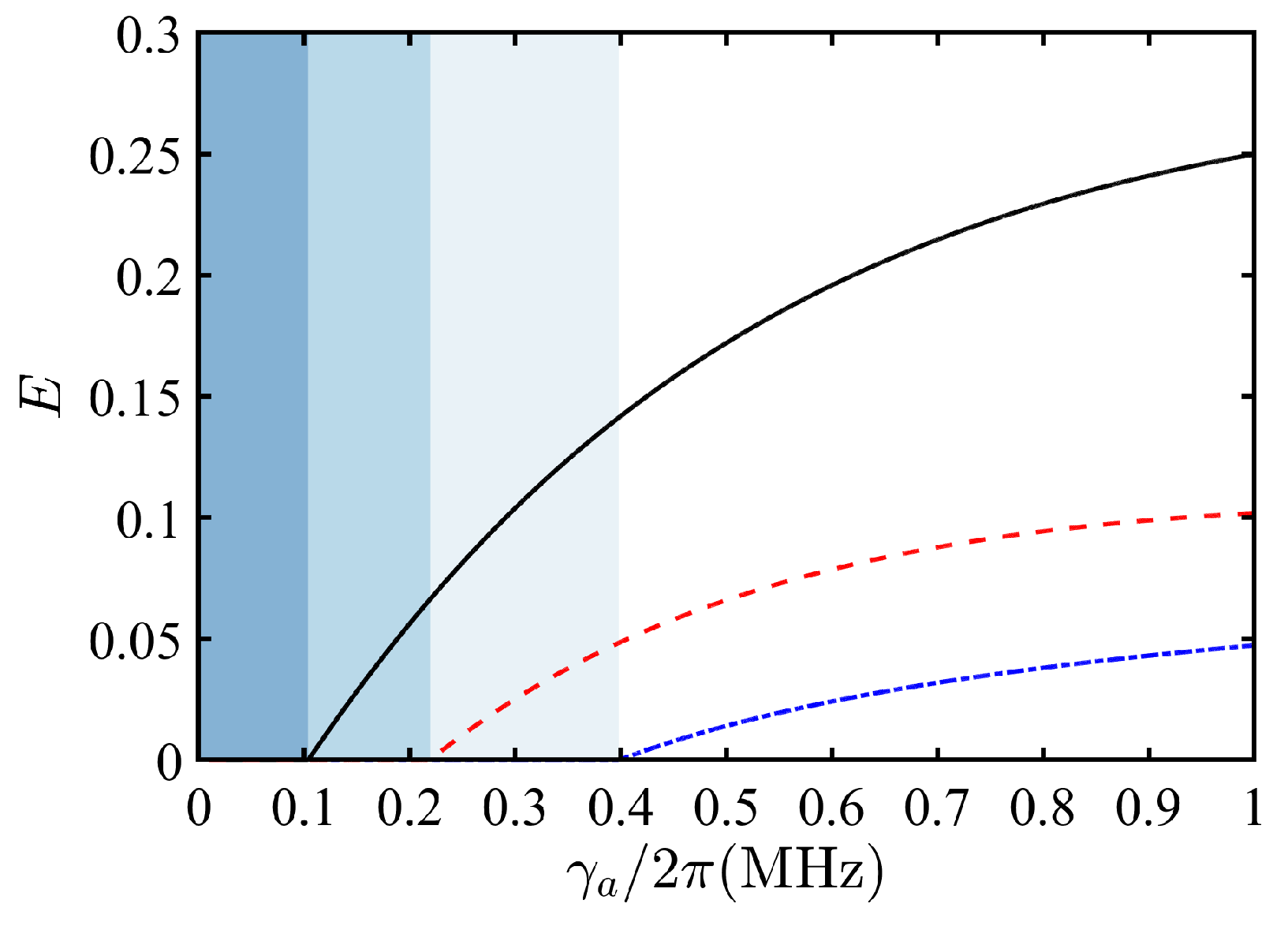
Figure 3 further reveals the critical decay rates governing the entanglement at
. Clearly, most cavity–mirror entanglement is redistributed and transferred, resulting in
for
. As
is further reduced, the redistribution and transfer of the cavity–mirror entanglement proceed progressively. When
,
, indicating the complete disappearance of cavity–mirror entanglement. At the threshold decay rate
, the weakened optomechanical coupling suppresses the cavity–superatom entanglement (
), leaving only the indirect superatom–mirror coupling entanglement (
). Remarkably, when
, all three entanglement types vanish (
). This collapse arises because ultralow atomic decay rates critically destabilize the optomechanical coupling, eroding the physical prerequisites for entanglement generation.
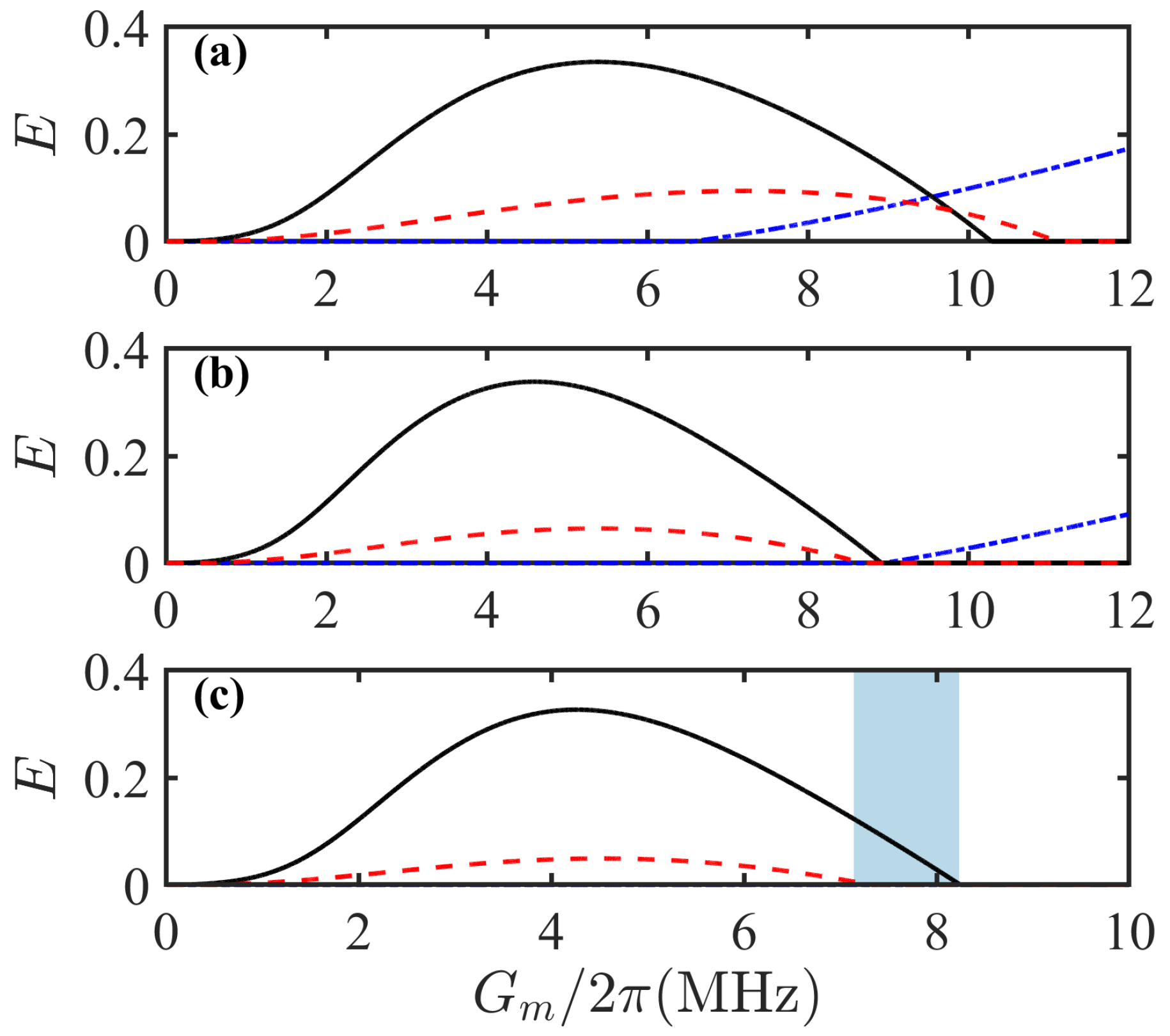
From Equation (
8) and prior analysis, the system’s entanglement exhibits pronounced sensitivity to the optomechanical coupling strength. As demonstrated in
Figure 4a, for
, the indirect superatom–mirror coupling entanglement persists within
, peaking at
for
. Within this regime, direct coupling entanglements coexist with indirect coupling entanglements. When
is reduced to
, as shown in
Figure 4b, the superatom–mirror entanglement window narrows to
, with the peak value
shifting to a lower coupling strength
. Notably, indirect coupling entanglement never occurs in isolation under these conditions. For
, as shown in
Figure 4c, the superatom–mirror entanglement persists within a narrower window of
, peaking at
for
. Collectively,
Figure 4 establishes optomechanical coupling as the fundamental driver of entanglement generation, with bipartite entanglement distribution arising from the intricate competition between the atomic decay rate and the coupling strength. To isolate indirect coupling entanglement, a strategic reduction in the optomechanical coupling strength enables the selective enhancement of superatom–mirror entanglement.
Figure 5 demonstrates that the system’s entanglement strongly depends on the cavity–superatom coupling coefficient
. Remarkably, regardless of atomic decay rate variations, enhancing
progressively suppresses the optomechanical coupling strength, thereby diminishing the cavity–mirror entanglement
until its eventual extinction. As evidenced in
Figure 5a, for
, the cavity–mirror entanglement
is sequentially transferred progressively to
and
with increasing
, completely vanishing at
. Beyond this critical threshold, further increasing
simultaneously enhances both
and
, with
consistently exceeding
.
Figure 5b exhibits a similar trend to
Figure 5a. Even at
, no parameter regime sustains solely indirect coupling entanglement, irrespective of
. However, for
, indirect superatom–mirror entanglement exclusively survives within
, peaking at
when
. These findings demonstrate that indirect coupling entanglement’s dominance can be engineered by strategically tuning
. Synthesizing the insights from
Figure 5, a fundamental trade-off emerges between
and
, dictating the entanglement redistribution pathways.
Finally, we discuss the temperature robustness of the system’s entanglement. Building on previous insights, to amplify indirect coupling entanglement, we propose a dual-parameter optimization strategy, i.e., reducing the optomechanical coupling strength
while enhancing the cavity–superatom coupling coefficient
. Specifically, with
and
, the cavity–mirror entanglement vanishes
, indicating complete entanglement redistribution. As shown in
Figure 6, for
, the superatom–mirror entanglement
decreases faster than the cavity–superatom entanglement
, with both approaching zero simultaneously at
(
). When
,
vanishes at
(
), while
vanishes earlier at
(
). For
, only the indirect coupling superatom–mirror entanglement
persists, exhibiting an approximately linear temperature dependence until its collapse at
(
). Similarly to noninteracting atomic systems [
44], excessively high temperatures critically destabilize optomechanical coupling, inducing entanglement collapse. Notably, observing regimes with solely indirect coupling entanglement using Rydberg atoms requires even stricter temperature conditions in our system.
Experimentally verifying the three types of bipartite entanglement requires the measurement of the corresponding covariance matrix. This involves distinct detection protocols for different subsystems. Specifically, the optomechanical quadratures (cavity field and mechanical variables) are accessible through homodyne detection of the cavity output, while atomic polarization quadratures are measured via Stokes parameter analysis, employing a laser beam transversely aligned relative to both the cavity axis and atomic cell. This probe laser is off-resonance-tuned to an auxiliary atomic transition for measurements [
37].