A Deep Learning Model for Spectral Reconstruction of Arrayed Micro-Resonators
Abstract
1. Introduction
2. Materials and Methods
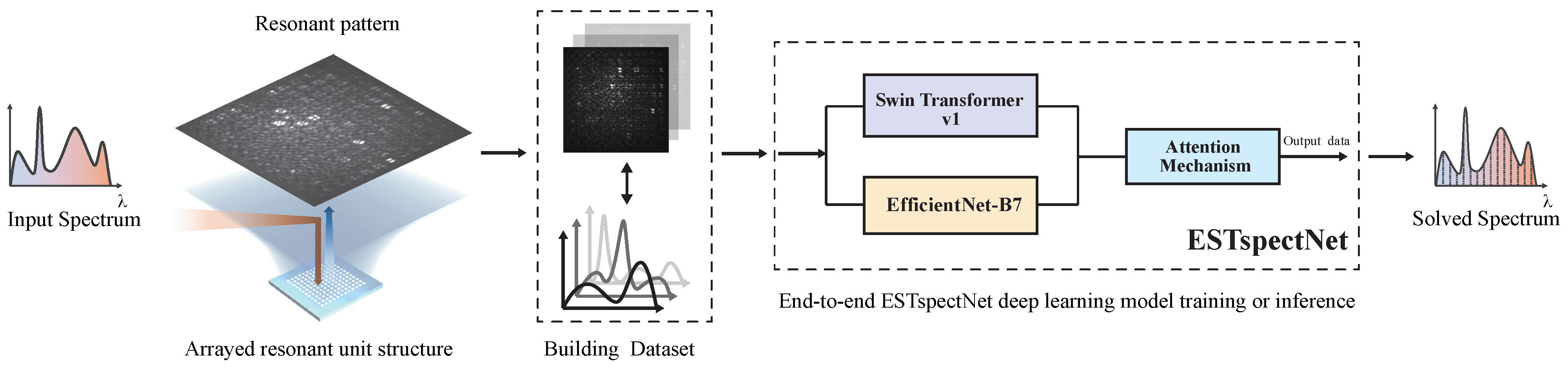
2.1. Principle of Spectrum Reconstruction Using an Array Strategy
- Ill-posedness: Due to the undersampling nature of array responses, the reconstruction problem is inherently ill-posed. Conventional methods require strong regularization constraints, which may lead to the loss of spectral details.
- Nonlinear responses: Practical systems are usually less ideal in detector’s nonlinearities and optical crosstalk. Conventional linear models struggle to accurately capture these nonlinear characteristics.
- Noise sensitivity: Various noise sources, including CMOS readout noise and dark current noise, significantly degrade reconstruction quality. Traditional denoising methods have limitations in preserving spectral features effectively.
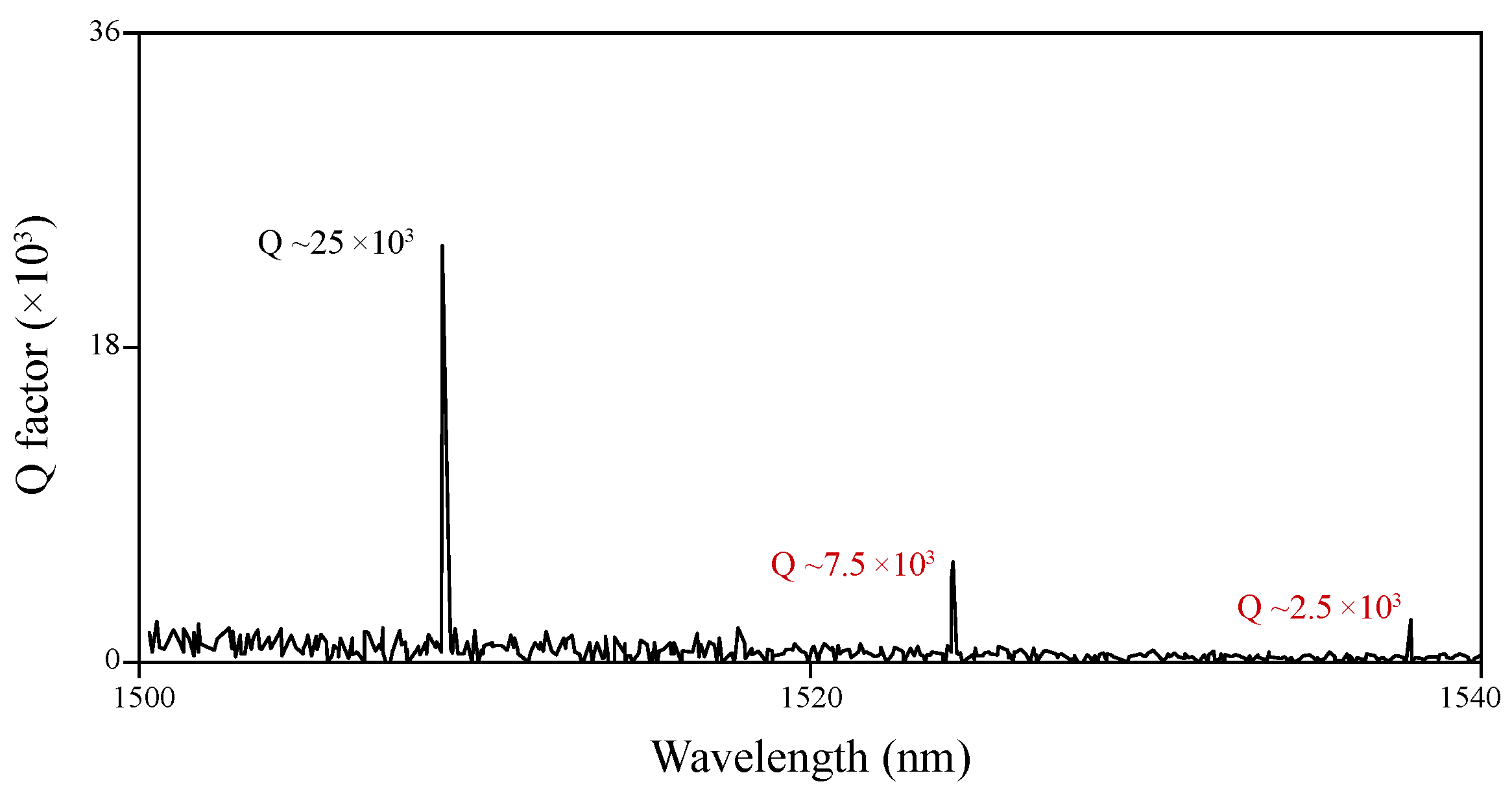
2.2. Photonic Crystal Microcavity Array: Design, Fabrication, and Testing
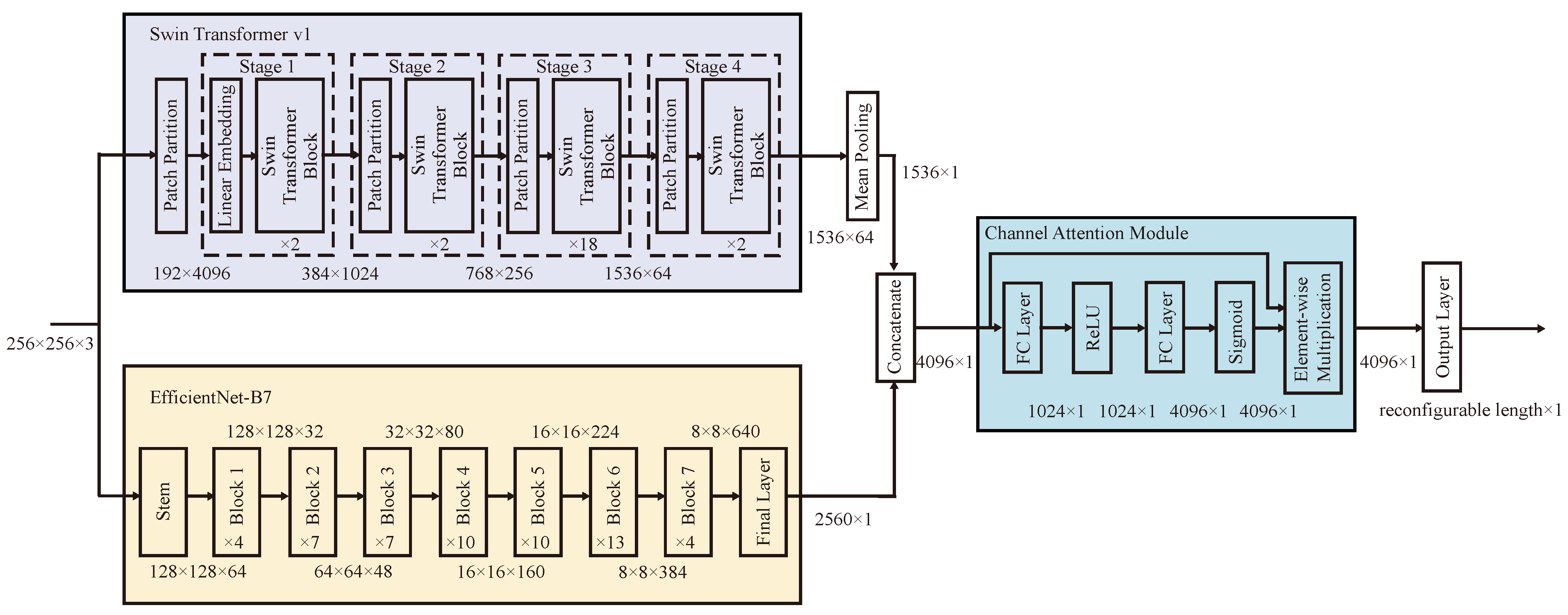
2.3. ESTspecNet: An End-to-End Learning Model for Image-to-Spectrum Reconstruction
- Dimension Compression: The first fully connected layer compresses the feature dimension from 4096 to 1024 using learnable parameters and :
- Non-Linear Activation applies ReLU activation to introduce non-linearity:
- Dimension Expansion: The second fully connected layer restores the original dimensionality with and :
- Adaptive Weighting generates channel-wise attention weights through sigmoid activation:
- Feature Enhancement performs element-wise multiplication to obtain the final weighted features:
3. Results
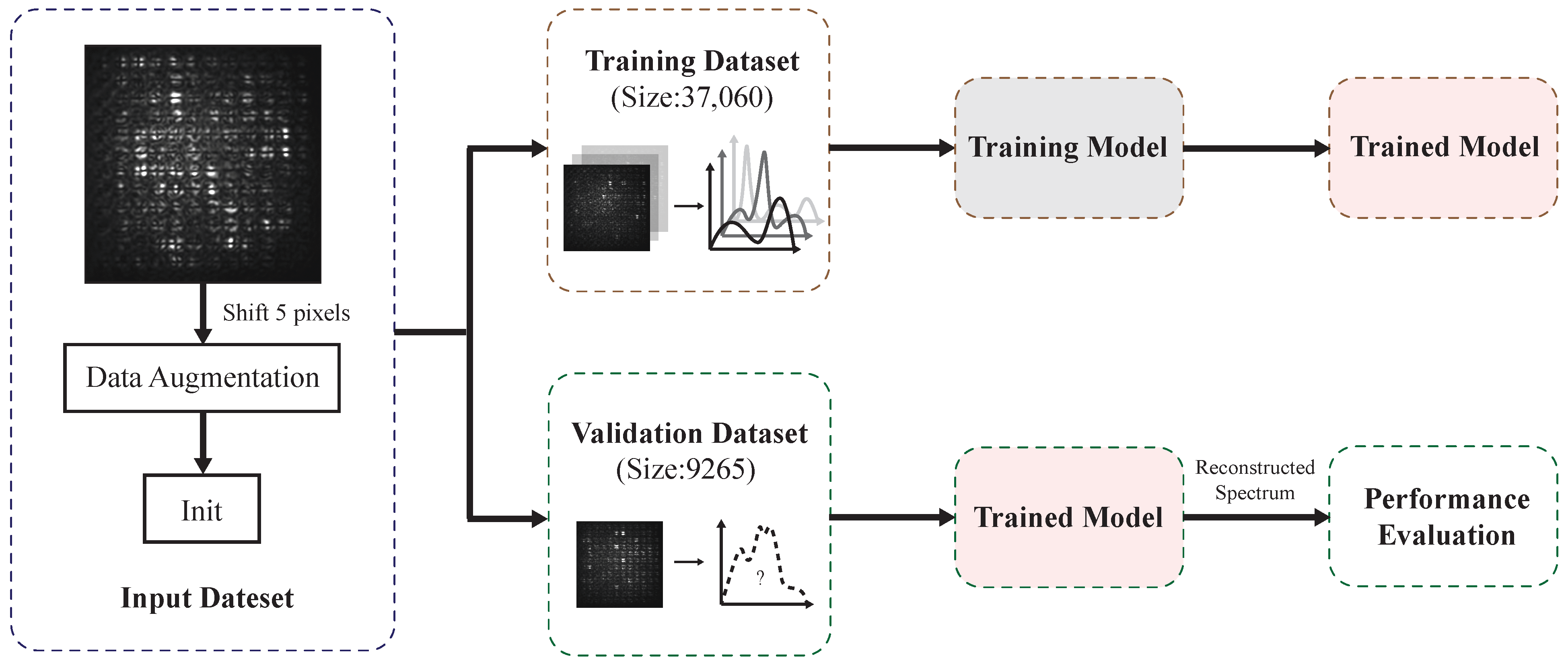
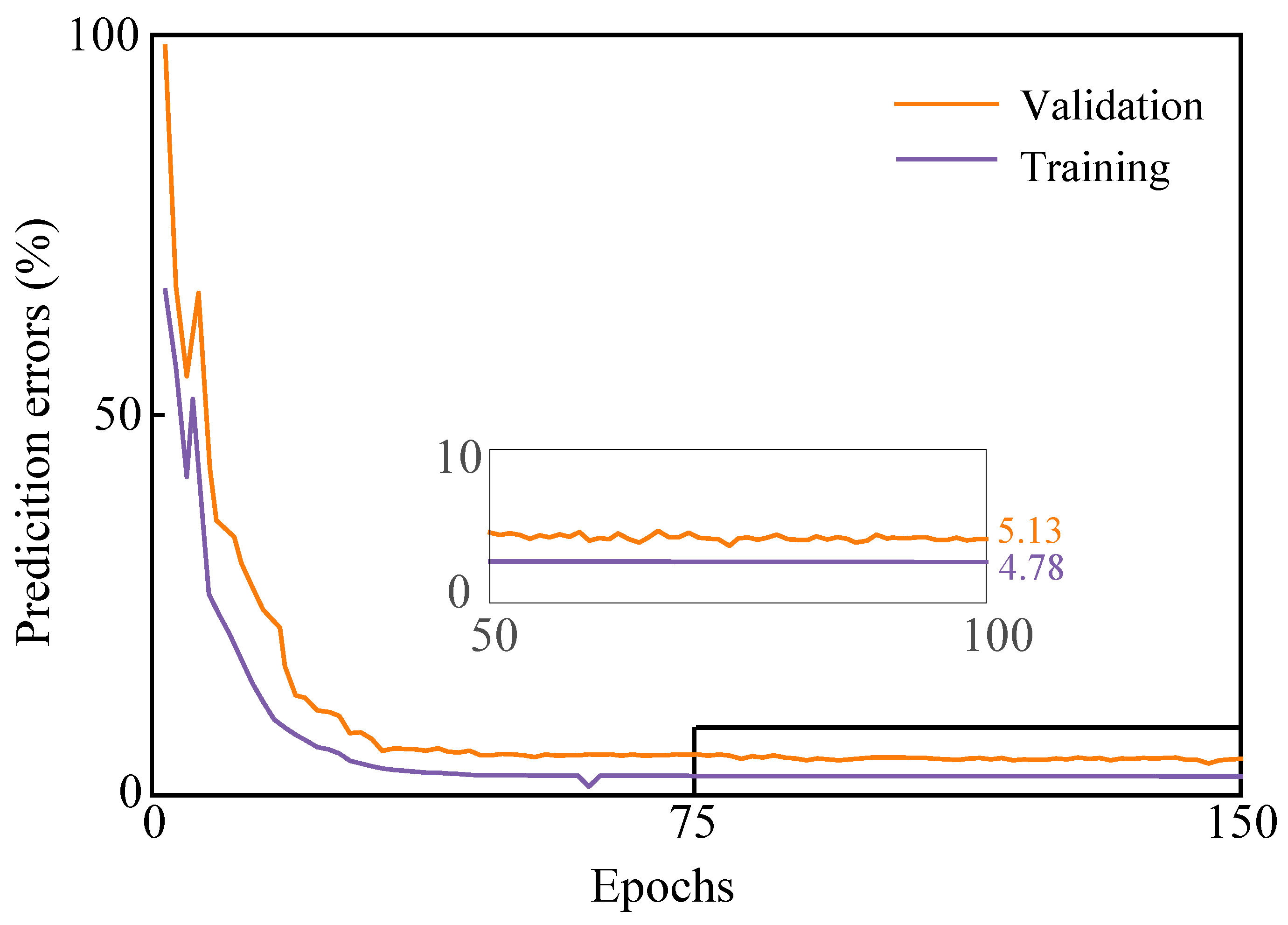
3.1. Experimental Data and Training Process
3.2. Metrics for Evaluating Spectral Reconstruction Performance
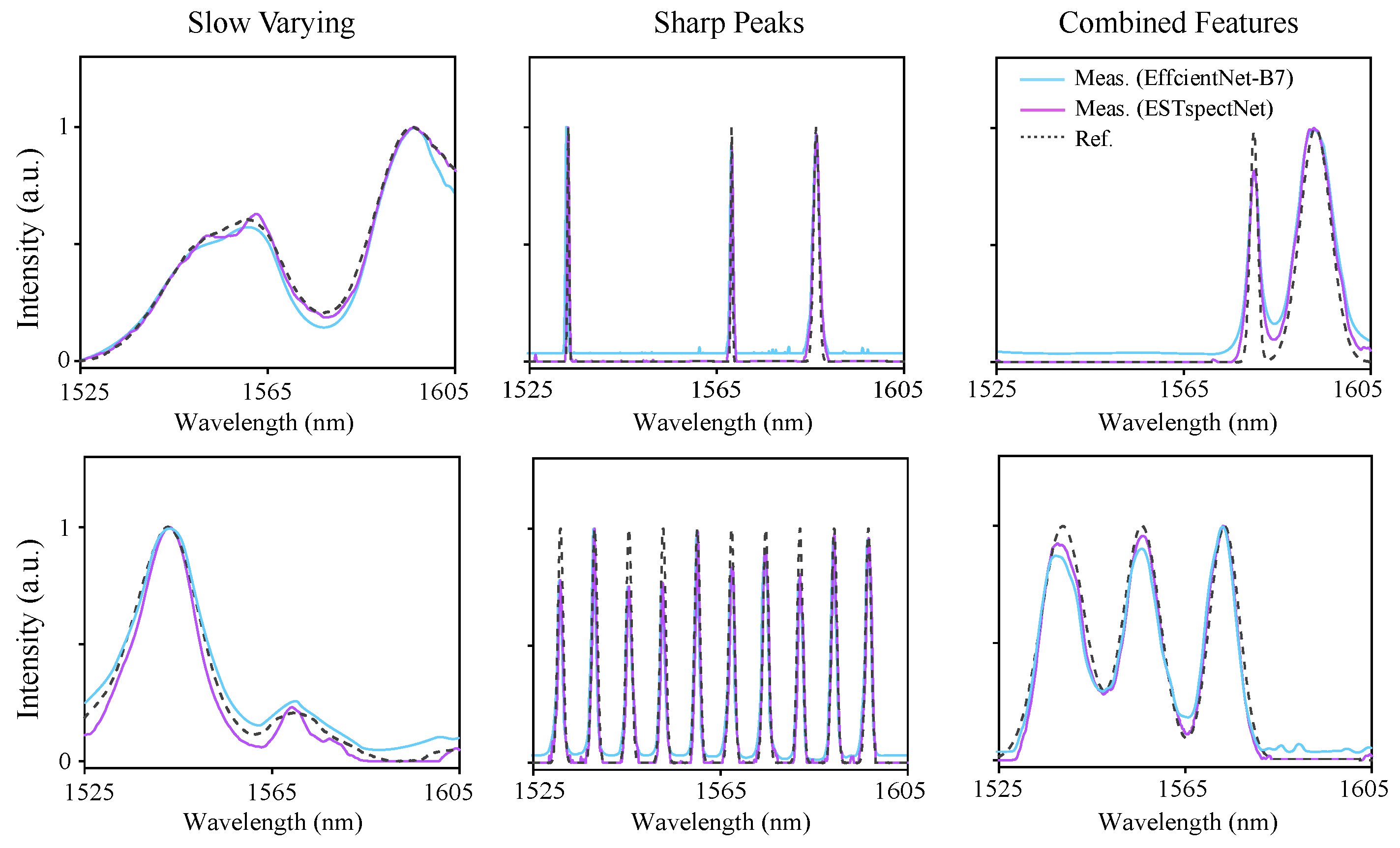
3.3. Model Performance and Analysis
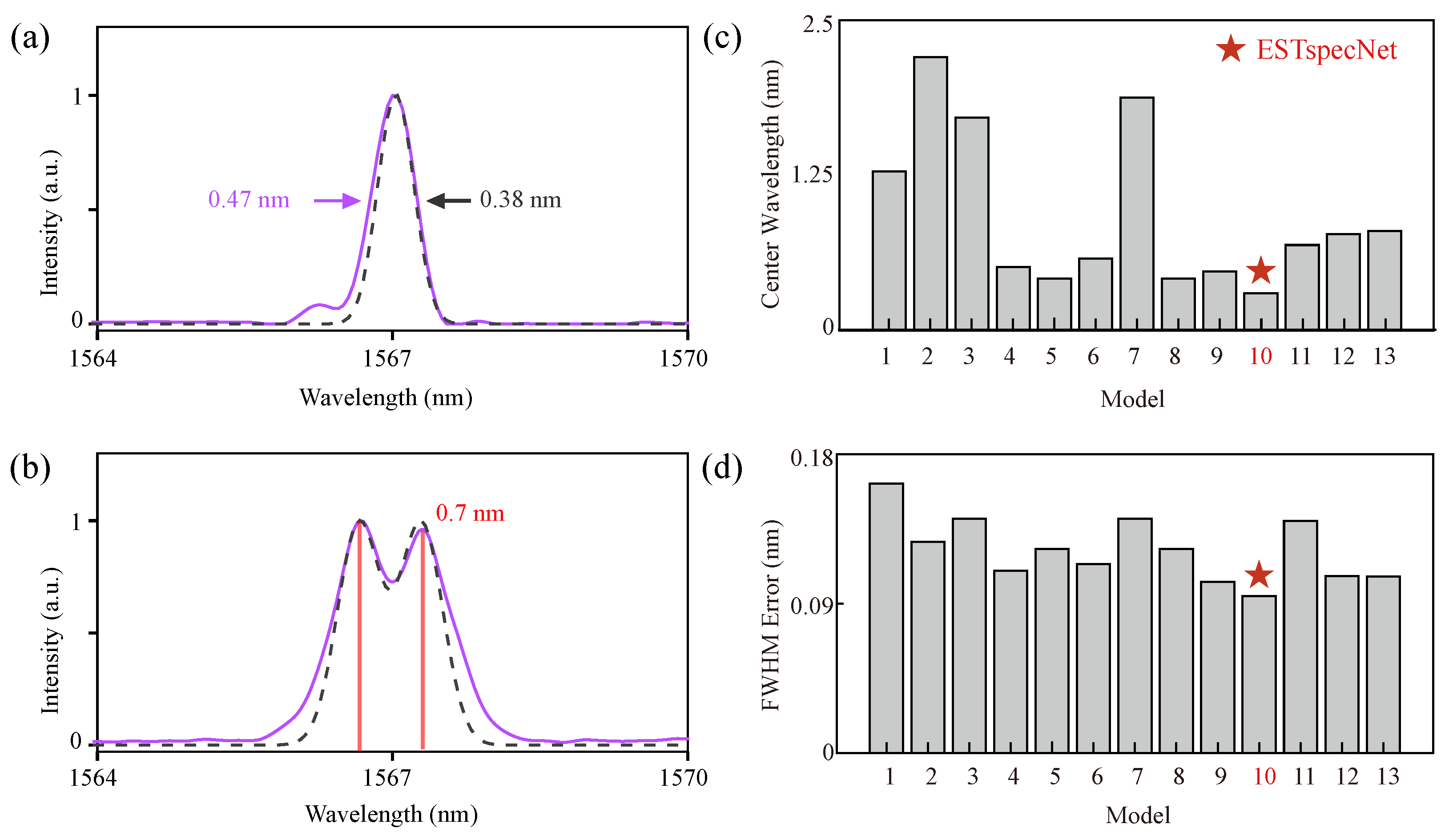
3.4. Model Performance Comparison
3.5. Impact of Data Augmentation
3.6. Effect of Attention Mechanism
3.7. Analysis of Model Fusion Strategies
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Q | quality factor |
| ML | machine learning |
| mini-BICs | miniaturized bound states in the continuum |
| ASE | amplified spontaneous emission |
| SOI | silicon-on-insulator |
| ICP | inductively coupled plasma |
| EBL | electron beam lithography |
| SNR | signal-to-noise ratios |
| MBConv | mobile inverted bottleneck convolution |
| CNNs | convolutional neural networks |
| DNNs | deep neural networks |
| SE | squeeze-and-excitation |
| MSE | mean square error |
| FWHM | full width at half maximum |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index |
| PE | Peak error |
| FE | full width at half maximum error |
| CMOS | Complementary Metal-Oxide-Semiconductor |
References
- Babos, D.V.; Tadini, A.M.; De Morais, C.P.; Barreto, B.B.; Carvalho, M.A.; Bernardi, A.C.; Oliveira, P.P.; Pezzopane, J.R.; Milori, D.M.; Martin-Neto, L. Laser-induced breakdown spectroscopy (LIBS) as an analytical tool in precision agriculture: Evaluation of spatial variability of soil fertility in integrated agricultural production systems. Catena 2024, 239, 107914. [Google Scholar] [CrossRef]
- Barulin, A.; Kim, Y.; Oh, D.K.; Jang, J.; Park, H.; Rho, J.; Kim, I. Dual-wavelength metalens enables Epi-fluorescence detection from single molecules. Nat. Commun. 2024, 15, 26. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Yao, C.; Xia, J.; Wang, H.; Cheng, Q.; Penty, R.; Fainman, Y.; Pan, S. Advances in cost-effective integrated spectrometers. Light. Sci. Appl. 2022, 11, 174. [Google Scholar] [CrossRef]
- Calafiore, G.; Koshelev, A.; Dhuey, S.; Goltsov, A.; Sasorov, P.; Babin, S.; Yankov, V.; Cabrini, S.; Peroz, C. Holographic planar lightwave circuit for on-chip spectroscopy. Light. Sci. Appl. 2014, 3, e203. [Google Scholar] [CrossRef]
- Zheng, S.; Cai, H.; Song, J.; Zou, J.; Liu, P.Y.; Lin, Z.; Kwong, D.L.; Liu, A.Q. A single-chip integrated spectrometer via tunable microring resonator array. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Kita, D.M.; Miranda, B.; Favela, D.; Bono, D.; Michon, J.; Lin, H.; Gu, T.; Hu, J. High-performance and scalable on-chip digital Fourier transform spectroscopy. Nat. Commun. 2018, 9, 4405. [Google Scholar] [CrossRef]
- Zheng, Q.; Nan, X.; Chen, B.; Wang, H.; Nie, H.; Gao, M.; Liu, Z.; Wen, L.; Cumming, D.R.; Chen, Q. On-Chip Near-Infrared Spectral Sensing with Minimal Plasmon-Modulated Channels. Laser Photonics Rev. 2023, 17, 2300475. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cui, H.; Alexander-Webber, J.; Gu, F.; Wang, X.; Wu, T.C.; Zhuge, M.; Williams, C.; Wang, P.; et al. Single-nanowire spectrometers. Science 2019, 365, 1017–1020. [Google Scholar] [CrossRef]
- Lin, X.; Wang, W.; Zhao, Y.; Yan, R.; Li, J.; Chen, H.; Lu, G.; Liu, F.; Du, G. High-accuracy direction measurement and high-resolution computational spectral reconstruction based on photonic crystal array. Opt. Express 2024, 32, 36085–36092. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, S.; Chen, A.; Zhou, M.; Luk, T.S.; James, A.; Nogan, J.; Ross, W.; Joe, G.; Shahsafi, A.; et al. Single-shot on-chip spectral sensors based on photonic crystal slabs. Nat. Commun. 2019, 10, 1020. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, H.; Zheng, Y.; Xu, Y.; Bao, J. Dual-layer broadband encoding spectrometer: Enhanced encoder basis orthogonality and spectral detection accuracy. Opt. Express 2024, 32, 39222–39244. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Bian, L.; Fu, H.; Wang, L.; Zou, B.; Dai, Q.; Zhang, J.; Zhong, H. Broadband perovskite quantum dot spectrometer beyond human visual resolution. Light. Sci. Appl. 2020, 9, 73. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Al Husseini, D.; Li, J.; Lin, Z.; Sukhishvili, S.; Cote, G.L.; Gutierrez-Osuna, R.; Lin, P.T. Mid-Infrared Serial Microring Resonator Array for Real-Time Detection of Vapor-Phase Volatile Organic Compounds. Anal. Chem. 2022, 94, 11008–11015. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Gan, X.; Zhu, Y.; Zhang, J. On-chip micro-ring resonator array spectrum detection system based on convex optimization algorithm. Nanophotonics 2023, 12, 715–724. [Google Scholar] [CrossRef]
- Guan, Q.; Lim, Z.H.; Sun, H.; Chew, J.X.Y.; Zhou, G. Review of miniaturized computational spectrometers. Sensors 2023, 23, 8768. [Google Scholar] [CrossRef]
- Björck, Å. Least squares methods. Handb. Numer. Anal. 1990, 1, 465–652. [Google Scholar]
- Oliver, J.; Lee, W.; Park, S.; Lee, H.N. Improving resolution of miniature spectrometers by exploiting sparse nature of signals. Opt. Express 2012, 20, 2613–2625. [Google Scholar] [CrossRef]
- Wang, W.; Dong, Q.; Zhang, Z.; Cao, H.; Xiang, J.; Gao, L. Inverse design of photonic crystal filters with arbitrary correlation and size for accurate spectrum reconstruction. Appl. Opt. 2023, 62, 1907–1914. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Silver, D.; Hasselt, H.; Hessel, M.; Schaul, T.; Guez, A.; Harley, T.; Dulac-Arnold, G.; Reichert, D.; Rabinowitz, N.; Barreto, A.; et al. The predictron: End-to-end learning and planning. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3191–3199. [Google Scholar]
- Chen, J.; Li, P.; Wang, Y.; Ku, P.C.; Qu, Q. Sim2Real in reconstructive spectroscopy: Deep learning with augmented device-informed data simulation. APL Mach. Learn. 2024, 2, 036106. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Wang, J.; Zhang, F.; Zhou, X.; Shen, X.; Niu, Q.; Yang, T. Miniaturized spectrometer based on MLP neural networks and a frosted glass encoder. Opt. Express 2024, 32, 30632–30641. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Wu, C.; Yu, M. Spectral Reconstruction for Internet of Things Based on Parallel Fusion of CNN and Transformer. IEEE Internet Things J. 2024, 12, 3549–3562. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, X.; Jin, J.; Zheng, Z.; Zhang, Z.; Wang, F.; He, L.; Zhen, B.; Peng, C. Observation of miniaturized bound states in the continuum with ultra-high quality factors. Sci. Bull. 2022, 67, 359–366. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, C.; Zhang, X.; Zuo, Y.; Zhang, Z.; Wang, F.; Chen, Z.; Li, H.; Peng, C. Miniaturized spectrometer enabled by end-to-end deep learning on large-scale radiative cavity array. arXiv 2024, arXiv:2411.13353. [Google Scholar]
- Peng, J.; Nie, W.; Li, T.; Xu, J. An end-to-end DOA estimation method based on deep learning for underwater acoustic array. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Gupta, A.; Mishra, R.; Zhang, Y. SenGLEAN: An End-to-End Deep Learning Approach for Super-Resolution of Sentinel-2 Multiresolution Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–19. [Google Scholar] [CrossRef]
- Signoroni, A.; Savardi, M.; Baronio, A.; Benini, S. Deep Learning Meets Hyperspectral Image Analysis: A Multidisciplinary Review. J. Imaging 2019, 5, 52. [Google Scholar] [CrossRef]
- Gao, L.; Qu, Y.; Wang, L.; Yu, Z. Computational spectrometers enabled by nanophotonics and deep learning. Nanophotonics 2022, 11, 2507–2529. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Bao, J. Solver-informed neural networks for spectrum reconstruction of colloidal quantum dot spectrometers. Opt. Express 2020, 28, 33656. [Google Scholar] [CrossRef]


| Model ID | Architecture | Training Configuration |
|---|---|---|
| Model 1 | EfficientNet-B7 | (baseline) |
| Model 2 | ResNet-50 | |
| Model 3 | Swin Transformer | |
| Model 4 | EfficientNet-B7 | + data augmentation |
| Model 5 | ResNet-50 | |
| Model 6 | Swin Transformer | |
| Model 7 | EfficientNet-B7 | + Attention + data augmentation |
| Model 8 | ResNet-50 | |
| Model 9 | Swin Transformer | |
| Model 10 | EfficientNet-B7 + ResNet-50 | + Attention + data augmentation |
| Model 11 | EfficientNet-B7 + Swin Transformer | |
| Model 12 | ResNet-50 + Swin Transformer | |
| Model 13 | EfficientNet-B7 + ResNet-50 + Swin Transformer | + Attention + data augmentation |
| Model | MSE () | PSNR (dB) | SSIM | Error (nm) | FWHM Error (nm) |
|---|---|---|---|---|---|
| Model 1 | 5.3 | 30.39 | 0.924 | 1.27 | 0.16 |
| Model 2 | 4.3 | 31.57 | 0.931 | 2.19 | 0.13 |
| Model 3 | 4.2 | 31.88 | 0.943 | 1.71 | 0.14 |
| Model 4 | 4.1 | 31.91 | 0.948 | 0.50 | 0.11 |
| Model 5 | 4.5 | 32.40 | 0.938 | 0.41 | 0.12 |
| Model 6 | 4.0 | 32.46 | 0.950 | 0.57 | 0.11 |
| Model | MSE () | PSNR (dB) | SSIM | Error (nm) | FWHM Error (nm) |
|---|---|---|---|---|---|
| Model 7 | 4.31 | 31.49 | 0.944 | 1.867 | 0.14 |
| Model 8 | 4.53 | 32.40 | 0.938 | 0.41 | 0.12 |
| Model 9 | 4.32 | 31.99 | 0.939 | 0.46 | 0.10 |
| Model | MSE () | PSNR (dB) | SSIM | Error (nm) | FWHM Error (nm) |
|---|---|---|---|---|---|
| Model 10 | 4.01 | 32.63 | 0.95 | 0.29 | 0.09 |
| Model 11 | 4.67 | 31.36 | 0.938 | 0.68 | 0.14 |
| Model 12 | 4.85 | 31.42 | 0.934 | 0.77 | 0.11 |
| Model 13 | 4.64 | 31.12 | 0.932 | 0.79 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Zhang, C.; Zheng, Z.; Li, H.; Peng, C. A Deep Learning Model for Spectral Reconstruction of Arrayed Micro-Resonators. Photonics 2025, 12, 449. https://doi.org/10.3390/photonics12050449
Zhou X, Zhang C, Zheng Z, Li H, Peng C. A Deep Learning Model for Spectral Reconstruction of Arrayed Micro-Resonators. Photonics. 2025; 12(5):449. https://doi.org/10.3390/photonics12050449
Chicago/Turabian StyleZhou, Xinyi, Cheng Zhang, Zhenyu Zheng, Hongbin Li, and Chao Peng. 2025. "A Deep Learning Model for Spectral Reconstruction of Arrayed Micro-Resonators" Photonics 12, no. 5: 449. https://doi.org/10.3390/photonics12050449
APA StyleZhou, X., Zhang, C., Zheng, Z., Li, H., & Peng, C. (2025). A Deep Learning Model for Spectral Reconstruction of Arrayed Micro-Resonators. Photonics, 12(5), 449. https://doi.org/10.3390/photonics12050449




