High-Performance Microwave-Frequency Comb Generation Based on Directly Modulated Laser with Filtering Operations
Abstract
1. Introduction
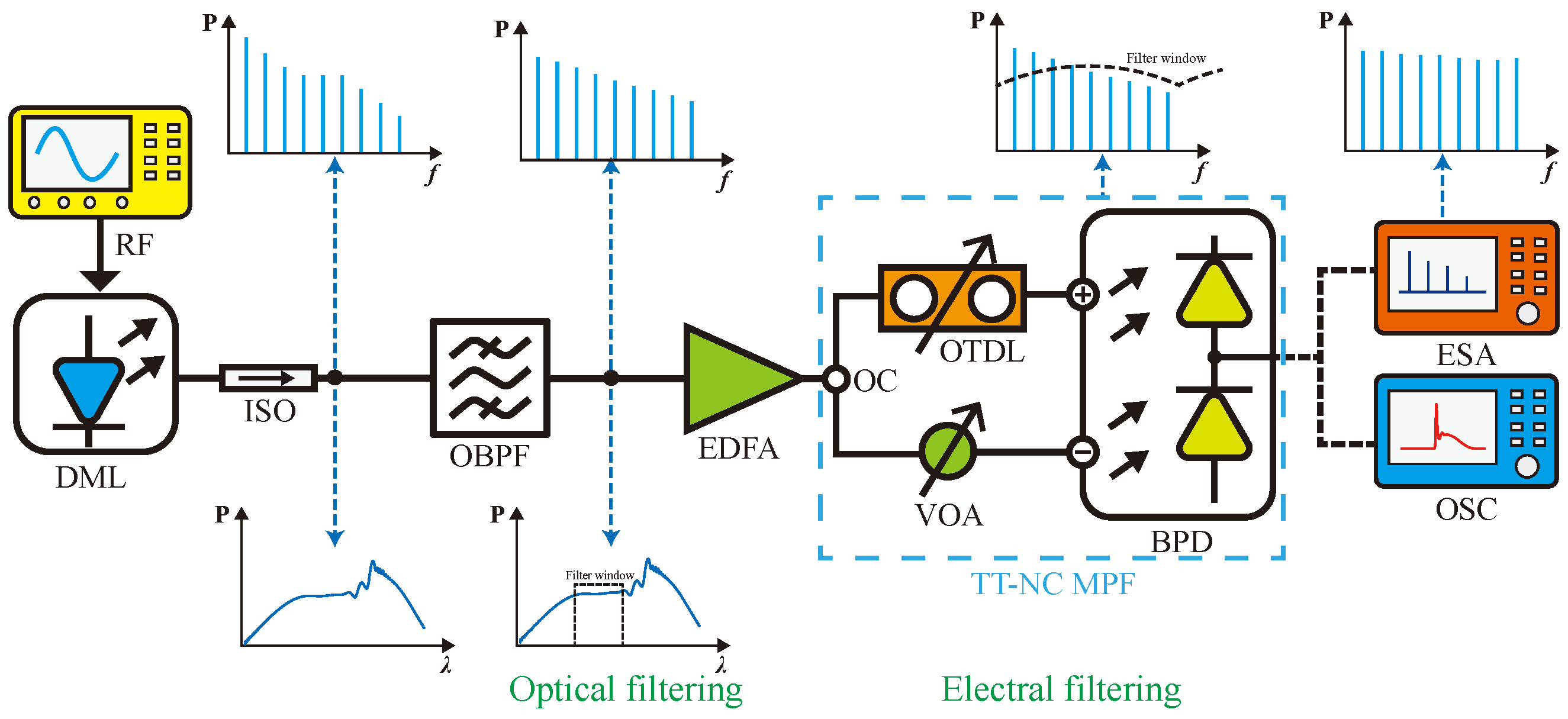
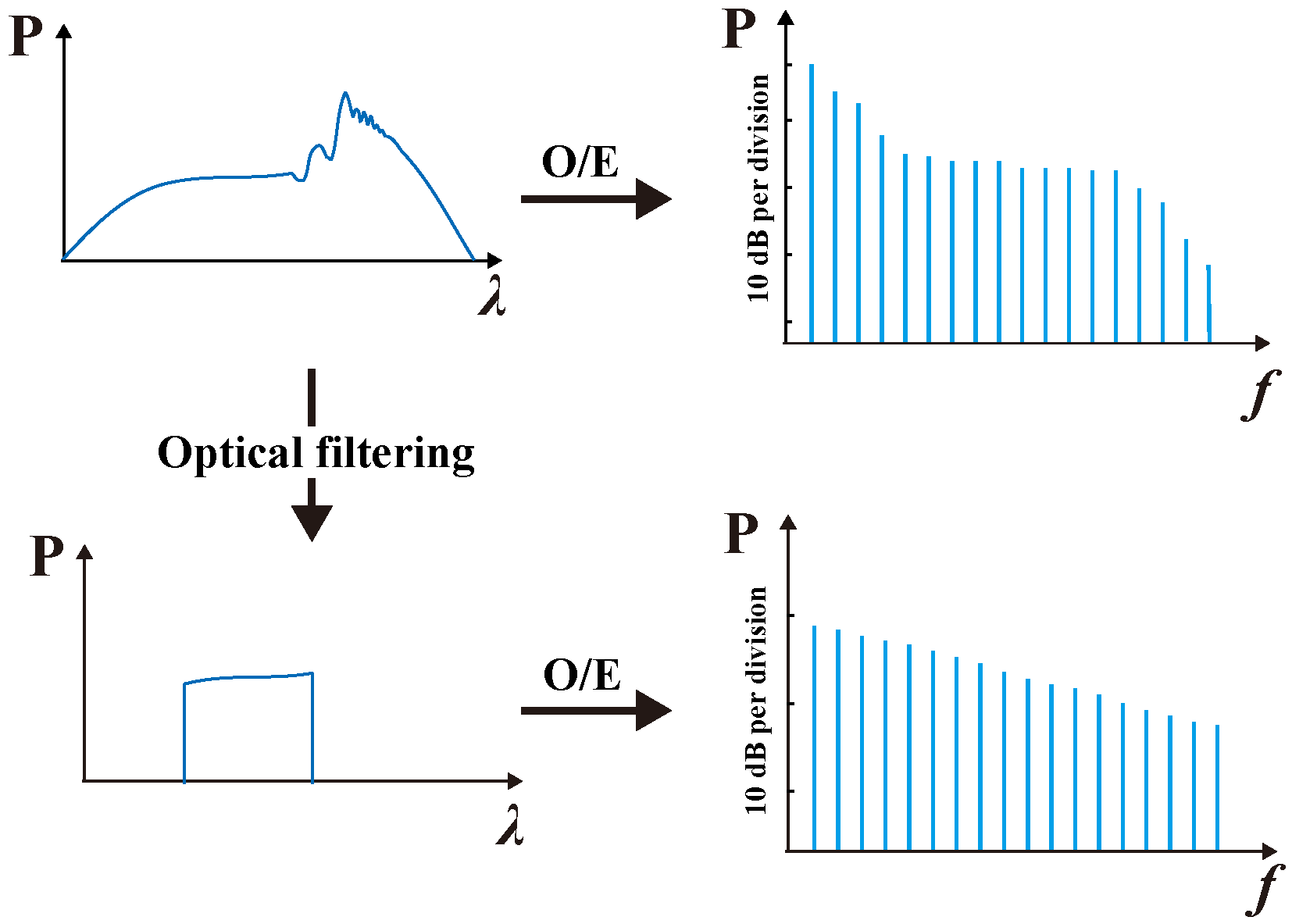
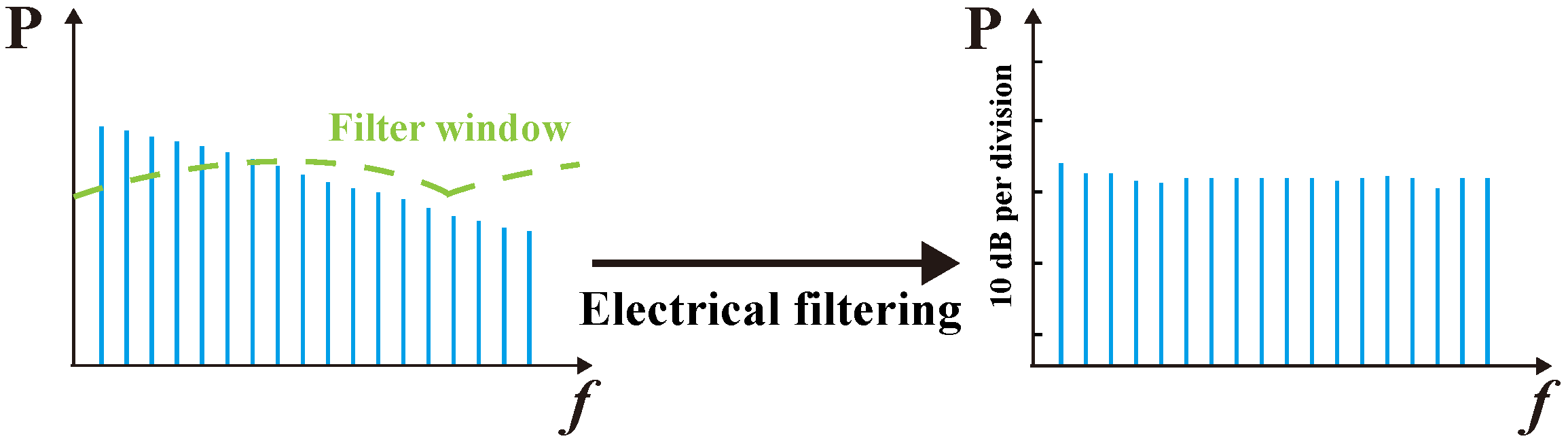
2. Principle
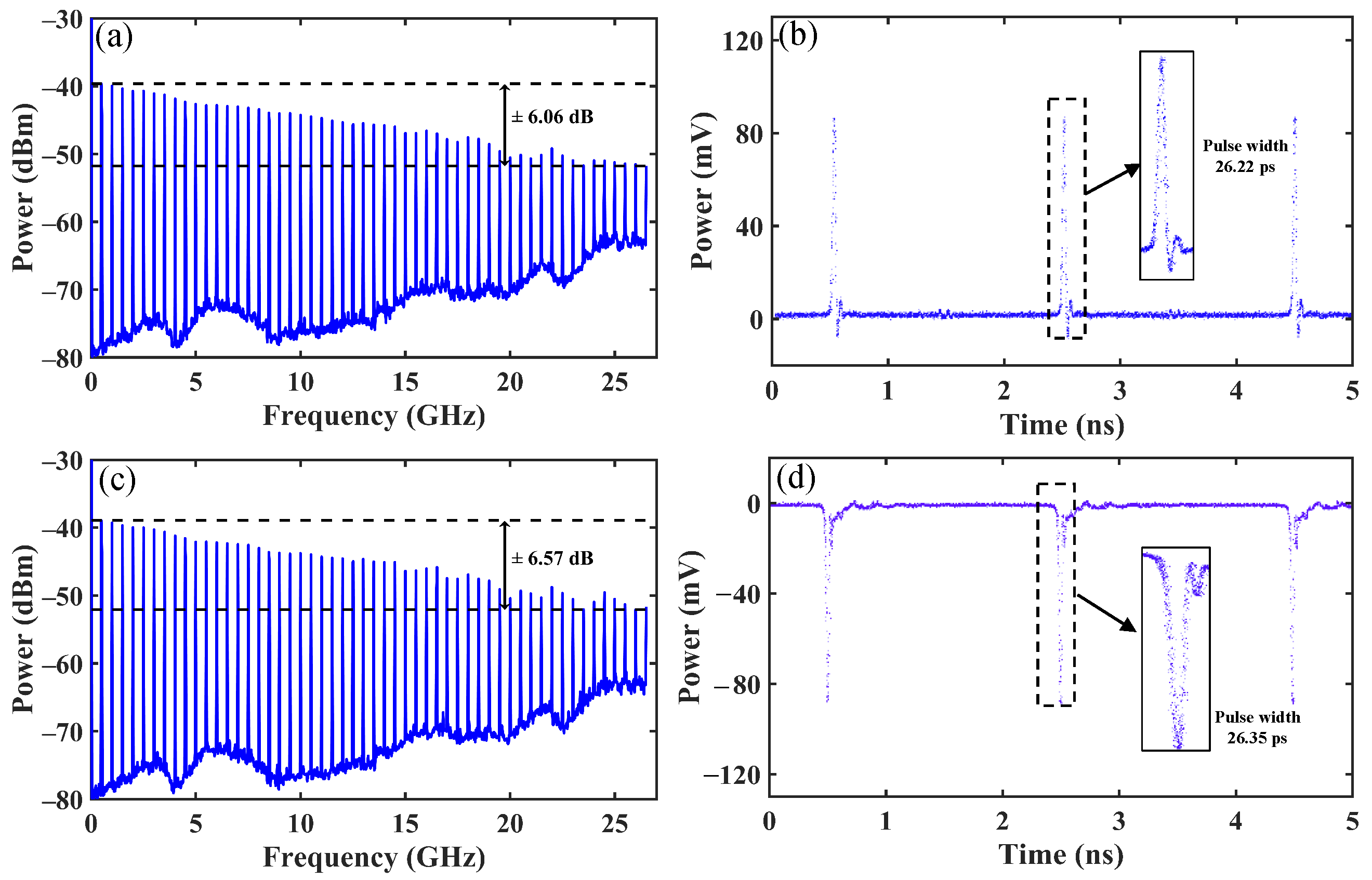
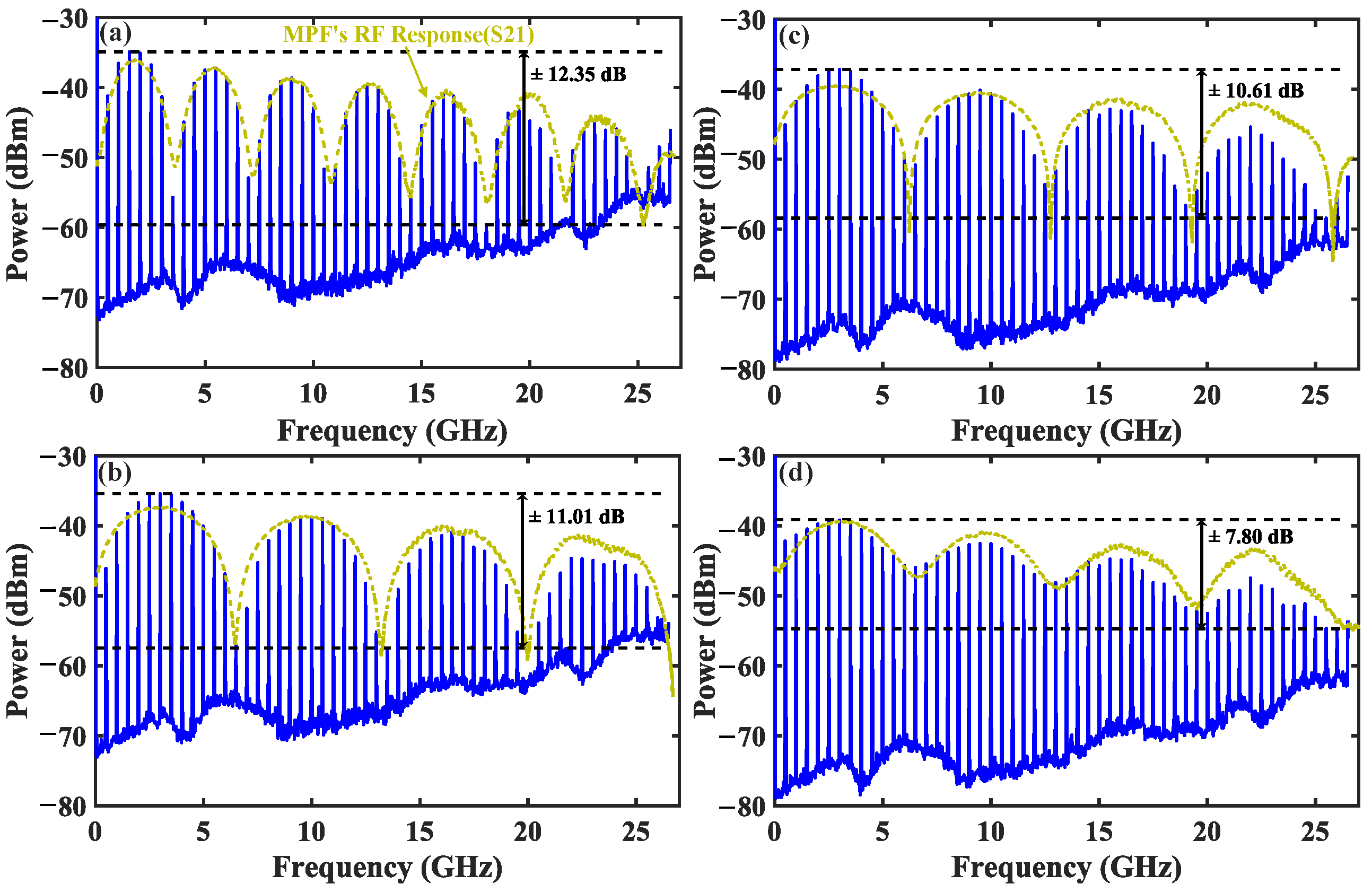
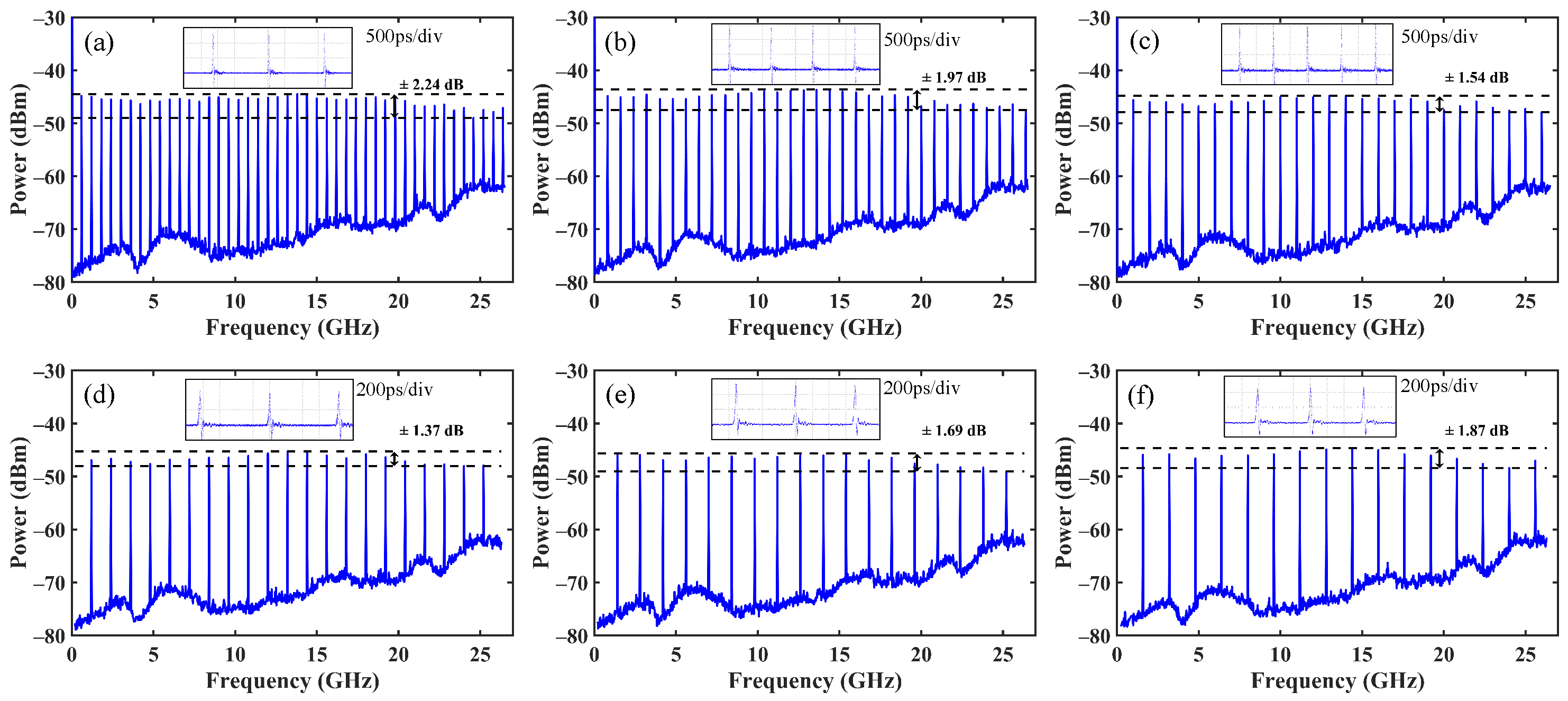
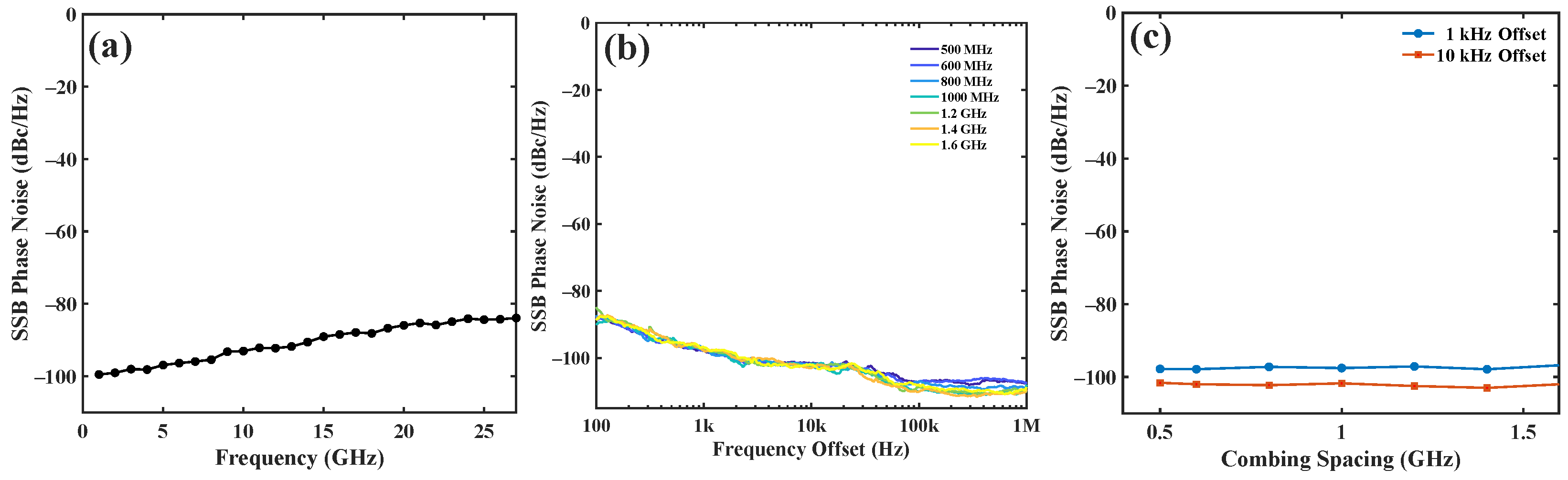
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shin, J.; Ryu, Y.; Miri, M.A.; Shim, S.B.; Choi, H.; Alù, A.; Suh, J.; Cha, J. On-Chip Microwave Frequency Combs in a Superconducting Nanoelectromechanical Device. Nano Lett. 2022, 22, 5459–5465. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lucas, E.; Raja, A.S.; He, J.; Riemensberger, J.; Wang, R.N.; Karpov, M.; Guo, H.; Bouchand, R.; Kippenberg, T.J. Photonic microwave generation in the X- and K-band using integrated soliton microcombs. Nat. Photonics 2020, 14, 486–491. [Google Scholar] [CrossRef]
- Zhang, L.H.; Liu, Z.K.; Liu, B.; Zhang, Z.Y.; Guo, G.C.; Ding, D.S.; Shi, B.S. Rydberg Microwave-Frequency-Comb Spectrometer. Phys. Rev. Appl. 2022, 18, 014033. [Google Scholar] [CrossRef]
- Wang, S.P.; Chen, Z.; Li, T. Controllable microwave frequency comb generation in a tunable superconducting coplanar-waveguide resonator*. Chin. Phys. B 2021, 30, 048501. [Google Scholar] [CrossRef]
- Corral, V.; Guzmán, R.; Gordón, C.; Leijtens, X.J.M.; Carpintero, G. Optical frequency comb generator based on a monolithically integrated passive mode-locked ring laser with a Mach–Zehnder interferometer. Opt. Lett. 2016, 41, 1937. [Google Scholar] [CrossRef]
- Wu, H.; Ma, T.; Lu, Q.; Ma, J.; Shi, L.; Mao, Q. Optical frequency combs based on a period-doubling mode-locked Er-doped fiber laser. Opt. Express 2018, 26, 577. [Google Scholar] [CrossRef]
- Akosman, A.E.; Sander, M.Y. Dual comb generation from a mode-locked fiber laser with orthogonally polarized interlaced pulses. Opt. Express 2017, 25, 18592. [Google Scholar] [CrossRef]
- Islam, M.S.; Kovalev, A.V.; Viktorov, E.A.; Citrin, D.S.; Locquet, A. Microwave Frequency Comb Generation by Gain-Switching Versus Relaxation Oscillations. IEEE Photonics Technol. Lett. 2021, 33, 491–494. [Google Scholar] [CrossRef]
- Li, B.; Wu, R.; Wang, Z.; Wang, X.; Zhang, X.; Hong, W.; Liu, H. Rational number harmonic mode-locked dual-loop optoelectronic oscillator with low supermode noise and low intermodulation distortions. Opt. Express 2022, 30, 30303–30311. [Google Scholar] [CrossRef]
- Shen, Z.; Jin, C.; Yang, J.; Zhang, S.; Tang, M.; Wang, K. Method for the generation of microwave frequency combs based on a Vernier optoelectronic feedback loop. Opt. Express 2020, 28, 35118–35127. [Google Scholar] [CrossRef]
- Tang, H.; Kong, Z.; Li, F.; Chen, X.; Li, M.; Zhu, N.; Li, W. Generation of Microwave Frequency Combs Based on Dual-Frequency Injected Optoelectronic Oscillator. J. Light. Technol. 2024, 42, 5522–5528. [Google Scholar] [CrossRef]
- He, Y.; Lopez-Rios, R.; Javid, U.A.; Ling, J.; Li, M.; Xue, S.; Vahala, K.; Lin, Q. High-speed tunable microwave-rate soliton microcomb. Nat. Commun. 2023, 14, 3467. [Google Scholar] [CrossRef] [PubMed]
- Parriaux, A.; Hammani, K.; Millot, G. Electro-optic frequency combs. In Advances in Optics and Photonics; Optica Publishing Group: Washington, DC, USA, 2020; Volume 12, pp. 223–287. [Google Scholar] [CrossRef]
- Rueda, A.; Sedlmeir, F.; Kumari, M.; Leuchs, G.; Schwefel, H.G.L. Resonant electro-optic frequency comb. Nature 2019, 568, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Eliason, T.; Parker, P.A.; Reber, M.A.R. Electro-optic frequency comb generation via cascaded modulators driven at lower frequency harmonics. Opt. Express 2024, 32, 36394–36404. [Google Scholar] [CrossRef]
- Zhang, M.; Buscaino, B.; Wang, C.; Shams-Ansari, A.; Reimer, C.; Zhu, R.; Kahn, J.M.; Lončar, M. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 2019, 568, 373–377. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, P.; Li, K.; Bao, H.; Li, N. Photonic generation of high-performance microwave frequency combs using an optically injected semiconductor laser with dual-loop optoelectronic feedback. Opt. Lett. 2021, 46, 4622–4625. [Google Scholar] [CrossRef]
- Juan, Y.S.; Lin, F.Y. Ultra broadband microwave frequency combs generated by an optical pulse-injected semiconductor laser. Opt. Express 2009, 17, 18596–18605. [Google Scholar] [CrossRef]
- Zhuang, J.P.; Li, X.Z.; Li, S.S.; Chan, S.C. Frequency-modulated microwave generation with feedback stabilization using an optically injected semiconductor laser. Opt. Lett. 2016, 41, 5764–5767. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, Y.; Li, J.; Li, S.; Zhang, Z.; Zhang, S.; Liu, Y. Tunable microwave frequency comb generation via periodic relaxation oscillation in directly modulated laser. Opt. Laser Technol. 2024, 170, 110295. [Google Scholar] [CrossRef]
- Lau, K.Y. Gain switching of semiconductor injection lasers. Appl. Phys. Lett. 1988, 52, 257–259. [Google Scholar] [CrossRef]
- Riecke, S.M.; Wenzel, H.; Schwertfeger, S.; Lauritsen, K.; Paschke, K.; Erdmann, R.; Erbert, G. Picosecond Spectral Dynamics of Gain-Switched DFB Lasers. IEEE J. Quantum Electron. 2011, 47, 715–722. [Google Scholar] [CrossRef]
- Cho, S.-D.; Lee, C.-H.; Shin, S.-Y. Limit of optical pulsewidth in the gain-switched DFB semiconductor laser. IEEE Photonics Technol. Lett. 1999, 11, 782–784. [Google Scholar] [CrossRef]
- Rosado, A.; Pérez-Serrano, A.; Tijero, J.M.G.; Valle, Á.; Pesquera, L.; Esquivias, I. Enhanced optical frequency comb generation by pulsed gain-switching of optically injected semiconductor lasers. Opt. Express 2019, 27, 9155. [Google Scholar] [CrossRef]
- Rosado, A.; Pérez-Serrano, A.; Tijero, J.M.G.; Valle, Á.; Pesquera, L.; Esquivias, I. Experimental study of optical frequency comb generation in gain-switched semiconductor lasers. Opt. Laser Technol. 2018, 108, 542–550. [Google Scholar] [CrossRef]
- Boerma, H.; Ganzer, F.; Runge, P.; Schell, M.; Fernandes, E.; Rudin, B.; Emaury, F. Microwave Photonic PS-Pulse and 140 GHz RF Comb Generator. J. Light. Technol. 2023, 41, 3533–3538. [Google Scholar] [CrossRef]
- Shen, C.; Li, P.; Zhu, X.; Zhang, Y.; Han, Y. Ultra-flat broadband microwave frequency comb generation based on optical frequency comb with a multiple-quantum-well electro-absorption modulator in critical state. Front. Optoelectron. 2019, 12, 382–391. [Google Scholar] [CrossRef]
- He, S.; Deng, Z.; Wang, S.; Xiong, S.; Zhang, M.; Di, Y.; Liu, C.; Li, X.; Luo, D.; Gu, C.; et al. A 62-fs All-Fiber Wideband Flat-Top Spectrum Electro-Optic Comb via Time-Frequency Domain Shaping. J. Light. Technol. 2024, 42, 4756–4762. [Google Scholar] [CrossRef]
- Yuan, J.; Yang, W.; Jing, M.; Zhang, H.; Jiao, Y.; Li, W.; Zhang, L.; Xiao, L.; Jia, S. Quantum sensing of microwave electric fields based on Rydberg atoms. Rep. Prog. Phys. 2023, 86, 106001. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, Q.; Jiang, Y.; Xu, J.; Lan, X.; Feng, J.; Yu, J.; Luo, Y.; Jiang, T.; Zhang, H.; Wu, Y. High-Performance Microwave-Frequency Comb Generation Based on Directly Modulated Laser with Filtering Operations. Photonics 2025, 12, 433. https://doi.org/10.3390/photonics12050433
Long Q, Jiang Y, Xu J, Lan X, Feng J, Yu J, Luo Y, Jiang T, Zhang H, Wu Y. High-Performance Microwave-Frequency Comb Generation Based on Directly Modulated Laser with Filtering Operations. Photonics. 2025; 12(5):433. https://doi.org/10.3390/photonics12050433
Chicago/Turabian StyleLong, Qianyou, Yang Jiang, Jing Xu, Xiaohong Lan, Jinjian Feng, Jiancheng Yu, Yunkun Luo, Tingyi Jiang, Hui Zhang, and Yu Wu. 2025. "High-Performance Microwave-Frequency Comb Generation Based on Directly Modulated Laser with Filtering Operations" Photonics 12, no. 5: 433. https://doi.org/10.3390/photonics12050433
APA StyleLong, Q., Jiang, Y., Xu, J., Lan, X., Feng, J., Yu, J., Luo, Y., Jiang, T., Zhang, H., & Wu, Y. (2025). High-Performance Microwave-Frequency Comb Generation Based on Directly Modulated Laser with Filtering Operations. Photonics, 12(5), 433. https://doi.org/10.3390/photonics12050433





