Comparison of Thin-Film Lithium Niobate, SOH, and POH for Silicon Photonic Modulators
Abstract
1. Introduction
2. An Overview of These Technologies
2.1. Silicon’s Modulating Characteristics
- Free-Carrier Dispersion Phenomenon: Electro-optic Effect
- Compared to lithium niobate and various other materials, silicon exhibits limited electro-optical effects due to the free-carrier dispersion effect on its refractive index. This effect comes from an increase or decrease in carriers (electrons and holes), which changes the refractive index of silicon, as shown in the following equation:Δn (at 1550 nm) = −[8.8 × 10−22 × ΔN + 8.5× 10−18 × ΔP0.8]Δn (at 1310 nm) = −[6.2 × 10−22 × ΔN + 6 × 10−18 × ΔP0.8]The change in absorption is described byΔα (at 1550 nm) = 8.5 × 10−18 × ΔN + 6 × 10−18 × ΔP [cm−1]where ΔN and ΔP are the carrier densities of electrons and holes.Δα (at 1310 nm) = 6 × 10−18 × ΔN + 4 × 10−1 8 × ΔP [cm−1]
- The change in refractive index affects the phase or amplitude of light passing through silicon, allowing interferometers to modify the phase or intensity.
- Silicon waveguide p-n junctions utilize free-carrier dispersion. Applying a voltage across the junction enables the movement of carriers, thereby modifying the optical characteristics of the silicon waveguide.
- 2.
- Plasma Dispersion Effect:
- The plasma dispersion effect can change silicon’s absorbance and refractive index by altering the concentration of free carriers (electrons and holes).
- Applying a forward or reverse bias across the p-n junction changes the number of silicon carriers. This changes the waveguide’s refractive index, the way it absorbs light, and how it moves.
- 3.
- Carrier Injection, Depletion, and Accumulation:
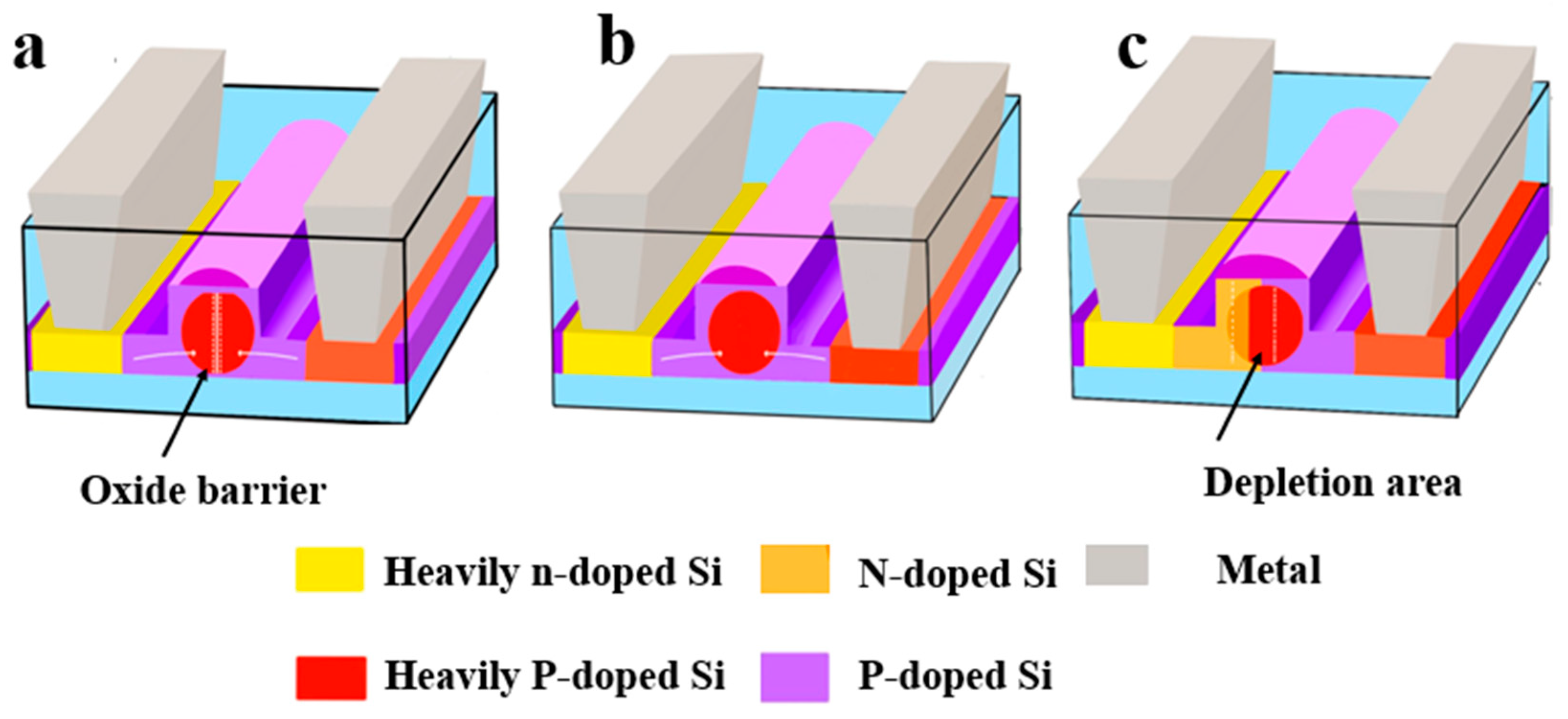
- Carrier injection: modulators introduce carriers into silicon waveguides through a forward-biased PN junction. Injection carriers alter the refractive index and absorption of the waveguide.
- Carrier depletion: Modulators use a reverse-biased p-n junction to remove carriers from a silicon waveguide.
- Carrier accumulation: When a voltage is applied across the silicon dioxide interface, it leads to the accumulation of carriers, which subsequently changes the refractive index.
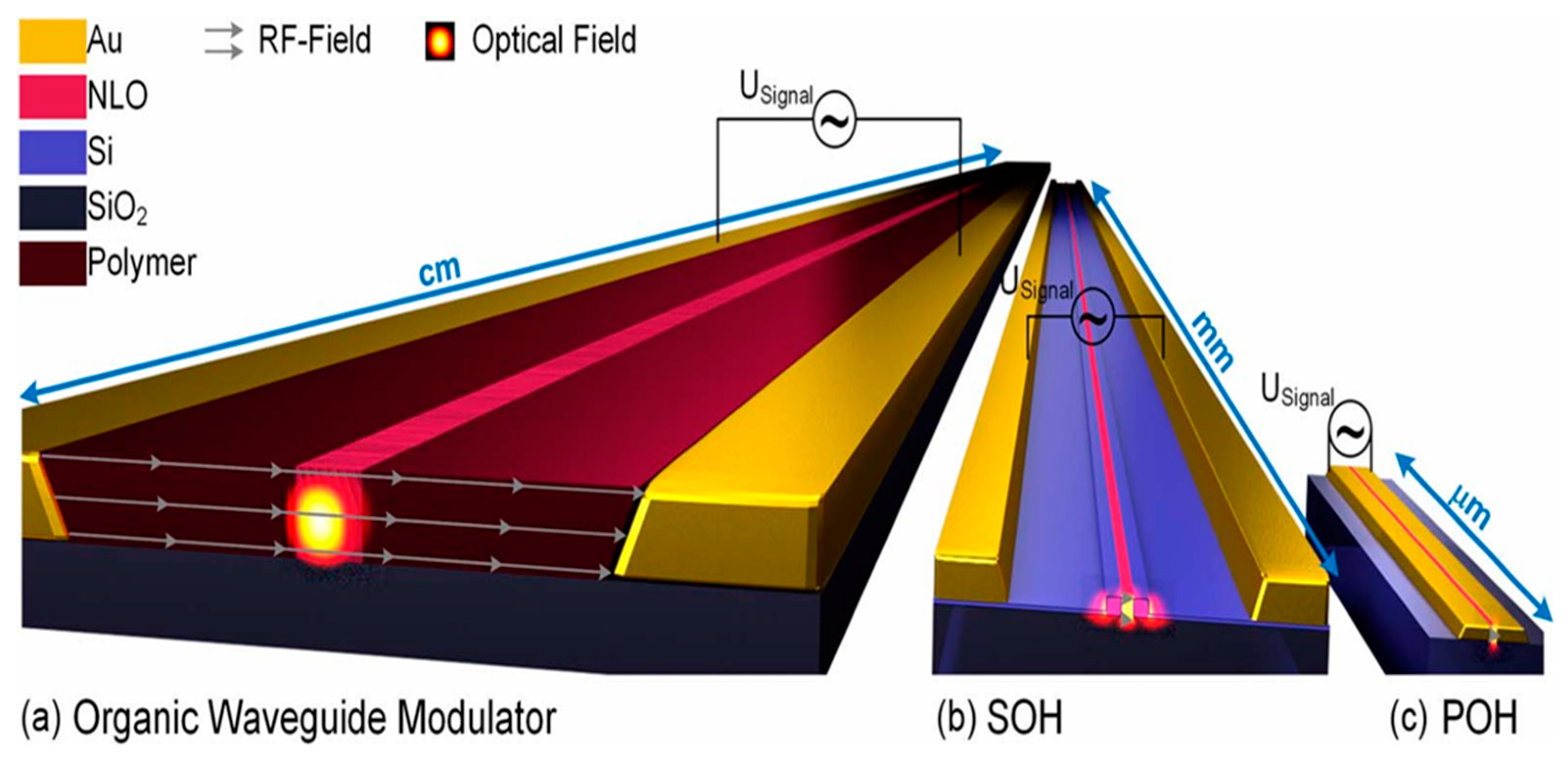
2.2. Overview of Technologies: TFLN/SOH/POH Modulator
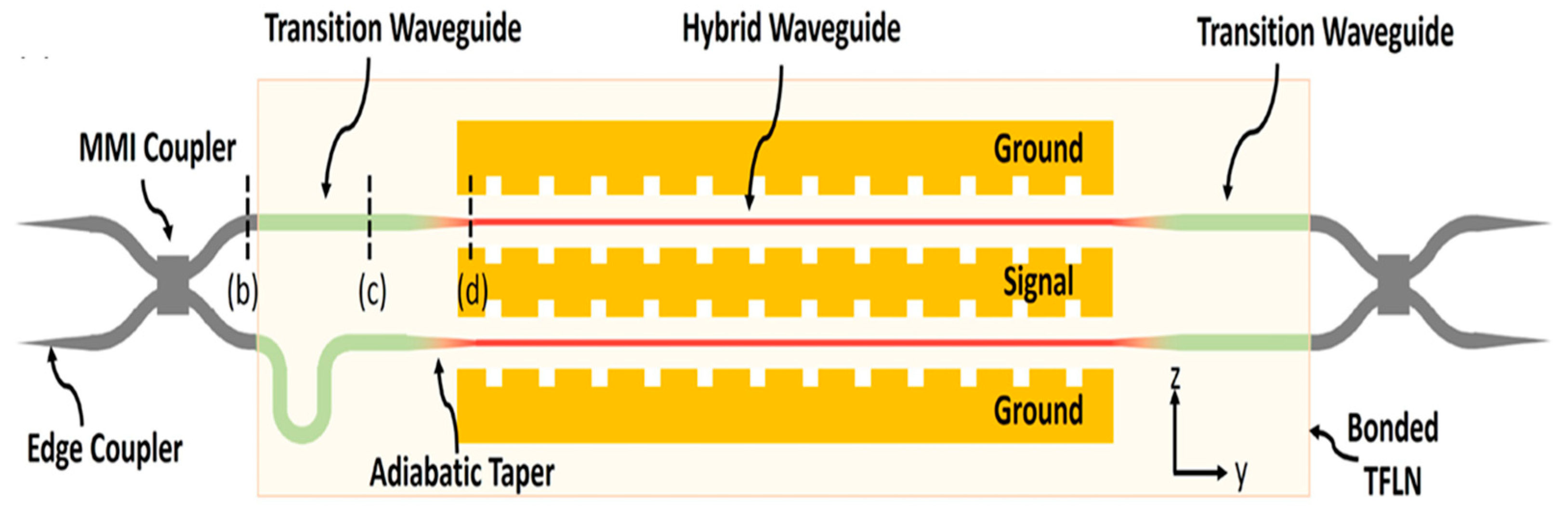
2.2.1. Thin-Film LiNbO3 Modulator Technology
- Fabrication Complexity: The highly complex bonding steps lead to non-uniform electro-optical performance and higher optical losses, which reduces production yields and makes the process more difficult to scale up.
- Optical Loss: Even though lithium niobate is a low-loss material, it can cause optical losses and manufacturing flaws that lower the efficiency and performance of modulators used for long-distance communication and applications that need to save power.
- Thermal Management: The refractive index of lithium niobate changes with temperature, which can affect the operation of TFLN modulators, especially in photonic circuits that are tightly mounted and cannot dissipate heat well. This results in phase drift and reduced efficiency.
- Driving voltage and power consumption: LN modulators need high driving voltages to provide a large modulation depth. This makes it difficult to lower the voltage without affecting performance or power and presents a challenge for applications that require power conservation.
- High-Frequency Operation: Due to the limitations of the electrode design and modulator signal transmission, high-frequency operation (e.g., above 100 GHz) with low loss and efficient modulation becomes difficult.
2.2.2. Silicon–Organic Hybrid Modulator Technology
- Material Long-Term Stability: The slot in the optical waveguide is narrow, so the chromophores are exposed to extremely high light intensities, leading to lifetime limitations. Another factor is the lack of eccentric order between chromophores due to operating at the glass-transition temperature, Tg. Both effects improve the half-wave voltage Vπ.
- Photochemical bleaching: When high optical intensities and oxygen are used in SOH devices, photochemical bleaching occurs. This breaks down electro-optic material permanently and raises the half-wave voltage Vπ [70].
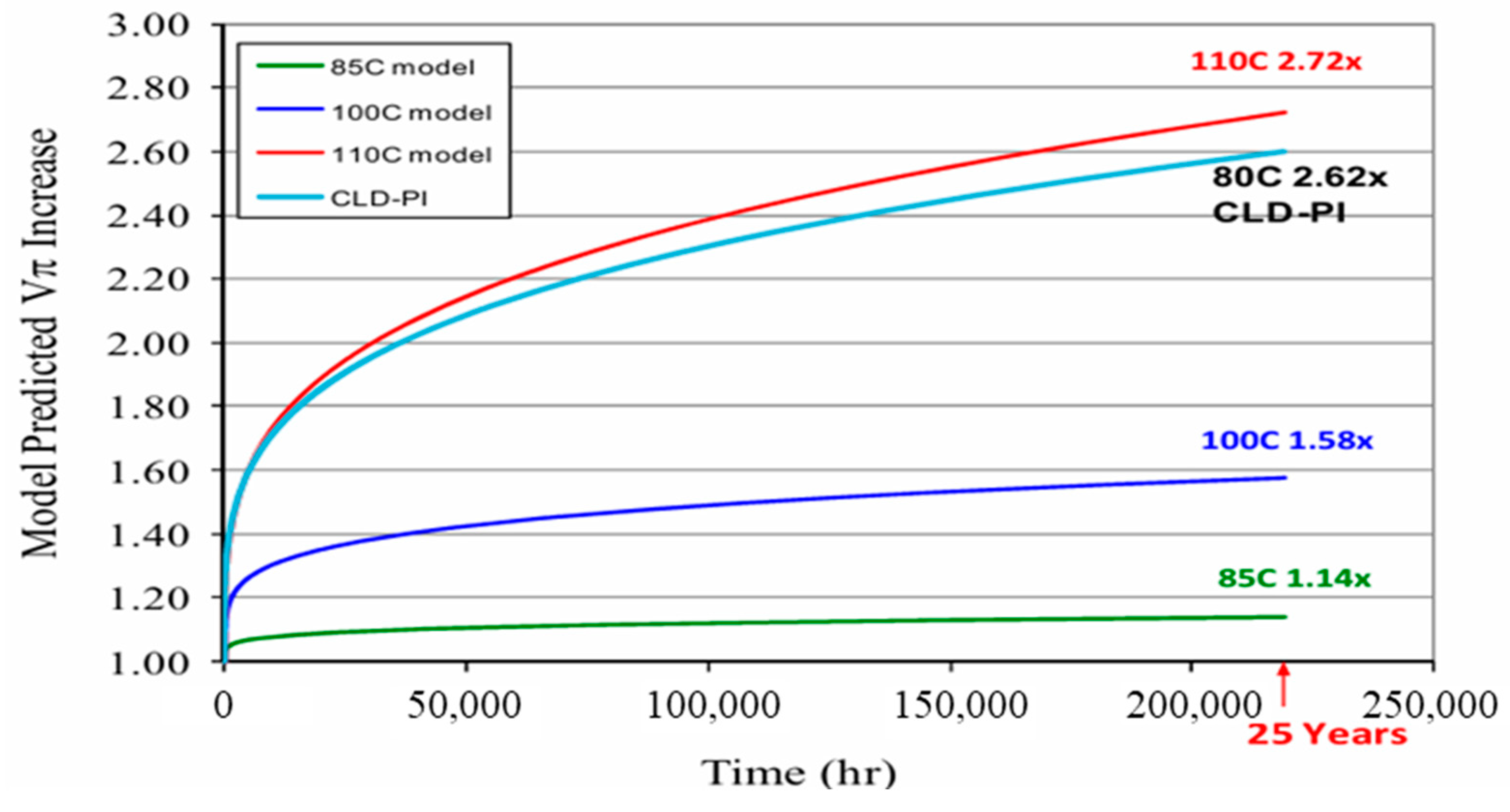
- Thermal deploying: As the device’s operational temperature nears the Tg of the organic EO material, depolarization occurs, resulting in an increase in the half-wave voltage Vπ. Photonic devices are required to adhere to the Telcordia standard [71], which delineates reliability criteria. The designated maximum operational temperature according to this standard is 85 °C. Exceeding this temperature can lead to premature aging and performance degradation of the device.
| Device | Line Rate (Gb/s, Overhead) | Modulation Scheme | Drive Voltage (Vpp) | VπL (Vmm) | Device Length (L, mm) | α [dB/mm] | VπLα (VdB) | EO Material | Tg [°C] | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| Slot-WG-IQ-MZM | 400 (20%) | 16QAM | 1.5 | 1 | 0.6 | - | - | SEO250 | 130 | [81] |
| Slot-WG-MZM | 280 (20%) 150 (7%) | PAM4 OOK | 0.86 0.82 | 0.46 | 0.75 | - | - | PerkinamineTM Series 5A | >175 | [77] |
| Strip-WG-MZM | 200 (-) 110 (-) | PAM4 OOK | - | 14.4 | 8 | 0.22 | 3.2 | Synthesized Based on | 172 | [83,84] |
| Strip-WG-MZM | 110 (-) | PAM4 | 1.6 | 22 | - | 0.22 | 3.6 | EO194 | 185 | [85] |
| Slot-WGIQ-MZM | 52 (7%) | 16QAM | 0.41 | 0.8 | 1.5 | - | - | EO100 | 140 | [86] |
| Strip-WG-MZM | 40 (-) | OOK | 0.14 | 0.32 | 1.5 | 9.3 | 7.4 | JRD1 | 82 | [82] |
| Strip-WG-MZM (Si/InP hybrid) | 252 (-) | PAM4 | - | - | 1.5 | 3.9 | - | Synthesized Based on | 172 | [87] |
| Slot-WG-CC-SOH MZM | 220 (20%) | PAM4 | 1 | 1.3 | 1 | - | - | YLD124 | 81 | [88] |
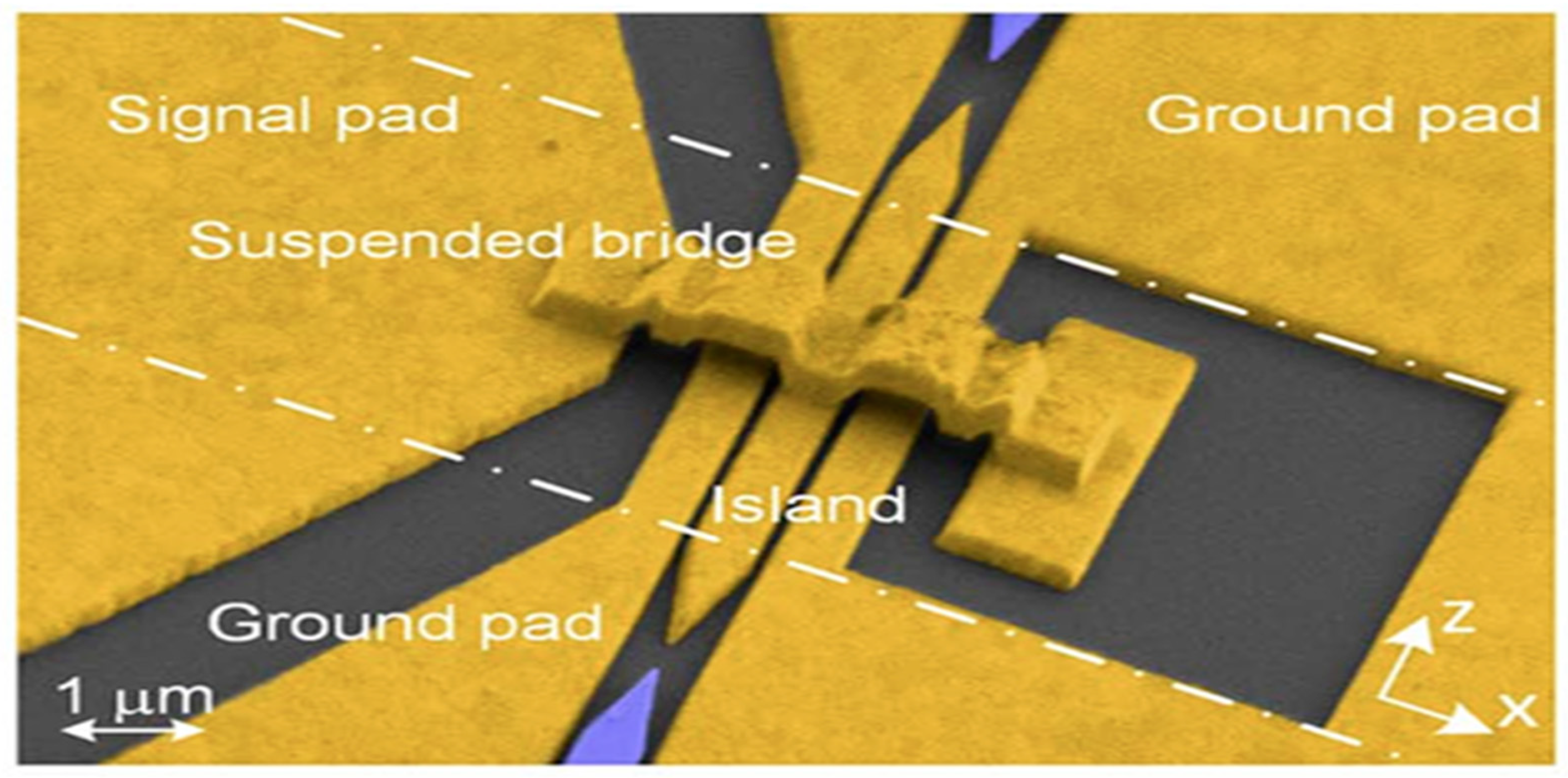
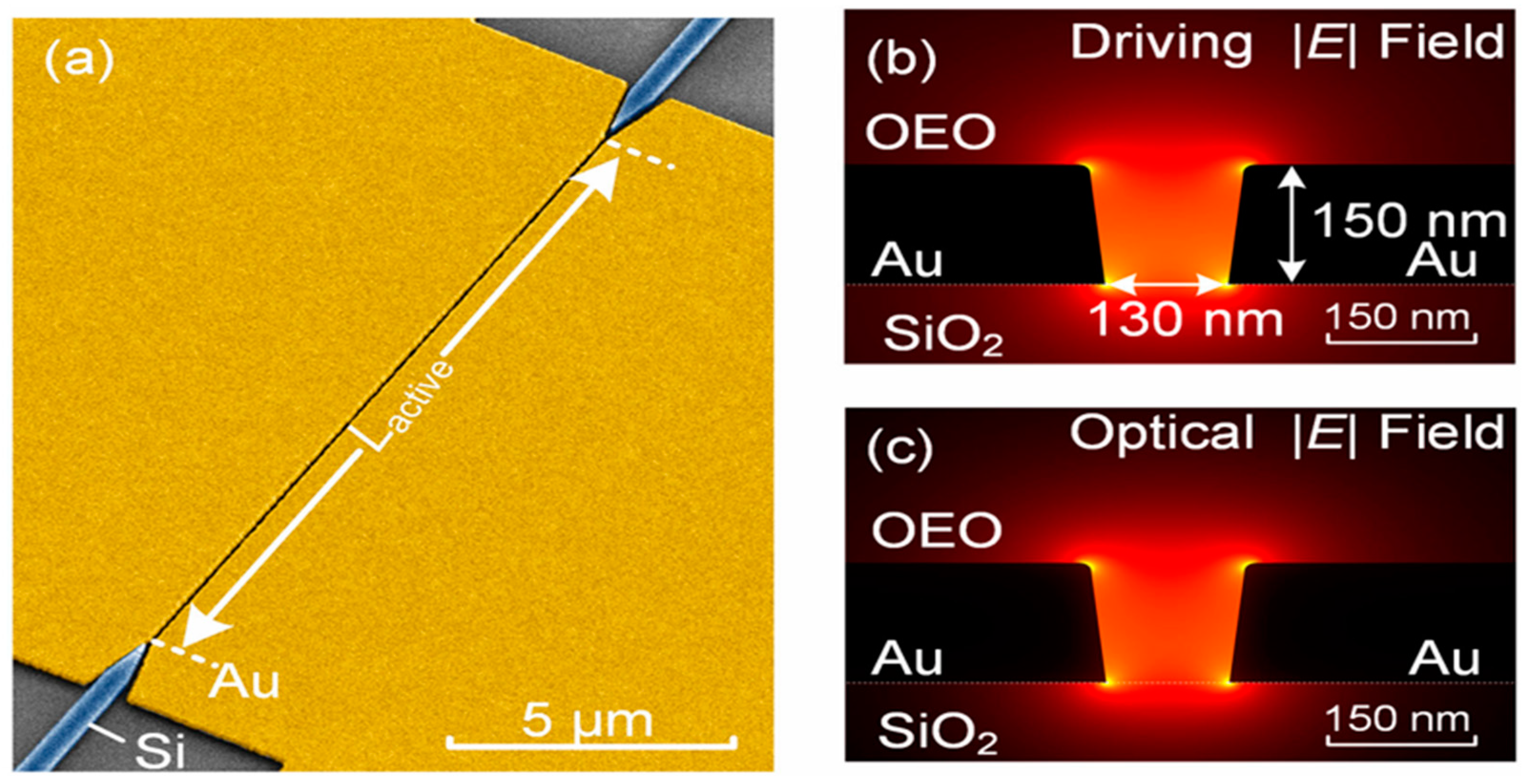
2.2.3. Plasma–Organic Hybrid Electro-Optic Modulator Technology
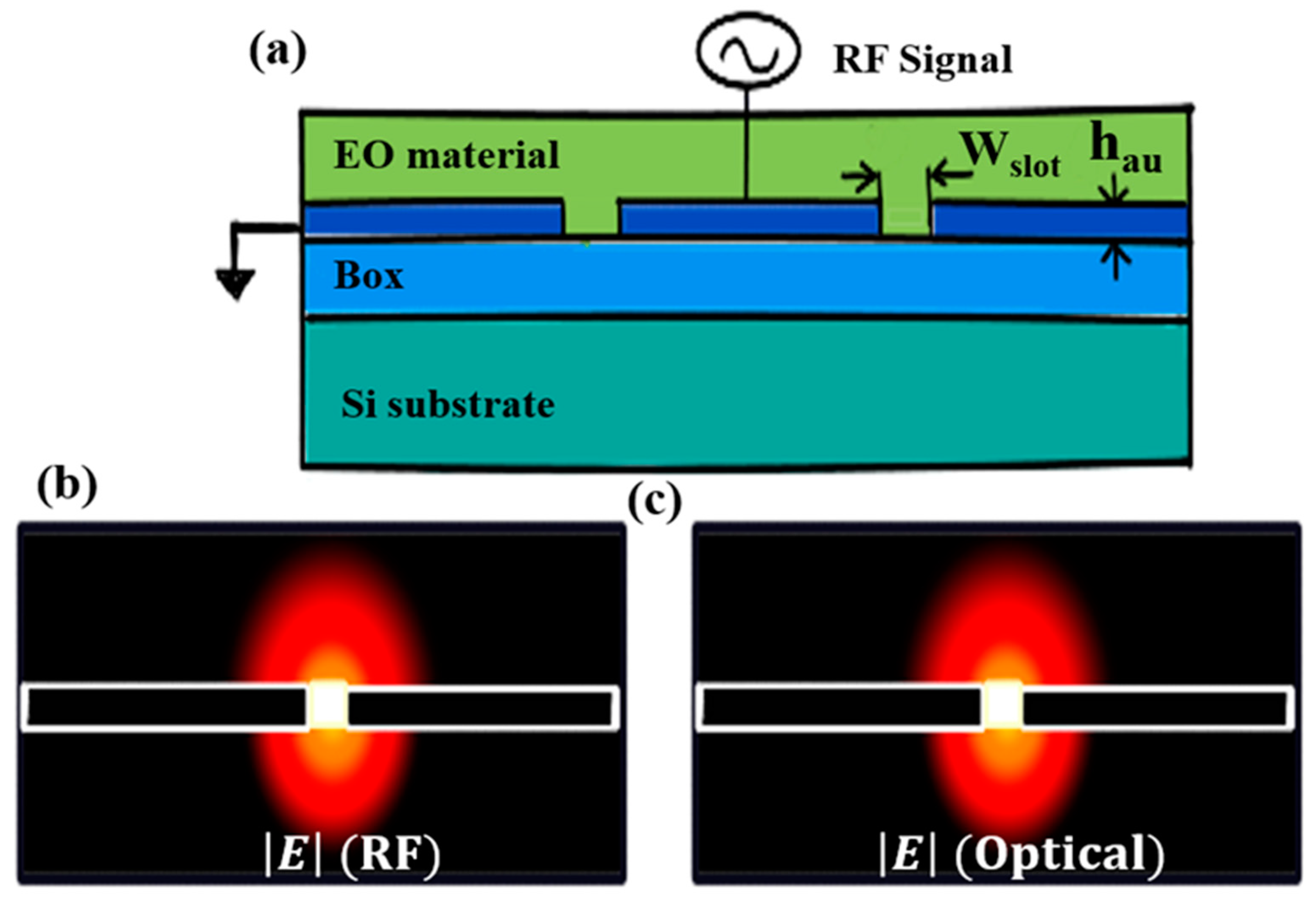
- (a)
- Significantly enhanced modulation efficiency, resulting in reduced VπL values.
- (b)
- Compact dimensions with cross-sections smaller than a wavelength.
- (c)
- Unmatched frequency and bandwidth capabilities compared to existing modulation techniques.
3. Comparative Analysis of Three Modulators: TFLN, SOH, and POH
- ●
- Modulation Efficiency:
- ●
- Modulator bandwidth:
- ●
- Energy consumption:
3.1. Modulation Efficiency
3.2. Modulation Bandwidth
3.3. Energy Consumption
3.4. Fabrication Complexity
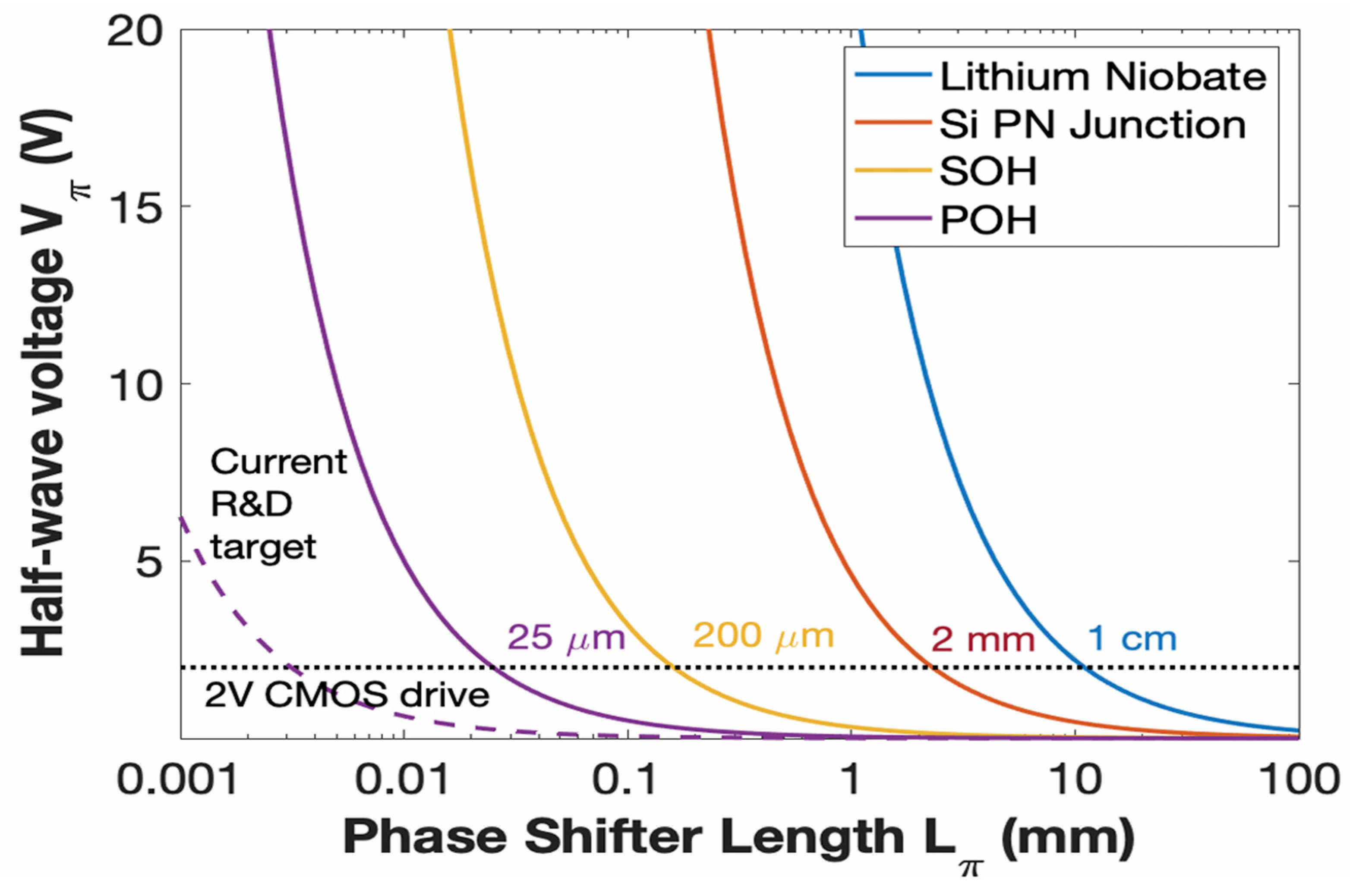
3.5. Footprint (Fixed Vπ)
3.6. Electro-Optic Coefficient, r33
3.7. Temperature Stability
- Thin-Film Lithium Niobate (TFLN) Modulator
- Silicon–Organic Hybrid (SOH) Modulators
- Plasma–Organic Hybrid (POH) Modulators
4. Challenges, and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, D.; Bauters, J.; Bowers, J.E. Passive technologies for future large-scale photonic integrated circuits on silicon: Polarization handling, light non-reciprocity and loss reduction. Light Sci. Appl. 2012, 1, e1–e12. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef]
- Rachel, W. Integrating silicon photonics. Nat. Photonics 2010, 4, 498–499. [Google Scholar]
- Shekhar, S.; Bogaerts, W.; Chrostowski, L.; Bowers, J.E.; Hochberg, M.; Soref, R.; Shastri, B.J. Roadmapping the next generation of silicon photonics. Nat. Commun. 2024, 15, 751. [Google Scholar] [CrossRef] [PubMed]
- Komljenovic, T.; Davenport, M.; Hulme, J.; Liu, A.Y.; Santis, C.T.; Spott, A.; Srinivasan, S.; Stanton, E.J.; Zhang, C.; Bowers, J.E. Heterogeneous silicon photonic integrated circuits. J. Light. Technol. 2015, 34, 20–35. [Google Scholar] [CrossRef]
- Timurdogan, E.; Sorace-Agaskar, C.M.; Sun, J.; Hosseini, E.S.; Biberman, A.; Watts, M.R. An ultralow power athermal silicon modulator. Nat. Commun. 2014, 5, 4008. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Sepehrian, H.; Rusch, L.A.; Shi, W. Single-carrier 72 GBaud 32QAM and 84 GBaud 16QAM transmission using a SiP IQ modulator with joint digital-optical pre-compensation. Opt. Express 2019, 27, 5610–5619. [Google Scholar] [CrossRef]
- Samani, A.; Patel, D.; Chagnon, M.; El-Fiky, E.; Li, R.; Jacques, M.; Abadía, N.; Veerasubramanian, V.; Plant, D.V. Experimental parametric study of 128 Gb/s PAM-4 transmission system using a multi-electrode silicon photonic Mach Zehnder modulator. Opt. Express 2017, 25, 13252–13262. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Kieninger, C.; Kutuvantavida, Y.; Elder, D.L.; Wolf, S.; Zwickel, H.; Blaicher, M.; Kemal, J.N.; Lauermann, M.; Randel, S.; Freude, W.; et al. Ultra-high electro-optic activity demonstrated in a silicon-organic hybrid modulator. Optica 2018, 5, 739–748. [Google Scholar] [CrossRef]
- Verbist, J.; Verplaetse, M.; Srinivasan, S.A.; Van Kerrebrouck, J.; De Heyn, P.; Absil, P.; De Keulenaer, T.; Pierco, R.; Vyncke, A.; Torfs, G.; et al. Real-time 100 Gb/s NRZ and EDB transmission with a GeSi electroabsorption modulator for short-reach optical interconnects. J. Light. Technol. 2017, 36, 90–96. [Google Scholar] [CrossRef]
- Tang, Y.; Peters, J.D.; Bowers, J.E. Over 67 GHz bandwidth hybrid silicon electro absorption modulator with asymmetric segmented electrode for 1.3 μm transmission. Opt. Express 2012, 20, 11529–11535. [Google Scholar] [CrossRef] [PubMed]
- Abel, S.; Eltes, F.; Ortmann, J.E.; Messner, A.; Castera, P.; Wagner, T.; Urbonas, D.; Rosa, A.; Gutierrez, A.M.; Tulli, D.; et al. Large Pockels effect in micro- and nanostructured barium titanate integrated on silicon. Nat. Mater. 2019, 18, 42–47. [Google Scholar] [CrossRef]
- Ossieur, P.; Moeneclaey, B.; Coudyzer, G.; Lambrecht, J.; Craninckx, J.; Martens, E.; Van Driessche, J.; Bruynsteen, C.; De Busscher, J.; Declercq, J.; et al. Integrated Photonics and Electronics for Optical Transceivers supporting AI/ML applications. IEEE J. Sel. Top. Quantum Electron. 2025, 31, 6000116. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D. Silicon optical modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef]
- Srinivasan, S.A.; Porret, C.; Balakrishnan, S.; Ban, Y.; Loo, R.; Verheyen, P.; Van Campenhout, J.; Pantouvaki, M. 60Gb/s waveguide-coupled O-band GeSi quantum-confined Stark effect electro-absorption modulator. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 6–10 June 2021; p. Tu1D.3. [Google Scholar]
- Jones, R.; Doussiere, P.; Driscoll, J.B.; Lin, W.; Yu, H.; Akulova, Y.; Komljenovic, T.; Bowers, J.E. Heterogeneously integrated InP\/silicon photonics: Fabricating fully functional transceivers. IEEE Nanotechnol. Mag. 2019, 13, 17–26. [Google Scholar] [CrossRef]
- Liang, D.; Bowers, J.E. Recent progress in heterogeneous III-V-on-silicon photonic integration. Light. Adv. Manuf. 2021, 2, 59–83. [Google Scholar] [CrossRef]
- Weigel, P.O.; Zhao, J.; Fang, K.; Al-Rubaye, H.; Trotter, D.; Hood, D.; Mudrick, J.; Dallo, C.; Pomerene, A.T.; Starbuck, A.L.; et al. Bonded thin film lithium niobate modulator on a silicon photonics platform exceeding 100 GHz 3-dB electrical modulation bandwidth. Opt. Express 2018, 26, 23728–23739. [Google Scholar] [CrossRef]
- Zhu, D.; Shao, L.; Yu, M.; Cheng, R.; Desiatov, B.; Xin, C.J.; Hu, Y.; Holzgrafe, J.; Ghosh, S.; Shams-Ansari, A.; et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 2021, 13, 242–352. [Google Scholar] [CrossRef]
- Li, Y.; Sun, M.; Miao, T.; Chen, J. Towards High-Performance Pockels Effect-Based Modulators: Review and Projections. Micromachines 2024, 15, 865. [Google Scholar] [CrossRef]
- Servizzi, A.J.; Boyd, J.T.; Sriram, S.; Kingsley, S.A. Extraordinary-mode refractive-index change produced by the linear electro-optic effect in LiNbO3 and reverse-poled LiNbO3. Appl. Opt. 1995, 34, 4248–4255. [Google Scholar] [CrossRef]
- Smolenskii, G.A.; Krainik, N.N.; Khuchua, N.P.; Zhdanova, V.V.; Mylnikova, I.E. The curie temperature of LiNbO3. Phys. Status Solidi 1966, 13, 309–314. [Google Scholar] [CrossRef]
- Castera, P.; Tulli, D.; Gutierrez, A.M.; Sanchis, P. Influence of BaTiO3 ferroelectric orientation for electro-optic modulation on silicon. Opt. Express 2015, 23, 15332–15342. [Google Scholar] [CrossRef]
- Gubinyi, Z.; Batur, C.; Sayir, A.; Dynys, F. Electrical properties of PZT piezoelectric ceramic at high temperatures. J. Electroceram. 2007, 20, 95–105. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Riemensberger, J.; Lihachev, G.; Churaev, M.; Kao, W.; Ji, X.; Zhang, J.; Blesin, T.; Davydova, A.; et al. Lithium tantalate photonic integrated circuits for volume manufacturing. Nature 2024, 629, 784–790. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, C.; Kharel, P.; Zhu, D.; Lončar, M. Integrated lithium niobate electro-optic modulators: When performance meets scalability. Optica 2021, 8, 652–667. [Google Scholar] [CrossRef]
- Valdez, F.; Mere, V.; Wang, X.; Boynton, N.; Friedmann, T.A.; Arterburn, S.; Dallo, C.; Pomerene, A.T.; Starbuck, A.L.; Trotter, D.C.; et al. 110 GHz, 110 mW hybrid silicon-lithium niobate Mach-Zehnder modulator. Sci. Rep. 2022, 12, 18611. [Google Scholar] [CrossRef]
- Hou, S.; Hu, H.; Liu, Z.; Xing, W.; Zhang, J.; Hao, Y. High-Speed Electro-Optic Modulators Based on Thin-Film Lithium Niobate. Nanomaterials 2024, 14, 867. [Google Scholar] [CrossRef]
- Liu, L.; Liu, N.; Zhang, J.; Zhu, Z.; Liu, K. High performance electro-optic modulator based on thin-film lithium niobate. Optoelectron. Lett. 2022, 18, 583–587. [Google Scholar] [CrossRef]
- Farzaneh, A.J.; Gholipour Vazimali, M.; Zhao, J.; Chen, X.; Le, S.T.; Chen, H.; Ordouie, E.; Fontaine, N.K.; Fathpour, S. Thin-Film Lithium Niobate Optical Modulators with an Extrapolated Bandwidth of 170 GHz. Adv. Photonics Res. 2023, 4, 2200216. [Google Scholar]
- Chen, N.; Lou, K.; Yu, Y.; He, X.; Chu, T. High-Efficiency Electro-Optic Modulator on Thin-Film Lithium Niobate with High-Permittivity Cladding. Laser Photonics Rev. 2023, 17, 2200927. [Google Scholar] [CrossRef]
- Chen, N.; Yu, Y.; Lou, K.; Mi, Q.; Chu, T. High-efficiency thin-film lithium niobate modulator with highly confined optical modes. Opt. Lett. 2023, 48, 1602–1605. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Fang, X.; Chen, X.; Zhu, L.; Zhang, F.; Chen, Z.; Li, Y. Monolithic thin film lithium niobate electro-optic modulator with over 110 GHz bandwidth. Chin. Opt. Lett. 2022, 20, 022502. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Liu, J.; Tan, S.; Lu, Q.; Guo, W. Low V π thin-film lithium niobate modulator fabricated with photolithography. Opt. Express 2021, 29, 6320–6329. [Google Scholar] [CrossRef]
- Ying, P.; Tan, H.; Zhang, J.; He, M.; Xu, M.; Liu, X.; Ge, R.; Zhu, Y.; Liu, C.; Cai, X. Low-loss edge-coupling thin-film lithium niobate modulator with an efficient phase shifter. Opt. Lett. 2021, 46, 1478–1481. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Chen, J.; Sua, Y.; Kumar, P.; Huang, Y. Efficient electro-optical modulation on thin-film lithium niobate. Opt. Lett. 2021, 46, 1884–1887. [Google Scholar] [CrossRef]
- Xu, M.; He, M.; Zhang, H.; Jian, J.; Pan, Y.; Liu, X.; Chen, L.; Meng, X.; Chen, H.; Li, Z.; et al. High-performance coherent optical modulators based on thin-film lithium niobate platform. Nat. Commun. 2020, 11, 3911. [Google Scholar] [CrossRef]
- Ruan, Z.; Chen, K.; Wang, Z.; Fan, X.; Gan, R.; Qi, L.; Xie, Y.; Guo, C.; Yang, Z.; Cui, N.; et al. High-Performance Electro-Optic Modulator on Silicon Nitride Platform with Heterogeneous Integration of Lithium Niobate. Laser Photonics Rev. 2023, 17, 2200327. [Google Scholar] [CrossRef]
- Chen, G.; Chen, K.; Gan, R.; Ruan, Z.; Wang, Z.; Huang, P.; Lu, C.; Lau, A.P.T.; Dai, D.; Guo, C.; et al. High performance thin-film lithium niobate modulator on a silicon substrate using periodic capacitively loaded traveling-wave electrode. APL Photonics 2022, 7, 026103. [Google Scholar] [CrossRef]
- Nelan, S.; Mercante, A.; Hurley, C.; Shi, S.; Yao, P.; Shopp, B.; Prather, D.W. Compact thin film lithium niobate folded intensity modulator using a waveguide crossing. Opt. Express 2022, 30, 9193–9207. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, H.; Jiang, Y.; Han, X.; Xiao, H.; Frigg, A.; Nguyen, T.G.; Boes, A.; Ren, G.; Su, Y.; et al. High-speed electro-optic modulator based on silicon nitride loaded lithium niobate on an insulator platform. Opt. Lett. 2021, 46, 5986–5989. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Liu, Y.; Li, Z.; Guan, H.; Wei, Q.; Tan, M.; Li, Z. 40 GHz high-efficiency Michelson interferometer modulator on a silicon-rich nitride and thin-film lithium niobate hybrid platform. Opt. Lett. 2021, 46, 2811–2814. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xiong, B.; Sun, C.; Wang, J.; Hao, Z.; Wang, L.; Han, Y.; Li, H.; Luo, Y. Sub-terahertz bandwidth capactively-loaded thin-film lithium niobate electro-optic modulators based on an undercut structure. Opt. Express 2021, 29, 41798–41807. [Google Scholar] [CrossRef]
- Ahmed, A.N.R.; Nelan, S.; Shi, S.; Yao, P.; Mercante, A.; Prather, D.W. Subvolt electro-optical modulator on thin-film lithium niobate and silicon nitride hybrid platform. Opt. Lett. 2020, 45, 1112–1115. [Google Scholar] [CrossRef]
- Li, Z.; Kim, H.; Chi, S.-H.; Hales, J.M.; Jang, S.-H.; Perry, J.W.; Jen, A.K.-Y. Effects of counterions with multiple charges on the linear and nonlinear optical properties of polymethine salts. Chem. Mater. 2016, 28, 3115–3121. [Google Scholar] [CrossRef]
- Honardoost, A.; Safian, R.; Teng, M.; Zhuang, L. Ultralow-power polymer electro–optic integrated modulators. J. Semicond. 2019, 40, 070401. [Google Scholar] [CrossRef]
- Witmer, J.D.; McKenna, T.P.; Arrangoiz-Arriola, P.; Van Laer, R.; Wollack, E.A.; Lin, F.; Jen, A.K.-Y.; Luo, J.; Safavi-Naeini, A.H. A silicon-organic hybrid platform for quantum microwave-to-optical transduction. Quantum Sci. Technol. 2020, 5, 034004. [Google Scholar] [CrossRef]
- Weimann, C.; Schindler, P.C.; Palmer, R.; Wolf, S.; Bekele, D.; Korn, D.; Pfeifle, J.; Koeber, S.; Schmogrow, R.; Alloatti, L.; et al. Silicon-organic hybrid (SOH) frequency comb sources for terabit/s data transmission. Opt. Express 2014, 22, 3629–3637. [Google Scholar] [CrossRef] [PubMed]
- Masafumi, A.; Fedoryshyn, Y.; Heni, W.; Baeuerle, B.; Josten, A.; Zahner, M.; Koch, U.; Salamin, Y.; Hoessbacher, C.; Haffner, C.; et al. High-speed plasmonic modulator in a single metal layer. Science 2017, 358, 630–632. [Google Scholar]
- Haffner, C.; Chelladurai, D.; Fedoryshyn, Y.; Josten, A.; Baeuerle, B.; Heni, W.; Watanabe, T.; Cui, T.; Cheng, B.; Saha, S.; et al. Low-loss plasmon-assisted electro-optic modulator. Nature 2018, 556, 483–486. [Google Scholar] [CrossRef]
- Robinson, B.H.; Salamin, Y.; Baeuerle, B.; Josten, A.; Ayata, M.; Koch, U.; Leuthold, J.; Dalton, L.R.; Johnson, L.E.; Elder, D.L.; et al. Optimization of plasmonic-organic hybrid electro-optics. J. Light. Technol. 2018, 36, 5036–5047. [Google Scholar] [CrossRef]
- Dalton, L.R. Theory-inspired development of organic electro-optic materials. Thin Solid Films 2009, 518, 428–431. [Google Scholar] [CrossRef]
- Koos, C.; Brosi, J.; Waldow, M.; Freude, W.; Leuthold, J. Silicon-on-insulator modulators for next-generation 100 Gbit/s-Ethernet. In Proceedings of the 33rd European Conference and Exhibition on Optical Communication—ECOC 2007, Berlin, Germany, 16–20 September 2007; p. 56. [Google Scholar]
- Juerg, L.; Koos, C.; Freude, W.; Alloatti, L.; Palmer, R.; Korn, D.; Pfeifle, J.; Lauermann, M.; Dinu, R.; Wehrli, S.; et al. Silicon-organic hybrid electro-optical devices. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 114–126. [Google Scholar]
- Wolfgang, H.; Kutuvantavida, Y.; Haffner, C.; Zwickel, H.; Kieninger, C.; Wolf, S.; Lauermann, M.; Fedoryshyn, Y.; Tillack, A.F.; Johnson, L.E.; et al. Silicon–organic and plasmonic–organic hybrid photonics. ACS Photonics 2017, 4, 1576–1590. [Google Scholar]
- Matthias, L. Silicon-Organic Hybrid Devices for High-Speed Electro-Optic Signal Processing; KIT Scientific Publishing: Karlsruhe, Germany, 2018; Volume 22. [Google Scholar]
- Zhou, Z.; Chao, M.; Su, X.; Fu, S.; Liu, R.; Li, Z.; Bo, S.; Chen, Z.; Wu, Z.; Han, X. Silicon–organic hybrid electro-optic modulator and microwave photonics signal processing applications. Micromachines 2023, 14, 1977. [Google Scholar] [CrossRef]
- Wolf, S.; Zwickel, H.; Hartmann, W.; Lauermann, M.; Kutuvantavida, Y.; Kieninger, C.; Altenhain, L.; Schmid, R.; Luo, J.; Jen, A.K.-Y.; et al. Silicon-Organic Hybrid (SOH) Mach-Zehnder Modulators for 100 Gbit/s on-off keying. Sci. Rep. 2018, 8, 2598. [Google Scholar] [CrossRef]
- Dalton, L.R.; Sullivan, P.A.; Bale, D.H. Electric field poled organic electro-optic materials: State of the art and future prospects. Chem. Rev. 2009, 110, 25–55. [Google Scholar] [CrossRef]
- Elder, D.; Tillack, A.; Johnson, L.; Dalton, L.R.; Robinson, B. Hybrid electro-optics and chipscale integration of electronics and photonics. In Proceedings of the Organic Sensors and Bioelectronics X, San Diego, CA, USA, 6–7 August 2017; Volume 10364. [Google Scholar]
- Johnson, L.E.; Elder, D.L.; Xu, H.; Hammond, S.W.; Benight, S.J.; O’Malley, K.; Robinson, B.H.; Dalton, L.R. New paradigms in materials and devices for hybrid electro-optics and optical rectification. In Proceedings of the Molecular and Nano Machines IV, San Diego, CA, USA, 1–5 August 2021; Volume 11812. [Google Scholar]
- Taghavi, I.; Moridsadat, M.; Tofini, A.; Raza, S.; Jaeger, N.A.F.; Chrostowski, L.; Shastri, B.J.; Shekhar, S. Polymer modulators in silicon photonics: Review and projections. Nanophotonics 2022, 11, 3855–3871. [Google Scholar] [CrossRef]
- Kieninger, C.; Füllner, C.; Zwickel, H.; Kutuvantavida, Y.; Kemal, J.N.; Eschenbaum, C.; Elder, D.L.; Dalton, L.R.; Freude, W.; Randel, S.; et al. Silicon-organic hybrid (SOH) Mach-Zehnder modulators for 100 GBd PAM4 signaling with sub-1 dB phase-shifter loss. Opt. Express 2020, 28, 24693–24707. [Google Scholar] [CrossRef]
- Freude, W.; Kotz, A.; Kholeif, H.; Schwarzenberger, A.; Kuzmin, A.; Eschenbaum, C.; Mertens, A.; Sarwar, S.; Erk, P.; Bräse, S.; et al. High-Performance Modulators Employing Organic Electro-Optic Materials on the Silicon Platform. IEEE J. Sel. Top. Quantum Electron. 2024, 30, 3400222. [Google Scholar] [CrossRef]
- Ullah, F.; Deng, N.; Qiu, F. Recent progress in electro-optic polymer for ultra-fast communication. PhotoniX 2021, 2, 13. [Google Scholar] [CrossRef]
- Kieninger, C.; Kutuvantavida, Y.; Miura, H.; Kemal, J.N.; Zwickel, H.; Qiu, F.; Lauermann, M.; Freude, W.; Randel, S.; Yokoyama, S.; et al. Demonstration of long-term thermally stable silicon-organic hybrid modulators at 85 °C. Opt. Express 2018, 26, 27955–27964. [Google Scholar] [CrossRef]
- Pecinovsky, C.; Barry, J.; Ginelle, R. Nonlinear Optical Chromophores Having a Diamondoid Group Attached Thereto, Methods of Preparing the Same, and Uses Thereof. U.S. Patent No. 11,921,401, 5 March 2024. [Google Scholar]
- Xu, H.; Liu, F.; Elder, D.L.; Johnson, L.E.; de Coene, Y.; Clays, K.; Robinson, B.H.; Dalton, L.R. Ultrahigh electro-optic coefficients, high index of refraction, and long-term stability from Diels–Alder cross-linkable binary molecular glasses. Chem. Mater. 2020, 32, 1408–1421. [Google Scholar] [CrossRef]
- Tominari, Y.; Yamada, T.; Kaji, T.; Yamada, C.; Otomo, A. Photostability of organic electro-optic polymer under practical high intensity continuous-wave 1550 nm laser irradiation. Jpn. J. Appl. Phys. 2021, 60, 101002. [Google Scholar] [CrossRef]
- Gebizlioglu, O.S. GR-468-CORE; Generic Reliability Assurance Requirements for Optoelectronic Devices Used in Telecommunications Equipment. Telcordia Standard: Basking Ridge, NJ, USA, 2004.
- Schwarzenberger, A.; Mertens, A.; Kholeif, H.; Kotz, A.; Eschenbaum, C.; Johnson, L.E.; Elder, D.L.; Hammond, S.R.; O’Malley, K.; Dalton, L.; et al. First demonstration of a silicon-organic hybrid (SOH) modulator based on a long-term-stable crosslinked electro-optic material. IET Conf. Proc. 2023, 2023, 859–862. [Google Scholar] [CrossRef]
- Koch, U.; Uhl, C.; Hettrich, H.; Fedoryshyn, Y.; Hoessbacher, C.; Heni, W.; Baeuerle, B.; Bitachon, B.I.; Josten, A.; Ayata, M.; et al. A monolithic bipolar CMOS electronic–plasmonic high-speed transmitter. Nat. Electron. 2020, 3, 338–345. [Google Scholar] [CrossRef]
- Thraskias, C.A.; Lallas, E.N.; Neumann, N.; Schares, L.; Offrein, B.J.; Henker, R.; Plettemeier, D.; Ellinger, F.; Leuthold, J.; Tomkos, I. Survey of photonic and plasmonic interconnect technologies for intra-datacenter and high-performance computing communications. IEEE Commun. Surv. Tutorials 2018, 20, 2758–2783. [Google Scholar] [CrossRef]
- Teichler, A.; Perelaer, J.; Schubert, U.S. Inkjet printing of organic electronics—Comparison of deposition techniques and state-of-the-art developments. J. Mater. Chem. C 2012, 1, 1910–1925. [Google Scholar] [CrossRef]
- Kieninger, C.L.; Kutuvantavida, Y.; Elder, D.L.; Wolf, S.; Zwickel, H.; Blaicher, M.; Kemal, J.N.; Lauermann, M.; Randel, S.; Freude, W.; et al. Ultra-high in-device electro-optic coefficient of r33 = 390 pm/V demonstrated in a silicon-organic hybrid (SOH) modulator. arXiv 2017, arXiv:1709.06338. [Google Scholar]
- Eschenbaum, C. Thermally stable silicon-organic hybrid (SOH) Mach-Zehnder modulator for high speed signaling. In Proceedings of the Emerging Applications in Silicon Photonics III, Birmingham, UK, 6–8 December 2022; p. PC123340G. [Google Scholar]
- Heni, W.; Haffner, C.; Elder, D.L.; Tillack, A.F.; Fedoryshyn, Y.; Cottier, R.; Salamin, Y.; Hoessbacher, C.; Koch, U.; Cheng, B.; et al. Nonlinearities of organic electro-optic materials in nanoscale slots and implications for the optimum modulator design. Opt. Express 2017, 25, 2627–2653. [Google Scholar] [CrossRef]
- Hoessbacher, C.; Habegger, P.; Destraz, M.; Hammond, S.R.; Johnson, L.E.; Meier, N.; De Leo, E.; Baeuerle, B.; Heni, W. Plasmonic-Organic-Hybrid (POH) Modulators—A Powerful Platform for Next-Generation Integrated Circuits. In Integrated Photonics Research, Silicon and Nanophotonics; Optica Publishing Group: Washington, DC, USA, 2021; p. IW1B.5. [Google Scholar]
- Patrick, S.; Mai, C.; Villringer, C.; Dietzel, B.; Bondarenko, S.; Ksianzou, V.; Villasmunta, F.; Zesch, C.; Pulwer, S.; Burger, M.; et al. Silicon-organic hybrid photonics: An overview of recent advances, electro-optical effects and CMOS integration concepts. J. Phys. Photonics 2021, 3, 022009. [Google Scholar]
- Wolf, S.; Zwickel, H.; Kieninger, C.; Lauermann, M.; Hartmann, W.; Kutuvantavida, Y.; Freude, W.; Randel, S.; Koos, C. Coherent modulation up to 100 GBd 16QAM using silicon-organic hybrid (SOH) devices. Opt. Express 2018, 26, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Miura, H.; Qiu, F.; Spring, A.M.; Kashino, T.; Kikuchi, T.; Ozawa, M.; Nawata, H.; Odoi, K.; Yokoyama, S. High thermal stability 40 GHz electro-optic polymer modulators. Opt. Express 2017, 25, 28643–28649. [Google Scholar] [CrossRef]
- Lu, G.-W.; Hong, J.; Qiu, F.; Spring, A.M.; Kashino, T.; Oshima, J.; Ozawa, M.A.; Nawata, H.; Yokoyama, S. High-temperature-resistant silicon-polymer hybrid modulator operating at up to 200 Gbit s−1 for energy-efficient datacentres and harsh-environment applications. Nat. Commun. 2020, 11, 4224. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.-W.; Sato, H.; Mao, J.; Yokoyama, S. Silicon-polymer hybrid modulators with high-temperature resistance for energy-efficient data centers. In Proceedings of the 2023 Opto-Electronics and Communications Conference (OECC), Shanghai, China, 2–6 July 2023; pp. 1–3. [Google Scholar]
- Yokoyama, S.; Lu, G.-W.; Miura, H.; Qiu, F.; Spring, A.M. High temperature resistant 112 Gbit/s PAM4 modulator based on Electro-Optic Polymer modulator. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Stefan, W.; Lauermann, M.; Schindler, P.; Ronniger, G.; Geistert, K.; Palmer, R.; Köber, S.; Bogaerts, W.; Leuthold, J.; Freude, W.; et al. DAC-less amplifier-less generation and transmission of QAM signals using sub-volt silicon-organic hybrid modulators. J. Light. Technol. 2015, 33, 1425–1432. [Google Scholar]
- Junichi, F.; Sato, H.; Bannaron, A.; Lu, G.W.; Yokoyama, S. High-Performance EO Polymer/Si and InP Nano-Hybrid Optical Modulators in O-band and C-band Wavelengths. In Proceedings of the 2023 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 5–9 March 2023. [Google Scholar]
- Sandeep, U.; Kemal, J.N.; Alam, A.S.; Lauermann, M.; Kuzmin, A.; Kutuvantavida, Y.; Nandam, S.H.; Hahn, L.; Elder, D.L.; Dalton, L.R.; et al. Hybrid electro-optic modulator combining silicon photonic slot waveguides with high-k radio-frequency slotlines. Optica 2021, 8, 511–519. [Google Scholar]
- Veronis, G.; Fan, S. Modes of subwavelength plasmonic slot waveguides. J. Light. Technol. 2007, 25, 2511–2521. [Google Scholar] [CrossRef]
- Melikyan, A. Active and Passive Plasmonic Devices for Optical Communications; KIT Scientific Publishing: Karlsruhe, Germany, 2018; Volume 17. [Google Scholar]
- Haffner, C.; Heni, W.; Fedoryshyn, Y.; Josten, A.; Baeuerle, B.; Hoessbacher, C.; Salamin, Y.; Koch, U.; Dordevic, N.; Mousel, P.; et al. Plasmonic Organic Hybrid Modulators—Scaling Highest Speed Photonics to the Microscale. Proc. IEEE 2016, 104, 2362–2379. [Google Scholar] [CrossRef]
- Heni, W.; Hoessbacher, C.; Haffner, C.; Fedoryshyn, Y.; Baeuerle, B.; Josten, A.; Hillerkuss, D.; Salamin, Y.; Bonjour, R.; Melikyan, A.; et al. High speed plasmonic modulator array enabling dense optical interconnect solutions. Opt. Express 2015, 23, 29746–29757. [Google Scholar] [CrossRef]
- Melikyan, A.; Koehnle, K.; Lauermann, M.; Palmer, R.; Koeber, S.; Muehlbrandt, S.; Schindler, P.C.; Elder, D.L.; Wolf, S.; Sommer, M.; et al. Plasmonic-organic hybrid (POH) modulators. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) held jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016. [Google Scholar]
- Elder, D.L.; Dalton, L.R. Organic electro-optics and optical rectification: From mesoscale to nanoscale hybrid devices and chip-scale integration of electronics and photonics. Ind. Eng. Chem. Res. 2022, 61, 1207–1231. [Google Scholar] [CrossRef]
- Xu, H.; Elder, D.L.; Johnson, L.E.; Heni, W.; de Coene, Y.; De Leo, E.; Destraz, M.; Meier, N.; Ghinst, W.V.; Hammond, S.R.; et al. Design and synthesis of chromophores with enhanced electro-optic activities in both bulk and plasmonic–organic hybrid devices. Mater. Horizons 2021, 9, 261–270. [Google Scholar] [CrossRef] [PubMed]
- Ummethala, S. Plasmonic-Organic and Silicon-Organic Hybrid Modulators for High-Speed Signal Processing; KIT Scientific Publishing: Karlsruhe, Germany, 2024; p. 22. [Google Scholar]
- Ummethala, S.; Harter, T.; Koehnle, K.; Li, Z.; Muehlbrandt, S.; Kutuvantavida, Y.; Kemal, J.; Marin-Palomo, P.; Schaefer, J.; Tessmann, A.; et al. THz-to-optical conversion in wireless communications using an ultra-broadband plasmonic modulator. Nat. Photon- 2019, 13, 519–524. [Google Scholar] [CrossRef]
- Christian, H.; Heni, W.; Fedoryshyn, Y.; Niegemann, J.; Melikyan, A.; Elder, D.L.; Baeuerle, B.; Salamin, Y.; Josten, A.; Koch, U.; et al. All-plasmonic Mach–Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 2015, 9, 525–528. [Google Scholar]
- Heni, W.; Baeuerle, B.; Mardoyan, H.; Jorge, F.; Estaran, J.M.; Konczykowska, A.; Riet, M.; Duval, B.; Nodjiadjim, V.; Goix, M.; et al. Ultra-High-speed 2:1 digital selector and plasmonic modulator IM/DD transmitter operating at 222 GBaud for intra-datacenter applications. J. Light. Technol. 2020, 38, 2734–2739. [Google Scholar] [CrossRef]
- Christian, H.; Heni, W.; Fedoryshyn, Y.; Elder, D.L.; Melikyan, A.; Baeuerle, B.; Niegemann, J.; Emboras, A.; Josten, A.; Ducry, F.; et al. High-speed plasmonic Mach-Zehnder modulator in a waveguide. In Proceedings of the 2014 The European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014. [Google Scholar]
- Smajic, J.; Juerg, L. Plasmonic Electro-Optic Modulators–A Review. IEEE J. Sel. Top-Ics Quantum Electron. 2024, 30, 3300113. [Google Scholar]
- Li, M.; Wang, L.; Li, X.; Xiao, X.; Yu, S. Silicon intensity Mach–Zehnder modulator for single lane 100 Gb/s applications. Photonics Res. 2018, 6, 109–116. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef]
- Horst, Y.; Bitachon, B.I.; Kulmer, L.; Brun, J.; Blatter, T.; Conan, J.-M.; Montmerle-Bonnefois, A.; Montri, J.; Sorrente, B.; Lim, C.B.; et al. Tbit/s line-rate satellite feeder links enabled by coherent modulation and full-adaptive optics. Light. Sci. Appl. 2023, 12, 153. [Google Scholar] [CrossRef]
- Messner, A.; Jud, P.A.; Winiger, J.; Eppenberger, M.; Chelladurai, D.; Heni, W.; Baeuerle, B.; Koch, U.; Ma, P.; Haffner, C.; et al. Broadband metallic fiber-to-chip couplers and a low-complexity integrated plasmonic platform. Nano Lett. 2021, 21, 4539–4545. [Google Scholar] [CrossRef]
- Ma, P.; Zhang, X.Z.; Bitachon, B.I.; Habegger, P.; Chelladurai, D.; Heni, W.; Messner, A.; Eppenberger, M.; Moor, D.; Elder, D.L.; et al. Low-loss plasmonically enhanced graphene-organic hybrid phase modulator with > 270 GHz modulation bandwidth. In European Conference and Exhibition on Optical Communication; Optica Publishing Group: Washington, DC, USA, 2022. [Google Scholar]
- Palmer, R.; Freude, W.; Leuthold, J.; Koos, C.; Koeber, S.; Elder, D.L.; Woessner, M.; Heni, W.; Korn, D.; Lauermann, M.; et al. High-speed, low drive-voltage silicon-organic hybrid modulator based on a binary-chromophore electro-optic material. J. Light. Technol. 2014, 32, 2726–2734. [Google Scholar] [CrossRef]
- Witzens, J.; Baehr-Jones, T.; Hochberg, M. Design of transmission line driven slot waveguide mach-Zehnder interferometers and application to analog optical links. Opt. Express 2010, 18, 16902–16928. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hosseini, A.; Lin, X.; Subbaraman, H.; Chen, R.T. Polymer-based hybrid-integrated photonic devices for silicon on-chip modulation and board-level optical interconnects. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 196–210. [Google Scholar] [CrossRef]
- Koeber, S.; Palmer, R.; Lauermann, M.; Heni, W.; Elder, D.L.; Korn, D.; Woessner, M.; Alloatti, L.; Koenig, S.; Schindler, P.C.; et al. Femtojoule electro-optic modulation using a silicon–organic hybrid device. Light. Sci. Appl. 2015, 4, e255. [Google Scholar] [CrossRef]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Alloatti, L.; Palmer, R.; Diebold, S.; Pahl, K.P.; Chen, B.; Dinu, R.; Fournier, M.; Fedeli, J.M.; Zwick, T.; Freude, W.; et al. 100 GHz silicon–organic hybrid modulator. Light: Sci. Appl. 2014, 3, e173. [Google Scholar] [CrossRef]
- Burla, M.; Hoessbacher, C.; Heni, W.; Haffner, C.; Fedoryshyn, Y.; Werner, D.; Watanabe, T.; Massler, H.; Elder, D.L.; Dalton, L.R.; et al. 500 GHz plasmonic Mach-Zehnder modulator enabling sub-THz microwave photonics. APL Photonics 2019, 4, 056106. [Google Scholar] [CrossRef]
- Heni, W.; Melikyan, A.; Haffner, C.; Fedoryshyn, Y.; Baeuerle, B.; Josten, A.; Niegemann, J.; Hillerkuss, D.; Kohl, M.; Elder, D.L.; et al. Plasmonic mach-zehnder modulator with> 70 ghz electrical bandwidth demon-strating 90 gbit/s 4-ask. In Proceedings of the Optical Fiber Communication Conference, Optical Society of America, Los Angeles, CA, USA, 22–26 March 2015; p. Tu2A-2. [Google Scholar]
- Dalton, L.R.; Leuthold, J.; Robinson, B.H.; Haffner, C.; Elder, D.L.; Johnson, L.E.; Hammond, S.R.; Heni, W.; Hosessbacher, C.; Baeuerle, B.; et al. Perspective: Nanophotonic electro-optics enabling THz bandwidths, exceptional modulation and energy efficiencies, and compact device footprints. APL Mater. 2023, 11, 050901. [Google Scholar] [CrossRef]
- Alam, S.; Li, X.; Jacques, M.; Berikaa, E.; Koh, P.-C.; Plant, D.V. Net 300 Gbps/λ transmission over 2 km of SMF with a silicon photonic Mach-Zehnder modulator. IEEE Photonics Technol. Lett. 2021, 33, 1391–1394. [Google Scholar] [CrossRef]
- Chan, D.W.U.; Wu, X.; Lu, C.; Lau, A.P.T.; Tsang, H.K. Efficient 330-Gb/s PAM-8 modulation using silicon microring modulators. Opt. Lett. 2023, 48, 1036–1039. [Google Scholar] [CrossRef]
- Berikaa, E.; Alam, S.; Samani, A.; El-Fiky, E.; Hu, Y.; Lessard, S.; Plant, D.V. Silicon photonic single-segment IQ modulator for net 1 Tbps/λ transmission using all-electronic equalization. J. Light. Technol. 2022, 41, 1192–1199. [Google Scholar] [CrossRef]
- Aalto, T.; Bryant, K.; Harjanne, M.; Eschenbaum, C.; Pitwon, R.; Debrégeas, H. Development of dynamic data centre networks and fast-tunable lasers in the DYNAMOS project. In Optical Interconnects XXIV; SPIE: Washington, DC, USA, 2024; Volume 12892. [Google Scholar]
- Jin, D.; Chen, H.; Barklund, A.; Mallari, J.; Yu, G.; Miller, E.; Dinu, R. EO polymer modulators reliability study. In Organic Photonic Materials and Devices XII; SPIE: Washington, DC, USA, 2010; Volume 7599. [Google Scholar]
- Hammond, S.R.; O’Malley, K.M.; Xu, H.; Elder, D.L.; Johnson, L.E. Organic electro-optic materials combining extraordinary nonlinearity with exceptional stability to enable commercial applications. In Organic Photonic Materials and Devices XXIV; SPIE: Washington, DC, USA, 2022; Volume 11998. [Google Scholar]
- Valdez, F.; Mere, V.; Wang, X.; Mookherjea, S. Integrated O-and C-band silicon-lithium niobate Mach-Zehnder modulators with 100 GHz bandwidth, low voltage, and low loss. Opt. Express 2023, 31, 5273–5289. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Gan, R.; Chen, K.; Chen, G.; Ruan, Z.; Zhang, J.; Liu, J.; Dai, D.; Guo, C.; Liu, L. Breaking the bandwidth limit of a high-quality-factor ring modulator based on thin-film lithium niobate. Optica 2022, 9, 1131–1137. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Li, J.; Wang, H.; Feng, C.; Zhang, L.; Sun, L.; Xu, J.; Liu, M.; Wang, Y.; et al. High-speed electro-optic modulation in topological interface states of a one-dimensional lattice. Light. Sci. Appl. 2023, 12, 206. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Wang, H.; Chen, B.; Ruan, Z.; Guo, C.; Chen, K.; Liu, L. Compact slow-light waveguide and modulator on thin-film lithium niobate platform. Nanophotonics 2023, 12, 3603–3611. [Google Scholar] [CrossRef]



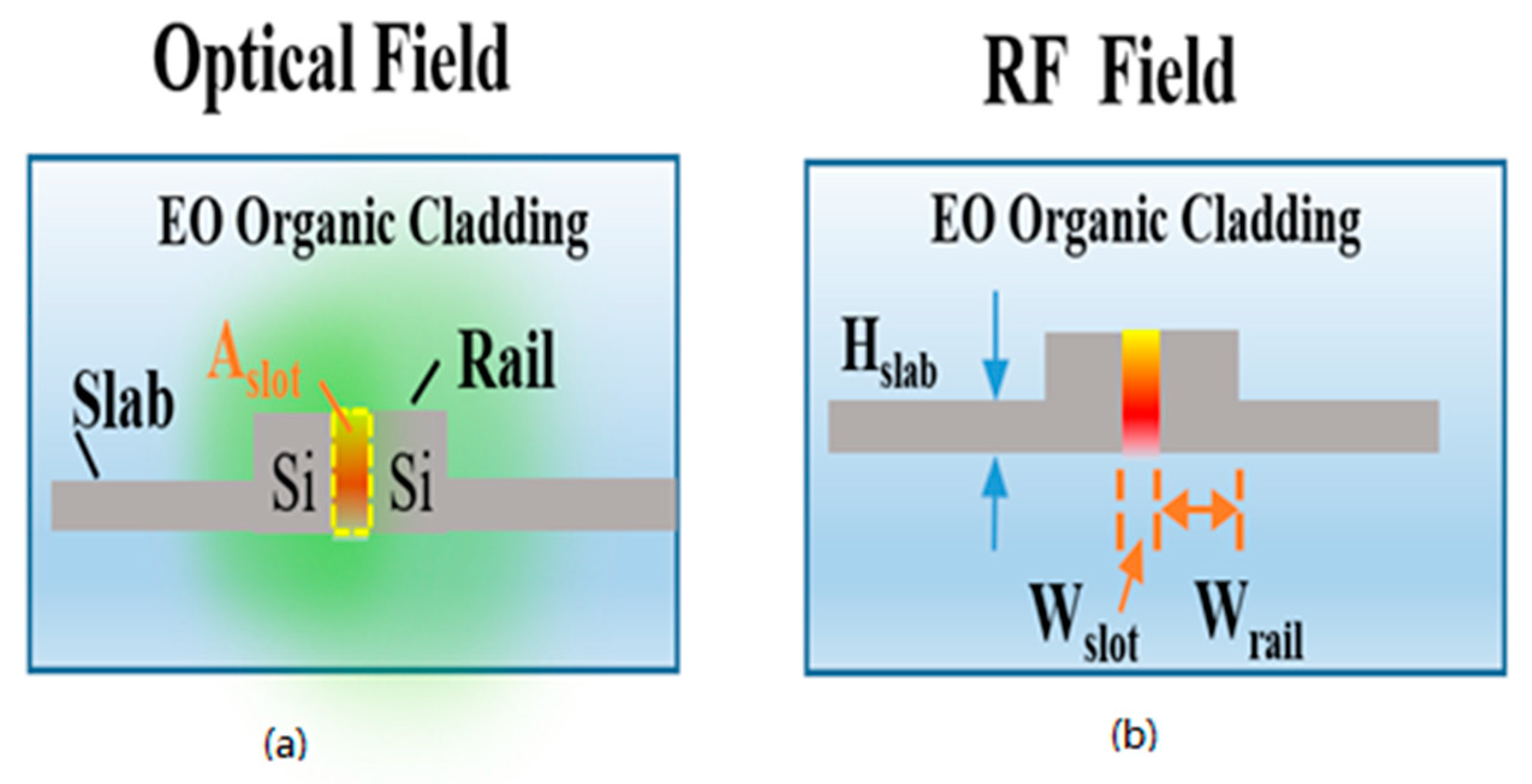
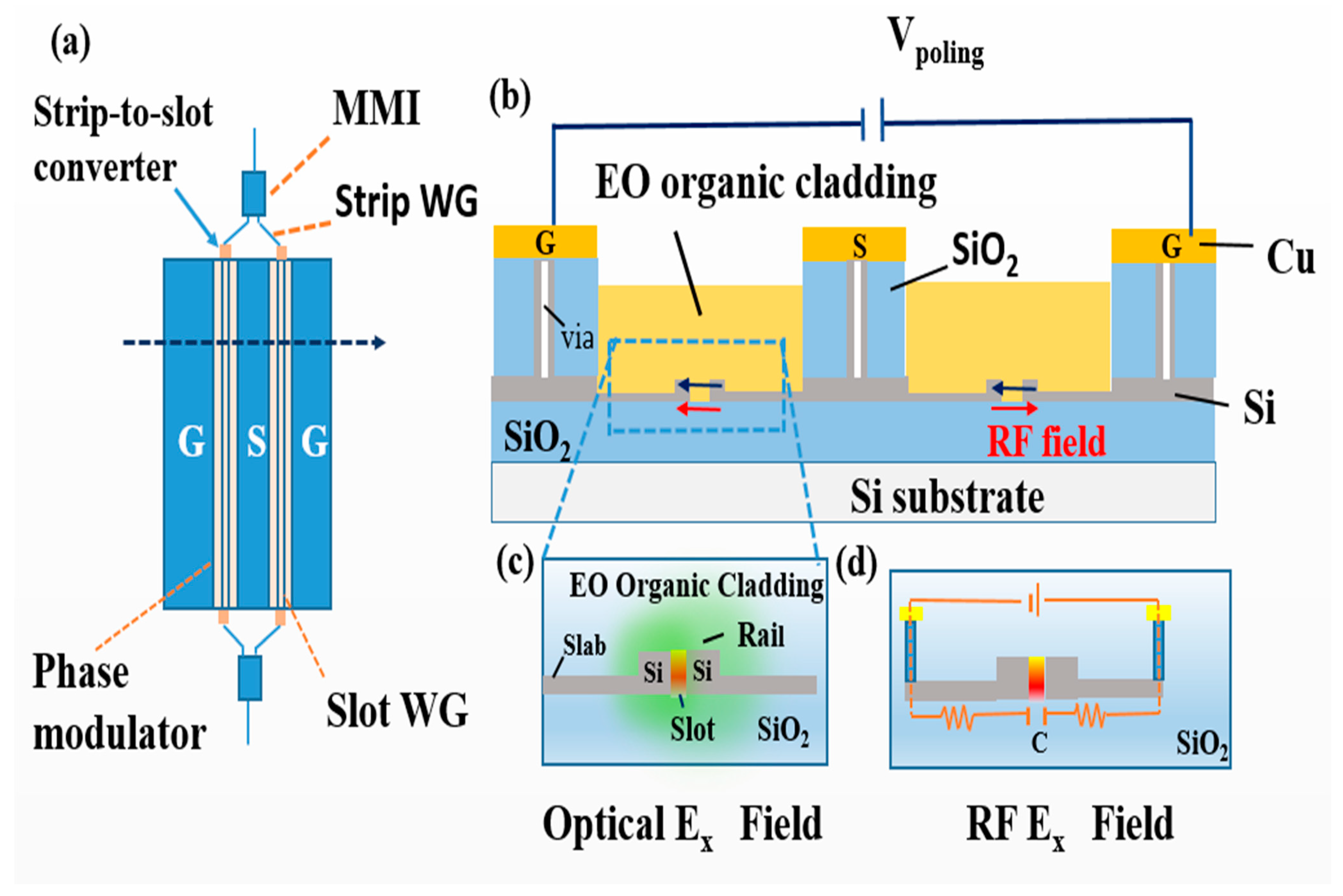






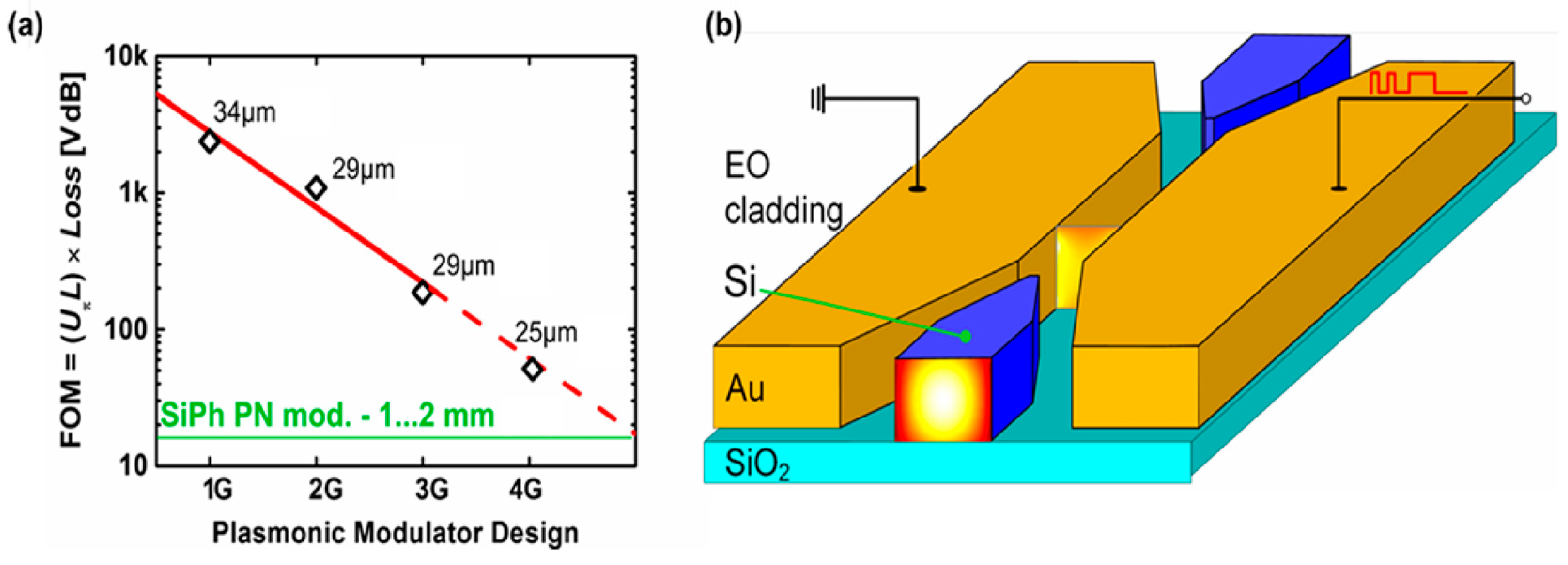


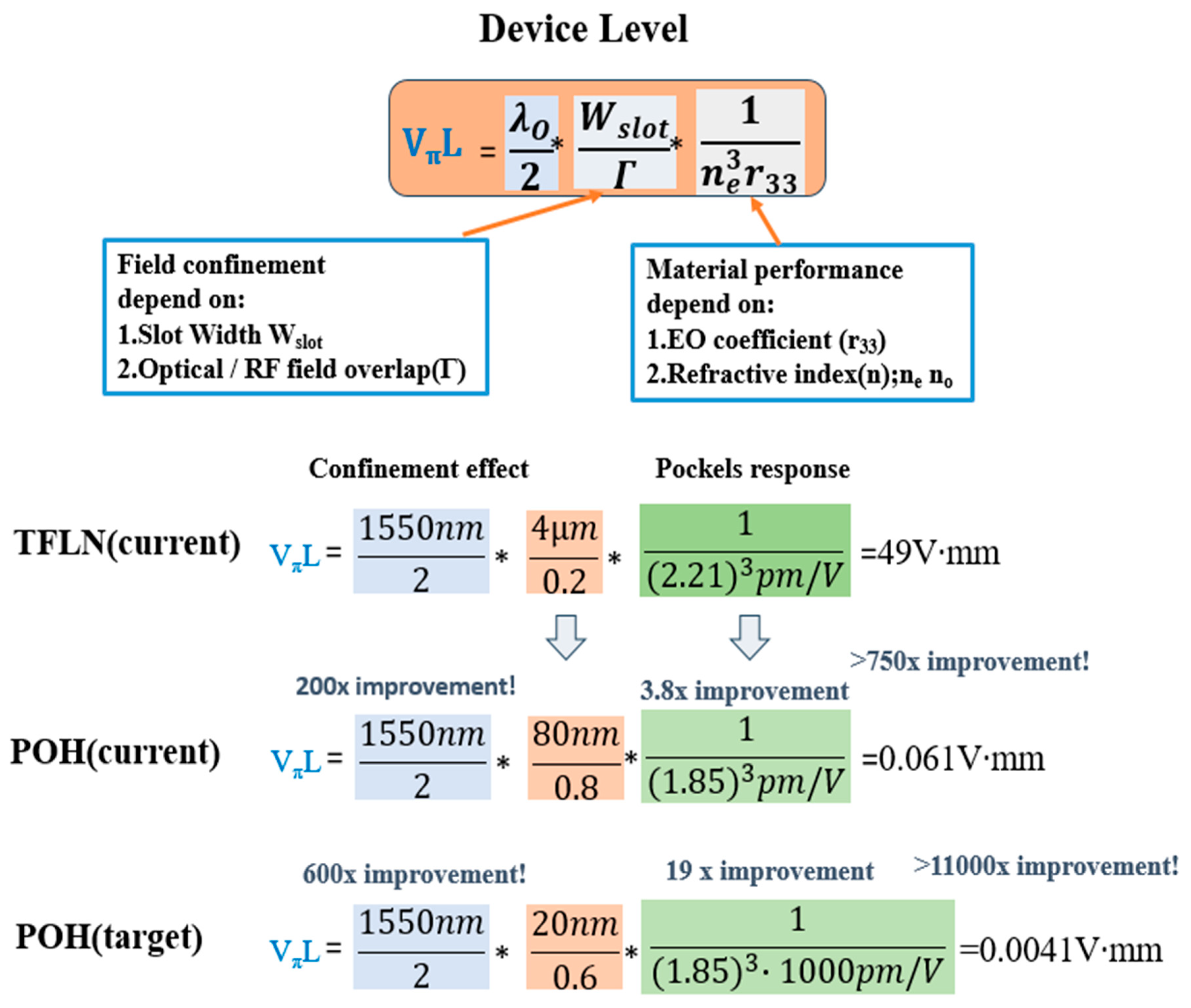
| Material | Point Group | EO Coefficient (pm/V) | Refractive Index | Curie Temp (°C) | Reference |
|---|---|---|---|---|---|
| LiNbO3 | 3 m | r13 = 96 | no = 2.286 ne = 2.2 | 1140 | [22,23] |
| r22 = 6.8 | |||||
| r33 = 30.9 | |||||
| r42 = 32.6 | |||||
| BaTiO3 | 4 m | r13 = 8 | no = 2.444 ne = 2.383 | 120 | [24] |
| r33 = 28 | |||||
| r51 = 800 | |||||
| PZT | 4 m | rc(001) = 270.2 | no = 2.453 ne = 2.458 | 340 | [25] |
| rc(011) = 198.2 | |||||
| rc(111) = 125.3 | |||||
| LiTaO3 | 4 m | r33 = 30.5 | no = 2.119 ne = 2.123 | 610–700 | [26] |
| Year | Scheme | Structure | Length | Vπ | VπL | Bandwidth | Insertion Loss | Ref. |
|---|---|---|---|---|---|---|---|---|
| (mm) | (V) | (V·cm) | (GHz) | (dB) | ||||
| 2023 | LNOI | MZM | 5 | 6.6 | 3.3 | 170 | NA | [31] |
| 2023 | LNOI | MZM | 4 | 3.52 | 1.41 | >67 | 0.5 | [32] |
| 2023 | LNOI | MZM | 4 | 3 | 1.2 | >40 | 2.43 | [33] |
| 2022 | LNOI | MZM | 5 | 4.74 | 2.37 | >110 | NA | [34] |
| 2021 | LNOI | MZM | 5 | 3.5 | 1.75 | >40 | NA | [35] |
| 2021 | LNOI | MZM | 13 | 2.36 | 3.068 | 60 | 2 | [36] |
| 2021 | LNOI | MZM | 4 | 1.6 | 0.64 | >3 | NA | [37] |
| 2020 | LNOI | IQM | 13 | 1.9 | 2.4 | >48 | 1.8 | [38] |
| 2023 | SiN + LN | MZM | 7 | 4.3 | 3 | 37 | 1 | [39] |
| 2022 | Si + LN | MZM | 5 | NA | 3.1 | 110 | 1.8 | [28] |
| 2022 | Si + LN | MZM | 10 | 2.2 | 2.2 | >67 | 0.2 | [40] |
| 2022 | SiN + LN | MZM | 6 | 4 | 4 | 37.5 | NA | [41] |
| 2022 | SiN + LN | MZM | 7.8 | 2.8 | 2.18 | 30 | NA | [42] |
| 2021 | SiN + LN | MIM | NA | 17.8 | 1.06 | >40 | NA | [43] |
| 2021 | TFLN | MZM | 10 | NA | 1.2 | >300 | <1 | [44] |
| 2020 | SiN + LN | MZM | 24 | 0.875 | 2.11 | NA | 5.4 | [45] |
| Modulator Variant | VπL [Vμm] | VπLα [VdB] | Length L [μm] | On-Chip Loss α [dB] | Bandwidth [GHz] | Ref. |
|---|---|---|---|---|---|---|
| SOI | 600 | 1.2 | 2000 | 5.4 | 60 | [102] |
| Photonic (SOH) | 400 | 1 | 280 | 2.2 | 100 | [64] |
| Photonic (LNOI) | 22,000 | 2.2 | 50,000 | 1.5 | 100 | [103] |
| Plasmonic (POH), horizontal | 60 | 30 | 19 | 6 | >500 | [104] |
| Plasmonic (POH), vertical | 100 | 50 | 11 | 5.5 | >300 | [105] |
| Hybrid plasmonic (POH) | 350 | 87 | 10 | 2.5 | >270 | [106] |
| Platform | Topology | EO BW | Propagation Loss α [dB/mm] | Insertion Loss IL [dB] | Half-Wave Voltage Vπ (V) | Modulation Efficiency VπL (V·mm) | Loss Efficiency VπLα | Line Rate (Gbps) | Energy Consumption | Footprint (mm) | Ref |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LiNbO3 | MZM | 45 | 0.025 | 0.5 | 1.4 | 28 | 0.7 | 210 | 14 | 20 | [103] |
| LiNbO3 | MZM | 108 | 1.5 | 7.6 | 13.4 | 67 | 102 | 150 | 1500 | 5 | [19] |
| LiNbO3 | MZM | 70 | 0.83 | 2.5 | 7.3 | 22 | 18.3 | 100 | 170 | 3 | [111] |
| SOH | MZM | 68 | 0.22 | 1.76 | 1.8 | 14.4 | 3.16 | 200 | 42 | 8 | [83] |
| SOH | MZM | 70 | 7.2 | 8 | 0.9 | 0.99 | 7.2 | 100 | 98 | 1.1 | [81] |
| SOH | MZM | 100 | 4.23 | 2 | 2 | 46.53 | 140 | - | 0.5 | 0.5 | [112] |
| POH | MZM | 70 | 375 | 6 | 12 | 0.192 | 72 | 72 | 110 | 0.016 | [50] |
| POH | MZM | 500 | 500 | 10 | 3 | 0.06 | 30 | - | - | 0.02 | [113] |
| POH | MZM | >70 | 544 | 13.6 | 3.6 | 0.09 | 49 | - | - | 0.025 | [114] |
| TFLN | SOH | POH | |
|---|---|---|---|
| Operation voltage (V) [119] | High (~6 V) | Extremely Low (<1 V) | Low (1.4 V) |
| Insertion Loss IL (dB) [63] | Low (0.5~7.6 dB) | Medium (1.76~8 dB) | Large (6~13.6 dB) |
| VπL (Vmm) [119] | High (22 Vmm) | Low (0.3 Vmm) | Ultra-low (0.05 Vmm) |
| 3 dB-BW(GHz) [119] | >100 GHz | >100 GHz | Ultra-high > 350 GHz |
| Footprint (Fixed Vπ) [94] | Large (1 cm) | Small (200 um) | Ultra-small (25 um) |
| Propagation Loss α (dB/mm) [119] | 1.5 (dB/mm) | 2 (dB/mm) | Ultra-high 200 (dB/mm) |
| Integration with Silicon | Complex [29] | Easier [58] | Medium complexity [90] |
| Thermal Stability | High (excellent) | Moderate | Moderate |
| Energy Efficiency [63] | Moderate | High (low power consumption) | Ultra-high (very low power consumption) |
| Challenge | Material quality and fabrication complexity | Material stability | Losses, material stability |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.-C.; Liu, A.-C.; Huang, W.-T.; Wu, C.-C.; Li, C.-H.; Kao, T.-S.; Chang, S.-W.; Sher, C.-W.; Lin, H.-Y.; Chow, C.-W.; et al. Comparison of Thin-Film Lithium Niobate, SOH, and POH for Silicon Photonic Modulators. Photonics 2025, 12, 429. https://doi.org/10.3390/photonics12050429
Yu T-C, Liu A-C, Huang W-T, Wu C-C, Li C-H, Kao T-S, Chang S-W, Sher C-W, Lin H-Y, Chow C-W, et al. Comparison of Thin-Film Lithium Niobate, SOH, and POH for Silicon Photonic Modulators. Photonics. 2025; 12(5):429. https://doi.org/10.3390/photonics12050429
Chicago/Turabian StyleYu, Tai-Cheng, An-Chen Liu, Wei-Ta Huang, Chang-Chin Wu, Chung-Hsun Li, Tsung-Sheng Kao, Shu-Wei Chang, Chin-Wei Sher, Huang-Yu Lin, Chi-Wai Chow, and et al. 2025. "Comparison of Thin-Film Lithium Niobate, SOH, and POH for Silicon Photonic Modulators" Photonics 12, no. 5: 429. https://doi.org/10.3390/photonics12050429
APA StyleYu, T.-C., Liu, A.-C., Huang, W.-T., Wu, C.-C., Li, C.-H., Kao, T.-S., Chang, S.-W., Sher, C.-W., Lin, H.-Y., Chow, C.-W., & Kuo, H.-C. (2025). Comparison of Thin-Film Lithium Niobate, SOH, and POH for Silicon Photonic Modulators. Photonics, 12(5), 429. https://doi.org/10.3390/photonics12050429








