Adaptive Freeform Optics Design and Multi-Objective Genetic Optimization for Energy-Efficient Automotive LED Headlights
Abstract
1. Introduction
2. Design and Evaluation of Freeform-Based Low-Beam Headlight
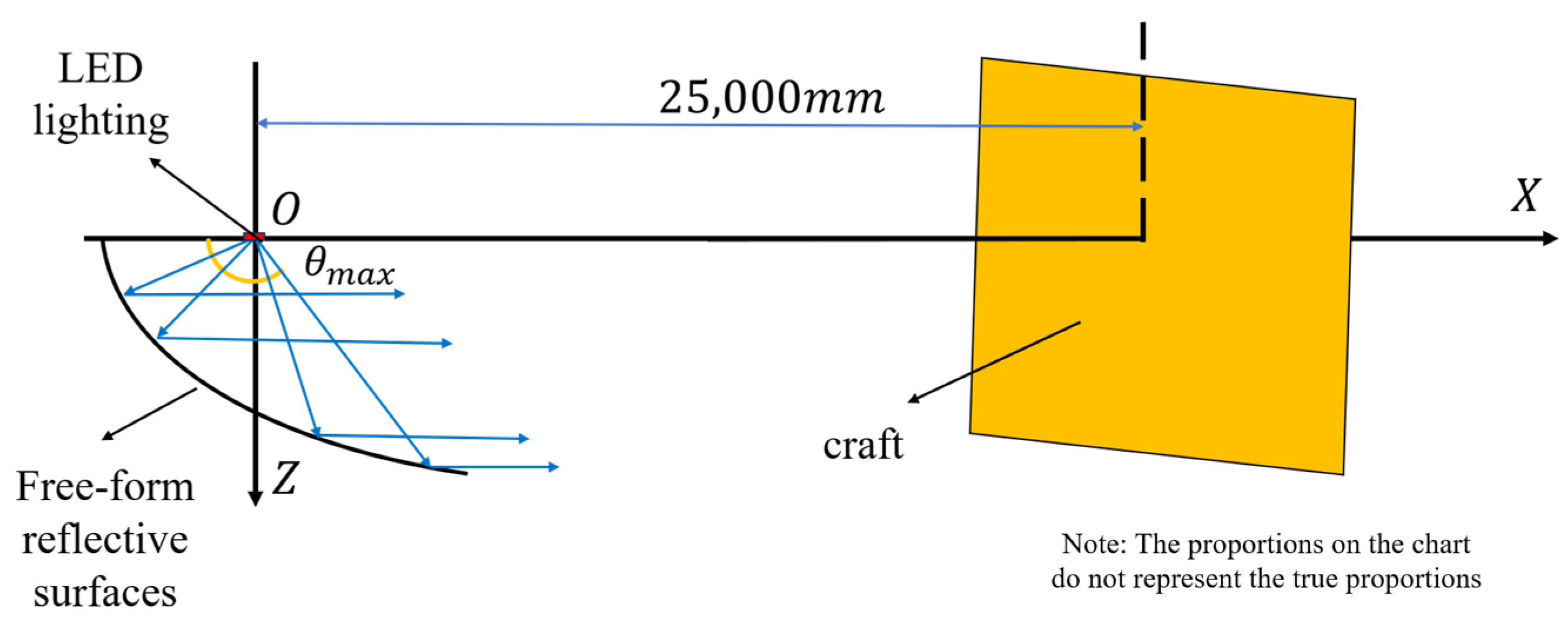
2.1. Design Requirements of the Low-Beam Headlight
2.2. LED Light Source Energy Division
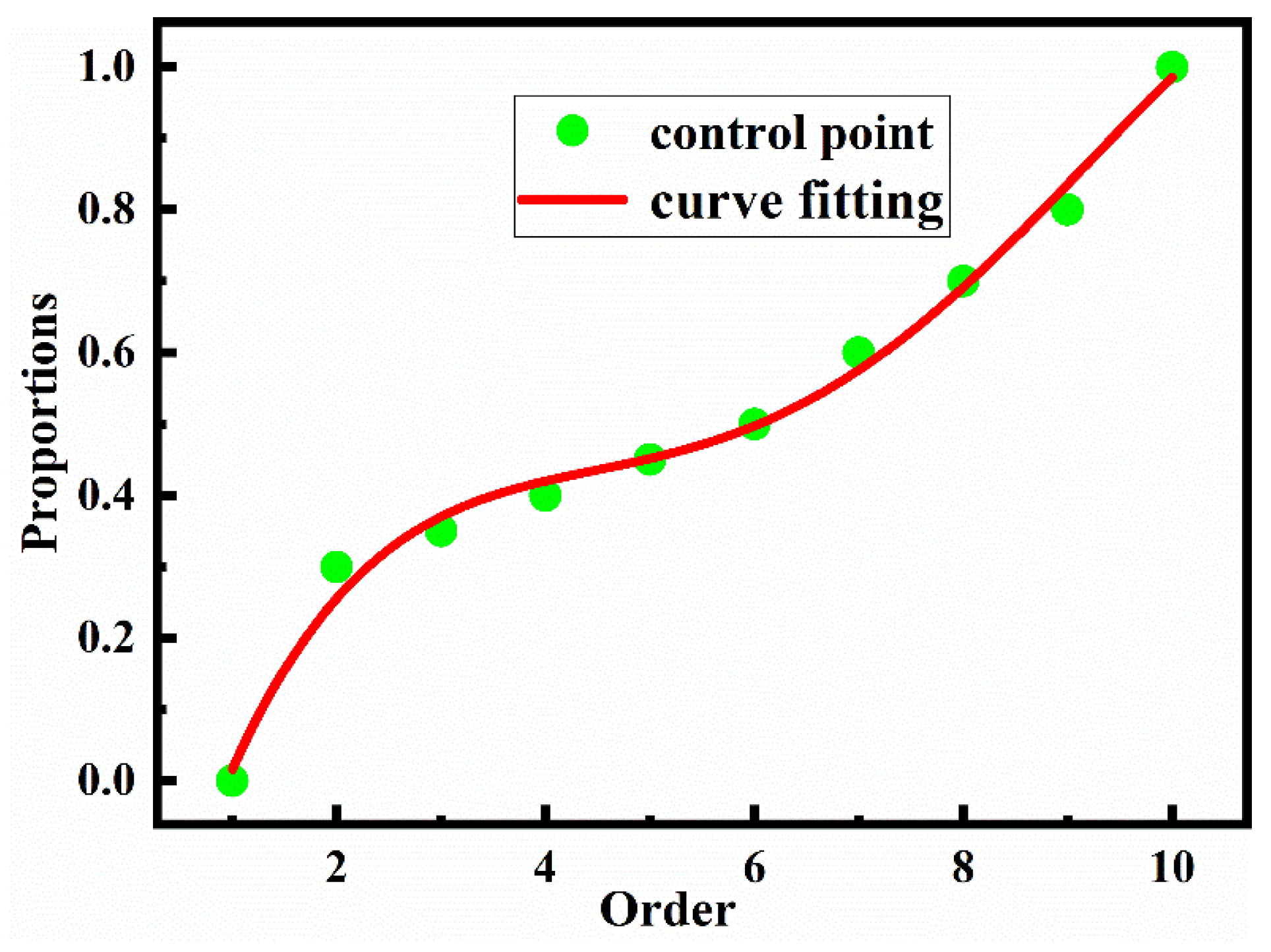
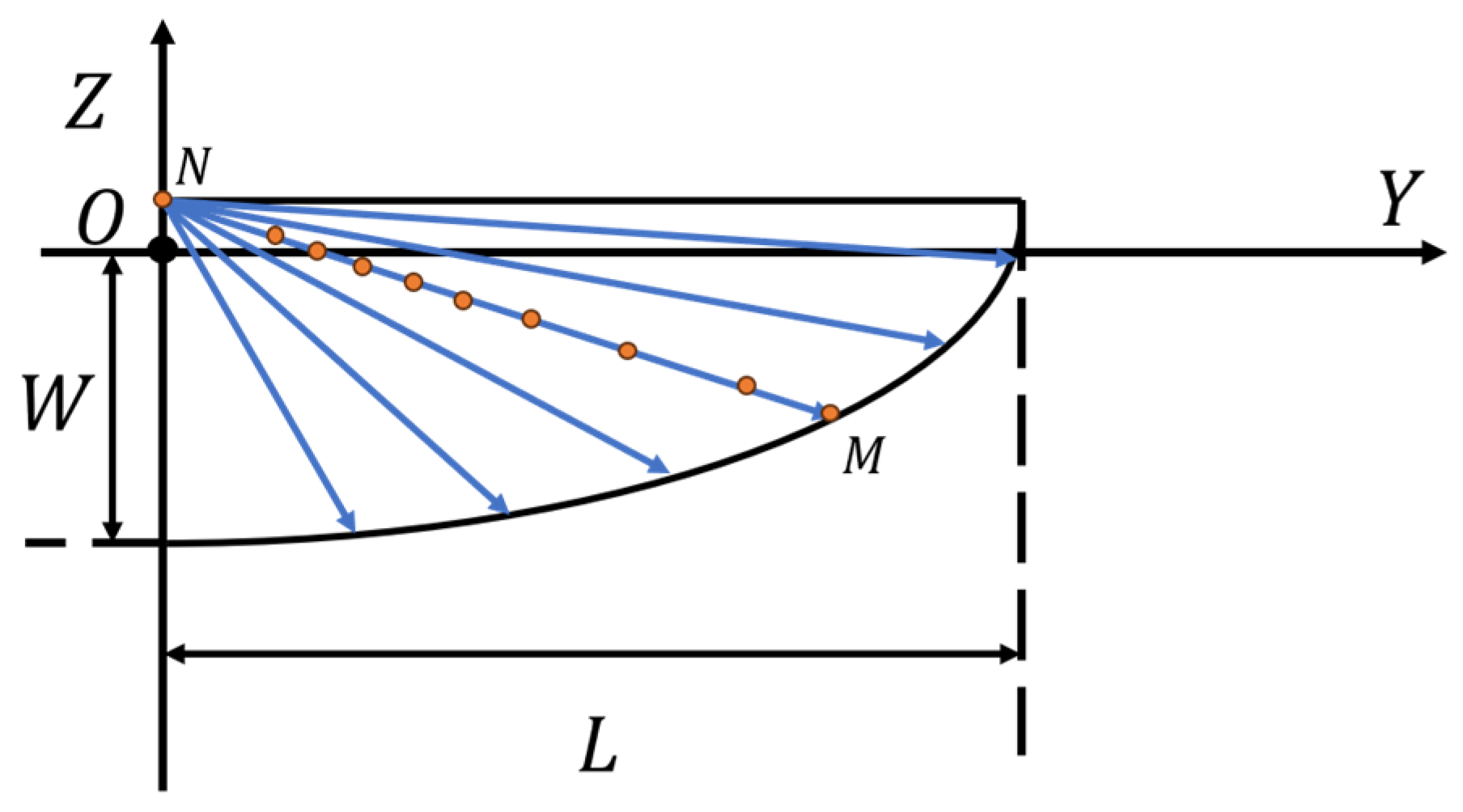
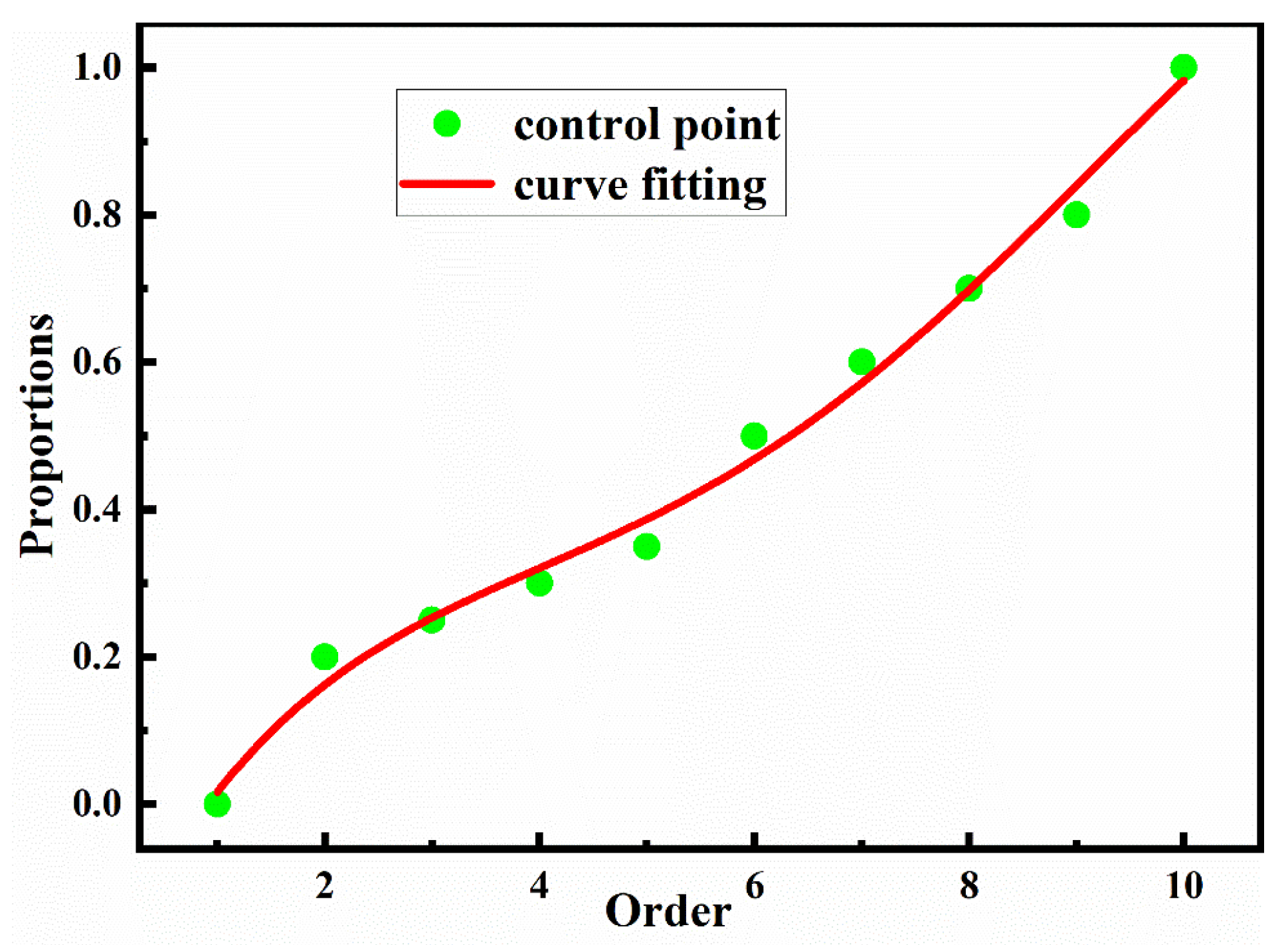
2.3. The Division of the Low Beam Target Surface
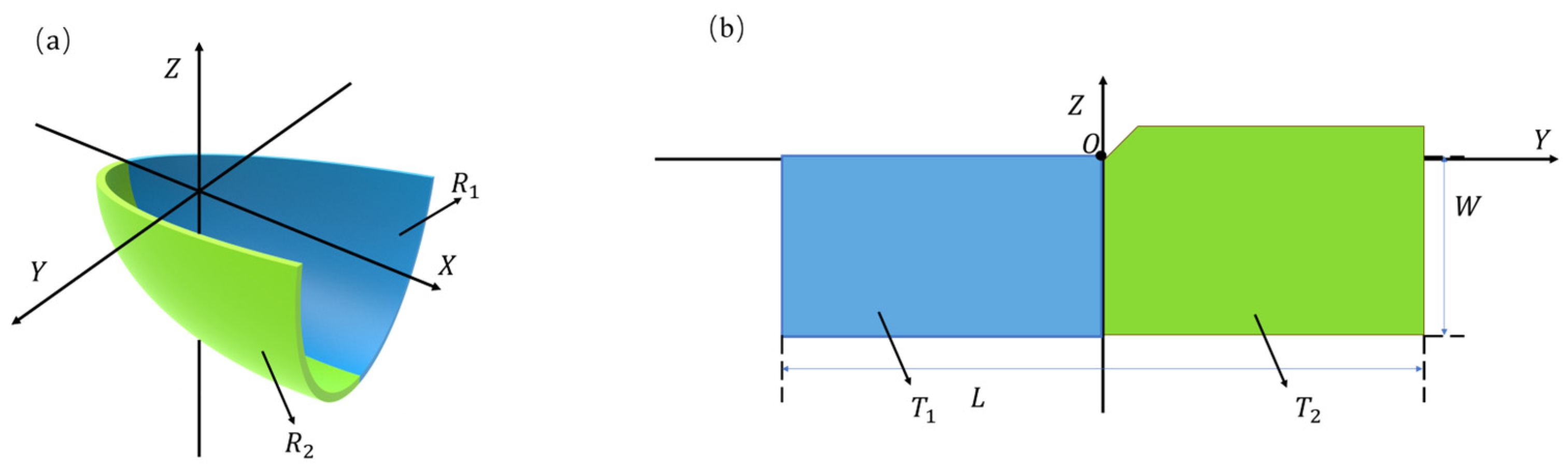
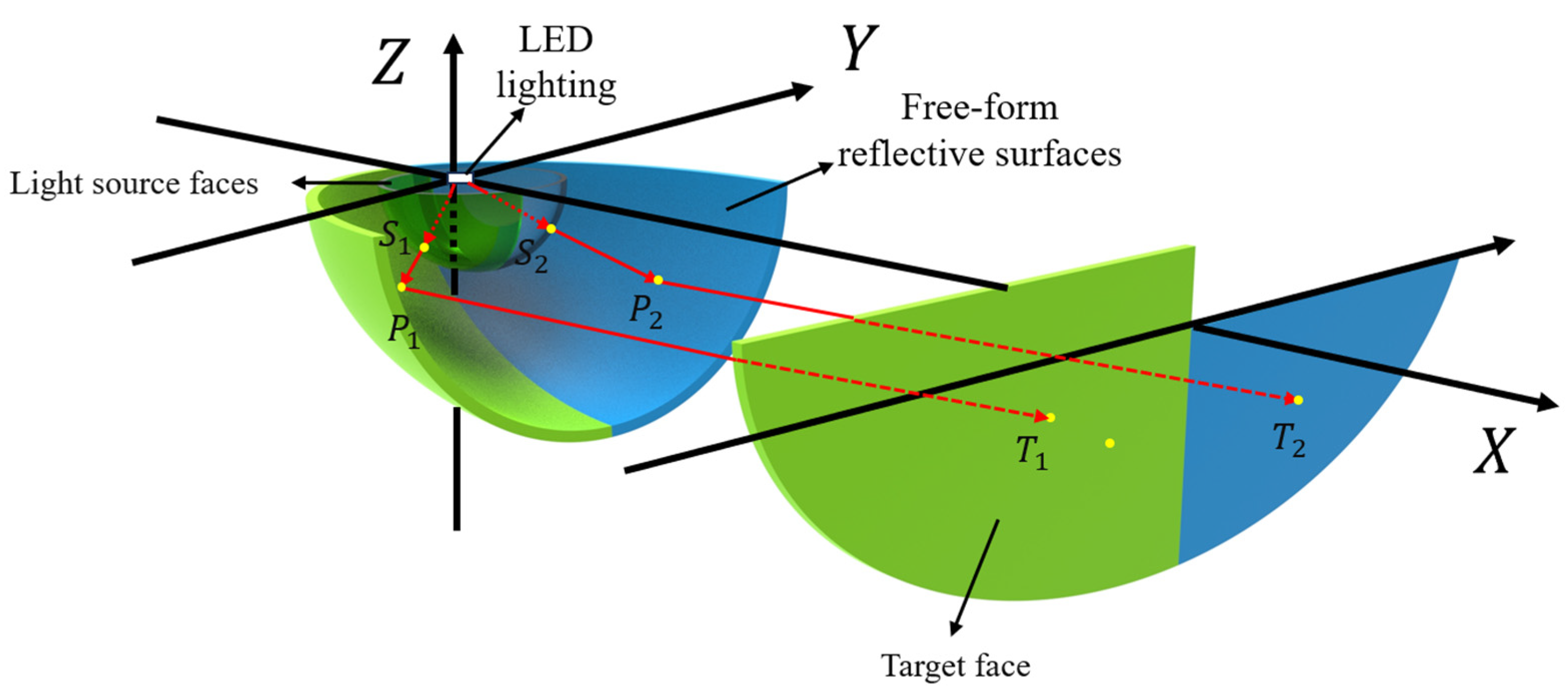
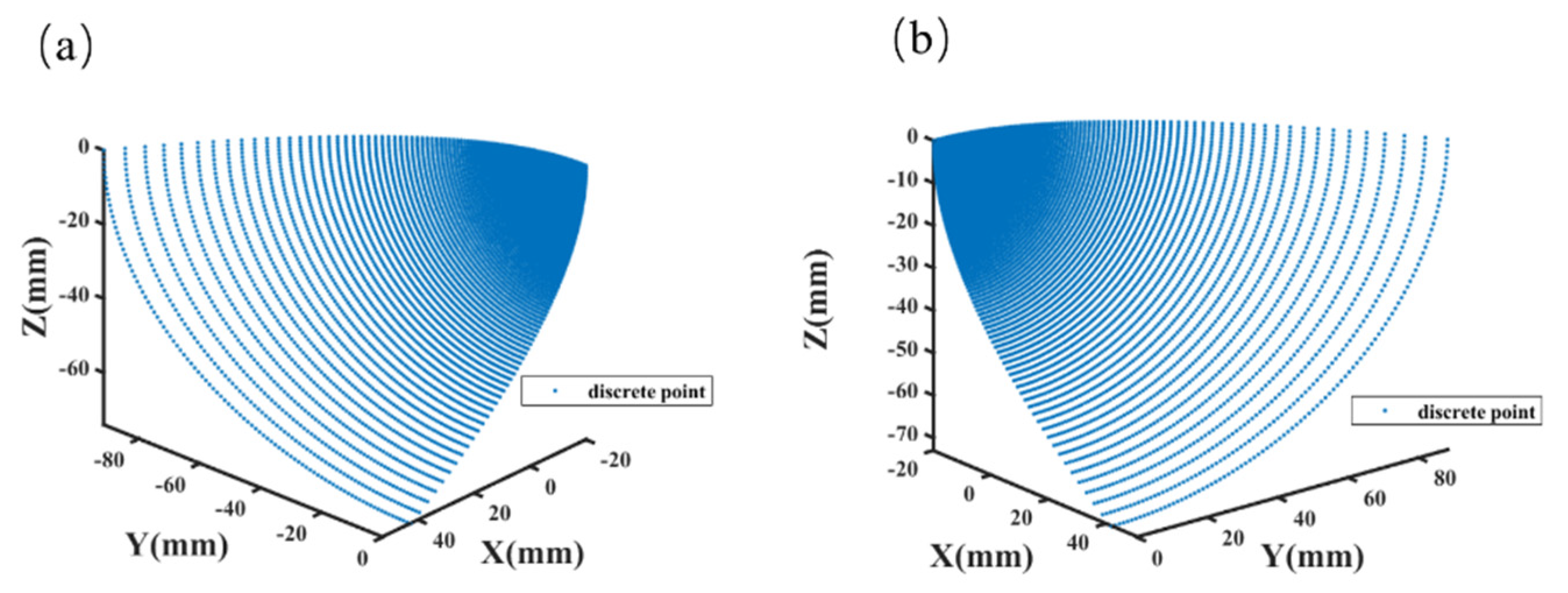
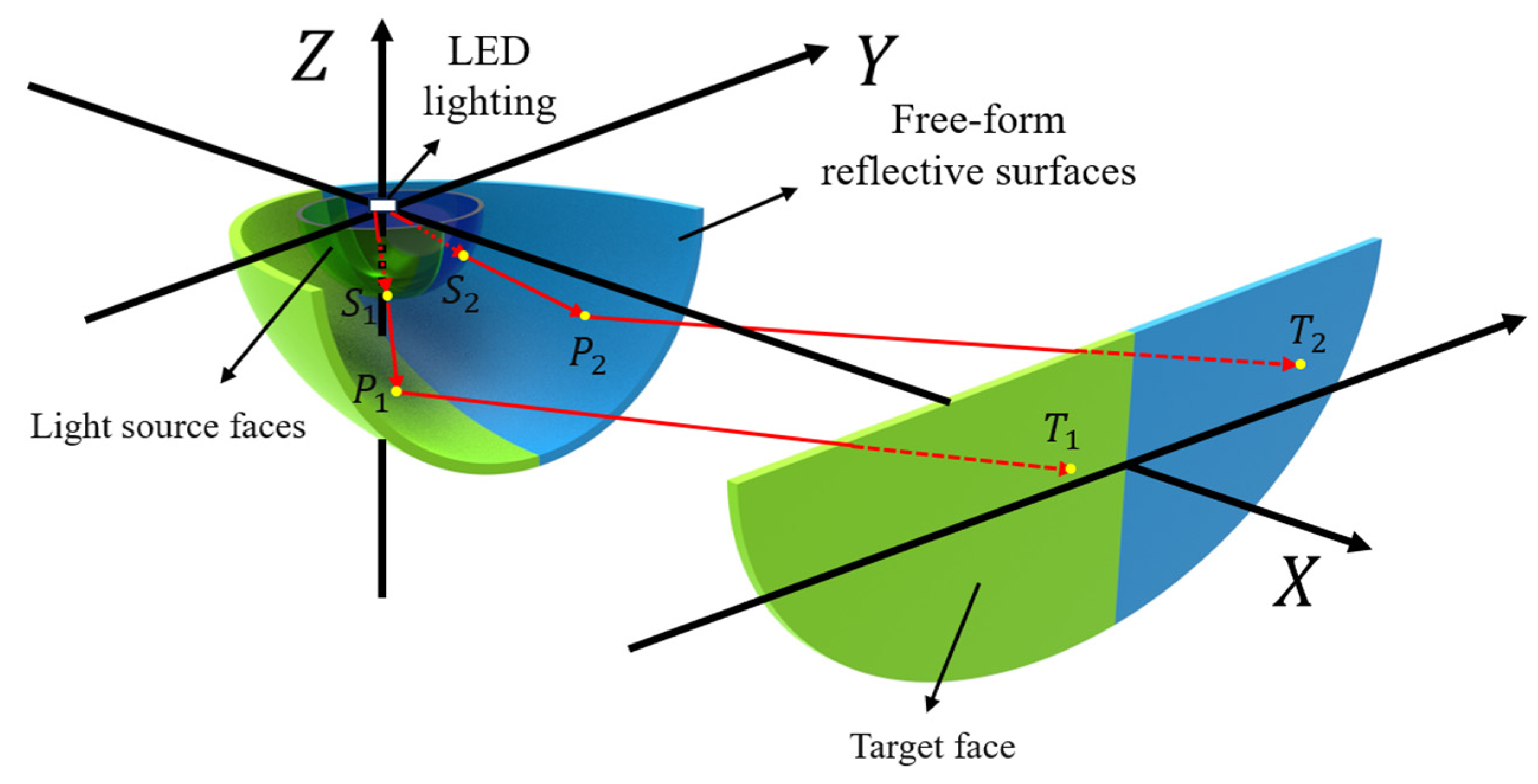
2.4. Calculation of Free-Form Surfaces for Low-Beam Headlight
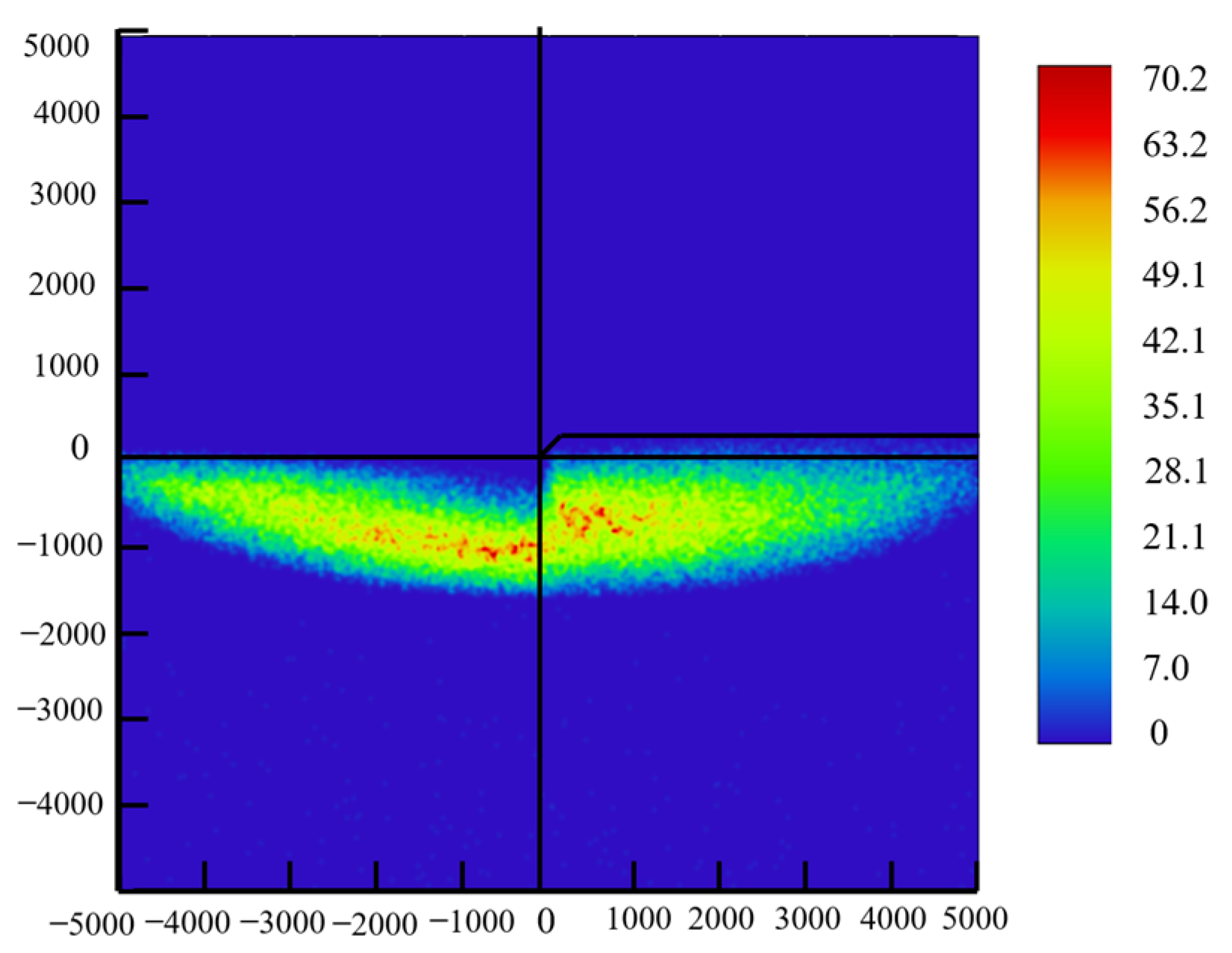
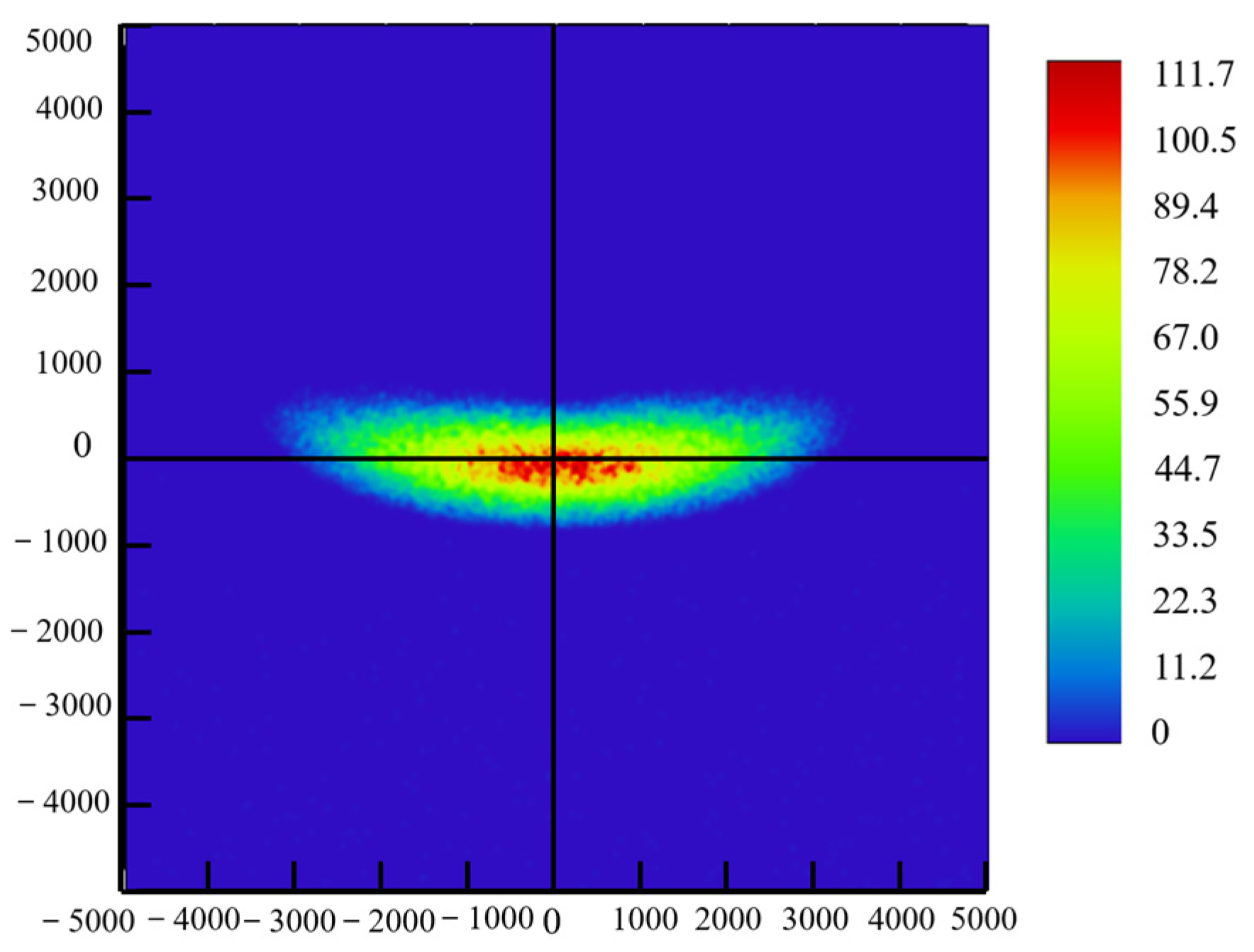
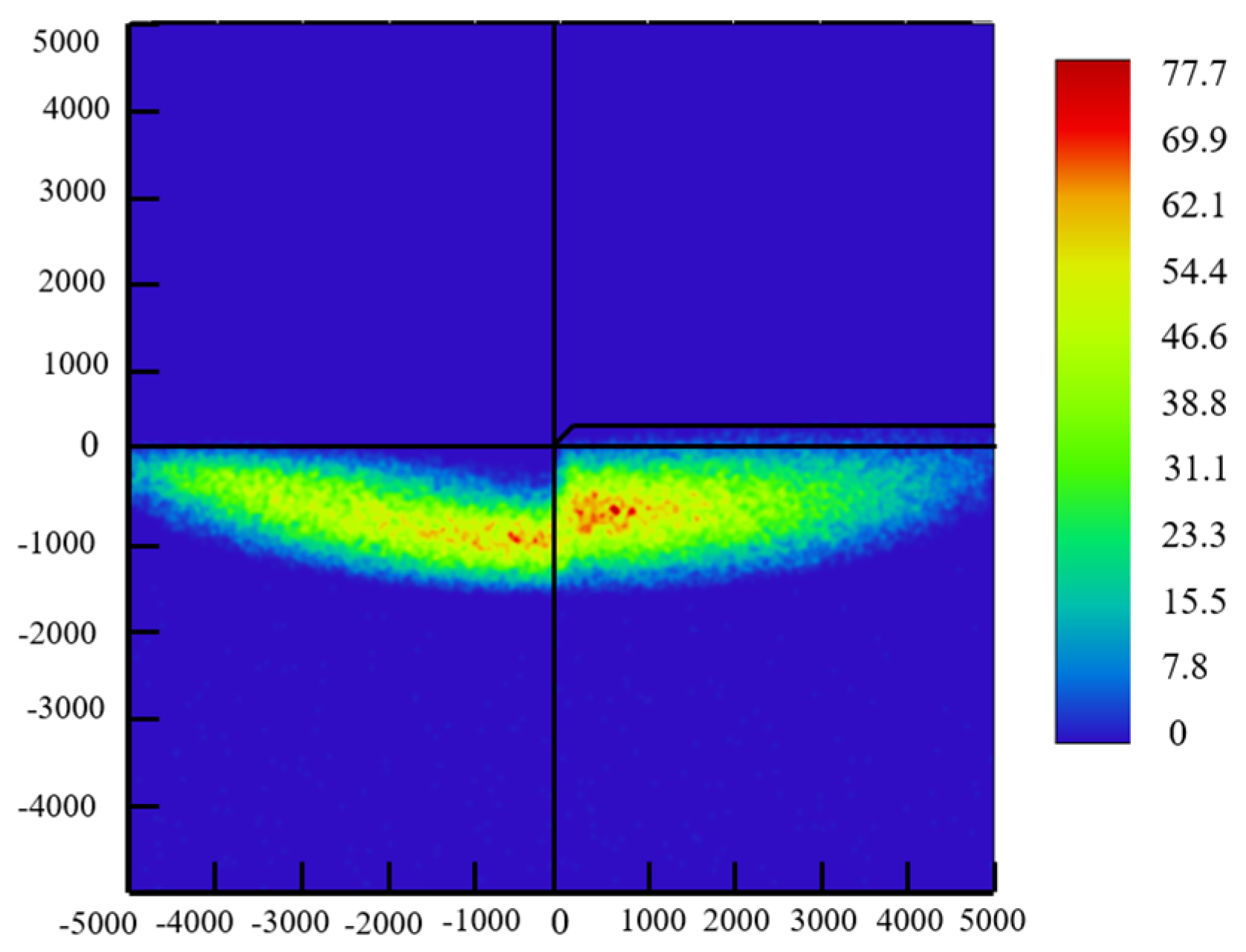
2.5. Modeling and Simulation of the Low-Beam Headlight
3. Freeform-Based High-Beam Headlight Design and Evaluation
3.1. Design Requirements of the High-Beam Headlight
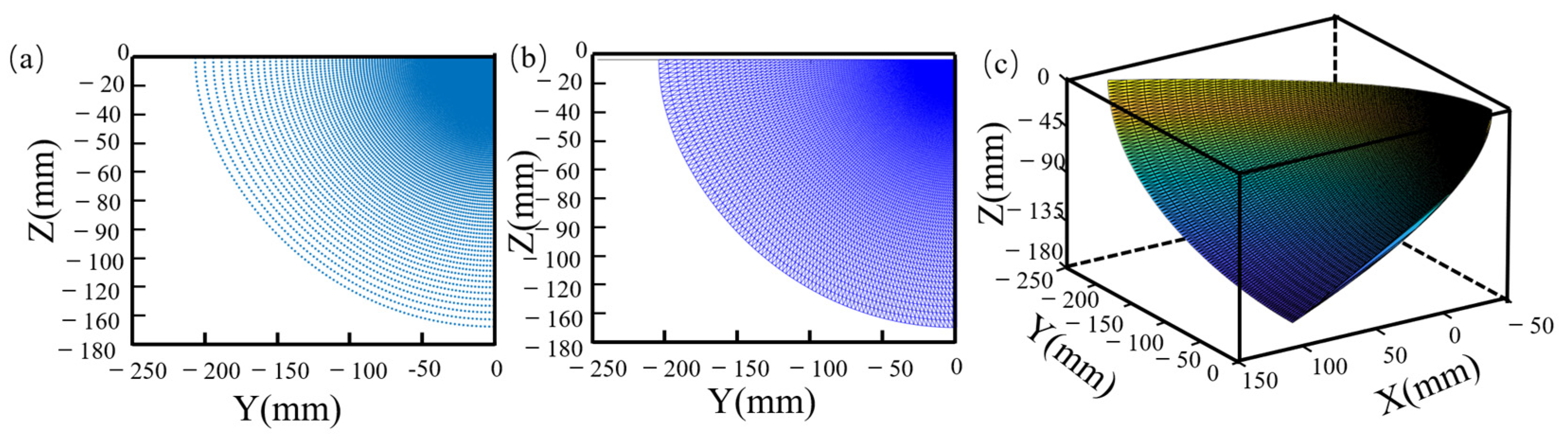
3.2. High-Beam Reflector Design
3.3. Calculation and Simulation of the Reflective Surface of High-Beam Headlight
4. Genetic Algorithm-Based Intelligent Optimization Method for Headlight Optical Structures
4.1. The Optimization Model Establishment
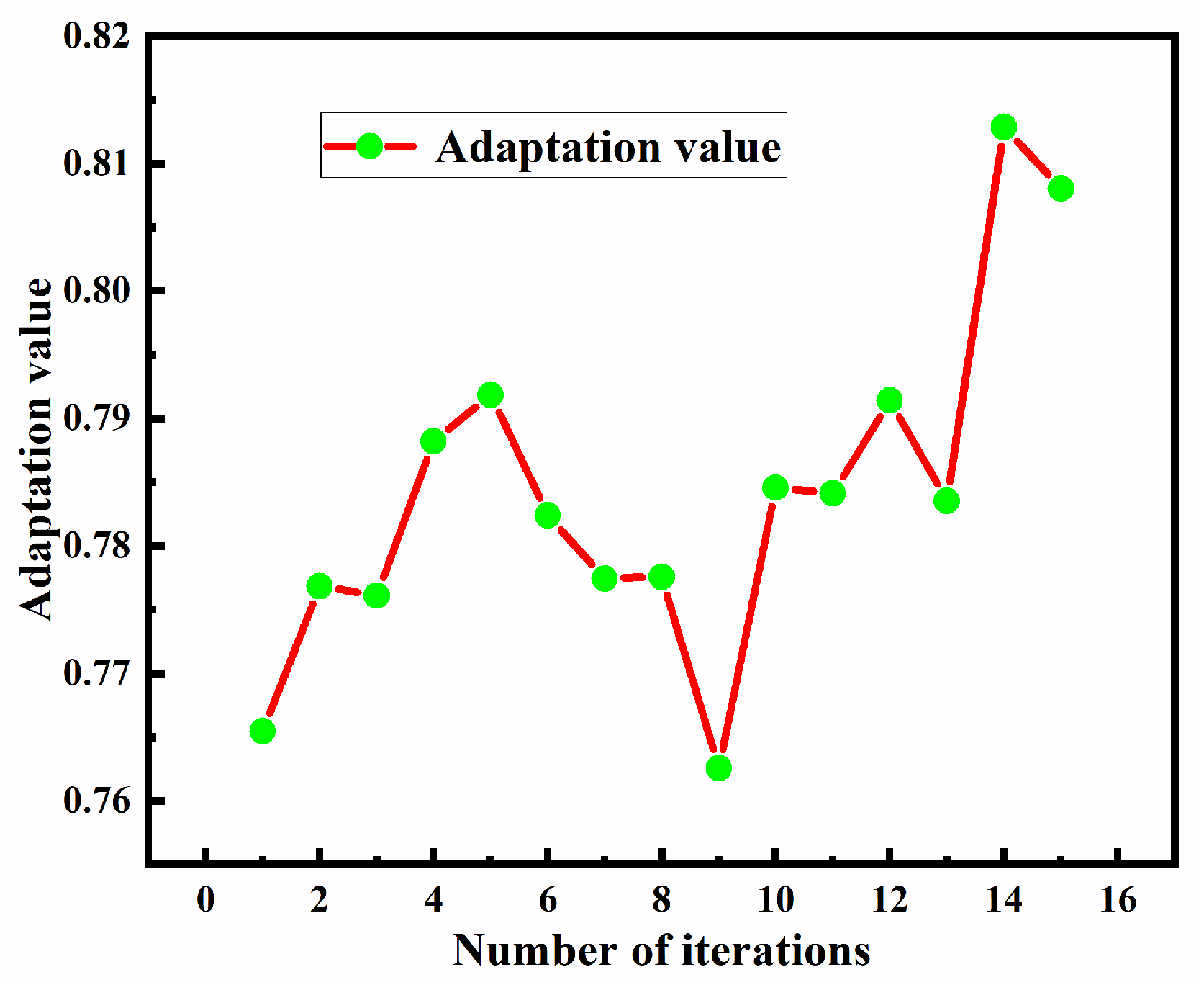
4.2. Optimization Process for Headlight Optical Structures
4.3. Results and Analyses
4.4. Manufacturing Process of Automotive Freeform Mirrors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, C.C.; Zheng, Y.J.; Hsu, Y.F.; Ye, Z.T. Design and Application of Liquid Silicone Rubber Light Guide in Compact Automotive Headlamps. Int. J. Optomechatron. 2024, 18, 2343407. [Google Scholar] [CrossRef]
- Qin, R.S. New Trends in Accounting Reform and Development in the ‘14th Five-Year Plan’ Period. XinLiCai 2021, 9, 12–17. [Google Scholar]
- Zhang, H.; Liu, D.; Wei, Y.; Wang, H. Asymmetric double freeform surface lens for integrated LED automobile headlamp. Micromachines 2021, 12, 663. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Lin, L. Design of a new pixel LED automobile headlamp. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optical Systems, Optoelectronic Instruments, Novel Display, and Imaging Technology, Online, 8–10 April 2022; pp. 140–146. [Google Scholar]
- Zhu, Z.; Wei, S.; Liu, R.; Hong, Z.; Zheng, Z.; Fan, Z.; Ma, D. Freeform surface design for high-efficient LED low-beam headlamp lens. Opt. Commun. 2020, 477, 126269. [Google Scholar] [CrossRef]
- Siddula, S. Design of Modern Technology Lighting System for Automobiles Check for updates. Emerg. Technol. Sustain. Dev. Sel. Proc. EGTET 2023, 2022, 1061. [Google Scholar]
- Zeng, Y. Free-form Automotive Laser Headlight Lighting System Based on Free-form Surface Design. Master’s Thesis, Changchun University of Science and Technology, Changchun, China, 2021. [Google Scholar]
- Xie, S.S. Design and Performance Analysis of Automobile Headlamp Based on Light-Emitting Diode. J. Nanoelectron. Optoelectron. 2023, 18, 1203–1210. [Google Scholar] [CrossRef]
- Bielawny, A.; Schupp, T.; Neumann, C. Automotive lighting continues to evolve. Opt. Photonics News 2016, 27, 36–43. [Google Scholar] [CrossRef]
- Feng, Z.X.; Froese, B.D.; Liang, R.G.; Cheng, D.; Wang, Y. Simplified freeform optics design for complicated laser beam shaping. Appl. Opt. 2017, 56, 9308–9314. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.S.; Qiu, D.; Zeng, Y.; Li, R.; Duan, W.; Fan, R. Design of a reflective LED automotive headlamp lighting system based on a free-form surface. Appl. Opt. 2021, 60, 8910–8914. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chen, Z.J.; Wu, H.; Ge, P. Free-form LED automotive front-illuminated optical lens design method. Infrared Laser Eng. 2014, 43, 1529–1534. [Google Scholar]
- Hsieh, C.C.; Tsai, C.L.; Hung, C.C.; Lin, H.H.; Li, T.C. Design of Multi-module LED Headlamp of Vehicle Under Federal Motor Vehicle Safety Standard. Sens. Mater. 2023, 35, 2433–2488. [Google Scholar] [CrossRef]
- Alfred, M.; Hossein, A. Folded light source: A technique for compact and efficient automotive lighting. Opt. Eng. 2023, 62, 095104. [Google Scholar]
- GB 25991-2010; Automotive Headlamps with LED Light Sources and/or LED Modules. Standardization Administration of China (SAC): Beijing, China, 2022.
- Oshima, R.; Masashige, S. Study of LED Spot Beam lighting for Headlights. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019. [Google Scholar]
- Tsai, C.Y. Design of free-form reflector for vehicle LED low-beam headlamp. Opt. Commun. 2016, 372, 1–13. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.M.; Ge, P. Design method of a light emitting diode front fog lamp based on a freeform reflector. Opt. Laser Technol. 2015, 72, 125–133. [Google Scholar] [CrossRef]
- Wang, L.P.; Su, P.; Ma, J.; Huang, J. LED high-beam module design for automotive headlight. AOPC 2021 Disp. Technol. 2021, 12063, 20–27. [Google Scholar]
- Mas, A.; Martín, I.; Patow, G. Heuristic driven inverse reflector design. Comput. Graph. 2018, 77, 1–15. [Google Scholar] [CrossRef]
- Tan, M.Y.; Chen, J. Dynamical optimized lamps distribution based on genetic algorithm for visible light communications. In Proceedings of the Eleventh International Conference on Information Optics and Photonics, Xi’an, China, 20 December 2019; pp. 1016–1021. [Google Scholar]
- Brunnstrom, K.; Andrew, J.S. Genetic algorithms for free-form surface matching. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; pp. 689–693. [Google Scholar]
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef]
- Rahbek, L.W.; Kirkegaard, P.H.; Alibrandi, U. Parametric grid mapping design tool for freeform surfaces using a genetic algorithm. Proc. IASS Annu. Symp. 2020, 22, 1–12. [Google Scholar]
- Lu, S.T. Characterization of Fabric Moisture Absorption and Quick-Drying Based on Segmentation Genetic Algorithm. Master’s Thesis, Zhongyuan University of Technology, Zhengzhou, China, 2023. [Google Scholar]
- Li, X.L. Research on the Key Technology of Magnetorheological Polishing of Complex Curved Aluminum Mirror. Master’s Thesis, National University of Defense Technology, Changsha, China, 2018. [Google Scholar]
- Xu, C.; Peng, X.Q.; Dai, Y.F. Current status of ultra-precision manufacturing of complex curved aluminum reflectors. Opto-Electron. Eng. 2020, 47, 200147. [Google Scholar]
- Xie, Y.J.; Mao, X.L.; Li, J.P.; Wang, F.; Wang, P.; Gao, R.; Li, X.; Ren, S.; Xu, Z.; Dong, R. Optical design and fabrication of an all-aluminum unobscured two-mirror freeform imaging telescope. Appl. Opt. 2020, 59, 833–840. [Google Scholar] [CrossRef] [PubMed]

















| Test Points or Areas | Required Illuminance (lx) | Simulated Illuminance (lx) | Fulfillment of Requirements |
|---|---|---|---|
| HV | ≤0.7 | 0.57 | Yes |
| B50L | ≤0.4 | 0 | Yes |
| 75R | ≥12 | 32.16 | Yes |
| 75L | ≤12 | 10.21 | Yes |
| 50L | ≤15 | 13.32 | Yes |
| 50R | ≥12 | 48.43 | Yes |
| 50V | ≥6 | 25.71 | Yes |
| 25L | ≥2 | 10.31 | Yes |
| 25R | ≥2 | 7.08 | Yes |
| III area | ≤0.7 | ≤0.14 | Yes |
| VI areas | ≥3 | ≥6.85 | Yes |
| I areas | ≤2 × 50R | ≤54.33 | Yes |
| Test Points or Areas | Required Illuminance (lx) |
|---|---|
| ≥48 and ≤250 | |
| HV Point | ≥ |
| 1125L to HV and HV to 1125R | ≥24 |
| 2250L to HV and HV to 2250R | ≥6 |
| Test Points or Areas | Required Illuminance (lx) | Simulated Illuminance (lx) |
|---|---|---|
| ≥48 and ≤250 | 111.7 | |
| HV Point | ≥ | 97.95 |
| 1125L to HV and HV to 1125R | ≥24 | 77.99 |
| 2250L to HV and HV to 2250R | ≥6 | 32.11 |
| Test Points or Areas | Required Illuminance (lx) | Simulated Illuminance (lx) |
|---|---|---|
| ≥48 and ≤250 | 127.4 | |
| HV Point | ≥ | 110.4 |
| 1125L to HV and HV to 1125R | ≥24 | 87.90 |
| 2250L to HV and HV to 2250R | ≥6 | 38.62 |
| Test Points or Areas | Simulated Illuminance (lx) | Fulfillment of Requirements |
|---|---|---|
| HV | 0.5 | Yes |
| B50L | 0 | Yes |
| 75R | 42.64 | Yes |
| 75L | 10.73 | Yes |
| 50L | 14.83 | Yes |
| 50R | 49.07 | Yes |
| 50V | 36.72 | Yes |
| 25L | 10.94 | Yes |
| 25R | 9.63 | Yes |
| III area | ≤0.46 | Yes |
| VI areas | ≥7.95 | Yes |
| I areas | ≤69.88 | Yes |
| Before Optimization | After Optimization | |||
|---|---|---|---|---|
| High Beam | Low Beam | High Beam | Low Beam | |
| (rad) | 2.09 | 2.2 | ||
| dimension (mm) | 157.78 × 60.35 × 69.89 | 179.08 × 62.08 × 72.91 | 218.94 × 101.14 × 90.82 | 255.72 × 105.81 × 96.04 |
| efficiency (%) | 80.69 | 80.59 | 89.40 | 88.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Peng, X.; Song, C. Adaptive Freeform Optics Design and Multi-Objective Genetic Optimization for Energy-Efficient Automotive LED Headlights. Photonics 2025, 12, 388. https://doi.org/10.3390/photonics12040388
Xu S, Peng X, Song C. Adaptive Freeform Optics Design and Multi-Objective Genetic Optimization for Energy-Efficient Automotive LED Headlights. Photonics. 2025; 12(4):388. https://doi.org/10.3390/photonics12040388
Chicago/Turabian StyleXu, Shaohui, Xing Peng, and Ci Song. 2025. "Adaptive Freeform Optics Design and Multi-Objective Genetic Optimization for Energy-Efficient Automotive LED Headlights" Photonics 12, no. 4: 388. https://doi.org/10.3390/photonics12040388
APA StyleXu, S., Peng, X., & Song, C. (2025). Adaptive Freeform Optics Design and Multi-Objective Genetic Optimization for Energy-Efficient Automotive LED Headlights. Photonics, 12(4), 388. https://doi.org/10.3390/photonics12040388






