Defect Detection Method for Large-Curvature and Highly Reflective Surfaces Based on Polarization Imaging and Improved YOLOv11
Abstract
1. Introduction
2. Method
2.1. Polarization Imaging Principle
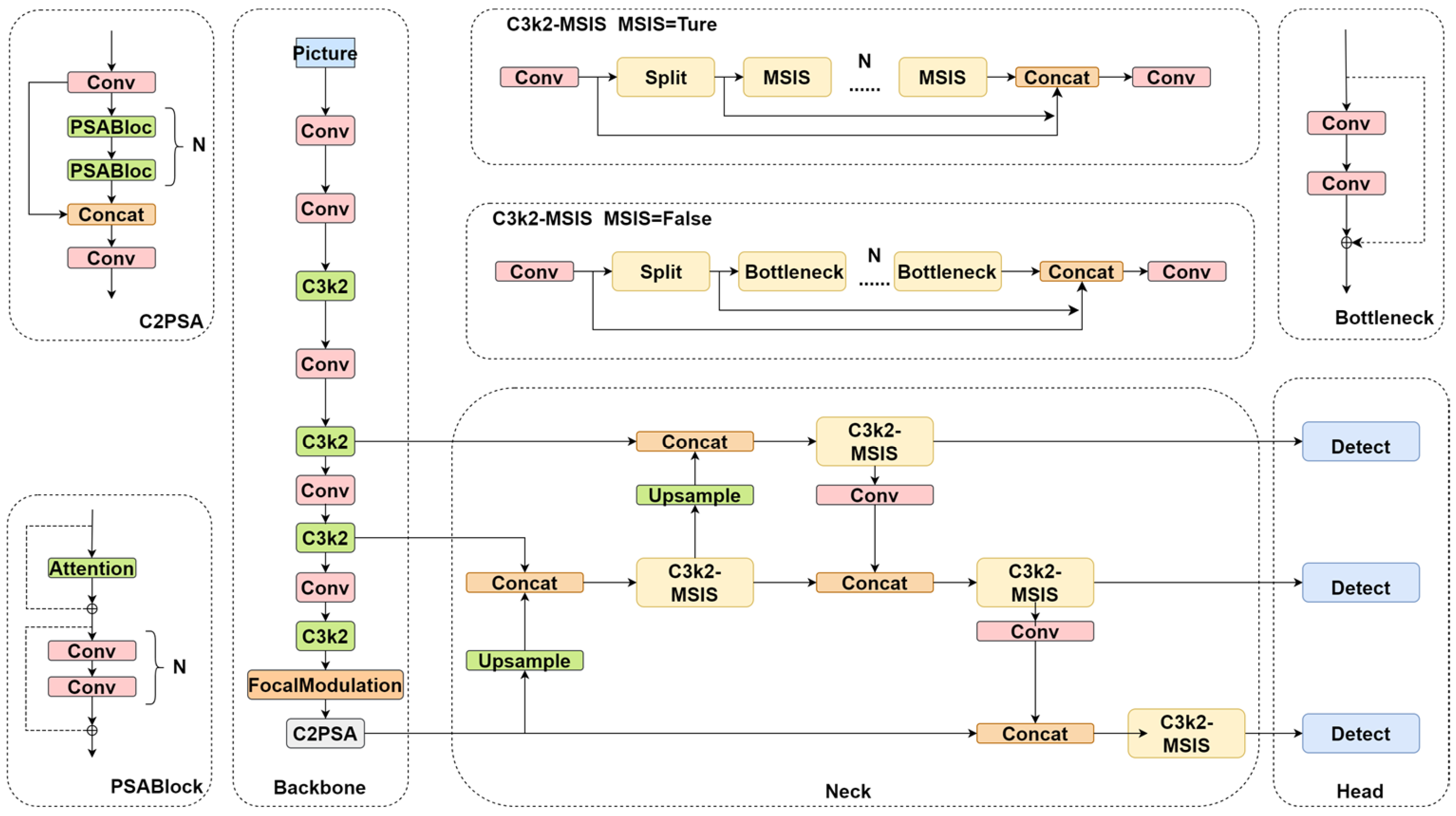
2.2. Improving the YOLOv11 Model
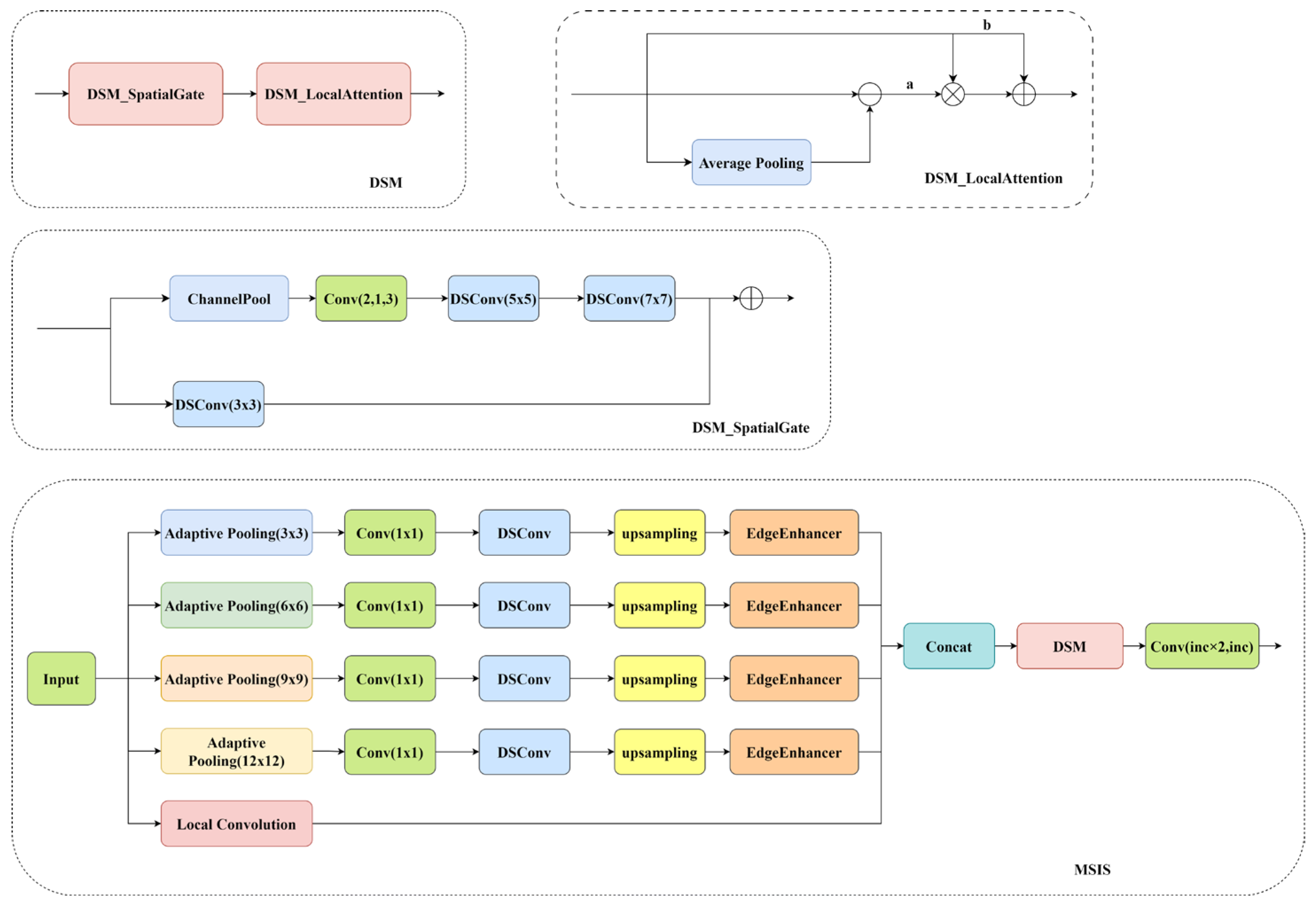
2.2.1. Multi-Scale Edge Information Selection Module
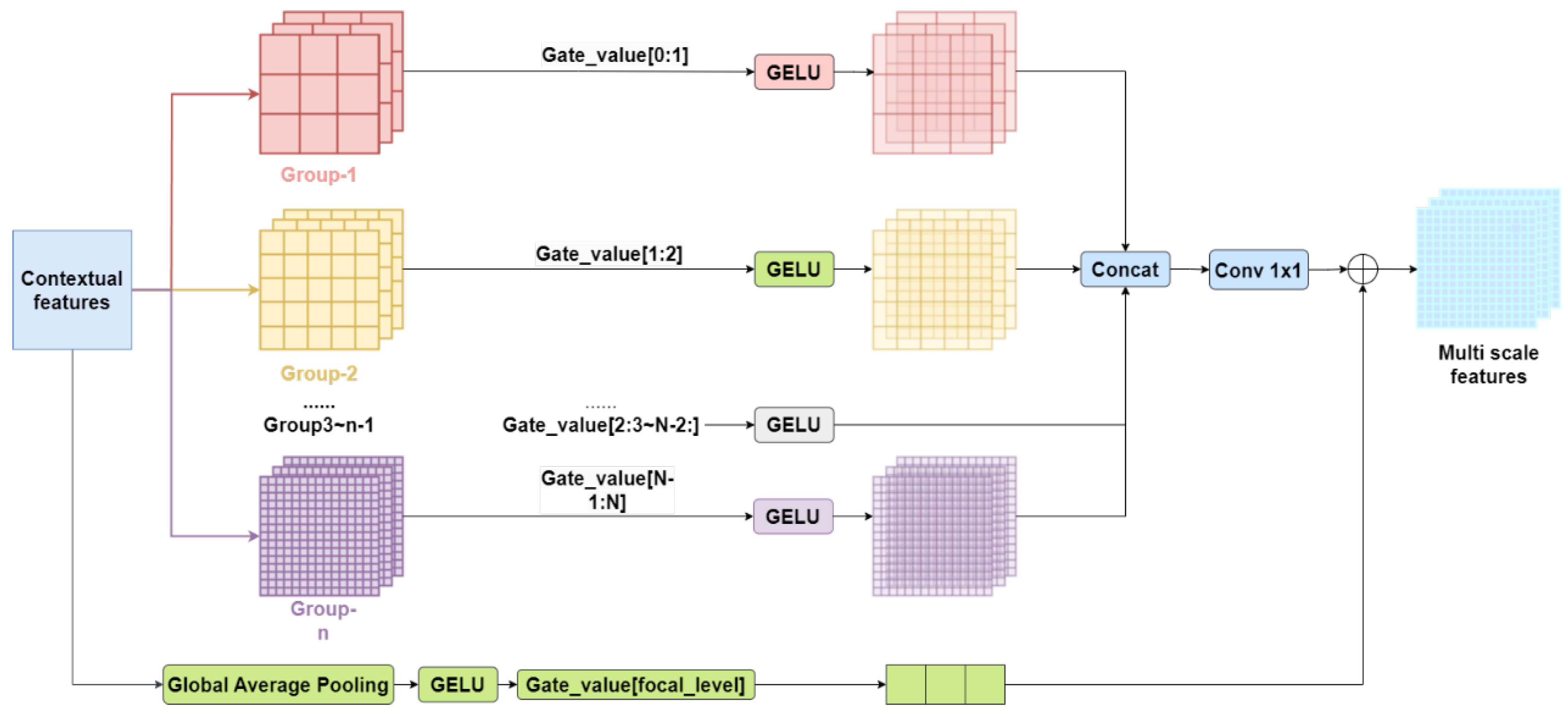
2.2.2. Focal Modulation Module
3. Experimental Results and Analysis
3.1. Test Equipment Construction
3.2. Polarization Imaging Performance Experiment
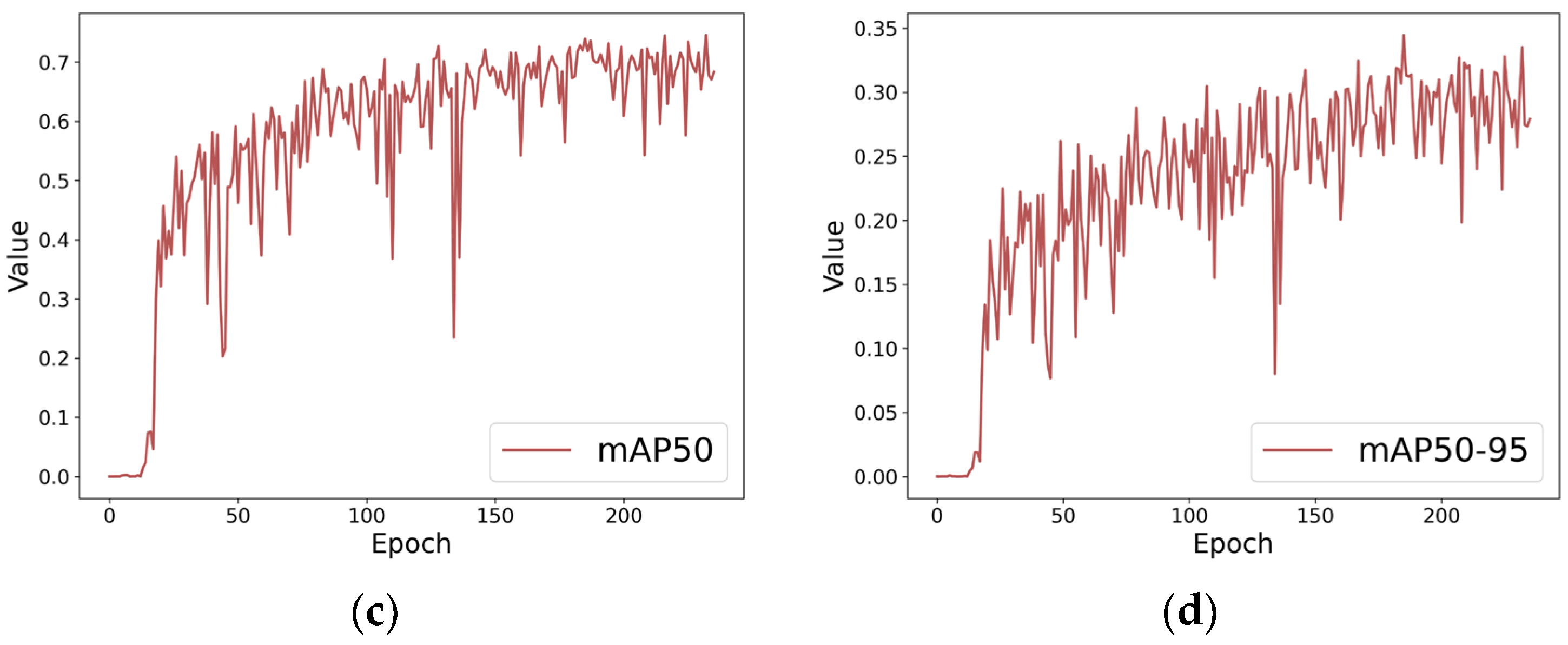
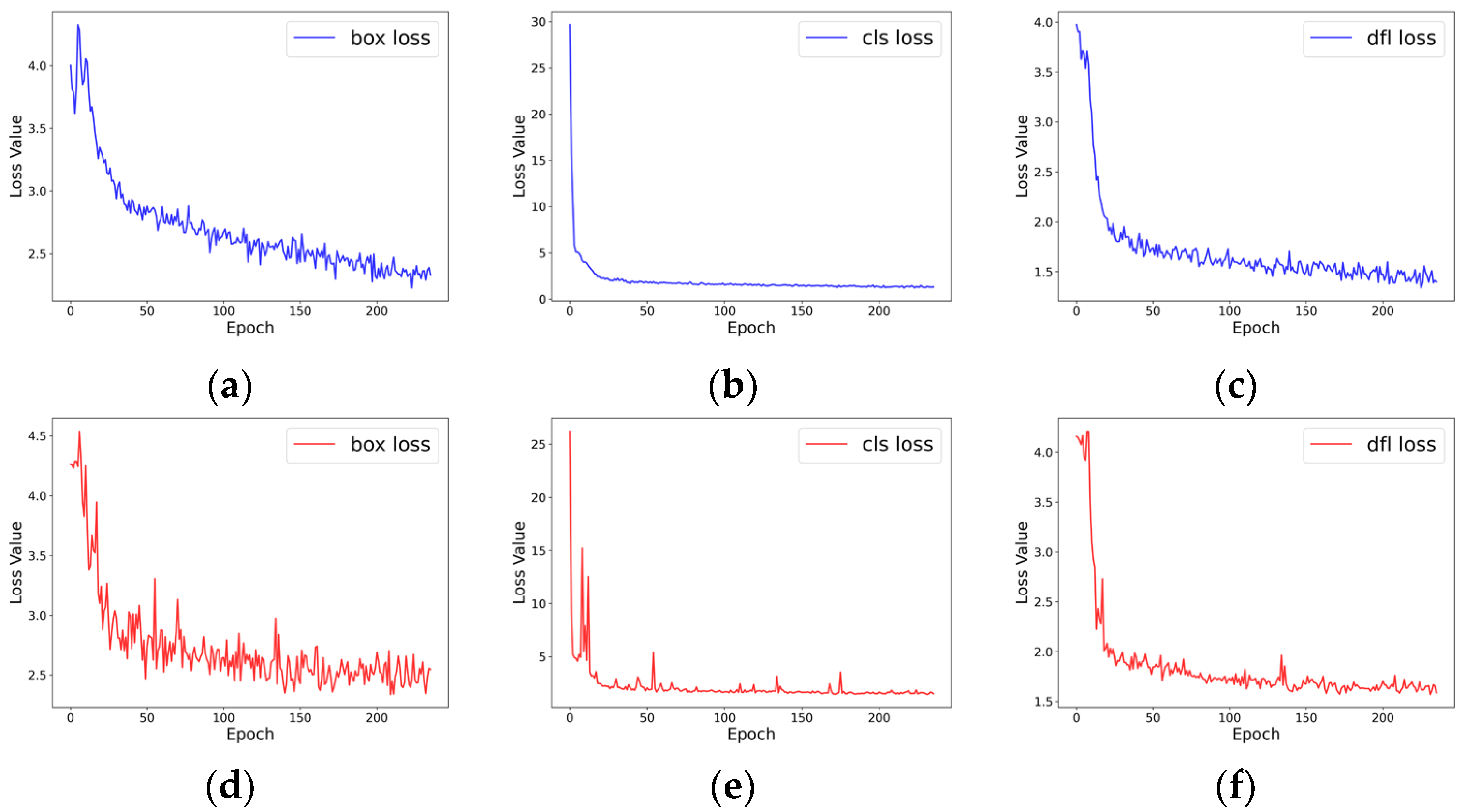
3.3. MF-YOLOv11 Model Performance Experiment
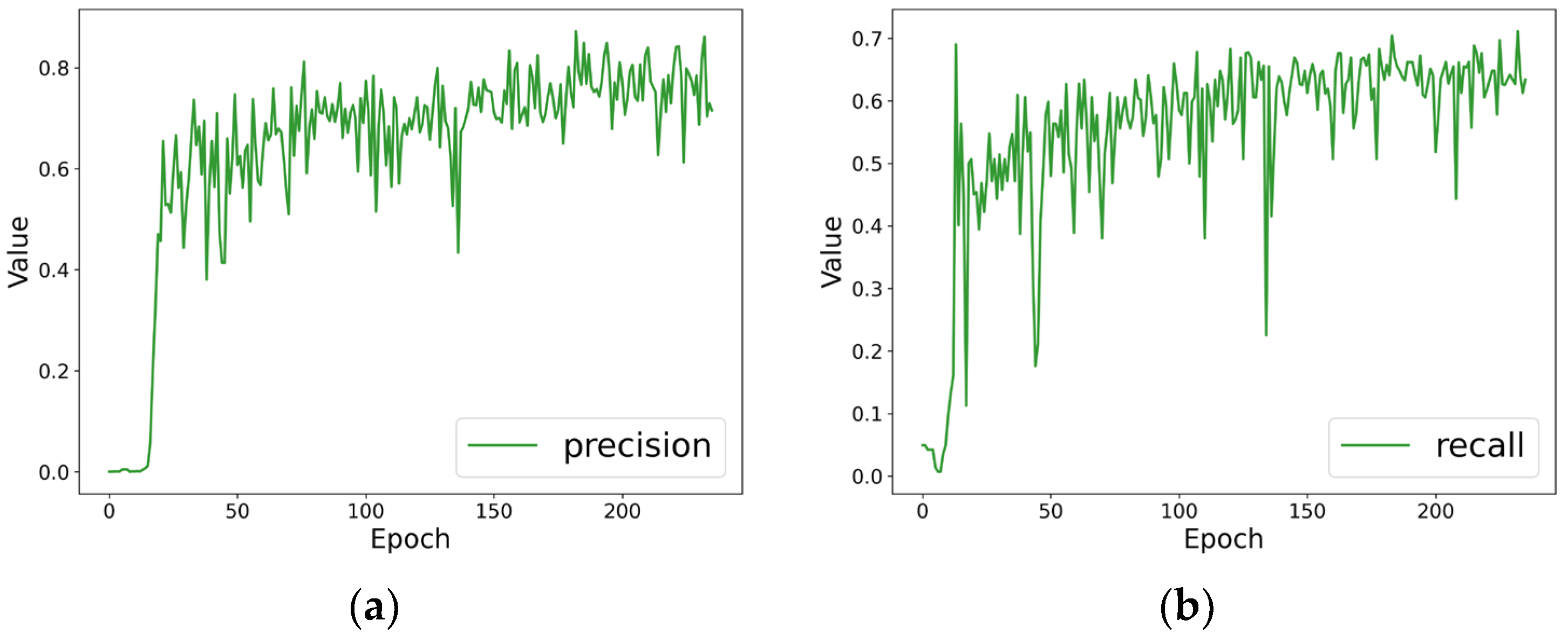
3.3.1. MF-YOLOv11 Model Checking Performance Evaluation
3.3.2. MF-YOLOv11 Model Detection Performance Comparison
3.3.3. Ablation Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zarei, A.; Pilla, S. Laser ultrasonics for nondestructive testing of composite materials and structures: A review. Ultrasonics 2024, 136, 107163. [Google Scholar] [CrossRef] [PubMed]
- Li, E.; Guo, W.; Cao, X.; Zhu, J. A magnetic head-based eddy current array for defect detection in ferromagnetic steels. Sens. Actuators A Phys. 2024, 379, 115862. [Google Scholar] [CrossRef]
- Chang, H.-L.; Ren, H.-T.; Wang, G.; Yang, M.; Zhu, X.-Y. Infrared defect recognition technology for composite materials. Front. Phys. 2023, 11, 1203762. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, F.; Yan, N.; Wu, Y. State of the Art in Defect Detection Based on Machine Vision. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 9, 661–691. [Google Scholar] [CrossRef]
- Wen, X.; Shan, J.; He, Y.; Song, K. Steel Surface Defect Recognition: A Survey. Coatings 2022, 13, 17. [Google Scholar] [CrossRef]
- Kim, T.; Behdinan, K. Advances in machine learning and deep learning applications towards wafer map defect recognition and classification: A review. J. Intell. Manuf. 2022, 34, 3215–3247. [Google Scholar] [CrossRef]
- Xie, Y.; Xu, X.; Liu, S. Machine vision-based detection of surface defects in cylindrical battery cases. J. Energy Storage 2024, 101, 113949. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, C.; Cheng, X.; Yang, J.; Chen, N. Stainless steel cylindrical pot outer surface defect detection method based on cascade neural network. Meas. Sci. Technol. 2023, 35, 036201. [Google Scholar] [CrossRef]
- Abdulrahman, Y.; Mohammed Eltoum, M.A.; Ayyad, A.; Moyo, B.; Zweiri, Y. Aero-engine Blade Defect Detection: A Systematic Review of Deep Learning Models. IEEE Access 2023, 11, 53048–53061. [Google Scholar] [CrossRef]
- Jing, J.; Liu, S.; Wang, G.; Zhang, W.; Sun, C. Recent advances on image edge detection: A comprehensive review. Neurocomputing 2022, 503, 259–271. [Google Scholar] [CrossRef]
- Tsai, D.-M.; Huang, C.-K. Defect Detection in Electronic Surfaces Using Template-Based Fourier Image Reconstruction. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 163–172. [Google Scholar] [CrossRef]
- Li, F.; Yuan, L.; Zhang, K.; Li, W. A defect detection method for unpatterned fabric based on multidirectional binary patterns and the gray-level co-occurrence matrix. Text. Res. J. 2019, 90, 776–796. [Google Scholar] [CrossRef]
- Sahu, D.; Dewangan, R.K.; Matharu, S.P.S. An Investigation of Fault Detection Techniques in Rolling Element Bearing. J. Vib. Eng. Technol. 2023, 12, 5585–5608. [Google Scholar] [CrossRef]
- Dong, G.; Pan, X.; Liu, S.; Wu, N.; Kong, X.; Huang, P.; Wang, Z. A review of machine vision technology for defect detection in curved ceramic materials. Nondestruct. Test. Eval. 2024, 1–27. [Google Scholar] [CrossRef]
- Zhou, A.; Ai, B.; Qu, P.; Shao, W. Defect detection for highly reflective rotary surfaces: An overview. Meas. Sci. Technol. 2021, 32, 062001. [Google Scholar] [CrossRef]
- Xu, L.M.; Yang, Z.Q.; Jiang, Z.H.; Chen, Y. Light source optimization for automatic visual inspection of piston surface defects. Int. J. Adv. Manuf. Technol. 2016, 91, 2245–2256. [Google Scholar] [CrossRef]
- Shao, W.; Liu, K.; Shao, Y.; Zhou, A. Smooth Surface Visual Imaging Method for Eliminating High Reflection Disturbance. Sensors 2019, 19, 4953. [Google Scholar] [CrossRef]
- Hui, M.; Li, M.; Babar, M. A Diffuse Reflection Approach for Detection of Surface Defect Using Machine Learning. Mob. Inf. Syst. 2022, 2022, 7771178. [Google Scholar] [CrossRef]
- Chen, H.; Gao, J.; Zhang, Z.; Yin, W.; Dong, N.; Zhou, G.; Meng, Z. CFRP delamination defect detection by dynamic scanning thermography based on infrared feature reconstruction. Opt. Lasers Eng. 2025, 187, 108884. [Google Scholar] [CrossRef]
- Bao, Y.; Zhou, Z.; Wei, S.; Xiang, J. Research on surface defect detection system and method of train bearing cylindrical roller based on surface scanning. J. Mech. Sci. Technol. 2023, 37, 4507–4519. [Google Scholar] [CrossRef]
- Wang, D.; Yin, J.; Wu, H.; Ge, B. Method for detecting internal cracks in joints of composite metal materials based on dual-channel feature fusion. Opt. Laser Technol. 2023, 162, 109263. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, W.; Huang, Y. A Novel Feature Extraction Method Based on Legendre Multi-Wavelet Transform and Auto-Encoder for Steel Surface Defect Classification. IEEE Access 2024, 12, 5092–5102. [Google Scholar] [CrossRef]
- Liu, Z.; Qu, B. Machine vision based online detection of PCB defect. Microprocess. Microsyst. 2021, 82, 103807. [Google Scholar] [CrossRef]
- Hussain, M. YOLO-v1 to YOLO-v8, the Rise of YOLO and Its Complementary Nature toward Digital Manufacturing and Industrial Defect Detection. Machines 2023, 11, 677. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Ameri, R.; Hsu, C.-C.; Band, S.S. A systematic review of deep learning approaches for surface defect detection in industrial applications. Eng. Appl. Artif. Intell. 2024, 130, 107717. [Google Scholar] [CrossRef]
- Song, K.; Sun, X.; Ma, S.; Yan, Y. Surface Defect Detection of Aeroengine Blades Based on Cross-Layer Semantic Guidance. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Y.; Deng, W. Defect Detection Using Shuffle Net-CA-SSD Lightweight Network for Turbine Blades in IoT. IEEE Internet Things J. 2024, 11, 32804–32812. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Xie, Q.; Wu, Y.; Yu, Z.; Wang, J. Tiny Defect Detection in High-Resolution Aero-Engine Blade Images via a Coarse-to-Fine Framework. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Liu, M.; Wang, H.; Du, L.; Ji, F.; Zhang, M. Bearing-DETR: A Lightweight Deep Learning Model for Bearing Defect Detection Based on RT-DETR. Sensors 2024, 24, 4262. [Google Scholar] [CrossRef]
- Chang, F.; Liu, M.; Dong, M.; Duan, Y. A mobile vision inspection system for tiny defect detection on smooth car-body surfaces based on deep ensemble learning. Meas. Sci. Technol. 2019, 30, 125905. [Google Scholar] [CrossRef]







| Number | Device Name | Brand | Model |
|---|---|---|---|
| 1 | Camera | Basler, Ahrensburg, Germany | Aca-2500-30gc |
| 2 | Lenses | ZLZK, Zoomlion, Changsha, China | LM0820MP5 |
| 3 | Light Source | V-Light, China | VLHBGLXD30X245B-24V |
| 4 | Industrial Computer | Hikvision, Hangzhou, China | MV-IPC-F487H |
| 5 | PLC | Siemens, Munich, Germany | S7-200 SMART |
| 6 | Frame grabber | Daheng Imaging, Beijing, China | PCIe-GIE72P |
| Name | Parameter |
|---|---|
| CPU | Intel i9-13900HX |
| GPU | NVIDIA RTX 4060 |
| WINDOW | WINDOW11 |
| PYTHON | 3.9 |
| CUDA | 11.7 |
| TORCH | 2.0.1 |
| Learning rates | 0.01 |
| Epochs | 250 |
| Batch size | 16 |
| Model Name | Precision | Recall | mAP50 | Model Size | GFLOPS |
|---|---|---|---|---|---|
| YOLOv11n | 82.2 | 68.3 | 71.1 | 5.9 | 7.3 |
| YOLOv11n-C3k2-MSIS | 83.7 | 69.2 | 71.6 | 5.8 | 7.4 |
| YOLOv11n-Focal Modulation | 84.3 | 69.7 | 71.8 | 5.8 | 7.4 |
| MF-YOLOv11n | 86.1 | 71.1 | 72.7 | 5.8 | 7.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Wang, D.; Wu, H. Defect Detection Method for Large-Curvature and Highly Reflective Surfaces Based on Polarization Imaging and Improved YOLOv11. Photonics 2025, 12, 368. https://doi.org/10.3390/photonics12040368
Yu Z, Wang D, Wu H. Defect Detection Method for Large-Curvature and Highly Reflective Surfaces Based on Polarization Imaging and Improved YOLOv11. Photonics. 2025; 12(4):368. https://doi.org/10.3390/photonics12040368
Chicago/Turabian StyleYu, Zeyu, Dongyun Wang, and Hanyang Wu. 2025. "Defect Detection Method for Large-Curvature and Highly Reflective Surfaces Based on Polarization Imaging and Improved YOLOv11" Photonics 12, no. 4: 368. https://doi.org/10.3390/photonics12040368
APA StyleYu, Z., Wang, D., & Wu, H. (2025). Defect Detection Method for Large-Curvature and Highly Reflective Surfaces Based on Polarization Imaging and Improved YOLOv11. Photonics, 12(4), 368. https://doi.org/10.3390/photonics12040368





