Study on the Wavelength-Dependent Temporal Waveform Characteristics of a High-Pressure CO2 Master Oscillator Power Amplifier System
Abstract
1. Introduction
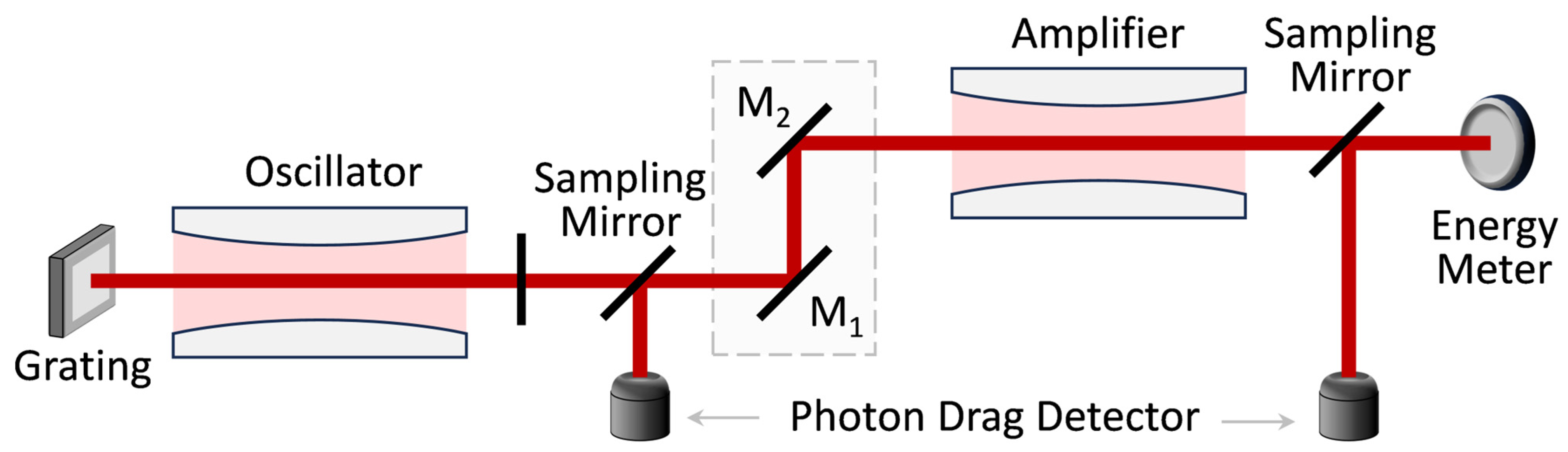
2. Experimental Setup
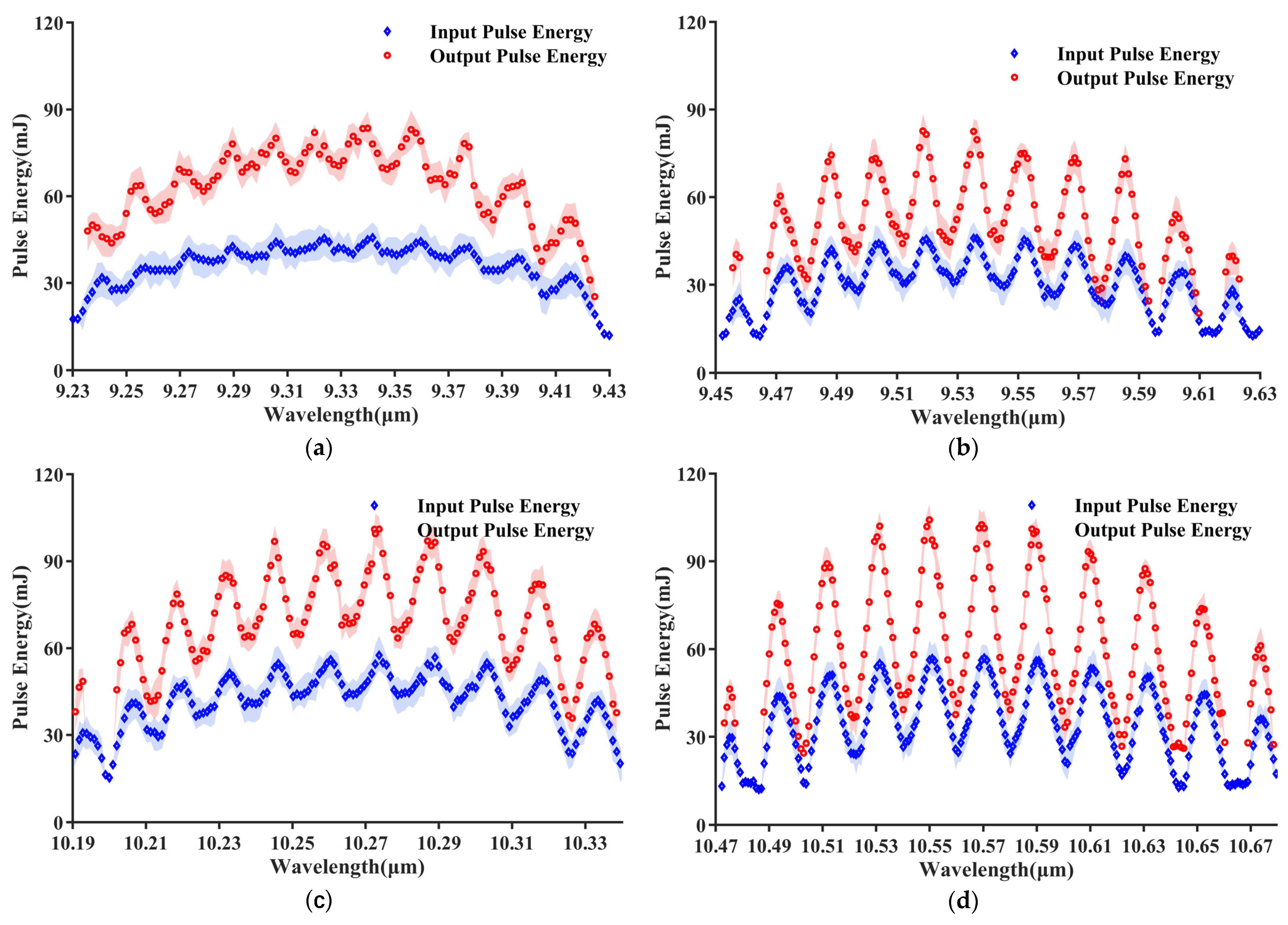
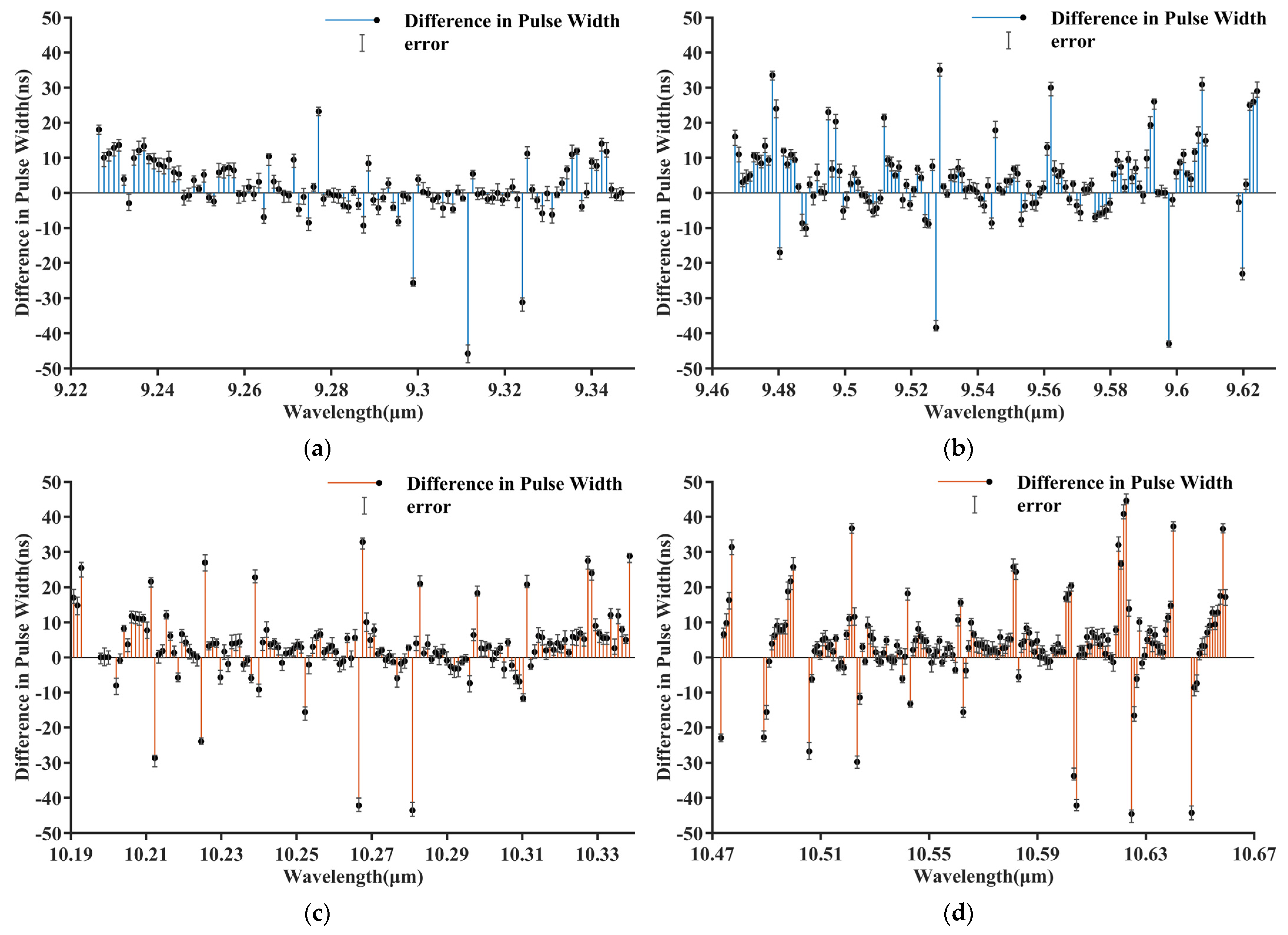
3. Results
4. Analysis and Discussion
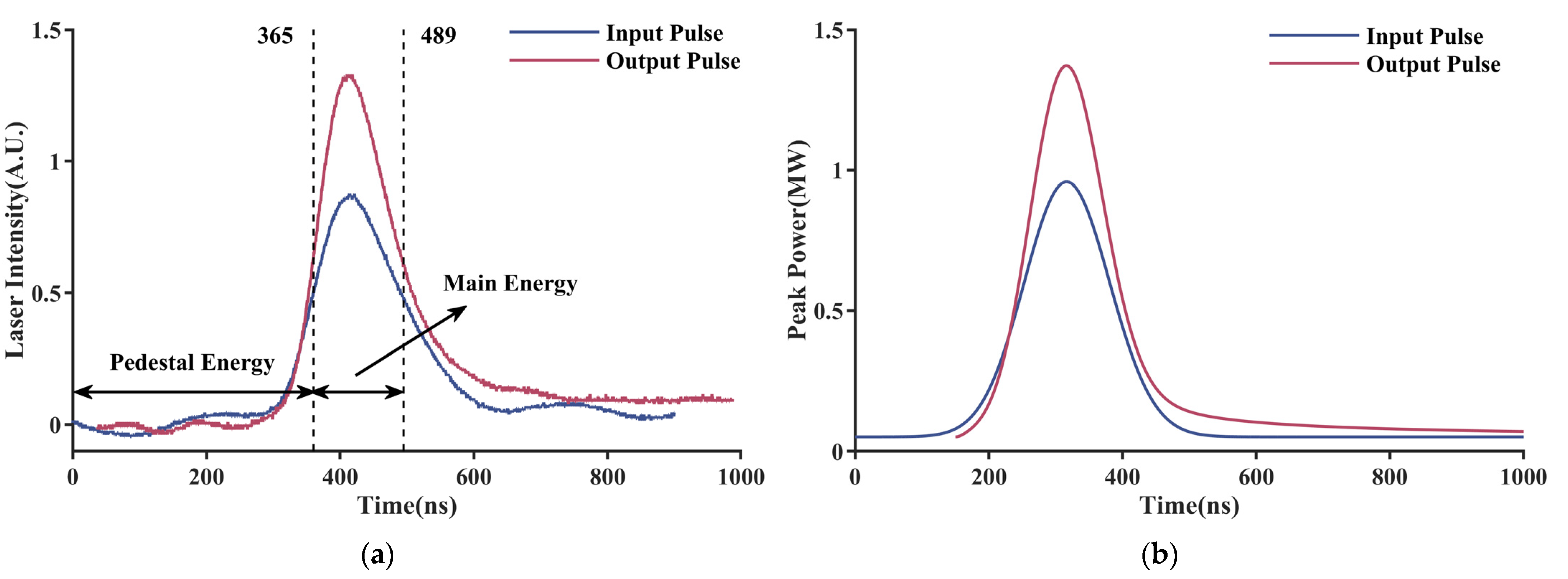
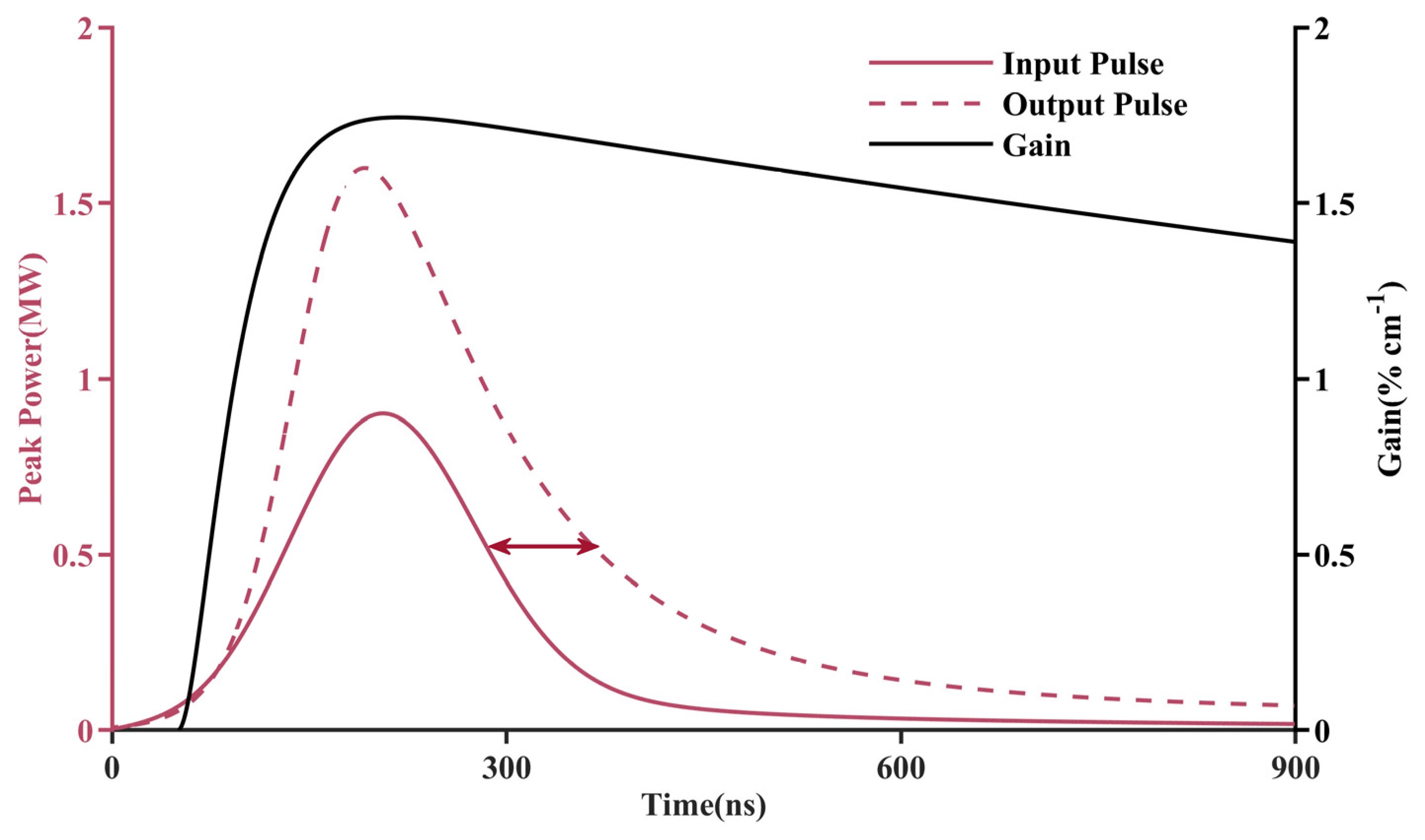
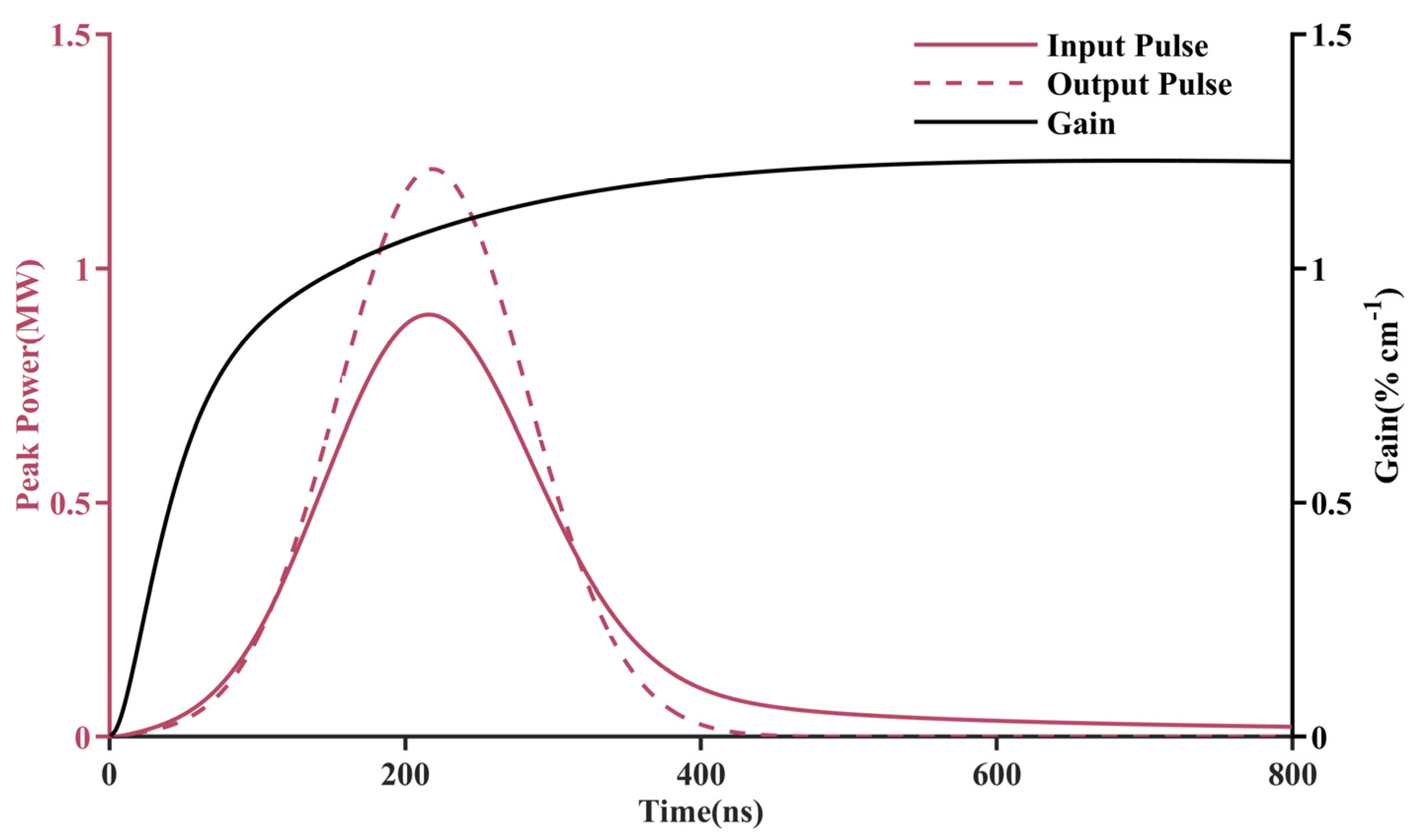
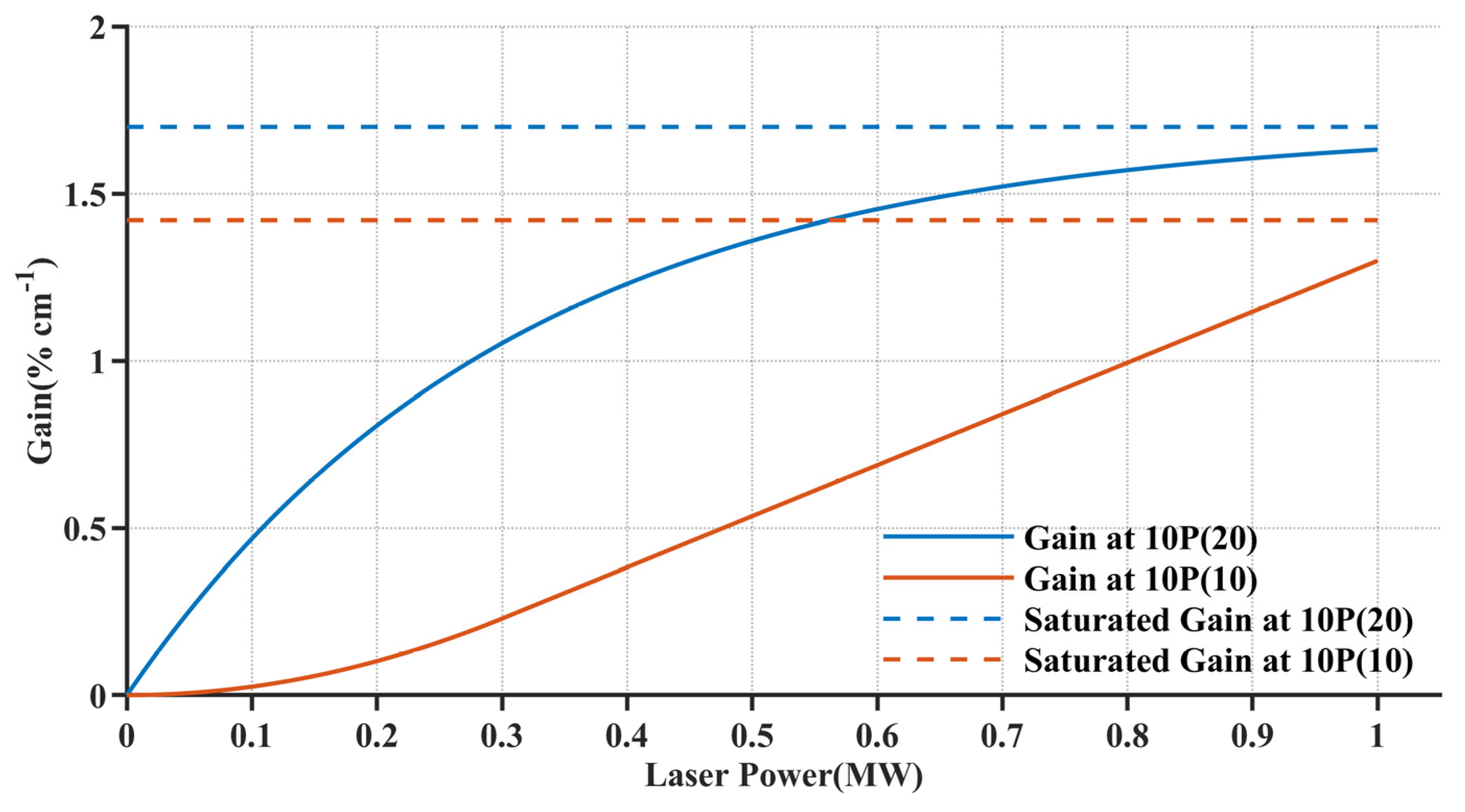
4.1. Analysis of Pulse Waveform and Gain Characteristics in High-Pressure CO2 Oscillator–Amplifier Systems
4.2. Limitations of the High-Pressure CO2 Six-Temperature Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laptev, V.B.; Pigul’skii, S.V. Efficient two-stage laser enrichment up to 99% of carbon-13 isotope by IR multiphoton dissociation of Freon molecules. Quantum Electron. 2022, 52, 371. [Google Scholar]
- Makarov, G.N.; Petin, A.N. Intense infrared laser-induced radiation–collision involvement of molecules that do not absorb laser radiation in resonance with a laser field in a two-component molecular medium. JETP Lett. 2022, 115, 256–260. [Google Scholar]
- Zhevlakov, A.P.; Seisyan, R.P.; Bespalov, V.G.; Elizarov, V.V.; Grishkanich, A.S.; Kascheev, S.V. High-efficiency bispectral laser source for EUV lithography. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXI; SPIE: San Francisco, CA, USA, 2016; Volume 9735, pp. 255–264. [Google Scholar]
- Amano, R.; Dinh, T.H.; Sasanuma, A.; Arai, G.; Hara, H.; Fujii, Y.; Hatano, T.; Ejima, T.; Jiang, W.; Sunahara, A.; et al. Influence of short pulse duration of carbon dioxide lasers on extreme ultraviolet emission from laser-produced plasmas. Jpn. J. Appl. Phys. 2018, 57, 070311. [Google Scholar]
- Parvin, P.; Sajad, B.; Silakhori, K.; Hooshvar, M.; Zamanipour, Z. Molecular laser isotope separation versus atomic vapor laser isotope separation. Prog. Nucl. Energy 2004, 44, 331–345. [Google Scholar] [CrossRef]
- Snyder, R. A proliferation assessment of third generation laser uranium enrichment technology. Sci. Glob. Secur. 2016, 24, 68–91. [Google Scholar]
- Versolato, O.O.; Sheil, J.; Witte, S.; Ubachs, W.; Hoekstra, R. Microdroplet-tin plasma sources of EUV radiation driven by solid-state lasers (Topical Review). J. Opt. 2022, 24, 054014. [Google Scholar] [CrossRef]
- Schafgans, A.A.; Brown, D.J.; Fomenkov, I.V.; Sandstrom, R.; Ershov, A.; Vaschenko, G.; Rafac, R.; Purvis, M.; Rokitski, S.; Tao, Y.; et al. Performance optimization of MOPA pre-pulse LPP light source. In Extreme Ultraviolet (EUV) Lithography VI.; SPIE: San Jose, CA, USA, 2015; Volume 9422, pp. 56–66. [Google Scholar]
- Welch, E.; Matteo, D.; Tochitsky, S.; Joshi, C. Generating quasi-single multi-terawatt picosecond pulses in the Neptune CO2 laser system. In IEEE Advanced Accelerator Concepts Workshop (AAC); IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Tochitsky, S.Y.; Narang, R.; Filip, C.; Clayton, C.E.; Marsh, K.A.; Joshi, C. Generation of 160-ps terawatt-power CO2 laser pulses. Opt. Lett. 1999, 24, 1717–1719. [Google Scholar] [PubMed]
- Haberberger, D.; Tochitsky, S.; Joshi, C. Fifteen terawatt picosecond CO2 laser system. Opt. Express. 2010, 18, 17865–17875. [Google Scholar] [PubMed]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Babzien, M.; Palmer, M.A. Demonstration of a 2 ps, 5 TW peak power, long-wave infrared laser based on chirped-pulse amplification with mixed-isotope CO2 amplifiers. OSA Contin. 2020, 3, 459–472. [Google Scholar]
- Feldman, B.J. Multiline short pulse amplification and compression in high gain CO2 laser amplifiers. Opt. Commun. 1975, 14, 13–16. [Google Scholar]
- Zhang, R.; Pan, Q.; Guo, J.; Chen, F.; Yu, D.; Sun, J.; Zhang, K.; Zhang, L. Theoretical and experimental study of nanosecond pulse amplification in a CW CO2 amplifier. Infrared Phys. Technol. 2020, 111, 103537. [Google Scholar]
- Ye, J.; Zhu, Z.; Lu, Y.; Bai, J.; Su, X.; Tan, R.; Zheng, Y. Investigation of the multi-spectral line output characteristics of a multi-atmospheric CO2 pulsed laser. Opt. Eng. 2023, 62, 056102. [Google Scholar] [CrossRef]
- Torabi, R.; Saghafifar, H.; Koushki, A.M.; Ganjovi, A.A. Simulation and initial experiments of a high power pulsed TEA CO2 laser. Phys. Scr. 2015, 91, 015501. [Google Scholar]
- Butcher, J.C. A history of Runge-Kutta methods. Appl. Numer. Math. 1996, 20, 247–260. [Google Scholar]
- Torabi, R.; Silakhori, K. Generalization of the 6-Temperature model for simulation of super-atmospheric pulsed CO2 lasers output. Phys. Scr. 2021, 96, 085402. [Google Scholar] [CrossRef]
| Spectral Band (μm) | Before Amplification (ns) | After Amplification (ns) |
|---|---|---|
| 9.277 | 64.8 | 88 |
| 9.299 | 93.5 | 67.8 |
| 9.311 | 121.8 | 76 |
| 9.324 | 118.4 | 87.2 |
| 9.478 | 115.5 | 149 |
| 9.527 | 124.6 | 86.2 |
| 9.528 | 93 | 128 |
| 9.597 | 174 | 131 |
| 9.607 | 114 | 144.9 |
| 10.212 | 157.7 | 129 |
| 10.226 | 105 | 132.4 |
| 10.266 | 115 | 72.8 |
| 10.268 | 70.2 | 103 |
| 10.281 | 141 | 97.4 |
| 10.522 | 84 | 120.7 |
| 10.524 | 131 | 101.2 |
| 10.602 | 147 | 93.2 |
| 10.603 | 151 | 88.8 |
| 10.621 | 97 | 137.8 |
| 10.622 | 125 | 169.6 |
| 10.625 | 160 | 115.4 |
| Parameter Description | Notation | Value | Units |
|---|---|---|---|
| CO2 symmetric excited level wave number | v1/c | 1337 | cm−1 |
| CO2 bending excited level wave number | v2/c | 667 | cm−1 |
| CO2 asymmetric excited level wave number | v3/c | 2349 | cm−1 |
| N2 excited level wave number | v4/c | 2330 | cm−1 |
| CO excited level wave number | v5/c | 2150 | cm−1 |
| Planck’s constant | h | 6.626 × 10−34 | J·s |
| Speed of light | c | 2.998 × 108 | m/s |
| Boltzmann constant | k | 1.38 × 10−23 | J/K |
| Rotational constant | BCO2 | 0.3871 | cm−1 |
| Collision cross section of CO2 molecules | QCO2 | 1.3 × 10−18 | m2 |
| Collision cross section of N2 molecules | QN2 | 1.14 × 10−18 | m2 |
| Collision cross section of He molecules | QHe | 3.7 × 10−19 | m2 |
| Collision cross section of CO molecules | QCO | 1.14 × 10−18 | m2 |
| CO2 symmetric excitation rate | X1 | 5 × 10−15 | m3/s |
| CO2 bending excitation rate | X2 | 3 × 10−15 | m3/s |
| CO2 asymmetric excitation rate | X3 | 8 × 10−15 | m3/s |
| N2 excitation rate | X4 | 2.3 × 10−14 | m3/s |
| CO excitation rate | X5 | 3 × 10−14 | m3/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Wen, M.; Zhu, Z.; Bai, J.; Fu, J.; Wang, H.; Wan, T.; Tan, R.; Zheng, Y. Study on the Wavelength-Dependent Temporal Waveform Characteristics of a High-Pressure CO2 Master Oscillator Power Amplifier System. Photonics 2025, 12, 346. https://doi.org/10.3390/photonics12040346
Huang Z, Wen M, Zhu Z, Bai J, Fu J, Wang H, Wan T, Tan R, Zheng Y. Study on the Wavelength-Dependent Temporal Waveform Characteristics of a High-Pressure CO2 Master Oscillator Power Amplifier System. Photonics. 2025; 12(4):346. https://doi.org/10.3390/photonics12040346
Chicago/Turabian StyleHuang, Zefan, Ming Wen, Ziren Zhu, Jinzhou Bai, Jingjin Fu, Heng Wang, Tianjian Wan, Rongqing Tan, and Yijun Zheng. 2025. "Study on the Wavelength-Dependent Temporal Waveform Characteristics of a High-Pressure CO2 Master Oscillator Power Amplifier System" Photonics 12, no. 4: 346. https://doi.org/10.3390/photonics12040346
APA StyleHuang, Z., Wen, M., Zhu, Z., Bai, J., Fu, J., Wang, H., Wan, T., Tan, R., & Zheng, Y. (2025). Study on the Wavelength-Dependent Temporal Waveform Characteristics of a High-Pressure CO2 Master Oscillator Power Amplifier System. Photonics, 12(4), 346. https://doi.org/10.3390/photonics12040346





