Filter-Assisted Self-Coherent Detection Field Recovery Scheme for Dual-Polarization Complex-Valued Double-Sideband Signals

Abstract

In this paper, we have proposed a filter-assisted self-coherent detection (FASCD) scheme that reconstructs the optical field of a dual-polarization complex-valued double-sideband (DP-CV-DSB) signal. At the receiver, the carrier is extracted using an optical bandpass filter (OBPF), and a pair of orthogonal carriers is constructed to achieve polarization-division multiplexing (PDM) by a Faraday rotator mirror (FRM). To address the issue of polarization crosstalk, channel estimation is performed using the least squares (LS) method, and the estimation results are further optimized through the intra-symbol frequency-domain averaging (ISFA) method. We demonstrate the system architecture and algorithms by simulation on a 224 Gbit/s 16-ary quadrature amplitude modulation DSB-PDM-OFDM system. The system performance is improved by 1 dB using the ISFA method.

1. Introduction

Driven by the rapid evolution of digital technologies and the emergence of innovative applications, including cloud computing, smart home systems, and autonomous driving, there has been a substantial increase in data traffic within short-reach optical networks [1,2,3]. Despite the benefits of coherent detection (CD), such as high spectral efficiency and enhanced sensitivity over long-haul transmissions, its adoption in short-reach optical networks has been constrained by the necessity for costly narrow-linewidth local oscillator (LO) lasers. In comparison, conventional DD eliminates the need for an LO, offering a simpler architecture and cost-effective implementation. However, traditional DD technology primarily relies on intensity modulation and direct detection (IM-DD), which is limited to amplitude modulation and detection, thereby resulting in low spectral efficiency (SE). Additionally, IM-DD systems are incapable of optical field recovery, preventing the digital compensation of linear signal impairments induced by fiber links, which further restricts the achievable transmission distance [4,5,6].

In recent years, to leverage the benefits of both DD and CD, a range of self-coherent detection (SCD) schemes have been introduced. These schemes are designed to enhance SE and mitigate the frequency-selective fading induced by dispersion [7]. At the transmitter, the carrier and signals are fed into the optical fiber. At the receiver, the desired signal can be retrieved from the carrier-signal beat term after photodiode (PD) detection. However, some schemes are limited to SSB modulation and thus cannot make full use of receiver bandwidth compared with CD, such as the Kramers–Kronig (KK) receiver [8] and iterative cancellation (IC) receiver [9]. To improve spectral efficiency, numerous DSB-SCD schemes have been proposed, such as carrier-assisted differential detection (CADD) [10,11,12,13], carrierless phase retrieval (CLPR) [14], asymmetric self-coherent detection (ASCD) [15], and carrier-assisted phase retrieval (CAPR) [16], as well as a filter-assisted direct detection (FADD) architecture that uses an OBPF or optical band-stop filter (OBSF) to obtain complex-valued double-sideband (CV-DSB) signals, as presented in our previous research [17].

PDM should be the next target to be achieved since it doubles the system capacity and spectral efficiency. The polarization fading phenomenon induced by random polarization rotation is a fundamental obstacle for PDM-SCD compared with PDM coherent detection, which seriously reduces system performance. Polarization fading occurs because the optical carrier cannot be split equally into X- or Y-polarization using a simple polarization beam splitter (PBS) without active polarization control [18,19], since the carrier undergoes random polarization state rotation in the fiber channel. Additionally, the SCD scheme relies on the reference optical carrier to reconstruct the optical field digitally [20]. As a result, the single-polarization optical field recovery is no longer fulfilled without a sufficiently strong carrier. To solve this problem, Zhu et al. proposed a filter-based PDM-SSB scheme [21]. At the transmitter, the generated PDM-SSB signals with two orthogonal carriers are located at opposite sides. At the receiver side, dual optical filters implementing polarization diversity are employed to suppress the undesired carrier on the opposite side. The scheme has been fully validated in other SSB systems [22,23]. In addition, the real-value DSB modulation format is also verified, but a multi-input-multi-output (MIMO) equalization algorithm with high complexity is required to eliminate the sideband crosstalk caused by OBPF [24]. In [25], a minimal coherent receiver architecture with Alamouti encoding and single-ended PD was proposed to reduce receiver complexity and cost, but it sacrificed half of the SE. To further increase the SE, PDM CV-DSB modulation has attracted extensive attention. In our previous research, we proposed a novel PDM-asymmetric-twin-SSB CADD (PDM-ATSSB CADD) scheme to realize the optical field recovery of PDM CV-DSB signals, which does not utilize the spectrum [26].

In this paper, we propose a dual-polarization (DP) field recovery scheme to fulfill polarization-fading-free detection, which is compatible with the detection of DSB signals and increases the SE. At the transmitter, a DSB signal and optical carrier at X-polarization is transmitted. At the receiver, the carrier is extracted using an OBPF. Polarization diversity is achieved by constructing a pair of orthogonal carriers using an FRM. The channel information is estimated based on the LS criterion using training sequences and optimized by ISFA. Moreover, the scheme achieves polarization recovery using MIMO equalization. In the proof-of-concept simulation, a 28GBaud PDM-OFDM-16-quadrature amplitude modulation (QAM) DSB signal is successfully recovered after 320 km single-mode fiber (SMF) transmission.

2. Principle

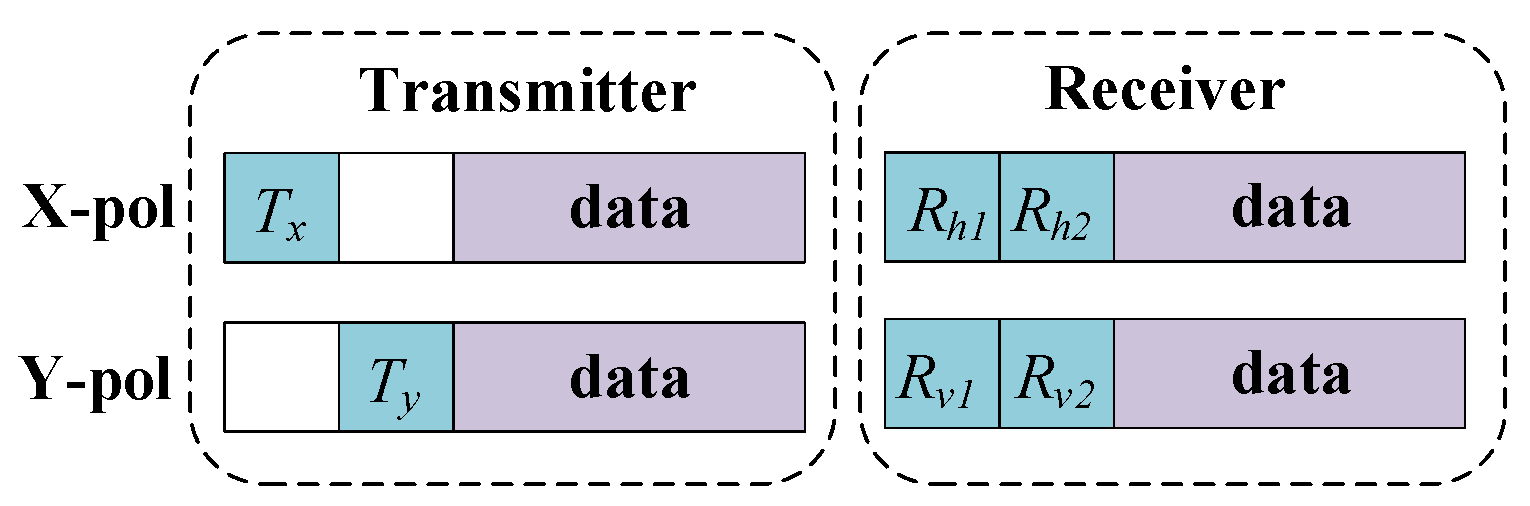
2.1. Principle of PDM-DSB FASCD

Figure 1 shows the schematic diagram of the PDM-DSB FASCD. In the transmitter, two independent OFDM signals form two pairs of symmetrical DSB signals corresponding to X-polarization and Y-polarization, respectively. As shown in Figure 1, the signal of the X-polarization and the Y-polarization are frequency overlapped to increase the SE. To ensure the carrier can be successfully extracted using an OBPF at the receiver, a guard band is set between the carrier and the signal. Note that in the Y-polarization, no carrier is present, and additionally, a spectral gap identical to that of the X-polarization is reserved. This is attributed to the requirement for signal equalization processing at the receiver end, where complicated channel estimation methods must be employed for the Y-polarization band at the same spectrum as the X-polarization guard band. Here, a part of the spectral efficiency is sacrificed in order to reduce the complexity of the algorithm. The generated optical signal is then fed into the single-mode fiber (SMF) for transmission, where the transmission signal can be expressed as ${\left(C_x+S_x\right)}_{x-pol}$ and ${\left(S_y\right)}_{y-pol}$, where $S_x$ and $S_y$ are the independent complex signals with equal power modulated on the X- and Y-polarization, respectively. The carrier-to-signal power ratio (CSPR) significantly impacts the performance of self-coherent systems. The CSPR is defined as the power ratio between the carriers and the PDM signals of X polarizations:

$$CSPR(dB)=10•{\log }_{10}{\displaystyle \frac{P_{x-carrier}}{P_{x-signal}}}$$

(1)

At the receiver, due to the PMD in the fiber, both the signal and the carrier undergo random rotations in their SOP. The use of a PBS can lead to polarization fading, which degrades the quality of signal transmission traditionally. The signal is split into two paths by OC: one path is directly injected into the hybrid, while the other path utilizes an OBPF to extract the carrier, as shown in Figure 1. Subsequently, a pair of orthogonal carriers can be constructed using FRM. The FRM transforms any input polarization state into an orthogonal output polarization state [27]. During transmission, the SOP of the signal undergoes random rotations; however, even if the polarization state is unknown, the orthogonality between the two signals remains unchanged throughout the transmission process. The polarization states of the signal and the carrier consistently remain aligned. As a result, the orthogonal optical carriers, when demodulated through a receiver (as shown in Figure 1), enable the recovery of the received signal and the restoration of the optical field information.

2.2. LS-Based MIMO Algorithm

During signal transmission, there is polarization crosstalk between the two polarization directions in the fiber link. Since the received OFDM signals are the polarization mixing of two transmitted OFDM signals with various SOP in the PDM-OFDM fiber link, channel estimation is necessary for polarization demultiplexing and signal demodulation. Each subcarrier is a subchannel in the OFDM system. The PDM fiber link can be dealt with as the two-input–two-output (2 × 2) channel model, where the Jones matrix $H$, consisting of $H_{fiber}$ and $H_{receiver}$, can be generally expressed as:

$$H=\left[\begin{array}{cc}{H}_{xx}& H_{xy}\\ H_{yx}& H_{yy}\end{array}\right]$$

(2)

Thus, the relationship between the transmitted signal and the received signal ${\left(R_H{R}_V\right)}^T$ is established.

$$\left[\begin{array}{c}{R}_H\\ R_V\end{array}\right]=\left[\begin{array}{cc}{H}_{xx}& H_{xy}\\ H_{yx}& H_{yy}\end{array}\right]\left[\begin{array}{c}{S}_x\\ S_y\end{array}\right]+\left[\begin{array}{c}{N}_H\\ N_V\end{array}\right]$$

(3)

Here, ${\left(N_H{N}_V\right)}^T$ are channel noise. Since the variation of H is slow compared to the signal duration, periodical channel estimation with the train sequences can obtain the channel transmission matrix H. Figure 2 demonstrates the distribution of the training sequences ${\left(T_x{T}_y\right)}^T$ and their corresponding received signals. There is also

$$\left[\begin{array}{cc}{R}_{h1}& R_{h2}\\ R_{v1}& R_{v2}\end{array}\right]=\left[\begin{array}{cc}{H}_{xx}& H_{xy}\\ H_{yx}& H_{yy}\end{array}\right]\left[\begin{array}{cc}{T}_x& 0\\ 0& T_y\end{array}\right]$$

(4)

Then, the channel matrix is obtained as

$$H=\left[\begin{array}{cc}{R}_{h1}/T_x& R_{h2}/T_y\\ R_{v1}/T_x& R_{v2}/T_y\end{array}\right]$$

(5)

2.3. Improved-MIMO-Algorithm-Based LS

In the aforementioned channel estimation method, the influence of noise is not taken into account. When the optical signal-to-noise ratio (OSNR) is relatively low, the accuracy of the channel estimation is compromised. Here, we employ an ISFA method to process the estimated channel. This method performs a weighted summation of each subchannel and its adjacent channels to derive new channel information. This process is equivalent to applying a windowed smoothing operation to the channel estimation results. The definition of the window is as follows:

$$w(m)=\left\{\begin{array}{c}{I}_0(m),1\le m\le 2n+1\\ 0,others\end{array}\right.$$

(6)

Here, $I_0\left(•\right)$ represents a Gaussian function. In this paper, we utilize a Gaussian function with a mean of 3 and a variance of 3. After applying the ISFA method, the channel matrix is given by:

$$\left[\begin{array}{cc}{H}_{xx}^{\prime }(q)& H_{xy}^{\prime }(q)\\ H_{yx}^{\prime }(q)& H_{yy}^{\prime }(q)\end{array}\right]={\displaystyle \sum _{k=q-n}^{q+n}\left[\begin{array}{cc}{H}_{xx}& H_{xy}\\ H_{yx}& H_{yy}\end{array}\right]•w(k-q+n+1)}/{\displaystyle \sum _{m=1}^{2n+1}w(m)}$$

(7)

In the summation on the right-hand side of the above equation, if the subcarriers exceed the valid range, their corresponding channel matrix elements are set to zero. Similarly, the window function weights at those positions are also set to zero. This ensures that only valid subcarriers contribute to the final result, maintaining the integrity and accuracy of the channel estimation. The averaging after summation utilizes the sum of the weights of the window function at each point. This ensures that the smoothed channel matrix maintains an amplitude comparable to that before smoothing, preserving the overall energy and characteristics of the channel while reducing noise and fluctuations.

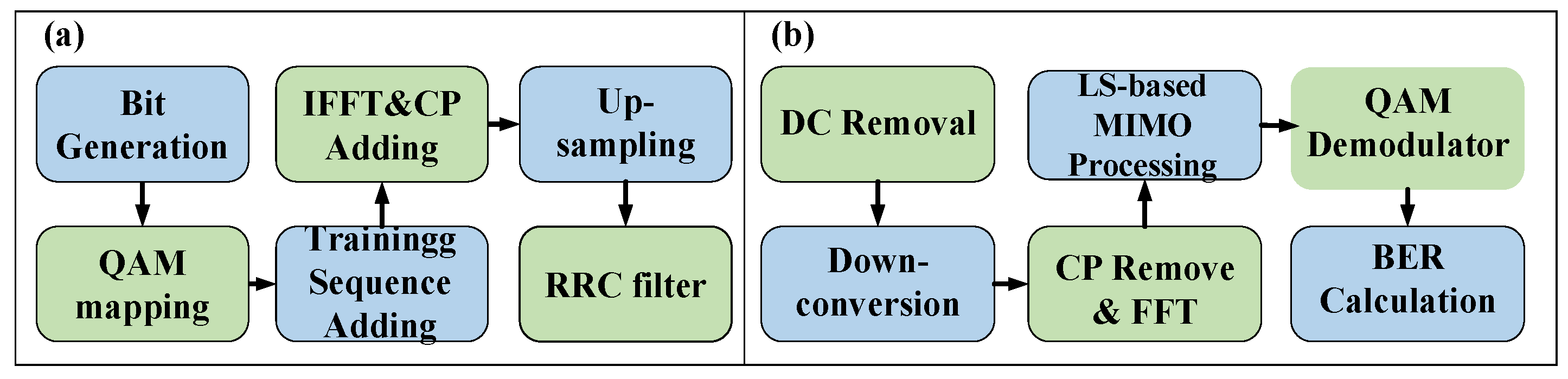
3. Simulation Setup

To investigate the performance of the proposed PDM-DSB FASCD and the improved algorithm ISFA, we use a 28GBaud PDM-OFDM 16-QAM simulation system with VPI 8.7 and MATLAB 2023b. The system structure is shown in Figure 1, and the specific DSP flow and spectral diagram are shown in Figure 3. The transmitter- and receiver-side DSP are performed in MATLAB 2023b, and the fiber, optical, and electrical devices are modelled in VPI. At the transmitter, the generated pseudo-random bit sequence is mapped to 16-QAM symbols, followed by a serial-to-parallel conversion. The resulting parallel symbols are then transformed into the time domain via an IFFT. Here, the IFFT length is set to 128, with 112 subcarriers used to carry data. The remaining subcarriers are set to zero, serving as a guard band to mitigate inter-symbol interference and improve signal robustness. The signal-to-carrier spacing is 2 GHz. Afterward, eight cyclic prefix samples are added to mitigate inter-symbol interference caused by channel impairments. The signal is then upsampled and shaped using a root raised cosine (RRC) filter with a roll-off factor of 0.01. We use an AWG and a linear EA to drive the DP-IQ modulator, which is biased at the null point to modulate the light from the laser. A reference carrier is added to align its polarization state with the x-polarization signal. This combined signal is then injected into a 320 km SMF. The parameters of the SMF are loss of 0.2 dB/km, chromatic dispersion coefficient of 17 ps/nm/km, and PMD coefficient of 0.1 ps/km^1/2.

At the receiver, the optical carrier is extracted using an OBPF, and its power is amplified by an EDFA to enhance the signal detection performance. The carrier is then evenly split into two parts: one part is used to receive the x-polarization signal, while the other part is passed through an FRM to construct its orthogonal polarization state, which serves as the carrier for detecting the y-polarization signal. The optical signal is converted into electrical signals using the receiver.

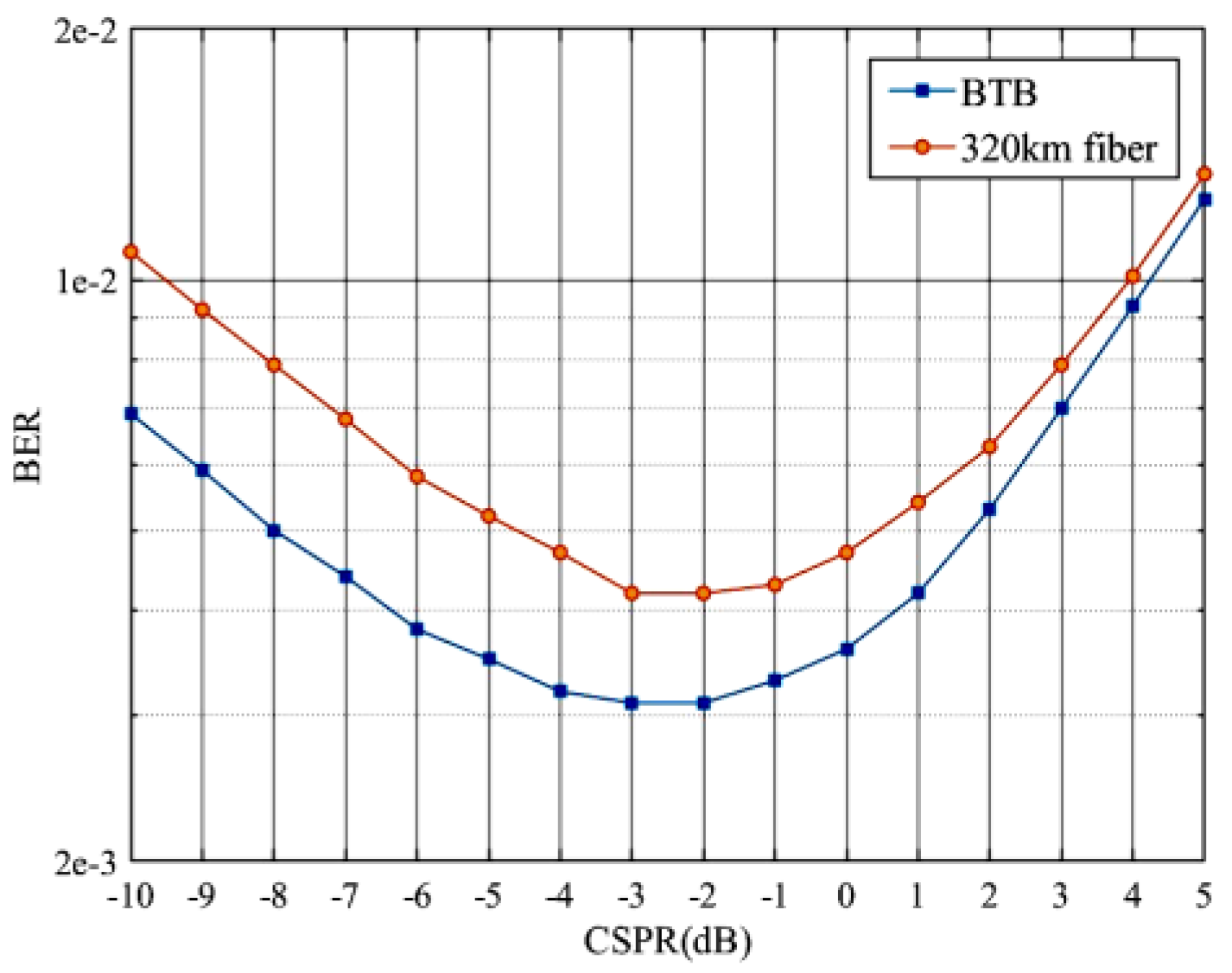
4. Results and Discussions

It is known that the CSPR is a critical parameter for self-coherent systems. Under a fixed transmit power, the CSPR affects the power proportion of the carrier in the transmitted signal. Regarding the impact of CSPR on signal transmission quality, Figure 4 presents the bit error rate (BER) versus CSPR for the PDM-OFDM FASCD at back-to-back (BTB) and 320 km of fiber transmission when the transmission rate is 224 Gbit/s. To identify the required CSPR, we fixed the bandwidth and Gaussian order of the OBPF to 3 GHz and 4, respectively. The OSNR are fixed as 23 dB. When the CSPR is small, it cannot amplify the signal term effectively. In order to effectively recover the signal during reception, we amplify the carrier using EDFA, which also amplifies the noise in the system, exacerbating the effect of noise on the system. OSNR in a system is defined as the ratio of the sum of the power of the signal and the carrier to the noise. When the CSPR is large, the signal-to-noise ratio in the system is small, which directly leads to the degradation of system performance. As we can see from the results, the optimal value for CSPR is −3 dB at 320 km transmission. Therefore, the CSPR is set to −3 dB in the following simulations.

In the description of the second section, extracting the optical carrier using an OBPF is a crucial step for achieving field recovery of the optical signal. To better align with practical scenarios, Gaussian filters of different orders are employed to simulate the OBPF. Figure 5 displays the system performance at different OSNR for back-to-back transmission under the optimal CSPR, with the Gaussian filter orders set to 2, 3, 4, and 5, respectively. When the filter order increases from 2 to 3, the system’s BER performance improves significantly. As the filter order increases, it effectively separates the signal and the carrier. When the filter order is further increased to 4, at an OSNR of 23 dB, the system’s BER is below the HD-FEC threshold of 3.8 × 10⁻³, enabling error-free transmission. Continuing to increase the filter order does not result in noticeable further improvement in the BER. Therefore, the OBPF order is set to 4, which will be used for the next simulations.

As mentioned in the second section, signals are subject to chromatic dispersion and polarization mode dispersion during transmission. For OFDM systems, a channel estimation method based on LS is commonly employed. However, since the noise in the channel is not taken into account, the estimated channel information is not entirely accurate. This leads to slight discrepancies between the equalized received signal and the actual signal during subsequent processing. Figure 6 illustrates the trend of the BER versus OSNR for both the conventional LS-based channel estimation method and the improved method after 320 km transmission. The improved method demonstrates about a 1 dB enhancement in OSNR performance.

To validate the proposed PDM-OFDM FASCD scheme in this paper, a comparison was made with traditional coherent detection under identical system parameter configurations. The BER curves as a function of OSNR for both reception schemes are depicted in Figure 7, with both schemes operating at a transmission rate of 224 Gbit/s. While the self-coherent system incurs an OSNR penalty of 3 dB due to the reduction of one laser, this trade-off is entirely acceptable given the high cost of lasers. Combined with the aforementioned analysis of carrier extraction, CSPR impact, and OSNR tolerance, this demonstrates the feasibility of the proposed scheme.

5. Conclusions

This paper proposes and simulates a filter-assisted direct detection system capable of receiving PDM-OFDM-DSB signals. At the transmitter, two independent 112 Gbit/s 16 QAM signals are up-converted to the optical domain using a DP-IQ modulator and then coupled with a central optical carrier aligned with the polarization state of one signal to form a DSB signal. At the receiver, the signal is detected using a filter-assisted receiver, achieving a transmission rate of 224 Gbit/s. Compared to other polarization-multiplexed direct detection schemes, this approach enables the detection of double-sideband signals, significantly improves receiver sensitivity, and addresses the issue of carrier fading, which has been a major obstacle to realizing polarization multiplexing. The simulation results show that compared with traditional CD results, an OSNR penalty of 3 dB is incurred without LO. Consequently, we believe that the proposed FASCD can deliver unexpected effects in short-distance optical communication.