Tunable All-Optical Pattern Recognition System Based on Nonlinear Optical Loop Mirror for Bit-Flip BPSK Targets

Abstract

As the basic physical infrastructure of various networks, optical networks are crucial to the advancement of information technology. Meanwhile, as new technologies emerge, the security of optical networks is facing serious threats. To improve the security of optical networks, optoelectronic firewalls primarily leverage all-optical pattern recognition to perform direct detection and analysis of data transmitted through the optical network at the optical layer. However, the current all-optical pattern recognition system still faces some problems when deployed in optical networks, including phase-lockingand relatively low recognition efficiency and scalability. In this paper, we propose a tunable all-optical pattern recognition system based on a nonlinear optical loop mirror (NOLM) for bit-flip BPSK targets. The operational principles and simulation setup of the proposed system are comprehensively described. Numerical simulations demonstrate that the system can accurately recognize and determine the position of 4-bit and 8-bit bit-flip BPSK targets in 16-bit input data with tunable frequencies of 192.8 THz and 193.4 THz at a data rate of 100 Gbps. Finally, the impact of input noise is evaluated by extinction ratio (ER), contrast ratio (CR), Q factor, bit error rate (BER), amplitude modulation (AM), and signal-to-noise ratio (SNR) under both frequencies.

1. Introduction

With the exponential growth of data interaction, edge computing, and high-definition live streaming, optical networks have attracted considerable attention over the past decade due to their favorable characteristics, including high speed, large capacity, and low power consumption. Meanwhile, the rapid advancement of emerging technologies has rendered optical network security increasingly vulnerable to sophisticated cyberattacks and malicious intrusions [1]. Optical networks can be affected by different threats depending on their coverage and type [2]. To enhance the security of optical networks, several approaches leveraging optical signal processing have been proposed, such as optical code-division multiple access (OCDMA) [3], all-optical encryption [4], optical steganography [5], and optoelectronic firewalls [6]. As an effective access control mechanism, an optoelectronic firewall leverages all-optical pattern recognition to perform direct detection and analysis of data transmitted through the optical network at the optical layer. Subsequently, it activates the appropriate protection scheme according to the predefined security protocols. Compared with conventional firewalls, it is efficient in filtering malicious traffic within a high-speed data stream since optical-electrical-optical conversion can be avoided. Given the increasing data rate and growing sophistication of malicious network attacks, it is essential to extend the functionality of the firewall to the optical layer and thus implement effective access control directly at the optical layer.

The widely investigated optoelectronic firewall originated from the Wirespeed Security Domains using Optical Monitoring (WISDOM) project led by the European Union. It was specifically designed to address inherent vulnerabilities and mitigate cyber threats within packet-switched network architectures. Experimental results show that it can recognize on-off keying (OOK) targets with lengths spanning from 8 to 256 bits with a data rate of 42.6 Gbps [7]. 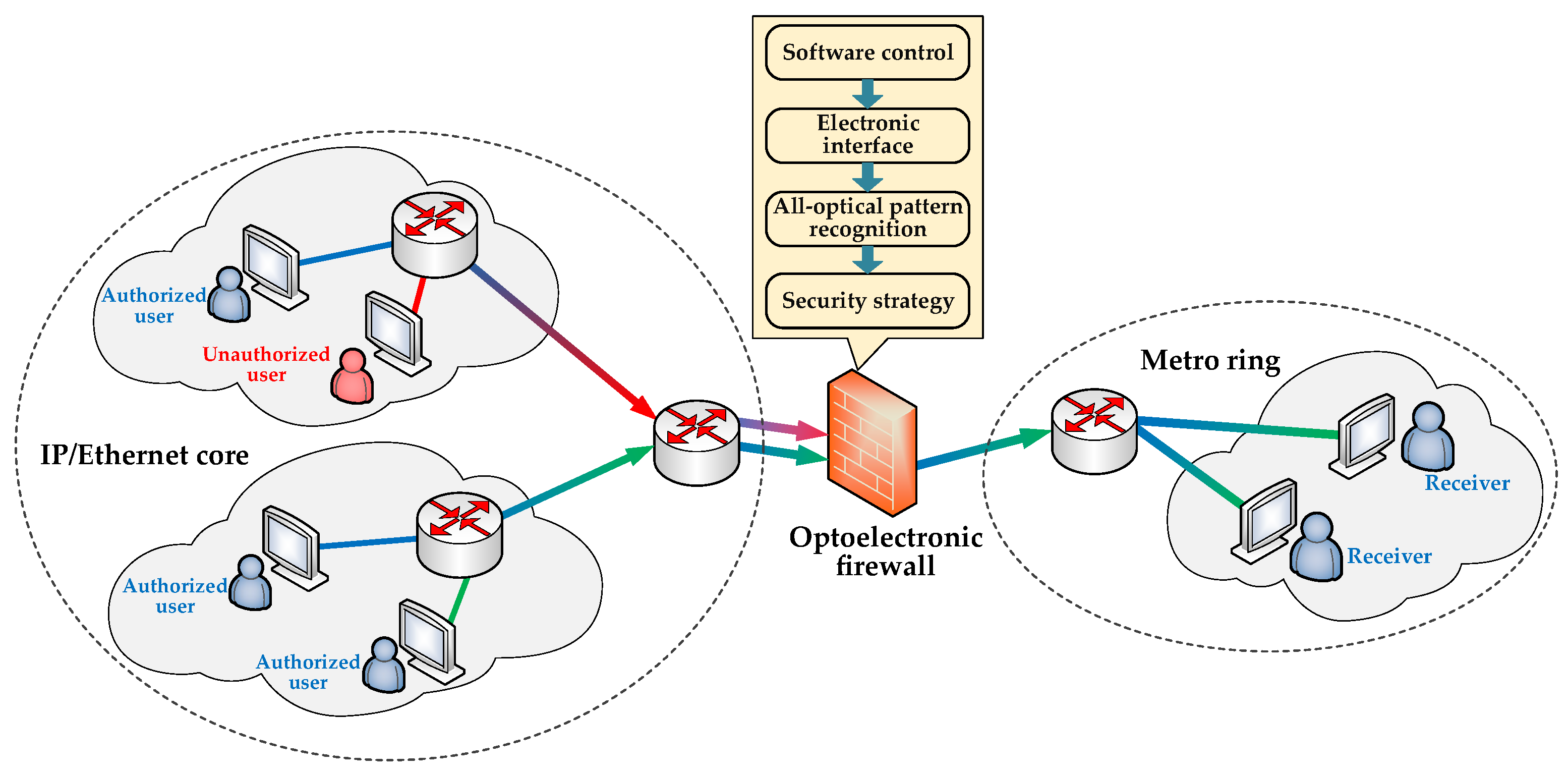Figure 1 shows the principle and deployment of an optoelectronic firewall. The optoelectronic firewall is located at the edge of optical networks, which provides primary optical information filtering at the router front end. It enables high-speed security monitoring of optical signals directly at the optical layer. Typically, an optoelectronic firewall can be deployed between the IP/Ethernet core and the metro ring, which belongs to the backbone network. When the input data is transmitted through a router to the optoelectronic firewall, the all-optical pattern recognition system inside the optoelectronic firewall conducts simple but high-speed comparison and inspection with the target sequence provided by the electronic interface. The all-optical pattern recognition system developed in WISDOM primarily comprises an XNOR gate, an AND gate, and a regenerator, all of which are implemented using semiconductor optical amplifier-based Mach-Zehnder interferometers (SOA-MZIs). Meanwhile, the electronic interface can be reconfigured by software control to obtain different target sequences. Finally, the security strategy module implements optical prefiltering based on the output results generated by the all-optical pattern recognition system.

To reduce recognition time, an all-optical binary recognition system with parallel structure was proposed for short sequence detection in [8]. It can recognize 8-bit OOK signals operating at 40 Gbps. However, the size of the system exhibits a linear correlation with the length of the target. Restricted by the carrier recovery time of SOA, a binary sequence matching system based on highly nonlinear fiber (HNLF) was proposed in [9]. Owing to the short response time of HNLF, it can recognize 8-bit targets in 64-bit OOK data at 160 Gbps. Meanwhile, phase modulation formats like binary phase shift keying (BPSK) and quadrature phase shift keying (QPSK) are extensively utilized in commercial optical communication devices because of their benefits, including extended transmission distances and robust resistance to noise [10]. An all-optical flexible matching system for OOK, BPSK, and polarization shift keying (PolSK) signals was developed in [11]. It can avoid phase-locking through all-optical format conversion and parallel structure. For higher-order phase-modulated signals, two all-optical pattern recognition systems based on format conversion [12] and parallel structure [13] were proposed to recognize QPSK symbols. To improve flexibility and scalability, a reconfigurable all-optical pattern-matching system for phase-modulated signals based on phase-sensitive amplification was proposed in [14]. Recently, a reconfigurable all-optical pattern recognition system was proposed for PSK and quadrature amplitude modulation (QAM) signals with two implementation architectures [15].

Although many works have studied the recognition of phase-modulated signals, there are still three issues that need to be addressed when an optoelectronic firewall is deployed in optical networks. First, frequency synchronization brought on by phase-locking leads to a complex system. Although the systems in [11,13] achieve a phase-locking-free architecture, the parallel structure makes the system complex and bulky when recognizing long target sequences. Other works all require additional frequency synchronization or phase-locking devices to maintain a stable frequency or phase relationship between the input data and the target, which also increases the complexity of the whole system. Second, a single pattern recognition system cannot recognize more than one target each time. As network attacks become sophisticated and insidious, it is necessary to recognize more than one target with arbitrary length without cost and complexity increasing. Third, the previous systems cannot support the recognition of input signals with tunable frequency. They can only achieve pattern recognition of input signals with a specific frequency.

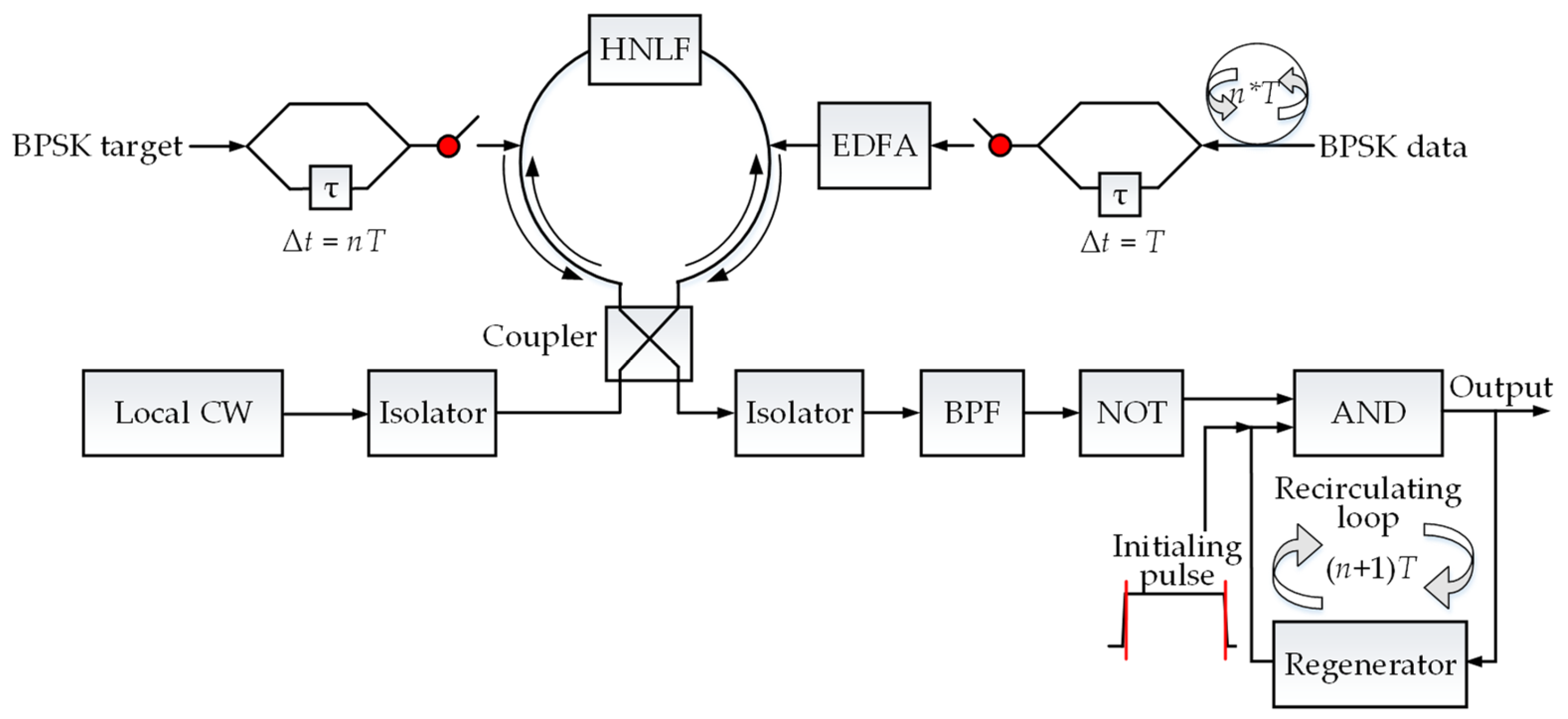
In this paper, we propose a tunable all-optical pattern recognition system based on a nonlinear optical loop mirror (NOLM). The system mainly consists of two delay interferometers (DLs), the NOLM, a NOT gate, and the recirculating loop, including an AND gate and a regenerator. The significant contributions of our study span four aspects: (1) our proposed system is phase-locking free. Benefiting from the signal reloading and the symmetric design of NOLM, the generation and maintenance of a stable phase relationship between the input data and target are inherently guaranteed, thereby eliminating the need for additional phase-locking or signal carrier extraction; (2) the system can recognize two bit-flip BPSK targets at the same time. Due to differential encoding, the phase difference between adjacent bits of the BPSK signal is mapped into a two-level power-modulated signal through DI. Then, two bit-flip BPSK targets are reloaded as the same output signal. By recognizing the reloaded signal, the recognition results for the original two bit-flip BPSK targets can be obtained; (3) the system can process the input signal with tunable frequency. By adjusting the gain of EDFA and controlling the signal power entering NOLM, the phase shift resulting from the XPM effect for the input signal with tunable frequency is ensured to be either π or 0. Thus, our proposed system can process the input signal with different frequencies; (4) the system can be extended to support higher-order modulation formats. By substituting the DI with an all-optical format conversion that transforms QPSK signals into four-level pulse amplitude modulation (PAM4) signals, the proposed system can be extended to support the recognition of QPSK targets, which enhances its compatibility and configurability. Detailed structure design and operation principles are illustrated. To evaluate the feasibility of the proposed system, simulations are conducted through VPItransmissionMaker 8.5, a photonics design and simulation software developed by VPIphotonics, with its headquarters located in Berlin, Germany. Numerical simulations demonstrate that the proposed system can accurately recognize and determine the position of bit-flip BPSK targets in the input data with a data rate of 100 Gbps and tunable frequency.

The rest of this paper is organized as follows. Section 2 details the operational principles of the proposed system. Section 3 describes the simulation setup and system parameters. Simulation results are presented and discussed in Section 4. Section 5 concludes this paper.

2. Principle of Operation

The schematic diagram of the proposed all-optical pattern recognition system is shown in Figure 2. Initially, the input BPSK data with a length of n bits is repeated m times via the storage loop with a duration of nT. Here, m represents the number of bits in the BPSK target, and T represents the bit period of the input data. The phase information is mapped into a power-modulated signal, which is characterized by an alternative mark inversion (AMI) pattern through the 1-bit DI. Assuming the two optional phases of the BPSK signal are 0 and π, the former is encoded as 0, and the latter is encoded as 1. Then, the output power of the AMI pattern, P_AMI = 0, corresponds to the consecutive bit sequence (10, 01), and P_AMI ≠ 0 corresponds to the consecutive bit sequence (00, 11). If the electrical field of the input BPSK signal is denoted as E_in, the electrical fields of the upper arm E_upper1-R and lower arm E_lower1-R after entering the first Y branch in the right DI can be expressed as

$$\left[\begin{array}{c}{E}_{upper1-R}\\ E_{lower1-R}\end{array}\right]=\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}{E}_{in}\\ 0\end{array}\right]=\left[\begin{array}{c}\sqrt{2}/2E_{in}\\ j\sqrt{2}/2E_{in}\end{array}\right].$$

(1)

Equation (1) describes the electric field distribution of the input BPSK signal E_in after passing through the first Y branch of the right DI. The lower arm signal acquires an additional j phase factor due to the DI, while the upper arm signal remains unchanged. The electrical fields of the upper arm E_upper2-R and lower arm E_lower2-R after entering the second Y branch in the right DI can be expressed as Equation (2), where Δφ_in is the adjacent bit phase difference of the input BPSK signal.

$$\left[\begin{array}{c}{E}_{upper2-R}\\ E_{lower2-R}\end{array}\right]=\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}\sqrt{2}/2E_{in}\\ j\sqrt{2}/2E_{in}\cdot e^{i\mathsf{\Delta }{\phi }_{in}}\end{array}\right]=\left[\begin{array}{c}1/2E_{in}\left(1-e^{i\mathsf{\Delta }{\phi }_{in}}\right)\\ j1/2E_{in}\left(1+e^{i\mathsf{\Delta }{\phi }_{in}}\right)\end{array}\right]$$

(2)

Equation (2) further illustrates the electric field distribution after passing through the second Y branch. Notably, signals in both the upper and lower arms are influenced by the phase difference Δφ_in between adjacent bits, causing rotation in the IQ plane. Equations (1) and (2) demonstrate how the phase information of the input BPSK signal is converted into amplitude information via the DI, which is the first step in achieving phase-modulated signal to amplitude signal conversion. Here, we select the lower arm as the output; the output power of the right DI P_AMI-R can be obtained as Equation (3), where P_in = |E_in|² denotes the power of the input signal.

$$\begin{array}{cc}\hfill P_{AMI-R}={\left|E_{lower2-R}\right|}^2& ={\left|j1/2E_{in}\left(1+e^{j\mathsf{\Delta }{\phi }_{in}}\right)\right|}^2\hfill \\ & ={\left|j1/2E_{in}\left(e^{j0}+e^{j\mathsf{\Delta }{\phi }_{in}}\right)\right|}^2\hfill \\ & ={\left|j1/2E_{in}{e}^{j\mathsf{\Delta }{\phi }_{in}/2}\left(e^{-j\mathsf{\Delta }{\phi }_{in}/2}+e^{j\mathsf{\Delta }{\phi }_{in}/2}\right)\right|}^2\hfill \\ & =|j{E}_{in}{e}^{j\mathsf{\Delta }{\phi }_{in}/2}\cos \left(\mathsf{\Delta }{\phi }_{in}/2\right){|}^2\hfill \\ & =P_{in}{\cos }^2\left(\mathsf{\Delta }{\phi }_{in}/2\right)\hfill \end{array}$$

(3)

Equation (3) calculates the output power P_AMI-R at the right DI, which depends on the input signal power P_in and the phase difference Δφ_in. For BPSK signals with phase states 0 or π, cos(2Δφ_in) can only be 1 or −1, resulting in two distinct power levels. This corresponds to the generation of alternate mark inversion (AMI) or duobinary signals. Equation (3) explains how the DI maps the phase information of BPSK signals into two power levels, enabling subsequent signal processing.

Next, the following optical switch is initially open and then closed at the beginning of the second loop. The output of the right DI enters the erbium-doped fiber amplifier (EDFA) to amplify the power to P_XPM, which is required in the subsequent cross-phase modulation (XPM) process. Similarly, the BPSK target is periodically generated with a duration of nT. Then, the phase information of the target is mapped into a power-modulated signal through the n-bit DI. Here, we assume that the electrical field of the BPSK target is denoted as E_t, then the electrical fields of the upper arm E_upper1-L and lower arm E_lower1-L after entering the first Y branch in the left DI can be expressed as

$$\left[\begin{array}{c}{E}_{upper1-L}\\ E_{lower1-L}\end{array}\right]=\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}{E}_t\\ 0\end{array}\right]=\left[\begin{array}{c}\sqrt{2}/2E_t\\ j\sqrt{2}/2E_t\end{array}\right].$$

(4)

The electrical fields of the upper arm E_upper2-L and lower arm E_lower2-L after entering the second Y branch in the left DI can be expressed as Equation (5), where Δφ_t is the adjacent bit phase difference of the BPSK target.

$$\left[\begin{array}{c}{E}_{upper2-L}\\ E_{lower2-L}\end{array}\right]=\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}\sqrt{2}/2E_t\\ j\sqrt{2}/2E_t\cdot e^{i\mathsf{\Delta }{\phi }_t}\end{array}\right]=\left[\begin{array}{c}1/2E_t\left(1-e^{i\mathsf{\Delta }{\phi }_t}\right)\\ j1/2E_t\left(1+e^{i\mathsf{\Delta }{\phi }_t}\right)\end{array}\right]$$

(5)

Again, we select the lower arm as the output, then the output power of the left DI P_AMI-L can be obtained as Equation (6), where P_t = |E_t|² denotes the power of the target. Equations (4)–(6) describe the processing of the BPSK target E_t by the left DI. Their physical meaning and function align with those of the right DI, but they apply to a different signal. The setting of the following optical switch is the same as that of the right one.

$$\begin{array}{cc}\hfill P_{AMI-L}={\left|E_{lower2-L}\right|}^2& ={\left|j1/2E_t\left(1+e^{j\mathsf{\Delta }{\phi }_t}\right)\right|}^2\hfill \\ & ={\left|j1/2E_t\left(e^{j0}+e^{j\mathsf{\Delta }{\phi }_t}\right)\right|}^2\hfill \\ & ={\left|j1/2E_t{e}^{j\mathsf{\Delta }{\phi }_t/2}\left(e^{-j\mathsf{\Delta }{\phi }_t/2}+e^{j\mathsf{\Delta }{\phi }_t/2}\right)\right|}^2\hfill \\ & =|j{E}_t{e}^{j\mathsf{\Delta }{\phi }_t/2}\cos \left(\mathsf{\Delta }{\phi }_t/2\right){|}^2\hfill \\ & =P_t{\cos }^2\left(\mathsf{\Delta }{\phi }_t/2\right)\hfill \end{array}$$

(6)

Meanwhile, the continuous wave (CW) with a center frequency of λ_CW generated by the local laser is separated into two branches after traversing a unidirectional isolator and a 50:50 coupler. These two branches are injected into the NOLM using bidirectional HNLF as a nonlinear medium, and transmitted clockwise and counterclockwise, respectively, in the NOLM. If the electrical field of the local CW is denoted as E_CW, the electrical fields of the clockwise carrier E_C and counterclockwise carrier E_CC can be expressed as

$$\left[\begin{array}{c}{E}_C\\ E_{CC}\end{array}\right]=\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}{E}_{CW}\\ 0\end{array}\right]=\left[\begin{array}{c}\sqrt{2}/2E_{CW}\\ j\sqrt{2}/2E_{CW}\end{array}\right]$$

(7)

Equation (7) describes the electric field distribution of the local CW E_CW divided into clockwise E_C and counterclockwise E_CC components. Then, the XPM effect occurs between the clockwise carrier, which serves as the probe, and the output of the left DI, which serves as the pump, inside the bidirectional HNLF. Similarly, the XPM effect occurs between the counterclockwise carrier and the output of the right DI at the same time. As the power of two pumps carries the phase information of the target and the input data, they are reloaded on the clockwise and counterclockwise carriers, respectively. Specifically, the phase shift φ_XPM induced by XPM is characterized as Equation (8), where γ and L_eff represent the nonlinear coefficient and the effective length of the bidirectional HNLF, respectively. P_XPM is the pump power required to make 2γL_effP_XPM = π.

$${\phi }_{XPM}=2\gamma L_{eff}{P}_{XPM}$$

(8)

Equation (8) defines the phase shift φ_XPM induced by XPM, which is proportional to the fiber’s nonlinear coefficient γ, effective interaction length L_eff, and pump power P_XPM. By controlling the pump power and fiber parameters, we can ensure that the probe signal is properly modulated, thereby achieving signal reloading. Here, we adjust P_AMI-R and P_AMI-L by setting the proper gain of the EDFA and controlling the output power of the target, such that P_AMI-R and P_AMI-L are either 0 or P_XPM for different consecutive bit sequences. After interacting inside the bidirectional HNLF, P_AMI-R = 0 is reloaded as φ_R-in = 0, where φ_R-in denotes the phase of the reloaded BPSK signal, while P_AMI-R ≠ 0 is reloaded as φ_R-in = π. Meanwhile, P_AMI-L = 0 is reloaded as φ_R-t = 0, where φ_R-t denotes the phase of the reloaded BPSK target, while P_AMI-L ≠ 0 is reloaded as φ_R-t = π. Here, the phase shift brought by the self-phase modulation (SPM) effect is ignored due to the low power of the probe. In this way, the phase-amplitude-phase conversion is completed. Two reloaded BPSK signals are coherently interfered at the output of the 50:50 coupler. Assuming the electrical field of the forward output which is close to the right isolator is denoted as E_fw, and the electrical field of the backward output which is close to the left isolator is denoted as E_bw, the above process can be expressed as Equation (9), where E_AMI-L and E_AMI-R are the electrical fields of the output of the left DI and right DI, respectively.

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{E}_{fw}\\ E_{bw}\end{array}\right]& =\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}{E}_C\cdot e^{j{\phi }_{R-t}}+E_{AMI-L}\\ E_{CC}\cdot e^{j{\phi }_{R-in}}+E_{AMI-R}\end{array}\right]\hfill \\ & =\left[\begin{array}{cc}\sqrt{2}/2& j\sqrt{2}/2\\ j\sqrt{2}/2& \sqrt{2}/2\end{array}\right]\left[\begin{array}{c}\sqrt{2}/2E_{CW}\cdot e^{j{\phi }_{R-t}}+E_{AMI-L}\\ j\sqrt{2}/2E_{CW}\cdot e^{j{\phi }_{R-in}}+E_{AMI-R}\end{array}\right]\hfill \\ & =\left[\begin{array}{c}1/2E_{CW}\cdot e^{j{\phi }_{R-t}}+\sqrt{2}/2E_{AMI-L}-1/2E_{CW}\cdot e^{j{\phi }_{R-in}}+j\sqrt{2}/2E_{AMI-R}\\ j1/2E_{CW}\cdot e^{j{\phi }_{R-t}}+j\sqrt{2}/2E_{AMI-L}+j1/2E_{CW}\cdot e^{j{\phi }_{R-in}}+\sqrt{2}/2E_{AMI-R}\end{array}\right]\hfill \end{array}$$

(9)

Equation (9) calculates the forward output electric field E_fw near the right isolator after passing through the NOLM. It incorporates interference between clockwise/counterclockwise carriers and AMI signals, as well as XPM-induced phase shifts. Next, the forward output E_fw is filtered through the band pass filter (BPF) with a center frequency of λ_CW. The electrical field of the output of the BPF, E_BPF, is shown in Equation (10).

$$\begin{array}{cc}\hfill E_{BPF}& =1/2E_{CW}\cdot e^{j{\phi }_{R-t}}-1/2E_{CW}\cdot e^{j{\phi }_{R-in}}\hfill \\ & =1/2E_{CW}\cdot \left(e^{j{\phi }_{R-t}}-e^{j{\phi }_{R-in}}\right)\hfill \\ & =\left\{\begin{array}{c}0,{\phi }_{R-t}={\phi }_{R-in}\pm 2k\pi \\ \pm E_{CW},{\phi }_{R-t}={\phi }_{R-in}\pm \left(2k+1\right)\pi \end{array}\right.\hfill \end{array}$$

(10)

Equation (10) represents the filtered output E_BPF after the BPF, which isolates the wavelength of the local CW λ_CW. Equations (7)–(10) model the signal transmission, interference in NOLM, and filtering processes, which are critical for achieving phase-locking-free bit-recognition.

It can be noted that the reloaded BPSK signal has π phase deflection because it goes through the 50:50 coupler twice. When the input signal is in phase with the target, there will be no pulse indicating logic “0” generated at the output of the BPF. Conversely, when the input signal is out of phase with the target, a pulse indicating logic “1” will be generated. Figure 3 shows the schematic diagram of the constellation transformation and corresponding bit sequence mapping during bit-recognition. The primary phases of signal processing include DI, XPM, and coupling. The original BPSK signal is first converted into the AMI pattern after the DI. Then, the AMI pattern is reloaded to the phase-modulated signal leveraging the XPM effect. The two reloaded signals are coupled to obtain the bit-recognition result. According to the bit-recognition result, when the adjacent bit phase difference of the input BPSK signal and the target are the same, which means both are π or 0, the output of the coupler is logic “0”. Otherwise, when the adjacent bit phase difference of the input BPSK signal and the target are different, the output of the coupler is logic “1”. Next, the bit-recognition result passes through an EDFA and a NOT gate. If the input signal is in phase with the target, there is a pulse indicating logic “1” generated after the NOT gate; otherwise, no pulse indicating logic “0” is generated after the NOT gate. Finally, a recirculating loop integrating an AND gate and a regenerator with (n + 1) bits delay is connected to recognize the target with variable length. This is the same as that in [7], so we will not go into detail here.

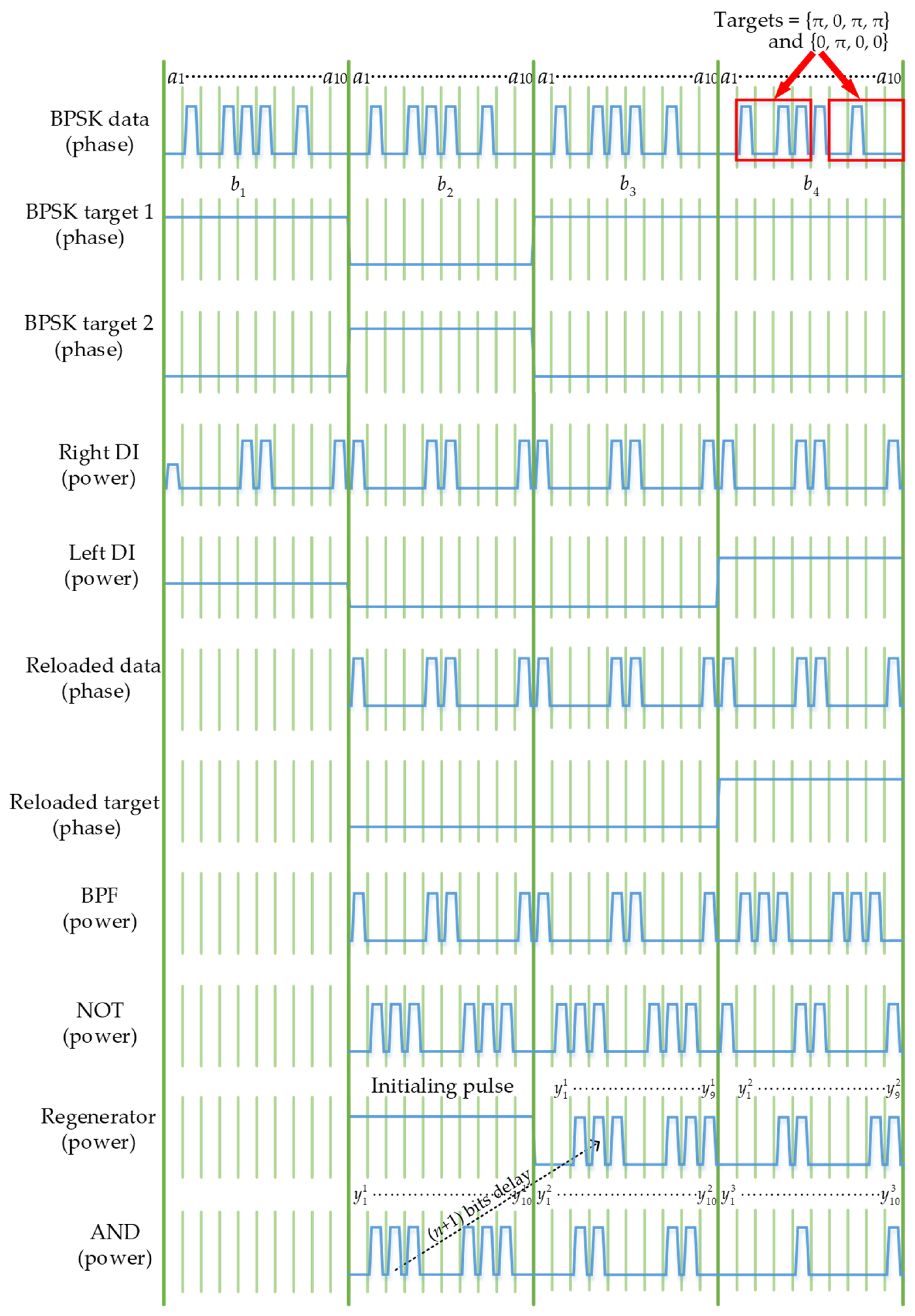
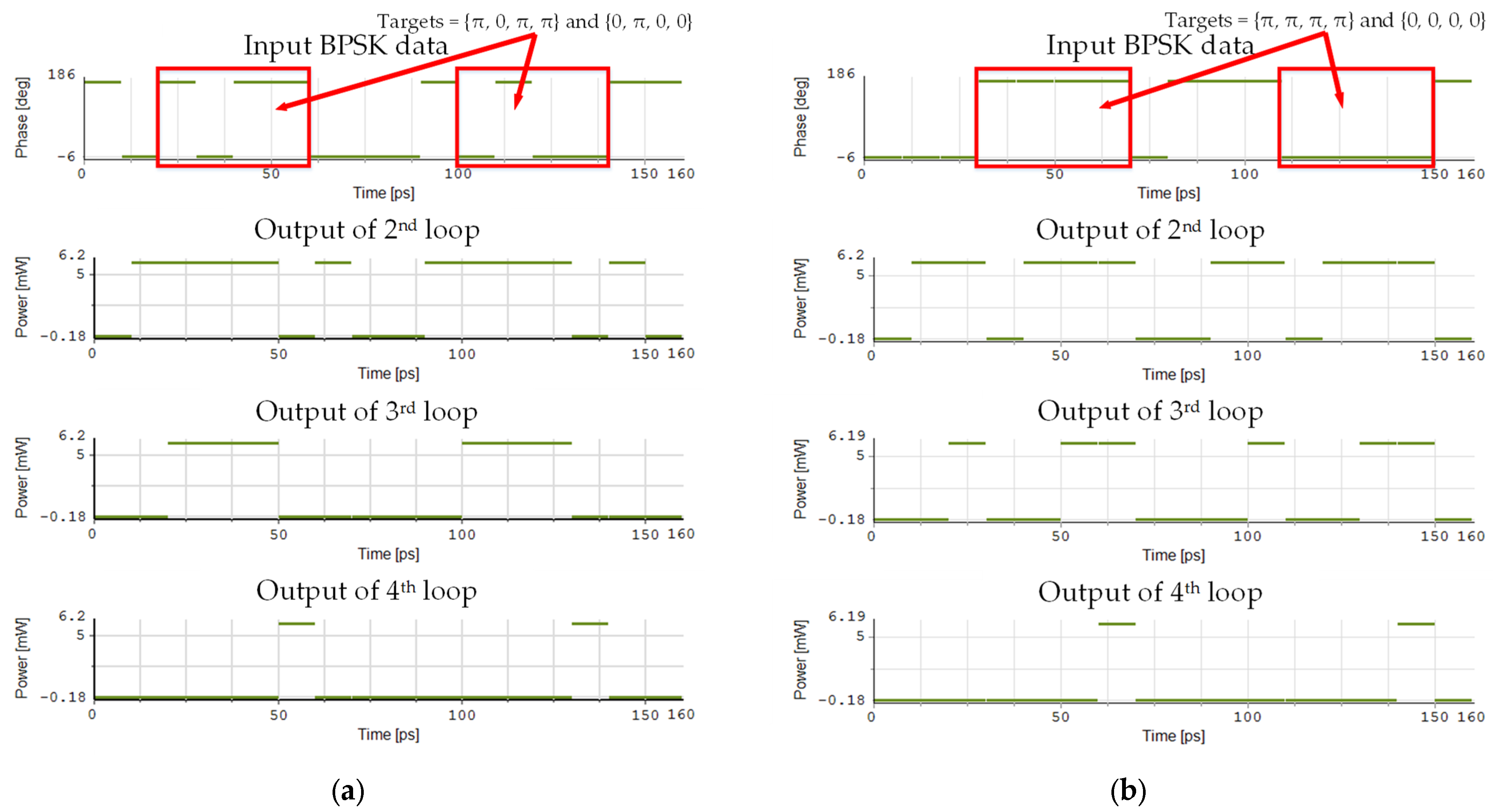
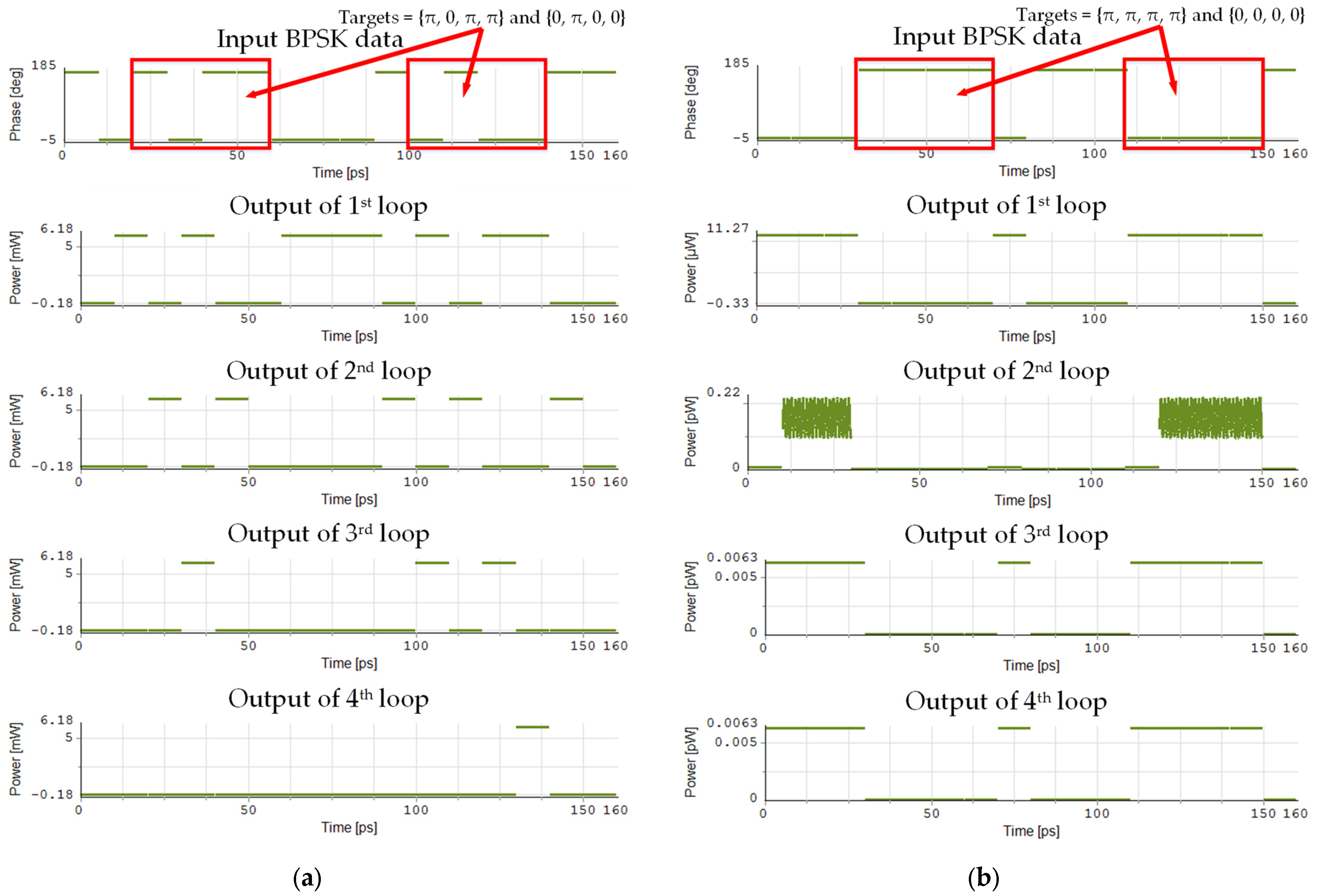
The procedure of searching targets {π, 0, π, π} and {0, π, 0, 0} in the input data {0, π, 0, π, π, π, 0, π, 0, 0} is shown in Figure 4. Here, we assume that the time for signals to pass through optical fibers and other components is ignored. In the first loop, the input BPSK data are first repeated four times via the storage loop with a duration of 10T. The repeated data are fed into the DI, where the current bit coherently interferes with the previous bit. Meanwhile, the first BPSK target with a length of 10T coherently interferes with the previous target bit. During the first loop, two optical switches are open, so the output of the DI will not enter the NOLM, and the other components in the system have no output.

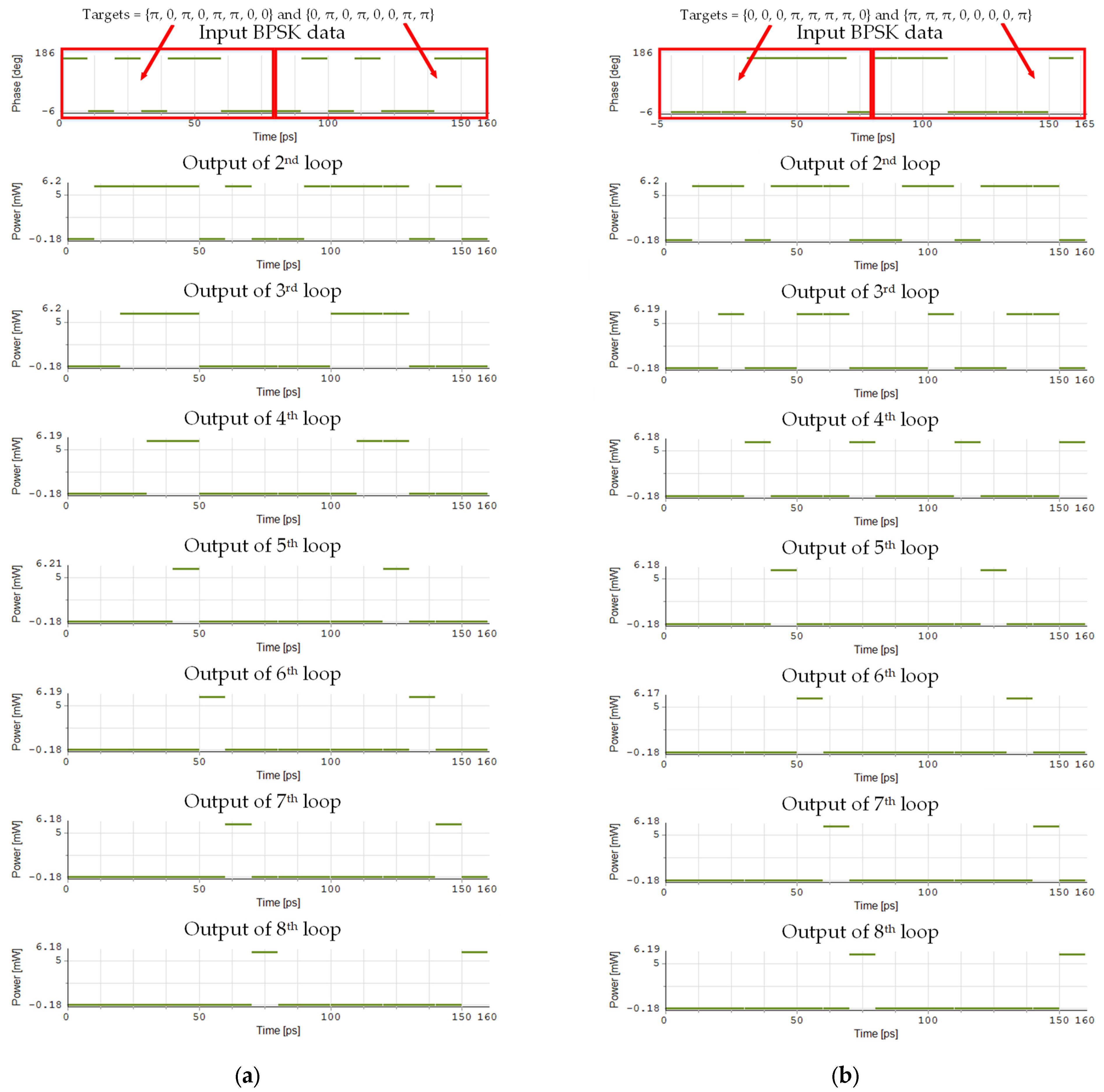
In the second loop, the input BPSK data coherently interferes with the previous bit. If these two bits have the same phase, the output power is high, which is denoted by logic “1”. Otherwise, the output power is low, which is denoted by logic “0”. Thus, the output of the right DI is {1, 0, 0, 0, 1, 1, 0, 0, 0, 1}. Similarly, the second BPSK target coherently interferes with the first BPSK target bit, and the output of the left DI is {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}. Assuming the initial phase of the local CW is 0, after passing through the isolator and coupler, the phase of the clockwise carrier remains the same, while the counterclockwise carrier introduces a phase shift of j. Then, the phase of the reloaded target in the clockwise direction is {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, and the phase of the reloaded data in the counterclockwise direction is {3π/2, π/2, π/2, π/2, 3π/2, 3π/2, π/2, π/2, π/2, 3π/2}. Subsequently, the signals in both directions pass through the coupler, and the counterclockwise carrier introduces another phase shift of j. After the isolator and the BPF, the signal at λ_CW is filtered out. Next, the output of the BPF is fed into the NOT gate, and the output is {0, 1, 1, 1, 0, 0, 1, 1, 1, 0}. The output of the NOT gate enters the recirculating loop together with an initializing pulse of 10T in length. The output of the AND gate is {0, 1, 1, 1, 0, 0, 1, 1, 1, 0}, which indicates the number and position of the first two bits of the targets in the input BPSK data. By repeating the process in the same manner, we can obtain the output from the AND gate in the fourth loop {0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1}, where the logic “1” indicates the number and position of the complete targets {π, 0, π, π} and {0, π, 0, 0} in the input BPSK data.

In the proposed system, it can be noticed that these two reloaded signals are phase-locking during signal generation. Additionally, they transmit through the same NOLM, which ensures the same optical path length and the strong coherence between them during signal transmission. Thus, in the bit-recognition process, the accuracy of phase-locking is rigorously guaranteed by the generation and maintenance of a stable phase relationship. Compared with previous pattern recognition systems that have phase-locking issues, the scheme is feasibly deployable in practical scenarios. The proposed system performs differential encoding on the input data and the target through two Dis, respectively, and then completes signal reloading and pattern recognition. Hence, it can support the recognition of two bit-flip BPSK targets simultaneously, which improves the recognition efficiency. Moreover, the proposed system can process the input signal with tunable frequency, which is especially suitable for wavelength-division multiplexing (WDM) optical networks. For an input signal with different frequencies, the EDFA followed by the DI should be precisely adjusted. Due to the limited gain of EDFA, the frequency variation in the input signal is within a range, but not random. Furthermore, the proposed system can be extended to support the recognition of QPSK targets by substituting the DI with an all-optical format conversion that transforms QPSK signals into PAM4 signals. Specifically, the input QPSK data and the QPSK target are first converted into PAM4 signals using an all-optical format conversion device [16]. During the conversion process, it is necessary to maintain phase-locking and enable wavelength conversion. After transforming the phase-modulated signals into power-modulated signals, the PAM4 signals are reloaded to QPSK signals via the XPM effect in the NOLM. Similarly, since the counterclockwise carrier passes through the 50:50 coupler twice, it introduces a π phase deflection. Consequently, when the reloaded QPSK data and reloaded QPSK target exhibit a π phase difference, the input QPSK symbol and the target QPSK symbol have the same phase. This means that when no signal is generated at the output of the BPF, the input QPSK symbol matches the target QPSK symbol. Conversely, a pulse output from the BPF indicates a mismatch between these two symbols. The output of the BPF is then amplified by a fixed-power EDFA to amplify the pulse power to a specific value, enabling it to serve as the pump in the subsequent NOT gate. Thus, if the input QPSK symbol and the QPSK target symbol are in phase, a pulse indicating logic “1” will be output after passing through the NOT gate. Otherwise, no pulse, indicating logic “0”, will be generated. Finally, the result is fed into the recirculating loop to complete the recognition and localization of the QPSK target within the input QPSK data. Compared with previous work, the proposed system can further improve flexibility and scalability, and accelerate the deployment of optoelectronic firewalls in optical networks.

3. Simulation Setup and System Parameters

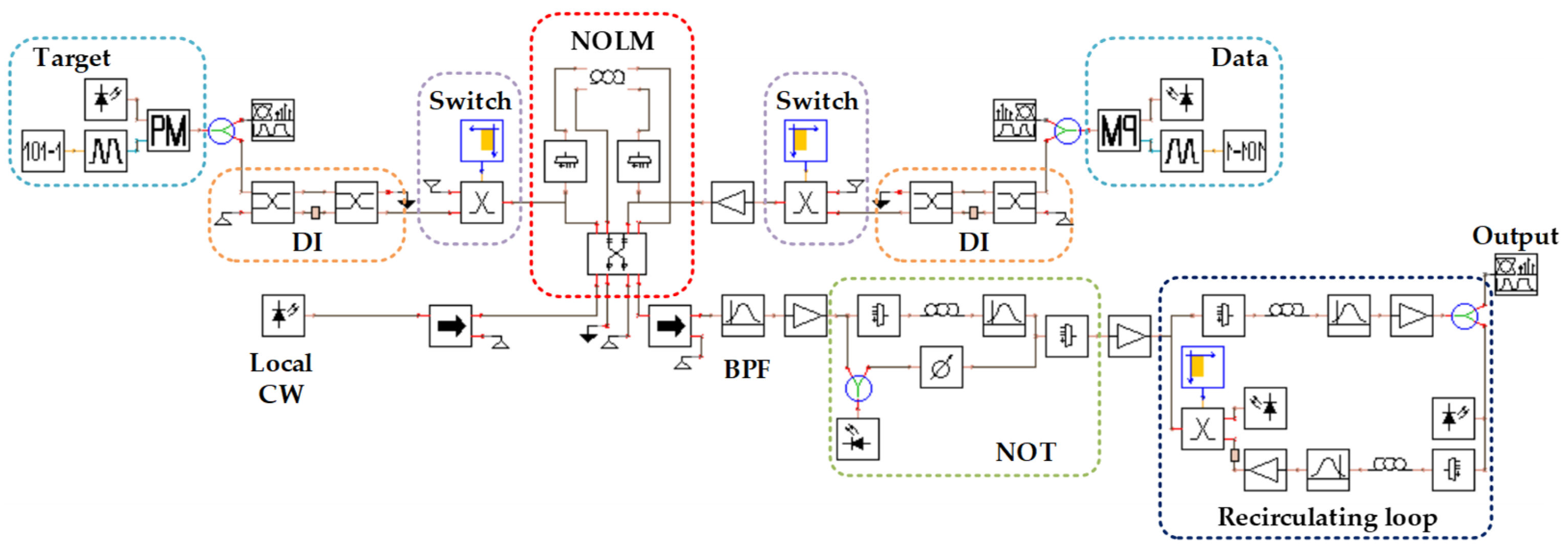
This section presents the simulation setup and parameter settings of the proposed all-optical pattern recognition system using VPItransmissionMaker 8.5. The data rate is set to 100 Gbps in our simulation considering the parameters of HNLF used in the system. Figure 5 shows the numerical simulation setup of the proposed system, and the parameter setting of various modules in simulation is displayed in

Table 1. Parameter setting of various modules in simulation.

Module	Parameter	Value
input data	center frequency	192.8 THz and 193.4 THz
	average power	0.5 mW [17]
	initial phase	{0, π}
target	center frequency	193.4 THz
	average power	63.22 mW
	initial phase	{0, π}
local CW	center frequency	193.1 THz
	average power	1 mW
all HNLFs	length	1007 m [18]
	attenuation	0.2 × 10−3 dB/m
	nonlinearity coefficient	~29 W−1 × km−1 [19]
	chromatic dispersion	−0.69 ps/nm × km
	dispersion slope	0.0074 ps/nm2 × km
all BPFs	bandwidth	100 GHz [20,21]
all lasers	line width	100 KHz [22]

.

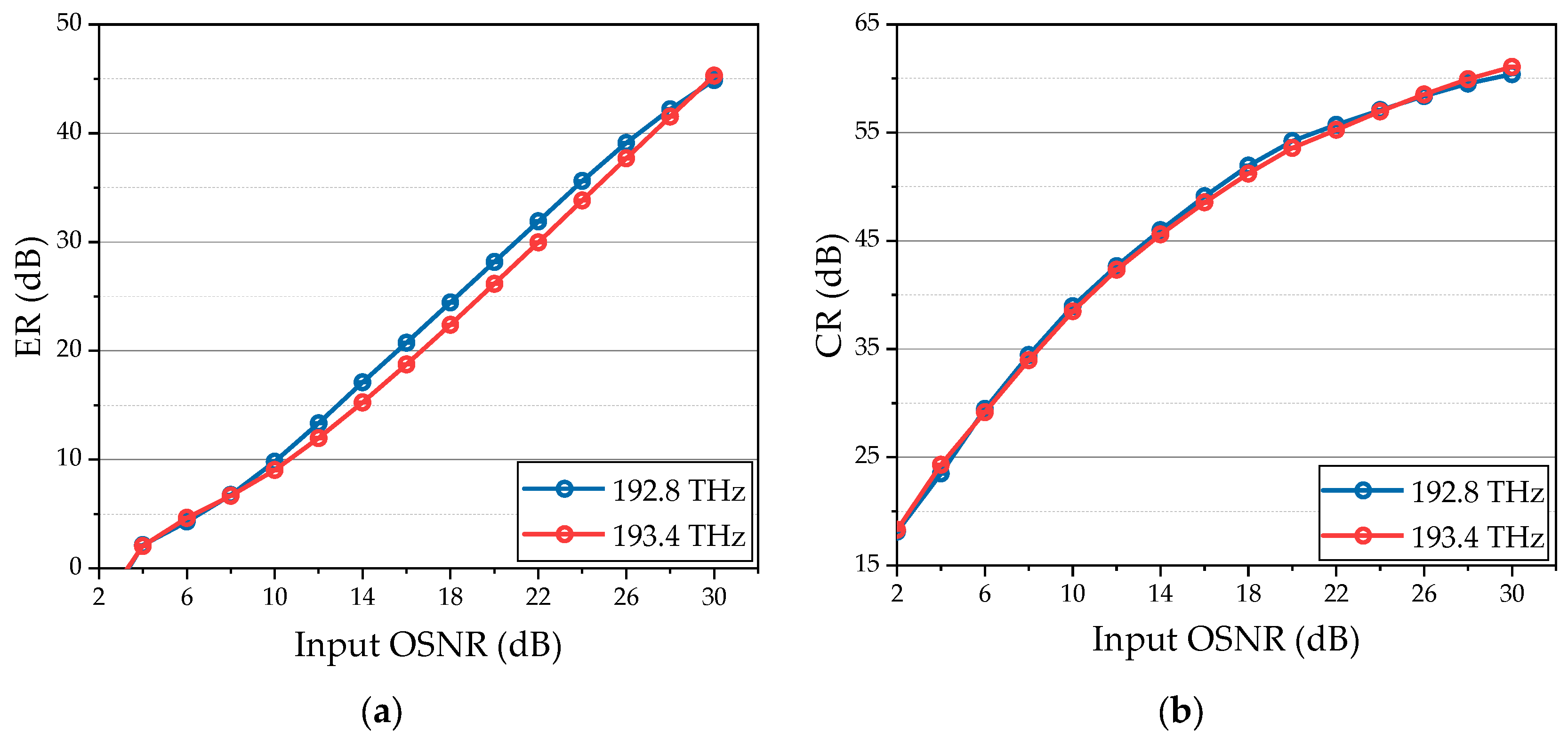
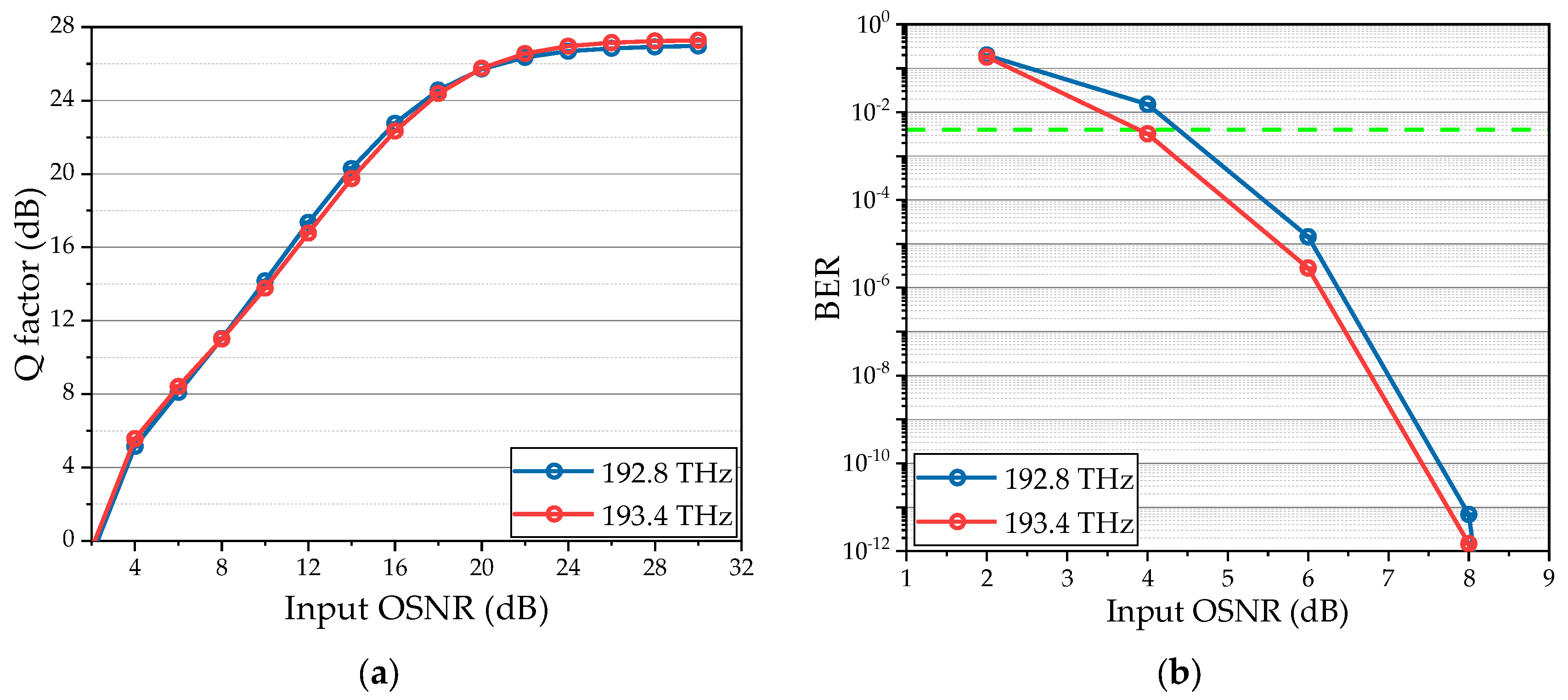
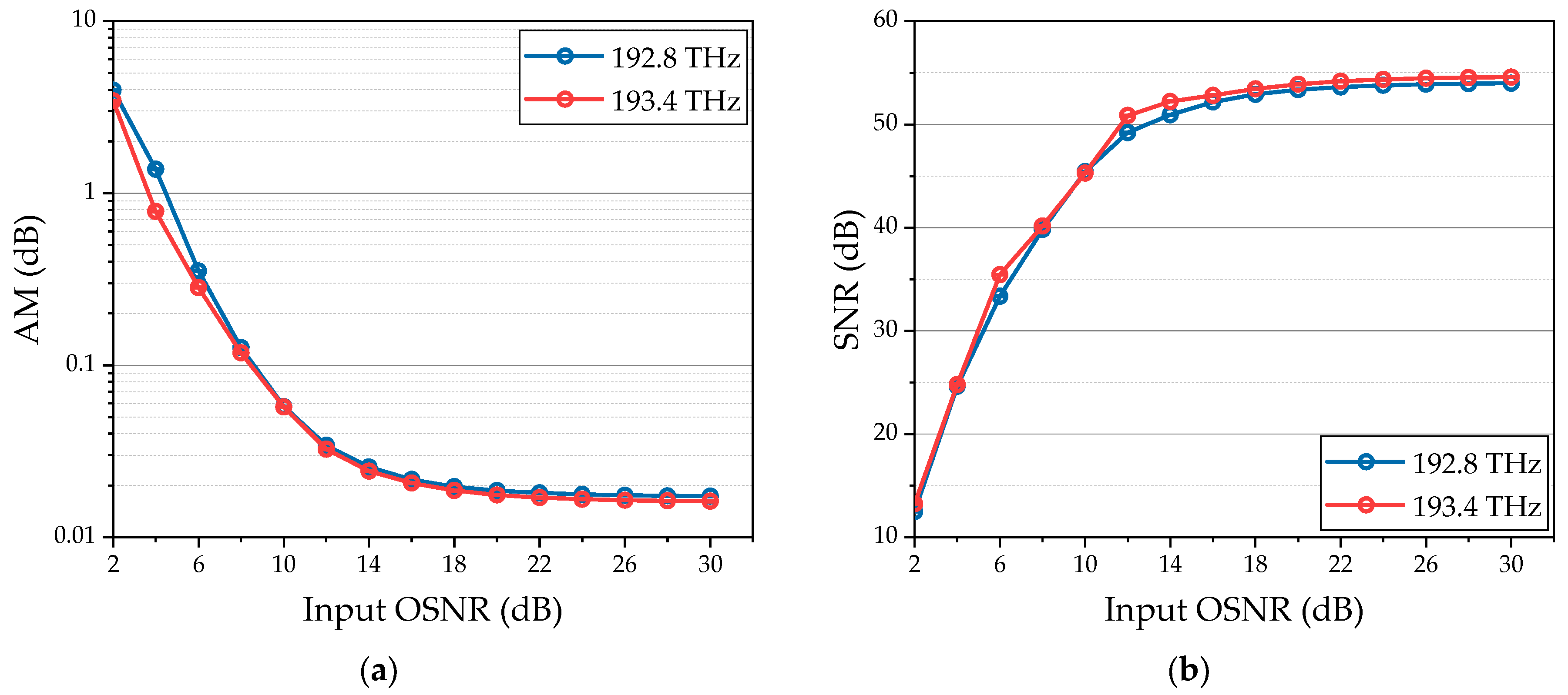
Data and Target: The incoming data and target sequence are represented by two synchronized BPSK signals, which are generated using predetermined data and ideal phase modulators. The input data stream is structured as a periodically replicated sequence, thereby avoiding the storage loop. The center frequency of the target is always set to 193.4 THz. To verify the performance of the system in processing the input data with tunable frequency, we set the center frequency of the input data to 192.8 THz and 193.4 THz in the simulation, which are symmetrical about the center frequency of the local CW.

DI: The DI module consists of two 50:50 couplers and an optical delay line (ODL). For the right DI following the input data, the delay time of the ODL is set to T, while for the left DI following the target, the delay time of the ODL is set to nT.

Switch: The switch module selects one of two input signals through a control signal. In the first loop, the optical switch selects a null source to pass through. After that, it selects the output of DI to pass through, so as to eliminate the interference brought about by the initial state. The output of the right switch is amplified by 20.06 dB and 20.02 dB when the center frequencies of the input data are 192.8 THz and 193.4 THz, respectively.

NOLM: The NOLM is constructed by a bidirectional 50:50 coupler, two multiplexers, and a bidirectional HNLF. First, the local CW with a center frequency of 193.1 THz passes through the unidirectional isolator and bidirectional coupler sequentially to generate the clockwise and counterclockwise carriers. Then, the input data and the counterclockwise carrier are injected into the HNLF through the right multiplexer. Meanwhile, the target and the clockwise carrier are injected through the left multiplexer. Subsequently, these two carriers are coherently interfered in the bidirectional coupler.

NOT: The output of the NOLM passes through another unidirectional isolator and a BPF with a center frequency of 193.1 THz to obtain the bit-recognition result. Before entering the NOT gate, an amplifier with a gain of 18.19 dB is used to increase the power of the bit-recognition result. Meanwhile, the probe with an average power of 0.5 mW at 192.8 THz inside the NOT gate is split into two branches. Then, the bit-recognition result, which serves as the pump, and the upper branch of the probe propagate through the following HNLF to generate the XPM effect. The upper branch of the probe experiences a phase shift induced by XPM, with its magnitude linearly dependent on the pump power. Thus, we modify the gain of the amplifier to achieve an XPM-induced phase shift of π. For the lower branch of the probe, an attenuator is used to match the output power of the upper branch. When the bit-recognition result is a logic “1”, destructive interference occurs at the multiplexer, resulting in an output of logic “0”. Conversely, when the bit-recognition result is a logic “0”, constructive interference occurs at the multiplexer, leading to an output of logic “1”. Therefore, the NOT gate is completed.

Loop: The output of the NOT gate is amplified by 4.97 dB using EDFA, and then enters the recirculating loop to complete the pattern recognition for variable target length. As the result of the first loop can be ignored, in the second loop, the initializing pulse which has an average power of 6 mW at 193.1 THz enters the subsequent AND gate with the output of the NOT gate. The AND gate operation is implemented by the FWM process within the HNLF. The output from this AND gate is then filtered using a BPF with a center frequency set at 192.5 THz. To ensure the power levels are consistent prior to entering the regenerator, an amplifier with a gain of 20.43 dB is employed. The regenerator itself also utilizes the FWM process within the HNLF to achieve frequency conversion. In the regenerator, the pump’s center frequency is 192.8 THz, and it maintains an average power of 6 mW. After interacting inside the HNLF, a BPF with a center frequency of 193.1 THz is utilized to extract the frequency-converted signal. An amplifier with a gain of 20.48 dB is positioned downstream. Finally, the output from the regenerator is fed back to the input of the AND gate after a delay of (n + 1)T. Upon completion of the second loop, the input to this AND gate is switched to the output of the regenerator via a control signal.

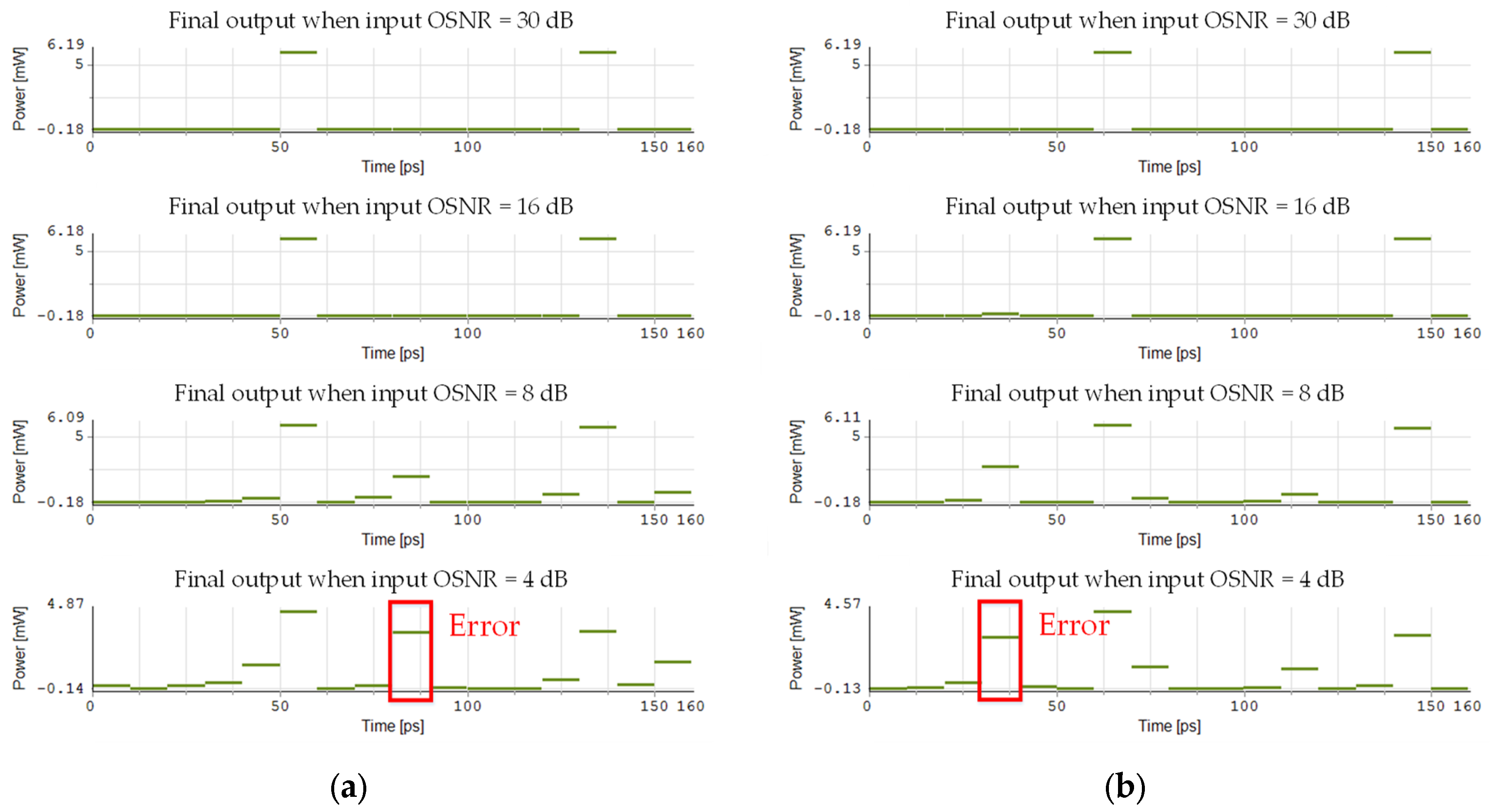
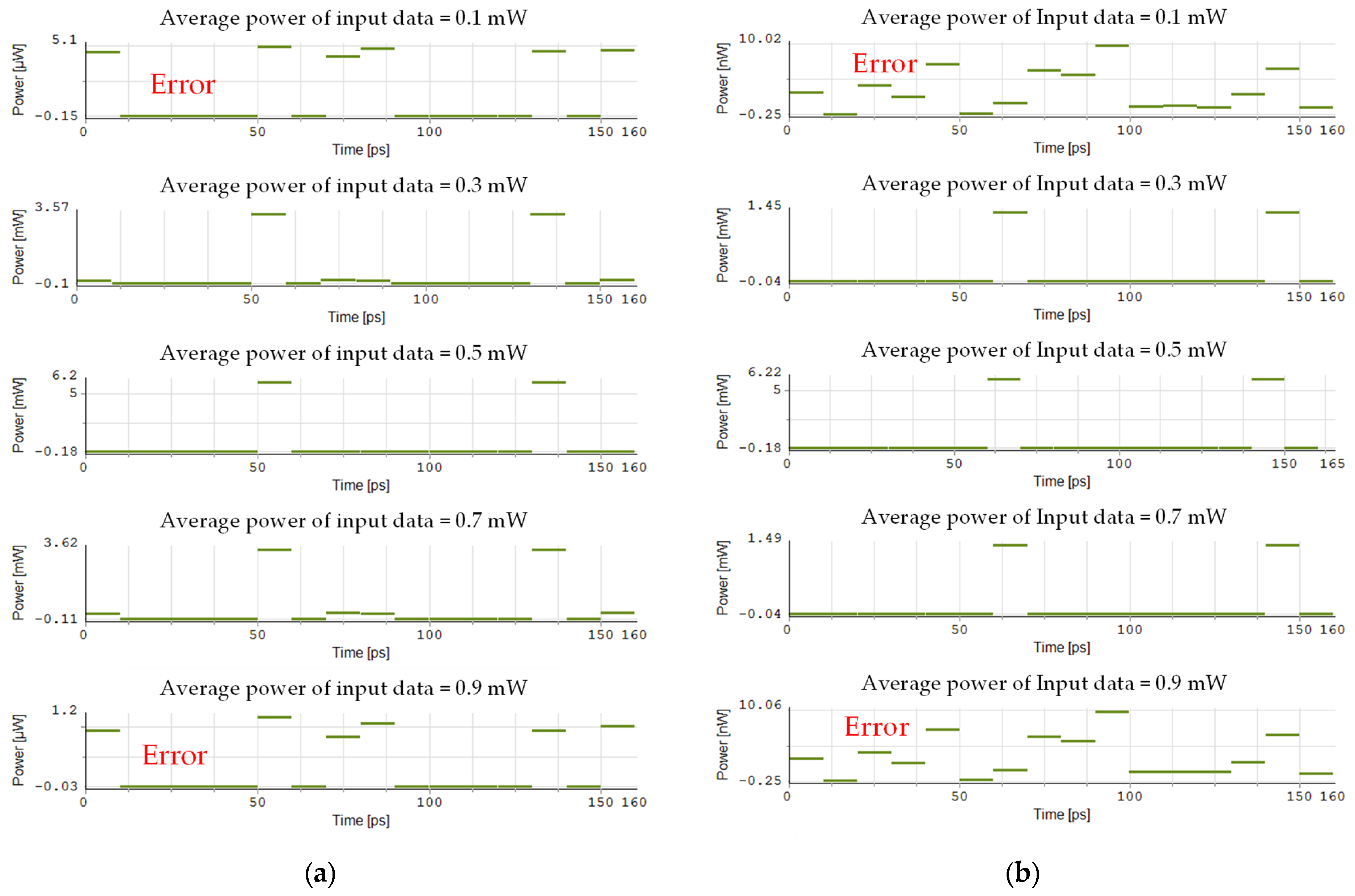
During the parameter selection process, we first clarified the average power of the input data. Considering the signal power transmitted in optical fibers, it is justified to set the value to 0.5 mW [17]. For the input signal frequencies, we chose 192.8 THz and 193.4 THz, which are centered around 193.1 THz. As the standard WDM channel spacing is 100 GHz, by setting the frequency spacing to 300 GHz, we ensure compatibility with existing optical network equipment while meeting the spectral occupancy requirements of high-data-rate signals. Moreover, the larger spacing reduces inter-channel crosstalk and mitigates nonlinear interference. Nonlinear effects such as FWM in HNLF can introduce noise. The 300 GHz spacing ensures that FWM-generated products are away from the main signal frequencies, allowing them to be easily filtered out by BPFs with a bandwidth of 100 GHz, thereby preserving signal integrity. The input frequencies of 192.8 THz and 193.4 THz are symmetrically distributed around the local CW frequency of 193.1 THz. This symmetric configuration aims to validate the system’s performance at dual frequency points and test its adaptability to tunable frequency. Through this symmetric frequency arrangement, the system’s flexibility in dynamically tunable WDM networks can be effectively evaluated. Subsequently, we set the parameters of the HNLF and chose a relatively lower power of 1 mW for the local CW [18]. However, during simulations, we observed that the phase shift induced by the XPM effect in the bidirectional HNLF failed to reach π. Therefore, we gradually increased the nonlinear coefficient to approximately 29 W⁻¹ × km⁻¹ [19]. We found that this value ensures significant XPM effects at 100 Gbps while avoiding signal distortion caused by excessive nonlinearity. The power of the target was determined through iterative optimization, ensuring that the XPM-induced phase shift reaches π when the left DI output is high, thereby completing signal reloading in the NOLM. Similarly, the gain of the EDFA before the input signal enters the NOLM was precisely calibrated to achieve a π-phase shift when the right DI output is high. All lasers were configured with a linewidth of 100 KHz, aligning with the typical ideal linewidth for CW lasers in coherent optical communication systems [22]. Additionally, setting this value to 100 KHz can effectively reduce the impact of phase noise on the system. All gain values of EDFA and output powers were optimized through multiple iterative simulations. By properly setting the gain value, the output signal power is maintained at the required level to drive subsequent logic operations.

4. Simulation Results and Discussion

4.1. Functional Verification

In this subsection, we choose 16-bit data as the search field to evaluate the output performance of the proposed all-optical pattern recognition system at 100 Gbps. The data rate represents the relatively high transmission rate that can be achieved using the BPSK modulation format in optical networks [23,24]. Through conducting simulations at this data rate, we can evaluate the system’s adaptability to such high-speed signals. Figure 6 presents the simulation results of recognizing 4-bit bit-flip BPSK targets in the input data using the proposed system at frequencies of 192.8 THz and 193.4 THz. When the frequency of the input data is 192.8 THz, as shown in Figure 6a, the phase of the input BPSK data is {π, 0, π, 0, π, π, 0, 0, 0, π, 0, π, 0, 0, π, π}, while the 4-bit bit-flip BPSK targets are {π, 0, π, π} and {0, π, 0, 0}. As the simulation result of the first loop is ignored, we observe the result from the second loop. The output of the second loop is {0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0}, which indicates all occurrences of {π, 0} and {0, π} in the data. The output of the third loop is {0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0}, which indicates all occurrences of {π, 0, π} and {0, π, 0} in the data. The output of the fourth loop is {0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0}, which clearly shows the number and position of the bit-flip BPSK targets {π, 0, π, π} and {0, π, 0, 0} in the data. Results demonstrate that two targets are hidden in the data, and their last bits are the sixth bit and the fourteenth bit of the input data, respectively. Figure 6b shows the simulation results of recognizing 4-bit bit-flip BPSK targets {π, π, π, π} and {0, 0, 0, 0} in the input data {0, 0, 0, π, π, π, π, 0, π, π, π, 0, 0, 0, 0, π} using the proposed system at a frequency of 193.4 THz. We find that the system can still accurately recognize 4-bit bit-flip BPSK targets when the frequency of the input data is 193.4 THz.

Figure 7 shows the simulation results of recognizing 8-bit bit-flip BPSK targets in the input data using the proposed system at frequencies of 192.8 THz and 193.4 THz. In Figure 7a where the input frequency is 192.8 THz, the input data are the same as that in Figure 6a, and the 8-bit bit-flip BPSK targets are {π, 0, π, 0, π, π, 0, 0} and {0, π, 0, π, 0, 0, π, π}. Similarly, we can observe that the output of the second loop is {0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0}, which indicates all occurrences of {π, 0} and {0, π} in the data. The output of the third loop is {0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0}, which indicates all occurrences of {π, 0, π} and {0, π, 0} in the data. The output of the fourth loop is {0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0}, which indicates all occurrences of {π, 0, π, 0} and {0, π, 0, π} in the data. The output of the fifth loop is {0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0}, which indicates all occurrences of {π, 0, π, 0, π} and {0, π, 0, π, 0} in the data. The output of the sixth loop is {0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0}, which indicates all occurrences of {π, 0, π, 0, π, π} and {0, π, 0, π, 0, 0} in the data. The output of the seventh loop is {0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0}, which indicates all occurrences of {π, 0, π, 0, π, π, 0} and {0, π, 0, π, 0, 0, π} in the data. The output of the eighth loop is {0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1}, which clearly demonstrates the presence of the entire target, and the logic “1” also indicates its temporal location within the data. Figure 7b presents the simulation results of recognizing 8-bit bit-flip BPSK targets {0, 0, 0, π, π, π, π, 0} and {π, π, π, 0, 0, 0, 0, π} in the input data using the proposed system at a frequency of 193.4 THz. Consequently, all the simulation results demonstrate that the proposed all-optical pattern recognition system can accurately determine the number and position of the bit-flip BPSK targets in the input data with tunable frequencies of 192.8 THz and 193.4 THz when the transmission rate is 100 Gbps.

Notably, our proposed system can also achieve accurate recognition of longer targets in longer input data. The system was also tested to recognize longer targets in longer input data, and no obvious signal degradation was observed in the output results. A longer input data sequence can provide more recognition opportunities, but it also takes more time. Consequently, to recognize the bit-flip BPSK targets, we choose targets of different lengths (4-bit and 8-bit) and recognize them in 16-bit input data to evaluate the system’s performance. For the specific values of the sequence, we ensure that each target appears at least once in the input data through careful design. However, in practical scenarios, the selection of the input data length and target length is determined based on actual application requirements.

To demonstrate the superiority of our proposed system more clearly, we conducted simulations that compared our proposed system with prior works [25]. After obtaining the bit-recognition results, the AND gate and regenerator in the recirculating loop of both systems, along with their corresponding parameter settings, are completely identical. Figure 8 shows the simulation results of recognizing 4-bit bit-flip BPSK targets in the input data using the reconfigurable system at frequencies of 192.8 THz and 193.4 THz. As shown in Figure 8a, when the input signal frequency is 192.8 THz, the input data and targets are the same as those in Figure 6a. However, in Figure 8a, through a single configuration of the target, a logic “1” in the output of each loop indicates that the input data has recognized the target symbols presented to the system. Consequently, when a complete target is recognized in the input data, a logic “1” appears in the output of the final loop, aligned with the position of the last symbol in the target sequence. According to the final output in Figure 8a, the reconfigurable system can only recognize a single target {0, π, 0, 0} under a single configuration. When the input signal frequency is 193.4 THz, as shown in Figure 8b, the input data and targets are set to be identical to those in Figure 6a. Moreover, to obtain accurate bit-recognition results, we set the frequency of the target to be consistent with the frequency of the input signal. However, the final simulation results indicate that the reconfigurable system fails to recognize input signals at another frequency without changing the parameters of the recirculating loop.

The simulation results in Figure 6 and Figure 7 demonstrate that the proposed system can recognize bit-flip BPSK targets simultaneously in the input data with tunable frequency, which greatly improves the efficiency and flexibility of the system. As attacks in optical networks become increasingly sophisticated, the limitations of existing systems that can only identify a single target at a time become apparent. To recognize multiple targets, multiple systems are typically cascaded. However, this approach not only substantially increases the cost of an optoelectronic firewall but also significantly raises its size and complexity. Therefore, our proposed system can improve recognition efficiency without increasing structural complexity. Meanwhile, as a key transmission technology in the physical layer of optical networks, WDM has become an indispensable part of backbone transmission and data center optical interconnections. However, current related research mainly focuses on processing optical signals with a specific frequency. Since the all-optical sequence recognition system primarily consists of all-optical logic gates, BPF, and other components, the parameters and performance of these components are highly dependent on the frequency of the input signal. If the parameters of these components need to be adjusted individually to accommodate optical signals of different frequencies, not only will the operational complexity be extremely high, but it will also significantly increase the maintenance cost of the system. Our proposed all-optical pattern recognition system can be reconfigured to support the recognition of input signals with tunable frequency in WDM optical networks, thereby improving the flexibility and versatility of the system. Consequently, our proposed system possesses unique advantages in dealing with relatively complex attacks within WDM optical networks, which addresses critical gaps and advances the state of the art in this field.

4.2. Impact of Input Noise

Next, we consider the impact of input noise on the proposed system. To emulate the actual input signal, variable white Gaussian noise (WGN) is introduced following the generation of BPSK data, which simulates the input BPSK signal under varying optical signal-to-noise ratios (OSNRs). The output results are evaluated when recognizing 4-bit bit-flip BPSK targets in the input signal with frequencies of 192.8 THz and 193.4 THz, respectively. The input data and the target are identical to those in Section 4.1. The seed of WGN remains consistent, while only the power spectral density of WGN is changed when varying the OSNR values of the input signal.

Figure 9 shows the simulation results when the OSNR of the input signal with frequencies of 192.8 THz and 193.4 THz varies from 30 dB to 4 dB. When the input OSNR is 30 dB, which means the input signal and transmission environment are relatively perfect, there is no obvious difference between the final outputs and the results in Figure 6. As the input OSNR decreases, the output quality gradually deteriorates because the power of logic “0” increases, while the power of logic “1” decreases. When the input OSNR is 4 dB, it can be noticed that the maximum power value of logic “0” is almost the same as the minimum power value of logic “1” in both Figure 9a,b, which will lead to errors.

To further quantify the output performance under different input OSNR values, we evaluate the metrics of extinction ratio (ER), contrast ratio (CR), Q factor, bit error rate (BER), amplitude modulation (AM), and signal-to-noise ratio (SNR). The definitions of ER, CR, Q factor, BER, AM, and SNR are shown in Equations (11)–(16) [26,27], where $P_{\min }^1$ represents the minimum power value of logic “1”; $P_{\max }^0$ represents the maximum power value of logic “0”; and $P_{\mathrm{mean}}^1$ ($P_{\mathrm{mean}}^0$) and σ₁ (σ₀) represent, respectively, the mean power values and standard deviation of the power values at logic “1” (logic “0”) state.

$$ER\left(dB\right)=10\log \left({\displaystyle \frac{P_{\min }^1}{P_{\max }^0}}\right)$$

(11)

$$CR\left(dB\right)=10\log \left({\displaystyle \frac{P_{mean}^1}{P_{mean}^0}}\right)$$

(12)

$$Q={\displaystyle \frac{P_{mean}^1-P_{mean}^0}{{\sigma }_1+{\sigma }_0}}$$

(13)

$$BER={\displaystyle \frac{1}{2}}erfc\left({\displaystyle \frac{Q}{\sqrt{2}}}\right)$$

(14)

$$AM\left(dB\right)=10\log \left({\displaystyle \frac{P_{\max }^1}{P_{\min }^1}}\right)$$

(15)

$$SNR={\left({\displaystyle \frac{P_{mean}^1}{{\sigma }_1}}\right)}^2$$

(16)

Equation (11) quantifies the power difference between minimum logic “1” ($P_{\min }^1$) and maximum logic “0” ($P_{\max }^0$). Equation (12) measures the mean power ratio between logic “1” and logic “0”. Equation (13) measures the quality of the output signal, which is closely related to BER. Equation (14) provides the error probability in signal transmission. Equation (15) reflects the dynamic range of the power level of logic “1”. Equation (16) measures the ratio of output signal power to noise power. Equations (11)–(16) are used to evaluate the quality of the output signal, which is important for guiding system optimization. The larger the ER, CR, Q factor, and SNR, the smaller the BER, indicating better logical discrimination at the receiver; otherwise, it indicates a higher probability of errors. To eliminate the impact of different sequences on output performance, the phase of the input BPSK signal is {π, 0, π, 0, π, π, 0, 0, 0, π, 0, π, 0, 0, π, π} for both frequencies with a transmission rate of 100 Gbps, while the 4-bit bit-flip BPSK targets are set to {π, 0, π, π} and {0, π, 0, 0} for both frequencies. Furthermore, to obtain good statistical confidence in the results, the seed of the WGN is changed 10 times for each input OSNR under identical noise power density and noise bandwidth, and we take the average of the results.

The output ER and CR performances under different input OSNRs are plotted in Figure 10. As shown in Figure 10a, the output ER decreases as the input OSNR decreases for both input frequencies. However, the input frequency of 192.8 THz can achieve a larger output ER value by about 4.86% on average compared with the input frequency of 193.4 THz, where the maximum ER improvement can reach 2.04 dB when the input OSNR is around 18 dB. Some studies indicate that the output exhibits comparatively superior quality when the typical empirical value of ER is above 9 dB [28]. Note that even at an input OSNR of 10 dB, where the quality of the input signal deteriorates seriously, the output ER values remain superior to the empirical benchmarks of 0.81 dB and 0.04 dB for 192.8 THz and 193.4 THz, respectively. In Figure 10b, it can be observed that as the input OSNR decreases, the output CR also decreases for both input frequencies. These two curves are very close, where the input frequency of 192.8 THz can achieve a slightly larger output CR value by about 0.33% on average compared with the input frequency of 193.4 THz, which means they have very similar CR performance. This is because these two frequencies are symmetrical about the center frequency of the local CW, and the gains of the amplifier following the right switch are 20.06 dB and 20.02 dB for the two input frequencies, which are almost the same. Then, the impact of input noise on the bit-recognition result should be almost the same. Therefore, when the input frequencies are 192.8 THz and 193.4 THz and the transmission rate is 100 Gbps, the output ER and CR results of the proposed system exhibit similar performance.

Figure 11 shows the Q factor and BER performances under different input OSNRs. In Figure 11a, the Q factor results exhibit a similar trend to those of ER and CR, where the value of the Q factor decreases as the input OSNR decreases for both input frequencies. When the input OSNR is larger than 20 dB or less than 8 dB, the input frequency of 193.4 THz can achieve a larger Q factor value compared with the input frequency of 192.8 THz. On the other side, the input frequency of 192.8 THz shows better performance when the input OSNR is between 8 dB and 20 dB. Generally, the input frequency of 193.4 THz can achieve a slightly larger Q factor value by about 0.14% on average compared with the input frequency of 192.8 THz. The BER performance under different qualities of input signal is shown in Figure 11b. Once the BER exceeds 10^−2.4, the signal becomes uncorrectable due to the forward error correction threshold limitation. Then, the BER performance is analyzed based on the green reference line in the figure. The results indicate that the OSNR at the input frequency of 193.4 THz is approximately 0.50 dB higher than that at 192.8 THz when the BER is 10^−2.4.

Figure 12 presents the AM and SNR performances at two frequencies of 192.8 THz and 193.4 THz under different input OSNRs. From Figure 12a, it is evident that the output AM progressively rises as the input OSNR decreases. This indicates that the higher the quality of the input signal, the smaller the amplitude fluctuation of logic “1” and the more stable the signal. In the high OSNR regime (OSNR > 18 dB), the value of AM is very small, and as input OSNR increases, the rate of decrease in AM gradually slows down. This may be because the system is approaching its optimal performance under high OSNR conditions, and further increasing OSNR has a diminishing effect on reducing AM. In the low OSNR regime (OSNR < 12 dB), the value of AM is relatively large, and as input OSNR increases, the rate of decrease in AM is relatively fast. This indicates that the system is more sensitive to changes in OSNR under low OSNR conditions, and increasing OSNR can significantly reduce the amplitude fluctuation of logic “1”. The two curves for 192.8 THz and 193.4 THz nearly overlap, indicating that the system’s response to input OSNR in terms of AM is highly similar at these two frequencies. In Figure 12b, the output SNR increases as the input OSNR increases at both 192.8 THz and 193.4 THz. This indicates that the higher the quality of the input signal, the higher the quality of the output signal. These two figures are very similar in trend and conclusion, further verifying the consistency and stability of the system’s response to input OSNR at 192.8 THz and 193.4 THz. According to Figure 10, Figure 11 and Figure 12, we can conclude that our proposed all-optical pattern recognition system exhibits stable performance when the input frequencies are 192.8 THz and 193.4 THz at 100 Gbps.

Although input noise is inevitable during signal transmission, there are two solutions that can be incorporated into our system design to reduce the influence of noise. Firstly, the regenerator in the recirculating loop can be further improved. It is mainly designed to achieve frequency conversion in the proposed pattern recognition system. However, it can be redesigned to achieve not only frequency conversion, but also suppressing the accumulated distortion and noise during transmission. There are many works that focus on all-optical frequency conversion and all-optical regeneration [29,30,31]. They can be achieved by cross-gain modulation (XGM), XPM, and FWM, and have been successfully tested in different nonlinear media. Secondly, an additional noise compression structure can be designed and placed in the recirculating loop to reduce the accumulation of noise caused by multiple loops. We propose a cascaded noise suppression structure based on FWM to improve the output performance of the pattern recognition system for OOK signals [32]. This structure helps to separate noise from signals by generating a step-shaped power transmission curve. The simulation results show that the proposed structure can effectively reduce errors. In future work, we will verify the effectiveness and performance of these two solutions. We hope to further improve the proposed all-optical pattern recognition system, and provide a more secure and reliable solution for future optical networks.

In the simulation, only the impact of input noise is considered. However, in practical optical systems, the sources and effects of noise are far more complex. The following specific noise parameters can be integrated into future research: (1) Amplified spontaneous emission (ASE) noise. ASE noise generated by optical amplifiers is a critical factor in fiber transmission systems. It degrades the OSNR and impacts output performance. We will model the generation and propagation of ASE noise in detail and analyze its specific impact on the output quality. (2) Nonlinear effect-induced noise. In HNLF, nonlinear effects such as XPM, while enabling signal reloading and logic operation, may also introduce additional noise. We will investigate the origin and characteristics of such nonlinear noise and explore parameter optimization to mitigate its impact. (3) Fiber loss and dispersion-induced noise. Fiber attenuation reduces signal power, while dispersion causes pulse broadening and distortion, both degrading signal integrity. We will quantify the impact of fiber loss and dispersion on system performance and explore compensation techniques to improve signal quality. (4) Phase noise. Phase noise arises from fluctuations in signal phase due to environmental factors (e.g., temperature variations, mechanical vibrations). We will analyze its impact on both BPSK signals and the output results and evaluate phase stabilization methods to suppress it.

4.3. Sensitivity Analysis of Input Power

Component tolerances and sensitivities play an important role in practical implementations. For example, variations in fiber length and dispersion characteristics can affect system performance. Similarly, fluctuations in signal and pump powers can also influence the efficiency of nonlinear processes. Here, we take the variation in signal power as an example to discuss the system’s sensitivity to changes in signal power. To evaluate the influence of input power on system performance, we conduct simulations under different average powers of input data while keeping other parameters fixed. Similarly, the output performance is evaluated when recognizing 4-bit bit-flip BPSK targets in the input signal with frequencies of 192.8 THz and 193.4 THz, respectively. Both the input data and target remain the same as those specified in Section 4.1.

Figure 13 shows the simulation results when the average power of input data with frequencies of 192.8 THz and 193.4 THz varies from 0.1 mW to 0.9 mW. It should be noted that in Figure 13, the simulation output aligns with those in Figure 6 only when the input power is 0.5 mW, as the input power in Figure 6 is also set to 0.5 mW. However, when the input power deviates from 0.5 mW, the power of the logic “1” in the output exhibits a significant decrease. Specifically, when the input power is 0.5 mW, the power of the logic “1” in the output is around 6 mW. However, in Figure 13a, when the input power is 0.3 mW or 0.7 mW, the power of the logic “1” in the output drops from around 6 mW to approximately 3.5 mW. In Figure 13b, when the input power is 0.3 mW or 0.7 mW, the power of the logic “1” in the output decreases from around 6 mW to approximately 1.5 mW. The simulation results indicate that when the input power is below 0.3 mW, the XPM-induced phase shift is insufficient to reach π; when the input power is above 0.7 mW, the XPM-induced phase shift exceeds π. Both scenarios degrade the coherent interference results after the optical coupler. If we set the output ER of 9 dB as the threshold, the system can achieve correct results when the output ER exceeds 9 dB; otherwise, it may fail to recognize the results accurately. Then, according to the simulation results, the proposed system still achieves correct results within the input power range of 0.3–0.7 mW (i.e., ±0.2 mW deviation from the nominal 0.5 mW). Thus, we conclude that the proposed system can tolerate input power fluctuations of approximately ±0.2 mW.

5. Conclusions

In this paper, a tunable all-optical pattern recognition system based on NOLM is proposed for bit-flip BPSK targets. Benefiting from the differential encoding and signal reloading, the proposed system can achieve phase-locking-free architecture and recognize two bit-flip BPSK targets simultaneously in the input signal with tunable frequency. We evaluate the feasibility of the proposed system, and the simulation results demonstrate that our proposed system can correctly recognize and locate 4-bit and 8-bit bit-flip BPSK targets in the input data, operating at a transmission rate of 100 Gbps and frequencies of 192.8 THz and 193.4 THz. Similar output performance can be observed when evaluating input noise tolerance of the system based on ER, CR, Q factor, BER, AM, and SNR under the input frequencies of 192.8 THz and 193.4 THz. Our proposed system provides an effective method for pattern recognition and can help to accelerate the deployment of optoelectronic firewalls in optical networks. Additionally, the scalability of the proposed pattern recognition system to support the recognition of QPSK targets is discussed. In actual experiments and deployment, our proposed system may still require precise time synchronization among the input data, target, and initializing pulse to obtain correct outputs.