Optical Field-to-Field Translation Under Atmospheric Turbulence: A Conditional GAN Framework with Embedded Turbulence Parameters
Abstract
1. Introduction
2. Network Design
2.1. The Laser Beam Model
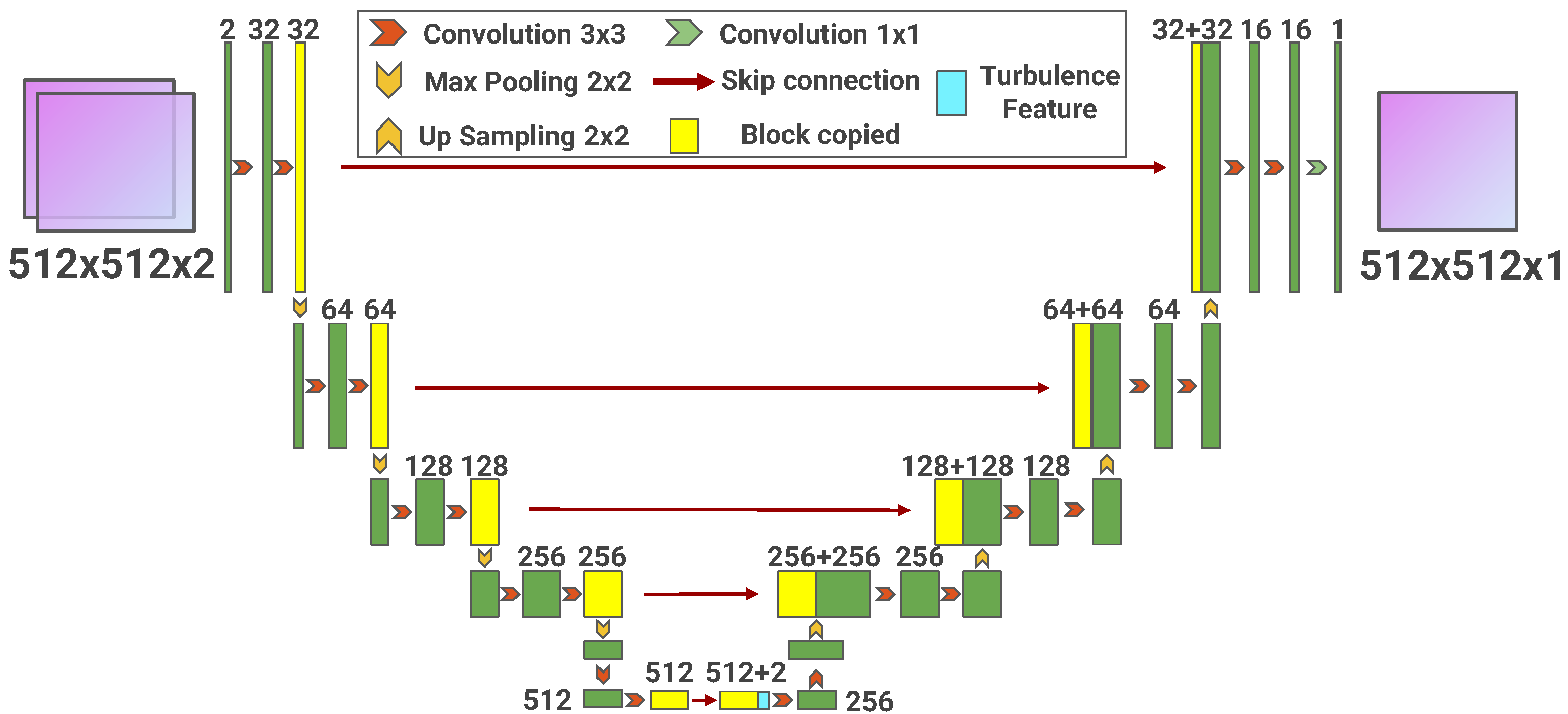
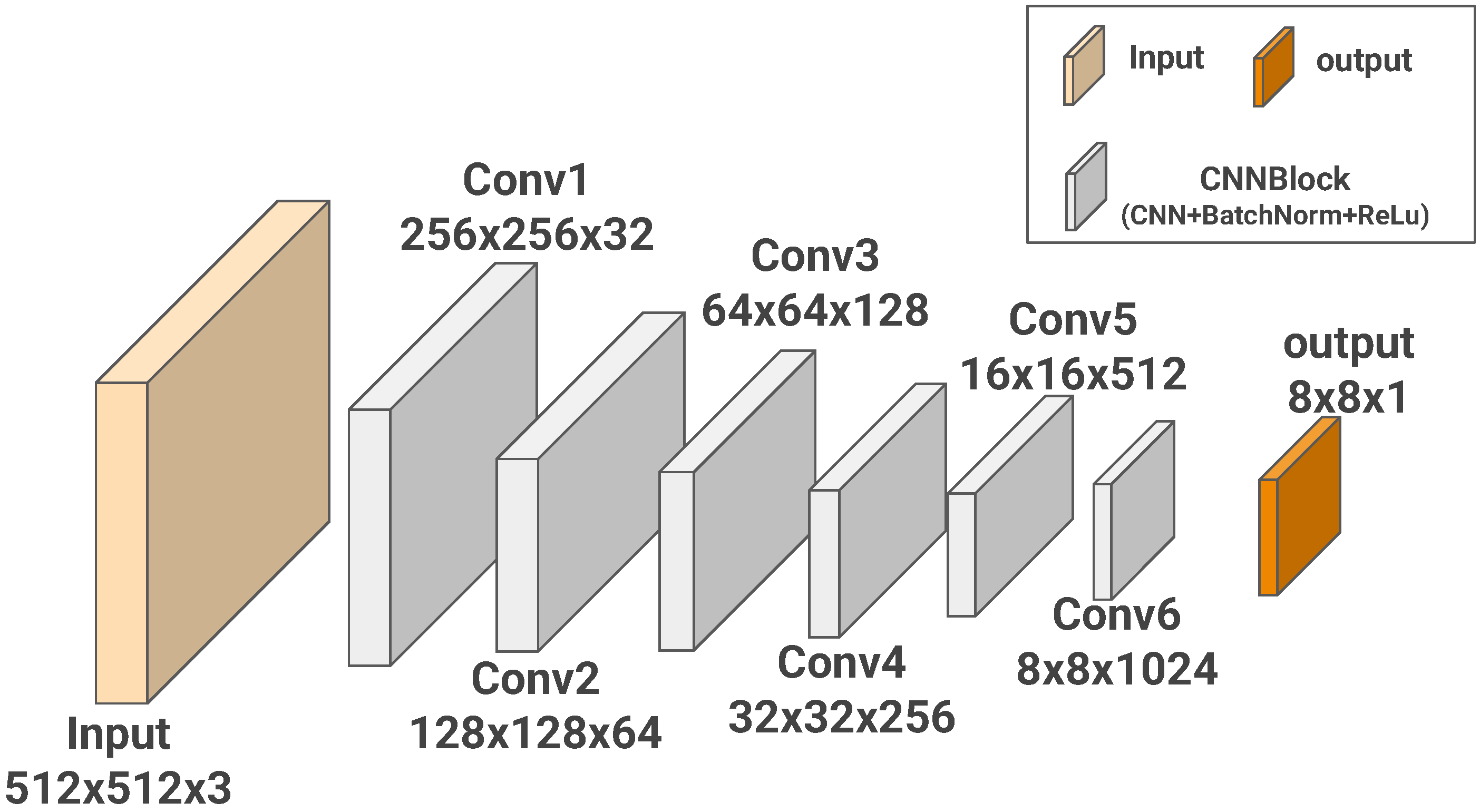
2.2. Proposed GAN Architecture
3. Training Data and Network Training
3.1. Building the Training Dataset
- The input optical field is a fundamental-mode Gaussian beam with a beam waist radius of 0.1 m and a wavelength of 1.08 μm. This Gaussian beam can be in a collimated or focused state. In the focused state, the focal length is set equal to the corresponding transmission distance;
- Regarding the turbulence-related parameters, the refractive index structure constant is linearly sampled 100 times from to . The outer scale parameter is 100 m, and the inner scale parameter is 0.01 m. The number of phase screens on the transmission path is set to 20;
- For the receiving-plane and transmission parameters, the physical dimension of the receiving plane is . The transmission distance ranges from 0 to 10,000 m, with a linear separation of 200 m intervals.
3.2. Loss Function
3.3. Training Method
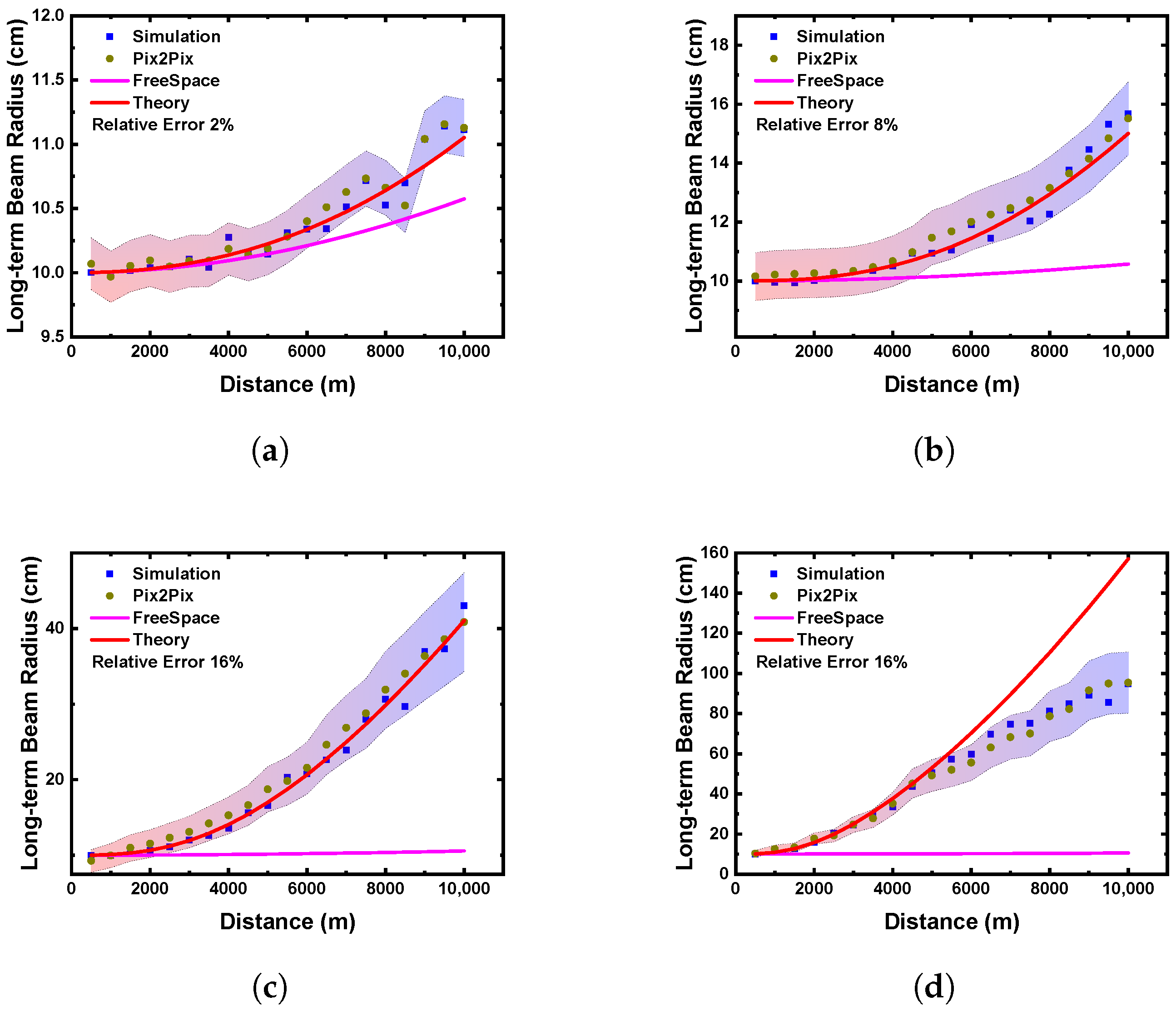
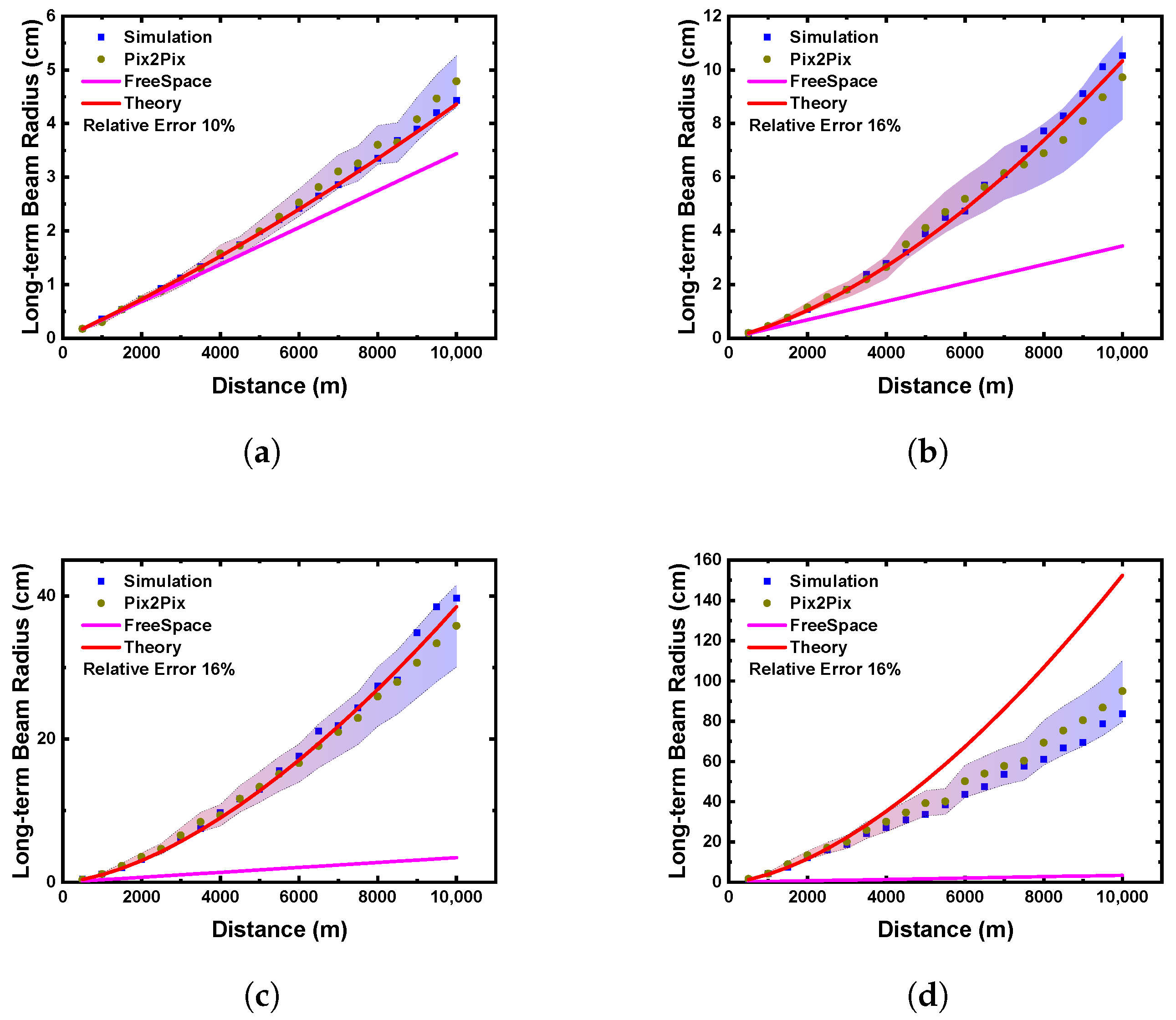
4. Results
5. Discussion
- The GANs prioritize learning low-frequency global features (e.g., overall intensity distribution) while struggling to synthesize high-frequency stochastic details (e.g., sub-pixel speckle breakups).
- The square symmetry of convolutional kernels inherently biases the generator toward blocky outputs with sharp edges when high-frequency turbulence effects are underlearned, rather than producing rotationally symmetric Gaussian or random speckles.
- Strong turbulence induced speckles exhibit extreme multimodality (infinite possible spatial configurations for a given turbulence strength). When GANs cannot cover all modes, they may collapse to a “statistical average” state.
- The generator learns that regular square patterns can partially match certain global statistics (e.g., total energy conservation or pixel mean) to fool the discriminator. This strategy, though unphysical, becomes a local Nash equilibrium in adversarial training.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Khare, K.; Lochab, P.; Senthilkumaran, P. Theory of wave propagation in a turbulent medium. In Orbital Angular Momentum States of Light; IOP Publishing: London, UK, 2020; pp. 7-1–7-39. [Google Scholar] [CrossRef]
- Hulea, M.; Tang, X.; Ghassemlooy, Z.; Rajbhandari, S. A review on effects of the atmospheric turbulence on laser beam propagation—An analytic approach. In Proceedings of the 2016 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Murty, S.S.R. Laser beam propagation in atmospheric turbulence. Proc. Indian Acad. Sci. USA 1979, 2, 179–195. [Google Scholar] [CrossRef]
- Salmanowitz, J.; Zandt, N.R.V. Phase Screen Generation for Non-Kolmogorov Turbulence. In Proceedings of the Imaging and Applied Optics Congress 2022 (3D, AOA, COSI, ISA, pcAOP), Vancouver, BC, Canada, 11–15 July 2022. [Google Scholar]
- Frehlich, R. Simulation of laser propagation in a turbulent atmosphere. Appl. Opt. 2000, 39, 393–397. [Google Scholar] [PubMed]
- Mcglamery, B.L. Computer Simulation Studies of Compensation of Turbulence Degraded Images. Proc. SPIE-Int. Soc. Opt. Eng. 1976, 74, 225–233. [Google Scholar]
- Jiang, R.; Wang, K.; Tang, X.; Wang, X. Investigation of Oceanic Turbulence Random Phase Screen Generation Methods for UWOC. Photonics 2023, 10, 832. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Yang, L.; Gong, L.; Wang, L.G.; Wang, X. Waveform Distortion of Gaussian Beam in Atmospheric Turbulence Simulated by Phase Screen Method. J. Math. 2022, 2022, 5939293. [Google Scholar] [CrossRef]
- Herman, B.J.; Strugala, L.A. Method for inclusion of low-frequency contributions in numerical representation of atmospheric turbulence. Proc. SPIE-Int. Soc. Opt. Eng. 1990, 1221, 183–192. [Google Scholar]
- Charnotskii, M. Sparse spectrum model for a turbulent phase. J. Opt. Soc. Am. A 2013, 30, 479. [Google Scholar]
- Charnotskii, M. Sparse spectrum model for the turbulent phase simulations. In Proceedings of the Atmospheric Propagation X, Baltimore, MD, USA, 29 April–3 May 2013; Thomas, L.M.W., Spillar, E.J., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8732, p. 873208. [Google Scholar] [CrossRef]
- Paulson, D.A.; Wu, C.; Davis, C.C. Randomized Spectral Sampling for Efficient Simulation of Laser Propagation through Optical Turbulence. J. Opt. Soc. Am. B 2019, 36, 3249–3262. [Google Scholar] [CrossRef]
- Cubillos, M.; Luna, K. Sinc method for generating and extending phase screens of atmospheric turbulence. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2024, 41, 14. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Chen, Z.; Xiao, C.; Qin, M.; Wu, H. Accurate simulation of turbulent phase screen using optimization method. Optik 2019, 178, 1023–1028. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, D.X.; Xiao, C.; Qin, M.Z. Precision analysis of turbulence phase screens and its influence on simulation of Gaussian-beam propagating in the turbulent atmosphere. Appl. Opt. 2020, 59, 3726–3735. [Google Scholar] [PubMed]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 10684–10695. [Google Scholar]
- Chen, Y.; Liu, X.; Jiang, J.; Gao, S.; Liu, Y.; Jiang, Y. Reconstruction of degraded image transmitting through ocean turbulence via deep learning. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2023, 40, 8. [Google Scholar]
- Rai, S.N.; Jawahar, C.V. Removing Atmospheric Turbulence via Deep Adversarial Learning. IEEE Trans. Image Process. 2022, 31, 2633–2646. [Google Scholar] [CrossRef] [PubMed]
- Chunbo, M.A.; Ke, H.; Jun, A.O. Numerical Simulation of Random Phase Screen Under the Kolmogorov and Non-Kolmogorov Turbulence Model. Comput. Digit. Eng. 2019, 7, 3596–3602. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Zhang, Q.; Wang, H.; Lu, H.; Won, D.; Yoon, S.W. Medical Image Synthesis with Generative Adversarial Networks for Tissue Recognition. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 199–207. [Google Scholar]
- Xie, X.C.; Yang, P.L.; Zhao, H.C.; Wang, Z.B.; Wu, Y.; Fei, W. Simulation of Characteristics of Far Field Laser Beam Spot Under Different Atmospheric Transmission Conditions. Mod. Appl. Phys. 2019, 10, 020301-1–020301-5. [Google Scholar]
- Xu, Z.Q.J.; Zhang, Y.; Xiao, Y. Training Behavior of Deep Neural Network in Frequency Domain. In Neural Information Processing; Gedeon, T., Wong, K.W., Lee, M., Eds.; Springer: Cham, Switzerland, 2019; pp. 264–274. [Google Scholar]
- Zhang, J.J.; Meng, D. Quantum-inspired analysis of neural network vulnerabilities: The role of conjugate variables in system attacks. Natl. Sci. Rev. 2024, 11, nwae141. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, J.; Meng, D.; Wang, X. Exploring the uncertainty principle in neural networks through binary classification. Sci. Rep. 2024, 14, 28402. [Google Scholar] [CrossRef]
- Zhang, J.J.; Zhang, D.X.; Chen, J.N.; Pang, L.G.; Meng, D. On the uncertainty principle of neural networks. iScience 2025, 28, 112197. [Google Scholar] [CrossRef] [PubMed]


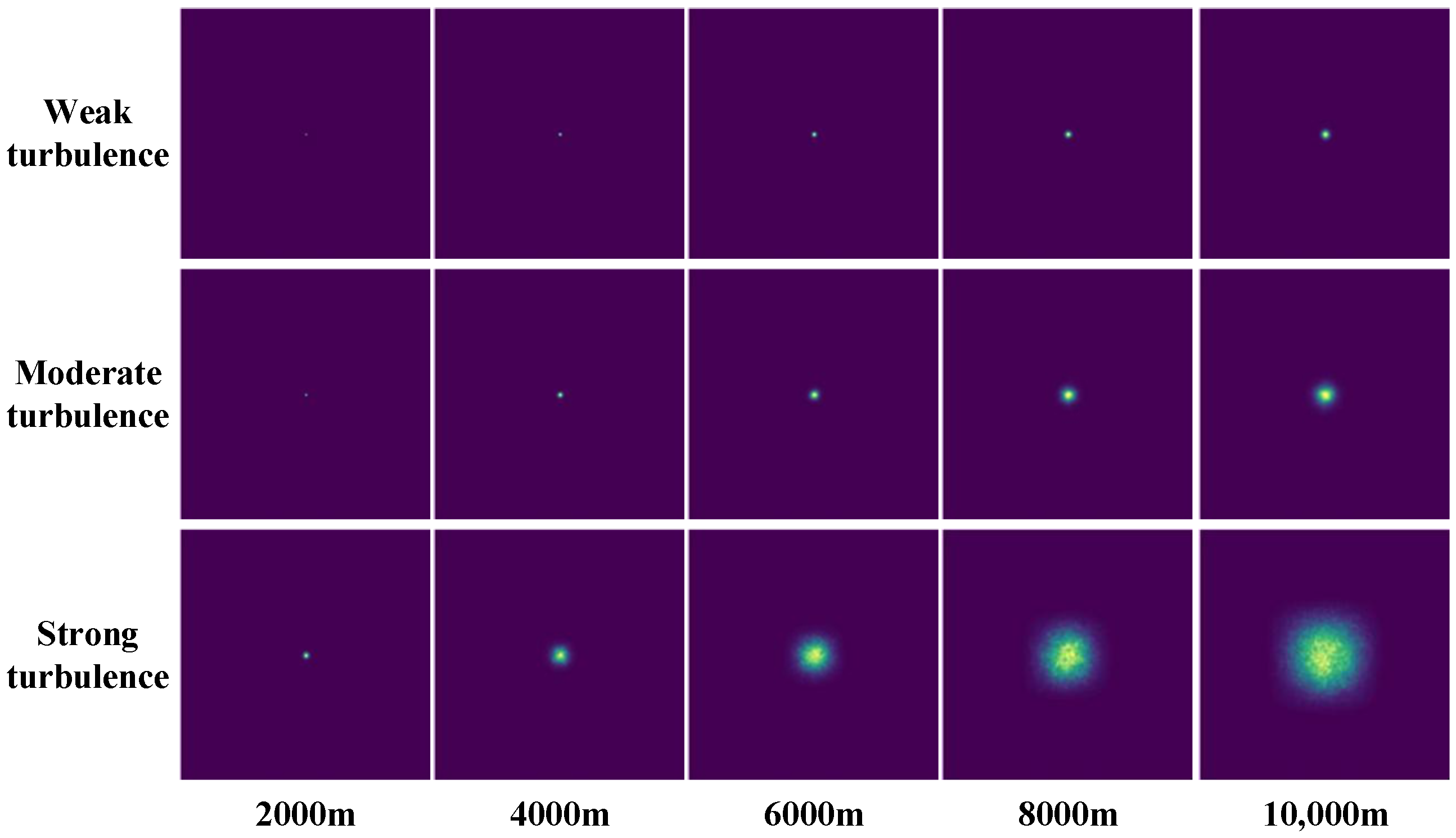
| () | Distance | |||||
|---|---|---|---|---|---|---|
| 2000 m | 4000 m | 6000 m | 8000 m | 10,000 m | ||
| Rytov Variance | 0.01 | 0.04 | 0.08 | 0.14 | 0.2 | |
| 0.1 | 0.38 | 0.81 | 1.37 | 2.06 | ||
| 1.08 | 3.85 | 8.10 | 13.73 | 20.68 | ||
| Fried Parameter (m) | 0.532 | 0.351 | 0.275 | 0.231 | 0.202 | |
| 0.134 | 0.088 | 0.069 | 0.058 | 0.051 | ||
| 0.033 | 0.022 | 0.017 | 0.014 | 0.013 | ||
| () | Value Range * | |
|---|---|---|
| Rytov Variance | 0.001–0.207 | |
| 0.008–2.067 | ||
| 0.085–20.67 | ||
| 0.851–206.7 | ||
| Fried Parameter (m) | 1.222–0.202 | |
| 0.307–0.051 | ||
| 0.077–0.013 | ||
| 0.019–0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhang, J.; Gao, Y.; Du, T. Optical Field-to-Field Translation Under Atmospheric Turbulence: A Conditional GAN Framework with Embedded Turbulence Parameters. Photonics 2025, 12, 339. https://doi.org/10.3390/photonics12040339
Zhang D, Zhang J, Gao Y, Du T. Optical Field-to-Field Translation Under Atmospheric Turbulence: A Conditional GAN Framework with Embedded Turbulence Parameters. Photonics. 2025; 12(4):339. https://doi.org/10.3390/photonics12040339
Chicago/Turabian StyleZhang, Dongxiao, Junjie Zhang, Yinjun Gao, and Taijiao Du. 2025. "Optical Field-to-Field Translation Under Atmospheric Turbulence: A Conditional GAN Framework with Embedded Turbulence Parameters" Photonics 12, no. 4: 339. https://doi.org/10.3390/photonics12040339
APA StyleZhang, D., Zhang, J., Gao, Y., & Du, T. (2025). Optical Field-to-Field Translation Under Atmospheric Turbulence: A Conditional GAN Framework with Embedded Turbulence Parameters. Photonics, 12(4), 339. https://doi.org/10.3390/photonics12040339




