Novel Spectrum Inversion-Based Double-Sideband Modulation with Low Complexity for a Self-Coherent Detection System
Abstract
1. Introduction
2. Principle of the SI-DSB FADD
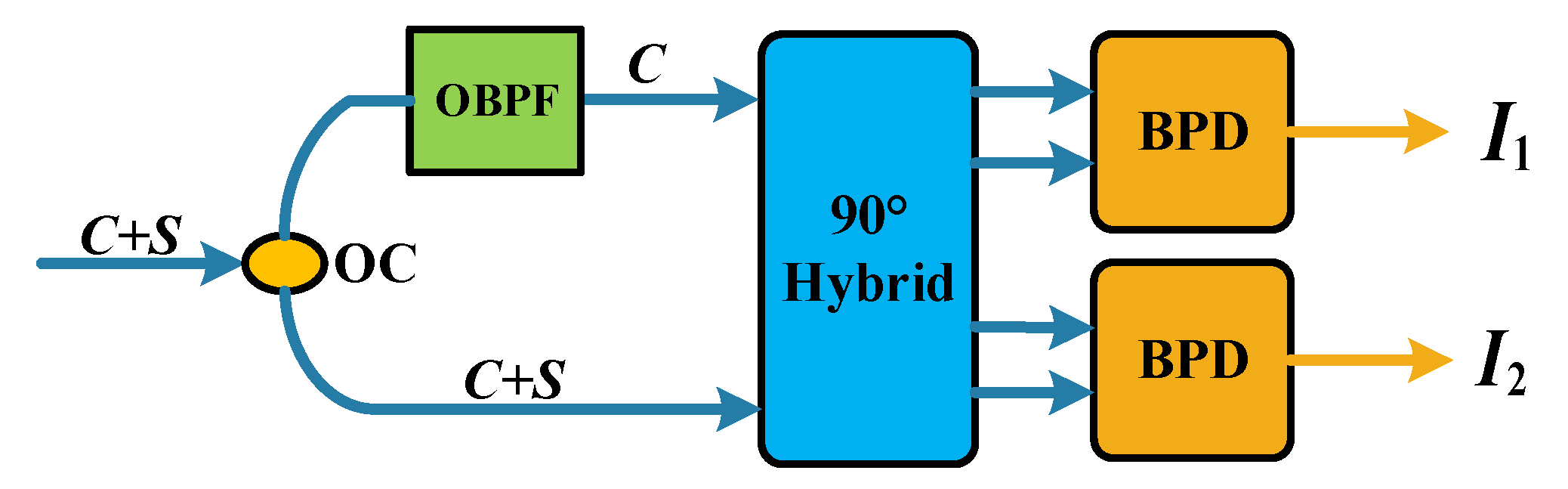
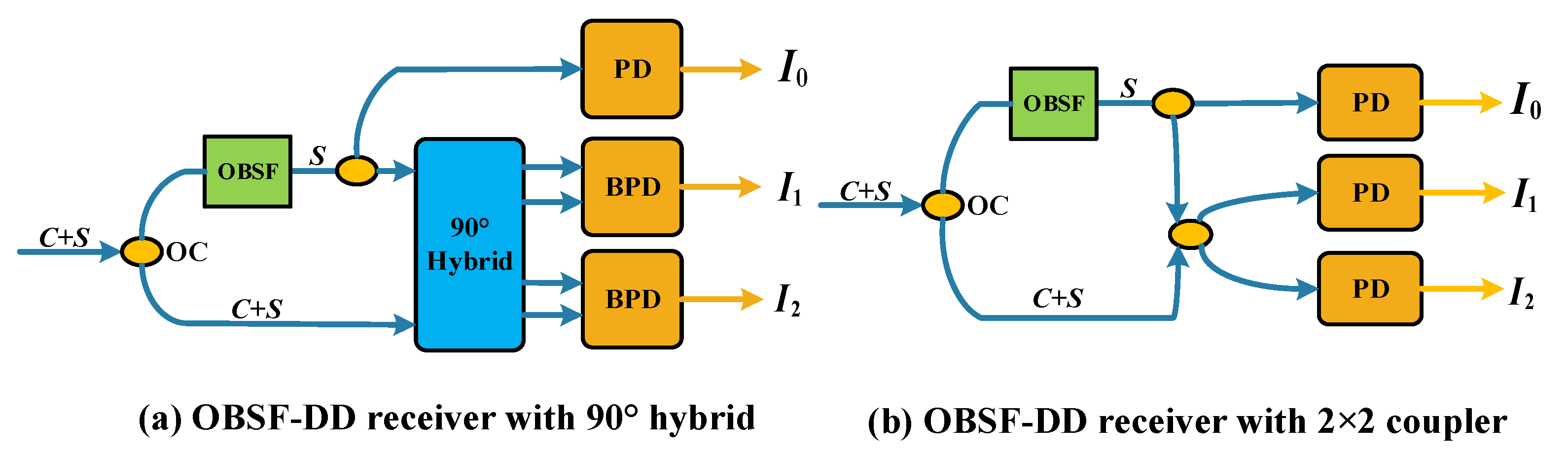
2.1. Structure of the FADD Receiver
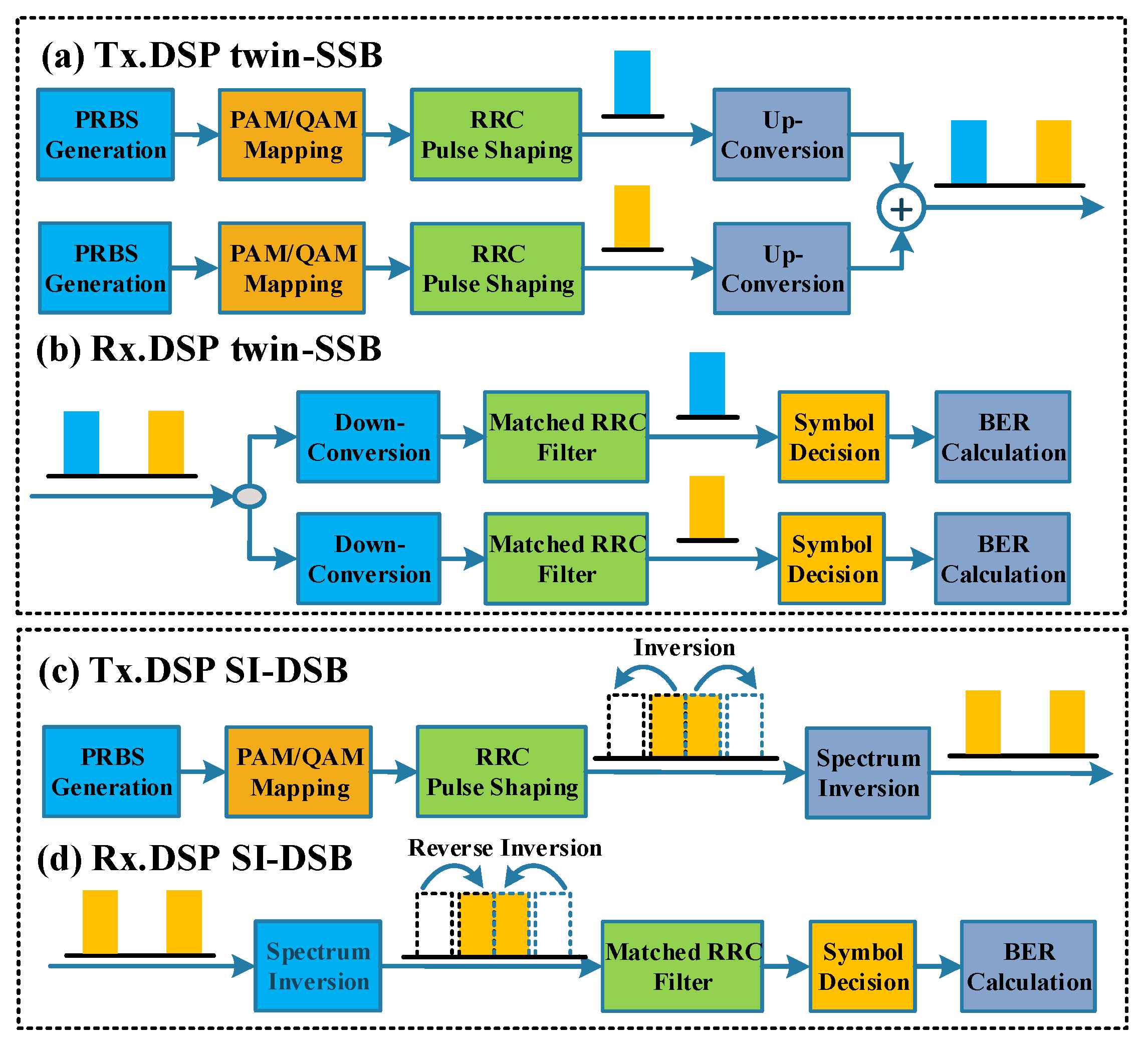
2.2. Principle of the PAM/QAM SI-DSB Modulation Scheme
3. Results and Discussion
3.1. Simulation Setup
3.2. Parameter Optimization of SI-DSB FADD
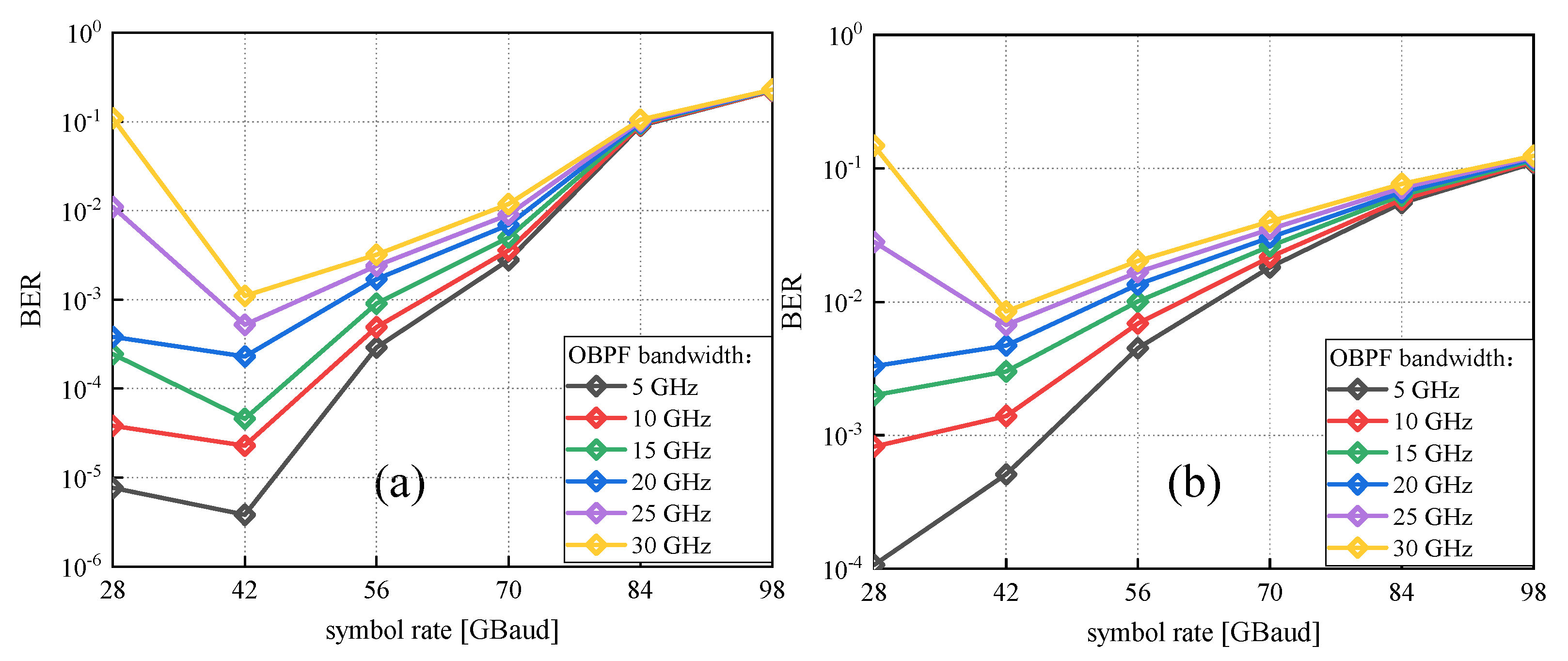
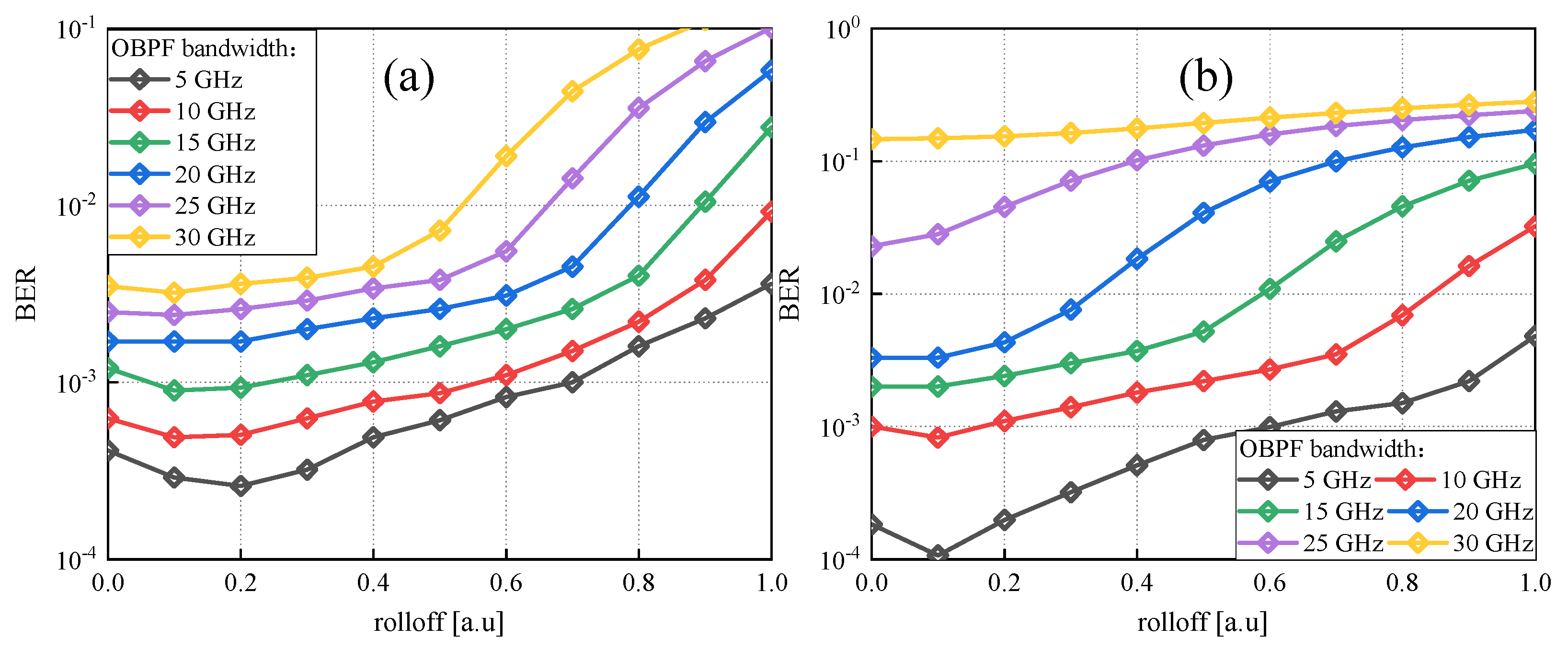
3.2.1. Guard Band of the SI-DSB Modulation
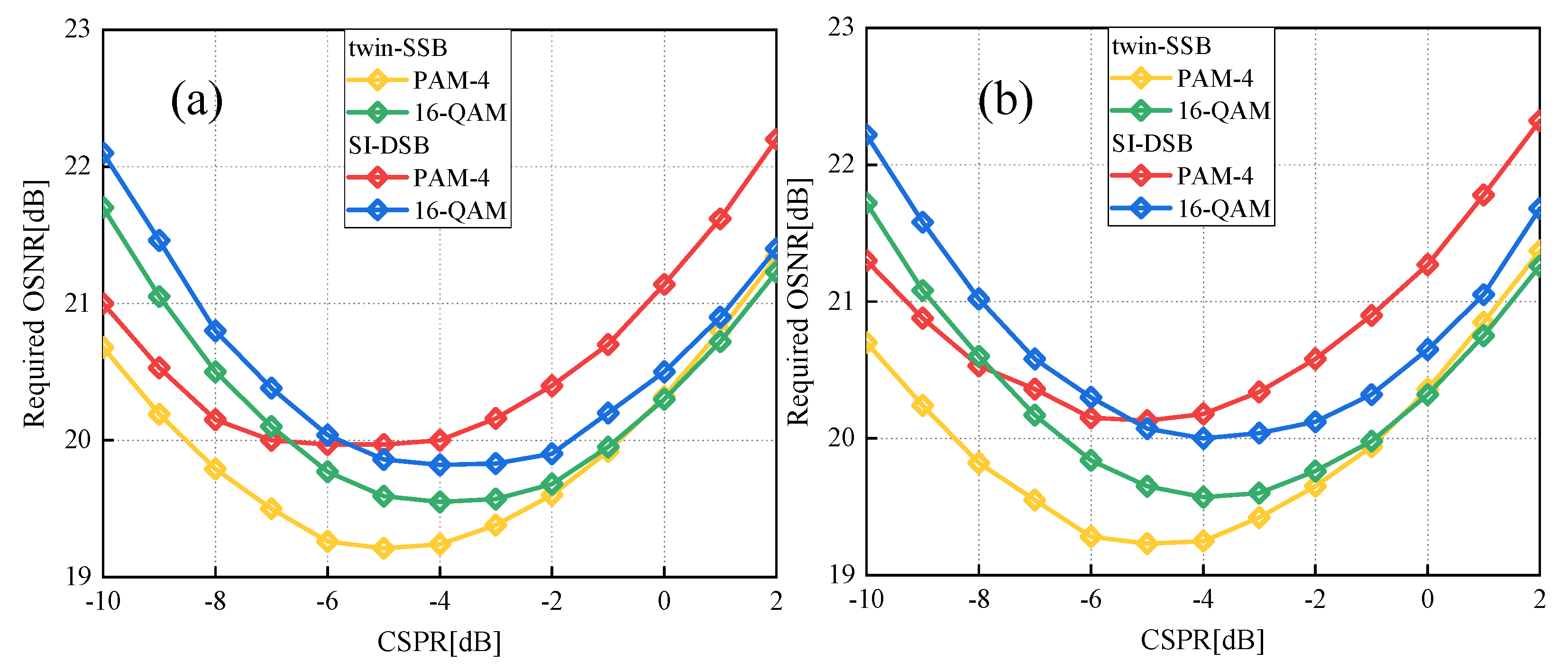
3.2.2. Optimal CSPR
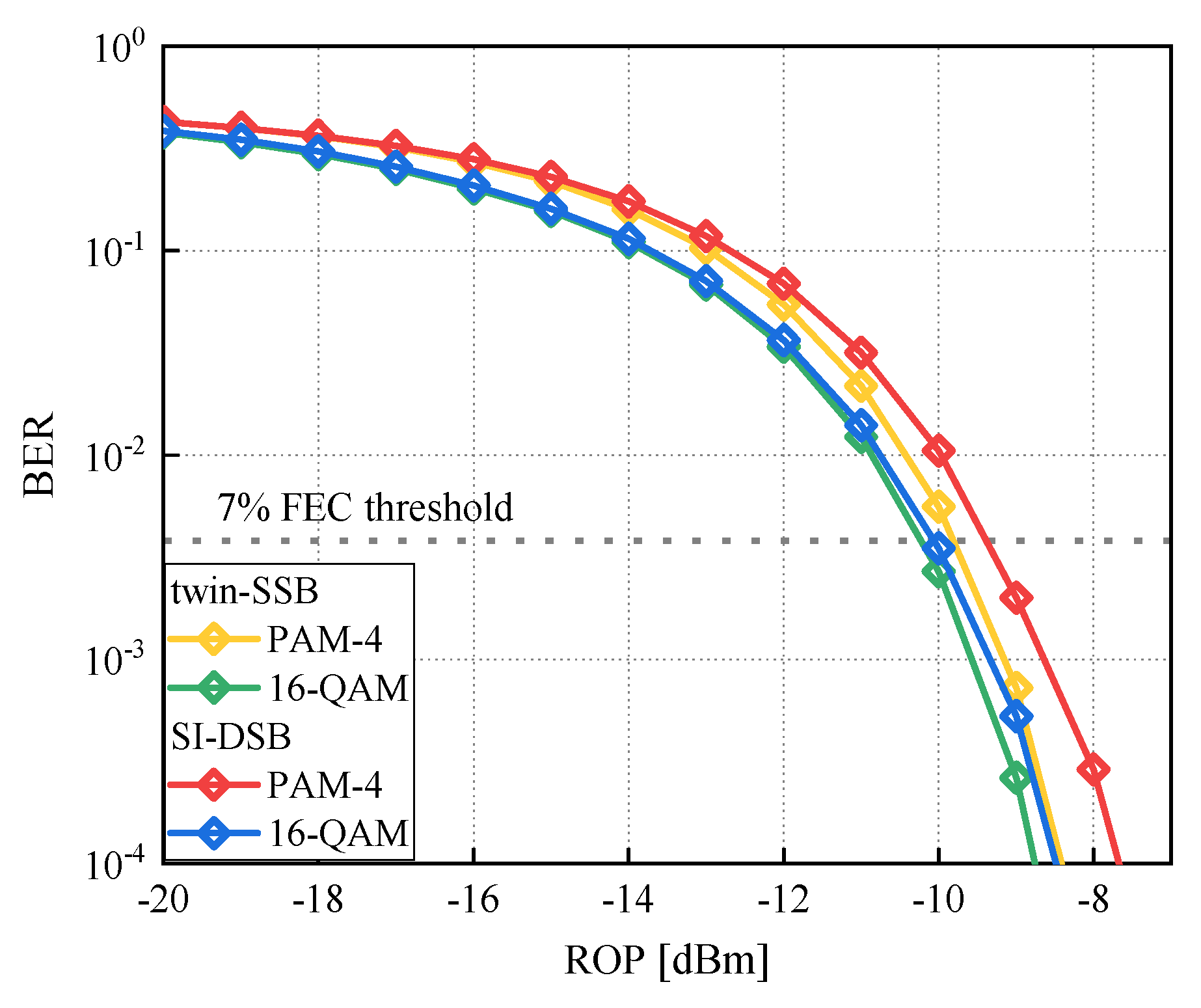
3.3. Comparison with Twin-SSB Modulation Scheme
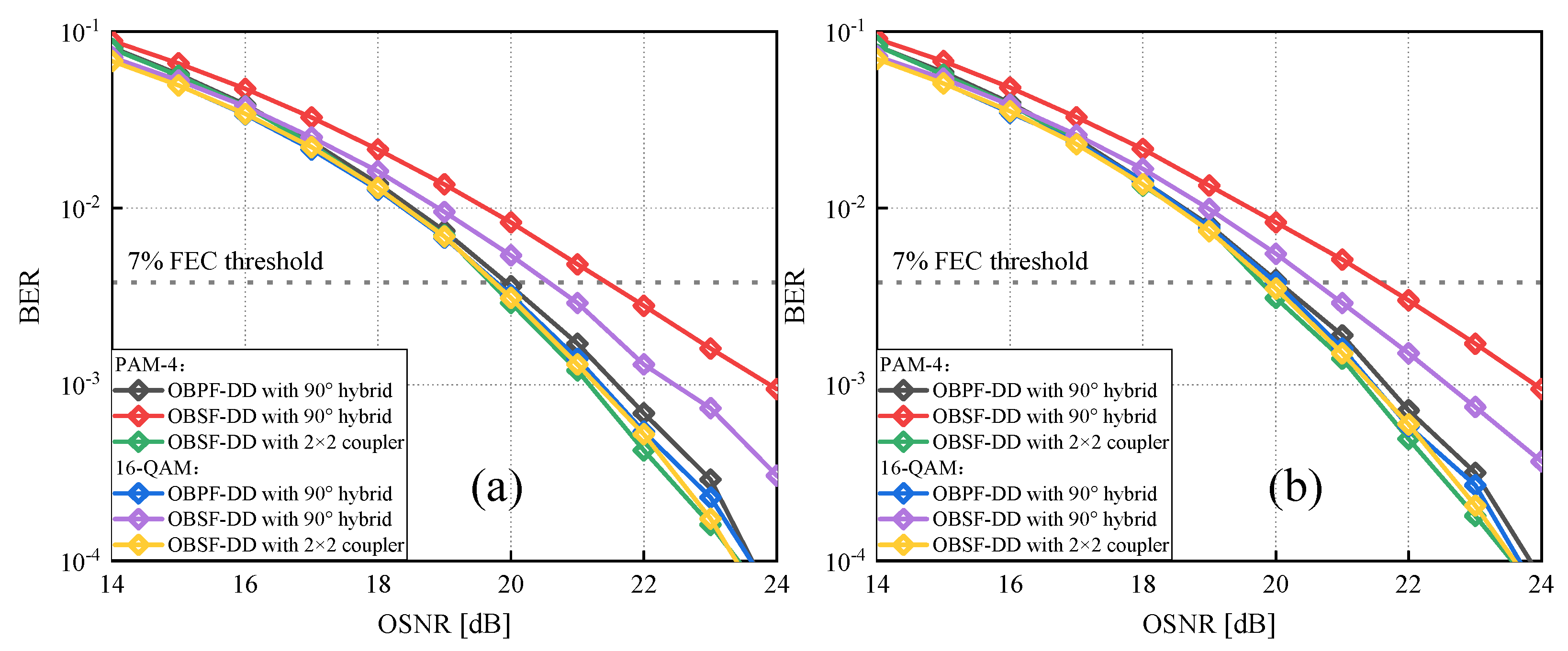
3.4. Performance Evaluation of SI-DSB FADD Systems
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital signal processing for short-reach optical communications: A review of current technologies and future trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Che, D.; Hu, Q.; Shieh, W. Linearization of direct detection optical channels using self-coherent subsystems. J. Light. Technol. 2016, 34, 516–524. [Google Scholar] [CrossRef]
- Lin, J.; Yan, L.; Yi, A.; Pan, Y.; Zhang, B.; Hu, Q.; Pan, W.; Luo, B. Integrated components and solutions for high-speed short-reach data transmission. Photonics 2021, 8, 77. [Google Scholar] [CrossRef]
- Winzer, P.J.; Essiambre, R.-J. Advanced Optical Modulation Formats. Proc. IEEE 2006, 94, 952–985. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Kramers-kronig coherent receiver. Optica 2016, 3, 1220–1227. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Kramers–Kronig receivers. Adv. Opt. Photon. 2019, 11, 480–517. [Google Scholar] [CrossRef]
- Sun, C.; Che, D.; Ji, H.; Shieh, W. Investigation of single-and multi-carrier modulation formats for Kramers–Kronig and SSBI iterative cancellation receivers. Opt. Lett. 2019, 44, 1785–1788. [Google Scholar] [PubMed]
- Le, S.T.; Schuh, K.; Chagnon, M.; Buchali, F.; Dischler, R.; Aref, V.; Buelow, H.; Engenhardt, K.M. 1.72Tb/s virtual-carrier assisted direct-detection transmission over 200 km. J. Light. Technol. 2018, 36, 1347–1353. [Google Scholar] [CrossRef]
- Shieh, W.; Sun, C.; Ji, H. Carrier-assisted differential detection. Light Sci. Appl. 2020, 9, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Ji, T.; Ji, H.; Xu, Z.; Shieh, W. Experimental demonstration of complex-valued DSB signal field recovery via direct detection. IEEE Photon. Technol. Lett. 2020, 32, 585–588. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, L.; Fu, Y.; Hu, W. Symmetric carrier assisted differential detection receiver with low-complexity signal-signal beating interference mitigation. Opt. Express 2020, 28, 19008–19022. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; An, S.; Ji, H.; Li, X.; Shieh, W.; Su, Y. Carrier-assisted differential detection with reduced guard band and high electrical spectral efficiency. Opt. Express 2021, 29, 33502–33511. [Google Scholar] [PubMed]
- Huang, Z.; Li, J.; Yu, X.; He, J.; Zhang, J.; Zhong, K.P.; Qin, Y. Joint signal-to-signal beat interference mitigation for the field recovery of symmetric carrier-assisted differential detection with low carrier-to-signal power ratio. Opt. Express 2024, 32, 18044–18054. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; O’Sullivan, M.; Xing, Z.; Alam, M.; Mousa-Pasandi, M.E.; Plant, D.V. Asymmetric self-coherent detection. Opt. Express 2021, 29, 25412–25427. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhu, Y.; Hu, W. Carrier-assisted phase retrieval. J. Light. Technol. 2022, 40, 5583–5596. [Google Scholar] [CrossRef]
- Qin, P.; Huo, J.; Bai, C. Filter-assisted direct detection-based field recovery scheme for complex-valued double-sideband signals. Opt. Fiber Technol. 2024, 85, 103811. [Google Scholar] [CrossRef]

| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Sample pre-symbol | 2 | Bandwidth of RX | 33 GHz |
| Symbol length | 32,768 | OBPF transfer function | Gaussian |
| Laser center frequency | 193.4 THz | OBPF order | 4 |
| Fiber length | 80 km | OBPF center frequency | 193.4 THz |
| Dispersion | 17 ps/nm/km | PD responsivity | 0.7 A/W |
| Dispersion slope | 0.08 ps/nm2/km | PD thermal noise | 10 pA/Hz1/2 |
| Core area | 80 µm | PD dark current | 3 × 10−9 A |
| Bandwidth of TX | 33 GHz | PD shot noise | on |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, P.; Huo, J.; Bai, H.; Zhang, X.; Tao, J.; Long, K. Novel Spectrum Inversion-Based Double-Sideband Modulation with Low Complexity for a Self-Coherent Detection System. Photonics 2025, 12, 302. https://doi.org/10.3390/photonics12040302
Qin P, Huo J, Bai H, Zhang X, Tao J, Long K. Novel Spectrum Inversion-Based Double-Sideband Modulation with Low Complexity for a Self-Coherent Detection System. Photonics. 2025; 12(4):302. https://doi.org/10.3390/photonics12040302
Chicago/Turabian StyleQin, Peng, Jiahao Huo, Haolin Bai, Xiaoying Zhang, Jianlong Tao, and Keping Long. 2025. "Novel Spectrum Inversion-Based Double-Sideband Modulation with Low Complexity for a Self-Coherent Detection System" Photonics 12, no. 4: 302. https://doi.org/10.3390/photonics12040302
APA StyleQin, P., Huo, J., Bai, H., Zhang, X., Tao, J., & Long, K. (2025). Novel Spectrum Inversion-Based Double-Sideband Modulation with Low Complexity for a Self-Coherent Detection System. Photonics, 12(4), 302. https://doi.org/10.3390/photonics12040302





