Multiplet Network for One-Shot Mixture Raman Spectrum Identification
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
- (1)
- RRUFF Dataset. We utilized data from the RRUFF database (https://rruff.info/, accessed on 16 May 2024) as the source for our training dataset. Developed by Professor Robert Downs at Arizona State University in 2006, this database offers a comprehensive collection of mineral Raman spectra with varying quality. From this database, we selected three datasets, ‘excellent_oriented’, ‘excellent_unoriented’, and ‘unrated_oriented’, comprising 16,998 spectra across 1723 classes. To align with the model’s input requirements, all spectra were interpolated or resampled to a length of 256. The procedure for generating the training spectra was as follows:
- (2)
- Experimental Dataset. The Experimental Dataset included the Raman spectra of 28 common organic and inorganic compounds, such as urea and sodium urate, as well as their mixtures. These spectra were acquired using a self-built transmission Raman spectrometer. The dataset was divided into two parts: (1) the Raman spectra of 28 pure compounds, which served as the candidate spectral library, and (2) the Raman spectra of 9 mixtures, which were used as the test set. All spectra had a resolution of 7 cm−1 and covered a wavenumber range of 200–2000 cm−1. The spectra were acquired using an excitation wavelength of 785 nm with an excitation power of 300 mW. The integration time was adjusted between 1 and 10 s based on the Raman scattering intensity of different materials.
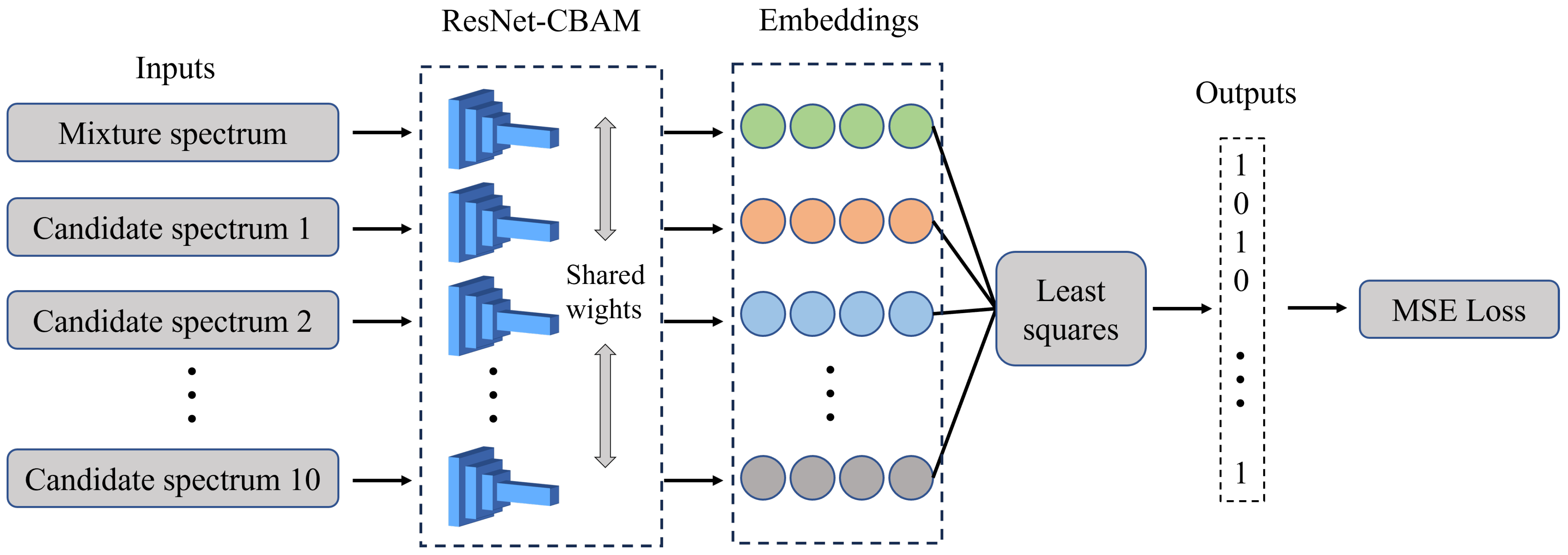
2.2. Multiplet Network
2.2.1. Mathematical Foundations of Mixture Decomposition
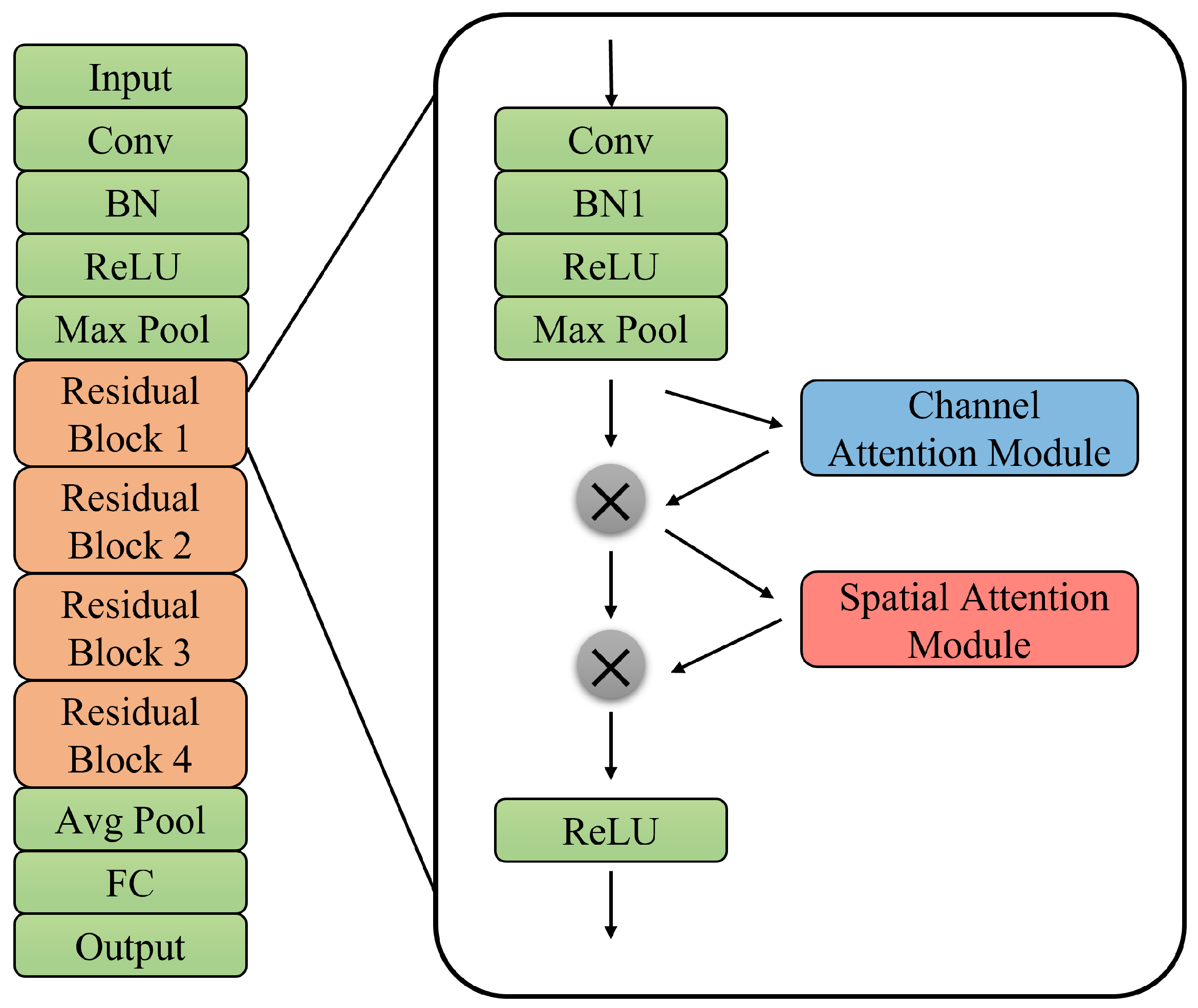
2.2.2. Network Architecture
2.3. Performance Evaluation
3. Results
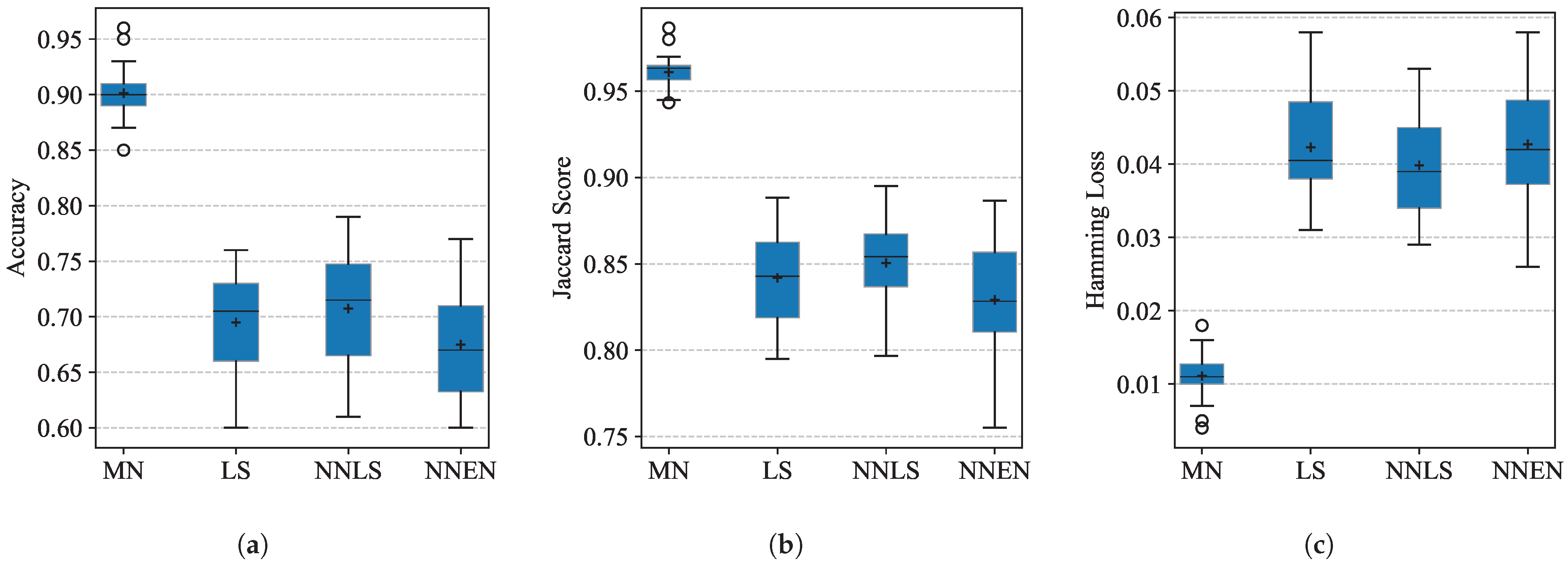
3.1. Performance on the RRUFF Dataset
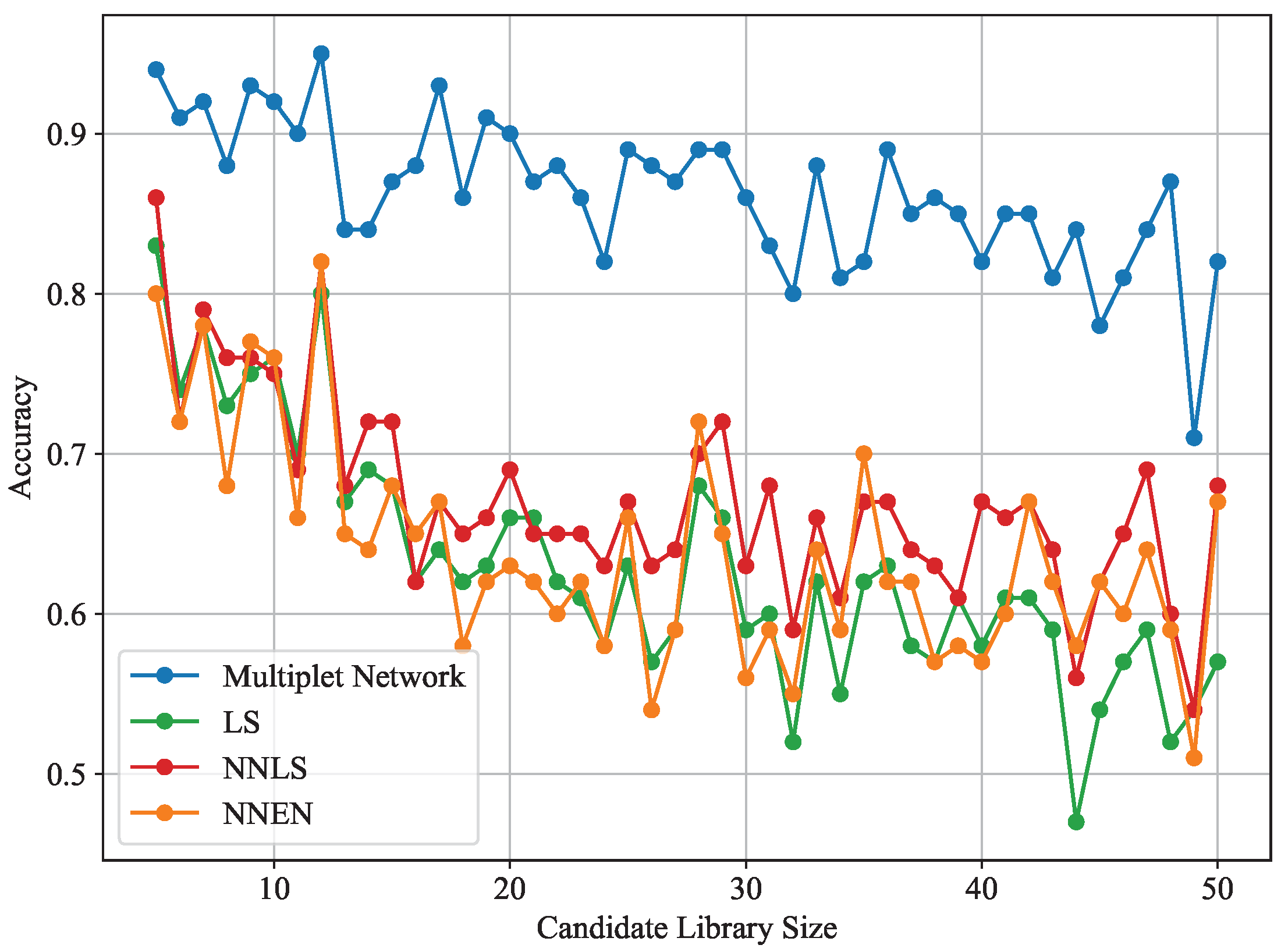
3.2. Impact of Support Set Size
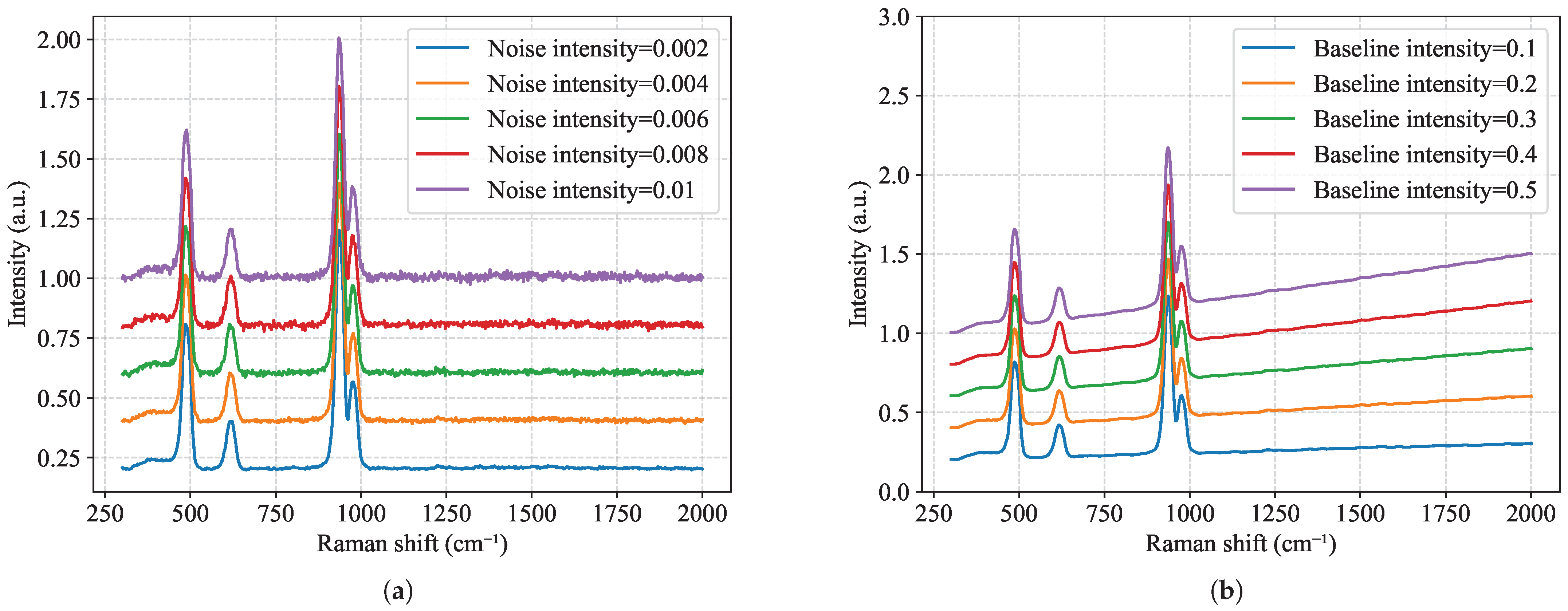
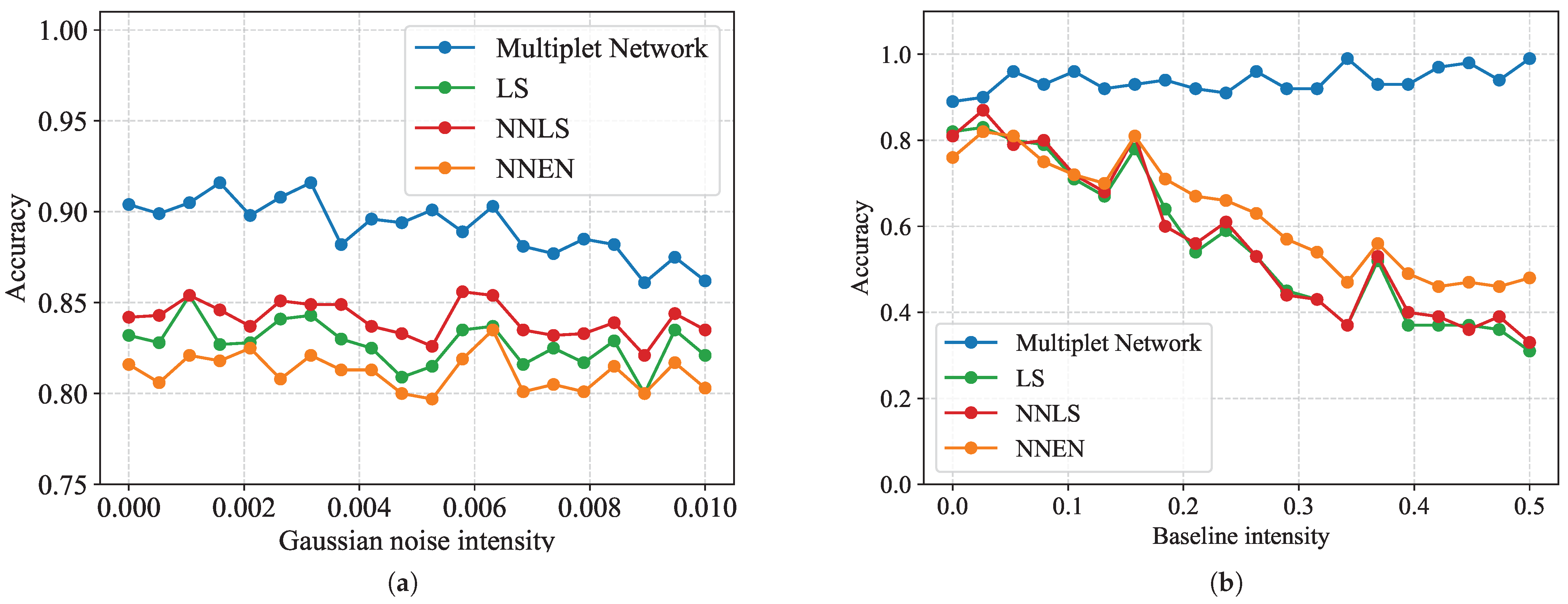
3.3. Robustness to Noise and Baseline Interference
3.4. Performance on Real-World Mixtures
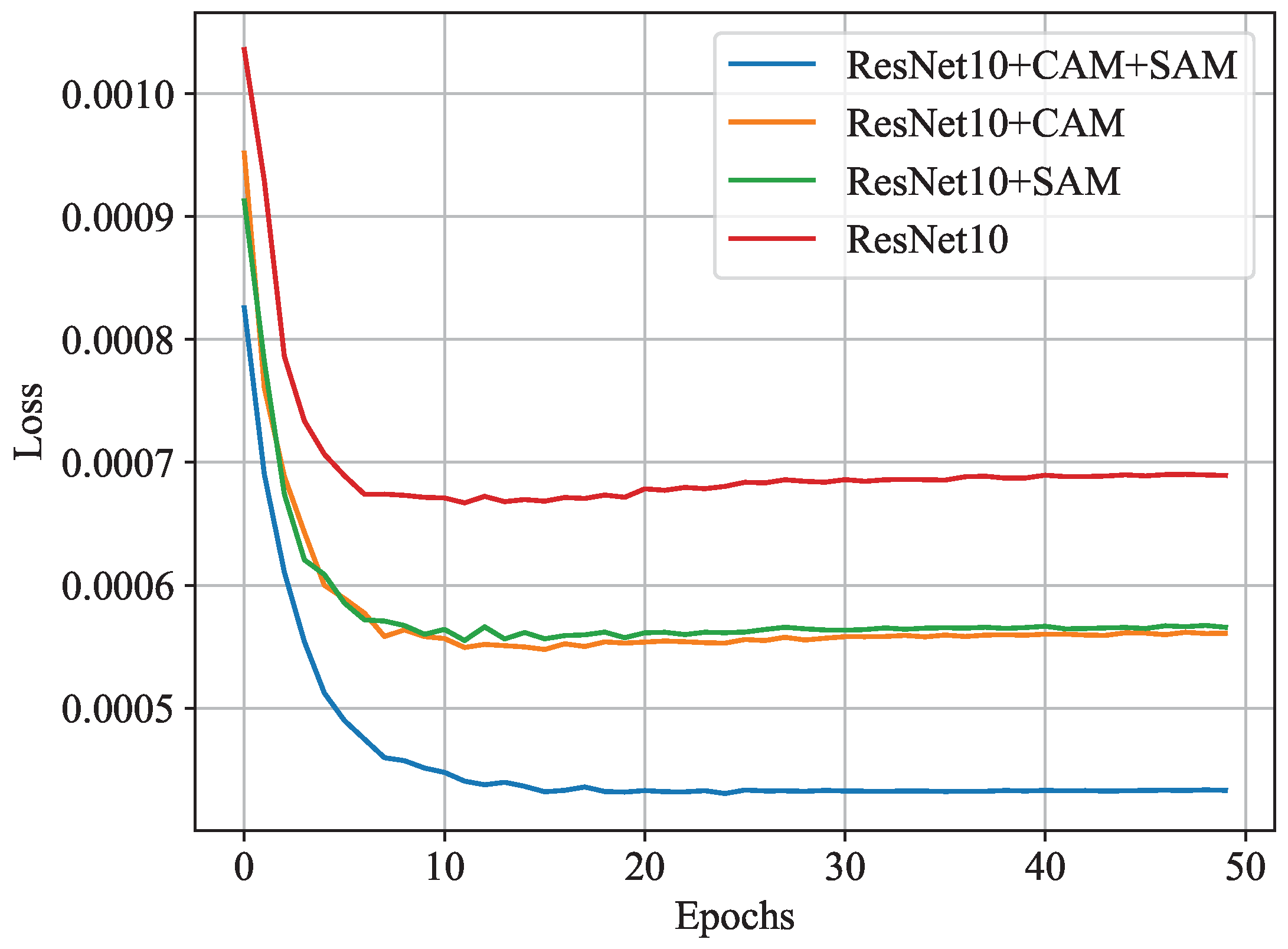
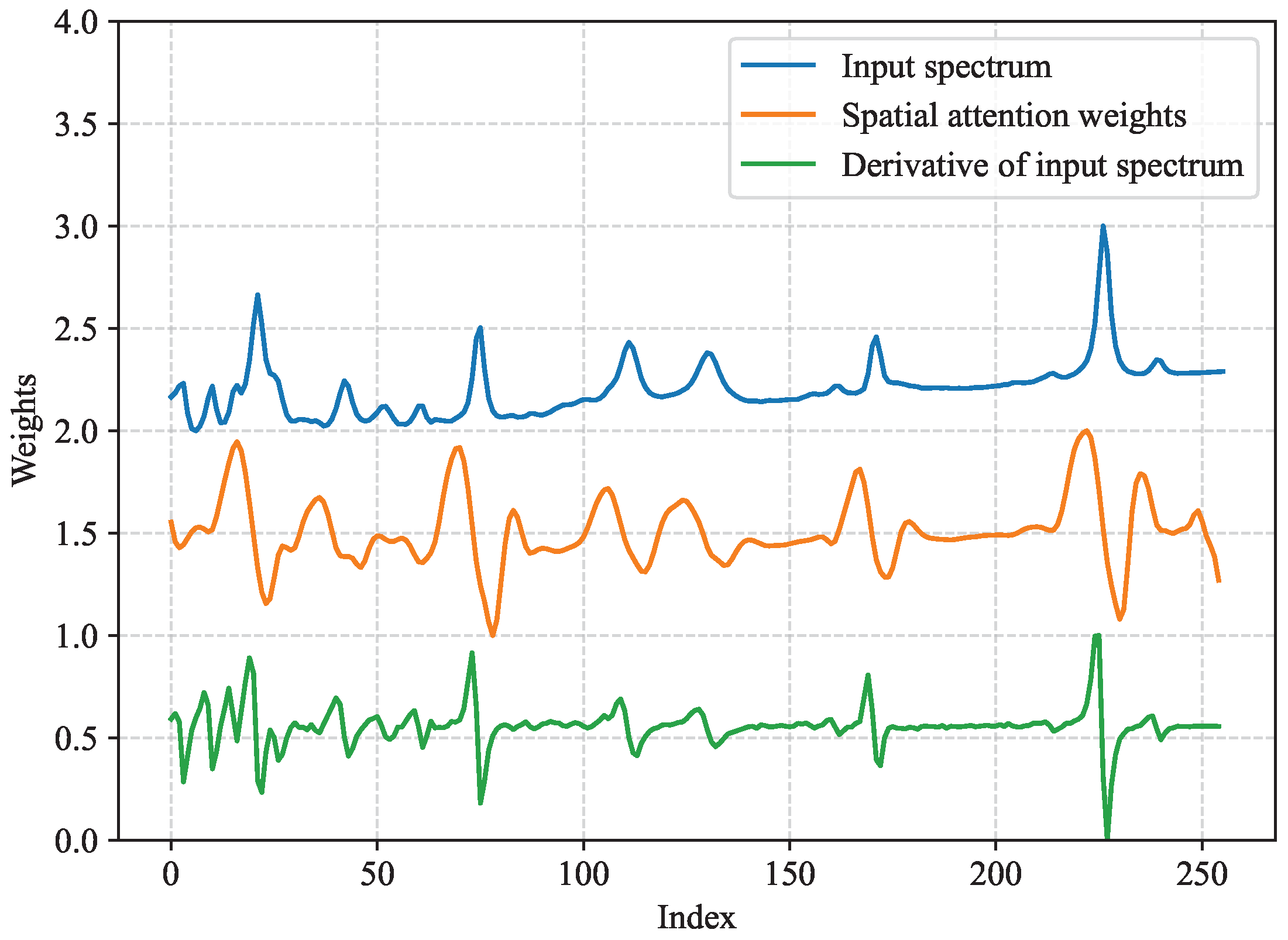
3.5. Effectiveness of Channel and Spatial Attention Modules
4. Discussion
4.1. Advantages of the Proposed Model
4.2. Robustness in Complex Environments
4.3. Practical Applicability
4.4. Comparison with Existing Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNN | Deep Neural Network |
| DeepCID | Deep Learning-Based Component Identification |
| PSNN | Pseudo-Siamese Neural Network |
| MN | Multiplet Network |
| RMSLoss | Root Mean Square Loss |
| LS | Least Squares |
| NNLS | Non-Negative Least Squares |
| NNEN | Non-Negative Elastic Nets |
| ResNet-CBAM | ResNet Integrated with the Convolutional Block Attention Module |
| CAM | Channel Attention Module |
| SAM | Spatial Attention Module |
References
- Ong, T.T.; Blanch, E.W.; Jones, O.A. Surface Enhanced Raman Spectroscopy in environmental analysis, monitoring and assessment. Sci. Total Environ. 2020, 720, 137601. [Google Scholar] [CrossRef] [PubMed]
- Sivaprakasam, V.; Hart, M.B. Surface-enhanced Raman spectroscopy for environmental monitoring of aerosols. ACS Omega 2021, 6, 10150–10159. [Google Scholar] [PubMed]
- Mojica, E.R.; Dai, Z. New Raman spectroscopic methods’ application in forensic science. Talanta Open 2022, 6, 100124. [Google Scholar] [CrossRef]
- Bērziņš, K.; Boyd, B.J. Surface-Enhanced, Low-Frequency Raman Spectroscopy: A Sensitive Screening Tool for Structural Characterization of Pharmaceuticals. Anal. Chem. 2024, 96, 17100–17108. [Google Scholar] [CrossRef]
- Petersen, M.; Yu, Z.; Lu, X. Application of Raman spectroscopic methods in food safety: A review. Biosensors 2021, 11, 187. [Google Scholar] [CrossRef]
- Dong, R.; Wang, J.; Weng, S.; Yuan, H.; Yang, L. Field determination of hazardous chemicals in public security by using a hand-held Raman spectrometer and a deep architecture-search network. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 258, 119871. [Google Scholar]
- Samuel, A.Z.; Mukojima, R.; Horii, S.; Ando, M.; Egashira, S.; Nakashima, T.; Iwatsuki, M.; Takeyama, H. On selecting a suitable spectral matching method for automated analytical applications of Raman spectroscopy. ACS Omega 2021, 6, 2060–2065. [Google Scholar] [CrossRef]
- Carey, C.; Boucher, T.; Mahadevan, S.; Bartholomew, P.; Dyar, M. Machine learning tools formineral recognition and classification from Raman spectroscopy. J. Raman Spectrosc. 2015, 46, 894–903. [Google Scholar] [CrossRef]
- Tan, X.; Chen, X.; Song, S. A computational study of spectral matching algorithms for identifying Raman spectra of polycyclic aromatic hydrocarbons. J. Raman Spectrosc. 2017, 48, 113–118. [Google Scholar] [CrossRef]
- Liu, J.; Osadchy, M.; Ashton, L.; Foster, M.; Solomon, C.J.; Gibson, S.J. Deep convolutional neural networks for Raman spectrum recognition: A unified solution. Analyst 2017, 142, 4067–4074. [Google Scholar] [CrossRef]
- Hu, J.; Zou, Y.; Sun, B.; Yu, X.; Shang, Z.; Huang, J.; Jin, S.; Liang, P. Raman spectrum classification based on transfer learning by a convolutional neural network: Application to pesticide detection. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 265, 120366. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Pan, X.; Yu, H.; Hua, S.; Wang, D.; Chen, D.Z.; Zhou, M.; Wu, J. A deep learning approach for detecting colorectal cancer via Raman spectra. BME Front. 2022, 2022, 9872028. [Google Scholar] [CrossRef] [PubMed]
- Vignesh, T.; Shanmukh, S.; Yarra, M.; Botonjic-Sehic, E.; Grassi, J.; Boudries, H.; Dasaratha, S. Estimating probabilistic confidence for mixture components identified using a spectral search algorithm. Appl. Spectrosc. 2012, 66, 334–340. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Chen, X.Q.; Lu, H.M.; Liang, Y.Z.; Fan, W.; Xu, D.; Zhou, J.; Ye, F.; Yang, Z.Y. Mixture analysis using reverse searching and non-negative least squares. Chemom. Intell. Lab. Syst. 2014, 137, 10–20. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, C.; Zhao, Z.; Zhu, Q.; Huang, M. Performance Improvement of Handheld Raman Spectrometer for Mixture Components Identification Using Fuzzy Membership and Sparse Non-Negative Least Squares. Appl. Spectrosc. 2022, 76, 548–558. [Google Scholar] [PubMed]
- Zeng, H.T.; Hou, M.H.; Ni, Y.P.; Fang, Z.; Fan, X.Q.; Lu, H.M.; Zhang, Z.M. Mixture analysis using non-negative elastic net for Raman spectroscopy. J. Chemom. 2020, 34, e3293. [Google Scholar]
- Van de Sompel, D.; Garai, E.; Zavaleta, C.; Gambhir, S.S. A hybrid least squares and principal component analysis algorithm for Raman spectroscopy. PLoS ONE 2012, 7, e38850. [Google Scholar]
- Fan, X.; Ming, W.; Zeng, H.; Zhang, Z.; Lu, H. Deep learning-based component identification for the Raman spectra of mixtures. Analyst 2019, 144, 1789–1798. [Google Scholar]
- Fan, X.; Wang, Y.; Yu, C.; Lv, Y.; Zhang, H.; Yang, Q.; Wen, M.; Lu, H.; Zhang, Z. A universal and accurate method for easily identifying components in Raman spectroscopy based on deep learning. Anal. Chem. 2023, 95, 4863–4870. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. Adv. Neural Inf. Process. Syst. 1993, 7, 25. [Google Scholar]
- Zhao, Z.; Liu, Z.; Ji, M.; Zhao, X.; Zhu, Q.; Huang, M. ConInceDeep: A novel deep learning method for component identification of mixture based on Raman spectroscopy. Chemom. Intell. Lab. Syst. 2023, 234, 104757. [Google Scholar] [CrossRef]
- Koyun, O.C.; Keser, R.K.; Şahin, S.O.; Bulut, D.; Yorulmaz, M.; Yücesoy, V.; Toreyin, B.U. RamanFormer: A Transformer-Based Quantification Approach for Raman Mixture Components. ACS Omega 2024, 9, 23241–23251. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Pipitsunthonsan, P.; Daengngam, C.; Channumsin, S.; Sreesawet, S.; Chongcheawchamnan, M. Identification of complex mixtures for Raman spectroscopy using a novel scheme based on a new multi-label deep neural network. IEEE Sensors J. 2021, 21, 10834–10843. [Google Scholar] [CrossRef]
- Liang, J.; Mu, T. Recognition of big data mixed Raman spectra based on deep learning with smartphone as Raman analyzer. Electrophoresis 2020, 41, 1413–1417. [Google Scholar] [CrossRef]
- Lafuente, B.; Downs, R.T.; Yang, H.; Stone, N.; Armbruster, T.; Danisi, R.M. The power of databases: The RRUFF project. Highlights Mineral. Crystallogr. 2015, 1, 25. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep metric learning using triplet network. In Proceedings of the Similarity-Based Pattern Recognition: Third International Workshop, SIMBAD 2015, Copenhagen, Denmark, 12–14 October 2015; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2015; pp. 84–92. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, arXiv:1912.01703. [Google Scholar]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaudoise Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Jaccard, P. The distribution of the flora in the alpine zone. 1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Hamming, R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]

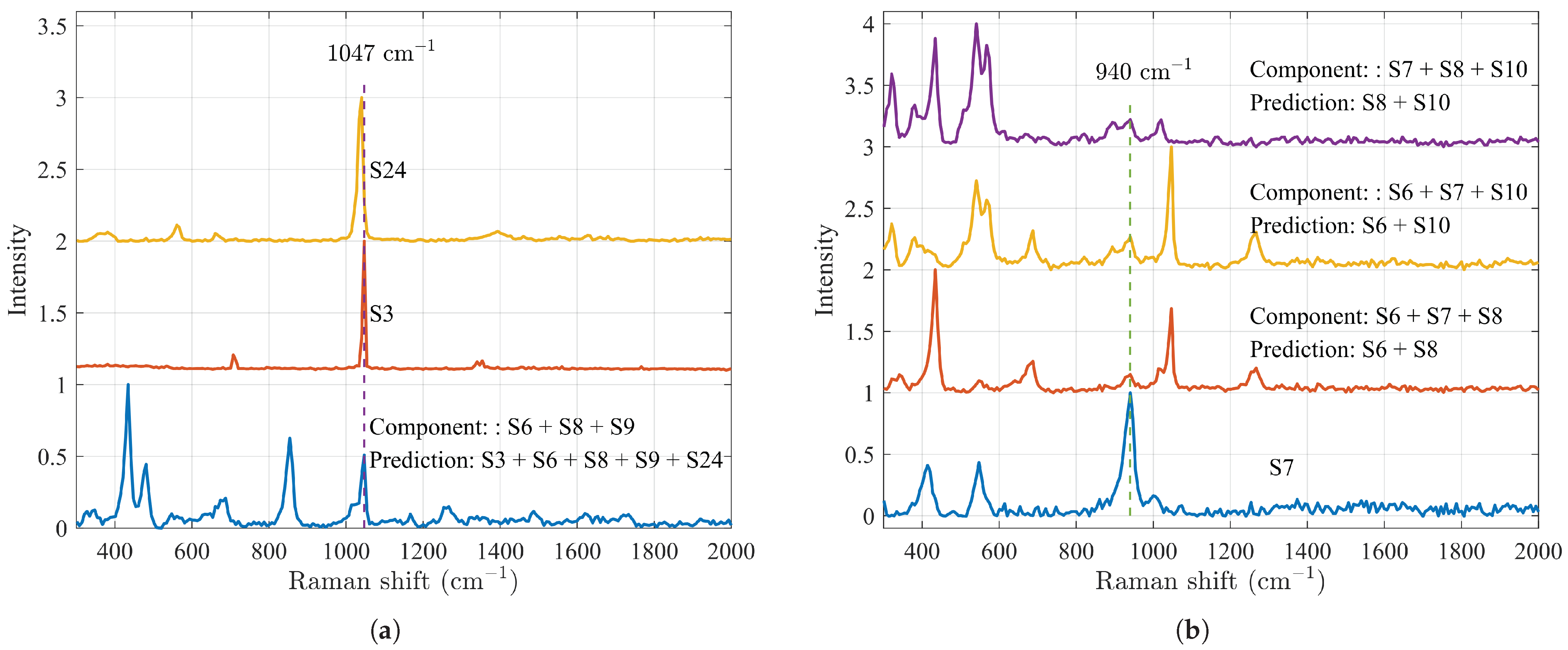
| True Components | Predicted Components | Confidence | Jaccard Score |
|---|---|---|---|
| S1, S3, S5 | S1, S5 | [0.89, 0.67] | 0.67 |
| S1, S3 | S1, S3 | [0.69, 0.75] | 1.00 |
| S2, S5 | S2, S5 | [0.84, 0.56] | 1.00 |
| S4, S5 | S4, S5 | [0.87, 0.88] | 1.00 |
| S1, S5 | S1, S5 | [0.94, 0.66] | 1.00 |
| S6, S7, S8 | S6, S8 | [0.69, 1.07] | 0.67 |
| S6, S7, S10 | S6, S10 | [0.89, 0.86] | 0.67 |
| S6, S8, S9 | S3, S6, S8, S9, S24 | [0.45, 0.59, 0.85, 0.85, 0.44] | 0.6 |
| S7, S8, S10 | S8, S10 | [0.92, 1.06] | 0.67 |
| Mean Jaccard Score: | 0.81 | ||
| Model | Accuracy | Loss |
|---|---|---|
| ResNet10 | 0.77 | |
| ResNet10 + CAM | 0.82 | |
| ResNet10 + SAM | 0.82 | |
| ResNet10 + CAM + SAM (ResNet-CBMA) | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhang, P.; Zhu, X.; Wang, H.; Ren, W.; Jin, C.; Zhao, W. Multiplet Network for One-Shot Mixture Raman Spectrum Identification. Photonics 2025, 12, 295. https://doi.org/10.3390/photonics12040295
Wang B, Zhang P, Zhu X, Wang H, Ren W, Jin C, Zhao W. Multiplet Network for One-Shot Mixture Raman Spectrum Identification. Photonics. 2025; 12(4):295. https://doi.org/10.3390/photonics12040295
Chicago/Turabian StyleWang, Bo, Pu Zhang, Xiangping Zhu, Hua Wang, Wenzhen Ren, Chuan Jin, and Wei Zhao. 2025. "Multiplet Network for One-Shot Mixture Raman Spectrum Identification" Photonics 12, no. 4: 295. https://doi.org/10.3390/photonics12040295
APA StyleWang, B., Zhang, P., Zhu, X., Wang, H., Ren, W., Jin, C., & Zhao, W. (2025). Multiplet Network for One-Shot Mixture Raman Spectrum Identification. Photonics, 12(4), 295. https://doi.org/10.3390/photonics12040295





