Bit Error Rate of Multi-Gaussian Correlated Asymmetric Bessel Beam Through Turbulent Ocean

Abstract

We investigate the underwater propagation of multi-Gaussian correlated asymmetric Bessel beam with partial coherence in the condition of quadrature amplitude modulation. The oceanic turbulence optical power spectrum is used to characterize turbulence effects under variable temperature and salinity. Based on the derivation of orbital angular momentum mode distribution, the theoretical model of bit error rate (BER) is constructed. Numerical analyses show that the low-temperature oceanic channel is more beneficial to BER reduction than the low-salinity channel. Due to the better resistance to turbulence, low-order modulation is superior in BER performance. As for beam optimization, the increments in wavelength and source coherence width, or the decrements of topological charge and asymmetry factor, help to obtain a lower BER. The research is instructive for the construction of underwater transmission links based on vortex beams.

1. Introduction

Compared to traditional acoustic communication, underwater wireless optical communication has advantages of high data bit rate, large information capacity, high confidentiality, and low energy consumption [1]. The research on the transmission characteristics of beam carriers in the ocean has been a popular topic in recent years. To describe the effects of oceanic turbulence on beam propagation, several power spectra of seawater refractive index fluctuation were proposed. Nikishov et al. developed the turbulence power spectrum assuming that seawater was stably stratified while Li et al. considered the unstable stratification [2,3]. Nevertheless, these spectra are only applicable to fixed seawater temperature and salinity. To quantify the dependence of oceanic turbulence on temperature and salinity concentration, Yao et al. established the oceanic turbulence optical power spectrum (OTOPS) [4]. This spectrum is applicable to all natural waters with an average temperature range of 0~30 °C and salinity concentration range of 0~40 ppt.

Vortex beams have great potential for underwater communication. As one typical feature of vortex beams, orbital angular momentum (OAM) is characterized by its topological charge, whose modulus and sign can be measured using interference or diffraction methods [5,6,7]. The multiplexing of OAM modes with different topological charges is able to enhance channel capacity [8]. Bessel beams are one kind of diffraction-resistant vortex beams, which are suitable information carriers due to their self-healing property [9]. Wang et al. experimentally demonstrated that the Bessel–Gaussian beam had a lower bit error rate for underwater communication than the Gaussian beam [10]. Zhou et al. reported the generation of caustic structured light based on Bessel superposition, which could be applied in communication because the curved trajectory enhanced the robustness of signal [11].

Since coherence is an important property of light field, its impacts on beam propagation attract much research interest [12,13]. As for partially coherent beams, source coherence is usually characterized by the correlation function in its cross-spectral density. Compared with the common correlation function of the Gaussian Schell model, the multi-Gaussian Schell model has an additional parameter of beam index in addition to source coherence width, which offers a way to adjust the far-field intensity profile [14]. By introducing the correlation factor of multi-Schell mode, Zhu et al. proposed the multi-modified Bessel–Gaussian Schell beam, which had flatter intensity distribution in the far field [15]. Liu et al. investigated the propagation of the partially coherent anomalous hollow beam generated by the multi-Gaussian Schell model source in oceanic turbulence, and elaborated the evolution characteristics of its spectral density distributions [16]. Wang et al. further analyzed the detection probability and channel capacity of the multi-Gaussian correlated Hankel–Bessel beam in oceanic turbulence [17].

In contrast with the direct light field transmission from beam source to receiver, signal modulation regulates the beam characteristics such as amplitude and phase by adopting appropriate modulation strategies, which can enhance the ability of vortex beams to resist interference and improve spectral efficiency [18]. On-off keying (OOK) is a commonly used amplitude modulation technique, which controls the presence or absence of beam carriers to achieve amplitude changes, thereby representing two different signal states. The two different states distinguished by amplitude are used to carry binary information in signal transmission. Although it is easy to implement in terms of hardware, it exhibits limitations on frequency range and transmission distance [19]. Binary phase shift keying is a phase modulation technique with two different phase states. By mapping the phase states, binary information is carried by phase states during signal transmission. The significant difference between the two phase states makes the distinction relatively easy even under a certain degree of noise interference. But it is unsuitable for high-speed communication due to the limited bandwidth utilization [20]. Quadrature amplitude modulation (QAM) is an efficient digital modulation technique, which combines the advantages of amplitude modulation and phase modulation. Through different combinations of amplitude and phase, it can modulate multiple bits simultaneously. This not only enhances the flexibility of signal transmission, but also significantly increases the information capacity available [21]. Zhu et al. demonstrated the higher received power and lower BER of the quasi-ring Airy vortex beam in atmospheric turbulence when 16-QAM discrete multi-tone signals were utilized [22].

Based on the investigations on traditional circular symmetric beams above, asymmetric vortex beams are developed gradually, such as the asymmetric Laguerre–Gaussian beam, the asymmetric Bessel–Gaussian beam, and the Pearcey beam [23,24,25,26,27]. As one typical asymmetric vortex beam, the asymmetric Bessel–Gaussian beam can have integral or fractional orbital angular momentum and diverse transverse intensity patterns by changing the asymmetry factor [23]. In this way, the adjustment of the beam field becomes more flexible. Kotlyar et al. demonstrated the generation of the asymmetric Bessel–Gaussian beam and its field distribution in free space [28]. Yu et al. analyzed the channel capacity of the asymmetric Bessel–Gaussian beam transmitted in turbulent atmosphere [29]. Although source coherence and signal modulation are both important factors affecting beam propagation performance, relevant investigations on the asymmetric Bessel–Gaussian beam have not been reported.

As a generalized extension of the common Bessel–Gaussian beam by considering source coherence and asymmetry simultaneously, the multi-Gaussian correlated asymmetric Bessel (MGCAB) beam provides more flexibility for field adjustment and application. Despite the fact that some research progress has been made on the propagation characteristics and field regulations of several multi-Gaussian correlated beams mentioned above, the discussions on BER under signal modulation are relatively scarce. Therefore, exploring the BER characteristics of the MGCAB beam can help to enrich the investigations on underwater communication using vortex beams. This paper combines the factors of source coherence, asymmetry, and modulation strategy together and explores their effects on signal transmission, which is expected to provide a theoretical basis for optimizing optical communication systems in turbulent ocean environments.

In this paper, the propagation of the MGCAB beam with partial coherence is investigated under modulation of QAM. The spectrum of OTOPS is adopted to characterize oceanic turbulence, which quantifies the influences of ocean temperature and salinity concentration on turbulence. By using Rytov approximation and spiral harmonic decomposition, we derive the expressions of signal reception probability and then BER of the MGCAB beam. Based on the established theoretical model, numerical simulations are conducted in different oceanic turbulence conditions. The influences of signal modulation and beam features on BER are analyzed, from which some instructive conclusions are given.

2. Theoretical Analysis

In the cylindrical coordinate system, the complex amplitude of asymmetric Bessel–Gaussian beam at the source plane is expressed as [28]

$$U\left(r,\phi ,0\right)=\exp \left(-{\displaystyle \frac{r^2}{{\omega }_0^2}}\right)\times {\displaystyle \sum _{p=0}^{\infty }\frac{c^p\exp \left(i{l}_0\phi +ip\phi \right)}{p!}{J}_{l_0+p}\left(\alpha r\right)},$$

(1)

where $r$ and $\phi$ represent the polar radius and polar angle, respectively, ${\omega }_0$ is the Gaussian waist radius, $c$ is the asymmetry factor, and $l_0$ is the topological charge of OAM mode. $\alpha =k\sin {\theta }_0$ is the scale factor with ${\theta }_0$ indicating Bessel cone angle, $k=2\pi /\lambda$ is beam wavenumber inverse to wavelength $\lambda$, $p$ is an integer, and $J_{l_0+p}\left(\cdot \right)$ indicates Bessel function of the first kind.

From the view of beam generation, the asymmetric Bessel–Gaussian beam is a fully coherent beam which can be regarded as the combination of Gaussian source with asymmetry Bessel mode. If the Gaussian source is replaced by the multi-Gaussian Schell-model source, the partially coherent MGCAB beam is generated. The multi-Gaussian Schell-model source can be conceptualized as a superposition of finite Gaussian functions, whose form $G(r,r^{\prime },\phi ,{\phi }^{\prime })$ is represented by the correlation factor $g(r,\phi )$ as follows [14]:

$$G\left(r,r^{\prime },\phi ,{\phi }^{\prime }\right)=g\left(r,\phi \right)g^{*}\left(r^{\prime },{\phi }^{\prime }\right)={\displaystyle \frac{1}{C_0}}{\displaystyle \sum _{n=1}^N\left(\begin{array}{c}N\\ n\end{array}\right)\frac{{\left(-1\right)}^{n-1}}{n}}\exp \left[{\displaystyle \frac{2r{r}^{\prime }\cos \left(\phi -{\phi }^{\prime }\right)-r^2-{r^{\prime }}^2}{2n{\sigma }^2}}\right],$$

(2)

where $C_0={\displaystyle {\sum }_{n=1}^N\left(\begin{array}{c}N\\ n\end{array}\right)\frac{{(-1)}^{n-1}}{n}}$ is the normalization factor, $\left(\begin{array}{c}N\\ n\end{array}\right)$ is the binomial coefficient, $N$ is beam index, and $\sigma$ is the source coherence width. In the case of $N=1$, the multi-Gaussian Schell-model degenerates into the common Gaussian Schell-model. So the complex amplitude of the MGCAB beam at the source plane can be expressed as

$$E\left(r,\phi ,0\right)=U\left(r,\phi ,0\right)g\left(r,\phi \right).$$

(3)

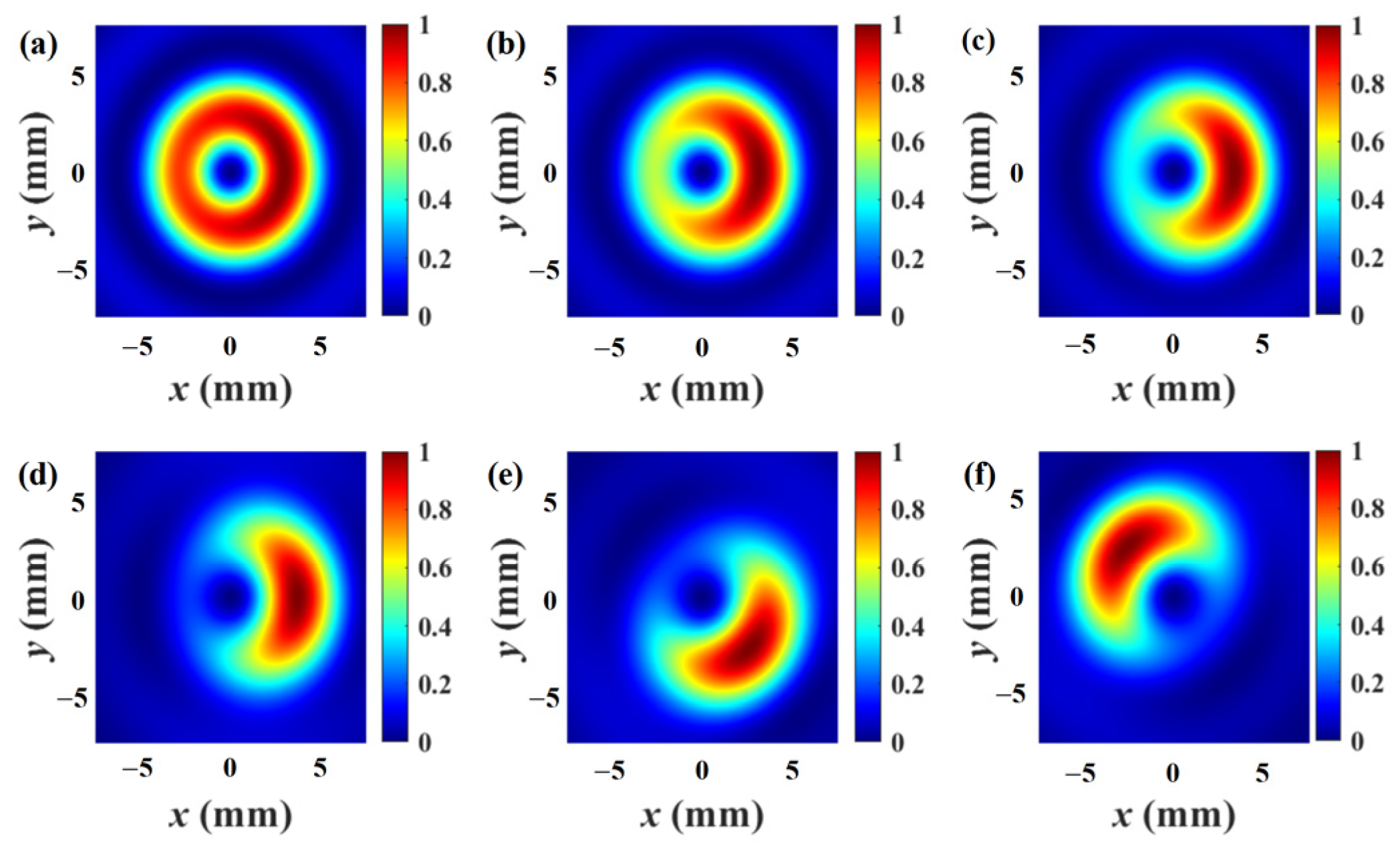
Figure 1 illustrates the corresponding spectral density distributions of the MGCAB beam under different asymmetry factors $c$. In contrast with the symmetric case (i.e., multi-Gaussian correlated Bessel beam) corresponding to $c=0$, the transverse spectral density distribution of the MGCAB beam has higher asymmetry when $c$ increases. The peak position of the transverse spectral density can also be altered by adjusting $c$.

When MGCAB beam propagates in oceanic turbulence, the fluctuation in the seawater refractive index brings wavefront distortion to the beam. Based on Rytov approximation theory, the disturbed complex amplitude $E\left(r,\phi ,z\right)$ of the MGCAB beam is expressed as [30]

$$E\left(r,\phi ,z\right)=U\left(r,\phi ,z\right)g\left(r,\phi \right)\exp \left[\psi \left(r,\phi ,z\right)\right],$$

$$U\left(r,\phi ,z\right)={\displaystyle \frac{1}{q}}\exp \left(ikz-{\displaystyle \frac{i{\alpha }^{2}z}{2kq}}-{\displaystyle \frac{r^2}{q{\omega }_0^2}}\right)\times {\displaystyle \sum _{p=0}^{\infty }\frac{c^p\exp \left(i{l}_0\phi +ip\phi \right)}{p!}{J}_{l_0+p}\left(\frac{\alpha r}{q}\right)},$$

(4)

where $U\left(r,\phi ,z\right)$ represents the complex amplitude of the asymmetric Bessel–Gaussian beam at propagation distance $z$ and $\psi \left(r,\phi ,z\right)$ is the turbulence-induced phase perturbations. The term $q=1+iz/z_0$ is related to the Rayleigh range $z_0=k{\omega }_0^2/2$. As a result, partial energy of the transmitted OAM signal mode transfers to adjacent modes and modal crosstalk happens. The received mode distribution can be obtained by using spiral harmonic decomposition, so Equation (4) is rewritten as [31]

$$E\left(r,\phi ,z\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\displaystyle \sum _l{a}_l\left(r,z\right)}\exp \left(il\phi \right),$$

(5)

where $l$ is the topological charge of each spiral harmonic component, $a_l\left(r,z\right)$ is the weight coefficient with the form of

$$a_l\left(r,z\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\displaystyle {\int }_0^{2\pi }E\left(r,\phi ,z\right)}\exp \left(-il\phi \right)d\phi .$$

(6)

If the receiving aperture has a radius of $R$, the spiral harmonic intensity $Q_l$ is calculated by the ensemble averaged $〈a_l\left(r,z\right)〉$ as follows:

$$Q_l={\displaystyle {\int }_0^R〈a_l\left(r,z\right)a_l^{*}\left(r,z\right)〉rdr}={\displaystyle {\int }_0^R〈{\left|a_l\left(r,z\right)\right|}^2〉rdr}.$$

(7)

Then, substituting Equations (4) and (6) into Equation (7), $Q_l$ is given by

$$\begin{array}{ll}{Q}_l=& {\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_0^R{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{2\pi }U\left(r,\phi ,z\right)U^{*}\left(r,{\phi }^{\prime },z\right)}}}g\left(r,\phi \right)g^{*}\left(r,{\phi }^{\prime }\right)\exp \left[-il\left(\phi -{\phi }^{\prime }\right)\right]\\ & \times 〈\exp \left[\psi \left(r,\phi ,z\right)+{\psi }^{*}\left(r,{\phi }^{\prime },z\right)\right]〉rdrd\phi d{\phi }^{\prime }\end{array}.$$

(8)

The exponential term $〈\exp \left[\psi \left(r,\phi ,z\right)+{\psi }^{*}\left(r,\phi ,z\right)\right]〉$ in Equation (8) describes the oceanic turbulence effects on the beam, whose value is related to spatial coherence radius ${\rho }_0$ as follows [30]:

$$〈\exp \left[\psi \left(r,\phi ,z\right)+{\psi }^{*}\left(r,{\phi }^{\prime },z\right)\right]〉=\exp \left\{-{\displaystyle \frac{2r^2\left[1-\cos \left(\phi -{\phi }^{\prime }\right)\right]}{{\rho }_0^2}}\right\}.$$

(9)

As for oceanic turbulence characterized by OTOPS, its power spectrum ${\mathsf{\Phi }}_n\left(\kappa \right)$ has the form of [4,32]

$${\mathsf{\Phi }}_n(\kappa )=A^2{\mathsf{\Phi }}_T(\kappa )+B^2{\mathsf{\Phi }}_S(\kappa )+2AB{\mathsf{\Phi }}_{TS}(\kappa ),$$

(10)

where $\kappa$ denotes the spatial frequency, $〈T〉$ is the average temperature, $〈S〉$ is the average salinity concentration, $A$ and $B$ are linear coefficients calculated by

$$\begin{array}{l}A=a_2\langle S\rangle +2a_3\langle T\rangle \langle S\rangle +2a_4\langle T\rangle +a_6{\lambda }^{-1}\\ B=a_1+a_2\langle T\rangle +a_3{\langle T\rangle }^2+a_5{\lambda }^{-1}\end{array},$$

(11)

with constants $a_1=1.779\times {10}^{-4}$, $a_2=-1.05\times {10}^{-6}$, $a_3=1.6\times {10}^{-8}$, $a_4=-2.02\times {10}^{-6}$, $a_5=0.01155$, and $a_6=-0.00423$. The spatial power spectra ${\mathsf{\Phi }}_T(\kappa )$ of temperature, ${\mathsf{\Phi }}_S(\kappa )$ of salinity, and their co-spectrum ${\mathsf{\Phi }}_{TS}(\kappa )$ are written as

$$\begin{array}{l}{\mathsf{\Phi }}_j(\kappa )={\displaystyle \frac{{\beta }_0{\epsilon }^{-1/3}{\kappa }^{-11/3}{\chi }_j}{4\pi }}\left[1+21.61{\left(\kappa \eta \right)}^{0.61}{f}_j^{0.02}-18.18{\left(\kappa \eta \right)}^{0.55}{f}_j^{0.04}\right]\exp \left[-174.90{(\kappa \eta )}^2{f}_j^{0.96}\right]\\ f_j=({0.072}^{4/3}{\beta }_0)/P{r}_j,j\in \left[T,S,TS\right]\end{array},$$

(12)

where ${\beta }_0=0.72$ is the Obukhov–Corrsin constant; $\epsilon$ is the kinetic energy dissipation rate; $\eta$ is the Kolmogorov microscale; $P{r}_T$, $P{r}_S$, and $P{r}_{TS}$ are the temperature Prandtl number, salinity Schmidt number, and the coupled Prandtl–Schmidt number, respectively. By means of the temperature–salinity gradient ratio $H$ and eddy diffusivity ratio $d_r$, the dissipation rates ${\chi }_T$ of temperature, ${\chi }_S$ of salinity, and their coupled value ${\chi }_{TS}$ have relationships as follows:

$${\chi }_S={\chi }_T{\displaystyle \frac{dr}{H^2}},{\chi }_{TS}={\chi }_T{\displaystyle \frac{(1+dr)}{2H}},$$

(13)

$$d_r\approx \left\{\begin{array}{c}{R}_P+R_p^{0.5}{(R_P-1)}^{0.5},R_P\ge 1\hfill \\ 1.85R_P-0.85,0.5\le R_P<1,\hfill \\ 0.15R_P,R_p<0.5\hfill \end{array}\right.$$

(14)

where $R_P$ is the density ratio with the form of $R_P={\alpha }_T\left|H\right|/{\beta }_S$, ${\alpha }_T$ and ${\beta }_S$ are the thermal expansion coefficient and saline contraction coefficient, respectively. Under the assumption of atmospheric pressure, the values of ${\alpha }_T$ and ${\beta }_S$ under different temperatures and salinity concentrations can be calculated using the TEOS-10 toolbox [33].

Then, the expression of ${\rho }_0$ can be obtained after some lengthy derivations based on the power spectrum ${\mathsf{\Phi }}_n\left(\kappa \right)$ of OTOPS and has the form of [32]

$${\rho }_0={\left[0.7246k^{2}z{\beta }_0{\epsilon }^{-1/3}\left(A^2{\chi }_T+B^2{\chi }_S+2AB{\chi }_{TS}\right)\right]}^{-1/2}.$$

(15)

Furthermore, based on the expressions given by Equations (2), (4), and (9), the spiral harmonic intensity $Q_l$ in Equation (8) is expanded as

$$\begin{array}{l}{Q}_l={\displaystyle \frac{1}{2\pi }}{\displaystyle \frac{1}{q}}{\displaystyle \frac{1}{q^{*}}}\exp \left(-{\displaystyle \frac{{\alpha }^2}{k}}\cdot {\displaystyle \frac{z_0}{1+z_0^2/z^2}}\right){\displaystyle \frac{1}{C_0}}{\displaystyle \sum _{n=1}^N\left(\begin{array}{c}N\\ n\end{array}\right)\frac{{(-1)}^{n-1}}{n}}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^R\exp }}}\left(-{\displaystyle \frac{r^2}{{\omega }_0^2}}\cdot {\displaystyle \frac{2}{1+z^2/z_0^2}}\right)\\ \times {\displaystyle \sum _{p=0}^{\infty }{\displaystyle \sum _{p^{\prime }=0}^{\infty }\frac{c^p{(c^{*})}^{p^{\prime }}\exp \left[i{l}_0\left(\phi -{\phi }^{\prime }\right)+ip\phi -i{p}^{\prime }{\phi }^{\prime }\right]}{p!p^{\prime }!}}}\exp \left[-r^2{\displaystyle \frac{1-\cos \left(\phi -{\phi }^{\prime }\right)}{n{\sigma }^2}}\right]\exp \left[-2r^2{\displaystyle \frac{1-\cos \left(\phi -{\phi }^{\prime }\right)}{{\rho }_0^2}}\right]\\ \times J_{l_0+p}\left({\displaystyle \frac{\alpha r}{q}}\right)J_{l_0+p^{\prime }}\left({\displaystyle \frac{\alpha r}{q^{*}}}\right)\exp \left[-il\left(\phi -{\phi }^{\prime }\right)\right]rdrd\phi d{\phi }^{\prime }\end{array}.$$

(16)

Considering the following integral formulae [34]

$$\begin{array}{c}{\displaystyle {\int }_0^{2\pi }\exp \left[-in\phi +x\cos \left(\phi -{\phi }^{\prime }\right)\right]}d\phi =2\pi \exp \left(-in{\phi }^{\prime }\right)I_n\left(x\right)\\ {\displaystyle {\int }_0^{2\pi }\exp \left(in\phi \right)}d\phi =2\pi \delta \left(n\right)\left[n\in N\right]\end{array},$$

(17)

where $I_n\left(\cdot \right)$ is the modified Bessel function of the first kind and $\delta \left(\cdot \right)$ is Dirac delta function, the simplified expression of Equation (16) is

$$\begin{array}{l}{Q}_l=2\pi {\left[1+z^2/z_0^2\right]}^{-1}\exp \left(-{\displaystyle \frac{{\alpha }^2}{k}}\cdot {\displaystyle \frac{z_0}{1+z_0^2/z^2}}\right){\displaystyle \frac{1}{C_0}}{\displaystyle \sum _{n=1}^N\left(\begin{array}{c}N\\ n\end{array}\right)\frac{{\left(-1\right)}^{n-1}}{n}}\\ \times {\displaystyle \sum _{p=0}^{\infty }\frac{{\left|c^2\right|}^p}{{\left(p!\right)}^2}}{\displaystyle {\int }_0^R\exp \left[-2r^2\left(\frac{1}{{\omega }_0^2}\cdot \frac{1}{1+z^2/z_0^2}+\frac{1}{{\rho }_0^2}+\frac{1}{2n{\sigma }^2}\right)\right]}\\ \times I_{l-l_0-p}\left({\displaystyle \frac{r^2}{n{\sigma }^2}}+{\displaystyle \frac{2r^2}{{\rho }_0^2}}\right)J_{l_0+p}\left({\displaystyle \frac{\alpha r{z}_0}{z_0+iz}}\right)J_{l_0+p}\left({\displaystyle \frac{\alpha r{z}_0}{z_0-iz}}\right)rdr\end{array}.$$

(18)

As a result, the reception probability of each spiral harmonic component has the form of

$$P_l={\displaystyle \frac{Q_l}{{\displaystyle {\sum }_{l^{\prime }=-\infty }^{\infty }{Q}_{l^{\prime }}}}},$$

(19)

When the topological charge $l$ of the received OAM mode equals to the topological charge $l_0$ of the transmitted mode, $P_l$ denotes the signal mode probability. While in the case of $l\ne l_0$, $P_l$ denotes the crosstalk mode probability. The signal-to-noise ratio $SNR$ is defined as [35]

$$SNR={\displaystyle \frac{P_{l=l_0}}{{\displaystyle {\sum }_{l=-\infty }^{\infty }{P}_{l\ne l_0}+N_0/P_{TX}}}}.$$

(20)

Here, the noise consists of two parts, namely the crosstalk noise induced by oceanic turbulence and system background noise $N_0$. Assuming that the power of the MGCAB beam at the transmitter is $P_{TX}$, the terms $P_{TX}\cdot P_{l=l_0}$ and $P_{TX}\cdot {\displaystyle {\sum }_{l=-\infty }^{\infty }{P}_{l\ne l_0}}$ represent the received signal power and crosstalk power, respectively. $N_0/P_{TX}$ reflects the level of background noise relative to the transmission power, which is usually given by the basal signal-to-noise ratio $SN{R}_0$ in decibel through the conversion of $N_0/P_{TX}={10}^{-SN{R}_0\left(\mathrm{dB}\right)/10}$.

Under the condition of signal modulation, the BER of the system is closely related to $SNR$. As for the modulation format of QAM with constellation points labeled by Gray code, the expression of BER has the form of [18]

$$\begin{array}{l}BER={\displaystyle \frac{2}{{\log }_{2}M}}\left(1-{\displaystyle \frac{1}{\sqrt{M}}}\right)erfc\sqrt{{\displaystyle \frac{3{\log }_{2}M}{2(M-1)}}SNR}\\ \times \left[1-{\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{1}{\sqrt{M}}}\right)erfc\sqrt{{\displaystyle \frac{3{\log }_{2}M}{2(M-1)}}SNR}\right]\end{array}$$

(21)

where $M$ is the modulation order and $erfc\left(\cdot \right)$ indicates the complementary error function.

3. Numerical Simulations and Discussions

In this section, we investigate the reception probability and BER of OAM modes for the MGCAB beam propagating in oceanic turbulence. The effects of turbulent environment are numerically analyzed and recommendations on beam parameters are given to optimize beam transmission under QAM. Except for specific instruction, the parameters of beam and turbulence in the following simulations are set as follows: $l_0=1$, $c=0.1$, $SN{R}_0=25\mathrm{dB}$, $N=5$, ${\theta }_0=0.05\mathrm{mrad}$, ${\omega }_0=0.01\mathrm{m}$, $\sigma =0.05\mathrm{m}$, $\lambda =532\mathrm{nm}$, $z=100\mathrm{m}$, $R=0.02\mathrm{m}$, $M=8$, ${\chi }_T{=10}^{-7}{\mathrm{K}}^2/\mathrm{s}$, $\epsilon ={10}^{-3}{\mathrm{m}}^2/{\mathrm{s}}^3$, $〈T〉=15$ °C, $〈S〉=15\mathrm{ppt}$, and $H=-10$ °C/ppt.

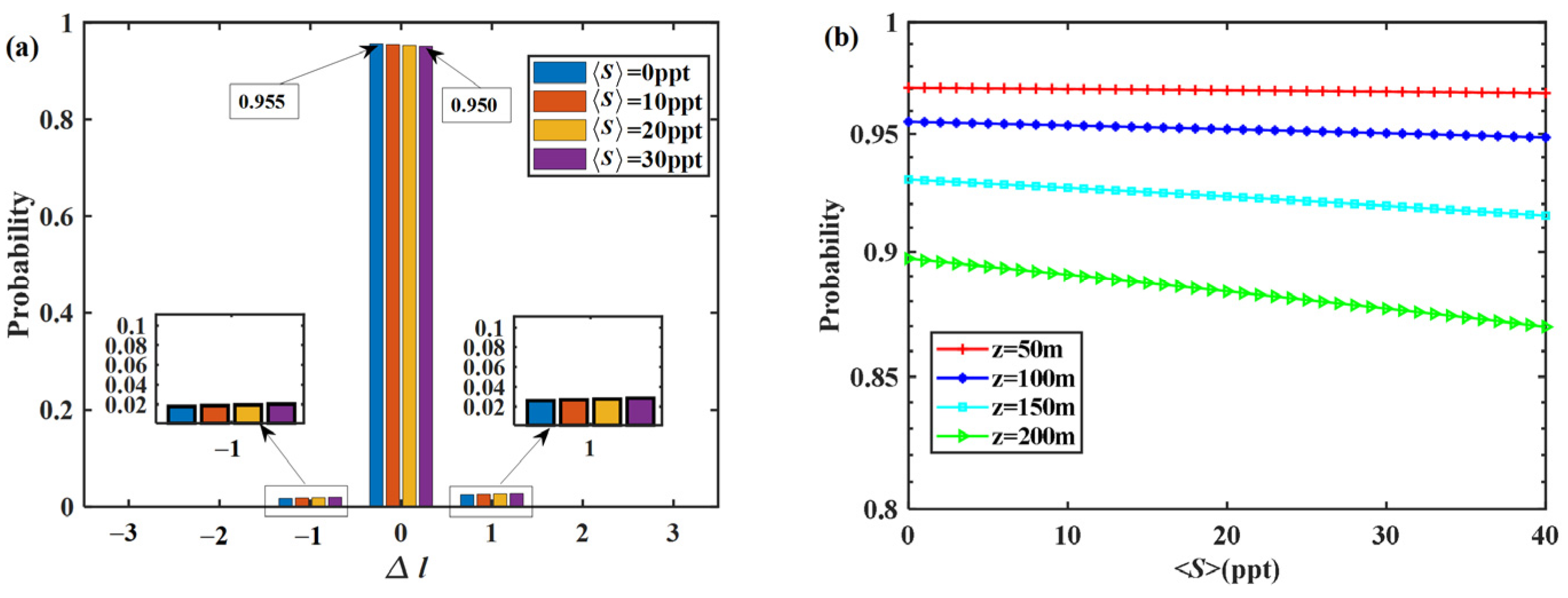
Figure 2 illustrates the received mode probability distribution of the MGCAB beam and the effects of average temperature $〈T〉$ on the reception probability of OAM signal mode under different transmission distances $z$. When $\mathsf{\Delta }l=0$ (i.e., $l=l_0$ in Equation (19)), the reception probability refers to that of signal mode. Otherwise, $\mathsf{\Delta }l\ne 0$ refers to the crosstalk case. As shown in Figure 2a, the signal reception probability gradually decreases as the average temperature rises, while the mode crosstalk continuously enhances. This phenomenon can be attributed to the fact that the higher temperature accelerates the thermal motion and expansion of water molecules. Then, the instability of stratified turbulence structure is enhanced, leading to stronger turbulence effects on beam propagation. As a result, the relatively severe wavefront distortion elevates crosstalk within OAM modes. Moreover, the received modes probability distribution exhibits asymmetry with respect to the signal mode (i.e., the crosstalk probability $P_{\mathsf{\Delta }l=1}>P_{\mathsf{\Delta }l=-1}$), and this can be ascribed to the high-order mode components in the amplitude of the MGCAB beam. Figure 2b shows that the transmission distance has a large influence on the signal reception probability of the MGCAB beam. When the transmission distance increases, the signal reception probability reduces due to the cumulative turbulence effects on beam intensity and phase patterns, and this phenomenon is more pronounced in high-temperature oceanic conditions.

The received mode probability distribution of the MGCAB beam versus average salinity concentration $〈S〉$ is reported in Figure 3a. Similar to the case presented in Figure 2a, the probability distribution of received modes also exhibits asymmetry relative to the signal mode. The signal reception probability of the MGCAB beam slightly decreases with the increment in salinity concentration. On one hand, the rise of salinity leads to smaller seawater density fluctuation, which causes less refractive effect on beam propagation, thereby reducing the wavefront distortion of OAM mode. On the other hand, the higher salinity causes larger concentration fluctuation and thus more scattering effect in seawater, resulting in the attenuation of signal mode [36]. Since the scattering effect of seawater is greater than refraction, the signal reception probability reduces with the rising salinity. When the transmission distance $z$ increases, there is a relatively obvious decrease in the signal reception probability of the MGCAB beam, as shown in Figure 3b. This is mainly due to the cumulative effect of salinity concentration in turbulent ocean.

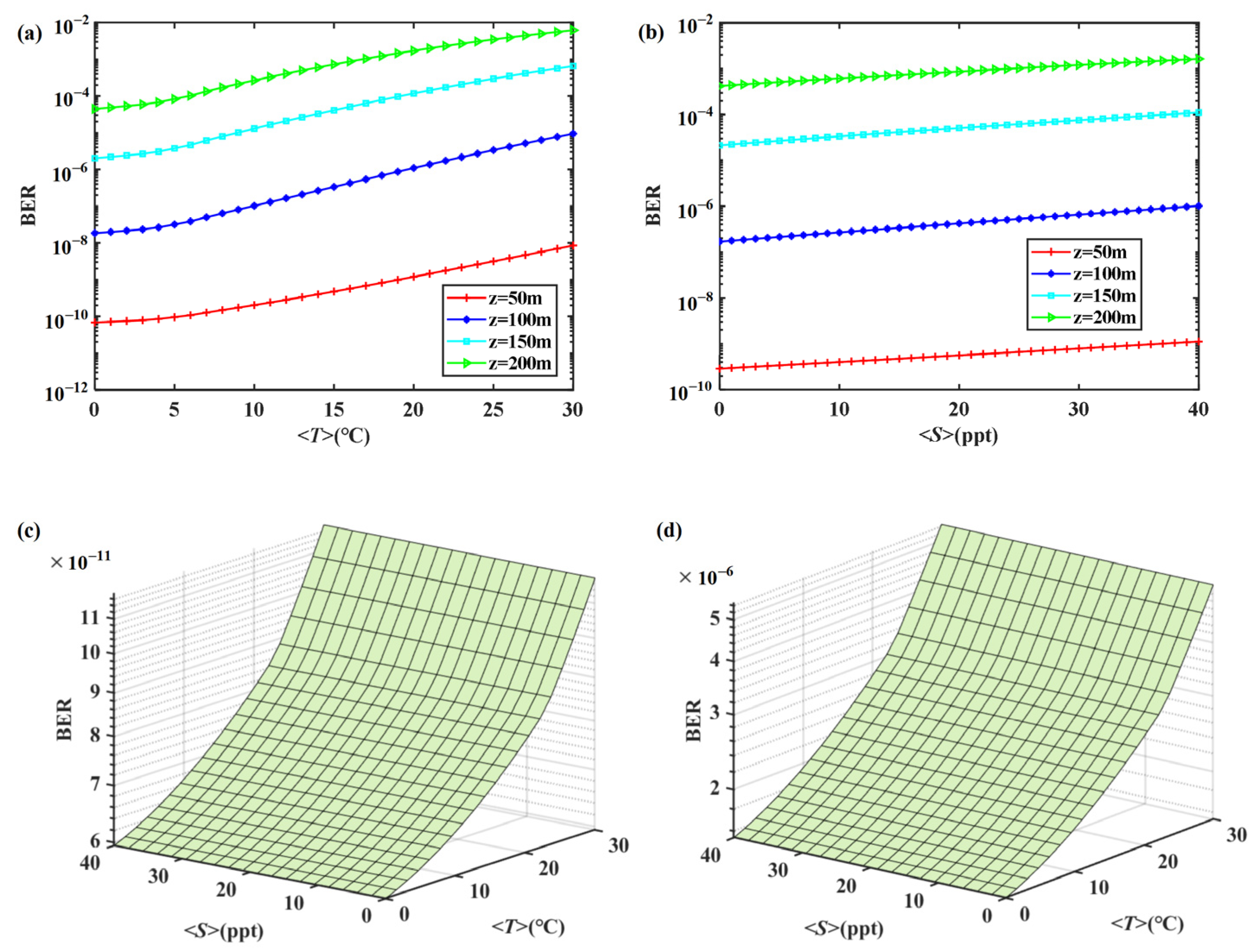
Based on the analysis of reception probability, Figure 4 shows the effects of average temperature $〈T〉$ and average salinity concentration $〈S〉$ on the BER of the MGCAB beam at different transmission distances $z$. The temperature and salinity ranges selected according to the spectrum of OTOPS cover all the natural water conditions [32]. As the temperature and salinity increase, the BER keeps rising because the lower reception probability of OAM signal mode at this time brings the reduction in SNR. Further observation reveals that there exists significant differences in the impacts of temperature and salinity changes on the level of BER. Under the same transmission distance, the change in temperature has a greater impact on BER, while the impact of salinity is relatively gentle. This indicates that the propagation of the MGCAB beam is more sensitive to the variation in seawater temperature. Since the surface temperature is higher than the deep temperature in actual oceanic environments, the selection of a deep cold ocean channel will result in better signal transmission quality.

In addition to temperature and salinity concentration, the temperature–salinity gradient ratio $H$ also contributes to turbulence effects. As shown in Figure 5, the BER of the MGCAB beam slowly increases with $H$ at first. When $H$ reaches about $-5$ °C/ppt, the BER decreases but later experiences a rapid rise with further elevation of $H$. This can be attributed to the variation in beam spatial coherence radius ${\rho }_0$. An increase in $H$ at small values causes the diminution in turbulence eddy diffusivity. As a result, the beam spatial coherence radius reduces, implying the occurrence of more wavefront distortion and modal crosstalk. Nevertheless, as $H$ increases to about $-5$ °C/ppt, the water expansion coefficient becomes negative [32]. The spatial coherence radius increases first but later decreases with the further rise of $H$, causing a “groove” in the curve of BER within the [−5,0) interval.

The influences of other turbulence parameters such as the temperature dissipation rate ${\chi }_T$ and kinetic energy dissipation rate $\epsilon$ on BER are also reflected in Figure 5. A lower level of BER can be obtained in conditions of smaller ${\chi }_T$ and larger $\epsilon$ due to the weaker oceanic turbulence. Compared with $\epsilon$, ${\chi }_T$ has a more significant impact on beam propagation performance. The results are consistent with the conclusions about ${\chi }_T$ and $\epsilon$ in previous reports based on the Nikishov oceanic turbulence spectrum [37].

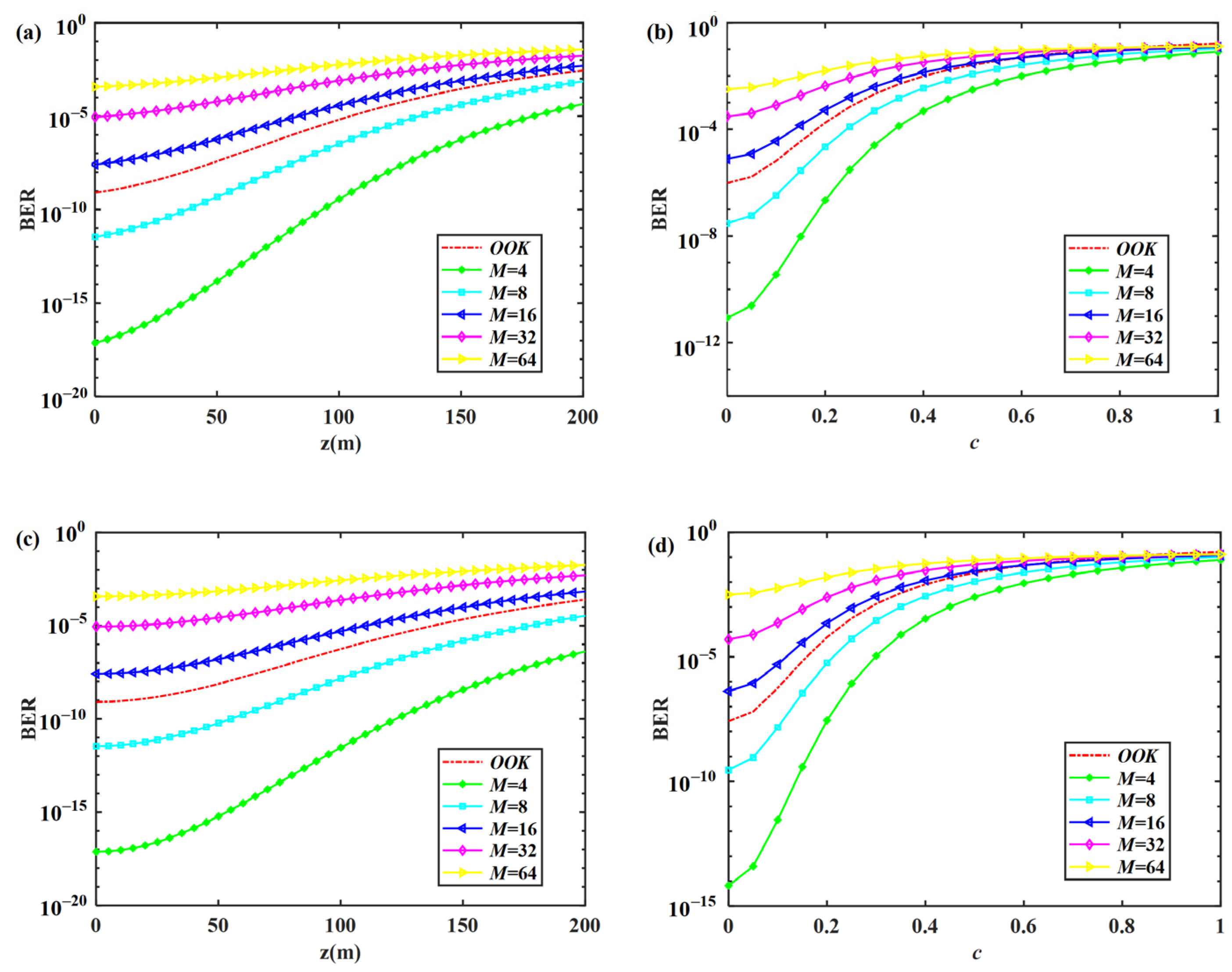
To investigate the impact of modulation system on the BER of the MGCAB beam, Figure 6a,c illustrate the relationship between BER and modulation order $M$ under various transmission distances $z$. During the transmission process, the BER of high-order modulation is higher than that of low-order modulation. The reason is that, when the modulation order increases, the constellation point number of QAM increases and their mutual distances become smaller, which makes the modal interference more severe in oceanic turbulence. Compared with the traditional OOK modulation [18], the low-order modulation of QAM not only has a lower BER but also carries a larger amount of information per symbol, which can significantly enhance the signal transmission efficiency. To further investigate the BER characteristics of the MGCAB beam under different turbulent conditions, we reduce the value of temperature dissipation rate ${\chi }_T$ in Figure 6c to construct a weaker turbulence condition than that in Figure 6a. It can be observed that the BER of low-order modulation decreases more significantly when turbulence weakens. Since high-order modulation can carry more data bits, the QAM modulation order should be selected adaptively to make a balance between information capacity and BER according to specific requirements.

Considering the properties of the beam itself, Figure 6b,d shows the relationship between BER and modulation order $M$ under different asymmetry factors $c$ of the MGCAB beam. The BER increases with $c$ due to the larger OAM modal crosstalk of asymmetric mode in turbulence. Low-order modulation has a lower BER and a smaller $c$ is preferable under low-order modulation. By comparing Figure 6b,d, we find that the BER decreases significantly in weaker oceanic turbulence, which makes high-order modulation a viable alternative option. The variation in BER with $c$ is relatively gentle under high-order modulation, which indicates that the change in $c$ has a small impact on beam propagation in this condition. Since $c$ is an important parameter controlling the transverse intensity pattern of the MGCAB beam, the optical field available is more flexible and diverse with the adjustment of beam asymmetry [23].

As a new degree of freedom of the vortex beam, the topological charge $l_0$ affects the BER of the MGCAB beam given in Figure 7a. Generally, the spot size expands with topological charge [38], which is also applicable to the MGCAB beam. The larger spot makes the beam more vulnerable to oceanic turbulence perturbations and exacerbates crosstalk between OAM modes. As a result, the SNR of transmission link decreases and BER increases. Therefore, the construction of the MGCAB beam with lower topological charge is preferable in multiplexing systems, which reduces not only BER but also the size of receiving aperture. Aiming at the problem of higher BER caused by large topological charge, the approach of low-order modulation of QAM can be adopted to reduce BER, which is intuitively demonstrated in Figure 7b. In addition, by introducing the adaptive feedback correction technique to measure the wavefront distortion caused by turbulence and conduct phase compensation, the BER can also be reduced [38]. Compared to topological charge $l_0$, the impact of beam index $N$ on BER is relatively smaller. The beam index affects the far-field intensity distribution of the MGCAB beam. With the increase in $N$, the perturbations of turbulence on the beam become larger and the BER gradually increases. On the other hand, a larger $N$ brings a flatter center intensity profile and a steeper edge in the far field [14]. Therefore, it is advisable to select the beam index according to the adaptability of beam field to different receiving systems within the acceptable range of BER.

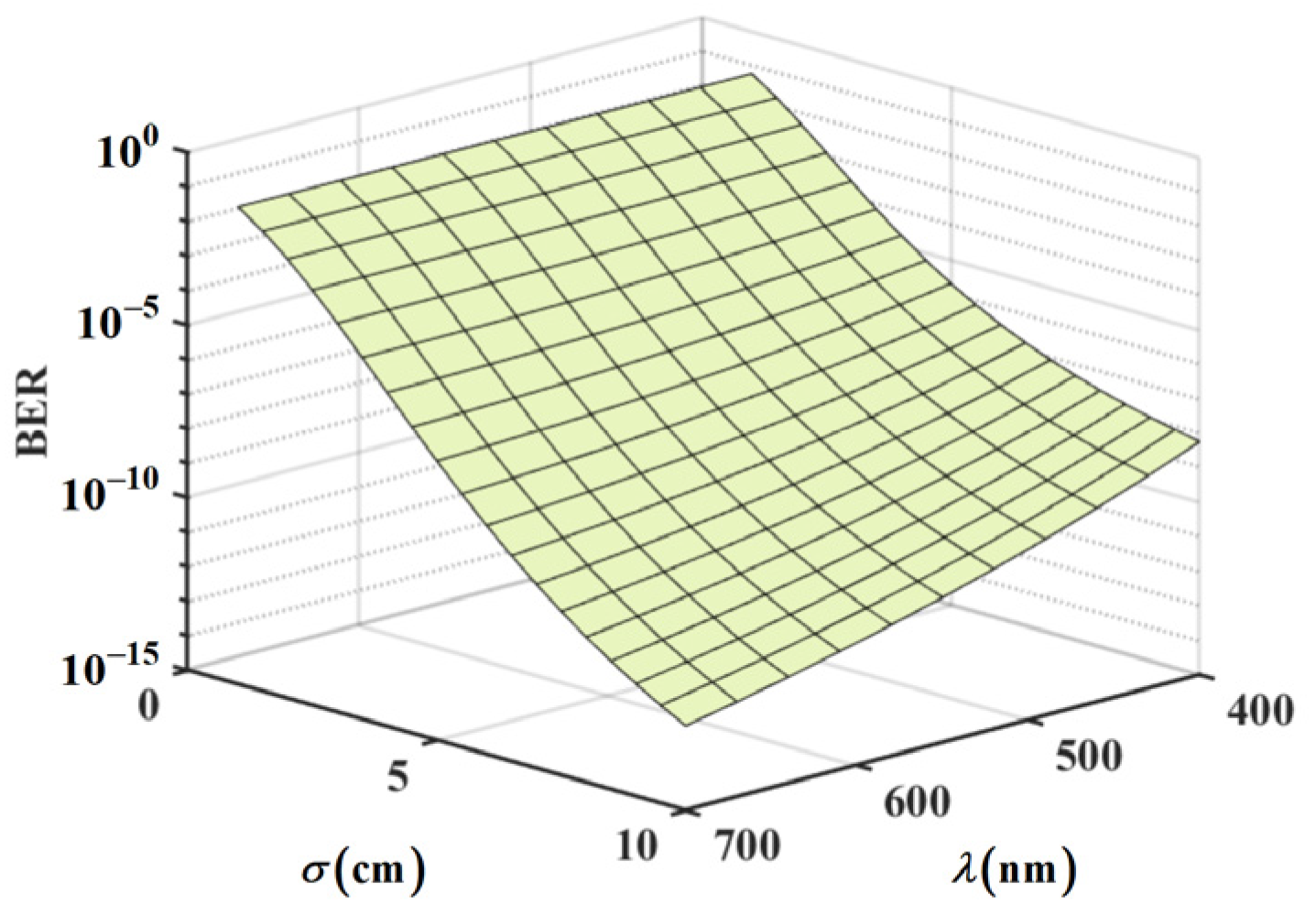
The influences of wavelength $\lambda$ and source coherence width $\sigma$ on the BER of the MGCAB beam are shown in Figure 8. With the increment in wavelength, a lower BER is obtained. The wavefront distortion and OAM modal crosstalk of the long-wavelength beam are weaker than those of the short-wavelength one due to the larger beam spatial coherence radius, demonstrating better resistance of long wavelength to turbulence perturbations. On the other hand, the increment in source coherence width $\sigma$ also reduces BER. A larger $\sigma$ corresponds to higher beam coherence, which mitigates the dispersal of the OAM spiral spectrum and decreases crosstalk. When $\sigma$ tends to infinity, the partially coherent beam grows to the fully coherent one. Therefore, a laser source with higher coherence and longer wavelength is beneficial to signal transmission in oceanic turbulent channels.

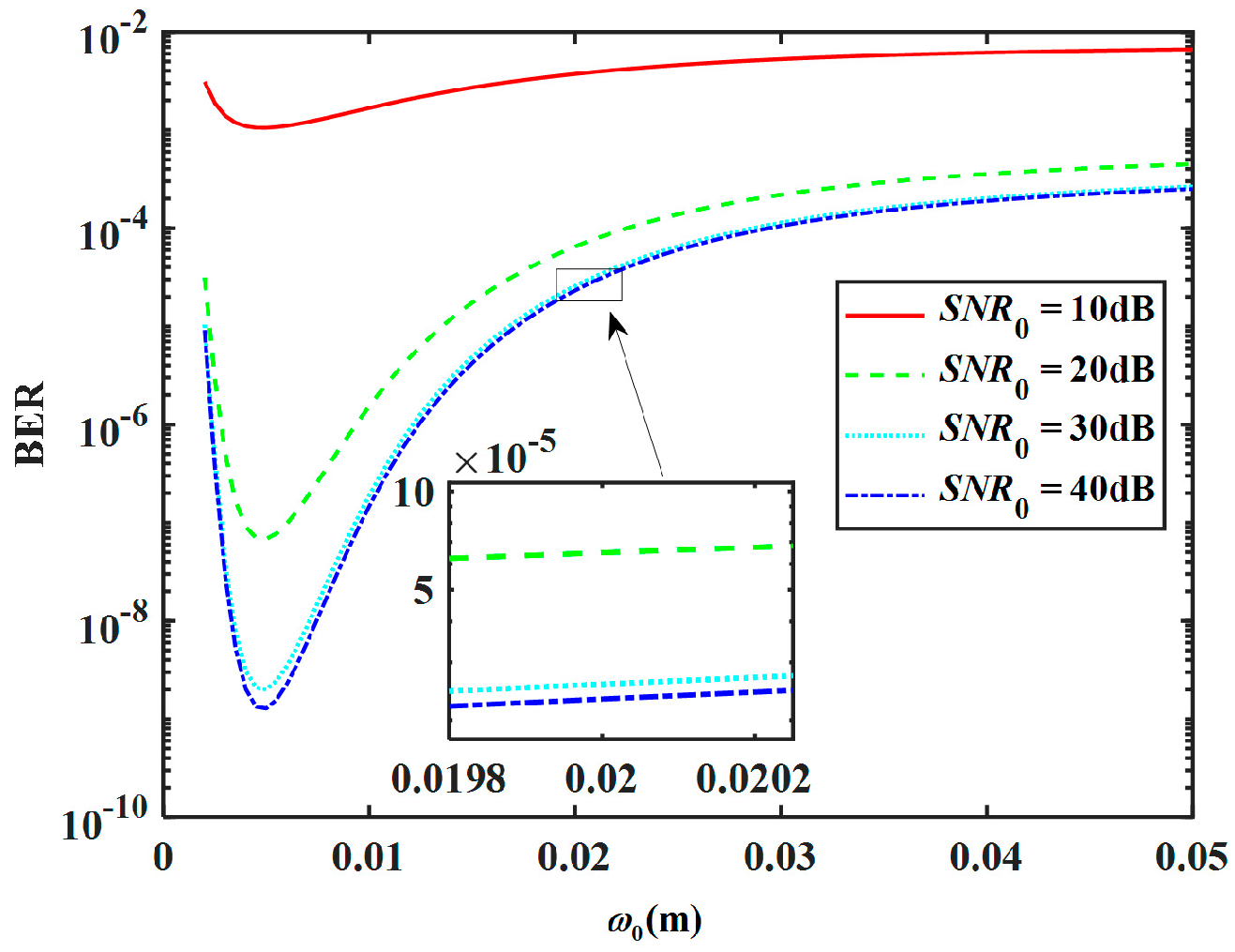
Figure 9 reports the relationship between BER and the waist radius ${\omega }_0$ of the MGCAB beam under different basal signal-to-noise ratios $SN{R}_0$. There exists an optimal value for the selection of ${\omega }_0$. The severe spreading brought by small ${\omega }_0$ and wide initial waist brought by large ${\omega }_0$ both result in a larger spot size during propagation, which makes the beam suffer more turbulence disturbances and the consequent modal crosstalk. Therefore, a moderate ${\omega }_0$ is preferable to mitigate turbulence effects and reduce BER. Apart from the crosstalk noise induced by oceanic turbulence, the system background noise also has an impact. As for given transmitted power, a larger $SN{R}_0$ means smaller background noise and thus lower BER. When $SN{R}_0$ exceeds about 30 dB, the background noise is extremely low and its impact can be negligible.

In summary, oceanic turbulence and the basal signal-to-noise ratio of the communication system both have impacts on the BER of the MGCAB beam. Oceanic turbulence can affect beam wavefront and cause modal crosstalk of the MGCAB beam. When the transmission distance increases, the cumulation of turbulence effects will increase the BER. It is worth noting that the high-temperature and high-salinity oceanic environment further exacerbates the turbulence perturbations, causing the BER to be at a high level and seriously affecting the signal transmission quality. In terms of the optimization of signal modulation strategy, we find that, compared with the traditional OOK modulation, the MGCAB beam under low-order QAM exhibits better anti-turbulence characteristics. The BER can also be reduced by adjusting the beam parameters such as wavelength, coherence width, and beam waist radius. In addition, the transverse spectral density distribution of the beam can be made more diverse by adjusting beam asymmetry, thus meeting the requirements of different application scenarios.

Based on the above-mentioned research results, the subsequent research in the future can focus on the effective transmission of beams in extreme oceanic environments of high temperature and high salinity concentrations. The research directions may include designing new types of light beams with special anti-turbulence structures, exploring more suitable modulation strategies, which are expected to promote the development of underwater optical communication in complex oceanic environments.

4. Conclusions

Taking source coherence into account, we construct a theoretical model to investigate the propagation of the MGCAB beam under QAM. With OTOPS to characterize oceanic turbulence, the reception probability of OAM mode is derived by use of spiral harmonic decomposition and then the expression of BER is given. Numerical simulations show that oceanic channels with lower temperature and salinity both induce less turbulence perturbations, but the former is more significant. In contrast with OOK modulation, low-order QAM has better turbulence resistance and BER performance. In terms of the MGCAB beam, lower coherence and lower asymmetry are preferable. Moreover, beam field optimizations towards long wavelength, small topological charge, and moderate waist radius are also beneficial to the reduction in BER. The research provides references for the underwater propagation of the vortex beam combined with signal modulation.