A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects
Abstract
1. Introduction
2. Model and Design
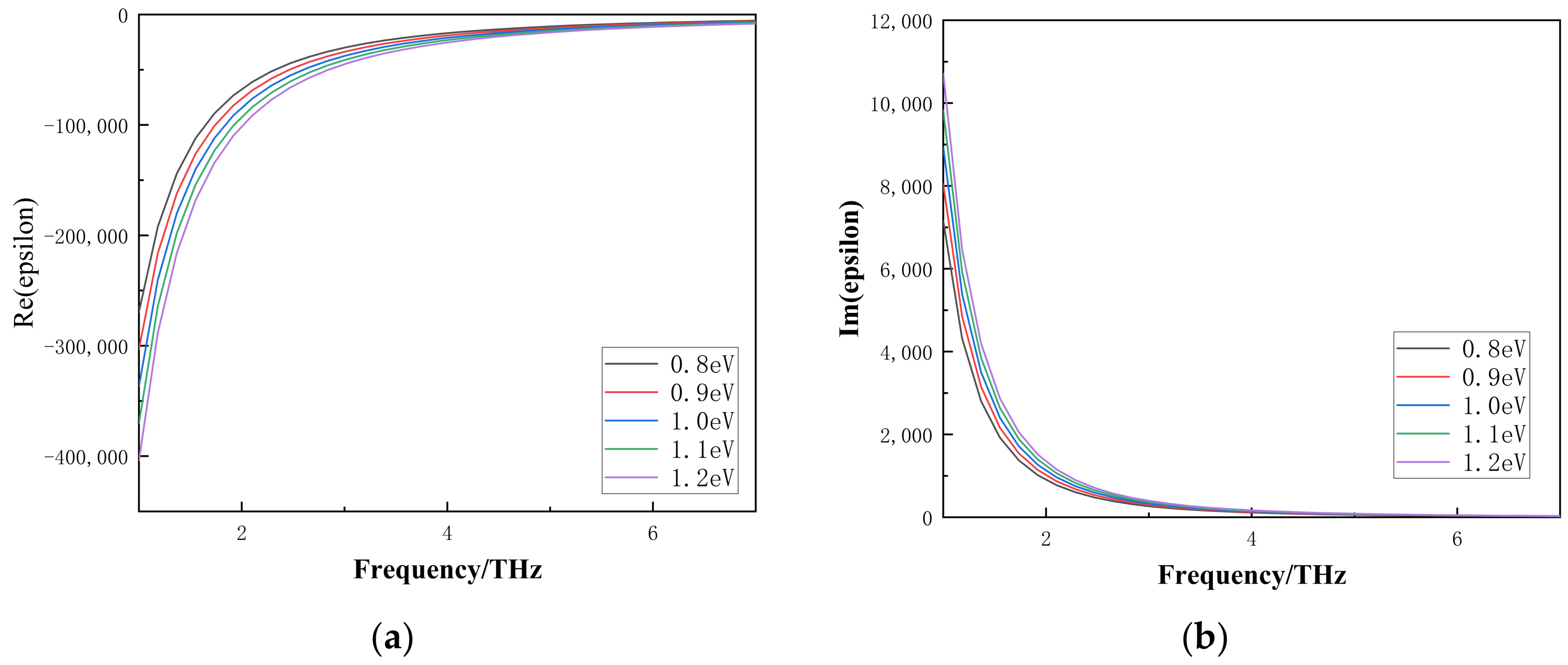
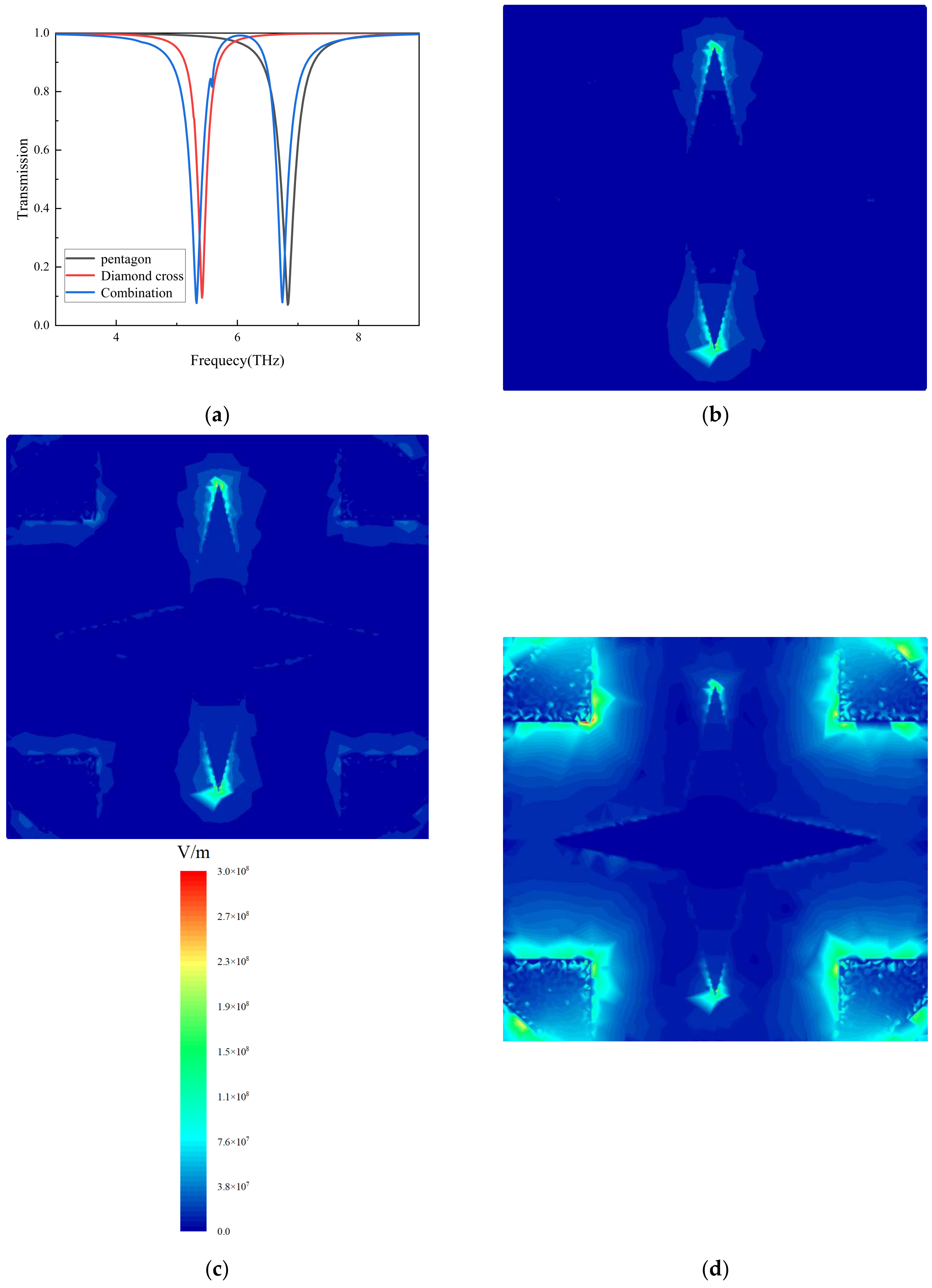
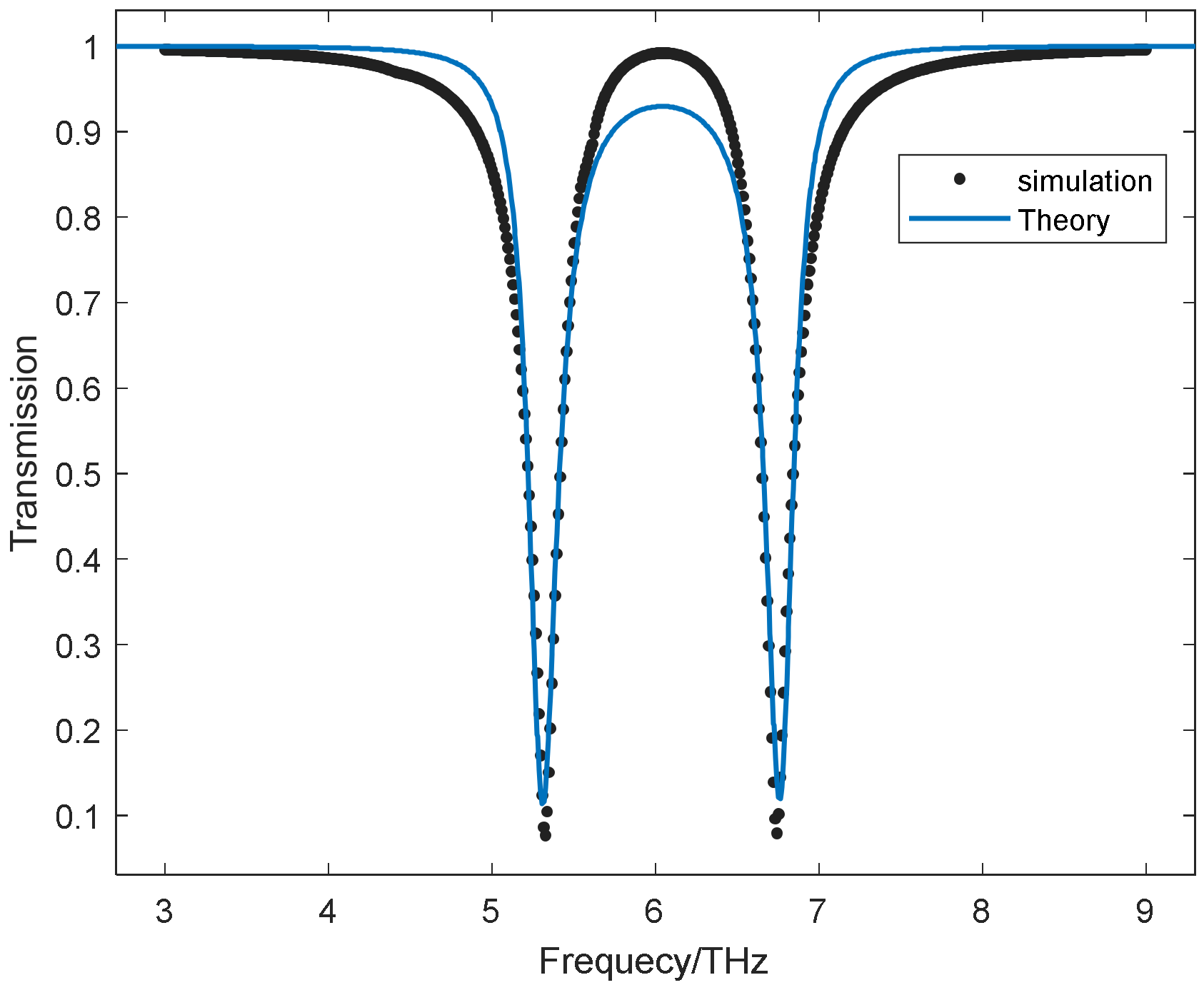
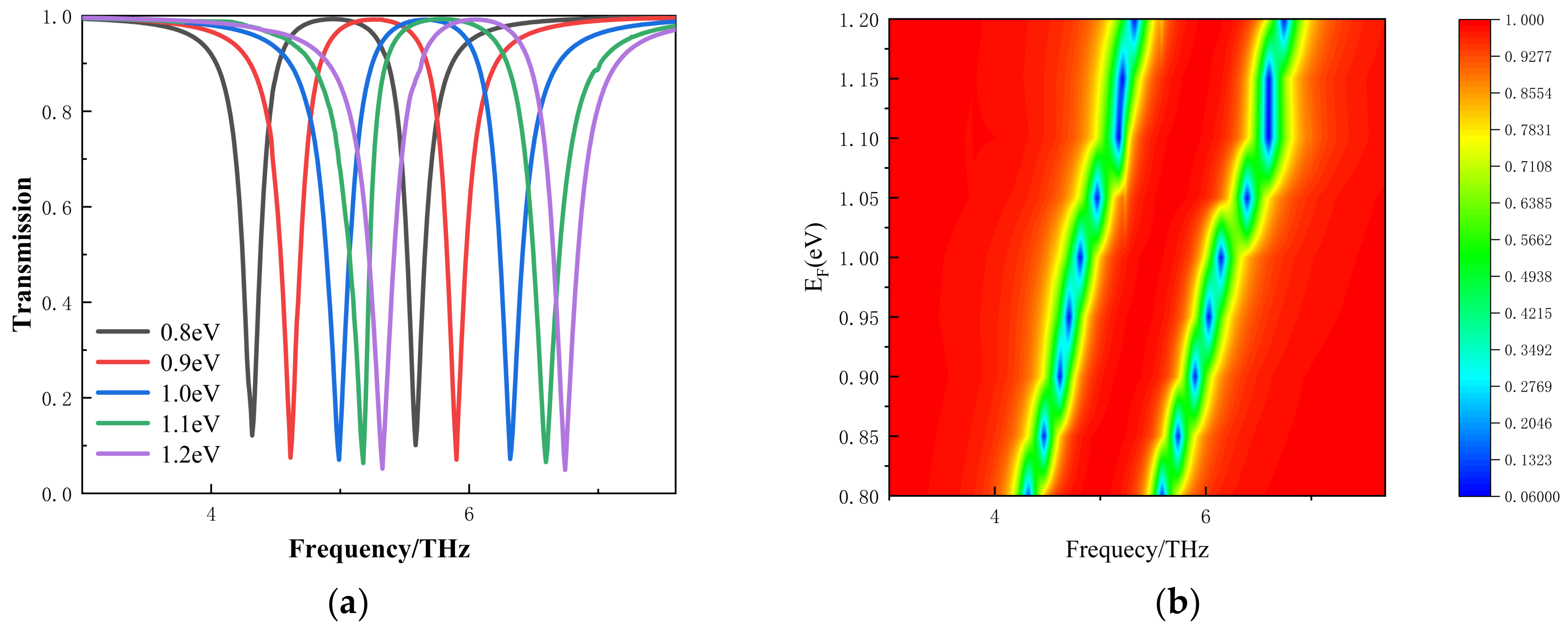
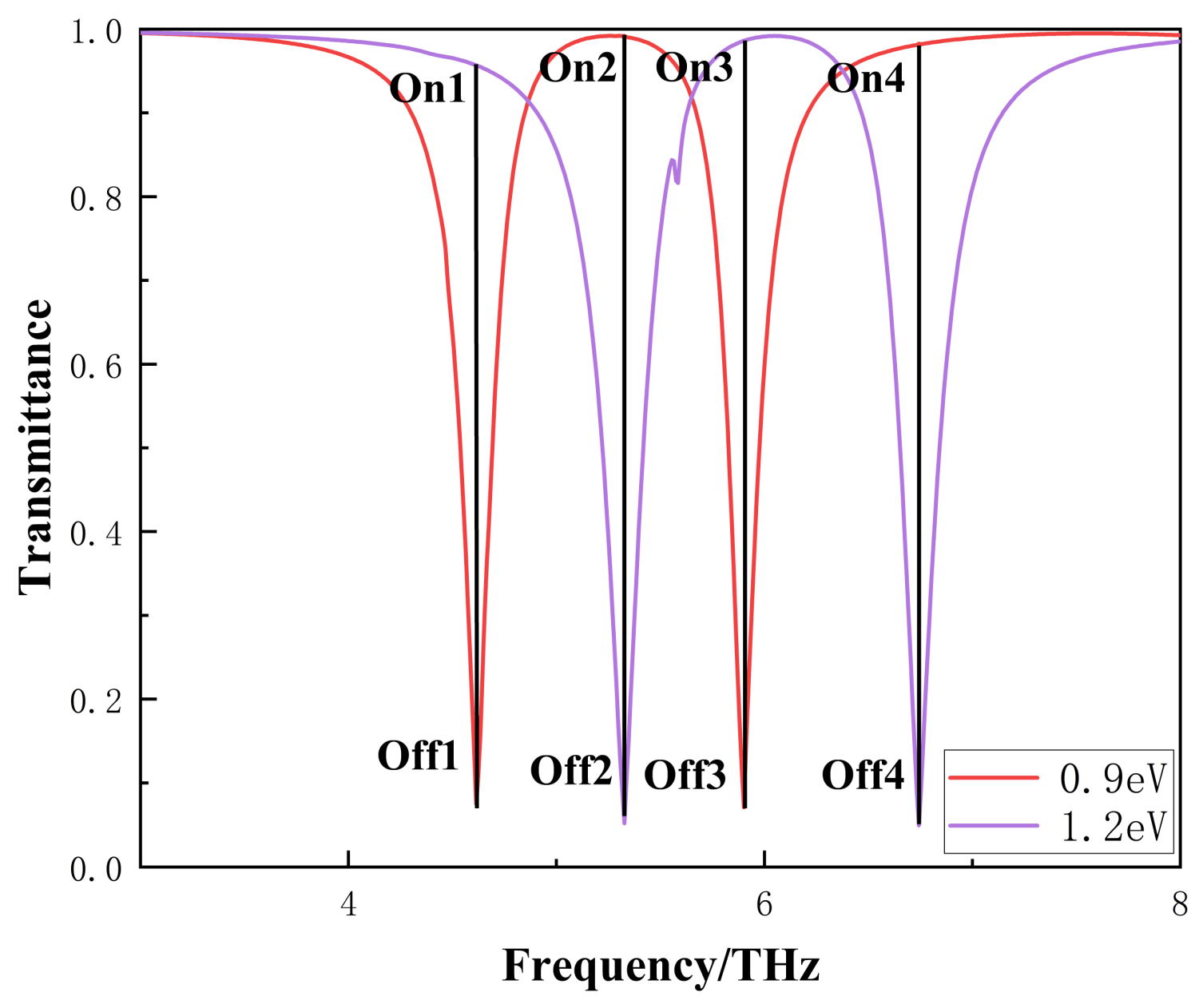
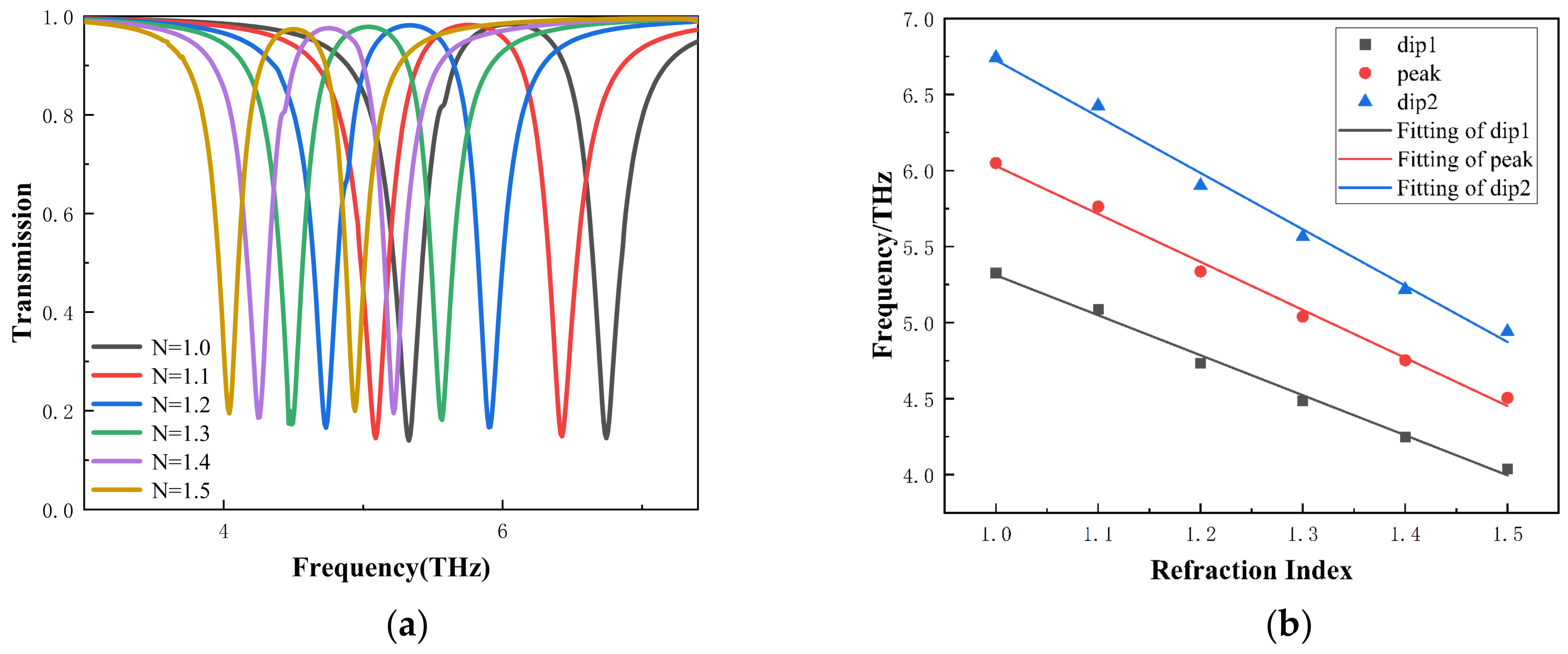
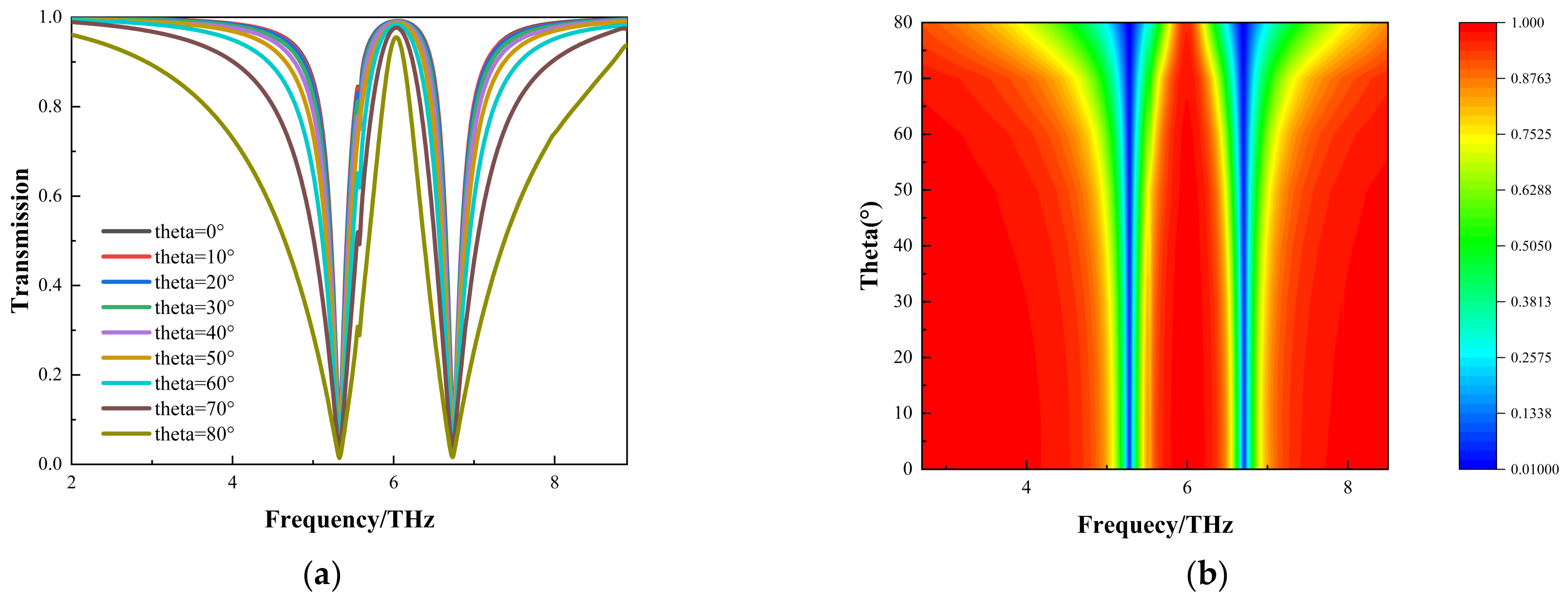
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, P.; Yao, Y.; Zhong, W.; Gu, P.; Yan, Z.; Liu, F.; Yan, B.; Tang, C.; Chen, J.; Zhu, M. Optical sensing based on classical analogy of double Electromagnetically induced transparencies. Results Phys. 2022, 39, 105732. [Google Scholar] [CrossRef]
- Jamshidi, M.; Park, C.B.; Azhari, F. An EIT-based piezoresistive sensing skin with a lattice structure. Mater. Des. 2023, 233, 112227. [Google Scholar] [CrossRef]
- Li, J.-S.; Xue, Y.-Y.; Guo, F.-L. Triple frequency bands terahertz metasurface sensor based on EIT and BIC effects. Opt. Commun. 2023, 554, 130225. [Google Scholar] [CrossRef]
- Foong, L.K.; Shabani, M.; Sharghi, A.; Reihanisaransari, R.; Al-Bahrani, M.; Le, B.N.; Khalilian, A. Electromagnetically induced transparency for efficient optical modulation in a graphene-dielectric metasurface with surface roughness. Surfaces Interfaces 2022, 35, 102423. [Google Scholar] [CrossRef]
- Lu, Z.; Yuan, J.; Xu, G.; Luo, B.; Tan, J. Optically implemented deep terahertz switch based on perovskite film and electromagnetically induced transparency metasurface. Opt. Laser Technol. 2024, 183, 112303. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, G.; Xu, C.; Qin, X.; Zhao, Q.; Zhou, H.; Wang, B.-X. Triple-band graphene-based tunable electromagnetically induced transparency terahertz metamaterial with multi-frequency optical switching. Diam. Relat. Mater. 2024, 143, 110939. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, F.; Zhou, P.; Zhang, X.; Yang, Y.; Yan, X.; Gao, S.; Zong, M.; Wang, M.; Yao, H.; et al. Frequency-tunable hybrid metamaterial terahertz logic gate with liquid crystal based on electromagnetically induced transparency. Results Phys. 2023, 56, 107295. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Cui, W.; Ren, X.; Li, C.; Xue, W.; Cao, D.; Li, G.; Lei, W. Tunable plasmon induced transparency in the ellipse-shaped resonators coupled waveguide. Results Phys. 2020, 16, 102981. [Google Scholar] [CrossRef]
- Tassin, P.; Zhang, L.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Low-Loss Metamaterials Based on Classical Electromagnetically Induced Transparency. Phys. Rev. Lett. 2009, 102, 053901. [Google Scholar] [CrossRef]
- Liang, D.; Chen, T. Optical modulated graphene metamaterial based on plasmon-induced transparency in the terahertz band: Application for sensing. Diam. Relat. Mater. 2022, 131, 109613. [Google Scholar] [CrossRef]
- Guo, X.; Cong, J.; Li, C. Dynamic tunable multiple plasmon induced transparency sensor and optical switch in dual-polarization excitation in a terahertz graphene metamaterial. Opt. Commun. 2023, 551, 130058. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, T. A triple plasmon-induced transparency terahertz sensor based on graphene metamaterials. Diam. Relat. Mater. 2024, 149, 111608. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, F.; Xu, Y.; Cheng, S.; Yang, W.; Yao, D.; Yi, Z. Multi-frequency polarization and electro-optical modulator based on triple plasmon- induced transparency in monolayer graphene metamaterials. Diam. Relat. Mater. 2023, 138, 110216. [Google Scholar] [CrossRef]
- Dai, C.; Li, B.; Zeng, L.; Wang, Q.; Chen, Z.; Zeng, Y.; Zhang, X.; Deng, C. Graphene modulator and 2-bit encoder based on plasma induced transparency effect. Diam. Relat. Mater. 2024, 150, 111715. [Google Scholar] [CrossRef]
- Zhu, A.; Li, Z.; Hou, W.; Cheng, L.; Hu, C.; Zhao, T.; Xu, C.; Mahapatra, R. Double plasmon-induced transparency 3 bit graphene encoder. Diam. Relat. Mater. 2024, 142, 110800. [Google Scholar] [CrossRef]
- Zhu, A.; Li, Z.; Hou, W.; Yang, X.; Cheng, L.; Hu, C.; Qiao, F.; Mahapatra, R. A 2-bit graphene encoder based on the plasmon-induced transparency effect and its sensing characteristics. Results Phys. 2024, 59, 107608. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Liu, W.; Cheng, H.; Tian, J. From Single-Dimensional to Multidimensional Manipulation of Optical Waves with Metasurfaces. Adv. Mater. 2019, 31, 1802458. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Zhong, F.; Li, J.; Liu, H.; Zhu, S. 12-Photon Entanglement and Scalable Scattershot Boson Sampling with Optimal Entangled-Photon Pairs from Parametric Down-Conversion. Phys. Rev. Lett. 2018, 120, 243901. [Google Scholar] [CrossRef]
- Su, Z.; Yang, Y.; Xiong, B.; Zhao, R.; Wang, Y.; Huang, L. Planar Chiral Metasurface Based on Coupling Quasi-Bound States in the Continuum. Adv. Opt. Mater. 2024, 12, 2303195. [Google Scholar] [CrossRef]
- Shao, Y.; Su, Z.; He, H.; Jing, X.; Liu, Y.; Geng, G.; Li, J.; Wang, Y.; Huang, L. Multispectral imaging through metasurface with quasi-bound states in the continuum. Opt. Express 2024, 32, 23268–23279. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Pu, M.; Chen, P.; Wang, C.; Wang, Y.; Zhao, Z.; Hu, C.; Huang, C.; Luo, X. Broadband anomalous reflection based on gradient low-Q meta-surface. AIP Adv. 2013, 3, 052136. [Google Scholar] [CrossRef]
- Lopato, P.; Herbko, M.; Gora, P.; Mescheder, U.; Kovacs, A.; Filbert, A. Numerical Analysis of the Influence of Fabrication Process Uncertainty on Terahertz Metasurface Quality. Electronics 2023, 12, 2198. [Google Scholar] [CrossRef]
- Seong, J.; Jeon, Y.; Yang, Y.; Badloe, T.; Rho, J. Cost-Effective and Environmentally Friendly Mass Manufacturing of Optical Metasurfaces Towards Practical Applications and Commercialization. Int. J. Precis. Eng. Manuf. Technol. 2023, 11, 685–706. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.; Zhang, F.; Zhao, Q.; Wu, H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Graphene Plasmonics: A Platform for 2D Optics. Adv. Opt. Mater. 2018, 7, 1800537. [Google Scholar] [CrossRef]
- Nan, J.; Zhang, Y.; Xie, Y.; Li, Z.; Yang, R.; Xu, J.; Fu, Q.; Zhang, F.; Fan, Y. Coupling Controlled Dual-Band Tunable Electromagnetic Extraordinary Transmission in Graphene Hybrid Metasurfaces. Adv. Electron. Mater. 2023, 9, 2300065. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, G.; Luo, X.; Zhou, F.; Cheng, Z.; Yi, Z. Tunable quintuple plasmon-induced transparency and the effect of symmetry breaking based on monolayer graphene split rings metasurface. Diam. Relat. Mater. 2024, 142, 110786. [Google Scholar] [CrossRef]
- Xie, Q.; Guo, L.; Zhang, Z.; Gao, P.; Wang, M.; Xia, F.; Zhang, K.; Sun, P.; Dong, L.; Yun, M. Versatile terahertz graphene metasurface based on plasmon-induced transparency. Appl. Surf. Sci. 2022, 604, 154575. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, B.; Xue, J.; Cao, X.; Xu, H.; He, H.; Cui, W.; He, Z. Sensing and slow light applications based on graphene metasurface in terahertz. Diam. Relat. Mater. 2022, 123, 108881. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, H.; Jiang, X.; Yin, J. Versatile Functionalization of the Micropatterned Hydrogel of Hyperbranched Poly(ether amine) Based on “Thiol-yne” Chemistry. Adv. Funct. Mater. 2014, 24, 1679–1686. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, L.; Wang, Y.; Shi, Z.; Shi, D.; Gao, H.; Wang, E.; Zhang, G. An Anisotropic Etching Effect in the Graphene Basal Plane. Adv. Mater. 2010, 22, 4014–4019. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.; Ren, P.-W.; Tian, Y.-C.; Fan, C.-Z. Dynamically tunable optical properties in graphene-based plasmon-induced transparency metamaterials. Chin. Phys. B 2019, 28, 026102. [Google Scholar] [CrossRef]
- Chen, D.-C.; Li, H.-J.; Xia, S.-X.; Qin, M.; Zhai, X.; Wang, L.-L. Dynamically tunable electromagnetically-induced-transparency-like resonances in graphene nanoring and nanodisk hybrid metamaterials. EPL Europhys. Lett. 2017, 119, 47002. [Google Scholar] [CrossRef]
- Tian, Y.-C.; Jia, W.; Ren, P.-W.; Fan, C.-Z. Tunable plasmon-induced transparency based on asymmetric H-shaped graphene metamaterials. Chin. Phys. B 2018, 27, 124205. [Google Scholar] [CrossRef]
- Liu, T.; Wang, H.; Liu, Y.; Xiao, L.; Zhou, C.; Xu, C.; Xiao, S. Dynamically tunable electromagnetically induced transparency in a terahertz hybrid metamaterial. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 104, 229–232. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Y.; Zhang, X.; Wang, J.; Liu, Z.; Luo, X.; Zhang, Z.; Gao, E. Dynamically adjustable plasmon-induced transparency and switching application based on bilayer graphene metamaterials. J. Phys. D Appl. Phys. 2020, 54, 054002. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Jiang, J.; Ren, L.; Cheng, S.; Wang, B.; Zhou, X.; Wang, Z. Dual dynamically tunable plasmon-induced transparency and absorption in I-type-graphene-based slow-light metamaterial with rectangular defect. Optik 2021, 246, 167837. [Google Scholar] [CrossRef]
- Hu, F.; Fan, Y.; Zhang, X.; Jiang, W.; Chen, Y.; Li, P.; Yin, X.; Zhang, W. Intensity modulation of a terahertz bandpass filter: Utilizing image currents induced on MEMS reconfigurable metamaterials. Opt. Lett. 2018, 43, 17–20. [Google Scholar] [CrossRef]
- Tang, B.; Jia, Z.; Huang, L.; Su, J.; Jiang, C. Polarization-Controlled Dynamically Tunable Electromagnetically Induced Transparency-Like Effect Based on Graphene Metasurfaces. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 4700406. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Yang, J.; Zhou, Z. Controlled and tunable plasmon-induced transparency based on graphene metasurfaces in atmospheric windows. Diam. Relat. Mater. 2022, 127, 109210. [Google Scholar] [CrossRef]
- Agravat, D.; Patel, S.K.; Almawgani, A.H.M.; Alsuwian, T.; Armghan, A.; Daher, M.G. Investigation of a Novel Graphene-Based Surface Plasmon Resonance Solar Absorber to Achieve High Absorption Efficiency Over a Wide Spectrum of Wavelengths, from Ultraviolet to Infrared. Plasmonics 2023, 19, 1071–1083. [Google Scholar] [CrossRef]
- Zhu, J.; Xiong, J. Tunable terahertz graphene metamaterial optical switches and sensors based on plasma-induced transparency. Measurement 2023, 220, 113302. [Google Scholar] [CrossRef]
- Qin, Y.; Zhou, F.; Liu, Z.; Zhang, X.; Zhuo, S.; Luo, X.; Ji, C.; Yang, G.; Zhou, Z.; Sun, L.; et al. Triple plasmon-induced transparency and dynamically tunable electro-optics switch based on a multilayer patterned graphene metamaterial. J. Opt. Soc. Am. A 2022, 39, 377–382. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, F.; Xu, Y.; Cheng, S.; Yang, W.; Yao, D.; Yi, Z. Tunable terahertz double plasmon induced-transparency based on monolayer patterned graphene structure. Photonics Nanostruct. Fundam. Appl. 2023, 54, 101132. [Google Scholar] [CrossRef]
- Wu, Z.; An, P.; Ding, M.; Qi, Y.; Zhang, L.; Han, S.; Lian, D.; Chen, C.; Yang, X. Tunable Electromagnetically Induced Transparent Window of Terahertz Metamaterials and Its Sensing Performance. Appl. Sci. 2022, 12, 7057. [Google Scholar] [CrossRef]
- Li, J.; Weng, J.; Li, J.; Chen, S.; Guo, Z.; Xu, P.; Liu, W.; Wen, K.; Qin, Y. Dynamic manipulation of plasmon induced transparency with parallel-orthometric graphene strips structure. Results Phys. 2022, 40, 105816. [Google Scholar] [CrossRef]
- Li, G. Tunable Fano resonance for advanced sensing in graphene-based metasurface. Diam. Relat. Mater. 2024, 142, 110823. [Google Scholar] [CrossRef]
- Li, Z.; Yang, N.; Liu, Y.; Zhong, Z.; Song, C.; He, Z.; Cui, W.; Xue, W.; Li, L.; Li, C.; et al. Tunable plasmonic optical responses and the sensing application in graphene-based metasurface. Diam. Relat. Mater. 2022, 126, 109071. [Google Scholar] [CrossRef]
- He, Z.; Cui, W.; Ren, X.; Li, C.; Li, Z.; Xue, W.; Zhang, B.; Zhao, R. Ultra-high sensitivity sensing based on tunable plasmon-induced transparency in graphene metamaterials in terahertz. Opt. Mater. 2020, 108, 110221. [Google Scholar] [CrossRef]
- Wang, M.; Cui, W.; Wang, Y.; Li, M.; Qie, X. Tunable fano-like resonances in graphene metasurface for quad-frequency optoelectronic sensing. Phys. E Low-Dimens. Syst. Nanostruct. 2025, 168, 116191. [Google Scholar] [CrossRef]
- Tan, C.; Wang, S.; Li, S.; Liu, X.; Wei, J.; Zhang, G.; Ye, H. Cancer Diagnosis Using Terahertz-Graphene-Metasurface-Based Biosensor with Dual-Resonance Response. Nanomaterials 2022, 12, 3889. [Google Scholar] [CrossRef] [PubMed]


| MD (%) | IL (dB) | ER (dB) | Ref |
|---|---|---|---|
| 95.6 | 0.315 | / | [44] |
| 94.3 | / | 12.43 | [45] |
| 94.5 | 1.360 | 7.77 | [46] |
| 93.3 | 0.250 | 11.75 | [47] |
| 89.0 | 0.55 | / | [48] |
| 95.04 | 0.08 | 13.00 | This work |
| Structure | Sensitivity (THz/RIU) | FOM (max) | Ref |
|---|---|---|---|
| Graphene | 1.1 | / | [49] |
| Graphene | 3.4269 | 21.92 | [50] |
| Graphene | 0.7928 | 8.12 | [31] |
| Graphene | 1.7134 | 6.998 | [51] |
| Graphene | 1.40 | 17.30 | [10] |
| Graphene | 1.8424 | 44.27 | [52] |
| Graphene | 1.21 | 2.75 | [53] |
| Graphene | 3.70 | 22.40 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, A.; Zhang, M.; Hou, W.; Cheng, L.; Hu, C.; Xu, C. A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects. Photonics 2025, 12, 218. https://doi.org/10.3390/photonics12030218
Zhu A, Zhang M, Hou W, Cheng L, Hu C, Xu C. A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects. Photonics. 2025; 12(3):218. https://doi.org/10.3390/photonics12030218
Chicago/Turabian StyleZhu, Aijun, Mengyi Zhang, Weigang Hou, Lei Cheng, Cong Hu, and Chuanpei Xu. 2025. "A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects" Photonics 12, no. 3: 218. https://doi.org/10.3390/photonics12030218
APA StyleZhu, A., Zhang, M., Hou, W., Cheng, L., Hu, C., & Xu, C. (2025). A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects. Photonics, 12(3), 218. https://doi.org/10.3390/photonics12030218




