Flat Emission Silicon Nitride Grating Couplers for Lidar Optical Antennas
Abstract
1. Introduction
2. Layerstack and Antenna Design Considerations
3. Design of the Single Radiator Element
3.1. Principle of Operation
3.2. Uniform Design
3.3. Non-Uniform Design
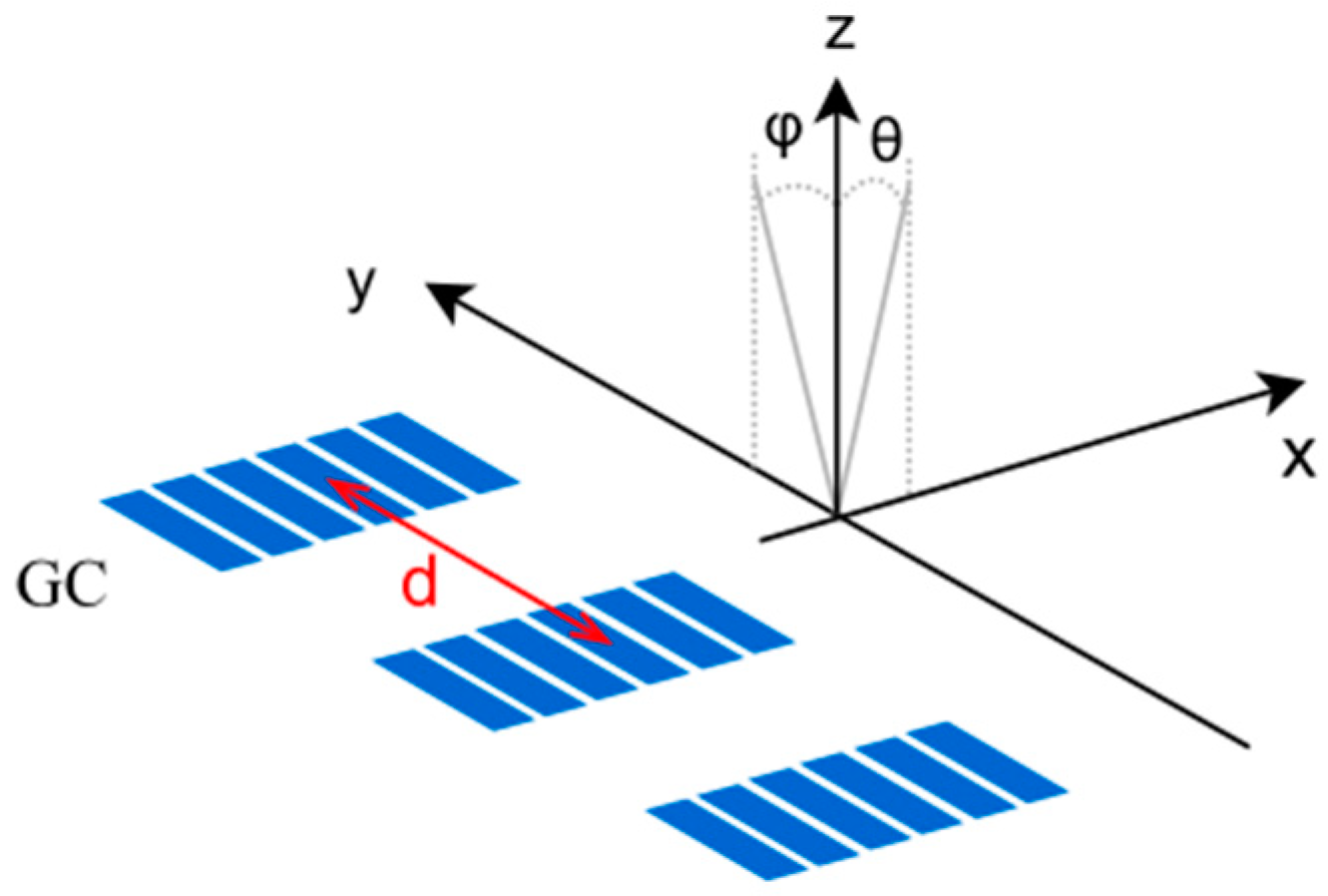
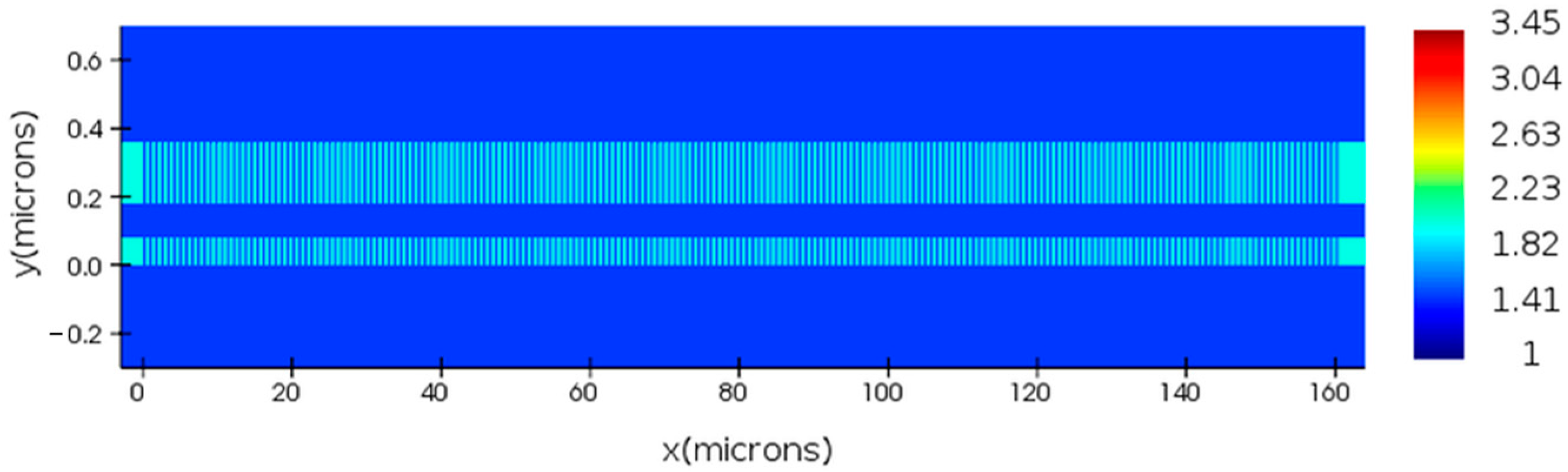
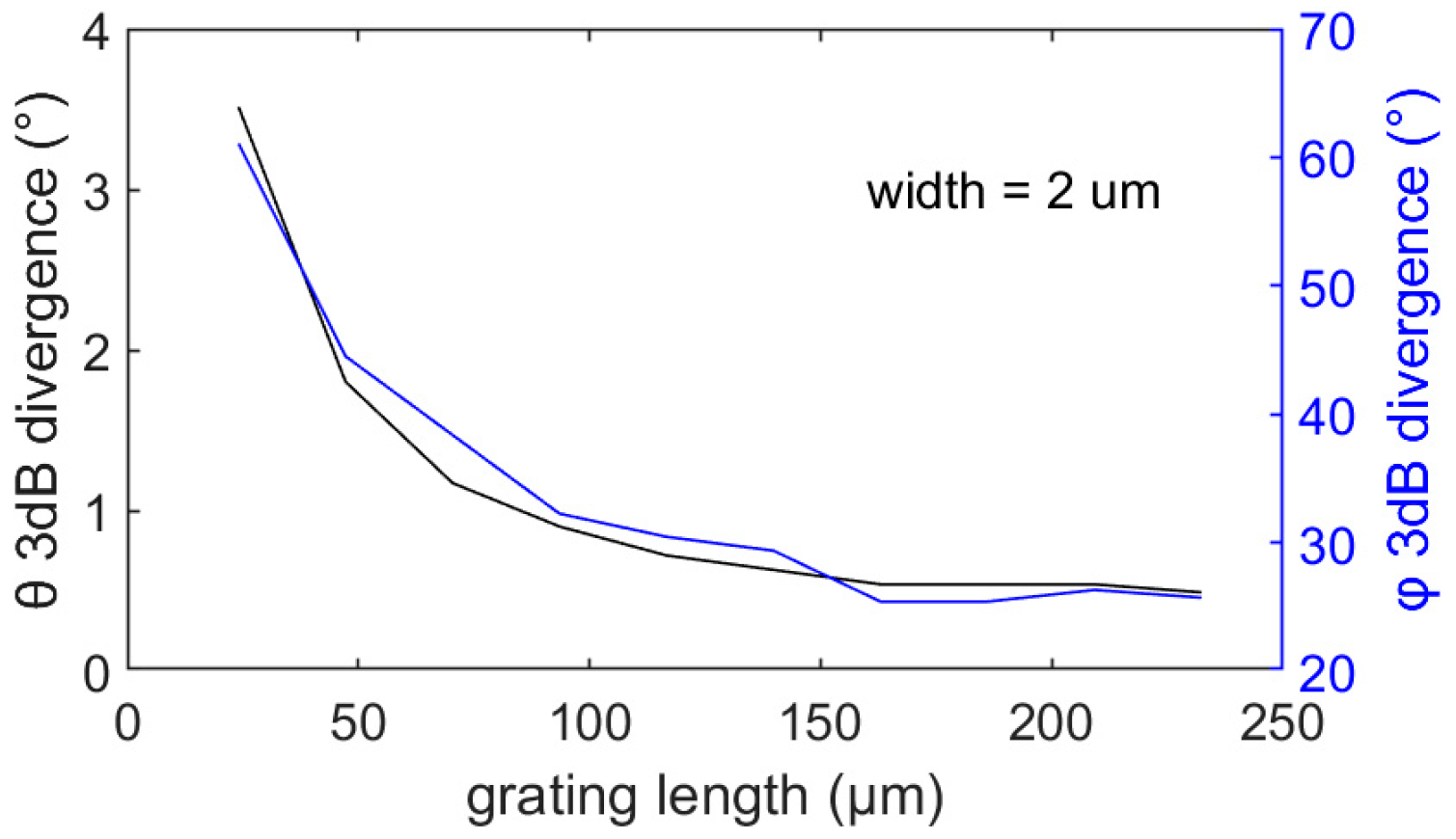
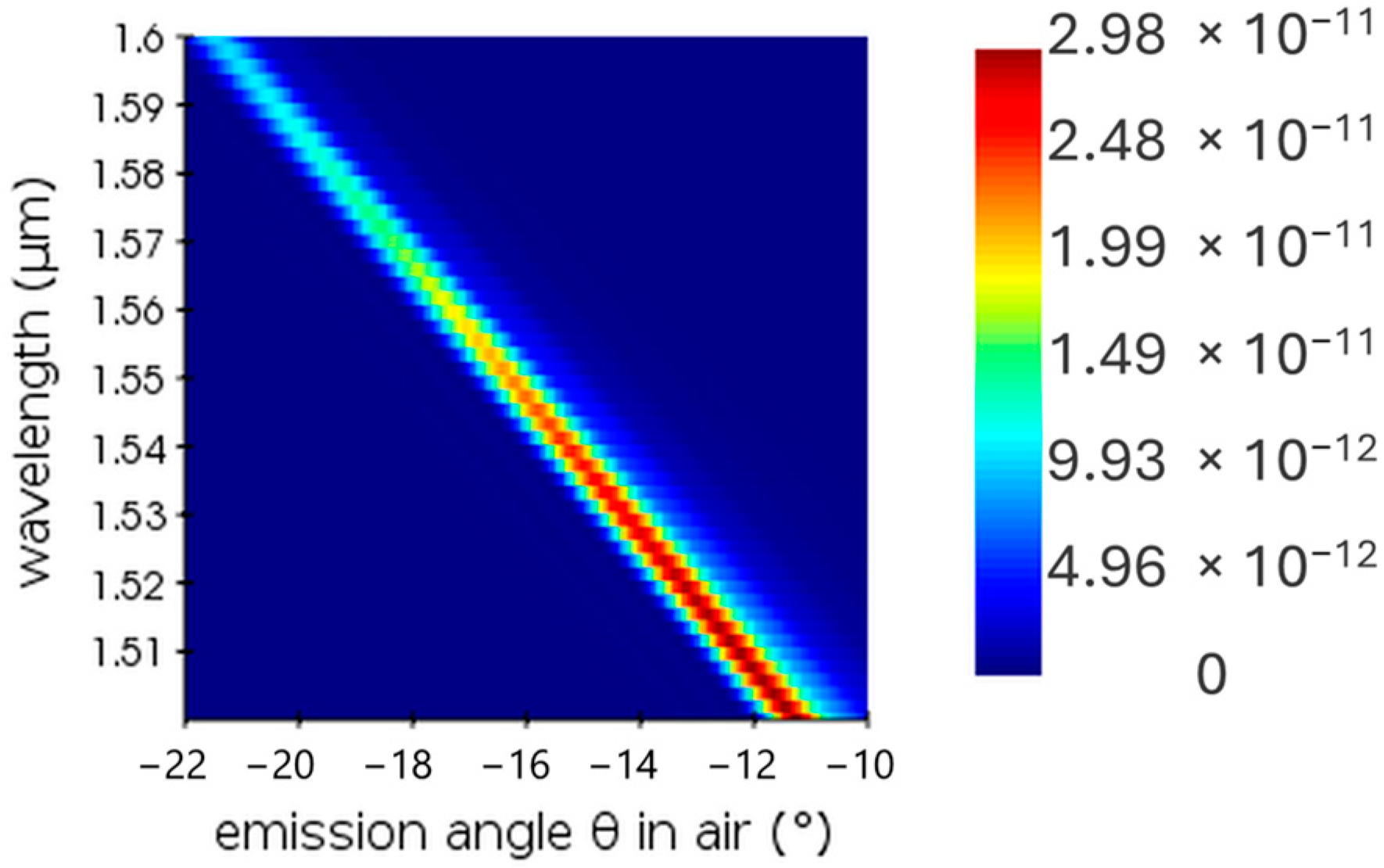
4. Design of the OPA Structure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Lidar | Light detection and ranging |
| PIC | Photonic integrated circuit |
| OPA | Optical phased array |
| UAM | Automated urban air mobility |
| Radar | Radio detection and ranging |
| 3D | Three-dimensional |
| FOV | Field of view |
| MEMS | Micro-electromechanical system |
| SOI | Silicon on insulator |
| CMOS | Complementary metal-oxide semiconductor |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| Si3N4 | Silicon nitride |
| ADS | Asymmetric double stripe |
| MPW | Multi-project wafer |
| GC | Grating coupler |
| SiO2 | Silicon dioxide |
| neff | Effective refractive index |
| FDE | Finite-difference eigenmode |
| FDTD | Finite-difference time domain |
| FF | Filling factor |
References
- Ahmed, F.; Mohanta, J.C.; Keshari, A.; Yadav, P.S. Recent Advances in Unmanned Aerial Vehicles: A Review. Arab. J. Sci. Eng. 2022, 47, 7963–7984. [Google Scholar] [CrossRef]
- Bathla, G.; Bhadane, K.; Singh, R.K.; Kumar, R.; Aluvalu, R.; Krishnamurthi, R.; Kumar, A.; Thakur, R.N.; Basheer, S. Autonomous Vehicles and Intelligent Automation: Applications, Challenges, and Opportunities. Mob. Inf. Syst. 2022, 2022, 7632892. [Google Scholar] [CrossRef]
- Ayala, R.; Mohd, T.K. Sensors in Autonomous Vehicles: A Survey. J. Auton. Veh. Syst. 2021, 1, 031003. [Google Scholar] [CrossRef]
- Falconi, F.; Melo, S.; Scotti, F.; Malik, M.N.; Scaffardi, M.; Porzi, C.; Ansalone, L.; Ghelfi, P.; Bogoni, A. A Combined Radar & Lidar System Based on Integrated Photonics in Silicon-on-Insulator. J. Light. Technol. 2021, 39, 17–23. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, J.; Zhang, F.; Zhang, L.; Yang, T.; Li, Q.; Pan, S. Photonics-Based Radar-Lidar Integrated System for Multi-Sensor Fusion Applications. IEEE Sens. J. 2020, 20, 15068–15074. [Google Scholar] [CrossRef]
- Li, Y.; Ibanez-Guzman, J. Lidar for Autonomous Driving: The Principles, Challenges, and Trends for Automotive Lidar and Perception Systems. IEEE Signal Process. Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Royo, S.; Ballesta-Garcia, M. An Overview of Lidar Imaging Systems for Autonomous Vehicles. Appl. Sci. 2019, 9, 4093. [Google Scholar] [CrossRef]
- Holzhüter, H.; Bödewadt, J.; Bayesteh, S.; Aschinger, A.; Blume, H. Technical concepts of automotive LiDAR sensors: A review. Opt. Eng. 2023, 62, 031213. [Google Scholar] [CrossRef]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- Hu, M.; Pang, Y.; Gao, L. Advances in Silicon-Based Integrated Lidar. Sensors 2023, 23, 5920. [Google Scholar] [CrossRef]
- Li, N.; Ho, C.P.; Xue, J.; Lim, L.W.; Chen, G.; Fu, Y.H.; Lee, L.Y.T. A Progress Review on Solid-State LiDAR and Nanophotonics-Based LiDAR Sensors. Laser Photonics Rev. 2022, 16, 2100511. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-Range LiDAR and Free-Space Data Communication with High-Performance Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 7700108. [Google Scholar] [CrossRef]
- Hashemi, H. A Review of Silicon Photonics LiDAR. In Proceedings of the 2022 IEEE Custom Integrated Circuits Conference (CICC), Newport Beach, CA, USA, 24–27 April 2022; pp. 1–8. [Google Scholar]
- Yoon, J.; Yoon, H.; Kim, J.-Y.; Kim, J.; Kang, G.; Kwon, N.-H.; Kurt, H.; Park, H.-H. Demonstration of high-accuracy 3D imaging using a Si optical phased array with a tunable radiator. Opt. Express 2023, 31, 9935. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Liang, Q.; Feng, J.; Liu, H.; Hu, J.; Yuan, S.; Xia, X.; Jiang, W.; Zhan, Q.; Zeng, H. Free-space beam shaping and steering based on a silicon optical phased array. Photonics Res. 2023, 11, 2093. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Han, X.; Wang, Q.; Wang, Z.; Fang, Y.; He, Y.; Geng, W.; Pan, Z.; Yue, Y. Solid-State Photonics-Based Lidar with Large Beam-Steering Angle by Seamlessly Merging Two Orthogonally Polarized Beams. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 8300608. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Bogaerts, W.; Baets, R. Two-Dimensional Dispersive Off-Chip Beam Scanner Fabricated on Silicon-On-Insulator. IEEE Photonics Technol. Lett. 2011, 23, 1270–1272. [Google Scholar] [CrossRef]
- Im, C.-S.; Bhandari, B.; Lee, K.-P.; Kim, S.-M.; Oh, M.-C.; Lee, S.-S. Silicon nitride optical phased array based on a grating antenna enabling wavelength-tuned beam steering. Opt. Express 2020, 28, 3270. [Google Scholar] [CrossRef]
- Xu, W.; Guo, Y.; Li, X.; Liu, C.; Lu, L.; Chen, J.; Zhou, L. Fully Integrated Solid-State LiDAR Transmitter on a Multi-Layer Silicon-Nitride-on-Silicon Photonic Platform. J. Light. Technol. 2023, 41, 832–840. [Google Scholar] [CrossRef]
- Malhouitre, S.; Fowler, D.; Garcia, S.; Lemonnier, O.; Tyler, N.; Rabaud, W. Silicon Nitride Photonic Platform for LIDAR Applications. In Proceedings of the 2018 IEEE 15th International Conference on Group IV Photonics (GFP), Cancun, Mexico, 29–31 August 2018; pp. 1–2. [Google Scholar]
- Wang, Q.; Wang, S.; Jia, L.; Cai, Y.; Yue, W.; Yu, M. Silicon nitride assisted 1×64 optical phased array based on a SOI platform. Opt. Express 2021, 29, 10509. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Raval, M.; Su, Z.; Li, N.; Timurdogan, E.; Coolbaugh, D.; Vermeulen, D.; Watts, M.R. Large-scale silicon nitride nanophotonic phased arrays at infrared and visible wavelengths. Opt. Lett. 2017, 42, 21. [Google Scholar] [CrossRef]
- Wörhoff, K.; Heideman, R.G.; Leinse, A.; Hoekman, M. TriPleX: A versatile dielectric photonic platform. Adv. Opt. Technol. 2015, 4, 189–207. [Google Scholar] [CrossRef]
- Roeloffzen, C.G.H.; Hoekman, M.; Klein, E.J.; Wevers, L.S.; Timens, R.B.; Marchenko, D.; Geskus, D.; Dekker, R.; Alippi, A.; Grootjans, R.; et al. Low-Loss Si3N4 TriPleX Optical Waveguides: Technology and Applications Overview. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 4400321. [Google Scholar] [CrossRef]
- Raval, M.; Poulton, C.V.; Watts, M.R. Unidirectional waveguide grating antennas with uniform emission for optical phased arrays. Opt. Lett. 2017, 42, 2563. [Google Scholar] [CrossRef]
- Shang, K.; Qin, C.; Zhang, Y.; Liu, G.; Xiao, X.; Feng, S.; Yoo, S.J.B. Uniform emission, constant wavevector silicon grating surface emitter for beam steering with ultra-sharp instantaneous field-of-view. Opt. Express 2017, 25, 19655. [Google Scholar] [CrossRef] [PubMed]
- Yepez, P.A.K.; Scholz, U.; Zimmermann, A. Temperature Dependence of the Steering Angles of a Silicon Photonic Optical Phased Array. IEEE Photonics J. 2020, 12, 6800813. [Google Scholar] [CrossRef]
- Spencer, D.T.; Davenport, M.; Srinivasan, S.; Khurgin, J.; Morton, P.A.; Bowers, J.E. Low kappa, narrow bandwidth Si_3N_4 Bragg gratings. Opt. Express 2015, 23, 30329. [Google Scholar] [CrossRef] [PubMed]












| d | 1.5λ | 2λ | 2.5λ | |
|---|---|---|---|---|
| Width | ||||
| 1 μm | 45 μm | 250 μm | 1400 μm | |
| 1.5 μm | 40 μm | 300 μm | 2280 μm | |
| 2 μm | 20 μm | 185 μm | 1600 μm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prousalidi, T.; Syriopoulos, G.; Kyriazi, E.; Botter, R.; Zervos, C.; Poulopoulos, G.; Apostolopoulos, D. Flat Emission Silicon Nitride Grating Couplers for Lidar Optical Antennas. Photonics 2025, 12, 214. https://doi.org/10.3390/photonics12030214
Prousalidi T, Syriopoulos G, Kyriazi E, Botter R, Zervos C, Poulopoulos G, Apostolopoulos D. Flat Emission Silicon Nitride Grating Couplers for Lidar Optical Antennas. Photonics. 2025; 12(3):214. https://doi.org/10.3390/photonics12030214
Chicago/Turabian StyleProusalidi, Thenia, Georgios Syriopoulos, Evrydiki Kyriazi, Roel Botter, Charalampos Zervos, Giannis Poulopoulos, and Dimitrios Apostolopoulos. 2025. "Flat Emission Silicon Nitride Grating Couplers for Lidar Optical Antennas" Photonics 12, no. 3: 214. https://doi.org/10.3390/photonics12030214
APA StyleProusalidi, T., Syriopoulos, G., Kyriazi, E., Botter, R., Zervos, C., Poulopoulos, G., & Apostolopoulos, D. (2025). Flat Emission Silicon Nitride Grating Couplers for Lidar Optical Antennas. Photonics, 12(3), 214. https://doi.org/10.3390/photonics12030214





