Design and Analysis of Enhanced IM/DD System with Nonorthogonal Code Shift Keying and Parallel Transmission
Abstract
1. Introduction
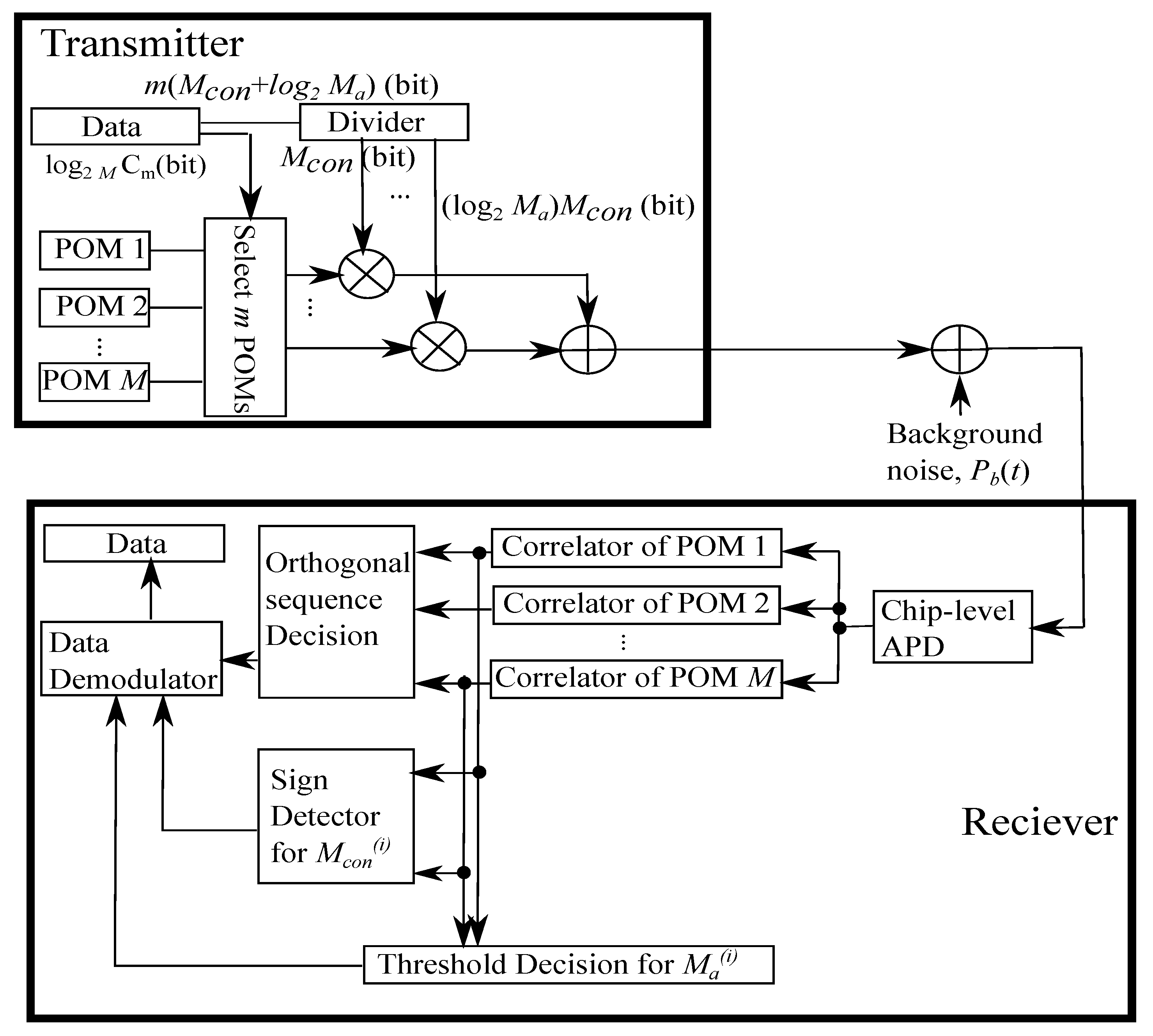
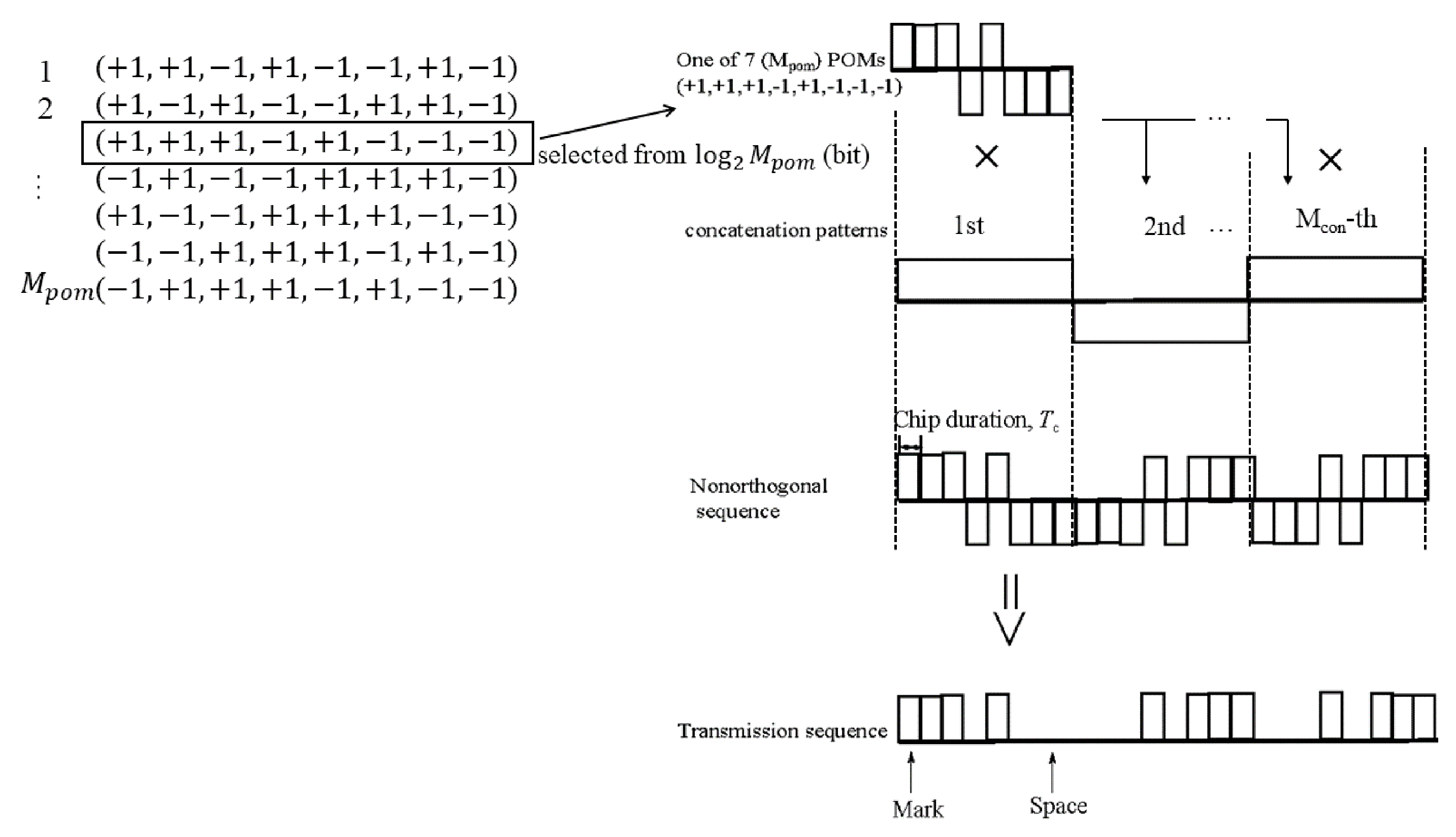
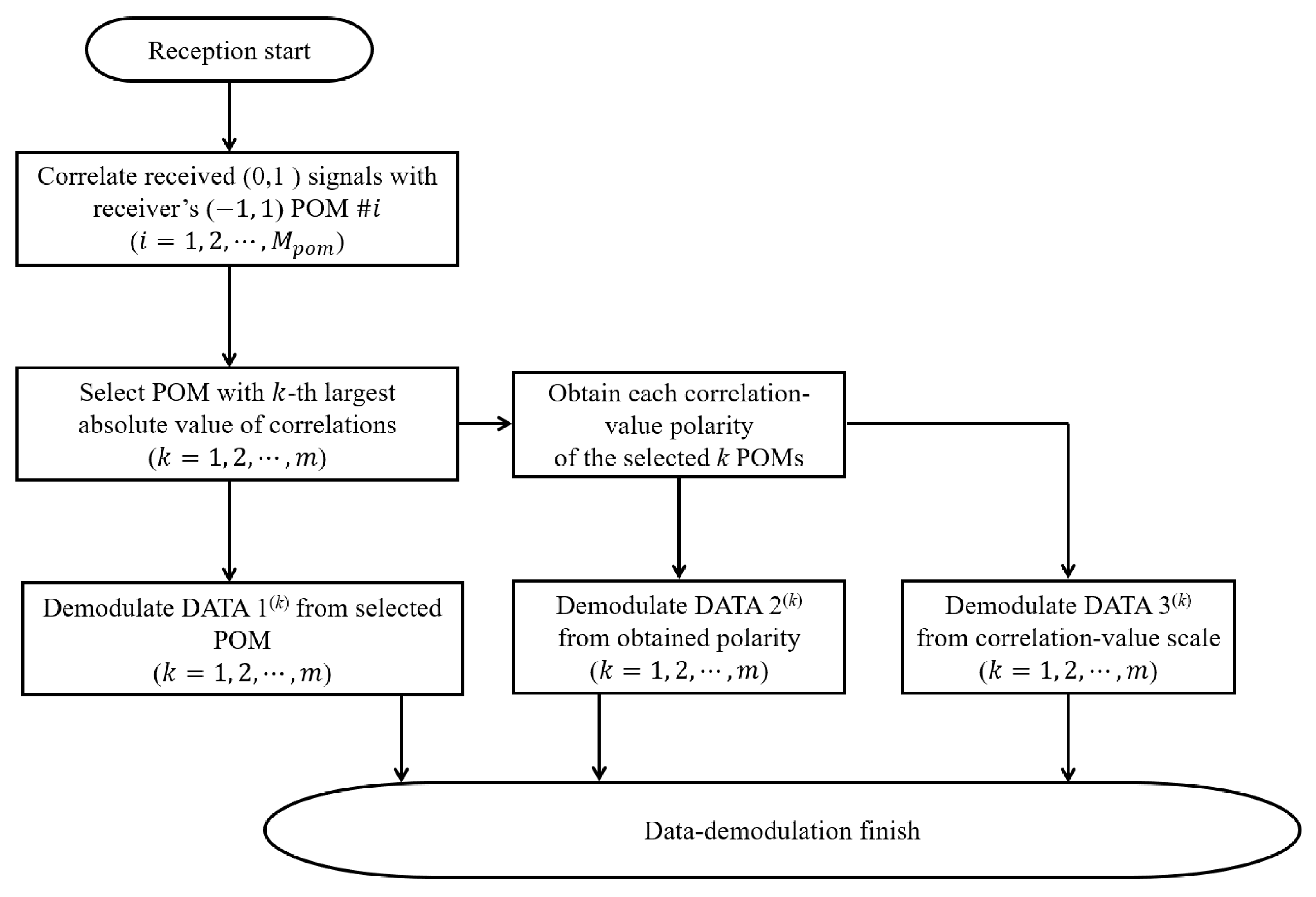
2. Proposed System Framework
2.1. Design of Nonorthogonal Codes
2.2. System Architecture
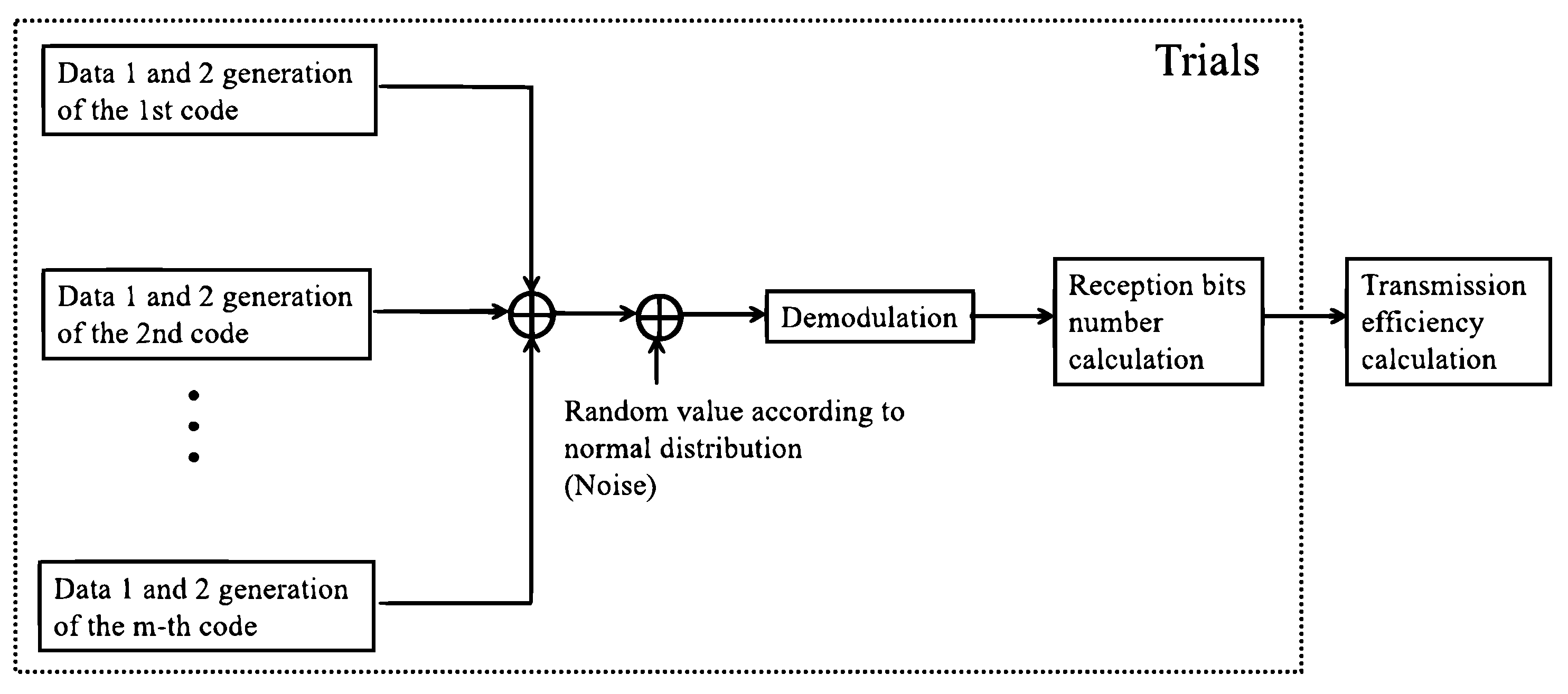
3. Theoretical Analysis
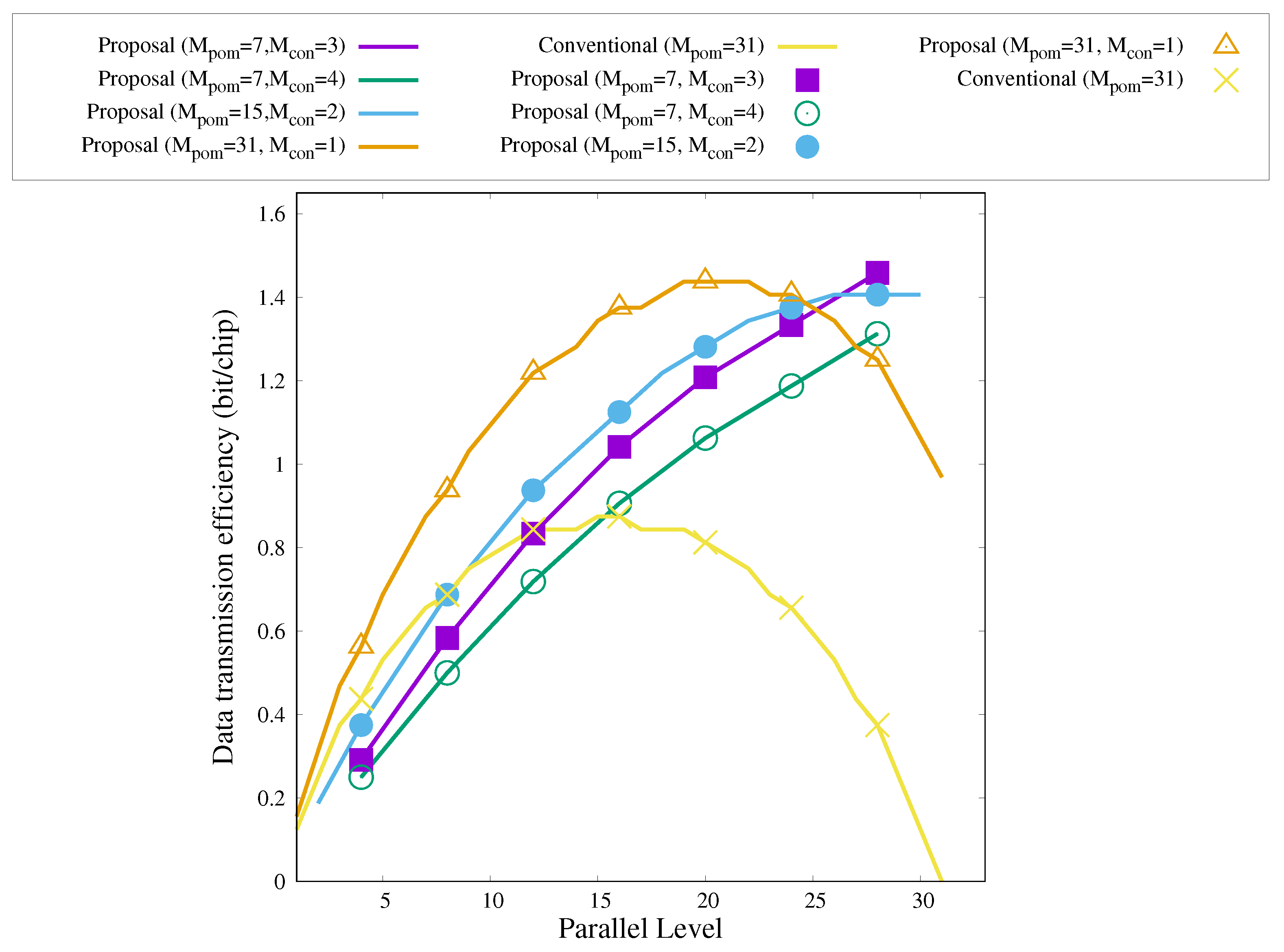
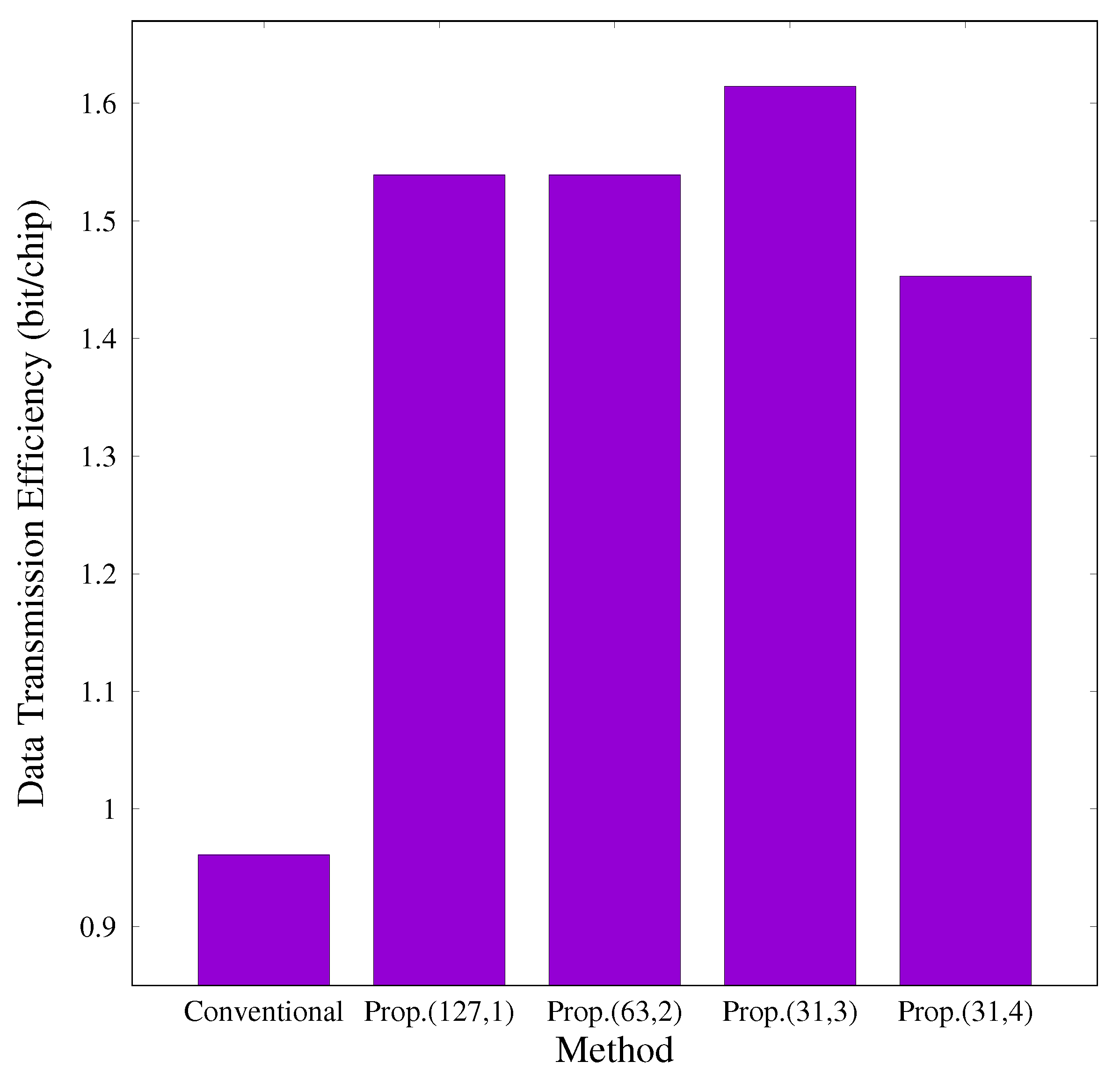
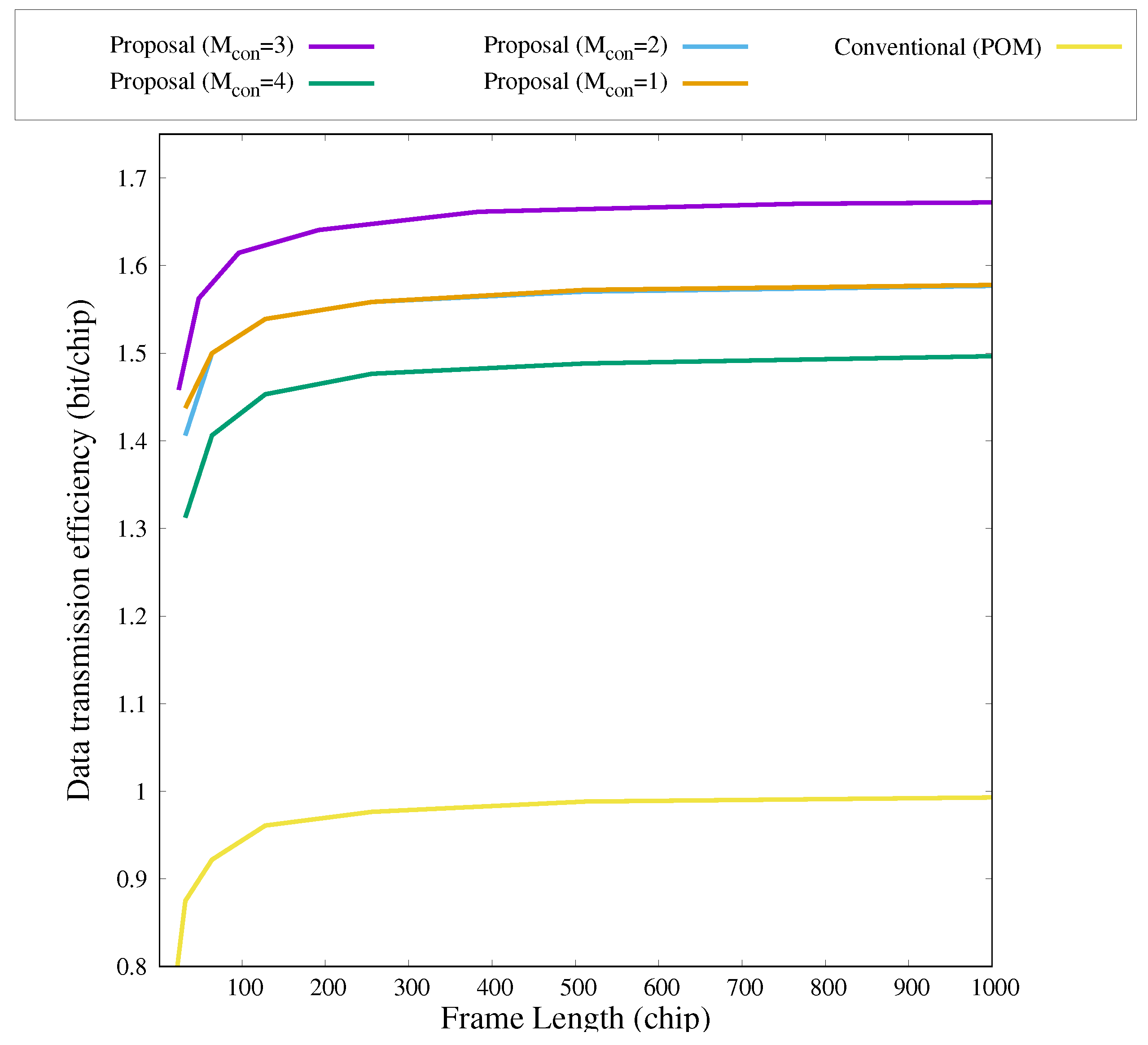
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwon, H. Optical Orthogonal Code-division Multiple-access system – Part I: APD Noise and Thermal Noise. IEEE Trans. Commun. 1994, 42, 2470–2479. [Google Scholar] [CrossRef]
- Qiu, Y.; Chen, S.; Chen, H.; Meng, W. Visible Light Communication based on CDMA Technology. IEEE Wirel. Commun. 2018, 25, 178–185. [Google Scholar] [CrossRef]
- Liu, M.; Wang, T.; Tseng, S. Throughput Performance Analysis of Asynchronous Optical CDMA Networks with Channel Load Sensing Protocol. IEEE Photonics J. 2017, 9, 7202313. [Google Scholar] [CrossRef]
- Chen, S.; Chow, C. Color-shift Keying Code-division Multiple-access Transmission for RGB-LED Visible Light Communications using Mobile Phone Camera. IEEE Photonics J. 2014, 7, 7904106. [Google Scholar] [CrossRef]
- Kiasaleh, K. Performance of APD-based, PPM Free-space Optical Communication Systems in Atmospheric Turbulence. IEEE Trans. Commun. 2014, 53, 1455–1461. [Google Scholar] [CrossRef]
- Zhu, X.; Kahn, J. Free-space Optical Communication through Atmospheric Turbulence Channels. IEEE Trans. Commun. 2002, 50, 1293–1300. [Google Scholar]
- Kumari, M.; Sharma, A.; Chaudhary, S. High-Speed Spiral-Phase Donut-Modes-Based Hybrid FSO-MMF Communication System by Incorporating OCDMA Scheme. Photonics 2023, 10, 94. [Google Scholar] [CrossRef]
- Hadi, M.; Pakravan, M. Analysis and Design of Adaptive OCDMA Passive Optical Networks. J. Light. Technol. 2017, 35, 2853–2863. [Google Scholar] [CrossRef]
- Hien, T.; Pham, T.; Dang, N.T. Analog network coding aided multiuser visible light communication networks using optical CDMA. OSA Contin. 2019, 2, 2569–2580. [Google Scholar]
- Yeh, B.C. Utilizing States of Polarization in One-Dimensional Corite Codes with Two-Code Keying for Optical Code-Division Multiple Access. Photonics 2024, 11, 819. [Google Scholar] [CrossRef]
- Li, J.; Uysal, M. Optical Wireless Communications: System Model, Capacity and Coding. Proc. IEEE VTC 2003, 1, 168–172. [Google Scholar]
- Babar, Z.; Izhar, M.; Nguyen, H.; Botsinis, P.; Alanis, D.; Chandra, D.; Ng, S. Unary-Coded Dimming Control Improves On-Off Keying Visible Light Communication. IEEE Trans. Commun. 2018, 66, 255–264. [Google Scholar] [CrossRef]
- Fuji-Hara, R.; Miao, Y. Optical orthogonal codes: Their bounds and new optimal constructions. IEEE Trans. Inf. Theory 2000, 46, 2396–2406. [Google Scholar]
- Kwong, W.; Perrier, P.; Pruncnal, P. Performance comparison of asynchronous and synchronous code-division multiple-access techniques for fiber-optic local area networks. IEEE Trans. Commun. 1991, 39, 1625–1634. [Google Scholar] [CrossRef]
- Matsushima, T.; Nagano, T.; Ochiai, N.; Teramachi, Y. Generalization of modified prime sequence codes and its properties. IEICE Trans. Fundam. 2008, E91-A, 559–573. [Google Scholar]
- Yamashita, T.; Hanawa, M.; Tanaka, Y.; Takahara, M. An Optical Code Division Multiplexing System using Hadamard Codes and SIK. IEICE Tech. Rep. 1998, OCS98-1, 1–6. [Google Scholar]
- Kozawa, Y.; Habuchi, H. Theoretical Analysis of Atmospheric Optical DS/SS with On-off Orthogonal M-sequence Pairs. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007; p. P0686. [Google Scholar]
- Islam, A.; Majumder, S.P. Effect of atmospheric turbulence on the BER performance of an optical CDMA FSO link with SIK receiver. Optik 2019, 179, 867–874. [Google Scholar] [CrossRef]
- Kozawa, Y.; Habuchi, H. Theoretical Analysis of Optical Wireless CDMA with Modified Pseudo Orthogonal M-Sequence Sets. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Honolulu, HI, USA, 30 November–4 December 2009; p. 11170402. [Google Scholar]
- Ochiai, N.; Kushibiki, S.; Matsushima, T.; Teramachi, Y. Performance Analysis of Synchronous Optical CDMA System with EWO signaling. IEICE Trans. Fundam. 2003, J86-A, 957–968. [Google Scholar] [CrossRef]
- Hsieh, C.P.; Chang, C.Y.; Yang, G.C.; Kwong, W. A Bipolar-bipolar Code for Asynchronous Wavelength-time Optical CDMA. IEEE Trans. Commun. 2006, 54, 2572–2578. [Google Scholar]
- Haas, H.; Yin, L.; Wang, Y.; Chen, C. What is LiFi? J. Light. Technol. 2016, 34, 1533–1544. [Google Scholar] [CrossRef]
- Elgala, H.; Mesleh, R.; Haas, H. Indoor optical wireless communication: Potential and state-of-the-art. IEEE Commun. Mag. 2011, 49, 56–62. [Google Scholar] [CrossRef]
- Oubei, H.M.; Shen, C.; Kammoun, A.; Zedini, E.; Park, K.H.; Sun, X.; Liu, G.; Kang, C.H.; Ng, T.K.; Alouini, M.S.; et al. Light based underwater wireless communications. Jpn. J. Appl. Phys. 2018, 57, 08PA06. [Google Scholar] [CrossRef]
- Luo, P.; Ghassemlooy, Z.; Le Minh, H.; Bentley, E.; Burton, A.; Tang, X. Fundamental analysis of a car to car visible light communication system. In Proceedings of the 2014 9th International Symposium on Communication Systems, Networks & Digital Sign (CSNDSP), Manchester, UK, 23–25 July 2014; pp. 1011–1016. [Google Scholar]
- Cove, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 689–721. [Google Scholar]
- Ansari, I.S.; AlQuwaiee, H.; Zedini, E.; Alouini, M.S. Information Theoretical Limits of Free-Space Optical Links. In Optical Wireless Communications: An Emerging Technology; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 171–208. [Google Scholar]
- Otsuki, T. Performance Analysis of Atmospheric Optical PPM CDMA Systems. J. Light. Technol. 2003, 2, 406–411. [Google Scholar] [CrossRef]
- Azim, A.W.; Bazzi, A.; Fatima, M.; Shubair, R.; Chafii, M. Dual-Mode Time Domain Multiplexed Chirp Spread Spectrum. IEEE Trans. Veh. Technol. 2023, 72, 16086–16097. [Google Scholar] [CrossRef]
- Hazu, R.; Kozawa, Y.; Habuchi, H. Visual Secret Sharing Based RGB Parallel Transmission System. In Proceedings of the 24th International Symposium On Wireless Personal Multimedia Communications (WPMC2021), Okayama, Japan, 14–16 December 2021; pp. 1–5. [Google Scholar]
- Tokunaga, T.; Habuchi, H.; Kozawa, Y. New two-layered pseudo-noise code for optical-wireless code-shift keying/SCDMA. In Proceedings of the 2017 Eighth International Workshop on Signal Design and Its Applications in Communications (IWSDA), Sapporo, Japan, 24–28 September 2017; pp. 149–153. [Google Scholar]
- Komuro, N.; Habuchi, H.; Tsuboi, T. Nonorthogonal CSK/CDMA with Received-Power Adaptive Access Control Scheme. IEICE Trans. Fundam. 2008, E91-A, 2779–2786. [Google Scholar] [CrossRef]
- Komuro, N.; Habuchi, H. Intensity Modulation Direct Detection Optical Wireless Communication with Nonorthogonal Code Shift Keying. In Proceedings of the IEEE Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; pp. 723–726. [Google Scholar]
- Komuro, N.; Habuchi, H. Design and Analysis of Optical Wireless Code Shift Keying with Nonorthogonal Sequences. OSA Contin. 2021, 4, 1437–1451. [Google Scholar] [CrossRef]
- Luong, D.; Thang, T.; Pham, A. Effect of Avalanche Photodiode and Thermal Noises on the Performance of Binary Phase-shift keying-subcarrier-intensity Modulation/free-space Optical Systems over Turbulence Channels. IET Commun. 2013, 7, 738–744. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Chip duration, | |
| APD effective ionization ratio, | 0.02 |
| Average APD gain, G | 100 |
| Modulation extinction ratio of the laser diode output power | 100 |
| in the mark and space states, | |
| Boltzmann’s constant, | |
| Receiver noise temperature, | 300 (K) |
| Receive load resistor, | 1030 () |
| Elementary charge, e | (C) |
| Planck’s constant, h | |
| APD bulk leakage current, | 0.1 (nA) |
| APD surface leakage current, | 10 (nA) |
| Quantum efficiency, | 0.6 |
| Laser wavelength, | 830 (nm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komuro, N.; Habuchi, H. Design and Analysis of Enhanced IM/DD System with Nonorthogonal Code Shift Keying and Parallel Transmission. Photonics 2025, 12, 166. https://doi.org/10.3390/photonics12020166
Komuro N, Habuchi H. Design and Analysis of Enhanced IM/DD System with Nonorthogonal Code Shift Keying and Parallel Transmission. Photonics. 2025; 12(2):166. https://doi.org/10.3390/photonics12020166
Chicago/Turabian StyleKomuro, Nobuyoshi, and Hiromasa Habuchi. 2025. "Design and Analysis of Enhanced IM/DD System with Nonorthogonal Code Shift Keying and Parallel Transmission" Photonics 12, no. 2: 166. https://doi.org/10.3390/photonics12020166
APA StyleKomuro, N., & Habuchi, H. (2025). Design and Analysis of Enhanced IM/DD System with Nonorthogonal Code Shift Keying and Parallel Transmission. Photonics, 12(2), 166. https://doi.org/10.3390/photonics12020166






