Behavior of Finite-Energy Fresnel–Bessel Beams in Long Free-Space Optical Communication Links
Abstract
1. Introduction
2. Theoretical Formulations
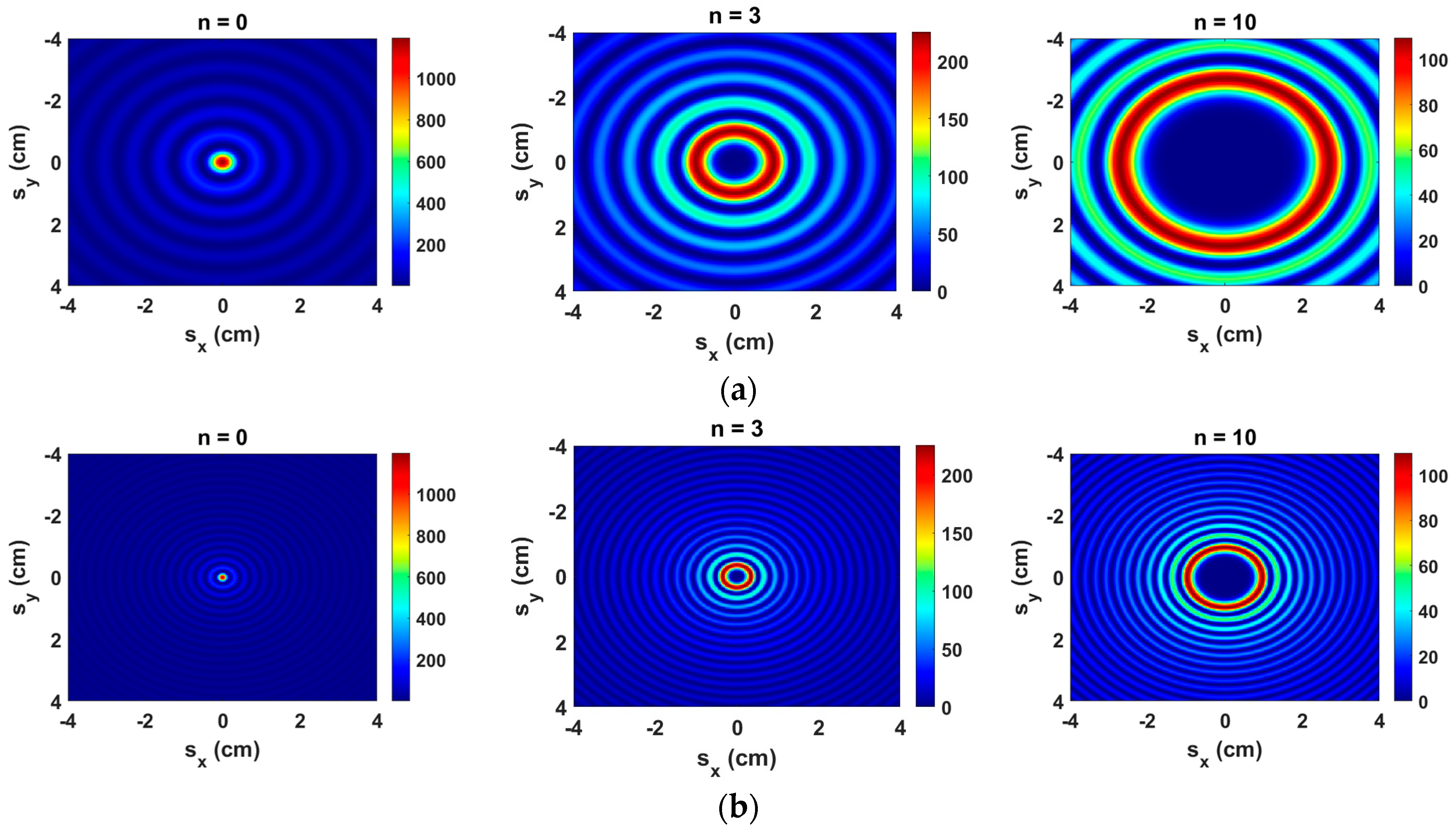
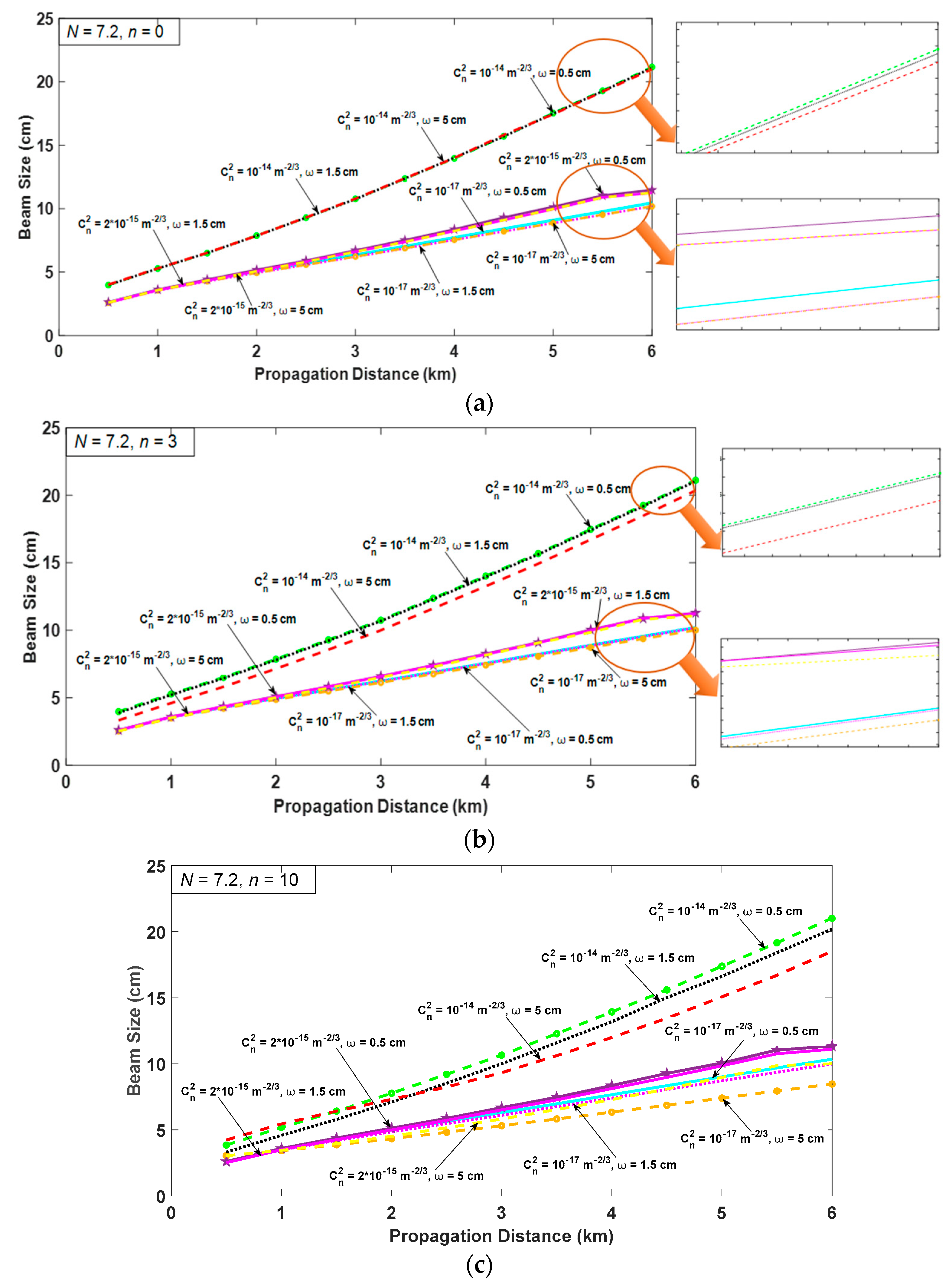
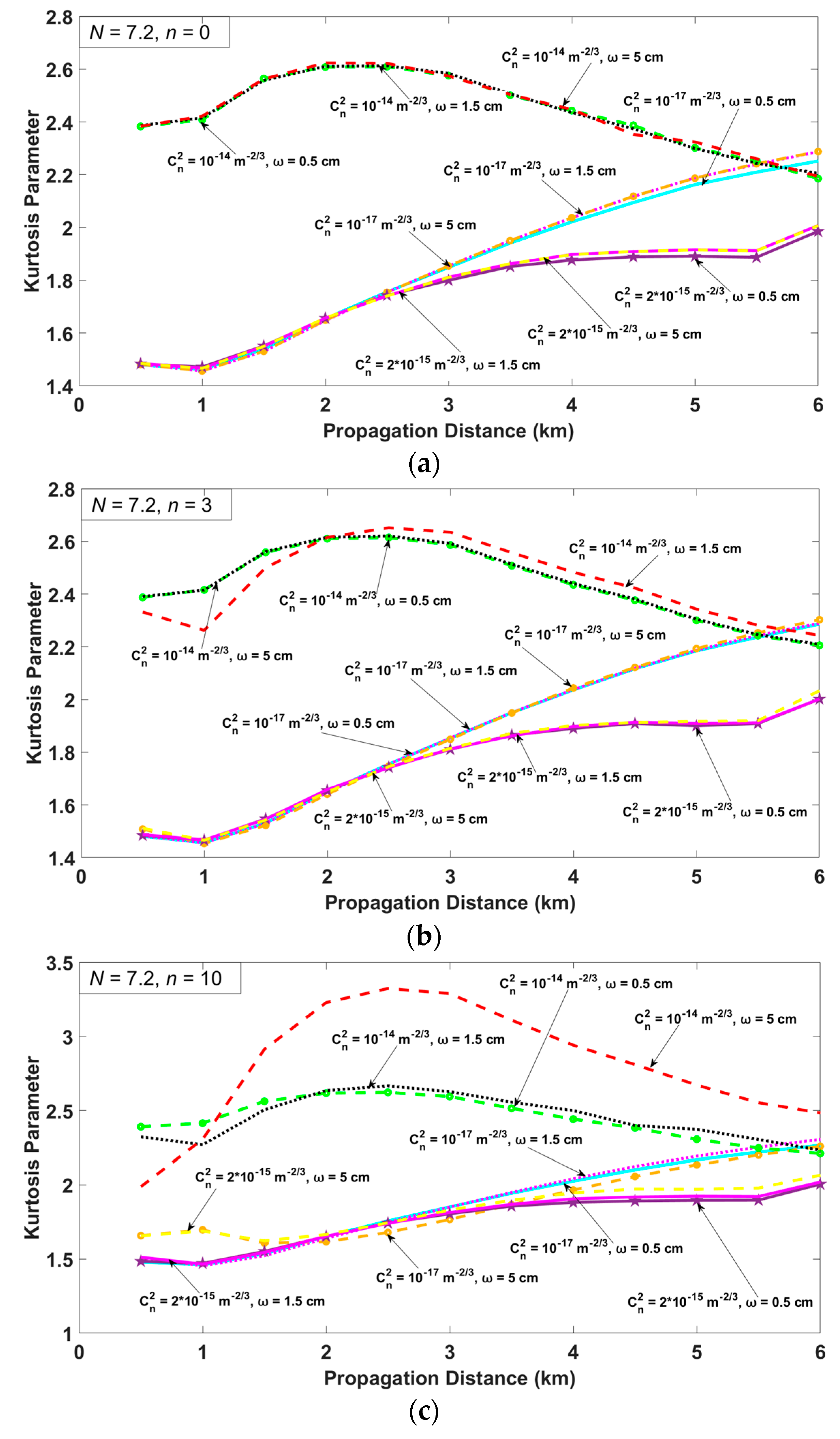
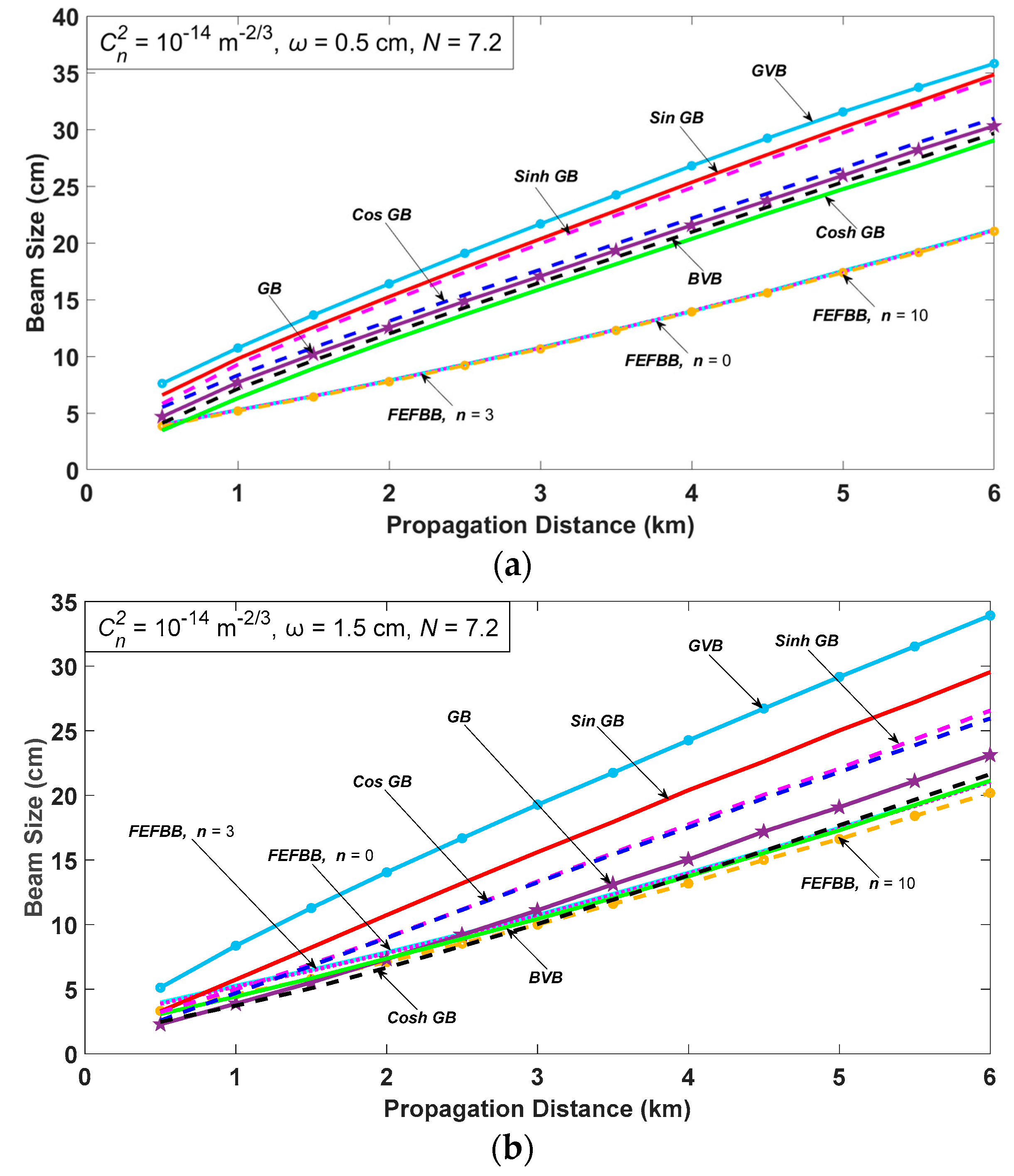
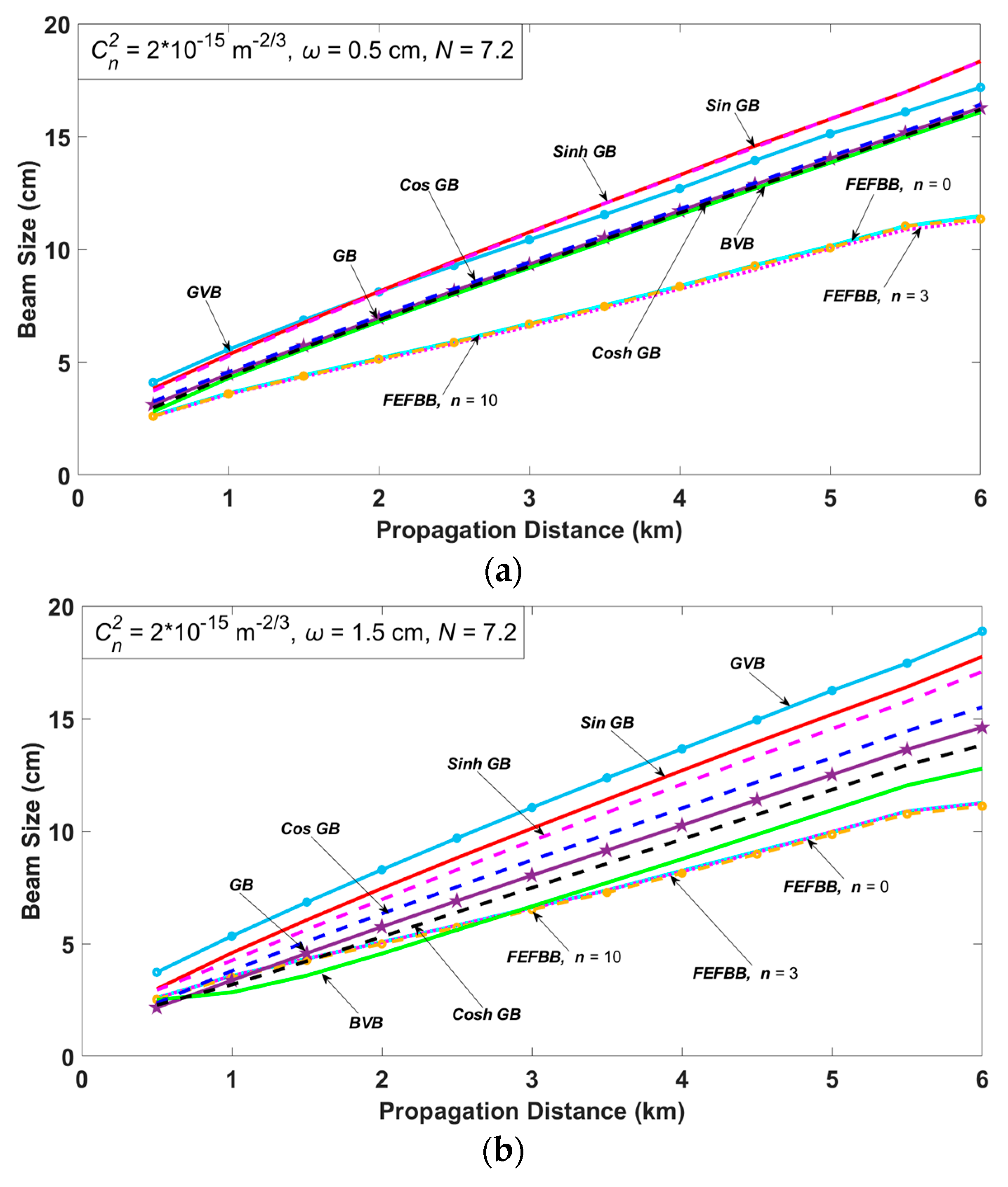
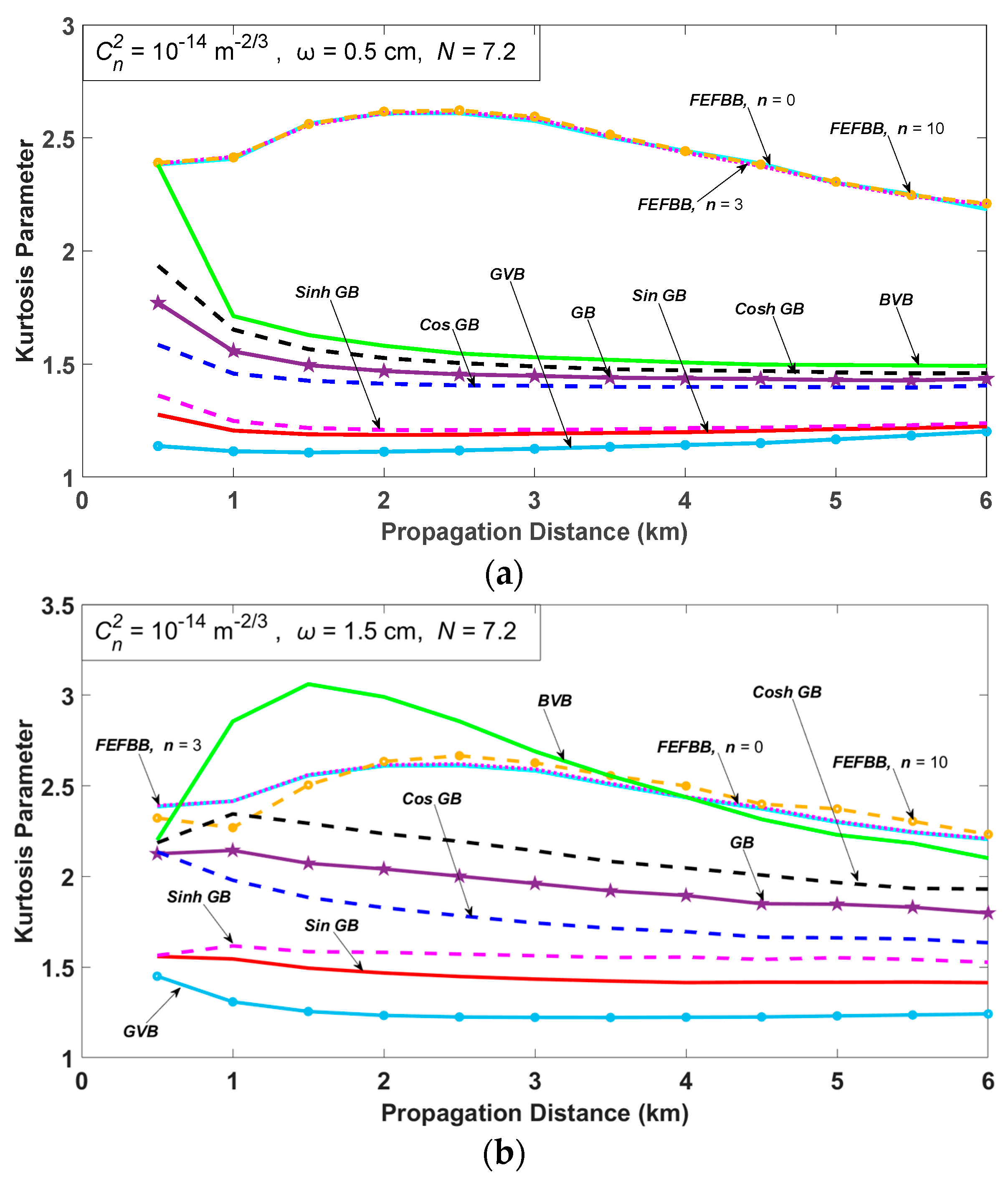
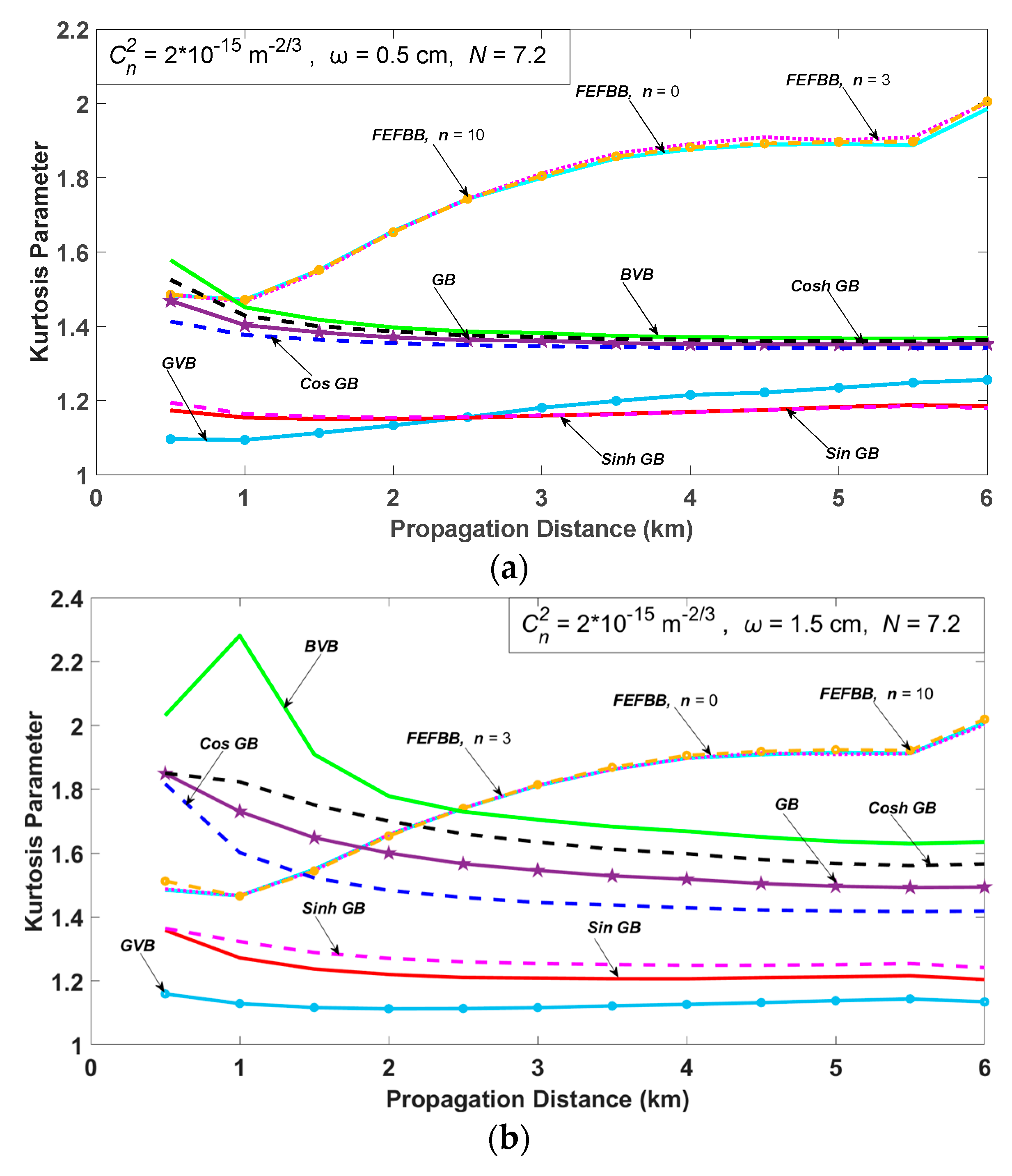
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2022, 11, 645–680. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Young, C.Y. Laser Beam Scintillation with Applications; SPIE: Bellingham, WA, USA, 2001. [Google Scholar]
- Pu, J.-X.; Wang, T.; Lin, H.-C.; Li, C.-L. Propagation of cylindrical vector beams in a turbulent atmosphere. Chin. Phys. B 2010, 19, 089201. [Google Scholar] [CrossRef]
- Bayraktar, M. Performance of Airyprime beam in turbulent atmosphere. Photon-Netw. Commun. 2021, 41, 274–279. [Google Scholar] [CrossRef]
- Bayraktar, M. Scintillation and bit error rate calculation of Mathieu-Gauss beam in turbulence. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2671–2683. [Google Scholar] [CrossRef]
- El Mechate, B.; Chafiq, A.; Belafhal, A. Ince–Gaussian beams propagation through turbulent atmospheric medium. Opt. Quantum Electron. 2024, 56, 667. [Google Scholar] [CrossRef]
- Eyyuboğlu, H.T.; Voelz, D.; Xiao, X. Scintillation analysis of truncated Bessel beams via numerical turbulence propagation simu-lation. Appl Opt. 2013, 52, 8032–8039. [Google Scholar] [CrossRef]
- Saad, F.; El Halba, E.M.; Belafhal, A. A theoretical study of the on-axis average intensity of generalized spiraling Bessel beams in a turbulent atmosphere. Opt. Quantum Electron. 2017, 49, 94. [Google Scholar] [CrossRef]
- Soifer, V.A.; Korotkova, O.; Khonina, S.N.; Shchepakina, E.A. Vortex beams in turbulent media: Review. Comput. Opt. 2016, 40, 605–624. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, D.; Yuan, X.; Zhou, Z. Numerical investigation of flat-topped vortex hollow beams and Bessel beams propagating in a turbulent atmosphere. Appl. Opt. 2016, 55, 9211–9216. [Google Scholar] [CrossRef]
- Yuan, Y.; Lei, T.; Li, Z.; Li, Y.; Gao, S.; Xie, Z.; Yuan, X. Beam wander relieved orbital angular momentum communication in turbulent atmosphere using Bessel beams. Sci. Rep. 2017, 7, srep42276. [Google Scholar] [CrossRef] [PubMed]
- Lukin, I.P. Mean intensity of vortex Bessel beams propagating in turbulent atmosphere. Appl. Opt. 2014, 53, 3287–3293. [Google Scholar] [CrossRef] [PubMed]
- Litvin, I.A.; Munar-Vallespir, P.; Nötzel, J. The channel capacity of the free space communication link based on Bessel-like beams. J. Opt. 2024, 27, 015701. [Google Scholar] [CrossRef]
- Wen, W. Quantitative Analysis of the Effect of Atmospheric Turbulence on a Bessel–Gaussian Beam. Photonics 2023, 10, 932. [Google Scholar] [CrossRef]
- Lorenser, D.; Christian Singe, C.; Curatolo, A.; Sampson, D.D. Energy-efficient low-Fresnel-number Bessel beams and their application in optical coherence tomography. Opt. Lett. 2014, 39, 548–551. [Google Scholar] [CrossRef]
- El Halba, E.M.; Ez-Zariy, L.; Belafhal, A. Creation of generalized spiraling bessel beams by fresnel diffraction of Bessel–Gaussian laser beams. Opt. Quantum Electron. 2017, 49, 236. [Google Scholar] [CrossRef]
- Akcan, C.I.; Bayraktar, M.; Elmabruk, K. Analysis of finite energy fresnel bessel beams scintillation level in turbulent commu-nication links. Phys. Scr. 2024, 99, 065505. [Google Scholar] [CrossRef]
- Adrews, L.C.; Philips, R.L.; Weeks, A.R. Propagation of a Gaussian-beam wave through a random phase screen. Waves Ran-Dom Media 1997, 7, 229. [Google Scholar] [CrossRef]
- Whitfield, E.M.; Banerjee, P.P.; Haus, J.W. Propagation of Gaussian beams through a modified von Karman phase screen. In Proceedings of the Laser Communication and Propagation through the Atmosphere and Oceans, San Diego, CA, USA, 12–16 August 2012; p. 85170P. [Google Scholar]
- Lukin, I.P.; Rychkov, D.S.; Falits, A.V.; Lai, K.S.; Liu, M.R. A phase screen model for simulating numerically the propagation of a laser beam in rain. Quantum Electron. 2009, 39, 863–868. [Google Scholar] [CrossRef]
- Eyyuboğlu, H.T. Propagation analysis of Ince–Gaussian beams in turbulent atmosphere. Appl. Opt. 2014, 53, 2290–2296. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media, 2nd ed.; SPIE Press Monograph; SPIE Press: Bellingham, WA, USA, 2005; 782p. [Google Scholar]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE-The International Society for Optical Engineering: Bellingham, WA, USA, 2010; ISBN 9780819483270. [Google Scholar]
- Elmabruk, K. Effect of system parameters on power scintillation of Ince Gaussian beam in turbulent atmosphere. Opt. Eng. 2022, 61, 126105. [Google Scholar] [CrossRef]
- Yüceer, M.; Eyyuboğlu, H.T. Laguerre-Gaussian beam scintillation on slant paths. Appl. Phys. B Laser Opt. 2012, 109, 311–316. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akcan, C.I.; Bayraktar, M.; Chatzinotas, S.; Elmabruk, K. Behavior of Finite-Energy Fresnel–Bessel Beams in Long Free-Space Optical Communication Links. Photonics 2025, 12, 158. https://doi.org/10.3390/photonics12020158
Akcan CI, Bayraktar M, Chatzinotas S, Elmabruk K. Behavior of Finite-Energy Fresnel–Bessel Beams in Long Free-Space Optical Communication Links. Photonics. 2025; 12(2):158. https://doi.org/10.3390/photonics12020158
Chicago/Turabian StyleAkcan, Cemre Irem, Mert Bayraktar, Symeon Chatzinotas, and Kholoud Elmabruk. 2025. "Behavior of Finite-Energy Fresnel–Bessel Beams in Long Free-Space Optical Communication Links" Photonics 12, no. 2: 158. https://doi.org/10.3390/photonics12020158
APA StyleAkcan, C. I., Bayraktar, M., Chatzinotas, S., & Elmabruk, K. (2025). Behavior of Finite-Energy Fresnel–Bessel Beams in Long Free-Space Optical Communication Links. Photonics, 12(2), 158. https://doi.org/10.3390/photonics12020158






