Optically Referenced Microwave Generator with Attosecond-Level Timing Noise
Abstract
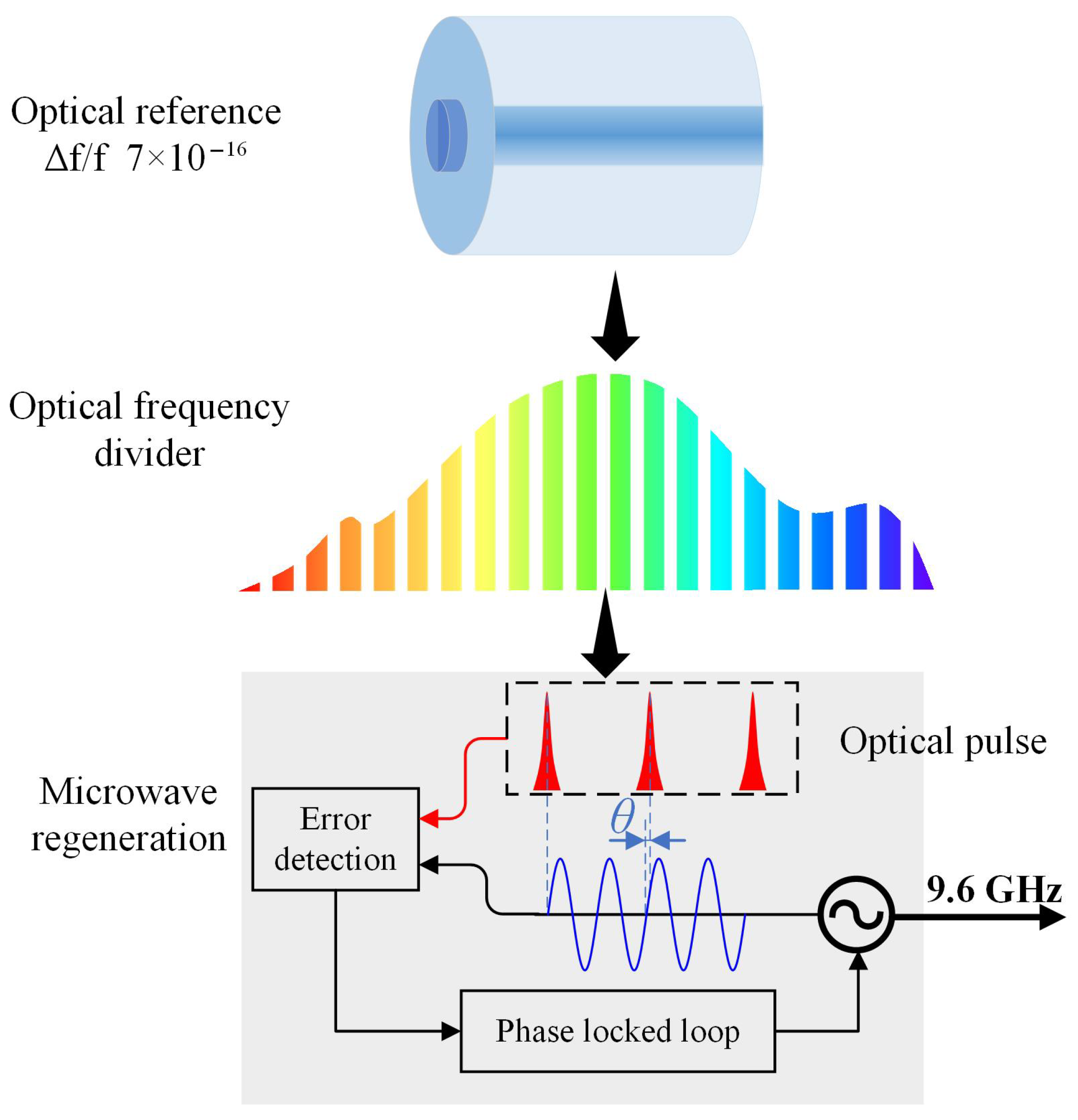
1. Introduction
2. Materials and Methods
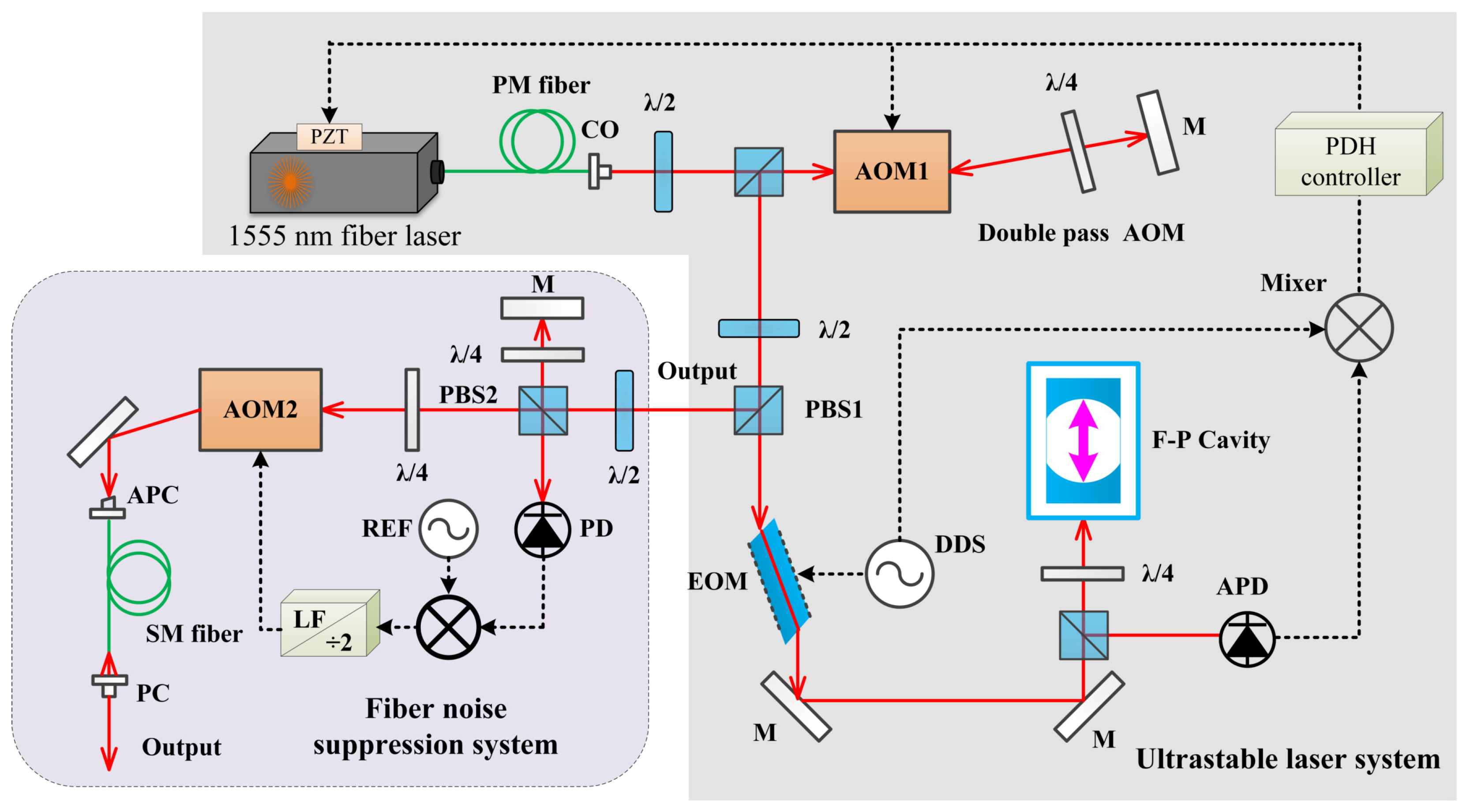
2.1. Ultrastable Laser
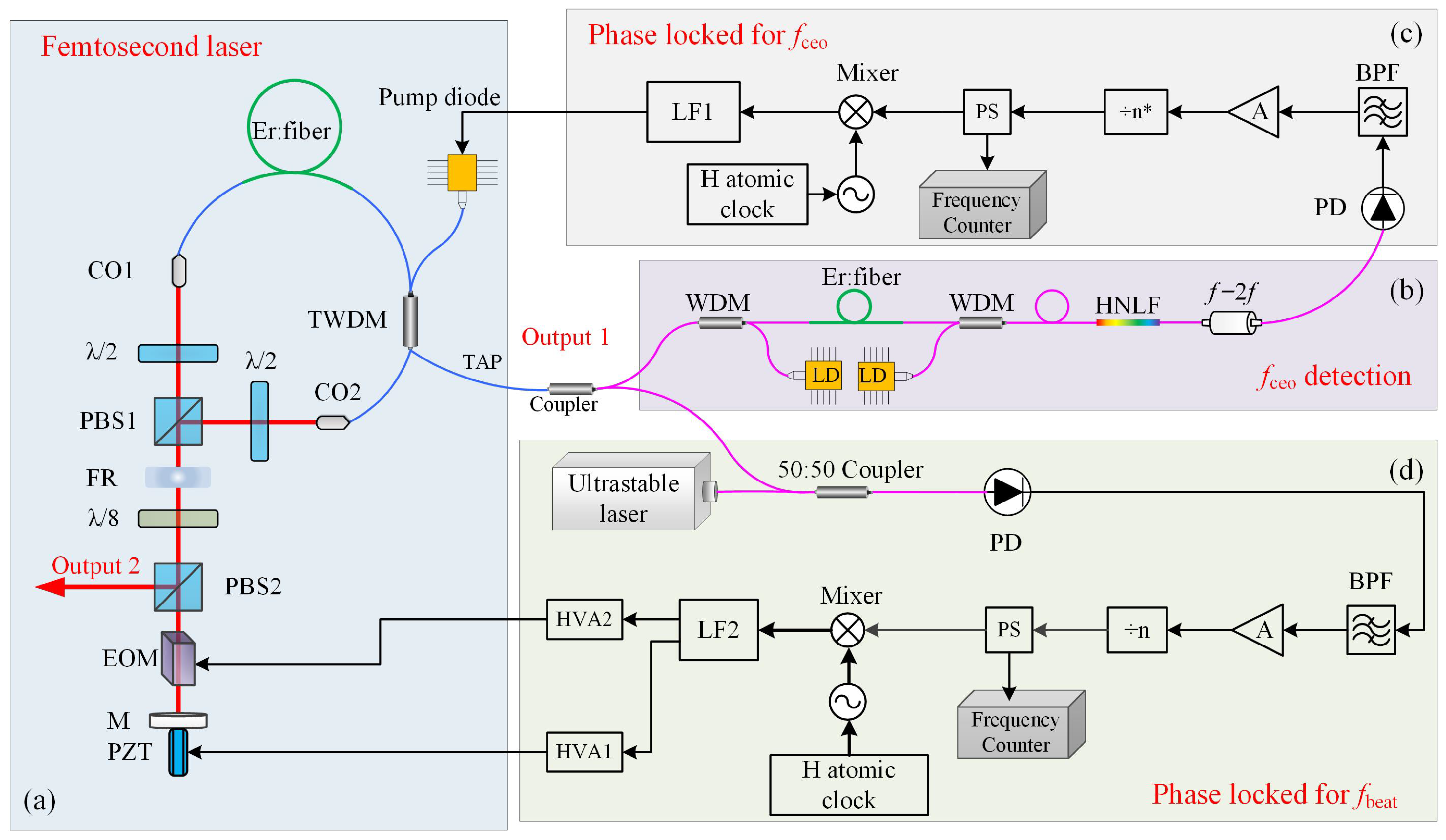
2.2. OFC
2.3. Optic-to-Electronic Converter
2.3.1. Experimental Setup of the Microwave Regeneration System
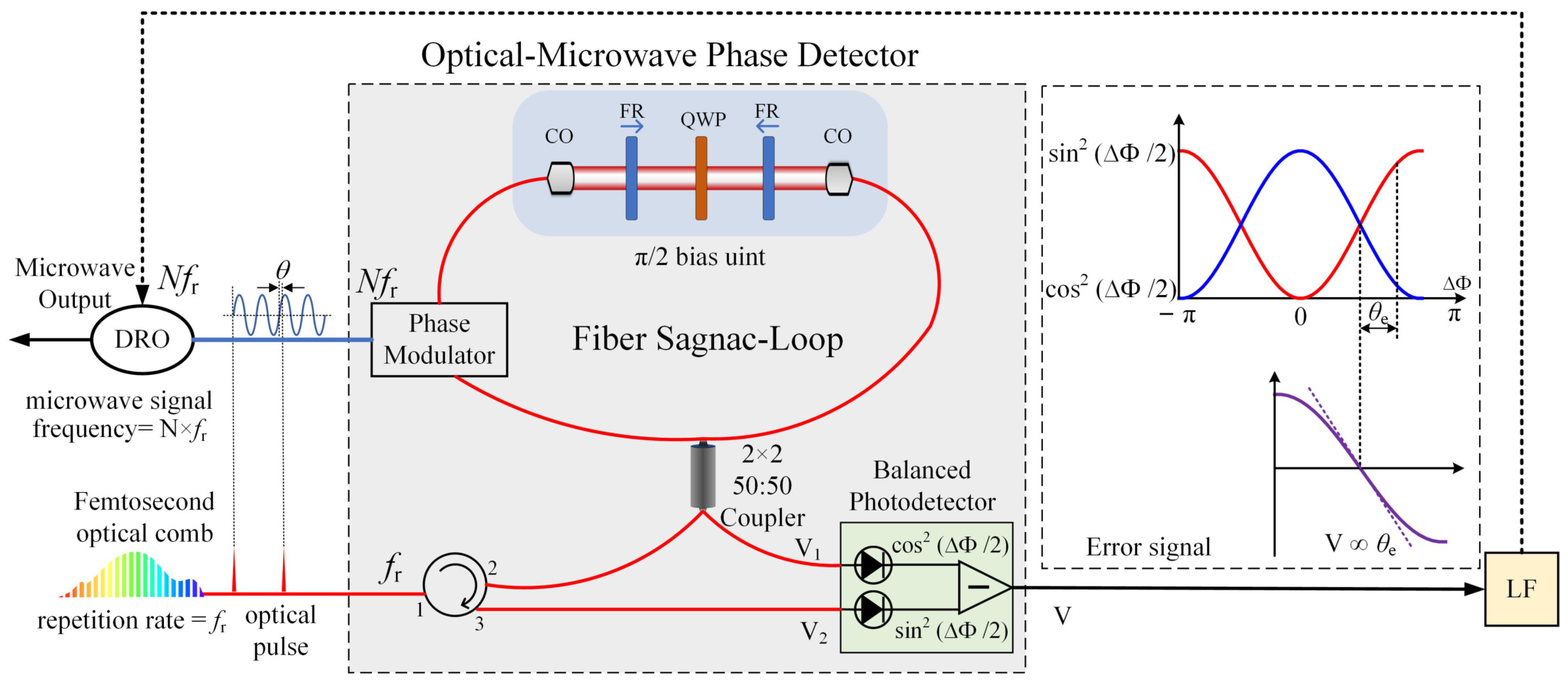
2.3.2. Principle Analysis of the Optical-to-Microwave Phase Detector
3. Results
3.1. Ultrastable Laser Performance Evaluation and Results
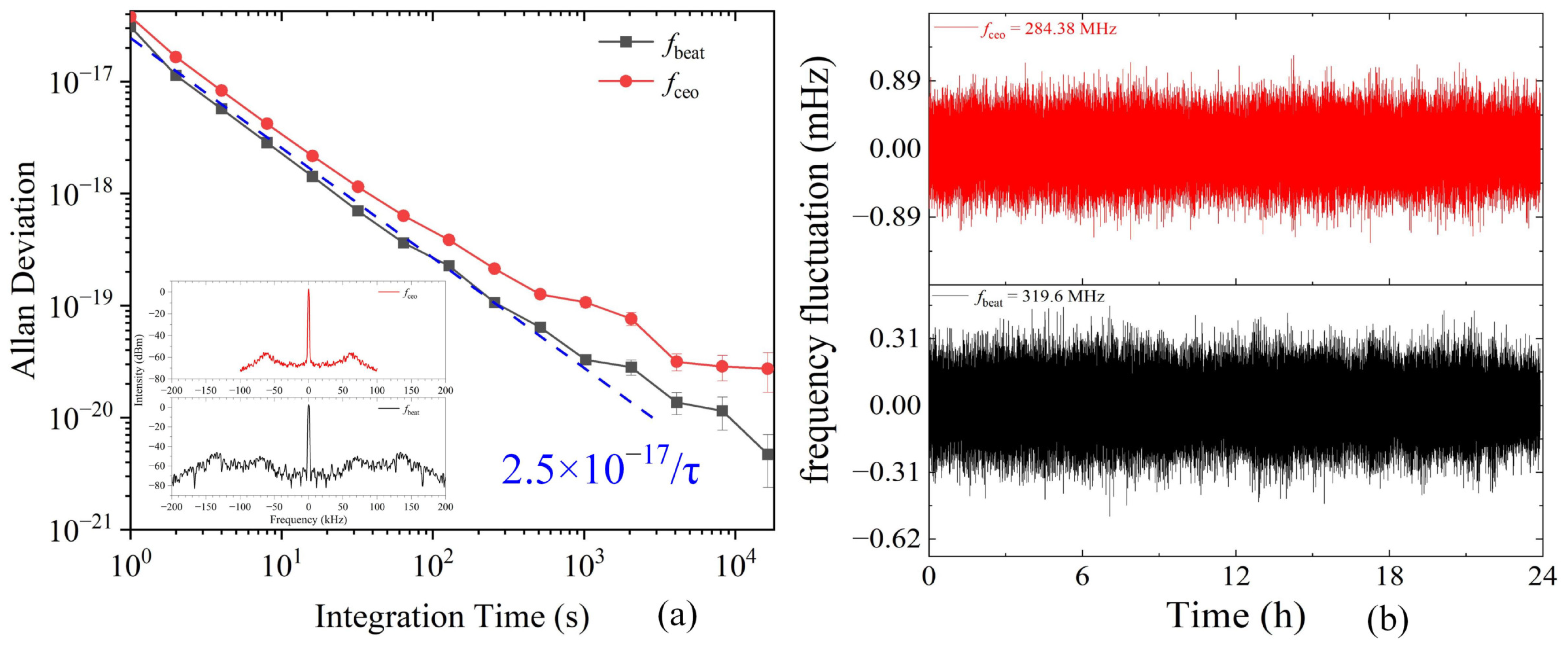
3.2. Performance Evaluation and Results of the Femtosecond OFC
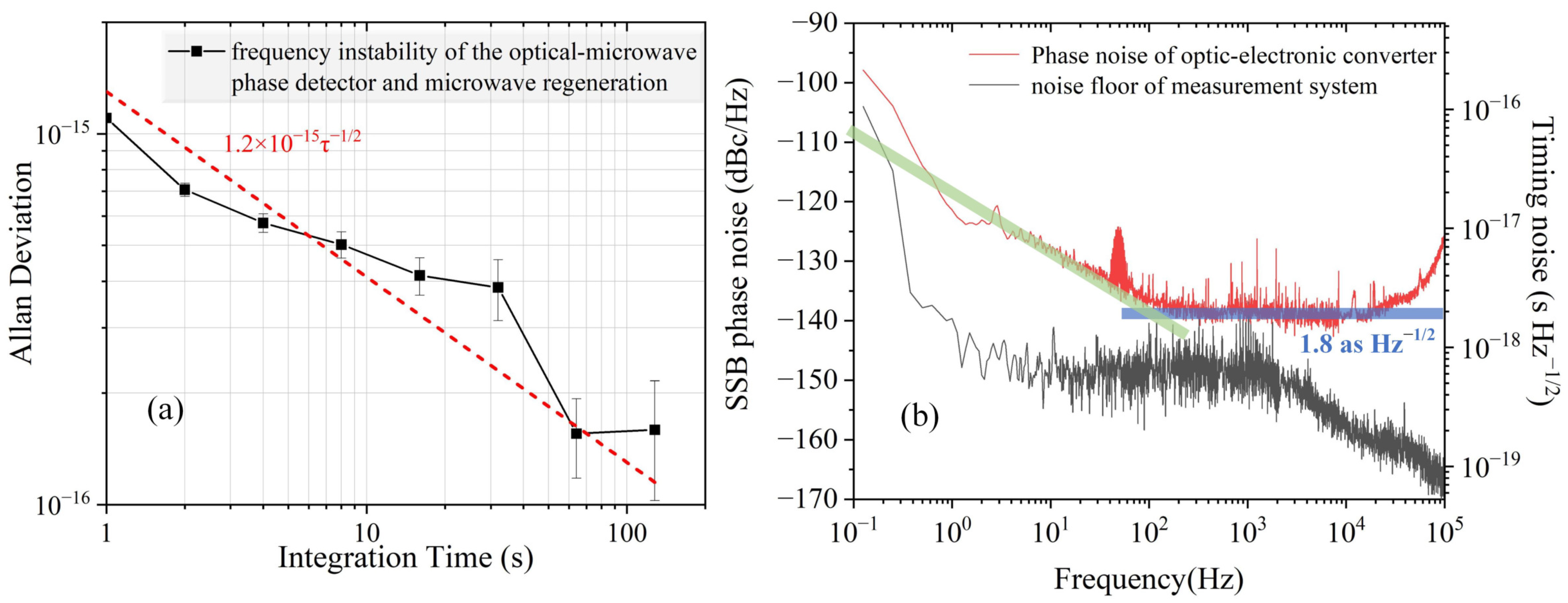
3.3. Performance Evaluation and Results of the Optic-to-Electronic Converter
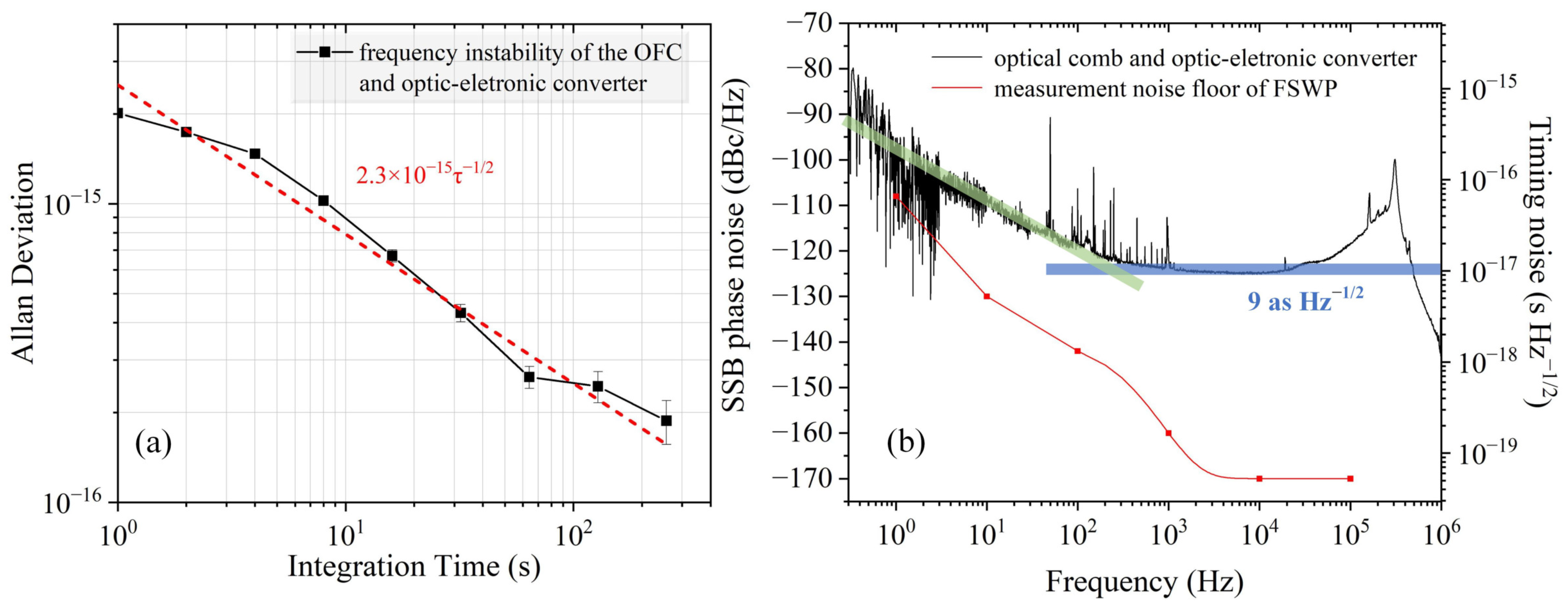
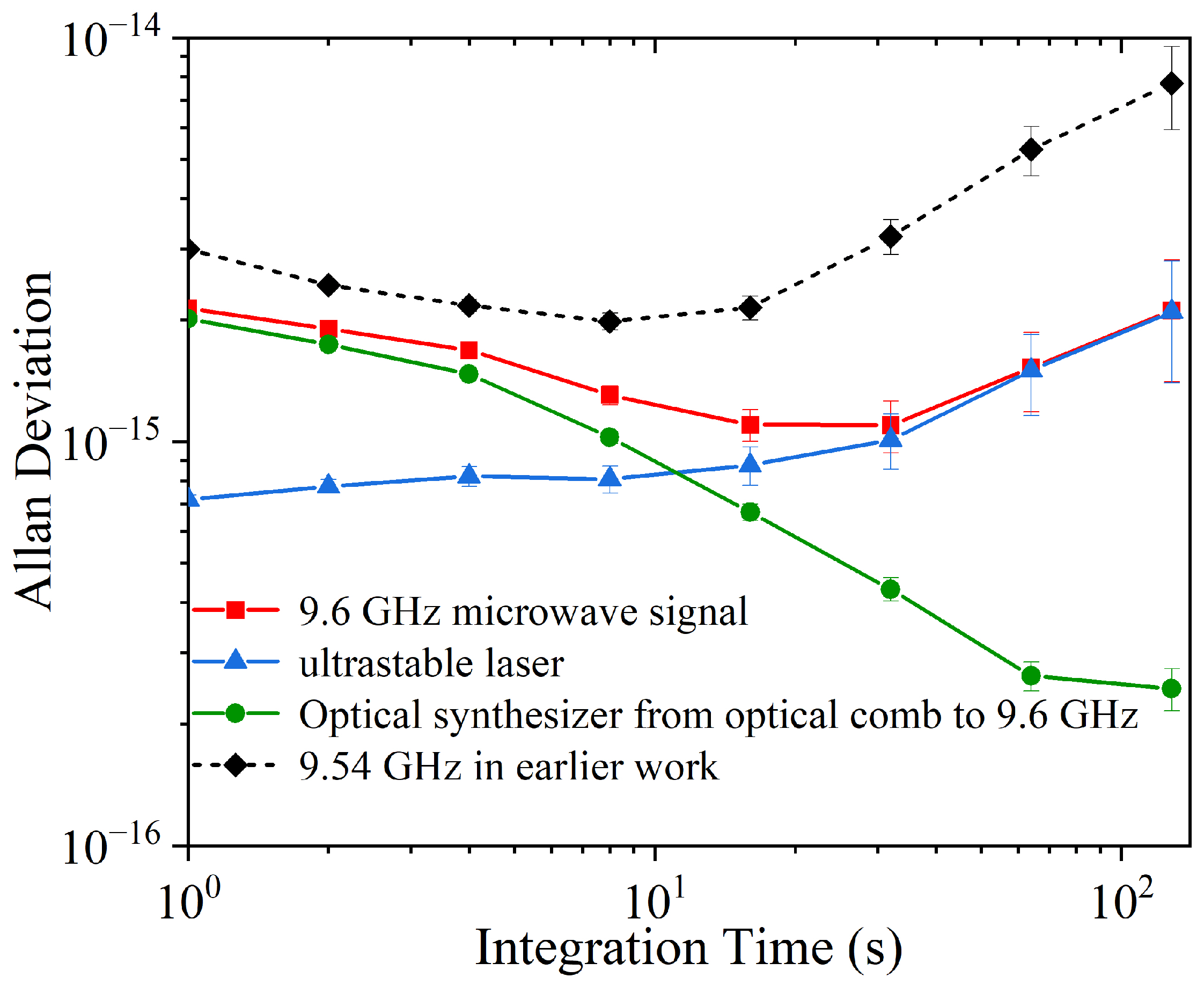
3.4. The Frequency Instability of the Photonic Microwave Generator
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fortier, T.M.; Kirchner, M.S.; Quinlan, F.; Taylor, J.; Bergquist, J.C.; Rosenband, T.; Lemke, N.; Ludlow, A.; Jiang, Y.; Oates, C.W.; et al. Generation of ultrastable microwaves via optical frequency division. Nat. Photonics 2011, 5, 425–429. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Ludlow, A.D.; Lemke, N.D.; Fox, R.W.; Sherman, J.A.; Ma, L.; Oates, C.W. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photonics 2011, 5, 158–161. [Google Scholar] [CrossRef]
- Abbott, B.P. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. Prospects for observing and localizing gravitational-wave transients with advanced LIGO and advanced virgo. Living Rev. Relativ. 2016, 19, 1. [Google Scholar] [CrossRef] [PubMed]
- Nand, N.R.; Hartnett, J.G.; Ivanov, E.N.; Santarelli, G. Ultra-stable very-low phase-noise signal source for very long baseline interferometry using a cryocooled sapphire oscillator. IEEE Trans. Microw. Theory Tech. 2011, 59, 2978–2986. [Google Scholar] [CrossRef]
- Xiao, X.; Li, S.; Peng, S.; Xing, L.; Xue, X.; Zheng, X.; Zhou, B. A large-range autofocus microwave photonic radar based on adaptive spatial filtering along the range direction. Opt. Commun. 2020, 477, 126354. [Google Scholar] [CrossRef]
- Chizh, A.L.; Mikitchuk, K.B.; Skotorenko, I.V. Optoelectronic reference X-band oscillator for radar systems. Quantum Electron. 2021, 51, 254–259. [Google Scholar] [CrossRef]
- Li, R.; Li, W.; Ding, M.; Wen, Z.; Li, Y.; Zhou, L.; Yu, S.; Xing, T.; Gao, B.; Luan, Y.; et al. Demonstration of a microwave photonic synthetic aperture radar based on photonicassisted signal generation and stretch processing. Opt. Express 2017, 25, 14334–14340. [Google Scholar] [CrossRef] [PubMed]
- Weyers, S.; Lipphardt, B.; Schnatz, H. Reaching the quantum limit in a fountain clock using a microwave oscillator phase locked to an ultrastable laser. Phys. Rev. A 2009, 79, 031803. [Google Scholar] [CrossRef]
- Santarelli, G.; Audoin, C.; Makdissi, A.; Laurent, P.; John Dick, G.J.; Clairon, A. Frequency stability degradation of an oscillator slaved to a periodically interrogated atomic resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 887–894. [Google Scholar] [CrossRef]
- Campbell, S.L.; Hutson, R.B.; Marti, G.E.; Goban, A.; Darkwah Oppong, N.; McNally, R.L.; Sonderhouse, L.; Robinson, J.M.; Zhang, W.; Bloom, B.J.; et al. A fermi-degenerate three-dimensional optical lattice clock. Science 2017, 358, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Beloy, K.; Bodine, M.I.; Bothwell, T.; Brewer, S.M.; Bromley, S.L.; Chen, J.; Deschênes, J.; Diddams, S.A.; Fasano, R.J.; Fortier, T.M.; et al. Frequency ration measurements at 18-digit accuracy using an optical clock network. Nature 2021, 591, 564–569. [Google Scholar]
- Brewer, S.M.; Chen, J.; Hankin, A.M.; Clements, E.R.; Chou, C.W.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. 27Al+ quantum-logic with a systematic uncertainty below 10−18. Phys. Rev. Lett. 2019, 123, 033201. [Google Scholar] [CrossRef] [PubMed]
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.; Ye, J.; Kennedy, C.J. JILA Srl optical lattice clock with uncertainty of 2.0 × 10−18. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Fasano, R.J.; Schäffer, S.A.; Beloy, K.; Nicolodi, D.; Brown, R.C.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Zhao, W.; Quan, H.; Xing, Y.; Zhang, S. Cascaded microwave transfer over 300-km fiber link with instability at the 10−18 level. Remote Sens. 2021, 13, 2182. [Google Scholar] [CrossRef]
- Schioppo, M.; Kronjager, J.; Silva, A.; Ilieva, R.; Paterson, J.W.; Baynham, C.F.A.; Bowden, W.; Hill, I.R.; Hobson, R.; Vianello, A.; et al. Comparing ultrastable lasers at 7 × 10−17 fractional frequency instability through a 2220 km optical fibre network. Nat. Commun. 2022, 13, 212. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Gui, S.; Wu, H.; Guo, Z.; Zhao, J. Remote Residual Instability Evaluation of Comb-Based Precise Frequency Transmission for Optical Clock. Photonics 2023, 10, 1188. [Google Scholar] [CrossRef]
- Matei, D.G.; Legero, T.; Häfner, S.; Grebing, C.; Weyrich, R.; Zhang, W.; Sonderhouse, L.; Robinson, J.M.; Ye, J.; Riehle, F.; et al. 1.5 μm lasers with sub-10 mHz linewidth. Phys. Rev. Lett. 2017, 118, 263202. [Google Scholar] [CrossRef]
- Xie, X.; Bouchand, R.; Nicolodi, D.; Giunta, M.; Hänsel, W.; Lezius, M.; Joshi, A.; Datta, S.; Alexandre, C.; Lours, M.; et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat. Photonics 2017, 11, 44–47. [Google Scholar] [CrossRef]
- Fortier, T.M.; Rolland, A.; Quinlan, F.; Baynes, F.N.; Metcalf, A.J.; Hati, A.; Ludlow, A.D.; Hinkley, N.; Shimizu, M.; Ishibashi, T.; et al. Optically referenced broadband electronic synthesizer with 15 digits of resolution. Laser Photonics Rev. 2016, 10, 780–790. [Google Scholar] [CrossRef]
- Yan, L.; Zhao, W.; Zhang, Y.; Tai, Z.; Zhang, P.; Rao, B.; Ning, K.; Zhang, X.; Guo, W.; Zhang, S.; et al. Photonic generation of RF and microwave signal with relative frequency instability of 10−15. Chin. Phys. B 2018, 27, 0330601. [Google Scholar] [CrossRef]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Tai, Z.; Yan, L.; Zhang, Y.; Zhang, X.; Guo, W.; Zhang, S.; Jiang, H. Transportable 1555-nm ultra-stable laser with sub-0.185-Hz linewidth. Chin. Phys. Lett. 2017, 34, 090602. [Google Scholar] [CrossRef]
- Tai, Z.; Yan, L.; Zhang, Y.; Zhang, X.; Guo, W.; Zhang, S.; Jiang, H. Electro-optic modulator with ultra-low residual amplitude modulation for frequency modulation and laser stabilization. Opt. Lett. 2016, 41, 5584–5587. [Google Scholar] [CrossRef] [PubMed]
- Donley, E.A.; Heavner, T.P.; Levi, F.; Tataw, M.O.; Jefferts, S.R. Double-pass acousto-optic modulator system. Rev. Sci. Instrum. 2005, 76, 063112. [Google Scholar] [CrossRef]
- Ma, L.; Jungner, P.; Ye, J.; Hall, J.L. Delivering the same optical frequency at two places: Accurate cancellation of phase noise introduced by an optical fiber or other time-varying path. Opt. Lett. 1994, 19, 1777–1779. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, Y.; Zhang, L.; Fan, S.; Zhang, X.; Guo, W.; Zhang, S.; Jiang, H. Attosecond-resolution Er:Fiber-based optical frequency comb. Chin. Phys. Lett. 2015, 32, 104207. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Li, M.; Rao, B.; Yan, L.; Chen, F.; Zhang, X.; Chen, Q.; Jiang, H.; Zhang, S. All polarization-maintaining Er:fiber-based optical frequency comb for frequency comparison of optical clocks. Chin. Phys. B 2022, 31, 054210. [Google Scholar] [CrossRef]
- Edelmann, M.; Hua, Y.; Şafak, K.; Kärtner, F.X. Intrinsic amplitude-noise suppression in fiber lasers mode-locked with nonlinear amplifying loop mirrors. Opt. Lett. 2021, 46, 1752–1755. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, E.N.; Hollberg, L.; Diddams, S.A. Analysis of noise mechanisms limiting the frequency stability of microwave signals generated with a femtosecond laser. IEEE J. Sel. Topics Quantum Electron. 2003, 9, 1059–1065. [Google Scholar] [CrossRef]
- Ivanov, E.N.; Diddams, S.A.; Hollberg, L. Study of the excess noise associated with demodulation of ultra-short infrared pulses. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1068–1074. [Google Scholar] [CrossRef] [PubMed]
- Haboucha, A.; Zhang, W.; Li, T.; Lours, M.; Luiten, A.N.; Le Coq, Y.; Santarelli, G. Optical-fiber pulse rate multiplier for ultralow phase-noise signal generation. Opt. Lett. 2011, 36, 3654–3656. [Google Scholar] [CrossRef]
- Kim, J.; Kartner, F.X. Femtosecond synchronization of radio frequency signals with optical pulse trains. Opt. Lett. 2004, 29, 2076–2078. [Google Scholar] [CrossRef]
- Jung, K.; Kim, J. Subfemtosecond synchronization of microwave oscillators with mode-locked Er-fiber lasers. Opt. Lett. 2012, 37, 2958–2960. [Google Scholar] [CrossRef]
- Jung, K.; Shin, J.; Kang, J.; Hunziker, S.; Min, C.; Kim, J. Frequency comb-based microwave transfer over fiber with 7 × 10−19 instability using fiber-loop optical-microwave phase detectors. Opt. Lett. 2014, 39, 1577–1580. [Google Scholar] [CrossRef] [PubMed]
- Dennis, M.L.; Duling, I.N.; Burns, W.K. Inherently bias drift free amplitude modulator. Electron. Lett. 1996, 32, 547–548. [Google Scholar] [CrossRef]
- Gopalakrishnan, G.K.; Burns, W.K.; McElhanon, R.W.; Bulmer, C.H.; Greenblatt, A.S. Performance and modeling of broadband LiNbO3 traveling wave optical intensity modulators. J. Light. Technol. 1994, 12, 1807–1819. [Google Scholar] [CrossRef]
- Taylor, J.; Datta, S.; Hati, A.; Nelson, C.; Quinlan, F.; Joshi, A.; Diddams, S.A. Characterization of power-to-phase conversion in high-speed P-I-N photodiodes. IEEE Photonics J. 2011, 3, 140–151. [Google Scholar] [CrossRef]
- Jiang, H.; Taylor, J.; Quinlan, F.; Diddams, S. Noise floor reduction of an Er:fiber laser-based photonic microwave generation. IEEE Photonics J. 2011, 3, 1004–1012. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Ruan, J.; Zhang, P.; Rao, B.; Li, M.; Du, Z.; Zhang, S. Optically Referenced Microwave Generator with Attosecond-Level Timing Noise. Photonics 2025, 12, 153. https://doi.org/10.3390/photonics12020153
Yan L, Ruan J, Zhang P, Rao B, Li M, Du Z, Zhang S. Optically Referenced Microwave Generator with Attosecond-Level Timing Noise. Photonics. 2025; 12(2):153. https://doi.org/10.3390/photonics12020153
Chicago/Turabian StyleYan, Lulu, Jun Ruan, Pan Zhang, Bingjie Rao, Mingkun Li, Zhijing Du, and Shougang Zhang. 2025. "Optically Referenced Microwave Generator with Attosecond-Level Timing Noise" Photonics 12, no. 2: 153. https://doi.org/10.3390/photonics12020153
APA StyleYan, L., Ruan, J., Zhang, P., Rao, B., Li, M., Du, Z., & Zhang, S. (2025). Optically Referenced Microwave Generator with Attosecond-Level Timing Noise. Photonics, 12(2), 153. https://doi.org/10.3390/photonics12020153




