Abstract
We present in this study a theoretical investigation of the near-field enhancement phenomenon within nanostructures, which have garnered recent attention due to their potential applications in sensing, imaging, and energy harvesting. The analysis reveals a significant intensification of electromagnetic fields proximal to periodically arranged arrays of gold nanoparticles sustaining a highly lossy mode. In addition to the existence of a localized surface plasmon (LSP) mode exhibiting suboptimal quality, our investigation unveils intricate aspects of near-field enhancement closely correlated to the dynamics of lasing mechanisms. Notably, our investigation is focused on elucidating the augmentation’s behavior across varying pumping energies. The achieved enhancement surpasses two orders of magnitude compared to the passive counterparts. We introduce a description of the energy conversion rate specific to the SPASER configuration. The conceptualized SPASER reveals a significant promise. It showcases energy conversion efficiency up to 80%, emphasizing the SPASER’s potential as a highly effective nano-scale energy source.
1. Introduction
In recent years, the manipulation of light at the nanoscale has emerged as a promising research area, holding promise for diverse applications in fields such as sensing [1,2,3], imaging [4], and optical communication. An interesting aspect of their exploration revolves around examining the near-field enhancement within nanostructures, with a particular focus on the domain of nano-lasers, known as SPASERs—surface plasmon amplification by stimulated emission of radiation. These unique nano-lasers harness surface plasmon resonances in metal nanostructures to amplify coherent light emission, transcending the boundaries of traditional macroscale lasers [5]. Operating at nanoscale dimensions, SPASERs offer distinct advantages, notably their compatibility with other nanodevices and structures [6,7,8,9,10,11,12,13,14], presenting novel avenues for technological integration.
The potential transformative impact of SPASERs on diverse domains, such as biomedicine, optical communications, and sensing [15], is undeniable. Their exceptional optical and electronic properties make them compelling candidates to revolutionize these fields. Yet, the path toward realizing their potential is accompanied by intricate technical challenges that necessitate careful consideration before their broad implementation.
Remarkably, the pursuit of nanoscale light manipulation not only uncovers phenomena inherent to very small dimensions but also holds promise for circumventing the diffraction limit of light—an issue that has long perplexed researchers. Notably, SPASERs exhibit characteristics crucial for addressing these challenges. The heart of their operation lies in the excitation of surface plasmons through a pump laser, followed by light emission via stimulated emission [15]. Compared to their conventional counterparts [16], SPASERs’ compactness stands out, paving the way for their integration with an array of nanoscale systems and devices [14,17,18,19].
The focus on nanoscale light offers a practical means to tackle the limitations posed by diffraction, enabling the creation of optical devices that push beyond conventional constraints. Central to this exploration is the phenomenon of near-field enhancement—wherein the electric field strength in proximity to a nanostructure surpasses that of the incident light. This enhancement emerges from the excitation of localized surface plasmons, collective oscillations within metal nanostructures [14]. Nonetheless, the allure of this enhancement often contends with the challenge of energy dissipation, limiting the overall efficiency of these systems.
In response to these hurdles, various strategies have emerged to mitigate the impact of the high loss rates inherent to plasmonic systems [20,21,22,23,24,25]. For instance, researchers have ventured into alternative materials with reduced loss rates, like aluminum-doped zinc oxide (AZO) and titanium nitride (TiN) [26]. Similarly, the design of nanostructures with tailored geometries seeks to curtail the influence of losses [27]. Encouragingly, advances in fabrication techniques have yielded hybrid structures that amalgamate plasmonic and non-plasmonic materials, concurrently elevating near-field enhancement and curtailing energy dissipation [28].
However, the intricate interplay between near-field enhancement and loss mitigation in nanostructures necessitates a multidisciplinary approach. To this end, this study builds upon a previously developed model [14] that impeccably aligns with experimental outcomes [16]. This investigation explores the lasing action within highly lossy materials, subsequently unveiling fundamental properties congruent with the SPASERs. The paper provides some insights that can be useful for harnessing the potential of nanoscale light manipulation, with applications spanning domains from communication to medicine and from sensing to fundamental scientific exploration.
This work is therefore concerned with the SPASER effect in periodic arrays sustaining a highly lossy mode. We use in our modeling methodology a semi-quantum approach in which we combine classical electrodynamics treatment for arrays of gold nanoparticles with a four-level quantum model of the laser dye photo-physics. The model was developed previously in reference [29] and shows excellent agreement with the experimental results [16]. While the foundation of this study is the previously developed model [29], this research offers a novel perspective by focusing on the near-field properties, which have not been explored in prior studies.
We investigate the properties of the near-field enhancement associated with the lasing action. We focus on the enhancement for different pumping energies, where we demonstrate an enhancement by two orders of magnitude higher than a passive structure. Then, we define the energy conversion rate in the SPASER system and show that the conceived SPASER could reach 80% of energy conversion, making it of great interest to act as a nano-source of energy. The efficiency at which systems convert incident energy into emitted electromagnetic radiation is a key parameter that directly impacts their performance. Improving energy conversion efficiency is essential for applications such as plasmonic lasers, sensors, and nanophotonic devices. The process is governed by the transfer of energy from optically excited four-level gain media to plasmons [16]. This energy transfer is a complex phenomenon, primarily driven by non-radiative energy interactions between the molecules in the gain medium and the surface plasmons [5,29]. The efficiency of this transfer depends on factors such as the spectral overlap between the gain medium’s emission peak and the plasmon resonance, the distance between the gain medium and the metallic surface, and the material properties of the system. More efficient energy transfer results in greater amplification of the plasmons, which enhances the intensity and coherence of the emitted electromagnetic field [17]. Optimizing this process involves fine-tuning the system’s design, material selection, and gain medium properties to achieve improved energy conversion and emission performance.
The paper proceeds as follows. In Section 2, we present the plasmonic nanostructure’s design and its accompanying gain medium. The methodology and numerical simulations are briefly presented in Section 2 as well. Moving on to Section 3, our exploration begins with a study of the fundamental properties of the resulting lasing. This includes a detailed analysis of the characteristics of the acquired near field. Subsequently, we introduce a crucial metric—the energy conversion rate. This metric serves to validate that the achieved lasing aligns with the characteristics of a SPASER. Our findings and insights are summarized in Section 4, providing a conclusive wrap-up of the study.
2. Methodology
The model employed in this study is elucidated in reference [14]. The model consists of a configuration comprising an array of nanocylinders (NCs), each with periodic dimensions Px and Py in two-dimensional space. These NCs are situated within a gain medium, specifically an active layer containing quantum dots (called an active structure, the passive structure has no added gain medium). The system is then subjected to illumination via an incident monochromatic photon source () as shown in Figure 1.
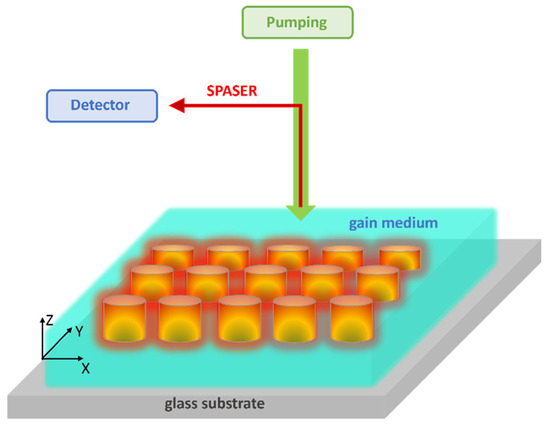
Figure 1.
Cartoon presentation of the structure composed of gold nanocylinders situated within a gain medium, containing quantum dots (green layer), all placed on a glass substrate (gray layer).
The parameters of the nanostructure are based on previous theoretical work [14]. These parameters include the diameter of each nanocylinder in the array d = 100 nm, the height h = 50 nm, and the period of the array p = 300 nm. Regarding the choice of gain medium, a previous study [14] investigated various options. It was demonstrated that a poor overlap between the emission peak of rhodamine and the resonance mode hindered energy transfer, thereby suppressing the lasing action of the system. In contrast, theoretical estimations suggested that gain media resembling quantum dots could significantly enhance lasing performance. Based on these findings, the present study adopts identical gain medium parameters, which are summarized as follows: absorption wavelength λa = 600 nm, emission wavelength λe = 720 nm, spectral bandwidth of emission Δλe = 70 nm, and absorption bandwidth Δλa = 70 nm.
One should note that the system’s response to incident electromagnetic fields is significantly influenced by parameters such as the size, shape, and type of nanoparticles, as well as the characteristics of the gain medium. While these factors play a crucial role in determining the overall behavior, their detailed analysis falls outside the scope of this work and will be addressed in future studies.
In Figure 2, we show the spectrum of the incident source for the active structure (a pic located at nm (red solid line)). For the passive structure without the gain medium, the incident field is rather very broad as presented in blue dashed line in Figure 2.
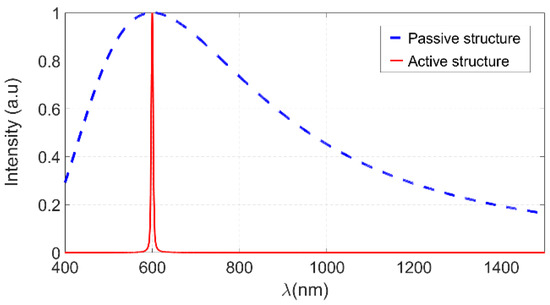
Figure 2.
Spectra of the incident field in passive and active structures.
The theoretical framework adopted for modeling this system has a semi-classical methodology. The electromagnetic field at the surface of the NCs, nestled within the gain medium, is computed by applying Maxwell’s equations [29]. The inclusion of the gain medium into the model entails a quantum depiction of four electronic energy levels (depicted in Figure 2 in reference [14]). When this configured system is subjected to a photon pumping flux, the behavior of the molecules within the gain medium is characterized at the microscopic level through the polarization (μi) of each molecule. On the macroscopic scale, this is achieved by averaging the polarization () across the entire molecular population.
The latter is governed by the following equation:
where N is the molecular population density, is the average frequency, is the transition bandwidth (accounting for radiative, non-radiative, and collisional effects), and .
An important observation is that molecules in states |1⟩ and |2⟩ exhibit opposing polarizations. This signifies that the overall polarization is contingent upon the population difference ΔN = N2 − N1, rather than the absolute population N(t). The temporal evolution of ΔN and its interplay with the electromagnetic field , mediated by rate equations, enables the exploration of nonlinear optical phenomena stemming from incident light—specifically absorption, emission, and relaxation processes.
Within our model, the aggregate polarization implies changes to the entire electromagnetic (EM) of the system. This time-varying polarization begets a persistent current , which finds incorporation into the Maxwell equations. To comprehensively capture the interactions between the EM field and the gain medium, establishing a self-consistent set of equations necessitates determining the time progression of ΔN(t) and, consequently, the evolution of all population densities. This is achieved by adopting the familiar rate-equation framework. Each molecule is conceptualized as a four-level entity: the ground state |0⟩ and three first excited states |1⟩, |2⟩, and |3⟩, as stated previously. The resulting rate equations are defined as
where and represent macroscopic polarizations resulting from transitions between states |0⟩ ↔ |3⟩ and |2⟩ ↔ |1⟩, respectively. This model captures the interactions between the gain medium and electromagnetic field, providing a comprehensive framework for studying the SPASER mechanism.
To solve this set of equations we use the Finite-Difference Time-Domain (FDTD) algorithm [30,31].
This semi-quantum model has been previously validated by comparison with experimental measurements of the far-field emission of SPASER systems [13,16]. This validation underscores the reliability of our approach and supports the extension of the model to investigate near-field properties with confidence.
3. Results and Discussion
3.1. Enhancement of the Near Field
In this section, we explore the near-field characteristics surrounding the nanoparticle within the SPASER configuration. Initially, our focus centers on the investigation of the enhancement of the electromagnetic (EM) field. Within plasmonic structures, owing to the interplay between photons and the cloud of electrons, the EM field can be both amplified and confined within dimensions smaller than the diffraction limit.
The SPASER mechanism has been discussed in previous work [29]. Briefly, we found that the achieved lasing mode is a purely plasmonic mode with no photonic characteristics. The far-field photons are primarily generated through near-field coupling between the gain molecules and the nanostructure. In this study, we propose that the near-field enhancement is predominantly governed by electron–photon coupling, where photons are emitted due to population inversion within the gain medium. However, we acknowledge that other physical processes, such as electron–phonon coupling, surface plasmon scattering, and loss mechanisms, may also influence near-field enhancement and energy conversion efficiency. Consequently, several questions emerge:
Firstly, does the plasmonic field experience enhancement within the context of a SPASER?
Secondly, when considering an active sample containing gain molecules, does the enhancement of the EM field surpass that observed in a passive structure? Put differently, does the utilization of a SPASER offer a more pertinent avenue for obtaining nanoscale light sources compared to passive structures?
Lastly, does the EM field within the active structure exhibit greater confinement than that within a passive structure?
However, comparing near-field behaviors in passive and active structures proves intricate due to the distinctive manners in which the two structures are illuminated. Specifically, within a passive structure, plasmons can be excited through a broad-spectrum white-light source (see Figure 2). This circumstance enables the adoption of a classical enhancement definition, quantified as the ratio:
Here, E represents the field in the immediate vicinity of the nanoparticles, and signifies the incident electric field. It is essential to underscore that these two fields are evaluated at identical wavelengths—typically the resonance wavelength. However, the scenario changes significantly in the context of an active structure. As we explained earlier and as corroborated by Stockman’s theoretical framework [5], the excitation of plasmons occurs through a non-radiative energy transfer from the gain medium. This gain medium necessitates stimulation via monochromatic photons, in stark contrast to the wide-spectrum white-light excitation employed in passive structures.
The distinction in excitation mechanisms between passive and active structures underscores the challenge of comparing near-field characteristics between the two. In passive configurations, the assessment of the EM field enhancement follows a straightforward classical definition, quantified by the ratio of the total field near the nanoparticle to the incident electric field . This evaluation method aligns with the coherent behavior of white-light illumination.
Conversely, in active structures, the interaction between the plasmonic field and the gain medium introduces a layer of complexity. The excitation of plasmons through non-radiative energy transfer hinges on the precise manipulation of the gain medium’s energy levels. This necessitates a meticulous adjustment of the pumping photons’ energy to match the specific transition frequencies within the gain medium. This targeted and selective excitation contrasts markedly with the broad-spectrum nature of white-light illumination.
The unique optical response of an active structure further complicates the comparison. Here, the EM field enhancement involves not only the ratio of to but also the complex interplay between the plasmon field, the gain medium, and the distinct excitation mechanisms. This intricate interdependence results in a qualitatively different field enhancement profile compared to passive structures, necessitating more sophisticated methodologies for evaluation and comparison.
The contrast between active and passive structures extends beyond the field enhancement measurements. It encapsulates the complexity of how plasmons are excited, how gain media are stimulated, and how these interactions collectively shape the near-field characteristics. This differentiation underscores the necessity of considering a broader array of parameters and perspectives when evaluating the near-field behaviors of plasmonic systems in both active and passive configurations.
An important consequence of this is that the definition we used to measure the enhancement as is no longer valid and has no physical meaning because at the wavelength of resonance is negligible. Certainly, we still can calculate this ratio; however, comparing it to the ratio obtained in passive and active structures, this ratio loses its sense because it could be artificially very high for the simple reason that is negligible in the active structure.
Figure 3 displays the spectra of the enhancement of the near field at nm, which is very close to the resonance wavelength in the far field nm, as it is well known that the resonance in the far field is slightly shifted compared to the near field [29].
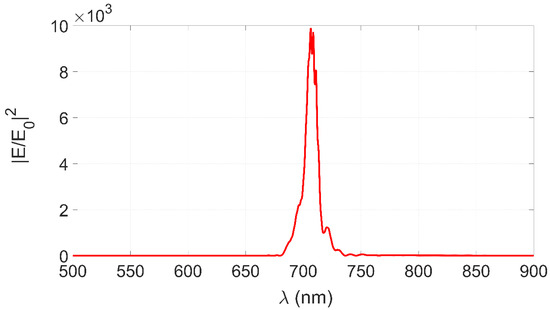
Figure 3.
Enhancement spectra in the near field as function of the wavelength.
In a previous work [14], we proposed a way to overcome this issue by integrating over the whole wavelength range for both the active and passive structures. In the present work, we propose a new strategy to calculate the enhancement of the electromagnetic field by considering as the field collected in the gain medium without nanoparticles. This method of normalization allows the elimination of the eventual field created in the gain medium without nanoparticles, intrinsic to the gain medium, such as spontaneous emission.
In Figure 4, we illustrate a cross section of the nanocylinder in the (z, x) plane. The field enhancement is plotted on a logarithmic scale, revealing significant enhancement in the proximity of the nanoparticle. The cross section was taken at the midpoint of the nanocylinder.
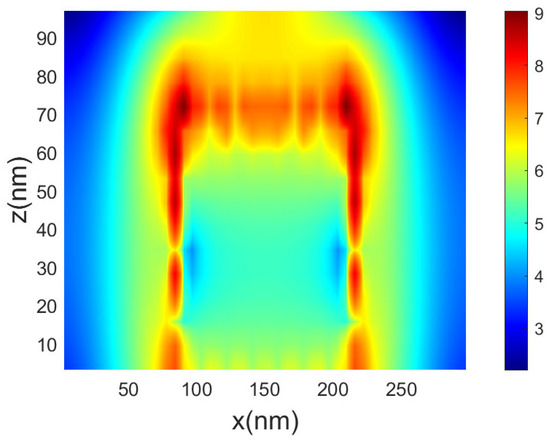
Figure 4.
Cross section of the nanocylinder in the (z, x) plane. The field enhancement is plotted on a logarithmic scale. Regions with higher field enhancement are presented in red.
We present in Figure 5 the results of the calculated enhancement using this method as a function of the pumping power at the wavelength of resonance. Multiple interesting observations could be concluded from this result.
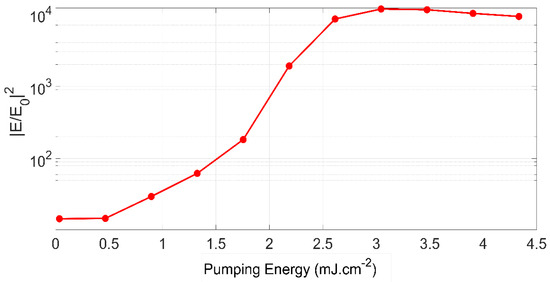
Figure 5.
Enhancement as a function of the pumping energy.
The electric field stays negligible compared to , which means that the gain medium after the withdrawal of the nanoparticles is not able to generate a field at the wavelength of resonance.
The enhancement depends significantly on the pumping, and it follows the same trend as the SPASER effect with the threshold of emission.
The enhancement is two orders of magnitude greater than the passive structure, where there is no medium gain.
3.2. Energy Conversion
In this section, we introduce an alternative approach that provides an enhanced solution for addressing the complexities associated with calculating and understanding enhancement phenomena. Our proposed method centers around assessing the energy conversion rate of the SPASER, a metric that provides a more comprehensive perspective. This rate is defined as the following ratio:
This definition draws inspiration from its common usage within the field of laser physics [1]. Particularly in laser systems, the most essential aspect lies in the conversion of incident light into coherent emitted light via population inversion. In this context, the conversion rate is expressed as a function of the spatial parameters.
Figure 6 supports this perspective by visualizing the conversion rate’s dependence on the pumping energy, near and far away from the NP. Close to the NP, the red solid line, corresponding to a location next to the nanoparticle (z = 0 nm), clearly illustrates a markedly elevated energy conversion compared to the region distanced from the NP (represented by the blue dashed line, corresponding to a location 40 nm away from the nanoparticle along the z-axis).
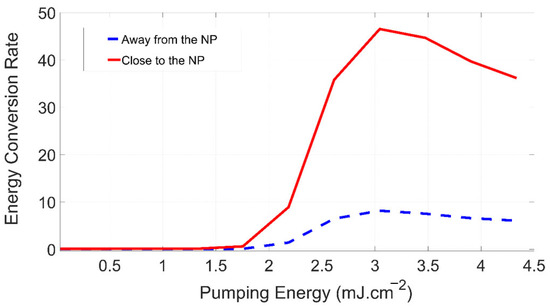
Figure 6.
Energy conversion rate as function of pumping energy, near (red) and far away (black) from the NP.
This disparity in conversion rates is also depicted in a two-dimensional representation in Figure 7. We showcase a top view of the energy conversion rate, employing a pumping of approximately 2.6 mJ/cm2. The left panel corresponds to a location away from the nanoparticle (z = 40 nm), while the right panel corresponds to the energy conversion rate in the vicinity of the nanoparticle (z = 0 nm). A white dashed circle is drawn, in the left panel, to represent the diameter of the nanocylinder, where one could notice the absence of a high value of energy conversion.
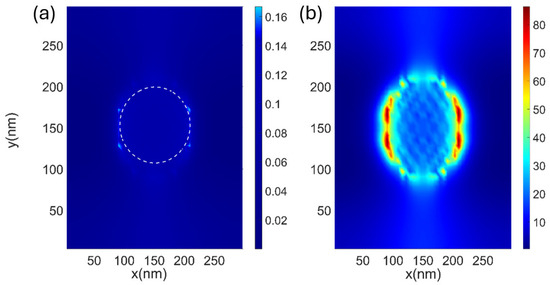
Figure 7.
Energy conversion rate in (x, y) plane at two different positions, (a): z = 40 nm, (b): z = 0 nm. Regions with higher energy conversion rates are depicted in red.
The salient observation underscores the presence of localized locations within the studied SPASER configuration where the conversion rate attains remarkable magnitudes (visible in the right panel of Figure 7).
Crucially, this outcome resonates with the earlier observations, reaffirming that high conversion rates are particularly pronounced within the immediate vicinity of the nanoparticle. These insights, collectively, corroborate the proposition that the conversion rate serves as a robust indicator of plasmon generation via stimulated emission, notably contributing to a deeper understanding of the intricate interplay of energy dynamics within the SPASER framework.
4. Conclusions
In conclusion, this study provides a nuanced understanding of near-field enhancement in highly lossy nanoarrays. These nanostructures hold compelling potential for sensing, imaging, and energy harvesting applications. The theoretical discourse uncloaks the amplification of electromagnetic fields in close proximity to precisely arranged arrays of gold nanoparticles. Despite the concurrent existence of a localized surface plasmon (LSP) mode marked by modest quality, we uncover intricate aspects of near-field enhancement intertwined with lasing dynamics. This exploration, focused on diverse pumping energies, unveils significant enhancement surpassing two orders of magnitude when compared to passive structures. This enhancement strongly depends on the pump energy, with a threshold observed around 0.5 mJ cm−2, beyond which a significant increase in enhancement occurs. A plateau in performance is reached at a pump energy of approximately 2.5 mJ cm−2. The observed enhancement is most pronounced in the immediate vicinity of the nanoparticles, where the electromagnetic field is strongly localized. However, this effect diminishes significantly with increasing distance from the nanoparticles, highlighting the localized nature of energy amplification. Furthermore, our findings suggest prospective avenues. The revealed sensitivity of enhancement to varying pumping energies could steer nanoarray design and optimization for tailored applications. Notably, our proposed SPASER design demonstrates a potential energy conversion efficiency of 80%, which can lead to efficient nanoscale energy sourcing and harvesting.
Author Contributions
The manuscript was written through contributions of all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work received no external funding.
Data Availability Statement
No data were used for the research described in the article.
Acknowledgments
This work was conducted as an outside activity and does not reflect A. M.’s capacity as an employee of The Jet Propulsion Laboratory, California Institute of Technology.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
NPs: nanoparticles; EM: electromagnetic field; LSP: localized surface plasmon; SE: spontaneous emission; StE: stimulated emission.
References
- Wang, S.; Li, B.; Wang, X.-Y.; Chen, H.-Z.; Wang, Y.-L.; Zhang, X.-W.; Dai, L.; Ma, R.-M. High-Yield Plasmonic Nanolasers with Superior Stability for Sensing in Aqueous Solution. ACS Photonics 2017, 4, 1355–1360. [Google Scholar] [CrossRef]
- Ma, R.-M.; Ota, S.; Li, Y.; Yang, S.; Zhang, X. Explosives Detection in a Lasing Plasmon Nanocavity. Nat. Nanotechnol. 2014, 9, 600–604. [Google Scholar] [CrossRef]
- Galanzha, E.I.; Weingold, R.; Nedosekin, D.A.; Sarimollaoglu, M.; Nolan, J.; Harrington, W.; Kuchyanov, A.S.; Parkhomenko, R.G.; Watanabe, F.; Nima, Z.; et al. Spaser as a Biological Probe. Nat. Commun. 2017, 8, 15528. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, J.; Song, P.; Kang, B.; Xu, J.; Chen, H. Spaser Nanoparticles for Ultranarrow Bandwidth STED Super-Resolution Imaging. Adv. Mater. 2020, 32, 1907233. [Google Scholar] [CrossRef]
- Stockman, M.I. Spasers Explained. Nat. Photonics 2008, 2, 327–329. [Google Scholar] [CrossRef]
- Nezhad, M.P.; Tetz, K.; Fainman, Y. Gain Assisted Propagation of Surface Plasmon Polaritons on Planar Metallic Waveguides. Opt. Express 2004, 12, 4072. [Google Scholar] [CrossRef]
- De Leon, I.; Berini, P. Modeling Surface Plasmon-Polariton Gain in Planar Metallic Structures. Opt. Express 2009, 17, 20191. [Google Scholar] [CrossRef]
- Li, Y.-F.; Feng, J.; Dong, F.-X.; Ding, R.; Zhang, Z.-Y.; Zhang, X.-L.; Chen, Y.; Bi, Y.-G.; Sun, H.-B. Surface Plasmon-Enhanced Amplified Spontaneous Emission from Organic Single Crystals by Integrating Graphene/Copper Nanoparticle Hybrid Nanostructures. Nanoscale 2017, 9, 19353–19359. [Google Scholar] [CrossRef]
- Hill, M.T.; Marell, M.; Leong, E.S.P.; Smalbrugge, B.; Zhu, Y.; Sun, M.; van Veldhoven, P.J.; Geluk, E.J.; Karouta, F.; Oei, Y.-S.; et al. Lasing in Metal-Insulator-Metal Sub-Wavelength Plasmonic Waveguides. Opt. Express 2009, 17, 11107. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G.; Liu, X.; Qian, F.; Li, Y.; Sum, T.C.; Lieber, C.M.; Xiong, Q. A Room Temperature Low-Threshold Ultraviolet Plasmonic Nanolaser. Nat. Commun. 2014, 5, 4953. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, J.; Mi, Y.; Sui, X.; Zhang, S.; Du, W.; Wang, R.; Shi, J.; Wu, X.; Qiu, X.; et al. All-Inorganic CsPbBr3 Nanowire Based Plasmonic Lasers. Adv. Opt. Mater. 2018, 6, 1800674. [Google Scholar] [CrossRef]
- Wan, M.; Gu, P.; Liu, W.; Chen, Z.; Wang, Z. Low Threshold Spaser Based on Deep-Subwavelength Spherical Hyperbolic Metamaterial Cavities. Appl. Phys. Lett. 2017, 110, 031103. [Google Scholar] [CrossRef]
- Yang, A.; Li, Z.; Knudson, M.P.; Hryn, A.J.; Wang, W.; Aydin, K.; Odom, T.W. Unidirectional Lasing from Template-Stripped Two-Dimensional Plasmonic Crystals. ACS Nano 2015, 9, 11582–11588. [Google Scholar] [CrossRef]
- Dridi, M.; Jaouadi, A.; Colas, F.; Compère, C. Theoretical Study of High Near-Field Enhancement Associated with the Lasing Action in Strongly Coupled Plasmonic Nanocavity Arrays. J. Phys. Chem. C 2021, 125, 749–756. [Google Scholar] [CrossRef]
- Azzam, S.I.; Kildishev, A.V.; Ma, R.-M.; Ning, C.-Z.; Oulton, R.; Shalaev, V.M.; Stockman, M.I.; Xu, J.-L.; Zhang, X. Ten Years of Spasers and Plasmonic Nanolasers. Light Sci. Appl. 2020, 9, 90. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Zhou, W.; Dridi, M.; Suh, J.Y.; Kim, C.H.; Co, D.T.; Wasielewski, M.R.; Schatz, G.C.; Odom, T.W. Lasing Action in Strongly Coupled Plasmonic Nanocavity Arrays. Nat. Nanotechnol. 2013, 8, 506–511. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Prosvirnin, S.L.; Papasimakis, N.; Fedotov, V.A. Lasing Spaser. Nat. Photonics 2008, 2, 351–354. [Google Scholar] [CrossRef]
- Noginov, M.A.; Zhu, G.; Belgrave, A.M.; Bakker, R.; Shalaev, V.M.; Narimanov, E.E.; Stout, S.; Herz, E.; Suteewong, T.; Wiesner, U. Demonstration of a Spaser-Based Nanolaser. Nature 2009, 460, 1110–1112. [Google Scholar] [CrossRef]
- Andrianov, E.S.; Baranov, D.G.; Pukhov, A.A.; Dorofeenko, A.V.; Vinogradov, A.P.; Lisyansky, A.A. Loss Compensation by Spasers in Plasmonic Systems. Opt. Express 2013, 21, 13467. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Cooper, T.A.; Zeng, L.; Ni, G.; Tong, J.K.; Tsurimaki, Y.; Huang, Y.; Meroueh, L.; Mahan, G.; Chen, G. Losses in Plasmonics: From Mitigating Energy Dissipation to Embracing Loss-Enabled Functionalities. Adv. Opt. Photonics 2017, 9, 775. [Google Scholar] [CrossRef]
- Garcia-Blanco, S.M.; Sefunc, M.A.; van Voorden, M.H.; Pollnau, M. Loss Compensation in Metal-Loaded Hybrid Plasmonic Waveguides Using Yb3+ Potassium Double Tungstate Gain Materials. In 2012 14th International Conference on Transparent Optical Networks (ICTON); IEEE: Coventry, UK, 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Gjerding, M.N.; Pandey, M.; Thygesen, K.S. Band Structure Engineered Layered Metals for Low-Loss Plasmonics. Nat. Commun. 2017, 8, 15133. [Google Scholar] [CrossRef] [PubMed]
- Güney, D.Ö.; Koschny, T.; Soukoulis, C.M. Reducing Ohmic Losses in Metamaterials by Geometric Tailoring. Phys. Rev. B 2009, 80, 125129. [Google Scholar] [CrossRef]
- Khurgin, J.B. How to Deal with the Loss in Plasmonics and Metamaterials. Nat. Nanotechnol. 2015, 10, 2–6. [Google Scholar] [CrossRef] [PubMed]
- Izyumskaya, N.; Fomra, D.; Ding, K.; Morkoç, H.; Kinsey, N.; Özgür, Ü.; Avrutin, V. High-Quality Plasmonic Materials TiN and ZnO:Al by Atomic Layer Deposition. Phys. Status Solidi RRL—Rapid Res. Lett. 2021, 15, 2100227. [Google Scholar] [CrossRef]
- Hu, H.; Tian, Y.; Chen, P.; Chu, W. Perspective on Tailored Nanostructure-Dominated SPP Effects for SERS. Adv. Mater. 2023, 36, 2303001. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J.; Wei, B. Hybrid Nanostructures of Metal/Two-Dimensional Nanomaterials for Plasmon-Enhanced Applications. Chem. Soc. Rev. 2016, 45, 3145–3187. [Google Scholar] [CrossRef]
- Dridi, M.; Mahjoub, A.; Jaouadi, A. Plasmonic Lasing in Highly Lossy Nanocylinder Arrays under Optical Pumping. Appl. Phys. B 2023, 129, 171. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House Antennas and Propagation Library; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Böhringer, K.; Hess, O. A Full-Time-Domain Approach to Spatio-Temporal Dynamics of Semiconductor Lasers. I. Theoretical Formulation. Prog. Quantum Electron. 2008, 32, 159–246. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).