Abstract
The pump heating effect of DFB fiber laser is normally ignored due to the short length of the laser cavity. However, by fabricating a phase-shifted FBG on high concentration Er-Yb codoped fiber to obtain a 16 mm long DFB fiber laser, the gradient surface temperature distributions along the active grating with different pump powers were observed. The average surface temperature rose by 16.82 K with a variation of less than 1.11 K, and the position with the highest temperature moved towards the center of the grating by 5.5 mm, when the pump power was increased from 0 mW to 191.6 mW. The transmission spectrum of the active phase-shifted FBG at different pump powers were measured, and an additional drift of the transmission peak in the stopband was testified. It was identified as an equivalent phase shift up to −0.1 π, which was induced by the gradient longitudinal temperature distribution. Considering that the initial phase shift of the grating was about 1.15 π, the increasing chirp of the active grating due to the pump heating could compensate the phase shift deviation from π surprisingly. The experimental results coincided with the simulation results by using the transmission matrix method under the assumption of piecewise-uniform structure for the chirped phase-shifted grating. The modified model of the active phase-shifted FBG reveals the difference between the cool cavity and the hot cavity at different pump powers, which may be used as a self-optimization mechanism for DFB fiber laser operation.
1. Introduction
Distributed-feedback (DFB) fiber lasers have attracted widely interests since 1990s, because of the robust single mode operation and compact structure [1,2,3]. DFB fiber laser consists of a piece of rare earth doped fiber and a phase-shifted FBG, which can be fabricated through UV exposure. Due to the phase shift of the active grating, a narrow transmission peak is created in the middle of the stopband of the transmission spectrum, which defined the lasing wavelength of the DFB fiber laser [3]. Based on the mode competition theory, efficient single mode operation is realized with the lowest fundamental mode pump threshold when the phase shift is π [4], which is taken as the phase shift condition for DFB fiber laser in common cases. However, it is not always so easy to strictly meet the perfect π phase shift, and the phase shift condition is relaxed in the fabrication, only if the laser can obtain stable single mode output with. When pump power is launched into the fiber laser, it has been observed that the lasing wavelength increased with pump power [3], and the laser cavity was detuned. The phase shift deviated from the original value with increased pump power as well, while the output power of the laser decreased with stopband broadening until lasing stopped. The surface temperature distribution along a DFB fiber laser was measured by a second DFB fiber laser. Exponentially decayed temperature along the laser cavity was noticed, indicating a sign of increasing chirp caused by the non-uniform heat distribution. When the pump power was increased further, a second transmission peak was observed, and lasing started again with a new laser mode. The reported results reveals an actual conflict between the design and operation of DFB fiber lasers: in the design of DFB fiber laser, the phase shift is set to close to π, and is expected to be unchanged. However, the actual phase shift varies with different pump power due to the pump induced thermal effect, and even deviates from π further with higher pump power. Refractive index change was found to be induced due to the thermal-optical effect rather than complex susceptibility change [5], and nonlinear tuning of Bragg wavelength in high concentration active fiber Bragg gratings (FBGs) was reported [6]. Bragg wavelength mismatch of the two FBG reflectors and unequal bandwidth broadening were observed in Er-Yb codoped DBR fiber lasers [5], and 0.32 nm shift in lasing wavelength was measured, corresponding to a temperature rise of 38 K. In addition to the wavelength shift, laser frequency fluctuation of up to 1.7 GHz was measured, when the DBR fiber laser was pumped with 68 mW of pump power. Due to the pump heating, fiber lasers might be unstable and even stop lasing at certain pump power [7]. In order to reduce the negative effects of pump induced thermal effect to linear cavity fiber lasers, possible solutions have been proposed [3,5,7], such as fabricating the fiber laser in low concentration active fiber, cooling the fiber laser by TEC thermoelectric cooler, or placing the fiber laser onto materials with high heat conductivity. In most cases, DFB fiber lasers are designed as short as possible, which is not easy to be achieved in low concentration active fiber. When DFB fiber lasers act as laser sources, TEC thermoelectric coolers and high thermal conductivity heat dissipation materials are widely used to enhance the stability of the laser output, which may not be applicable for DFB fiber laser sensors. Therefore, a solution to mitigate the negative effects of pump heating with self-organizing mechanism of DFB fiber laser is of great value. Although the pump heating is regarded as negative effects in most cases, the thermal effect of DFB fiber laser may also be utilized for self-feedback and sensing. By regulation of the thermal expansion coefficient of the DFB fiber laser cavity with specially designed mechanical structure, the inherent photothermal effect was used to reduce frequency noise of the laser [8]. By fusing a piece of cobalt-doped fiber fused at the rear end of the fiber laser, an intensity demodulated fiber-optic hot-wire sensing method was proposed, based on the thermally induced chirp effect of DFB fiber laser [9]. In this paper, a short DFB fiber laser was fabricated on high concentration Er-Yb codoped fiber, while the surface temperature distribution along the grating and the transmission spectrum of the active phase-shifted FBG were measured synchronously. The impact of the pump-induced gradient temperature distribution was found to induce an equivalent phase shift compensating the phase shift deviation from π with no obvious stopband broadening. It provides a further understanding on the operating mechanism of the DFB fiber laser, and a possible approach for self- stabilization in the laser operation.
2. Theoretical Analysis
The structure of a DFB fiber laser is illustrated in Figure 1. A centimeter-level fiber Bragg grating (FBG) is fabricated on a section of rare earth ions (e.g., Er3+, Er3+/Yb3+) doped fiber to form a linear resonator. An ideal phase shift of π is introduced in the middle of the FBG to obtain the zero-order resonant wavelength.
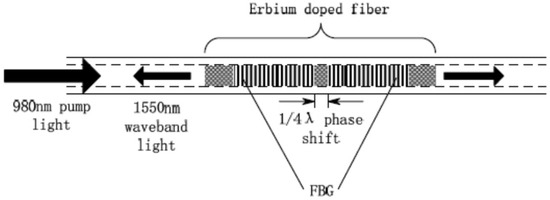
Figure 1.
Configuration of DFB fiber laser.
Since the temperature and strain response of a DFB fiber laser is identical to that of a standard Bragg grating [2], the resonant wavelength shift of the DFB fiber laser due to the ambient temperature change can be attributed to the following four aspects: the thermal-optical effect of the fiber, the thermal expansion effect of the fiber, the elasto-optical effect caused by the thermal expansion of the fiber, and the waveguide effect caused by changes in the fiber core due to the thermal expansion. In general, the following assumptions are usually made for the DFB fiber laser: the effect of pump heating is ignored, and the temperature distribution along the FBG is often taken as a uniform field, while the longitudinal waveguide effect induced by the non-uniform temperature distribution is barely considered. Based on these assumptions, the temperature sensitivity of the DFB fiber laser can be computed as [10]:
where λB is the Bragg wavelength of the grating, neff is the effective refractive index of the active fiber core, ξ is the thermal-optical coefficient of the FBG, p11 and p12 are the elasto-optical coefficients of the fiber, and α is the thermal expansion coefficient of the fiber. In this relation thermo-optic coefficient (for Germania doped Silica) is ξ = Δneff/ΔT ≈ 6.8 × 10−6 neff K−1, p11 = 0.113, p12 = 0.252, and thermal expansion coefficient (for Silica) is α = ΔΛ/(ΛΔT) ≈ 0.55 × 10−6 K−1 (Λ is the period of the grating), which denotes a temperature sensitivity of about 6.97 × 10−6 K−1. Considering that the effective refractive index of the fiber core is close to 1.45, the thermo-optic coefficient is about 9.86 × 10−6 K−1. As the thermo-optic coefficient is ten times larger than the thermal expansion coefficient, the temperature response of the grating is mainly decided by the thermo-optic coefficient of the fiber.
For the phase-shifted FBG in a DFB fiber laser, it keeps the periodic structure when there is no pump light injection. However, in the laser operation process, the injection of the pump light causes heat accumulation along the DFB fiber laser cavity. Due to the exponential decay characteristics of the pump absorption, the pump power continuously attenuates along the DFB fiber laser cavity. The thermal effect accumulates in the laser cavity as well, which inevitably forms a non-uniform longitudinal temperature distribution along the laser, and makes the phase-shifted FBG into a hot cavity state. As a result, the active phase-shifted FBG in the DFB fiber laser is both a heat source with a non-uniform temperature distribution and a temperature-sensitive sensor. The thermal effect chirps the phase-shifted FBG, and changes the initial periodic waveguide structure with an unexpected phase shift.
To calculating the transmission spectrum of a non-uniform grating, piecewise-uniform approach with transmission matrix is one of the most commonly used methods [11]. For the piecewise-uniform approach with transmission matrix, the grating is divided into a number of uniform pieces. The number of segments should not be made arbitrarily large and ~100 segments is sufficient, since the coupled-mode-theory approximations are not valid when a uniform grating section is only a few grating periods long [11]. When the pump light is injected into the fiber laser, due to the relatively low pump power, the temperature rise is on the order of dozens of K with a variation of less than 10 K along the fiber laser [3,5]. By multiplying the thermal expansion coefficient by a temperature rise of 50 K, the length change due to the thermal expansion effect of a DFB fiber laser with a length of 50 mm is less than 1.375 μm. Considering that the number of segments is around 100, the length of each uniform section of grating is less than 1 mm. The length difference between different sections due the non-uniform temperature distribution is less than 100 nm, which is almost negligible in the uniform segmentation of the chirped grating. Given that the thermo-optic coefficient of the fiber is around 10−5 K−1, the difference of the refractive index between different sections is on the order of 10−5, which is close to the modulation depth of the refractive index for typical FBGs. Therefore, the whole active phase-shifted FBG with different pump power can be taken as a piecewise-uniform structure and divided into several different segments. Each segment is considered as a short piece of uniform FBG with the same length, in which the temperature distribution can be taken as a constant.
In different segments, the temperature of the short piece of uniform FBG are different, which results in different refractive index change of the fiber core. As temperature at the fiber surface is proportional to temperature inside the active fiber [12], considering the limited temperature change in the fiber laser [3], the surface temperature can be approximated as the temperature inside the fiber laser. When the surface temperature rise of the segment is measured, the additional perturbation to the effective refractive index can be given as:
where ΔT is the surface temperature change due to the pump heating, and z is the position along the active grating. As the active grating is divided into several segments, for z locates in the same segment, it has the same value of ΔT.
Considering the periodic refractive index modulation and the refractive index change due to non-uniform temperature distribution, the total effective refractive index modulation of the segment can be expressed as:
where Λ is the period of the initial uniform grating, and v is the fringe visibility of the periodic index change.
In each segment of active FBG, the additional perturbation to the effective refractive index is a constant, and the transmission matrix of each segment can be given by the conventional transmission matrix method [11]. As there is an initial phase shift in the grating, a phase-shift matrix is inserted in the string of matrices. The phase-shift matrix is given by:
where φi is the phase shift, which is always designed to be close to π.
By multiplying these transmission matrices together in accordance with the position of each segment and the phase shift, the transmission matrix of the whole chirped phase-shifted FBG can be calculated to characterize the transmission spectrum of the chirped phase-shifted grating in the DFB laser [11].
3. Experiment and Results
3.1. Pump Characteristics of the DFB Fiber Laser
To operate in the C band, Erbium doped fiber and Erbium-Ytterbium (Er-Yb) co-doped fiber are used to fabricate DFB fiber lasers. Compared to Erbium doped fibers, the broad absorption band of Er-Yb co-doped fibers and the more than two orders of magnitude of higher pump absorption make them attractive for short cavity fiber lasers [7]. To make the pump heating effect more obvious, a DFB fiber laser was fabricated on a piece of high concentration Er-Yb co-doped fiber. Hydrogen loading was used to increase the photosensitivity of the active fiber. A 16 mm-long uniform FBG was written in a section of the Er-Yb co-doped fiber using a KrF excimer laser operated at 248 nm at first to fabricate a high reflectivity FBG. The period of the phase mask was 1057.65 nm. In order to increase the pump threshold to intensify the thermal effect, the UV irradiation continued for about two minutes after the reflectivity of the peak stopped rising, which broadened the spectra width of the FBG obviously. Then a phase-shift was introduced by exposing a tiny section near the center position of the FBG using a narrowed UV beam. A narrow transmission window was created in the stopband of the transmission spectrum, and there was a laser output when the phase-shifted FBG was pumped by a 980 nm semiconductor laser. After annealing at 120 °C for 24 h, the DFB fiber laser could produce a narrow line-width frequency in the C-band. The output of the DFB fiber laser at a pump power of 191.6 mW before and after annealing are shown in Figure 2a. The laser output power was measured with an optical power meter, and the output power as a function of pump power is shown in Figure 2b.
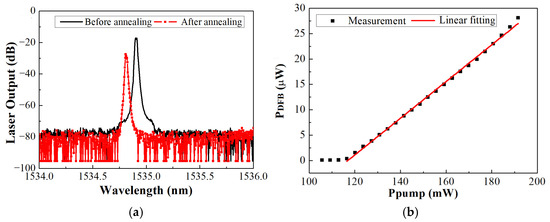
Figure 2.
Output characteristics the DFB fiber laser: (a) Laser output pumped at 191.6 mW before annealing and after annealing; (b) Output power versus input pump power.
After annealing, the signal-to-noise ratio (SNR) of the DFB fiber laser was about 53 dB, and the lasing wavelength was 1534.806 nm. The pump threshold was estimated to be ~116 mW, and the slope efficiency was very low (~0.362‰), indicating that most of the absorbed pump power was converted into heat.
3.2. Temperature Characteristics of the DFB Fiber Laser
The DFB fiber laser was pumped by a 980 nm semiconductor laser through a wavelength division multiplexer (WDM1). The DFB fiber laser was placed on the surface of the ceramic fabric paper with low thermal conductivity for a uniform temperature background. Amplified spontaneous emission(ASE) broadband light was injected into the DFB fiber laser through WDM2, and the transmission spectrum of the pumped phase-shifted FBG was monitored by an optical spectrum analyzer (OSA). Two optical isolators (ISO1 and ISO2) were put in the light path to prevent the reverse light transmission, and the unused pigtail of WDM2 was immersed in the refractive index matching gel to eliminate the possible optical feedback from the facet. The environmental temperature was set to a constant value, and the position of the DFB fiber laser was unchanged. An infrared camera with a resolution of 0.2 K fixed to a tripod was used to take images for the DFB fiber laser, which produced infrared images with 320 × 240 pixels. The experiment was conducted in a dust-free workshop to suppress airflows and convection with constant temperature of 295 K. The structure of the experimental setup is shown in Figure 3.
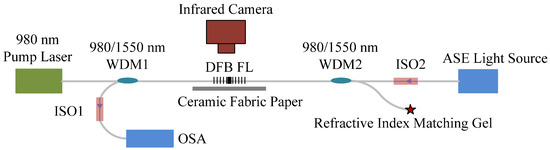
Figure 3.
Experimental setup for the temperature characteristics measurement of DFB fiber laser.
The infrared camera was used to calibrate the temperature of the active phase-shifted FBG and the ceramic fiber background before the pump light was injected. After the temperature calibration, the pump power was increased from 0 mW to 191.6 mW. After the surface temperature distribution of the pumped laser stabilized, the surface temperature distribution of the pumped DFB fiber laser was measured with the infrared camera. The infrared images of the pumped DFB fiber laser given by the infrared camera at pump power of 3.49 mW and 191.6 mW are shown in Figure 4.
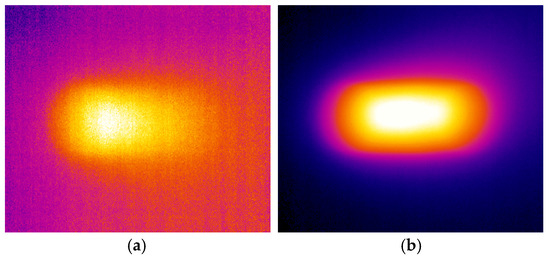
Figure 4.
The infrared images of the pumped DFB fiber laser: (a) Pumped at 3.49 mW; (b) Pumped at 191.6 mW.
It can be observed from the infrared images that, when the pump power was 3.49 mW, the surface temperature at the pump end of the DFB fiber laser was significantly higher than other positions. When the pump power was increased to 191.6 mW, the surface temperature of the whole DFB fiber laser increased obviously, while it was not easy to find the position with the highest temperature. The surface temperature at the horizontal center of the fiber was extracted at different longitudinal positions, and the pump end of the DFB fiber laser was set as the zero-point of the axial coordinate. The longitudinal surface temperature distribution curves at 3.49 mW and 191.6 mW are plotted in Figure 5.
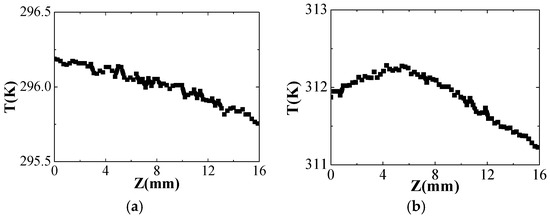
Figure 5.
The longitudinal surface temperature distribution curves of the pumped DFB fiber laser: (a) Pumped at 3.49 mW; (b) Pumped at 191.6 mW.
As revealed in Figure 5, there was 68 testing data points of temperature along the active grating given by the infrared images. The highest surface temperature in the pumped phase-shifted FBG at 3.49 mW was at the pump end of the grating, and the surface temperature decreases gradually along the grating. The highest surface temperature was 296.39 K at the pump input end of the active grating, and the lowest surface temperature was 295.50 K at the far end. When pumped at 191.6 mW, the highest surface temperature of the active grating was 312.31 K locating at around 5.5 mm from the pump input end, and the lowest surface temperature was 311.20 K at the far end. The position with the highest surface temperature moved towards the middle of the active grating by about 5.5 mm, and the surface temperature rose first and then fell along the laser cavity, coinciding with the results reported in Reference [3]. As the surface temperature of the active grating was 295 K without pump injection, the average surface temperature of the active grating with 191.6 mW pump power rose by 16.82 K, and the temperature difference along the DFB fiber laser was less than 1.11 K. The pump power was then increased by about 7 mW from 0 mW to 191.6 mW, and the surface temperature distributions of the active grating at different pump powers are shown in Figure 6.
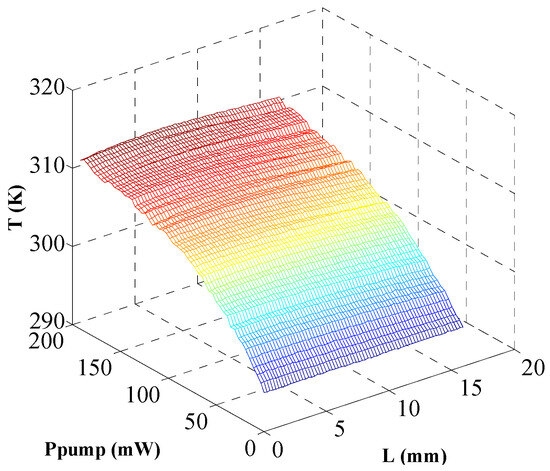
Figure 6.
Surface temperature distribution of the active grating at different pump powers.
As shown in Figure 6, when the pump power was low, the longitudinal temperature distribution was close to an exponential decay curve. As most of the lasing intensity in the DFB fiber laser was located around the phase shift, the phase shift position became a hot spot. It made the position of the highest surface temperature move from the pump end towards the middle of the grating gradually with increased pump power, even when the pump power was below the pump threshold with no laser operation in the phase-shifted FBG. The gradient temperature distribution along the active phase-shifted FBG acted as a heat source to itself, which resulted in resonant wavelength shift as temperature response of the active grating. The transmission spectrum of the active phase-shifted FBG at different pump powers were measured online, as shown in Figure 7.
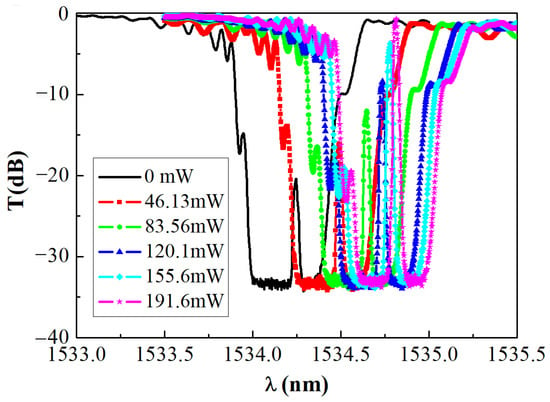
Figure 7.
Measured transmission spectrum of the phase-shifted FBG at different pump powers.
The transmission spectrum of the active phase-shifted FBG moved towards longer wavelengths as a whole with increased pump power. Due to the limitation of the power spectral density of ASE and the noise floor of OSA, there was a flat bottom in the stopband of the active phase-shifted FBG. When the pump power was 0 mW, the two edges of the flat bottom in the stopband located at around 1534 nm and 1534.33 nm with a depth of about 33 dB, and the transmission peak was near 1534.25 nm with a height of about 13 dB above the flat bottom of the stopband. When the pump power was 191.6 mW, the two edges of the flat bottom in the stopband moved to around 1534.61 nm and 1534.95 nm with a depth of about 32.5 dB, and the transmission peak was near 1534.81 nm with a height of about 33 dB above the flat bottom of the stopband. With increased pump power from 0 mW to 191.6 mW, the stopband did not broaden besides an overall shift of about 0.61 nm towards longer wavelength, while the transmission peak in the stopband drifted by 0.56 nm towards longer wavelength. As the wavelength shift of the transmission peak was smaller than that of the stopband, it indicated that besides the overall shift of the stopband with the increased pump power, there was an additional drift of the transmission peak of about 0.05 nm towards the center of the stopband. The shape and the width of the stopband maintained almost the same except the additional drift of the transmission peak, similar to the transmission spectrum of a uniform grating with a different phase shift. Therefore, the additional drift of the transmission peak could be identified as an additional equivalent phase shift due to the non-uniform temperature distribution.
4. Discussion
As revealed in Figure 7, transmission spectrum of the active grating could maintain the overall shape with increased pump power, and the thermally induced chirp mainly resulted in an additional phase shift. The transmission spectrum of the active phase-shifted FBG without pump injection was simulated based on the conventional transmission matrix method [11]. The simulation parameters were as follows: the length of the grating was L = 16 mm, and the effective refractive index of the fiber core was n1i = 1.45015 with a modulation depth of 4.10 × 10−4, while the phase shift was set to be φi = 1.15 π at the center of the grating. The simulated transmission spectrum of the phase-shifted FBG was compared with the measured results of the phase-shifted FBG without pump injection, as shown in Figure 8.
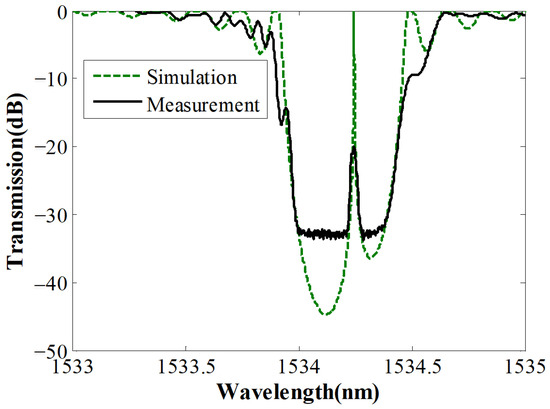
Figure 8.
Transmission spectrum of the active phase-shifted FBG pumped at 0 mW.
In Figure 8, the width of the stopband and the location of the transmission peak were almost the same in the simulation and measurement results, which showed that the simulated curve fitted the measurement results quite well. The initial phase shift of the active phase-shifted FBG without pump injection was considered the same as the phase shift in the simulation, which was 1.15π.
When the pump power was increased to 191.6 mW, the transmission spectrum of the active phase-shifted FBG was simulated under the piecewise-uniform assumption based on the transmission matrix method. The additional perturbation to the effective refractive index was given by addressing the temperature distribution along the grating in Figure 5b and substituting the thermo-optic coefficient of 9.86 × 10−6 K−1 to Equation (2). To coincide with the spatial resolution of the infrared images, the whole grating was divided into 68 segments in the simulation, and the length of each segment was about 0.235 mm. The stimulated transmission spectrum of the chirped phase-shifted FBG was compared with the measured transmission spectrum of the active grating pumped at 191.6 mW, as given in Figure 9.
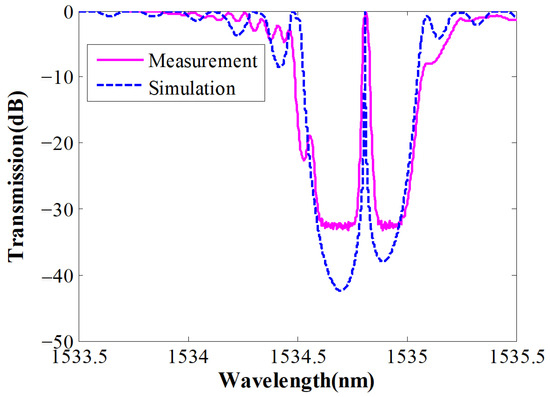
Figure 9.
Transmission spectrum of the active phase-shifted FBG pumped at 191.6 mW.
In Figure 9, it is revealed that, the calculated curve and the measured transmission spectrum were very close. The validity of the transmission matrix method under the assumption of piecewise-uniform structure for the thermally chirped active grating was testified. There were slight differences between the simulation and measurement results. In the measurement results, the two edges of the flat bottom in the stopband located at around 1534.61 nm and 1534.95 nm with a depth of about 32.5 dB, while in the simulation curve, the two “edges” wavelength located at 1534.57 nm and 1534.93 nm with the same depth. The simulation error was less than 0.1 nm, as the temperature inside the fiber core was approximated by the surface temperature of the fiber. The accuracy of the simulated results may be optimized when the active phase-shifted FBG is further subdivided with more segments, which needs infrared images with more pixels and higher temperature resolution.
As the measured transmission spectrum of the thermally chirped active grating given in Figure 7 was similar to the transmission spectrum of a uniform grating with a certain phase shift, the transmission spectrum of the active phase-shifted FBG pumped at 191.6 mW was simulated based on the conventional transmission matrix method. The measured transmission spectrum was close to the simulated transmission spectrum of a typical phase-shifted FBG of the same length with a phase shift of 1.05 π at the center position. Other simulation parameters were the same as in the simulation for the phase-shifted grating with no pump, except that the effective refractive index of the fiber core was set to be n2i = 1.45068. Compared to the initial 1.15 π phase shift of the active grating with no pump, there was an additional equivalent phase shift of −0.1 π. Through similar processes, the equivalent phase shifts of the active phase-shifted FBG at different pump powers were given in Table 1.

Table 1.
Additional equivalent phase shifts of the active phase-shifted FBG at different pump powers.
The gradient longitudinal temperature distribution induced a negative equivalent phase shift with increased value when the pump power was increased. As the initial phase shift was 1.15π, the additional equivalent phase shift could compensate the initial deviation from the perfect phase shift condition.
It’s worth noting that, when the pump power was increased from 0 mW to 191.6 mW, the transmission peak moved by about 0.56 nm. As the average surface temperature of the active grating rose by 16.82 K, the temperature sensitivity was 33.29 pm/K, which was much higher than the calculated result in Equation (1). There was an effective refractive index change of Δni = n2i − n1i = 1.45068 − 1.45015 = 0.00053, and the thermo-optic coefficient was about 3.15 × 10−5 K−1, which verified the assumption that the accumulated thermo-optic effect was the main influence factor for the thermal chirping.
The experiment results in Figure 7 showed the stable performance of the active phase-shifted FBG with no obvious stopband broadening, and a modified transmission spectrum with the assistance of the additional equivalent phase shift at higher pump power. It testified the possibility of enhanced laser operation with improved phase shift condition due to the pump heating.
The additional equivalent phase shift due to the pump heating may either cause DFB fiber laser quenching after long-term operation with increased phase shift deviation from π, or stabilize the laser operation with improved phase shift condition. It is decided by thermal coefficient of the active fiber and the temperature distribution along the active grating, which depends on the dopants of the active fiber, the design of the grating, the pump power, the pump wavelength and the pump configuration, as well as the thermal properties of the materials surrounding the laser. Lots of experimental and theoretical work should be carried out for further exploration, such as the pump heating performance comparison across various devices and operating conditions, and the influence to the linewidth of the laser output.
5. Conclusions
In this paper, a short phase-shifted FBG was fabricated on high concentration Er-Yb codoped fiber, acting as the resonant cavity of a DFB fiber laser with a pump efficiency of 0.362‰. Pump heating of the DFB fiber laser induced significant temperature variation along the fiber laser, which introduced notable chip to the designed uniform periodic structure. The gradient temperature distribution along the fiber grating and the transmission spectrum of the phase-shifted FBG were measured at different pump powers synchronously. Compared with the phase-shifted FBG with no pump injection, an average surface temperature rise of about 16.82 K was verified in the active grating with a variation of less than 1.11 K by the infrared images, when the active grating was pumped at 191.6 mW. An additional transmission peak drift of about 0.05 nm towards the center of the stopband was observed in the transmission spectrum besides an overall shift of 0.61 nm, which denoted an additional equivalent phase shift of −0.1π. Considering the initial phase shift of 1.15π, the equivalent phase shift due to the pump-induced thermal chirp can compensate the deviation from π, which can be utilized for the performance optimization of DFB fiber lasers.
Author Contributions
Conceptualization, W.L. and H.G.; methodology, S.Z.; software, Y.P.; validation, G.Y.; data curation, H.H.; writing—original draft preparation, W.L.; writing—review and editing, H.G.; supervision, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JD Project of Hubei Province, grant number 2023BAA013.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kringlebotn, J.T.; Archambault, J.-L.; Reekie, L.; Payne, D.N. Er3+:Yb3+-codoped fiber distributed-feedback laser. Opt. Lett. 1994, 19, 2101–2103. [Google Scholar] [CrossRef]
- Hill, D.J.; Nash, P.J.; Jackson, D.A.; Webb, D.J.; O’Neill, S.F.; Bennion, I.; Zhang, L. A fiber laser hydrophone array. In Proceedings of the Fiber Optic Sensor Technology and Applications, Boston, MA, USA, 20–22 September 1999. [Google Scholar]
- Hadeler, O. Application of a DFB fibre laser temperature sensor for characterizing pump induced temperature distributions along another DFB fibre laser. In Proceedings of the Fourteenth International Conference on Optical Fiber Sensors, Venice, Italy, 11–13 October 2000. [Google Scholar]
- Yamada, M.; Sakuda, K. Analysis of almost-periodic distributed feedback slab waveguides via a fundamental matrix approach. Appl. Opt. 1987, 26, 3474–3478. [Google Scholar] [CrossRef]
- Xu, Y.Z.; Tam, H.Y.; Liu, S.Y.; Demokan, M.S. Pump-induced thermal effects in Er-Yb fiber grating DBR lasers. Photon. Technol. Lett. 1998, 10, 1253–1255. [Google Scholar] [CrossRef]
- Qi, L.; Jin, L.; Liang, Y.; Cheng, L.; Guan, B. Efficiency enhancement of optical tuning for Bragg gratings in rare-earth doped fibers. Photon. Technol. Lett. 2014, 26, 1188–1191. [Google Scholar] [CrossRef]
- Man, W.S.; Xu, Y.Z.; Tam, H.Y.; Demokan, M.S. Frequency instability in Er/Yb fiber grating lasers due to heating by nonradiative transitions. Photon. Technol. Lett. 1999, 11, 1390–1392. [Google Scholar] [CrossRef]
- Ying, K.; Liang, H.; Chen, D.; Sun, Y.; Pi, H.Y.; Wei, F.; Yang, F.; Cai, H.W. Ultralow noise DFB fiber laser with self-feedback mechanics utilizing the inherent photothermal effect. Opt. Express 2020, 28, 400083. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Zhang, X.L.; Hong, Y.M.; Shang, Y.; Ni, J.S.; Song, Z.Q. Study on the mechanism of fiber-optic hot-wire sensing based on DFB-FL thermally induced chirp effect. Opt. Fiber Technol. 2024, 83, 103678. [Google Scholar] [CrossRef]
- Jiang, S.C.; Wang, J.; Sui, Q.M.; Ye, Q.L.; Wang, L.J. Study of three-component fbg vibration sensor for simultaneous measurement of vibration, temperature, and verticality. J. Sens. 2015, 2015, 382865. [Google Scholar]
- Erdogan, T. Fiber Grating Spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Davis, M.K.; Digonnet, M.J.F.; Pantell, R.H. Thermal effects in doped fibers. J. Light. Technol. 1998, 16, 1013–1023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).